Abstract
One of the key problems in social network analysis is influence maximization, which has great significance both in theory and practical applications. Given a complex network and a positive integer k, and asks the k nodes to trigger the largest expected number of the remaining nodes. Many mature algorithms are mainly divided into propagation-based algorithms and topology- based algorithms. The propagation-based algorithms are based on optimization of influence spread process, so the influence spread of them significantly outperforms the topology-based algorithms. But these algorithms still takes days to complete on large networks. Contrary to propagation based algorithms, the topology-based algorithms are based on intuitive parameter statistics and static topology structure properties. Their running time are extremely short but the results of influence spread are unstable. In this paper, we propose a novel topology-based algorithm based on local index rank (LIR). The influence spread of our algorithm is close to the propagation-based algorithm and sometimes over them. Moreover, the running time of our algorithm is millions of times shorter than that of propagation-based algorithms. Our experimental results show that our algorithm has a good and stable performance in IC and LT model.
Similar content being viewed by others
Introduction
One company develops some new products and wants to market them. It has a limited budget so that it can only select a small group of initial users to experience the products. The company hopes that these users (top-k nodes) would like the application and to start influencing their friends to use it, and their friends would influence their friends’friends and so on, which is called the word-of-mouth phenomenon1,2,3. This Top-k problem, referred to as influence maximization through the powerful viral marketing. Influence maximization problem also covers a lot of other grounds in real life such as virus transmission, outbreak detection4 and so on. However, today’s networks turn larger and have complex connection structures, which means that the solution to the problem needs to be very efficient and accurate5.
In the early stage, Domingos et al.2 first study influence maximization as an algorithmic problem. Kempe et al. prove that the optimization problem is NP-hard6, present a greedy approximation algorithm applicable to all three models, which guarantees that the influence spread is within (1 − 1/e) of the optimal influence spread. Then, they propose a propagation-based algorithm (called general greedy algorithm). It performs well in accuracy, which wholly depends on computer operation on each round of influence estimation and it is also a continuously greedy optimizing process. That is why they runs for hours in a network that has only several thousand vertices7. Propagation-based algorithm significantly outperforms the other algorithms in influence spread but spends so much running time in large networks. For overcoming the drawback of propagation-based algorithm, Leskovec et al.4 present an optimization in selecting seeds, which is referred to as the Cost-Effective LazyForward (CELF). It uses the sub-modularity8 property of the influence maximization objective to greatly reduce the number of evaluations on the influence spread of nodes. Their experimental results demonstrate that CELF optimization could achieve as many as 700 times speedup in selecting seeds, which is a very impressive result. However, CELF still takes a few hours to complete a graph with few tens of thousands of nodes. It is still not efficient to large-scale networks. Goyal et al.9 proposed CELF++ algorithm to optimize the running time, but still has this problem in large-scale networks. Chen et al.5 proposed NewGreedy algorithm. In this propagation-based algorithm, they first removed the edges that have no impact in influencing spreading process, and then simulate influence spreading in subgraph. NewGreedy has no need to consider the estimation in each round. Its running times are 15% to 34% shorter than CELFgreeedy. Then for further improvement, Chen et al. proposed MixGreedy algorithm. In the first round, they use NewGreedy to select the first seed and then use the CELF optimization to select the remaining seeds in the later5,10. Notice that all the algorithms above are belong to propagation-based algorithm which needs the optimization of influence spread process.
With the rapid development of network11, the scale of network becomes huge5,10,12. The calculations of these propagation-based algorithms are facing increasing pressure.
Another kind of algorithm is topology-based algorithm. It is based on intuition attributes or experience structure and take static topology structure of network or centralities into consideration. The topology-based algorithms have no optimization of influence spread process, so the running time of them are extremely short. But the deviation degree of its influence spread can not be controlled. In previous studies, some classical indicators are considered, such as Degree heuristics6, Betweenness13 closeness14 and so on. K-shell decomposition15 and Pagerank16 are also a good method to measure the influence spread capability of nodes. They could fast select top-k nodes based on their intuition attributes such as Degree: a simple method that selects the k nodes with the highest degree; Distance: a simple method that selects the k vertices with the smallest average shortest-path distances to all other nodes, which is also evaluated in literature6. These algorithms above are all belong to topology-based algorithm.
It is worth mentioning that Chen et al. proposed Degreediscount5 which is significantly better than topology-based algorithms and is close to the influence spread of propagation-based algorithm. What’s more, the second advantage of Degreediscount is its speed, which is much faster than all propagation-based algorithms. Moreover, several excellent topology-based algorithms were proposed in recent years whose accuracy almost reach the same orders of magnitude as propagation-based algorithm. By comparison, the topology-based algorithms are getting more and more attention from researchers.
In addition, there are many excellent algorithms based on many different perspectives. Wang et al.17 proposed a community-based algorithm, which Combined the general greedy algorithm with community structure. Jung et al.18 proposed influence ranking and influence estimation (IRIE) algorithm, which has the best performance both in running time and influence spread in weighted cascade model (WC)6 and Trivalency model (TR)10. Recently, Tang et al.19 proposed an algorithm based on martingale (IMM), which performs well in continuous-time independent cascade model (CTIC)20. F. Altarelli et al.21 have proposed a BP-based algorithm to solve inverse problems for irreversible dynamical processes defined over networks which is based on the cavity method of statistical physics and which is capable of identifying sets of seeds which maximize some objective function that depends on the activation times of each node. Different excellent algorithms perform well in different influence propagation model. The future directions for this research change to be more pluralistic by the contribution of statistical physics, mathematical calculation, dynamical propagation and social computing.
Notice that the key point of most algorithms is to avoid “rich-club” effect22,23,24, which appears in social networks frequently. Degree heuristic algorithm (hereafter referred as Degree) is frequently used for selecting seeds in influence maximization but the seeds with highest degree will cause large numbers of active nodes overlapped in propagation process23. Briefly, the nodes with high degree often connects lots of same neighbors. Because many complex networks especially the networks with social characteristics follow a heavy-tailed distribution. In this work, we propose an algorithm based on local index rank of each vertex (LIR). The advantage of our approach is fast and efficient comparing with other algorithms. The nodes selected by LIR are the local leaders, whose degree are higher than the neighbors. In this case, LIR avoids the “rich-club” effect quickly and guarantee that most seeds are not connected to each other, which efficiently improve the Degree heuristic algorithm. We are interested in testing the performance of LIR which contains influence spread and running time. So we choose five mature algorithms from two different categories. We compared the results of our method with two excellent propagation-based algorithms and three topology-based algorithms including the best topology-based algorithm (Degreediscount algorithm). Our experimental results show that the influence spread of LIR is higher than Degreediscount and performs better than most of other algorithms in IC model. As a supplement, we simulate the influence capability in LT model. The performance of LIR in LT model is both good and stable.
Results
Datasets
As is shown in Table 1, N is the number of network and E is the number of edge. The average degree is k and the max degree of network is denoted as kmax. CC refers to the average clustering coefficient of the networks and ρ refers to the network diameter. Ca-GrQc is a collaboration network of Arxiv General Relativity category. Each node in the network represents an author and each edge represents that two authors collaborated. Ca-Hepth is a collaboration network of Arxiv High Energy Physics Theory category from 1993 to 2003. GP2P, a sequence of snapshots of the Gnutella peer-to-peer file sharing network from August 2002. Power is an undirected, network represents the topology of the Western States Power Grid of the United States. The first three networks can be downloaded on the web at http://snap.stanford.edu/data/index.html and the last one can be downloaded on the web at http://www-personal.umich.edu/ mejn/. These four complex networks are obtained from real-life transaction. Ca-GrQc, Ca-Hepth and Gnutella follow the heavy-tailed distribution. Thus, the result curves of six algorithms in these three datasets are clear and intuitive. Notice that the max degree in Power Grid is only 19, so the influence spread of all algorithms are very close in IC and LT models. Although the importance of each nodes are hard to be distinguished, our LIR algorithm performs well in Power Grid networks.
Experiments and Results
We summarize our experiment results in IC and LT model and calculate the running time of different algorithms. All the experiments were conducted on hardware environment with Intel(R) CoreTM i5-3470 CPU 3.20 GHz and 4 G memory and software environment with Dev C++ 5.11 on Windows 7 operating system. In our work, we use two basic models (IC and LT model) to simulate the influence spreading on real world. Mixgreedy is one of the best propagation-based algorithm both in running time and influence spread. Similarly, Degreediscount is the state-of-the-art topology-based algorithm. We use the IC model with uniform influence probability. Because different algorithms are applied to different propagation models, the accuracy and running time can not be compared to all proposed algorithms. In order to ensure the integrity of our experiments, we choose five compared algorithms which includes two excellent propagation-based algorithms and three topology-based algorithms in our experiments. In each set of experiment, we set initial seed size parameter k = 50 and take 20000 times on simulation and estimation and finally take the average of the results to obtain the influence spread5.
First, we test the six algorithms in IC model. In literature6, they mainly report results on a small propagation probability of p = 0.01, but we also consider other values (p = 0.02 − p = 0.09) and add the experiments correspondingly. Notice that larger p values (e.g. p = 0.1) are not considered due to its insensitivity to different algorithms6. When the propagation probability p exceeds 0.1, the difference of influence spread almost disappeared. For testing the sensitiveness of propagation probability p, we shows the results of experiments of six algorithms in Fig. 1, which depict the variety of influence spread with p increasing (0.01 to 0.09). In Fig. 1, it is easy to find that our LIR algorithm performs better than other algorithms. Especially in Fig. 1(a), from p = 0.04 to p = 0.09 the influence spread of LIR surprisingly exceed all algorithms. The similar phenomenon also comes up in Fig. 1(b) when p > 0.04. In Fig. 1(c), LIR gets ahead of the rest algorithms from p = 0.03 to p = 0.07. When the propagation probability is low (e.g. p < 0.4), the influence spread of LIR and other algorithms are very close. In Fig. 1(d), Power Grid networks which max degree is very small, our LIR still performs better than Mixgreedy algorithm and has no big gap with Newgreedy and Degreediscount algorithms. The influence spread results are the average of the 20000 experiments, so the numerical difference of the six algorithms is not obvious. For example, in Fig. 1(b,c), the network size are large whereas the influence spread result of our LIR algorithm exceeds other algorithms within 100 nodes, which cause the overlapping of carves. In summary, our LIR algorithm as a topology-based algorithm performs better than other algorithms in IC model. For showing the details of the results clearly, we draw Fig. 2 which with the median of all propagation probability (i.e. p = 0.05).
Figure 2 reports the results on influence spreads of our algorithms as well as other algorithms for comparison. The difference between Fig. 1 is that the x-axis represents the parameter k (from 1 to 50). As Fig. 2 shows, the influence spread of various algorithms on the four graphs in the IC model with p = 0.05, which are very consistent. It is easy to read that the red dots are our LIR algorithm. Distance and Degree heuristics are significantly worse than the other algorithms. LIR is an improved method based on Degree. The influence spread of LIR is much higher than Degree except in Power gird network. In Fig. 2(a–c), the influence spread of LIR is higher than the other algorithms, even Mixgreedy and Newgreedy are lower than it. Notice that the influence spread of Degreediscount is lower than LIR in these four datasets all the time. Compared to Degree and Distance heuristics, LIR avoid the “Rich-club Effect” subtlety, so the influence spread of LIR must be higher than the other three topology-based algorithms.
Table 2 reports the standard deviation of different algorithms for selecting k = 50 seeds in IC model with p = 0.05. For each algorithm, we simulate 20000 times of influence spread and compute the standard deviation. As Table 2 shown, the gap between LIR and other mature algorithms is not large, which means that the rationality of LIR is proved.
Table 3 reports the running times of six algorithms. Our LIR algorithm only take O(m) time in a network, so the liner running time of LIR is amazingly short. It is obvious that LIR and Degreediscount run extremely fast, only take a few milliseconds to finish, and are nearly hundred-thousand times faster than the propagation-based algorithms. Although LIR spends a little more time than Degreediscount in the first three networks, the influence spread of LIR is higher than Degreediscount in the three networks. In GP2P, LIR is better than Degreediscount both in running time and influence spread. Generally, LIR take merely the same time as Degreediscount but has a higher influence spread than Degreediscount. The running time of Distance is almost same with the propagation-based algorithms while its influence spread is much worse than the propagation-based algorithms. Because LIR is a topology-based algorithm, the running time of it is not related to the influence model. Thus, we only show the time statistics in IC model in this work.
Figure 3 shows the influence spread of six algorithms on four datasets in LT model. The two propagation-based algorithms are not a surprise that it generates the best influence spread. The performance of LIR is not as good as the result in IC model. However, the influence spread of LIR essentially match the propagation-based algorithms. In Fig. 3(a), Degree heuristic performs worst, but the two propagation-based algorithms have a good performance. In Fig. 3(b), the influence spread of LIR is close to the two propagation-based algorithms and Degreediscount. In Fig. 3(c), LIR’s influence spread is higher than Mixgreedy and the influence spread of LIR is higher than Degreediscount and Mixgreedy. In Fig. 3(d), the accuracy of LIR and Degreediscount are almost same even higher than the other propagation-based algorithms.
In summary, our LIR runs fast and obtains a higher influence spread, which is generally close to propagation-based algorithms or exceeds the two propagation-based algorithms sometimes. Moreover, the running time of LIR is million times shorter than propagation-based algorithms. As for Degree heuristic, LIR is an excellent improved method, which avoid rich club effect successfully. Degreediscount performs well both in running time and influence spread accuracy. LIR takes almost the same running time as Degreediscount but gets a higher influence spread in IC model. Therefore LIR is a suitable choice for the influence maximization problem.
Discussion
Degree algorithm selects the seeds that with highest degree. However, in most real life network, the degree of nodes follows a heavy-tail distribution, which indicates that most nodes with high degree are connected with each other (rich-club phenomenon). So, only considering degree of nodes will cause the overlapping in the first step of influence spread. From this point of view, LIR solve the rich-club problem well and reduce the number of overlapped neighbors. Nodes with 0 LI value mean that they are the leader in local part and most of them are not linking to each others.
In Fig. 4, we show the number of edges that connect two seeds in the seed set selected by LIR and Degree algorithms. There are 961 edges among the seeds selected by Degree algorithm in Ca-GrQC, but only 2 edges among the seeds selected by our LIR algorithm. In other three datasets, the seeds selected by LIR are merely connected. In the four datasets, the edges among the seeds selected by LIR are very sparse. The probabilities of selecting two connected nodes by our method are lower than 0.5%. So it is obvious that LIR largely improves the Degree algorithm, and the combined influence spread ability of these dispersed seeds will be stronger.
Notice that the greater gap between two algorithms in the Fig. 4, the better LIR performs in influence spread. For example, in Ca-GrQC, LIR only has 2 edge connect seeds but Degree algorithm has 961 edges, which is a big difference. So in Fig. 2(a), Degree is the worst algorithm compared with other algorithms but LIR is the best. On the contrary, in Power network, the max degree is not high and many nodes have same degree, which makes our method insensitive. The difference between our algorithm (4 edges) and Degree (27 edges) is not large. So in Fig. 2(d), the performance of LIR and other algorithms are very close. Thus it can be seen that avoiding the rich-club is meaningful in identifying top-k influential nodes. We also assume that this idea is from the origin of the communities characteristic, which indicates the top-k nodes we finally select may located in different communities or at least there has a certain distance between each others14,17,25.
Several conclusions can be drawn from the experimental results reported above. First, comparing with original Degree algorithm, LIR is a well-performed improved method. Second, the liner running time of LIR is in same order of magnitude as Degreediscount while showing very impressive results in the independent cascade model. Last but not least, the influence spread of LIR match the propagation-based algorithms and even exceeds them.
To summarize, our LIR is a fantastic new approach for solving the influence maximization problem, which only takes less than one-millionth of time of propagation-based algorithms but performs considerably well in influence spread. There are also several plans for this research. First, our LIR performs well in the independent cascade model. We plan to optimize LIR to make it adapt to other propagation models and try to find a strategy to ensure all leaders are not connect to each others. Second, we will analysis poor performing results in LT model and find the reason. Third, we will continue to change the probability of IC model and explore the relevance of different probability and influence spread. We also plan to investigate the top-k problem based on the view of community structures in our future work.
Methods
LIR algorithm
G = {V, E} is a network or graph where V is set of vertices (or nodes) and E ⊆ V × V is a set of edges (or links between the nodes). di is the degree of node vi. N(vi) = {vj|vj ∈ V,(vj, vi) ∈ E} that is the neighborhood set of node vi. We define that  . Q(x) = 1 when (x > 0), otherwise Q(x) = 0. We compute the LI of each node first, which represents the local index of each node. Normally, if the LI value of node vi is 5, it indicates that there are 5 neighborhoods around node vi whose degree are higher than node vi. Notice that according to the definition of LI, it is possible that two adjacent nodes have the same LI value. (e.g. two connected nodes that have the highest degree in the network). In this case, there will be two nodes whose LI value are 0 simultaneously. But if the networks follow heavy-tailed distribution, this phenomenon will happen with extreme low probability, which has merely no impact on our experimental results. In this paper, We are interested in the nodes with 0 LI value. These 0-LI nodes have two advantages: one is that they all have the highest degree in their local part, the other is that most of them are not adjacent to each others. Finally, we rank these 0-LI nodes by their degree. The length of LIR is depended on k. Algorithm 1 as the following implements the steps of LIR.
. Q(x) = 1 when (x > 0), otherwise Q(x) = 0. We compute the LI of each node first, which represents the local index of each node. Normally, if the LI value of node vi is 5, it indicates that there are 5 neighborhoods around node vi whose degree are higher than node vi. Notice that according to the definition of LI, it is possible that two adjacent nodes have the same LI value. (e.g. two connected nodes that have the highest degree in the network). In this case, there will be two nodes whose LI value are 0 simultaneously. But if the networks follow heavy-tailed distribution, this phenomenon will happen with extreme low probability, which has merely no impact on our experimental results. In this paper, We are interested in the nodes with 0 LI value. These 0-LI nodes have two advantages: one is that they all have the highest degree in their local part, the other is that most of them are not adjacent to each others. Finally, we rank these 0-LI nodes by their degree. The length of LIR is depended on k. Algorithm 1 as the following implements the steps of LIR.

Illustrate examples
LIR is an improved approach based on Degree heuristic, which inherited the advantages of short running time. Degree heuristic is an intuitive method for the influence maximization problem14,26, but its fatal flaw is that it can’t deal with the “rich club” effect, which caused a large number of nodes overlapped in spread process. Most topology-based algorithms focus on finding a way to avoid the “rich-club” effect. The approach that selects 0-LI nodes solves the problem easily and fast. LIR is an ordered set by degree from high to low and the LI value of all the seeds we select are 0. In this way, LIR can obtain more neighbors of seed set in the first step of influence spread, which could make the influence spread larger.
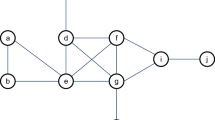
We display a sample network in Fig. 5 to demonstrate the difference between LIR and Degree. Nodes with yellow color are the neighbors of seeds (include seeds). Suppose that we want to choose two seeds in this network and get more nodes infected by the seeds. If we use Degree-based algorithm, we should find the nodes with high degree in the network. In this way, node 15(degree is 15) and 16(degree is 11) will be selected. Notice that seeds 15 and 16 leave 8 nodes (white color nodes) that have no chance to be active in the first step of influence spreading. Although the degree of node 15 and 16 are high, most of their neighbors are overlapped. In Fig. 5(b), Because node 15 and 16 are connected, the LI value of 16 is 1(not 0). The degree of node 2(degree is 9) is not high, but its LI value is 0. Then, we choose node 15 and 2 as seeds based on LIR algorithm, whose LI value is 0, the most nodes in the network turn to be the seeds’neighbors. It is obvious in Fig. 5(b) that only 2 nodes leave which have no chance to be active. In general, using LIR to choose seeds could make seeds more dispersed and then bring more neighbors.
IC Model
IC (independent cascade model)6. Given a network G = {V, E}, where the vertex set V has n nodes. There exists an edge e(uv) between vertex u and its neighbor v. puv ∈ [0, 1] is the probability that u infect v, which is independent in the whole diffusion process. If at time t, u is active and its neighbor v is not yet activated, u try to infect v with probability puv. If this process is successful, v will be active in t + 1 time. But whether it succeeds or not, u has only one chance to infect v. If v has many neighbors in time, the order of the neighbors try to infect v is arbitrary. The simulation process starts from the initial node, until no new node can be activated. In IC model with large or small propagation probability p, the influence spread is not very sensitive to different algorithms. We had test the probability 0.01 to 0.1. In order to show the curves clearly, we added Fig. 2 with the median p = 0.05.
LT Model
LT (liner threshold model)6. Given a network G = {V, E}, N(u) is the set of neighbors of u. Suppose u is active, u has an influential value on its neighbor, denoted as buv. The buv on edges could be learned from real data. In our experiment, we assign equal values to edges. For example, if a node has 10 neighbors, then buv of each edge is 0.1. All nodes in N(u) have influential value to u, but the summation is less than 1. That is ∑v∈N(u)buv ≤ 1. Each threshold of u has to be generated uniformly at random from 0 to 1. (i.e. with stochastic threshold, with random distribution), if ∑v∈N(u)buv ≥ θu, u will be active. In LT model, an active node u failed to infect his neighbor v, its influential value buv will be accumulated, which is a contribution to the other neighbors. The diffusion process is over until no new node can be activated.
Additional Information
How to cite this article: Liu, D. et al. A Fast and Efficient Algorithm for Mining Top-k Nodes in Complex Networks. Sci. Rep. 7, 43330; doi: 10.1038/srep43330 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Leskovec, J., Adamic, L. A. & Huberman, B. A. The dynamics of viral marketing. Acm Transactions on the Web 1, 5 (2005).
Richardson, M. & Domingos, P. Mining knowledge-sharing sites for viral marketing. In Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining, 61–70 (2002).
Licamele, L. & Getoor, L. Social capital in friendship-event networks, 959–964 (2006).
Leskovec, J. et al. Cost-effective outbreak detection in networks. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 420–429 (2007).
Chen, W., Wang, Y. & Yang, S. Efficient influence maximization in social networks. in: Kdd. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, June 28 - July, 199–208 (2009).
Kempe, D., Kleinberg, J. & Tardos, v. Maximizing the spread of influence through a social network. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 137–146 (2003).
Lu, W., Chen, W. & Lakshmanan, L. V. S. Influence maximization in continuous time diffusion networks. Cement and Concrete Composites 34, 684–691 (2012).
Vaze, R. & Ganapathy, H. Sub-modularity and antenna selection in mimo systems. IEEE Communications Letters 16, 1446–1449 (2011).
Goyal, A., Lu, W. & Lakshmanan, L. V. S. Celf++: optimizing the greedy algorithm for influence maximization in social networks. In International Conference on World Wide Web, WWW 2011, Hyderabad, India, March 28 - April, 47–48 (2011).
Chen, W., Yuan, Y. & Zhang, L. Scalable influence maximization in social networks under the linear threshold model, 88–97 (2010).
Leskovec, J., Backstrom, L., Kumar, R. & Tomkins, A. Microscopic evolution of social networks. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, Nevada, Usa, August, 462–470 (2008).
Liu, D., Jing, Y. & Chang, B. Identifying influential nodes in complex networks based on expansion factor. International Journal of Modern Physics C (2016).
Freeman, L. C. A set of measures of centrality based on betweenness. In Sociometry 35–41 (1977).
Zhao, Z., Wang, X., Zhang, W. & Zhu, Z. A community-based approach to identifying influential spreaders. Entropy 17, 2228–2252 (2015).
Garas, A., Schweitzer, F. & Havlin, S. A k-shell decomposition method for weighted networks. New Journal of Physics 14, 83030–83043(14) (2012).
Bryan, K. & Leise, T. The 25,000,000,000 eigenvector: The linear algebra behind google. Siam Review 48, 569–581 (2010).
Wang, Y., Cong, G., Song, G. & Xie, K. Community-based greedy algorithm for mining top-k influential nodes in mobile social networks. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, Dc, Usa, July, 1039–1048 (2010).
Jung, K., Heo, W. & Chen, W. Irie: Scalable and robust influence maximization in social networks. In Data Mining (ICDM), 2012 IEEE 12th International Conference on, 918–923 (2012).
Tang, Y., Shi, Y. & Xiao, X. Influence maximization in near-linear time: A martingale approach. In ACM SIGMOD International Conference on Management of Data, 1539–1554 (2015).
Chen, W., Lu, W. & Zhang, N. Time-critical influence maximization in social networks with time-delayed diffusion process. Chinese Journal of Engineering Design 19, 340–344 (2012).
Altarelli, F., Braunstein, A., DallAsta, L. & Zecchina, R. Optimizing spread dynamics on graphs by message passing. Mathematics 2013, 387–402 (2013).
Leskovec, J. & Faloutsos, C. Sampling from large graphs. In ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 631–636 (2006).
Colizza, V., Flammini, A., Serrano, M. A. & Vespignani, A. Detecting rich-club ordering in complex networks. Nature Physics 2, 110–115 (2006).
Zhou, S. & Mondragon, R. J. The rich-club phenomenon in the internet topology. Microscopy and Microanalysis 34, 109–113 (2003).
Goyal, A., Bonchi, F. & Lakshmanan, L. V. S. Discovering leaders from community actions. In Acm Conference on Information and Knowledge Management, 499–508 (2008).
Linyuan, L., Tao, Z., Qian-Ming, Z. & Eugene, S. H. The h-index of a network node and its relation to degree and coreness:. Nature Communications 7 (2016).
Acknowledgements
This work was supported by the joint funds of the national natural science foundation of China (No. U1404604), the science and technology project of Henan province (No. 152102310313) and the PhD research startup foundation of Henan Normal University (No. QD14135). This work is (partially) supported by Tianjin Key Laboratory of Advanced Networking (TANK). National High Technology Research and Development Program of China (2014AA015103), the National Natural Science Foundation of China (61572041).
Author information
Authors and Affiliations
Contributions
D.L. devised the study. D.L., Y.J. and W.J.W. conducted the experiments and analyzed the results. Y.J.and Z.J. prepared the figures and wrote the paper. D.L. and Y.J. authors reviewed the paper. G.J.S. and D.L. revised the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, D., Jing, Y., Zhao, J. et al. A Fast and Efficient Algorithm for Mining Top-k Nodes in Complex Networks. Sci Rep 7, 43330 (2017). https://doi.org/10.1038/srep43330
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep43330
This article is cited by
-
Time and cost-effective online advertising in social Internet of Things using influence maximization problem
Wireless Networks (2024)
-
Influence maximization based on SATS scheme in social networks
Computing (2023)
-
Identifying vital nodes for influence maximization in attributed networks
Scientific Reports (2022)
-
An efficient discrete differential evolution algorithm based on community structure for influence maximization
Applied Intelligence (2022)
-
A survey on meta-heuristic algorithms for the influence maximization problem in the social networks
Computing (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.