Abstract
We investigate prime factorization from two perspectives: quantum annealing and computational algebraic geometry, specifically Gröbner bases. We present a novel autonomous algorithm which combines the two approaches and leads to the factorization of all bi-primes up to just over 200000, the largest number factored to date using a quantum processor. We also explain how Gröbner bases can be used to reduce the degree of Hamiltonians.
Similar content being viewed by others
Introduction
Prime factorization is at the heart of secure data transmission because it is widely believed to be NP-complete. In the prime factorization problem, for a large bi-prime M, the task is to find the two prime factors p and q such that M = pq. In RSA cryptosystem, the message to be transmitted is encrypted using a public key which is, essentially, a large bi-prime that can only be decrypted using its prime factors, which are kept in a private key. Prime factorization also connects to many branches of mathematics; two branches relevant to us are computational algebraic geometry1 and quantum annealing2,3,4.
To leverage the problem of finding primes p and q into the realm of computational algebraic geometry, it suffices to transform it into a system of algebraic equations  . This is done using the binary representation
. This is done using the binary representation  and
and  , which is plugged into M = pq and expanded into a system of polynomial equations. The system
, which is plugged into M = pq and expanded into a system of polynomial equations. The system  is given by this initial system of equations in addition to the auxiliary equations expressing the binary nature of the variables Pi and Qi, carry-on, and connective variables. The two primes p and q are then given by the unique zero of
is given by this initial system of equations in addition to the auxiliary equations expressing the binary nature of the variables Pi and Qi, carry-on, and connective variables. The two primes p and q are then given by the unique zero of  . In theory, we can solve the system
. In theory, we can solve the system  using Gröbner bases; however, in practice, this alone does not work, since Gröbner basis computation (Buchberger’s algorithm) is exponential in the number of variables.
using Gröbner bases; however, in practice, this alone does not work, since Gröbner basis computation (Buchberger’s algorithm) is exponential in the number of variables.
The connection to quantum annealing can also be easily described. Indeed, finding p and q can be formulated into an unconstrained binary optimization problem  , where the cost function f is the sum of the squares of polynomials in
, where the cost function f is the sum of the squares of polynomials in  . The unique zero of
. The unique zero of  now sits on the unique global minimum of
now sits on the unique global minimum of  (which has minimum energy equal to zero). There are, however, a few non-trivial requirements we need to deal with before solving the cost function using quantum annealing. These requirements concern the nature of cost functions that quantum annealers can handle. In particular, we would like the cost function of
(which has minimum energy equal to zero). There are, however, a few non-trivial requirements we need to deal with before solving the cost function using quantum annealing. These requirements concern the nature of cost functions that quantum annealers can handle. In particular, we would like the cost function of  to be a positive quadratic polynomial. We also require that the coefficients of the cost function (coupling and external field parameters) be rather uniform and match the hardware-imposed dynamic range.
to be a positive quadratic polynomial. We also require that the coefficients of the cost function (coupling and external field parameters) be rather uniform and match the hardware-imposed dynamic range.
In the present paper, we suggest looking into the problem through both lenses, and demonstrate that indeed this approach gives better results. In our scheme, we will be using quantum annealing to solve  , but at the same time we will be using Gröbner bases to help us reduce the cost function f into a positive quadratic polynomial f+ with desired values for the coefficients. We will be also using Gröbner bases at the important step of pre-processing f+ before finally passing it to the quantum annealer. This pre-processing significantly reduces the size of the problem. The result of this combined approach is an algorithm with which we have been able to factorize all bi-primes up to 2 × 105 using the D-Wave 2X processor. The algorithm is autonomous in the sense that no a priori knowledge, or manual or ad hoc pre-processing, is involved. We refer the interested reader to Supplementary materials for a brief description of the D-Wave 2X processor, along with some statistics for several of the highest numbers that we embedded and solved. More detail about the processor architecture can be found in ref. 5. Another important reference is the work of S. Boixo et al. in ref. 6, which presents experimental evidence that the scalable D-Wave processor implements quantum annealing (with surprising robustness against noise and imperfections). Additionally, evidence that, during a critical portion of quantum annealing, the qubits become entangled and entanglement persists even as the system reaches equilibrium is presented in ref. 7.
, but at the same time we will be using Gröbner bases to help us reduce the cost function f into a positive quadratic polynomial f+ with desired values for the coefficients. We will be also using Gröbner bases at the important step of pre-processing f+ before finally passing it to the quantum annealer. This pre-processing significantly reduces the size of the problem. The result of this combined approach is an algorithm with which we have been able to factorize all bi-primes up to 2 × 105 using the D-Wave 2X processor. The algorithm is autonomous in the sense that no a priori knowledge, or manual or ad hoc pre-processing, is involved. We refer the interested reader to Supplementary materials for a brief description of the D-Wave 2X processor, along with some statistics for several of the highest numbers that we embedded and solved. More detail about the processor architecture can be found in ref. 5. Another important reference is the work of S. Boixo et al. in ref. 6, which presents experimental evidence that the scalable D-Wave processor implements quantum annealing (with surprising robustness against noise and imperfections). Additionally, evidence that, during a critical portion of quantum annealing, the qubits become entangled and entanglement persists even as the system reaches equilibrium is presented in ref. 7.
Relevant to us also is the work in ref. 8, which uses algebraic geometry to solve optimization problems (though not specifically factorization; see Methods for an adaptation to factorization). Therein, Gröbner bases are used to compute standard monomials and transform the given optimization problem into an eigenvalue computation. Gröbner basis computation is the main step in this approach, which makes it inefficient. In contrast to that work, we ultimately solve the optimization problem using a quantum annealing processor and pre-process and adjust the problem with algebraic tools, that is, we reduce the size of the cost function and adjust the range of its parameters. However, we share that work’s point of view of using real algebraic geometry, and our work is the first to introduce algebraic geometry, and Gröbner bases in particular, to solve quantum annealing-related problems. We think that this is a fertile direction for both practical and theoretical endeavours.
Mapping the factorization problem into a degree-4 unconstrained binary optimization problem is first discussed in ref. 9. There, the author proposes solving the problem using a continuous optimization method he calls curvature inversion descent. Another related work is the quantum annealing factorization algorithm proposed in ref. 10. We will discuss it in the next section and improve upon it in two ways. The first involves the addition of the pre-processing stage using Gröbner bases of the cost function. This dramatically reduces the number of variables therein. The second way concerns the reduction of the initial cost function, for which we propose a general Gröbner basis scheme that precisely answers the various requirements of the cost function. In Results, we present our algorithm (the column algorithm) which outperforms this improved algorithm (i.e., the cell algorithm). Using a reduction proposed in ref. 10 and ad-hoc simplifications, the paper11 reports the factorization of bi-prime 143 on a liquid-crystal NMR quantum processor. It has been then observed by ref. 12 that the same 4-qubit Hamiltonian can be used to factor biprimes 3599, 11663, and 56153. More recently, in ref. 13, the authors factored the bi-prime 551 using a 500 MHz NMR spectrometer.
This review will not be complete without mentioning Shor’s algorithm14 and Kitaev’s phase estimation15, which, respectively, solve the factorization problem and the abelian hidden subgroup problem in polynomial time, both for the gate model paradigm. The largest number factored using a physical realization of Shor’s algorithm is 1516; see ref. 17 also for a discussion about oversimplification in the previous realizations. Finally, in ref. 18, it has been proved that contextuality (Kochen-Specker theorem) is needed for any speed-up in a measurement-based quantum computation factorization algorithm.
Results
The binary multiplication of the two primes p and q can be expanded in two ways: cell-based and column-based procedures (see Methods). Each procedure leads to a different unconstrained binary optimization problem. The cell-based procedure creates the unconstrained binary quadratic programming problem

and the column-based procedure results in the problem

The two problems  and
and  are equivalent. Their cost functions are not in quadratic form, and thus must be reduced before being solved using a quantum annealer. The reduction procedure is not a trivial task. In this paper we define, for both scenarios: (1) a reduced quadratic positive cost function and (2) a pre-processing procedure. Thus, we present two different quantum annealing-based prime factorization algorithms. The first algorithm’s decomposition method (i.e., the cell procedure) has been addressed in ref. 10, without pre-processing and without the use of Gröbner bases in the reduction step. Here, we discuss it from the Gröbner bases framework and add the important step of pre-processing. The second algorithm, however, is novel in transformation of its quartic terms to quadratic, outperforming the first algorithm due to its having fewer variables.
are equivalent. Their cost functions are not in quadratic form, and thus must be reduced before being solved using a quantum annealer. The reduction procedure is not a trivial task. In this paper we define, for both scenarios: (1) a reduced quadratic positive cost function and (2) a pre-processing procedure. Thus, we present two different quantum annealing-based prime factorization algorithms. The first algorithm’s decomposition method (i.e., the cell procedure) has been addressed in ref. 10, without pre-processing and without the use of Gröbner bases in the reduction step. Here, we discuss it from the Gröbner bases framework and add the important step of pre-processing. The second algorithm, however, is novel in transformation of its quartic terms to quadratic, outperforming the first algorithm due to its having fewer variables.
We write  for the ring of polynomials in
for the ring of polynomials in  with real coefficients and
with real coefficients and  for the affine variety defined by the polynomial
for the affine variety defined by the polynomial  , that is, the set of zeros of the equation f = 0. Since we are interested only in the binary zeros (i.e.,
, that is, the set of zeros of the equation f = 0. Since we are interested only in the binary zeros (i.e.,  ), we need to add the binarization polynomials xi(xi − 1), where i = 1, …, n, to f and obtain the system
), we need to add the binarization polynomials xi(xi − 1), where i = 1, …, n, to f and obtain the system  . The system
. The system  generates an ideal
generates an ideal  by taking all linear combinations over
by taking all linear combinations over  of all polynomials in
of all polynomials in  ; we have
; we have  . The ideal
. The ideal  reveals the hidden polynomials which are the consequence of the generating polynomials in
reveals the hidden polynomials which are the consequence of the generating polynomials in  . To be precise, the set of all hidden polynomials is given by the so-called radical ideal
. To be precise, the set of all hidden polynomials is given by the so-called radical ideal  , which is defined by
, which is defined by  . In practice, the ideal
. In practice, the ideal  is infinite, so we represent such an ideal using a Gröbner basis
is infinite, so we represent such an ideal using a Gröbner basis  which one might take to be a triangularization of the ideal
which one might take to be a triangularization of the ideal  . In fact, the computation of Gröbner bases generalizes Gaussian elimination in linear systems. We also have
. In fact, the computation of Gröbner bases generalizes Gaussian elimination in linear systems. We also have  and
and  . A brief review of Gröbner bases is given in Methods.
. A brief review of Gröbner bases is given in Methods.
The cell algorithm
Suppose we would like to define the variety  by the set of global minima of an unconstrained optimization problem
by the set of global minima of an unconstrained optimization problem  , where f+ is a quadratic polynomial. For instance, we would like f+ to behave like f2. Ideally, we want f+ to remain in
, where f+ is a quadratic polynomial. For instance, we would like f+ to behave like f2. Ideally, we want f+ to remain in  (i.e., not in a larger ring), which implies that no slack variables will be added. We also want f+ to satisfy the following requirements:
(i.e., not in a larger ring), which implies that no slack variables will be added. We also want f+ to satisfy the following requirements:
- i
f+ vanishes on
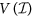 or, equivalently,
or, equivalently, 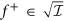 .
. - ii
f+ > 0 outside
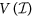 , that is, f+ > 0 over
, that is, f+ > 0 over 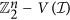 .
. - iii
Coefficients of the polynomial f+ are adjusted with respect to the dynamic range allowed by the quantum processor.
Let  be a Gröbner basis for
be a Gröbner basis for  . We can then go ahead and define
. We can then go ahead and define

where the real coefficients ai are subject to the requirements above; note that we already have  and thus the first requirement (i) is satisfied.
and thus the first requirement (i) is satisfied.
Let us apply this procedure to the optimization problem  above. There, f = Hij and the ring of polynomials is
above. There, f = Hij and the ring of polynomials is  . We obtain the following Gröbner basis (see Methods about algorithm used):
. We obtain the following Gröbner basis (see Methods about algorithm used):

We have used the lexicographic order  ; see Methods for definitions. Note that t1 = Hij. We define
; see Methods for definitions. Note that t1 = Hij. We define

where the real coefficients ak are to be found. We need to constrain the coefficients ak with the other requirements. The second requirement (ii), which translates into a set of inequalities on the unknown coefficients ak, can be obtained through a brute force evaluation of  over the 26 points of
over the 26 points of  . The outcome of this evaluation is a set of inequalities expressing the second requirement (ii) (see Supplementary materials).
. The outcome of this evaluation is a set of inequalities expressing the second requirement (ii) (see Supplementary materials).
The last requirement (iii) can be expressed in different ways. We can, for instance, require that the absolute values of the coefficients of  , with respect to the variables Pj, Qi, Si,j, Si+1,j−1, Zi,j, and Zi,j+1, be within [1 − ε, 1 + ε]. This, together with the set of inequalities from the second requirement, define a continuous optimization problem and can be easily solved. Another option is to minimize the distance between the coefficients to one specific coefficient. The different choices of the objective function and the solution of the corresponding continuous optimization problem are presented in Supplementary materials.
, with respect to the variables Pj, Qi, Si,j, Si+1,j−1, Zi,j, and Zi,j+1, be within [1 − ε, 1 + ε]. This, together with the set of inequalities from the second requirement, define a continuous optimization problem and can be easily solved. Another option is to minimize the distance between the coefficients to one specific coefficient. The different choices of the objective function and the solution of the corresponding continuous optimization problem are presented in Supplementary materials.
Having determined the quadratic polynomial  satisfyies the important requirements (i, ii, and iii) above, we can now phrase our problem
satisfyies the important requirements (i, ii, and iii) above, we can now phrase our problem  as the equivalent quadratic unconstrained binary optimization problem
as the equivalent quadratic unconstrained binary optimization problem  . Notice that this reduction is performed only once for all cases; it need not to be redone for different bi-primes M. Before passing the problem to the quantum annealer, we use Gröbner bases again, this time to reduce the size of the problem. In fact, what we pass to the quantum annealer is
. Notice that this reduction is performed only once for all cases; it need not to be redone for different bi-primes M. Before passing the problem to the quantum annealer, we use Gröbner bases again, this time to reduce the size of the problem. In fact, what we pass to the quantum annealer is  , where NF is the normal form and
, where NF is the normal form and  is now the Gröbner basis cutoff, which we discuss in the next section. The largest bi-prime number that we embedded and solved successfully using the cell algorithm is ~35 000. Table 1 presents a small sample of many bi-prime numbers M that we tested using the cell algorithm, the number of variables using both the customized reduction CustR (i.e., reduction explained above before pre-processing with Gröbner bases) and the window-based GB reduction (i.e., reduction CustR followed with pre-processing with Gröbner bases), the overall reduction percentage R%, and the embedding and solving status inside the D-Wave 2X processor Embed.
is now the Gröbner basis cutoff, which we discuss in the next section. The largest bi-prime number that we embedded and solved successfully using the cell algorithm is ~35 000. Table 1 presents a small sample of many bi-prime numbers M that we tested using the cell algorithm, the number of variables using both the customized reduction CustR (i.e., reduction explained above before pre-processing with Gröbner bases) and the window-based GB reduction (i.e., reduction CustR followed with pre-processing with Gröbner bases), the overall reduction percentage R%, and the embedding and solving status inside the D-Wave 2X processor Embed.
The column algorithm (factoring up to 200000)
The total number of variables in the cost function of the previous method is 2spsq, before any pre-processing. Here we present the column-based algorithm where the number of variables (before pre-processing) is bounded by  . Recall that here we are phrasing the factorization problem M = pq as
. Recall that here we are phrasing the factorization problem M = pq as

where Hi, for 1 ≤ i ≤ sp, is

The cost function is of degree 4 and, in order to use quantum annealing, it must be replaced with a positive quadratic polynomial with the same global minimum. The idea is to replace the quadratic terms QjPi−j inside the different Hi with new binary variables Wi−j,j, and add the penalty  to the cost function (now written in terms of the variables Wi−j,j). To find
to the cost function (now written in terms of the variables Wi−j,j). To find  , we run Gröbner bases computation on the system
, we run Gröbner bases computation on the system

Following the same steps as in the previous section, we get

with a, b,  such that −a − b − c > 0, −b − c > 0, −a − c > 0, c > 0 (e.g., c = 1, a = b = −2). The new cost function is now
such that −a − b − c > 0, −b − c > 0, −a − c > 0, c > 0 (e.g., c = 1, a = b = −2). The new cost function is now

We can obtain a better Hamiltonian by pre-processing the problem before applying the W transformation. Indeed, let us first fix a positive integer cutoff ≤(sp + sq + 1) and let  be a Gröbner basis of the set of polynomials
be a Gröbner basis of the set of polynomials

In practice, the cutoff is determined by the size of the maximum subsystem of polynomials Hi on which one can run a Gröbner basis computation; it is defined by the hardware. We also define a cutoff on the other tail of {Hi}, that is, we consider  . Notice that here we are working on the original Hi rather than the new Hi(W). This is because we would like to perform the replacement
. Notice that here we are working on the original Hi rather than the new Hi(W). This is because we would like to perform the replacement  after the pre-processing (some of the quadratic terms might be simplified by this pre-processing). Precisely, what we pass to the quantum annealer is the quadratic positive polynomial
after the pre-processing (some of the quadratic terms might be simplified by this pre-processing). Precisely, what we pass to the quantum annealer is the quadratic positive polynomial

Here LT stands for the leading term with respect to the graded reverse lexicographic order. The second summation is over all i and j such that  is still quadratic. The outer normal form in the first summation refers to the replacement
is still quadratic. The outer normal form in the first summation refers to the replacement  , which is again performed only if
, which is again performed only if  is still quadratic.
is still quadratic.
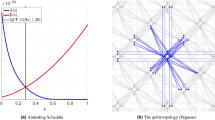
The columns of Table 2 present: a small sample of many bi-prime numbers that we tested and their prime factors, the number of variables using each of a naïve polynomial-to-quadratic transformation tool P2Q written mostly based on the algorithm discussed in ref. 19 (Other degree reduction procedures are discussed in refs 20, 21, 22, 23). Our novel polynomial-to-quadratic transformation CustR, and our window-based reduction GB after applying pre-processing. The overall reduction percentage R% and the embedding and solving status in the D-Wave 2X processor Embed are also shown. Figure 1 shows the adjacency matrix of the corresponding positive quadratic polynomial graph H and its embedded pattern inside the Chimera graph of the D-Wave 2X processor for one of the bi-primes. Details pertaining to the use of the hardware can be found in Supplementary materials.
Discussion
In this work, factorization is connected to quantum annealing through binarization of the long multiplication. The algorithm is autonomous in the sense that no a priori knowledge, or manual or ad hoc pre-processing, is involved. We have attained the largest bi-prime factored to date using a quantum processor, though more-subtle connections might exist. A future direction that this research can take is to connect factorization (as an instance of the abelian hidden subgroup problem), through Galois correspondence, to covering spaces and thus to covering graphs and potentially to quantum annealing. We believe that more-rewarding progress can be made through the investigation of such a connection.
Methods
Column factoring procedure
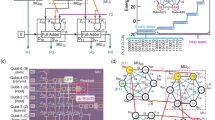
Here we discuss the two single-bit multiplication methods of the two primes p and q. The first method generates a Hamiltonian for each of the columns of the long multiplication expansion, while the second method generates a Hamiltonian for each of the multiplying cells in the long multiplication expansion. The column factoring procedure initially introduced in ref. 9, has been generalized. The generalized column factoring procedure of  and
and  is depicted Figure 2.
is depicted Figure 2.
The equation for an arbitrary column (i) can be written as the sum of the column’s multiplication terms (above) plus all previously generated carry-on terms from lower significant columns (j < i). This sum is equal to the column’s bi-prime term mi plus the carry-ons generated from higher significant columns. The polynomial equation for the i-th column is

The above equation is used as the main column procedure’s equation Hi. The Hamiltonian generation and reduction is discussed in detail in Results.
Cell factoring procedure
In the cell multiplication procedure the ultimate goal is to break each of the column equations discussed above into multiple smaller equations so that each equation contains only one quadratic term. This not only simplifies the generation of quadratic Hamiltonians, but also generates Hamiltonians with more-uniform quadratic coefficients in comparison to the column procedure. We generalized the procedure initially introduced in ref. 10. Figure 3 depicts our generalization:
Each cell contains one of the total (sp − 1) (sq − 1) quadratic terms in the form of QiPj. To chain a cell to its upper cell, one extra sum variable Si,j is added. Also, each carry-on variable Zi,j in a cell is the carry-on of the cell directly to its right, so each cell contains four variables. The sum of three terms QiPj, Si,j, and Zi,j is at most 3; thus, it generates an additional sum variable Si+1,j−1 and one carry-on variable Zi,j+1. Therefore, the equation for an arbitrary cell indexed (i, j), shown in the centre of the above table, is

As we can see, only six binary variables are involved in each cell equation and the equation contains one quadratic term, so it can be transformed into a positive Hamiltonian without adding slack variables. The Hamiltonian generation and reduction procedure is discussed in detail in Results.
Gröbner bases
Good references for the following definitions are chapters 1 and 2 of ref. 1 and chapter 1 of ref. 24.
Normal forms
A normal form is the remainder of Euclidean divisions in the ring of polynomials  . Precisely, the normal form of a polynomial
. Precisely, the normal form of a polynomial  , with respect to the set of polynomials
, with respect to the set of polynomials  (usually a Gröbner basis), is the polynomial
(usually a Gröbner basis), is the polynomial  , which is the image of f modulo
, which is the image of f modulo  . It is the remainder of the Euclidean of f by all
. It is the remainder of the Euclidean of f by all  .
.
Term orders
A term order on  is a total order
is a total order  on the set of all monomials
on the set of all monomials  , which has the following properties: (1) if
, which has the following properties: (1) if  , then
, then  for all positive integers a, b, and c; (2)
for all positive integers a, b, and c; (2)  for all strictly positive integers a. An example of this is the pure lexicographic order
for all strictly positive integers a. An example of this is the pure lexicographic order  . Monomials are compared first by their degree in x1, with ties broken by degree in x2, etc. This order is usually used in eliminating variables. Another example, is the graded reverse lexicographic order
. Monomials are compared first by their degree in x1, with ties broken by degree in x2, etc. This order is usually used in eliminating variables. Another example, is the graded reverse lexicographic order  . Monomials are compared first by their total degree, with ties broken by reverse lexicographic order, that is, by the smallest degree in xn, xn−1, etc.
. Monomials are compared first by their total degree, with ties broken by reverse lexicographic order, that is, by the smallest degree in xn, xn−1, etc.
Gröbner bases
Given a term order  on
on  , then by the leading term (initial term) LT of f we mean the largest monomial in f with respect to
, then by the leading term (initial term) LT of f we mean the largest monomial in f with respect to  . A (reduced) Gröbner basis to the ideal
. A (reduced) Gröbner basis to the ideal  with respect to the ordering
with respect to the ordering  is a subset
is a subset  of
of  such that: (1) the initial terms of elements of
such that: (1) the initial terms of elements of  generate the ideal
generate the ideal  of all initial terms of
of all initial terms of  ; (2) for each
; (2) for each  , the coefficient of the initial term of g is 1; (3) the set LT(g) minimally generates
, the coefficient of the initial term of g is 1; (3) the set LT(g) minimally generates  ; and (4) no trailing term of any
; and (4) no trailing term of any  lies in
lies in  . Currently, Gröbner bases are computed using sophisticated versions of the original Buchberger algorithm, for example, the F4 and F5 algorithms by J. C. Faugère25,26.
. Currently, Gröbner bases are computed using sophisticated versions of the original Buchberger algorithm, for example, the F4 and F5 algorithms by J. C. Faugère25,26.
Factorization as an eigenvalue problem
In this section, for completeness, we describe how the factorization problem can be solved using eigenvalues and eigenvectors. This is an adaptation of the method presented in ref. 8 to factorization, which is itself an adaption to real polynomial optimization of the method of solving polynomial equations using eigenvalues in ref. 1.
Let  be in
be in  as in (12), where we have used the notation xi instead of the Ps, Qs, Zs, and Ws. Define
as in (12), where we have used the notation xi instead of the Ps, Qs, Zs, and Ws. Define

which is in the larger ring  . We also define the set of polynomials
. We also define the set of polynomials

The variety  is the set of all binary critical points of
is the set of all binary critical points of  . Its coordinates ring is the residue algebra
. Its coordinates ring is the residue algebra  . We need to compute a basis for A. This is done by first computing a Gröbner basis for
. We need to compute a basis for A. This is done by first computing a Gröbner basis for  and then extracting the standard monomials (i.e., the monomials in
and then extracting the standard monomials (i.e., the monomials in  that are not divisible by the leading term of any element in the Gröbner basis). In the simple example below, we do not need to compute any Gröbner basis since
that are not divisible by the leading term of any element in the Gröbner basis). In the simple example below, we do not need to compute any Gröbner basis since  is a Gröbner basis with respect to plex(α, x). We define the linear map
is a Gröbner basis with respect to plex(α, x). We define the linear map

Since the number of critical points is finite, the algebra A is always finite-dimensional by the Finiteness Theorem (page 39 of ref. 1). Now, the key points are:
The value of
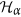 (i.e., values of
(i.e., values of 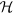 ), on the set of critical points
), on the set of critical points 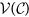 , are given by the eigenvalues of the matrix
, are given by the eigenvalues of the matrix 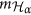 .
.Eigenvalues of
 and
and 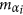 give the coordinates of the points of
give the coordinates of the points of 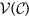 .
.If v is an eigenvector for
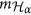 , then it is also an eigenvector for
, then it is also an eigenvector for 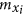 and
and 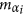 for 1 ≤ i ≤ n.
for 1 ≤ i ≤ n.
We illustrate this in an example. Consider M = pq = 5 × 3 and let

be the corresponding Hamiltonian as in (12), where x1 = p2, x2 = q1, x3 = w2,1, and x4 = z2,3. A basis for the residue algebra A is given by the set of the 16 monomials

The matrix  is
is

We expect the matrix’s smallest eigenvalue to be zero and, indeed, we get the following eigenvalues for  :
:

This is also the set of values which  takes on
takes on  . The eigenvector v which corresponds to the eigenvalue 0 is the column vector
. The eigenvector v which corresponds to the eigenvalue 0 is the column vector

This eigenvector is used to find the coordinates of  that cancel (minimize)
that cancel (minimize)  . The coordinates of the global minimum
. The coordinates of the global minimum  are defined by
are defined by  , and this gives x1 = x2 = x3 = 1, x4 = 0, and α1 = 2α2 = α3 = 2, α4 = 5.
, and this gives x1 = x2 = x3 = 1, x4 = 0, and α1 = 2α2 = α3 = 2, α4 = 5.
Additional Information
How to cite this article: Dridi, R. and Alghassi, H. Prime factorization using quantum annealing and computational algebraic geometry. Sci. Rep. 7, 43048; doi: 10.1038/srep43048 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
22 March 2017
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Cox, D. A., Little, J. B. & O’Shea, D. Using algebraic geometry. Graduate texts in mathematics (Springer, New York, 1998).
Kadowaki, T. & Nishimori, H. Quantum annealing in the transverse ising model. Phys. Rev. E 58, 5355–5363 (1998).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science 292, 472–475 (2001).
Das, A. & Chakrabarti, B. K. Colloquium: Quantum annealing and analog quantum computation. Rev. Mod. Phys. 80, 1061–1081 (2008).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194–198 (2011).
Boixo, S., Albash, T., Spedalieri, F. M., Chancellor, N. & Lidar, D. A. Experimental signature of programmable quantum annealing. Nat Commun 4 (2013).
Lanting, T. et al. Entanglement in a quantum annealing processor. Phys. Rev. X 4, 021041 (2014).
Parrilo, P. A. & Sturmfels, B. Minimizing polynomial functions. DIMACS Series in Discrete Mathematics and Theoretical Computer Science (2001).
Burges, C. Factoring as optimization. Tech. Rep. MSR-TR-2002-83, Microsoft Research (2002).
Schaller, G. & Schutzhold, R. The role of symmetries in adiabatic quantum algorithms. Quantum Information & Computation 10, 109–140 (2010).
Xu, N. et al. Quantum factorization of 143 on a dipolar-coupling nuclear magnetic resonance system. Phys. Rev. Lett. 108, 130501 (2012).
Dattani, N. S. & Bryans, N. Quantum factorization of 56153 with only 4 qubits. arXiv:1411.6758 (2014).
Pal, S., Moitra, S., Anjusha, V. S., Kumar, A. & Mahesh, T. S. Hybrid scheme for factorization: Factoring 551 using a 3-qubit NMR quantum adiabatic processor. arXiv:1611.00998 [quant-ph] (2016).
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26, 1484–1509 (1997).
Kitaev, A. Quantum measurements and the abelian stabilizer problem. arXiv:9511026 (1995).
Monz, T. et al. Realization of a scalable shor algorithm. Science 351, 1068–1070 (2016).
Smolin, J. A., Smith, G. & Vargo, A. Oversimplifying quantum factoring. Nature 499, 163–165 (2013).
Raussendorf, R. Contextuality in measurement-based quantum computation. Phys. Rev. A 88, 022322 (2013).
Boros, E. & Aritanan, G. On quadratization of pseudo-boolean functions. arXiv:1404.6538 (2014).
Anthony, M., Boros, E., Crama, Y. & Gruber, A. Quadratization of symmetric pseudo-boolean functions. Discrete Applied Mathematics 203, 1–12 (2016).
Babbush, R., O’Gorman, B. & Aspuru-Guzik, A. Resource efficient gadgets for compiling adiabatic quantum optimization problems. Annalen der Physik 525, 877–888 (2013).
Babbush, R., Denchev, V. S., Ding, N., Isakov, S. & Neven, H. Construction of non-convex polynomial loss functions for training a binary classifier with quantum annealing. CoRR abs/1406.4203 (2014).
Tanburn, R., Okada, E. & Dattani, N. S. Reducing multi-qubit interactions in adiabatic quantum computation without adding auxiliary qubits. part 1: The “deduc-reduc” method and its application to quantum factorization of numbers. arXiv:1508.04816 (2015).
Sturmfels, B. Gröbner bases and convex polytopes, vol. 8 of University Lecture Series (American Mathematical Society, Providence, RI, 1996).
Faugére, J.-C. A new efficient algorithm for computing Gröbner bases (f4). Journal of Pure and Applied Algebra 139, 61–88 (1999).
Faugère, J. C. A new efficient algorithm for computing Gröbner bases without reduction to zero (f5). In Proceedings of the 2002 International Symposium on Symbolic and Algebraic Computation, ISSAC ’02, 75–83 (ACM, New York, NY, USA, 2002).
Acknowledgements
We appreciate discussions with Pooya Ronagh and thank Marko Bucyk for proofreading the manuscript.
Author information
Authors and Affiliations
Contributions
R.D. and H.A. designed the algorithms. R.D. and H.A. conceived the experiments and analysed the results. All authors wrote and reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Dridi, R., Alghassi, H. Prime factorization using quantum annealing and computational algebraic geometry. Sci Rep 7, 43048 (2017). https://doi.org/10.1038/srep43048
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep43048
This article is cited by
-
Short-depth QAOA circuits and quantum annealing on higher-order ising models
npj Quantum Information (2024)
-
Effective prime factorization via quantum annealing by modular locally-structured embedding
Scientific Reports (2024)
-
Progress in the prime factorization of large numbers
The Journal of Supercomputing (2024)
-
Scalable set of reversible parity gates for integer factorization
Communications Physics (2023)
-
A quantum-inspired probabilistic prime factorization based on virtually connected Boltzmann machine and probabilistic annealing
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

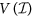 or, equivalently,
or, equivalently, 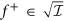 .
.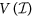 , that is, f+ > 0 over
, that is, f+ > 0 over 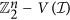 .
.


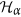 (i.e., values of
(i.e., values of 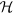 ), on the set of critical points
), on the set of critical points 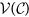 , are given by the eigenvalues of the matrix
, are given by the eigenvalues of the matrix 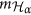 .
. and
and 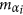 give the coordinates of the points of
give the coordinates of the points of 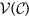 .
.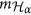 , then it is also an eigenvector for
, then it is also an eigenvector for 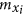 and
and 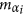 for 1 ≤ i ≤ n.
for 1 ≤ i ≤ n.