Abstract
The application of complex systems theory to physiology and medicine has provided meaningful information about the nonlinear aspects underlying the dynamics of a wide range of biological processes and their disease-related aberrations. However, no studies have investigated whether meaningful information can be extracted by quantifying second-order moments of time-varying cardiovascular complexity. To this extent, we introduce a novel mathematical framework termed complexity variability, in which the variance of instantaneous Lyapunov spectra estimated over time serves as a reference quantifier. We apply the proposed methodology to four exemplary studies involving disorders which stem from cardiology, neurology and psychiatry: Congestive Heart Failure (CHF), Major Depression Disorder (MDD), Parkinson’s Disease (PD), and Post-Traumatic Stress Disorder (PTSD) patients with insomnia under a yoga training regime. We show that complexity assessments derived from simple time-averaging are not able to discern pathology-related changes in autonomic control, and we demonstrate that between-group differences in measures of complexity variability are consistent across pathologies. Pathological states such as CHF, MDD, and PD are associated with an increased complexity variability when compared to healthy controls, whereas wellbeing derived from yoga in PTSD is associated with lower time-variance of complexity.
Similar content being viewed by others
Introduction
Physiological dynamics associated with oscillatory systems (such as the cardiovascular system) are commonly characterized through mathematical approaches in both the time and frequency domains. Most of these approaches assume intrinsic linearity and time-invariant properties. The inherent postulate is that the magnitude of physiological responses is proportional to the strength/amplitude of the input stimuli. Given the widespread accessibility of electrocardiographic (ECG) as well as pulseoximeter measurements, the analysis of Heart Rate Variability (HRV) has become a paradigmatic example of physiological time series analysis performed through linear techniques. HRV analysis is commonly based on indices such as mean heart rate, standard deviation, and low-frequency (LF) and high-frequency (HF) spectral powers derived from the RR interval series1. However, the cardiovascular system is constantly involved in a dynamical, mutual interplay with numerous other physiological subsystems (e.g., endocrine, neural, and respiratory), as well as in multiple self-regulating, adaptive biochemical processes2,3,4. In this context, it is well known that the effects of combined sympathetic and vagal stimulation on heart rate are not simply additive, as tonic sympathetic stimulation sensitizes the heart rate to vagal stimulation4. This is because sympathetic stimulation inhibits acetylcholine release by acting on adrenergic receptors on the vagal terminals, cytosolic adenosine 3,5-cyclic monophosphate mediates postjunctional interactions between the sympathetic and vagal systems, and acetylcholine released by vagal stimulation inhibits norepinephrine release by acting on muscarinic receptors on sympathetic nerve terminals. In addition, neuropeptide Y released from sympathetic nerve terminals also interacts with ACh acetylcholine, and the release of neuropeptide Y is prevented by simultaneous vagal stimulation4. As a results, cardiovascular dynamics exhibits an inherently complex structure characterized by non-stationary, intermittent, scale-invariant and nonlinear behaviors1,5.
In light of the above, methodological approaches derived from the theory of complex dynamical systems may provide access to a more complete description of the mechanisms underlying biological regulation of cardiac activity. Widely employed methods for characterizing heartbeat complexity include detrended fluctuation analysis and wavelet analysis (which quantify scaling properties, correlations, and fractal measures of variability), Lyapunov exponents as well as various measures of entropy such as sample entropy and its multiscale version (which quantify the degree of instability and predictability of the time series under investigation)6,7,8,9. The use of these methods has allowed improved characterization of abnormal cardiac rhythms1,10,11 and has aided in predicting the risk of acute adverse events such as sudden cardiac and sudden infant death (see refs 1,9, 10, 11, 12, 13, 14, 15, 16).
Current Limitations in Complexity Assessment
Despite the considerable achievements obtained by the measures and approaches outlined above, the application of these analysis strategies to physiological systems has resulted in several discrepancies in the literature. For example, changes in cardiovascular complexity have been observed to accompany aging17, whereas other findings suggest that fractal linear and nonlinear characteristics of cardiovascular dynamics do not change with age18. Similar controversies have been reported in the field of sleep analysis19. In this paper, we posit that these discrepancies may partly be due to several methodological and applicative issues inherent to these methods, which have not yet been satisfactorily addressed.
First, the intrinsically discrete nature of heartbeats, which are unevenly spaced in time, often leads to the use of interpolation procedures, which are likely to introduce bias in the estimation of nonlinear/complexity measures. Second, traditional complexity estimation approaches/algorithms provide a single value (or set of values) within a predetermined time window and hence can only represent average measures of the physiological system dynamics observed in the entire time window. However, it is well known that physiological dynamics commonly undergo rapid, transient changes in time which can also occur in a number of psycho-physiological states and pathologic conditions20,21,22,23. In the face of non-stationary behavior, collapsing across time into a single, more or less representative value may not allow to capture the subtleties of complex behavior within any particular analysis window. Moreover, even in case of windowing strategies that would allow for the computation of more than one reference point estimation, this may not be sufficient to properly catch the time-varying dynamics of the computed measure. Third, most of the nonlinearity and complexity measures employed to-date have been proven to be sensitive to the presence of uncorrelated (e.g. white) or correlated (e.g. 1/f) noise. As stochasticity plays a crucial role in physiological dynamics6,10, this sensitivity may lead to an overestimation of complexity which may become more evident in the presence of specific pathologies, such as certain cardiac arrhythmias including atrial fibrillation24. While when compared to healthy systems, these pathological situations appeared to be associated with the emergence of a more regular cardiovascular behavior(visible as a reduction in entropy)11, it was shown that the observed changes were due to modifications in the statistical properties of underlying physiological noise24.
A New Time-varying Model for Complexity Assessment
To overcome these limitations, we recently introduced novel time-varying complexity measures that can be applied to stochastic discrete series such as the ones related to heartbeat dynamics7,8. These novel measures are fully embedded in the probabilistic framework of the inhomogeneous point-process theory and are obtained by modeling the cardiovascular system through both deterministic and random terms. In turn, this caters for the simultaneous presence of both chaotic and stochastic behaviours. This idea has been successful applied in other studies6,25, and is in agreement with current views on the genesis and physiology of healthy heartbeat dynamics, which can be thought of as the output of a nonlinear deterministic system (the pacemaker cells of the sinus node) forced by a high-dimensional input (neural activity of fibers innervating the sinus node itself). The originality of the new definitions lies in the explicit mathematical formulations of the time-varying phase-space vectors, as well as in the definition of their distance7,8.The main advantages of these techniques are that the resulting, instantaneous estimates of complexity are free from bias due to either interpolation techniques or variability in statistical properties of noise.
Complexity Variability
Once instantaneous complexity series are available, basic time-domain features can be used to summarize cardiovascular complex dynamics. In particular, measures of central tendency, e.g., the median value, and variability, e.g., the median absolute deviation can be calculated.
The former (central tendency) can be considered equivalent to standard complexity estimates which collapse data across time by design. The latter (median absolute deviation) represents an innovation in the field of complexity analysis7,8, by defining a measure of complexity variability.
In this context, when adopting instantaneous Lyapunov exponents as a complexity measure7, we recently observed a notable (albeit preliminary) discriminant power associated with its variability. In a recent study on patients with congestive heart failure (CHF) and healthy subjects24 we found that neither standard sample (SampEn) and approximate (ApEn) entropy measures1,26 nor the median (over a given time-window) of the instantaneous dominant Lyapunov exponent are able to discriminate between the two populations. In contrast, heartbeat dynamics associated with CHF showed a significantly increased complexity variability when compared to healthy controls, hence providing a novel measure which could potentially aid in early discrimination and/or stratification of this kinds of patients27,28. Of note, these findings are in accordance with current literature indicating an effect of cardiovascular disorders on complexity and variability of biological processes29.
Novel Definitions and Applications of Complexity Variability
In this study, we hypothesize that the discriminative potential of complexity variability measures can serve as a potential biomarker able to discriminate subtle changes which are not evident in other complexity measures. To this end, in this study we aimed to broaden the spectrum of pathologies under study to patients suffering from neurological and mental disorders such as major depression disorder (MDD), Post Traumatic Stress Disorders (PTSD), and Parkinson’s Disorders (PD). In the rest of this paper, prior art concerning cardiovascular assessment of these pathologies is reported. Then, the basic mathematical formulation of inhomogeneous point-process models of heartbeat dynamics, as well as of instantaneous Lyapunov estimates are reported followed by experimental results, discussion and conclusion.
Heartbeat Dynamics in Cardiovascular, Mental and Neurological Disorders
HRV Assessment in Congestive Heart Failure
Congestive Heart failure (CHF) is a major public health problem, with a prevalence of more than 5.8 million in the United States and more than 23 million worldwide30. HRV analysis has been previously used to discern healthy subjects from patients suffering from congestive heart failure (CHF)31,32,33,34,35,36,37. It has been accepted that linear features of heartbeat dynamics (based on spectral analysis) are not sufficient for CHF patient characterization, and need to be complemented by nonlinear features, ranging from Entropy to Non-Gaussian metrics (see refs 7,8,23,31, 32, 33,37,38 and reference therein for reviews). Also, classic approximate and sample entropy, as expressed in their basic form, are not able to discern between heathy subjects and patients with CHF8,24.
Moreover, cardiovascular dynamics in CHF patients was associated with a loss of multifractality, whose information is encoded in the Fourier phases of HRV series23,32,33,37. Furthermore, in CHF patients, departures from Gaussianity have been used to evaluate increased mortality risk34,35,38.
HRV Assessment in Major Depression
According to epidemiological studies, almost 15% of the population in the United States has suffered from at least one episode of mood alteration39, and about 27% (equals 82.7 million; 95% confidence interval: 78.5–87.1) of the adult European population is or has been affected by at least one mental disorder40. To date, biological markers, especially those derived from applying advanced signal processing approaches to biological signals, are not commonly incorporated in clinical routine examinations41,42. Previous studies have focused on depression and sleep43,44 and circadian heart rate rhythms45,46 highlighting autonomic changes that may be considered predictors of clinical modifications. In the realm of HRV analysis, a decrement of HF power and an increment of LF/HF ratio was observed in MD patients when compared to controls47. However, several studies demonstrated that estimates of linear cardiovascular dynamics, i.e., quantifiers of the power distribution among frequencies only, are unable to adequately discern healthy subjects from MD patients22,43,48,49,50,51,52,53.
Nonlinear analysis of HRV data, which also quantifies nonlinear interactions among frequencies reflecting underlying ANS dynamics, represents a recent frontier in the assessment of psychiatric disorders. In this context, nonlinear measures have already allowed the discrimination of depressive patients from healthy subjects, consistently showing a significant decrease of complexity in the pathological cohort22,49,50,51. These findings support the hypothesis that complexity of physiologic signals could be used as dynamical biomarkers of depression.
HRV Assessment in Post Traumatic Stress Disorder with Insomnia
Sleep disturbances and insomnia related to post-traumatic stress disorder (PTSD) are a prototypical example of the comorbidity between autonomic dysfunction psychological distress. Among American adults, the estimated lifetime prevalence of PTSD is 6.8%54. Sleep disturbances such as insomnia and nightmares have much higher prevalence (up to 60%) in people with PTSD compared to those without PTSD55. As separate conditions, both PTSD and insomnia are characterized by chronic hyperarousal of Autonomic Nervous System (ANS) activity56, i.e., high sympathetic and hypothalamicpituitaryadrenal activity), and drug-nave subjects with PTSD display decreased cardiac vagal control when compared to subjects without PTSD and matched controls57. Clinically, this overlap is reflected in an entire cluster of the DSM-IV-TR diagnostic criteria for PTSD pertaining to hyperarousal58. Accordingly, the DSM-IV-TR PTSD hyperarousal cluster includes assessment of insomnia symptoms, and autonomic dysregulation has also been proposed as an important mechanism in the pathogenesis of insomnia59. While we are not aware of literature on ANS function in PTSD-related insomnia, one study suggested the existence of a relationship between sleep disturbances and baroreceptor sensitivity in women with PTSD60.
Among the approaches thought to aid in stress reduction and the prevention of mental disorders, yoga has been seen to be an effective strategy61. Mixed evidence suggests that yoga influences HRV dynamics in people without PTSD, including advanced yoga practitioners as well as adults exposed to acute trauma and chronic stress62,63,64. While some studies have shown that yoga reduces psychological symptoms in PTSD, no studies have directly investigated HRV dynamics in PTSD patients (with or without insomnia) who practice yoga65,66. Because insomnia and PTSD involve ANS dysregulation, and because yoga may balance ANS function, HRV analysis has the potential to serve as a biomarker to assess the therapeutic effect of yoga in reducing hyperarousal in PTSD.
HRV Assessment in Parkinson’s Disorders
Parkinson’s disease (PD) is the second most common neurodegenerative disorder after Alzheimer’s disease, and is classically associated with motor symptoms including tremor, balance problems, limb rigidity, bradykinesia and gait abnormalities67. The causes and aetiology of this disease are still largely unknown. Symptoms of ANS failure are known to be part of the disease68. They include cardiovascular, sexual, bladder, gastrointestinal, and sudo-motor abnormalities69, and previous studies reported a variable prevalence of cardiovascular autonomic dysfunction between 23% and 80%70,71.
HRV measures have been employed to non-invasively explore ANS alterations in PD by evaluating the modulatory effects of ANS dynamics on sinus node activity72. In one of these studies, all HRV spectral components (calculated from studying 24 h outpatient ECG recordings) were found to be significantly lower in the PD patients when compared to control subjects73. In another study on 10 minutes of data recorded at rest, HRV-HF power was significantly lower in untreated patients with PD with respect to healthy controls, whereas nonlinear HRV analysis based on entropy and geometrical measures was not able to distinguish between patients and controls74. However, PD patients displayed an increase in complexity of systolic arterial pressure series when compared to controls75. Taken together, these findings point towards a possible role of HRV analysis characterizing subtle autonomic alterations which accompany major motor symptoms in PD.
Experimental Setup and Results
In order to validate the complexity variability framework, in this paper we pooled four experimental datasets involving cardiovascular, neurological, and mental disorders such as Congestive Heart Failure (CHF), Major Depression Disorder (MDD), Parkinsonos Disease (PD), and Post-Traumatic Stress Disorder (PTSD) with insomnia. Within the CHF, MDD, and PD datasets the patient population was compared with age- and gender-matched healthy controls. In the PTSD dataset, we performed paired comparison of data gathered before and after all patients underwent yoga practice training. Details on each experimental setup follow below.
All features were instantaneously calculated with a δ = 5 ms temporal resolution from each recording of each subject. KS and autocorrelation plots were visually inspected to check that all points of the plot were within the 95% of the confidence interval, hence guaranteeing the independence of the model-transformed intervals76. NARL model order selection was performed by choosing orders that minimize KS distances (the smaller the KS distance, the better the model fit). Once the order p,q is determined, the initial NARL coefficients are estimated by the method of least squares76. Accordingly, our analysis indicated p = 3~5 and q = 1~3 with α = 0.2 as optimal choice.
Complex Dynamics in Congestive Heart Failure patients
This dataset was selected from data gathered from CHF patients and reference healthy subjects on a public source: Physionet (http://www.physionet.org/)77. All participants received information about the study procedures and gave written informed consent approved by the local Institutional Review Board. The experimental protocol was approved by the Hospitals’ Human Subjects Committees. Data were acquired in accordance with the approved guidelines78. RR time series were recorded from 14 CHF patients (from BIDMC-CHF Database) as well as 16 healthy subjects (from MIT-BIH Normal Sinus Rhythm Database). Each RR time series, extracted from the 20 h recording at the same day cycle, was artifact-free (upon visual inspection and artifact rejection based on the point-process model79) and lasted about 50 min. These recordings have been employed in multiple landmark studies of complex heartbeat interval dynamics7,8,12,15,27,80.
Results
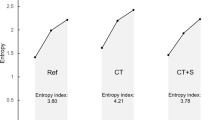
In this dataset, we tested the ability of instantaneous linear and complex nonlinear estimates of heartbeat dynamics to discriminate healthy subjects from CHF patients. Exemplary instantaneous tracking of complex heartbeat dynamics, along with the first-order moment, are shown in Fig. 1. Group statistics are reported in Table 1. The difference was expressed in terms of p-values calculated through a non-parametric Mann-Whitney test under the null hypothesis that the medians of the two sample groups were equal.
On average, CHF patients show significantly lower μRR, σRR, as well as lower LF and HF power. The median IDLE (IDLE) was not significantly different between the two groups. Conversely, the complexity variability measure, CVIDLE, showed significant statistical difference (p < 0.05). It is worth noting that we detected an increase in CVIDLE in the pathological state (as compared to controls), contrarily to classical nonlinear-based assessments7,8,23,31,32,33,38, in which pathology is consistently associated with a decrease of complexity. Our novel quantifier therefore provides an additional dimension associated with incremental knowledge about changes in cardiovascular complexity in CHF7,8,23,31,32,33,37,38.
Complex Dynamics in Major Depression Disorder Patients
48 outpatients (age: 22.6 ± 4.7 years) with Major Depression Disorder (MDD) were recruited through screening in a population of University students by applying the Zung-self-rating depression scale81. All patients were experiencing their first MDD episode and had not received psychotherapeutic or pharmacological treatment. A control group consisting of 48 age- and gender-matched healthy subjects was also included (age: 23.5 ± 4.9 years). Sixteen men (33.3%) and 32 women (66.6%) were included in each group. Exclusion criteria for both MDD and healthy subjects were: cardio-, cerebro-, or peripheral vascular diseases, the presence of neoplasm, diabetes mellitus, kidney or liver failure, infectious or systemic inflammatory disease and current neurological illnesses. All participants received information about the study procedures and gave written informed consent approved by the local Institutional Review Board of the Cardiovascular Foundation of Colombia, Bucaramanga, Colombia. The experimental protocol was approved by such ethical committee. Data were acquired in accordance with the approved guidelines. Participants abstained from smoking or consuming beverages containing caffeine, xanthines or alcohol the day before evaluation. Continuous ECG monitoring (lead II) was performed with a Finometer device (Finapress Medical System, The Netherlands) while subjects were asked to rest for 10 minutes in a reclining position. Further details can be found in ref. 51.
Results
Exemplary instantaneous tracking of complex heartbeat dynamics, along with the first-order moment, during 10 minutes of resting state are shown in Fig. 2. Group statistics are reported in Table 2. The difference was expressed in terms of p-values from a non-parametric Mann-Whitney test under the null hypothesis that the medians of the two sample groups are equal.
In summary, in presence of a severe depressive state CVIDLE provides significant statistical power in discerning MDD from healthy subjects. To our knowledge, this is the first time that a time-varying complexity assessment is proposed in mental disorders. Our results are also in agreement with previous studies demonstrating that estimates of linear cardiovascular dynamics are unable to adequately discern healthy subjects from MD patients22,43,48,49,50,51,52,53. Also, as in CHF (see above), classical complexity measures have been seen to decrease in MDD when compared to healthy controls48,49,53. In this study, we show that our CVIDLE measure is significantly increased in MDD as compared to controls, hence providing additional information about complex cardiovascular changes.
Complex Dynamics in Post-Traumatic Stress Disorder with Insomnia and Yoga Training
The overall objective of this experimental setup was to evaluate the potential of yoga as an adjunctive treatment for insomnia related to PTSD. Nineteen adults (over 18 years-old) were recruited to participate in this study. Insomnia and PTSD unrestricted by trauma history was confirmed in study participants using the Clinician-Administered PTSD Scale and the American Academy of Sleep Medicine’s Research Diagnostic Criteria for insomnia related to a mental health disorder82,83. All participants received information about the study procedures and gave written informed consent approved by the local Institutional Review Board (Partners Human Research Committee, Brigham and Women’s Hospital, Boston, MA, USA) The experimental protocol was approved by the Institutional Review Board. Data were acquired in accordance with the approved guidelines. Participants were asked to continue any other stable treatments they were on (pharmacological and behavioral) 6 weeks from baseline throughout the duration of the study. Also, all subjects were naive to yoga (<1 hour/week in the past 6 months). The intervention consisted of an 8-week, closed-group yoga program: classes met twice weekly for 90 minutes, with 15-minute personal practice on non-class days guided by DVD or online. This manualized program included ethics, postures, breath regulation, relaxation and basic meditation techniques taught in the Kripalu yoga style. The first 4 weeks focused upon learning all techniques except meditation, while building safety and trust; the second half involved more time in poses and breaths, and introduced meditation. Continuous ECG data was collected at baseline and at end of treatment 5 minutes of resting state with regular breathing. Out of the 19 participants who completed the study (50% attrition), 12 had evaluable baseline and end-treatment ECG data.
Results
Instantaneous linear and complex nonlinear estimates of heartbeat dynamics were used to investigate significant changes in ANS activity between before- and after-performing the yoga training. Exemplary instantaneous tracking of the complex heartbeat dynamics, along with the first-order moment are shown in Fig. 3. Paired group statistics are reported in Table 3. The difference was expressed in terms of p-values from a non-parametric Wilcoxon test under the null hypothesis that the medians of the two paired sample groups are equal.
In particular, in PTSD patients who improved their mental well-being by decreasing their psychological distress after yoga training (e.g., PTSD symptoms decreased with p < 0.005 from 57.1 ± 2.5 at baseline to 46.8 ± 2.9 based on the PTSD Checklist - Specific for the Diagnostic and Statistical Manual for Mental Health Disorders, 4th edition; from Noggle et al., in preparation), our complexity variability measure was significantly lower when comparing data acquired before and after training. To our knowledge, estimates of CVIDLE are able for the first time to provide an effective quantification of improved mental well-being employing exclusively cardiovascular dynamics.
Complex Dynamics in Parkinson’s Disease
Cardiovascular signals were recorded from 29 healthy controls (HC, 18 males) and 30 PD patients (23 males). Subjects were placed horizontally in a supine position and remained at rest during the whole recording (10 minutes). During the acquisition, all subjects were instructed not to talk and maintained relaxed spontaneous breathing. All participants gave written informed consent to participate in the study, which was approved by the Versilia Hospital, AUSL 12 Viareggio, Lido di Camaiore (LU), Italy, committee. The experimental protocol was approved by the local ethics committee. Data were acquired in accordance with the approved guidelines. Clinical assessment included history of disease-related symptoms and signs, and full neurological examination. All patients were screened for cardiovascular autonomic dysfunction which was considered as exclusion criterion. All patients had to satisfy the UK Brain Bank criteria for the diagnosis of PD84 and were in stage 1, 1.5 2 or 2.5 according to the Hoehn-Yahr (HY) system. As supportive criterion, a 123IFP-CIT SPECT to confirm nigrostriatal degeneration was performed. Severity of parkinsonism was evaluated by the Unified Parkinsonos Disease Rating Scale (UPDRS)85 and the HY staging system86.
Results
In this case, we tested the ability of instantaneous linear and complex nonlinear estimates of heartbeat dynamics in discriminating healthy subjects from PD patients. Exemplary instantaneous tracking of the complex heartbeat dynamics, along with the first-order moment, during 10 minutes of resting state are shown in Fig. 4. Group statistics are reported in Table 4 (reproduced from28 with permission). The difference was expressed in terms of p-values from a non-parametric Mann-Whitney test under the null hypothesis that the medians of the two sample groups are equal.
Importantly, our results suggest that PD states are associated with an increase of complexity variability, possibly pointing toward subtle autonomic changes which may accompany or precede autonomic dysfunctions, and can only be detected using an instantaneous, time resolved approach to quantifying autonomic complexity.
Discussion and Conclusion
We presented a novel complexity variability framework for the assessment of complex physiological dynamics. This work was motivated by the fact that a single complexity estimation, which collapses data across time, may not be sufficient to completely characterize physiological system complexity in the face of non-stationary behavior20,21,22,23. Importantly, accounting for temporal dynamics of stochastic events is fundament for the assessment of complex ecosystems, too87,88.
Our methodological approach is based on the time-varying assessment of Lyapunov exponents (e.g. the IDLE index) within a point-process paradigm which has been explicitly devised for modeling cardiovascular control. We performed instantaneous IDLE estimates in four exemplary datasets, involving data gathered in patients with cardiovascular disease such as CHF, as well as in neurological and psychiatric disorders such as MDD, PTSD with insomnia, and Parkinson’s Disease (PD). The time-varying IDLE information was summarized through measures of central tendency (median value) and variability (median absolute deviation).
In all statistical comparisons of patients vs controls or patients before treatment vs patients after treatment, the central tendency of complexity measures did not show any significant differences. Conversely, our complexity variability measures always showed statistically significant differences. Moreover, when compared to other instantaneous heartbeat estimates defined in the time and frequency domains76, only heartbeat complexity variability measures showed significant differences in the MDD, PTSD and insomnia treatment, and PD datasets.
Of note, in the attempt to provide a plausible comparison set, we were not able to find high time-resolution indices that were going beyond the standard heart rate variability indices (linear and nonlinear). Reasonably, we do not exclude that other indices derived by processing series of heartbeat dynamics might present meaningful characteristics able to effectively discern between, e.g., healthy control subjects and patients with major depression, Parkinson’s disease, congestive heart failure, or post traumatic stress disorder. Indeed, we aimed to study clinically meaningful, statistical properties of complexity variability, i.e., of the variance of a series quantifying the complexity level of a nonlinear system.
While the findings reported in this study will need further characterization before they can be directly translated into clinical practice, the presence of significant differences in complexity variability measures between MDD, PTSD and insomnia treatment, provides an indication that these physiological measurements could potentially aid in the early differential diagnosis between subjects experiencing normal grief or anxiety symptoms and those eventually evolving to clinical depression or PTSD in response to a stressful life event. This is of particular importance for clinical practitioners, given that normal grief, although sharing similar clinical symptoms with depression, neither involves the physiological alterations reported in MDD nor requires pharmacological interventions. Furthermore, consistently detecting altered autonomic features could provide an indication of how the modulation of peripheral physiology by cortical and subcortical pathways becomes disrupted during active MDD and PTSD. The study of complex ANS activity could therefore potentially be explored as an early physiological index for remission or relapse in patients under treatment. Interestingly, in the case of cardiovascular and mental/neurological disorders, complexity variability measures were significantly higher in the pathological groups as compared to controls (healthy subjects). Consistent with these findings, in case of PTSD patients who improved their mental well-being, complexity variability measures were significantly lower when comparing data acquired before and after yoga training. Additionally, we found an increased complexity variability in PD patients when compared to controls. While the etiology of ANS disturbances in PD (also known as dysautonomia) are not yet well-understood, it is known that they reflect neurodegenerative processes which involve additional circuits apart from the nigrostriatal dopaminergic system89,90, and develop in a manner which is largely independent of the evolution of dopaminergic symptoms. Accordingly, it has been shown that the assessment of cardiovascular autonomic failure can aid in early recognition and treatment of PD91,92, and previous studies have demonstrated parkinsonisms such as Multiple System Atrophy and Progressive supranuclear palsy display different patterns of disease-related alterations with respect to PD93,94. A better understanding, early recognition and treatment of ANS failure in PD may therefore aid in the differential diagnosis of Parkinsonisms as well as have an impact on patient management quality and therefore quality of life. In this context, currently the evaluation of ANS dysfunctions relies on combersome diagnostic tests only available in selected centers93,94,95 and it is associated with a large amount of diagnostic and financial overhead. We have shown that additional measures related higher-order, complexity statistics of heartbeat dynamics as well as from their variability over time are the most useful in discriminating PD patients from controls, possibly pointing towards their employment in a lightweight (i.e., ECG-based only) and therefore more widespread diagnostic environment.
Therefore, overall, opposite to the common concept that cardiovascular variability decreases with disease, we have found a measure of variability that increases in the presence of some pathological states, and decreases with states of mental well-being.
Taken together, these evidences suggest that our Lyapunov-based, heartbeat complexity variability measures could be employed as a putative biomarker of psychiatric and/or neurological well-being, where higher complexity variability is associated with a more severe pathological state. In addition, complexity variability might allow for better stratification of pathological subtypes, providing an additional discriminant dimension in building a feature space. These findings are in agreement with the current literature which posits that cardiovascular disorders affect complexity and variability1,9,10,11,12,13,14,15,16. On the methodological side, it is important to mention that our IDLE estimates are not affected by the intrinsically discrete nature of heartbeat dynamics, which are unevenly spaced in time. Additionally, our IDLE estimates are independent of signal background noise statistics7,8, which have been seen to heavily confound the detection of disease-related alterations in complexity24. Of note, we used discrete Laguerre expansions on cubic autoregressive Wiener-Volterra models to achieve long-term memory and improved performances in parameter estimation, as confirmed by goodness of fit measures7.
Also, unlike other methods that might require relatively long-term recordings, our method is potentially useful to obtain complexity measures from short recordings. Future work will investigate the potential of these time-varying complexity estimates in producing new real-time measures for the underlying complexity of physiological systems.
Methods for Cardiovascular Complexity Variability Estimation
In this section, details on the signal processing methodology for the cardiovascular complexity variability estimation are reported. A summary of all indices used in this study is reported in Table 5.
Lyapunov Exponents Estimation
The Lyapunov Exponent (LE) of a real valued function f(t) defined for t > 0 is ref. 96:

More generally, let us consider n-dimensional linear system in the form yi = Y(t)pi, where Y(t) is a fundamental solution matrix with Y(0) orthogonal, and {pi} is an orthonormal basis of  . Then, the sum of the corresponding n Lyapunov Exponents (λi) is minimized, and the orthonormal basis {pi} is called “normal”96. One of the key theoretical tools for determining LEs is the continuous QR factorization: Y(t) = Q(t)R(t)97,98 where Q(t) is orthogonal and R(t) is upper triangular with positive diagonal elements Rii, i = 1:n. Therefore we obtain96,97,98:
. Then, the sum of the corresponding n Lyapunov Exponents (λi) is minimized, and the orthonormal basis {pi} is called “normal”96. One of the key theoretical tools for determining LEs is the continuous QR factorization: Y(t) = Q(t)R(t)97,98 where Q(t) is orthogonal and R(t) is upper triangular with positive diagonal elements Rii, i = 1:n. Therefore we obtain96,97,98:

Considering N data samples, we evaluate the Jacobian over the time series, and determine the LE by means of the QR decomposition:

This decomposition is unique except in the case of zero diagonal elements. Then, leveraging on the estimation of the matrices R(n), the LEs λi are given by

where τ is the sampling time step, and R(n)ii is the value in the diagonal taken by the ith row and ith column.
Nonlinear Modeling of History Dependence
The expected value of a nonlinear autoregressive model can be written as follows:

Due to the autoregressive structure of (4), the system can be identified with only exact knowledge of the output data and with only few assumptions on the input data.
An important practical limitation in modeling high-order nonlinearities using the model in (4) is the high number of parameters that need to be estimated from the observed data. An advocated approach to solve such a limitation is the use of Laguerre functions99,100,101,102. Let us define the jth-order discrete time orthonormal Laguerre function:

where α is the discrete-time Laguerre parameter (0 < α < 1) which determines the rate of exponential asymptotic decline of these functions, and n ≥ 0. Given the Laguerre function, ϕj(n), and the signal, y(n), the jth-order Laguerre filter output is:

Time-Varying Modeling of Heartbeat Intervals
The iterative estimation along time of the time-varying complexity and related complexity variability index can be performed using several signal processing methods. For example, traditional recursive least-square and window-based methods can be applied. In addition, a simple Kalman filtering can be used to track the complex cardiovascular dynamics at each heartbeat, whereas an instantaneous estimation (i.e., at each moment in time) can be performed using point-process modeling.
A random point process is a stochastic process whose elements are point patterns specified as a locally finite counting measure103. Considering the R-waves detected from the Electrocardiogram (ECG) as such events, point process theory can be used to characterize their probability of occurrence76,104,105,106,107. Mathematically, in the time domain, a simple 1-D point process consists of series of timestamps marking the occurrence times t ∈ [0,∞) of the random events. Given a set of R-wave events  , let RRj = ujuj−1 > 0 denote the jth R–R interval, or equivalently, the waiting time until the next R-wave event. Assuming history dependence, the probability distribution of the waiting time tuj until the next R-wave event, where uj denotes the previous R-wave event occurred before time t, follows an inverse Gaussian (IG) model:
, let RRj = ujuj−1 > 0 denote the jth R–R interval, or equivalently, the waiting time until the next R-wave event. Assuming history dependence, the probability distribution of the waiting time tuj until the next R-wave event, where uj denotes the previous R-wave event occurred before time t, follows an inverse Gaussian (IG) model:

where  is the history of the point process, ξ(t) is the vector of the time-varing parameters,
is the history of the point process, ξ(t) is the vector of the time-varing parameters,  represents the first-moment statistic (mean) of the distribution, and ξ0(t) = θ > 0 denotes the shape parameter of the IG distribution (as θ/μ → ∞, the IG distribution becomes more like a Gaussian distribution). As
represents the first-moment statistic (mean) of the distribution, and ξ0(t) = θ > 0 denotes the shape parameter of the IG distribution (as θ/μ → ∞, the IG distribution becomes more like a Gaussian distribution). As  indicates the probability of having a beat at time t given that a previous beat has occurred at uj, its first moment
indicates the probability of having a beat at time t given that a previous beat has occurred at uj, its first moment  can be interpreted as the average (or expected) waiting time before the next beat. We can also estimate the second-moment statistic (variance) of the IG distribution as
can be interpreted as the average (or expected) waiting time before the next beat. We can also estimate the second-moment statistic (variance) of the IG distribution as  . The use of an IG distribution to characterize the R-R intervals is physiologically motivated: if the rise of the membrane potential to a threshold initiating the cardiac contraction is modeled as a Wiener process with drift, then the probability density of the times between threshold crossings (the RR intervals) is indeed the inverse Gaussian distribution76. It is important to note that, when compared with other distributions, the IG model always achieves the best fitting results105. The instantaneous RR mean,
. The use of an IG distribution to characterize the R-R intervals is physiologically motivated: if the rise of the membrane potential to a threshold initiating the cardiac contraction is modeled as a Wiener process with drift, then the probability density of the times between threshold crossings (the RR intervals) is indeed the inverse Gaussian distribution76. It is important to note that, when compared with other distributions, the IG model always achieves the best fitting results105. The instantaneous RR mean,  , can be modeled as a generic function of the past RR values
, can be modeled as a generic function of the past RR values  , where RRj−k denotes the previous kth R–R interval occurred prior to the present time t.
, where RRj−k denotes the previous kth R–R interval occurred prior to the present time t.
Here, we represent the nonlinear cardiovascular system by modeling the instantaneous RR mean within a inhomogeneous point-process modeling, taking into account up to the cubic nonlinear terms:

hereinafter called Nonlinear Autoregressive with Laguerre expansion (NARL) model, with g0,{g1(i)}, {g2(i,j)}, and {g3(i,j,k)} the Laguerre coefficients7,15.
When α = 0 the filter output becomes lj(n) = (−1)jy(n − j − 1) and the NARL model corresponds, apart for the sign, to the finite nonlinear autoregressive model (NAR) model in (4), whereas for α ≠ 0 the instantaneous RR mean is theoretically defined as follows:

thus having long-term (infinite) memory, and  . The use of the derivative RR series is aimed at improving model fits in highly non-stationary environments108.
. The use of the derivative RR series is aimed at improving model fits in highly non-stationary environments108.
Moreover, using the point-process modeling, as  is defined in a continuous-time fashion, we can obtain an instantaneous R–R mean estimate at a very fine timescale (with an arbitrarily small bin size Δ), which requires no interpolation between the arrival times of two beats. Given the proposed parametric model, the nonlinear indices of the HR and HRV will be defined as a time-varying function of the parameters ξ(t) = [θ(t), g0(t), g1(0, t),..., g1(P, t), g2(0, 0, t),..., g2(Q, Q, t), g3(0, 0, 0, t),..., g3(K, K, K, t)].
is defined in a continuous-time fashion, we can obtain an instantaneous R–R mean estimate at a very fine timescale (with an arbitrarily small bin size Δ), which requires no interpolation between the arrival times of two beats. Given the proposed parametric model, the nonlinear indices of the HR and HRV will be defined as a time-varying function of the parameters ξ(t) = [θ(t), g0(t), g1(0, t),..., g1(P, t), g2(0, 0, t),..., g2(Q, Q, t), g3(0, 0, 0, t),..., g3(K, K, K, t)].
A local maximum likelihood method76,109,110 is used to estimate the time-varying parameter set x (t). We use a Newton-Raphson procedure to maximize the local log-likelihood and compute the local maximum-likelihood estimate of x (t)109. Because there is significant overlap between adjacent local likelihood intervals, we start the Newton-Raphson procedure at t with the previous local maximum-likelihood estimate at time t − Δ in which Δ define how much the local likelihood time interval is shifted to compute the next parameter update. We determined the optimal orders {p,q,k} using the Kolmogorov-Smirnov (KS) statistic in the post hoc analysis76.
Calculation of the Complexity Variability Index
In our case, the matrix Y(t), described in section 5, corresponds to the Jacobian of the j-dimensional system of the NARL model parameters, where j is the value of the largest lag in the model6. Therefore, given the NARL model reported in (7) and using proper transformations7, it is possible to obtain an M-dimensional state space canonical representation:

where F(⋅) arises directly from (8).
The estimation of the LEs is performed at each time t from the corresponding time-varying vector of parameters, ξ(t). We define the first LE (λ1(t)) as the instantaneous dominant Lyapunov exponent (IDLE). In this paper, starting from each IDLE series, the time-varying information was condensed by means of the central tendency of the feature distribution, quantified as median (IDLE). In addition, we used the Median Absolute Deviation (MAD) with MAD(X) = |X − Median(X)|), of the IDLE to define the complexity variability index CVIDLE.
Additional Information
How to cite this article: Valenza, G. et al. Complexity Variability Assessment of Nonlinear Time-Varying Cardiovascular Control. Sci. Rep. 7, 42779; doi: 10.1038/srep42779 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
U. Rajendra Acharya, K. Paul Joseph, N. Kannathal, C. Lim & J. Suri, Heart rate variability: a review. Medical and Biological Engineering and Computing 44, no. 12, pp. 1031–1051 (2006).
P. C. Ivanov, L. N. Amaral, A. L. Goldberger & H. E. Stanley Stochastic feedback and the regulation of biological rhythms. EPL (Europhysics Letters) 43, no. 4, p. 363 (1998).
C. Schäfer, M. G. Rosenblum, J. Kurths & H.-H. Abel Heartbeat synchronized with ventilation. Nature 392, pp. 239–240 (1998).
K. Sunagawa, T. Kawada & T. Nakahara Dynamic nonlinear vago-sympathetic interaction in regulating heart rate. Heart and Vessels 13, no. 4, pp. 157–174 (1998).
G. B. West, J. H. Brown & B. J. Enquist A general model for the origin of allometric scaling laws in biology. Science 276, no. 5309, pp. 122–126 (1997).
A. Armoundas et al. A stochastic nonlinear autoregressive algorithm reflects nonlinear dynamics of heart-rate fluctuations. Annals of biomedical engineering 30, no. 2, pp. 192–201 (2002).
G. Valenza, L. Citi & R. Barbieri Estimation of instantaneous complex dynamics through lyapunov exponents: a study on heartbeat dynamics. PloS one 9, no. 8, p. e105622 (2014).
G. Valenza, L. Citi, E. P. Scilingo & R. Barbieri Inhomogeneous point-process entropy: An instantaneous measure of complexity in discrete systems. Physical Review E 89, no. 5, p. 052803 (2014).
A. Voss, S. Schulz, R. Schroeder, M. Baumert & P. Caminal Methods derived from nonlinear dynamics for analysing heart rate variability. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 367, no. 1887, pp. 277–296 (2009).
L. Glass Dynamical disease: Challenges for nonlinear dynamics and medicine. Chaos: An Interdisciplinary Journal of Nonlinear Science 25, no. 9, p. 097603 (2015).
A. L. Goldberger, C.-K. Peng & L. A. Lipsitz What is physiologic complexity and how does it change with aging and disease? Neurobiology of aging 23, no. 1, pp. 23–26 (2002).
L. Glass Introduction to controversial topics in nonlinear science: Is the normal heart rate chaotic? Chaos: An Interdisciplinary Journal of Nonlinear Science 19, no. 2, p. 028501 (2009).
J. K. Kanters, M. V. Højgaard, E. Agner & N.-H. Holstein-Rathlou, Short-and long-term variations in non-linear dynamics of heart rate variability. Cardiovascular Research 31, no. 3, pp. 400–409 (1996).
O. Stiedl & M. Meyer Fractal dynamics in circadian cardiac time series of corticotropin-releasing factor receptor subtype-2 deficient mice. Journal of mathematical biology 47, no. 2, pp. 169–197 (2003).
G. Valenza, L. Citi, E. P. Scilingo & R. Barbieri Point-process nonlinear models with laguerre and volterra expansions: Instantaneous assessment of heartbeat dynamics. Signal Processing, IEEE Transactions On 61, no. 11, pp. 2914–2926 (2013).
G. Wu et al. Chaotic signatures of heart rate variability and its power spectrum in health, aging and heart failure. PloS one 4, no. 2, p. e4323 (2009).
D. E. Vaillancourt, J. J. Sosnoff & K. M. Newell Age-related changes in complexity depend on task dynamics. Journal of Applied Physiology 97, no. 1, pp. 454–455 (2004).
D. T. Schmitt & P. C. Ivanov Fractal scale-invariant and nonlinear properties of cardiac dynamics remain stable with advanced age: a new mechanistic picture of cardiac control in healthy elderly. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology 293, no. 5, pp. R1923–R1937 (2007).
D. T. Schmitt, P. K. Stein & P. C. Ivanov Stratification pattern of static and scale-invariant dynamic measures of heartbeat fluctuations across sleep stages in young and elderly. Biomedical Engineering, IEEE Transactions on 56, no. 5, pp. 1564–1573 (2009).
A. Bunde et al. Correlated and uncorrelated regions in heart-rate fluctuations during sleep. Physical Review Letters 85, no. 17, p. 3736 (2000).
P. C. Ivanov et al. Scaling behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature 383, no. 6598, pp. 323–327 (1996).
G. Valenza, M. Nardelli, G. Bertschy, A. Lanata & E. Scilingo, Mood states modulate complexity in heartbeat dynamics: A multiscale entropy analysis. EPL (Europhysics Letters) 107, no. 1, p. 18003 (2014).
Y. Yamamoto & R. L. Hughson On the fractal nature of heart rate variability in humans: effects of data length and beta-adrenergic blockade. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology 266, no. 1, pp. R40–R49 (1994).
M. Costa, A. Goldberger & C. Peng Multiscale entropy analysis of complex physiologic time series. Physical Review Letters 89, no. 6, p. 68102 (2002).
K. Chon, J. Kanters, R. Cohen & N. Holstein-Rathlou Detection of chaotic determinism in time series from randomly forced maps. Physica D: Nonlinear Phenomena 99, no. 4, pp. 471–486 (1997).
J. Richman & J. Moorman Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology- Heart and Circulatory Physiology 278, no. 6, p. H2039 (2000).
G. Valenza, L. Citi & R. Barbieri Instantaneous nonlinear assessment of complex cardiovascular dynamics by laguerre-volterra point process models. In Engineering in Medicine and Biology Society (EMBC), 2013 35th Annual International Conference of the IEEE. 1em plus 0.5em minus 0.4em IEEE. pp. 6131–6134 (2013).
G. Valenza et al. Assessment of spontaneous cardiovascular oscillations in parkinson’s disease. Biomedical Signal Processing and Control 26, pp. 80–89 (2016).
P. J. Schwartz & G. M. De Ferrari Sympathetic–parasympathetic interaction in health and disease: abnormalities and relevance in heart failure. Heart failure reviews 16, no. 2, pp. 101–107 (2011).
V. L. Roger Epidemiology of heart failure. Circulation research 113, no. 6, pp. 646–659 (2013).
U. R. Acharya, K. P. Joseph, N. Kannathal, C. M. Lim & J. S. Suri Heart rate variability: a review. Medical and biological engineering and computing 44, no. 12, pp. 1031–1051 (2006).
H. V. Huikuri et al. Fractal correlation properties of RR interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation 101, no. 1, pp. 47–53 (2000).
P. C. Ivanov et al. Multifractality in human heartbeat dynamics. Nature 399, no. 6735, pp. 461–465 (1999).
K. Kiyono, J. Hayano, E. Watanabe, Z. R. Struzik & Y. Yamamoto Non-gaussian heart rate as an independent predictor of mortality in patients with chronic heart failure. Heart Rhythm 5, no. 2, pp. 261–268 (2008).
T. Mäkikallio et al. Fractal analysis and time- and frequency-domain measures of heart rate variability as predictors of mortality in patients with heart failure. Am. J. Cardiol. 87, pp. 178–182 (2001).
J. Nolan and et al. Prospective study of heart rate variability and mortality in chronic heart failure: Results of the united kingdom heart failure evaluation and assessment of risk trial. Circulation 98, pp. 1510–1516 (1998).
H. Wendt et al. Multiscale wavelet p-leader based heart rate variability analysis for survival probability assessment in chf patients. In Proc. Int. IEEE EMBS Conf., Chicago, USA, pp. 2809–2812 Aug. (2014).
J. Hayano et al. Increased non-gaussianity of heart rate variability predicts cardiac mortality after an acute myocardial infarction. Frontiers in Physiology 2, pp. 1–11 (2011).
R. Kessler et al. Lifetime and 12-month prevalence of dsm-iii-r psychiatric disorders in the united states: results from the national comorbidity survey. Archives of general psychiatry 51, no. 1, p. 8 (1994).
S. Pini et al. Prevalence and burden of bipolar disorders in european countries. European Neuropsychopharmacology 15, no. 4, pp. 425–434 (2005).
A. Andreazza et al. Oxidative stress markers in bipolar disorder: a meta-analysis. Journal of affective disorders 111, no. 2, pp. 135–144 (2008).
E. Vieta, M. Reinares & A. Rosa Staging bipolar disorder. Neurotoxicity research 19, no. 2, pp. 279–285 (2011).
G. Iverson et al. A new potential marker for abnormal cardiac physiology in depression. Journal of behavioral medicine 28, no. 6, pp. 507–511 (2005).
H. Stampfer The relationship between psychiatric illness and the circadian pattern of heart rate. Australasian Psychiatry 32, no. 2, pp. 187–198 (1998).
J. Taillard, P. Lemoine, P. Boule, M. Drogue & J. Mouret, Sleep and heart rate circadian rhythm in depression: The necessity to separate. Chronobiology International 10, no. 1, pp. 63–72 (1993).
J. Taillard, P. Sanchez, P. Lemoine & J. Mouret, Heart rate orcadian rhythm as a biological marker of desynchronization in major depression: A methodological and preliminary report. Chronobiology international 7, no. 4, pp. 305–316 (1990).
M. W. Agelink, C. Boz, H. Ullrich & J. Andrich Relationship between major depression and heart rate variability.: Clinical consequences and implications for antidepressive treatment. Psychiatry research 113, no. 1, pp. 139–149 (2002).
R. M. Carney, K. E. Freedland, G. E. Miller & A. S. Jaffe Depression as a risk factor for cardiac mortality and morbidity: a review of potential mechanisms. Journal of psychosomatic research 53, no. 4, pp. 897–902 (2002).
S. J. Leistedt et al. Decreased neuroautonomic complexity in men during an acute major depressive episode: analysis of heart rate dynamics. Translational psychiatry 1, no. 7, p. e27 (2011).
S. Schulz, M. Koschke, K.-J. Bär & A. Voss The altered complexity of cardiovascular regulation in depressed patients. Physiological measurement 31, no. 3, p. 303 (2010).
G. Valenza et al. Nonlinear digital signal processing in mental health: characterization of major depression using instantaneous entropy measures of heartbeat dynamics. Frontiers in physiology 6, pp. 1–8 (2015).
G. Valenza, L. Citi, C. Gentili, A. Lanata, E. P. Scilingo & R. Barbieri . Point-Process Nonlinear Autonomic Assessment of Depressive States in Bipolar Patients, Methods of Information in Medicine. 53, no. 4, pp. 296–302 (2014).
A. C. Yang & S.-J. Tsai Is mental illness complex? From behavior to brain. Progress in Neuro-Psychopharmacology and Biological Psychiatry 45, pp. 253–257 (2013).
E. M. Sledjeski, B. Speisman & L. C. Dierker Does number of lifetime traumas explain the relationship between ptsd and chronic medical conditions? Answers from the national comorbidity survey-replication (ncs-r). Journal of behavioral medicine 31, no. 4, pp. 341–349 (2008).
S. Mohsenin & V. Mohsenin Diagnosis and management of sleep disorders in posttraumatic stress disorder: A review of the literature. The primary care companion for CNS disorders. doi: 10.4088/PCC.14r01663 16, no. 6 (2014).
H. Cohen et al. Autonomic dysregulation in panic disorder and in post-traumatic stress disorder: application of power spectrum analysis of heart rate variability at rest and in response to recollection of trauma or panic attacks. Psychiatry research 96, no. 1, pp. 1–13 (2000).
H.-A. Chang et al. Decreased cardiac vagal control in drug-nave patients with posttraumatic stress disorder. Psychiatry investigation 10, no. 2, pp. 121–130 (2013).
A. P. Association et al. Diagnostic and statistical manual of mental disorders. 4th text revision ed. Washington, DC: American Psychiatric Association, pp. 553–557 (2000).
B. Farina, S. Dittoni, S. Colicchio, E. Testani, A. Losurdo et al. Heart rate and heart rate variability modification in chronic insomnia patients. Behavioral sleep medicine 12, no. 4, pp. 290–306 (2014).
C. S. Ulmer, P. S. Calhoun, J. D. Edinger, H. R. Wagner & J. C. Beckham Sleep disturbance and baroreceptor sensitivity in women with posttraumatic stress disorder. Journal of traumatic stress 22, no. 6, pp. 643–647 (2009).
C. Streeter, P. Gerbarg, R. Saper, D. Ciraulo & R. Brown Effects of yoga on the autonomic nervous system, gamma-aminobutyric-acid, and allostasis in epilepsy, depression, and post-traumatic stress disorder. Medical hypotheses 78, no. 5, pp. 571–579 (2012).
B. S. Cheema et al. Effect of an office worksite-based yoga program on heart rate variability: outcomes of a randomized controlled trial. BMC complementary and alternative medicine 13, no. 1, p. 82 (2013).
M. E. Papp, P. Lindfors, N. Storck & P. E. Wändell Increased heart rate variability but no effect on blood pressure from 8 weeks of hatha yoga–a pilot study. BMC research notes 6, no. 1, p. 59 (2013).
C.-K. Peng et al. Heart rate dynamics during three forms of meditation. International journal of cardiology 95, no. 1, pp. 19–27 (2004).
L. Stankovic Transforming trauma: a qualitative feasibility study of integrative restoration (irest) yoga nidra on combat-related post-traumatic stress disorder. International journal of yoga therapy 21, no. 1, pp. 23–37 (2011).
B. A. van der Kolk et al. Original research yoga as an adjunctive treatment for posttraumatic stress disorder: A randomized controlled trial. J Clin Psychiatry 75, no. 6, pp. e559–e565 (2014).
L. S. Forno Neuropathology of parkinson’s disease. Journal of Neuropathology & Experimental Neurology 55, no. 3, pp. 259–272 (1996).
C. Magerkurth, R. Schnitzer & P. D. D. S. Braune Symptoms of autonomic failure in parkinsonos disease: prevalence and impact on daily life. Clinical Autonomic Research 15, no. 2, pp. 76–82 (2005).
M. Asahina, E. Vichayanrat, D. A. Low, V. Iodice & C. J. Mathias Autonomic dysfunction in parkinsonian disorders: assessment and pathophysiology. Journal of Neurology, Neurosurgery & Psychiatry 84, no. 6, pp. 674–680 (2013).
P. M. Netten, K. de Vos, M. W. Horstink & W. H. Hoefnagels Autonomic dysfunction in parkinson’s disease, tested with a computerized method using a finapres device. Clinical Autonomic Research 5, no. 2, pp. 85–89 (1995).
J. Senard et al. Prevalence of orthostatic hypotension in parkinsonos disease. Journal of Neurology, Neurosurgery & Psychiatry 63, no. 5, pp. 584–589 (1997).
K. Kiyono, J. Hayano, S. Kwak, E. Watanabe & Y. Yamamoto Non-gaussianity of low frequency heart rate variability and sympathetic activation: lack of increases in multiple system atrophy and parkinson disease. Frontiers in physiology 3, pp. 1–10 (2012).
T. Haapaniemi et al. Ambulatory ecg and analysis of heart rate variability in parkinson’s disease. Journal of neurology, neurosurgery & psychiatry 70, no. 3, pp. 305–310 (2001).
M. Kallio et al. Comparison of heart rate variability analysis methods in patients with parkinson’s disease. Medical and Biological Engineering and Computing 40, no. 4, pp. 408–414 (2002).
A. Porta et al. Short-term complexity indexes of heart period and systolic arterial pressure variabilities provide complementary information. Journal of Applied Physiology 113, no. 12, pp. 1810–1820 (2012).
R. Barbieri, E. Matten, A. Alabi & E. Brown A point-process model of human heartbeat intervals: new definitions of heart rate and heart rate variability. American Journal of Physiology-Heart and Circulatory Physiology 288, no. 1, p. H424 (2005).
A. Goldberger et al. Physiobank, physiotoolkit, and physionet: Components of a new research resource for complex physiologic signals. Circulation 101, no. 23, p. e215 (2000).
D. S. Baim et al. Survival of patients with severe congestive heart failure treated with oral milrinone. Journal of the American College of Cardiology 7, no. 3, pp. 661–670 (1986).
L. Citi, E. N. Brown & R. Barbieri A real-time automated point-process method for the detection and correction of erroneous and ectopic heartbeats. Biomedical Engineering, IEEE Transactions on 59, no. 10, pp. 2828–2837 (2012).
C. Peng, S. Havlin, H. Stanley & A. Goldberger Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos An Interdisciplinary Journal of Nonlinear Science 5, no. 1, p. 82 (1995).
W. W. Zung A self-rating depression scale. Archives of general psychiatry 12, no. 1, pp. 63–70 (1965).
T. Morgenthaler et al. Practice parameters for the psychological and behavioral treatment of insomnia: an update. an american academy of sleep medicine report. Sleep 29, no. 11, p. 1415 (2006).
F. W. Weathers, T. M. Keane & J. R. Davidson Clinician-administered ptsd scale: a review of the first ten years of research. Depression and anxiety 13, no. 3, pp. 132–156 (2001).
W. Gibb & A. Lees The relevance of the lewy body to the pathogenesis of idiopathic parkinson’s disease. Journal of Neurology, Neurosurgery & Psychiatry 51, no. 6, pp. 745–752 (1988).
M. D. S. T. F. On Rating Scales for Parkinson’s Disease et al. The unified parkinson’s disease rating scale (updrs): status and recommendations. Movement disorders: official journal of the Movement Disorder Society 18, no. 7, p. 738 (2003).
M. M. Hoehn & M. D. Yahr, Parkinsonism: onset, progression, and mortality. Neurology 50, no. 2, pp. 318–318 (1998).
L. Li, Z. Jin & J. Li Periodic solutions in a herbivore-plant system with time delay and spatial diffusion. Applied Mathematical Modelling 40, no. 7, pp. 4765–4777 (2016).
G.-Q. Sun, S.-L. Wang, Q. Ren, Z. Jin & Y.-P. Wu Effects of time delay and space on herbivore dynamics: linking inducible defenses of plants to herbivore outbreak. Scientific Reports 5 (2015).
H. Braak & K. Del Tredici Nervous system pathology in sporadic parkinson disease. Neurology 70, no. 20, pp. 1916–1925 (2008).
H. Braak, E. Ghebremedhin, U. Rüb, H. Bratzke & K. Del Tredici Stages in the development of parkinsonos disease-related pathology. Cell and tissue research 318, no. 1, pp. 121–134 (2004).
M. Asahina, E. Vichayanrat, D. A. Low, V. Iodice & C. J. Mathias Autonomic dysfunction in parkinsonian disorders: assessment and pathophysiology. Journal of Neurology, Neurosurgery & Psychiatry pp. jnnp–2012 (2012).
S. Jain & D. S. Goldstein Cardiovascular dysautonomia in parkinson disease: from pathophysiology to pathogenesis. Neurobiology of disease 46, no. 3, pp. 572–580 (2012).
K. Kimpinski et al. The role of autonomic testing in the differentiation of parkinson’s disease from multiple system atrophy. Journal of the neurological sciences 317, no. 1, pp. 92–96 (2012).
A. Lipp et al. Prospective differentiation of multiple system atrophy from parkinson disease, with and without autonomic failure. Archives of neurology 66, no. 6, pp. 742–750 (2009).
K. H. Brodersen, C. S. Ong, K. E. Stephan & J. M. Buhmann The balanced accuracy and its posterior distribution. In Pattern recognition (ICPR), 2010 20th international conference on. 1em plus 0.5 em minus 0.4 em IEEE, pp. 3121–3124 (2010).
L. Dieci, R. Russell & E. Van Vleck On the computation of lyapunov exponents for continuous dynamical systems. SIAM journal on numerical analysis, pp. 402–423 (1997).
K. Geist, U. Parlitz & W. Lauterborn Comparison of different methods for computing lyapunov exponents. Prog. Theor. Phys 83, no. 5, pp. 875–893 (1990).
J. Holzfuss & U. Parlitz Lyapunov exponents from time series. Lyapunov Exponents pp. 263–270 (1991).
M. Akay Nonlinear Biomedical Signal Processing Vol. II: Dynamic Analysis and Modeling. 1em plus 0.5em minus 0.4em Wiley-IEEE Press (2000).
M. Korenberg Parallel cascade identification and kernel estimation for nonlinear systems. Annals of biomedical engineering 19, no. 4, pp. 429–455 (1991).
M. Korenberg & L. Paarmann Orthogonal approaches to time-series analysis and system identification. Signal Processing Magazine, IEEE 8, no. 3, pp. 29–43 (1991).
V. Marmarelis Identification of nonlinear biological system using laguerre expansions of kernels. Ann. Biomed. Eng. 21, pp. 573–589 (1993).
D. Daley & D. Vere-Jones An introduction to the theory of point processes, vol. I: Elementary Theory and Methods. 1em plus 0.5em minus 0.4em Springer Verlag, 2 (2003).
R. Barbieri & E. Brown Analysis of heartbeat dynamics by point process adaptive filtering. Biomedical Engineering, IEEE Transactions on 53, no. 1, pp. 4–12 (2006).
Z. Chen, E. Brown & R. Barbieri Assessment of autonomic control and respiratory sinus arrhythmia using point process models of human heart beat dynamics. Biomedical Engineering, IEEE Transactions on 56, no. 7, pp. 1791–1802 (2009).
Z. Chen, E. Brown & R. Barbieri Characterizing nonlinear heartbeat dynamics within a point process framework. Biomedical Engineering, IEEE Transactions on 57, no. 6, pp. 1335–1347 (2010).
Z. Chen and others. Dynamic assessment of baroreflex control of heart rate during induction of propofol anesthesia using a point process method. Annals of biomedical engineering pp. 1–17 (2011).
C. Granger & R. Joyeux An introduction to long-memory time series models and fractional differencing. Journal of time series analysis 1, no. 1, pp. 15–29 (1980).
C. Loader Local regression and likelihood. 1em plus 0.5 em minus 0.4 em Springer Verlag (1999).
R. Tibshirani & T. Hastie Local likelihood estimation. Journal of the American Statistical Association pp. 559–567 (1987).
Acknowledgements
The research leading to these results has received partial funding from the Department of Anesthesia, Critical Care & Pain Medicine, Massachusetts General Hospital, and Harvard Medical School, Boston, MA, USA, and the United States National Institutes of Health, National Center for Complementary and Alternative Medicine, Project #5F32AT006092, and European Union Seventh Framework Programme FP7/2007-2013 under Grant No. 601165 of the project “WEARHAP”.
Author information
Authors and Affiliations
Contributions
G.V., L.C. and R.B. devised the methodology and developed the software; J.N.T. defined the experimental setup and acquired experimental data from patients with P.T.S.D. and insomnia; R.G.G. defined the experimental setup and acquired experimental data from patients with M.D.D.; N.T. defined the experimental setup and acquired experimental data from patients with P.D.; G.V., L.C., N.T. and R.B. analyzed data; All authors wrote the manuscript and approved the final text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Valenza, G., Citi, L., Garcia, R. et al. Complexity Variability Assessment of Nonlinear Time-Varying Cardiovascular Control. Sci Rep 7, 42779 (2017). https://doi.org/10.1038/srep42779
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep42779
This article is cited by
-
Assessing Autonomic Function from Electrodermal Activity and Heart Rate Variability During Cold-Pressor Test and Emotional Challenge
Scientific Reports (2020)
-
Enhanced flow-motion complexity of skin microvascular perfusion in Sherpas and lowlanders during ascent to high altitude
Scientific Reports (2019)
-
The application of Lempel-Ziv and Titchener complexity analysis for equine telemetric electrocardiographic recordings
Scientific Reports (2019)
-
Detecting abnormality in heart dynamics from multifractal analysis of ECG signals
Scientific Reports (2017)
-
MEIS1 variant as a determinant of autonomic imbalance in Restless Legs Syndrome
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.