Abstract
Our experiment shows that the thermal emission of phonon can be controlled by magnetic resonance (MR) mode in a metasurface (MTS). Through changing the structural parameter of metasurface, the MR wavelength can be tuned to the phonon resonance wavelength. This introduces a strong coupling between phonon and MR, which results in an anticrossing phonon-plasmons mode. In the process, we can manipulate the polarization and angular radiation of thermal emission of phonon. Such metasurface provides a new kind of thermal emission structures for various thermal management applications.
Similar content being viewed by others
Introduction
In recent years, the research interest of thermal emission in the infrared wavelength range is growing fast due to its important applications in thermaophotovoltaic (TPV) devices1, radiative cooling2,3, incandescent source4, near-field heat transfer5, and infrared spectroscopy6. Up to now, various structures and systems have been used to control thermal emission, such as gratings7,8, nanoantennas9,10, photonic crystals11, surface plasmons12,13,14, metamaterials15,16,17 and metasurfaces (MTS)18,19. Some properties of thermal emission, such as the emission bandwidth20, coherent properties7 and dynamics switching21,22 are reported to be controlled in these systems.
In physics, thermal emission is caused by the elementary excitations in materials, such as phonon in polar dielectric7,18, exciton in semiconductor20,21, and plasmons in metals. Up to now, most of related published papers investigated thermal emission produced by only one elementary excitation. There are few work to explore the simultaneous contribution of different elementary excitations to thermal emission. In the infrared frequencies, phonons, the quantum emitter as the ‘fingerprints’ of materials characterizing the vibrations of constitution atoms, are the eigen states of materials. And manipulating thermal emission of phonons is important in electronics, optics, bimolecular, and integrated circuits23,24,25,26. However, the thermal emission of phonon is usually weak and hard to be controlled. On the other hand, plasmons of different metallic nanostructures can be easily controlled through structural designing. In this work, we will show that thermal emission of phonon can be well controlled through phonon-plasmons coupling in magnetic metasurfaces.
Compared with bulk metamaterials, 2-D MTS are more easily fabricated and the optical loss can be suppressed greatly27,28,29. Up to now, MTS has been widely used in anomalous negative refraction30,31,32, beam shaping33,34,35, surface wave excitation18,36,37, hologram38,39, reflection phase40, mathematical operation41, polarization controlling42,43,44,45,46,47, functional mirrors48,49, nonlinear devices50,51, invisible cloaking52 and subwavelength imaging53. Among different metasurface resonance unit designs, metal/insulation/metal (MIM) sandwich resonator has very strong local MR mode and is easily fabricated. MIM resonator has been used in magnetic field enhancement54, magnetic polariton55, magnetic plasmon waveguide56, magnetic nanolaser57, perfect absorber58,59, nonlinear generations60, negative optical pressure61 and dipolar response62.
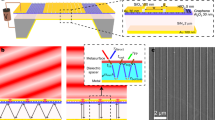
In this work, the MIM metasurface is used to control the emission of phonons. Using high temperature synthesized amorphous SiO2, we designed and fabricated the Al/SiO2/Al magnetic MTS with Al grating arrayed on the SiO2/Al film (see Fig. 1(a)). The MTS grating width is adjusted to produce the strong coupling between MR and phonon inside SiO2. Differ from the precedent studies about the active optical phonons of silica at λ = 10 μm63, here, we focus our attention on the relatively inactive optical phonon at λ = 12.5 um. The absorption and thermal emission spectra were measured by Fourier-transform infrared (FTIR) spectrometer in the wavelength range 11–16 μm. The anticrossing features in the spectra denoted that strong coupling occurred between phonon and magnetic resonance, albeit with big difference in radiation intensity of these two resonant states. Using commercial software FDTD solution and coupled mode theory64, we analysed the coupling physical mechanism. The theoretical calculations agree with experiments quite well.
Experiment result
The Al/SiO2/Al magnetic MTS were fabricated on Si wafer. In fabrication, Al film of thickness 150 nm was deposited on pre-cleaned Si wafer by electron beam evaporation. Amorphous silica films (500nm) were synthesized by plasma enhanced chemical evaporation (PECVD) at temperature 300 °C on the Al film, and subsequent in situ annealing was performed for 10 hours. An Al grating was fabricated on the amorphous SiO2 films by ultraviolent photolithography and subsequent lift-off. The schematic view in Fig. 1(a) exhibits both structure and material information. In experiment, the period and height of grating was fixed as Λ = 6.5 μm and h = 0.05 μm, the width d can be changed through tuning the exposure time in the course of photolithography. Figure 1(b) shows the morphology characterized by a commercial scanning electron microscopy (SEM) of sample with width d = 2.8 μm. The total thickness of MTS is 0.7 micron which is much smaller than the working wavelength range 11–16 μm.
We measured thermal emission and absorption of sample with FTIR spectrometer. The scanning wavelength range is 11–16 μm. At the same time, we also used FDTD method to calculate the absorption of structures and compare the results with experiment. Firstly, we investigated the MR and phonon separately without coupling effect between them. Figure 2(a) gives the thermal emission and absorption of SiO2/Al. Without grating, there is no MR and only phonon is found. Both the measured absorption (blue triangle symbolic line) and thermal emission (red brackets symbolic line) spectra show one faint and broad peak at 12.5 um, along with the measured ones was the simulated absorption spectrum by FDTD method as denoted by the black triangle symbolic line in Fig. 2(a). The data of SiO2 were referred to ref. 65. The agreement between measured and calculated absorption spectra consolidated our material research base and method reliability. Figure 2(b) gives the calculated absorption spectrum of MTS, where the refraction index of SiO2 n = 1.47 was used in simulation. In the simulation, the MTS grating periodic is Λ = 6.5 μm and width d = 3 μm under TM polarization (electric field perpendicular to the grating), as we can see, only MR resonance peak is found at 12.5 um. Compared with phonon, the absorption of MR is much stronger which is attributed to the strong magnetic resonance mode54,55,56,57,58,59,60,61. Here, the MR mode can be regarded as a kind of plasmonic cavity mode.
For the MTS given in Fig. 1, its thermal emission shows very strong polarization dependence. Figure 2(c) gives TE polarized emission (E field parallel to grating strip). Both the thermal emission and absorption spectra of the MTS in Fig. 2(c) show the similar peculiarity as phonon at 12.5 um given in Fig. 2(a). Here, MR cannot be excited, and only phonon contribute to the emission and absorption. Therefore, these curves are very like those in Fig. 2(a). The calculation agree with experiment quite well.
On the other hand, for TM polarized emission of MTS (E field perpendicular to grating strip) in Fig. 2(d), it is quite different from TE emission in Fig. 2(a). Here, phonon resonance can be still found at the wavelength 12.5 μm. At the same time, the MR can be excited at the same wavelength. This makes MR and phonon overlapped with each other. As a result, the strong coupling occurs between MR and phonon, which will produce two resonance peaks in the curve. In Fig. 2(d), two prominent peaks are obtained at wavelength 11.8 μm and 13.29 μm, which lie on the two sides of 12.5 μm, and are different from peaks of the phonon (Fig. 2(a)) and the MR (Fig. 2(b)). In simulations, with including phonon of SiO2 in the program, the simulated absorption spectra of sample with periodic Λ = 6.5 μm and width d = 3 μm also features two pronounced peaks as denoted by the black triangle symbolic line given in Fig. 2(d). The simulated and measured absorption spectra agree well, which are both in accordance with the thermal emission spectrum. In the following, we will provide a theory model to explain the coupling mechanism.
The absorption and emission polarization dependence of sample can be described by the ratio of TM over TE: P = ITM/ITE. For SiO2/Al film, there is no polarization dependence for phonon mode and P = 1. While, for MTS, strong anisotropic property is demonstrated for both theoretical and experimental results as shown in Fig. 3 (experimental result: red line, and theoretical result: blue line). We can see P is very large for the wavelength around the two resonance peaks, while it will approximate unit when the wavelength is far away from the peaks. It means that the polarization dependence is caused by the strong resonance mode of MTS. In the figure, P amounted to forty-fold in calculations, and only about five-fold in experiment. This large discrepancy between theory and experiment is caused by the defects of samples and the aberrations in adjusting the polarizations. Despite all this, the modified anisotropic thermal emission of phonon was still clearly discerned. Beside polarization dependence, the angular dependence of emission and absorption is also changed by MTS. Figure 4(a) and (c) give the results of SiO2/Al, in which only phonon exists. As given in ref. 63, phonon near 12.5 μm includes both LO and TO pair mode in the range 1160–1200 cm−1. Due to Berreman effect of LO phonon in thin film66, the interaction between phonon and light will be enhanced by increasing the angle. Then, as shown in Fig. 4(a) and (c), the absorption and thermal emission of SiO2/Al film became stronger at larger emission or incident angle. While for MTS in Fig. 4(b) and (d), both the two resonance modes obtain their maximum absorption and emission efficiency at normal angle. For the mode at wavelength 11.8 μm, the absorption and emission do not change much with angle. While, for the mode at wavelength 13.29 μm, the emission and absorption is reduced greatly around 50 degree. This is caused by strong Bragg scattering at this angle.
In above discussion, we know that the coupling between phonon and MR will produce two resonance peaks. In physics, it is like the normal mode splitting of atoms in cavity67,68,69. By putting atom into high-finesse optical cavity, and tuning the parameters of the cavity, the spontaneous emission spectra of the atom featured anti-crossing line-shape, which was attributed to the strong coupling occurred between the atom and cavity. Actually, such mode splitting was also possibly for magnetic polariton structures55. In our system, if the MR can be regarded as a cavity and phonon as an atom, the two peaks can be seen as the result of mode splitting. Then if we tune the MR by changing structure parameter, it is possible to produce anti-crossing line-shape near the phonon resonance. For the MTS in Fig. 1(a), its MR resonance wavelength is dependent on the grating width d. Then we can tune MR through changing d. FDTD simulations were performed with varied grating width d of MTS. Figure 5(a) depicted the simulated absorption spectra versus the photon energy and the grating width d, which was changed from 2.6 to 3.6 μm. Pronounced anticrossing behaviour was demonstrated in the absorption spectra, indicating the presence of the strong coupling between MR and the phonon. In experiment, a series of samples with varied width d and fixed period Λ = 6.5 μm were synthesized through changing the exposure time in the process of photolithography. The measured thermal emission spectra of the varied width d grating were shown in Fig. 5(b), where the measurements were performed in normal angle under TM polarization. The pronounced anticrossing behaviour near phonon energy ω = 0.1 ev (λ = 12.5 μm) was also demonstrated in both Fig. 5(a) and (b). The excellent agreement between simulation and experiment render the strong coupling convincible in this system.
Theory
In this part, a coupled mode theory64 is established to describe the physical mechanism of the strong coupling between the MR and the phonon. Firstly, let’s recur to the common equations that describe two coupled oscillators as:

where μ1, μ2 are the displacements of oscillators under excitation, respectively, and g1, g2 are coupling factor between oscillators and incident field, κ is the coupling factor between the two oscillators64. δ is the resonance frequency difference between μ1 and μ2. γ1 and γ2 are dissipation losses of oscillators μ1, μ2, respectively. Here, we choose oscillator μ2 as the phonon, with inherent resonant frequency ω0. And the MR oscillator μ1 can be manipulated through changing the parameters of the MTS. The Hamiltonian of this two oscillators system can be presented as:

Due to the coupling term in Hamiltonian, the mode splitting happens and the two eigen frequencies can be obtained as:


When the MR resonant frequency is near the phonon frequency ω = 0.1 ev, namely, δ ≈ 0, the strong coupling may occur if κ > > (γ1−γ2)2 67,68,69, and the coupled system has two eigen energies, the normal mode splits into two modes, and thus two peaks will be found in absorption spectra.
Here, the mode splitting is like the Rabi splitting of atom in cavity and the Rabi frequency is67,68,69:

Based on the equation (3), the eigen frequencies of the MTS with varied grating width were numerically calculated, where the parameters of SiO2 phonon γ2 = 0.65254(ev) were fitted from the Lorentz formulation. Figure 6 displays the eigen-wavelength versus the grating width d from coupled mode theory (the blanket triangles) and FDTD simulation (the solid red dots). The green dotted line in Fig. 6 indicates the phonon resonance wavelength, and the purple dotted line depicts the MR wavelength varied with the grating width, the error bar gave out the difference value between them and the experiment results. It is evident that the coupled mode theory calculation, the FDTD simulation and the experiment agrees quite well. All the three spectra feature anticrossing characterization. The narrowest frequency is located rightly at the phonon resonant frequency, ω = 0.1 ev, with γ1 = 1.06896(ev), and thus the detuning δ = 0. Substitute these parameters into formula (4), the coupling coefficient can be obtained as κ = 0.65265(ev). Clearly, κ2 >>(γ1−γ2)2, satisfies the strong coupling condition67,68,69. Substituting these parameters into Rabi splitting energy band formula (5)  67,70,71, and we get the Rabi splitting band gap in the anisotropic magnetic MTS as ħΩrabi = 1.237(ev). Hitherto, from the excellent agreement between simulation and experiment results, we conclude that the thermal emission of SiO2 phonon at ω = 0.1 ev can be controlled by MTS.
67,70,71, and we get the Rabi splitting band gap in the anisotropic magnetic MTS as ħΩrabi = 1.237(ev). Hitherto, from the excellent agreement between simulation and experiment results, we conclude that the thermal emission of SiO2 phonon at ω = 0.1 ev can be controlled by MTS.
Summary
In this work, we use MTS to control the thermal emission of phonon. The emission peak, polarization and radiation angle can be well manipulated in the process. A coupled mode theory is established to calculate the mode splitting and anti-crossing effect, which agrees with experiment well. In this work, we only consider the phonon inside SiO2. Actually, this method can be used to any other materials with different phonon wavelength as the MR can be flexibly tuned to any wavelength. If the fabrication is improved and the MTS have larger resonance Q factor, the plasmon-phonon coupling can be further enhanced. In the future, it can be anticipated that MTS will have many other interesting applications in thermal emission devices.
Additional Information
How to cite this article: Zhang, X. et al. Controlling thermal emission of phonon by magnetic metasurfaces. Sci. Rep. 7, 41858; doi: 10.1038/srep41858 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Lenert, A. et al. A nanophotonic solar thermophotovoltaic device. Nat Nanotechnol 9, 126–30 (2014).
Raman, A. P., Anoma, M. A., Zhu, L., Rephaeli, E. & Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 515, 540–544 (2014).
Shi, N. N. et al. Keeping cool: Enhanced optical reflection and radiative heat dissipation in Saharan silver ants. Science 349, 298–301 (2015).
Ilic, O. et al. Tailoring high-temperature radiation and the resurrection of the incandescent source. Nat Nano 11, 320–324 (2016).
St-Gelais, R., Zhu, L., Fan, S. & Lipson, M. Near-field radiative heat transfer between parallel structures in the deep subwavelength regime. Nat Nano 11, 515–519 (2016).
De Wilde, Y. et al. Thermal radiation scanning tunnelling microscopy. Nature 444, 740–743 (2006).
Greffet, J.-J. et al. Coherent emission of light by thermal sources. Nature 416, 61–64 (2002).
Dahan, N., Gorodetski, Y., Frischwasser, K., Kleiner, V. & Hasman, E. Geometric Doppler Effect: Spin-Split Dispersion of Thermal Radiation. Physical Review Letters 105, 136402 (2010).
Schuller, J. A., Taubner, T. & Brongersma, M. L. Optical antenna thermal emitters. Nat Photon 3, 658–661 (2009).
Ingvarsson, S., Klein, L. J., Au, Y.-Y., Lacey, J. A. & Hamann, H. F. Enhanced thermal emission from individual antenna-like nanoheaters. Optics Express 15, 11249–11254 (2007).
Luo, C., Narayanaswamy, A., Chen, G. & Joannopoulos, J. D. Thermal Radiation from Photonic Crystals: A Direct Calculation. Physical Review Letters 93, 213905 (2004).
Wang, C.-M. et al. Reflection and emission properties of an infrared emitter. Optics Express 15, 14673–14678 (2007).
Ye, Y.-H. et al. Coupling of surface plasmons between two silver films in a Ag/SiO2/Ag plasmonic thermal emitter with grating structure. Applied Physics Letters 93, 263106 (2008).
Mason, J. A., Smith, S. & Wasserman, D. Strong absorption and selective thermal emission from a midinfrared metamaterial. Applied Physics Letters 98, 241105 (2011).
Liu, X. et al. Taming the Blackbody with Infrared Metamaterials as Selective Thermal Emitters. Physical Review Letters 107, 045901 (2011).
Guo, Y., Cortes, C. L., Molesky, S. & Jacob, Z. Broadband super-Planckian thermal emission from hyperbolic metamaterials. Applied Physics Letters 101, 131106 (2012).
Lee, B. J., Wang, L. P. & Zhang, Z. M. Coherent thermal emission by excitation of magnetic polaritons between periodic strips and a metallic film. Optics Express 16, 11328–11336 (2008).
Shitrit, N. et al. Spin-Optical Metamaterial Route to Spin-Controlled Photonics. Science 340, 724–726 (2013).
Costantini, D. et al. Plasmonic Metasurface for Directional and Frequency-Selective Thermal Emission. Physical Review Applied 4, 014023 (2015).
De Zoysa, M. et al. Conversion of broadband to narrowband thermal emission through energy recycling. Nat Photon 6, 535–539 (2012).
Inoue, T., Zoysa, M. D., Asano, T. & Noda, S. Realization of dynamic thermal emission control. Nat Mater 13, 928–931 (2014).
Brar, V. W. et al. Electronic modulation of infrared radiation in graphene plasmonic resonators. Nat Commun 6 (2015).
Guo, J. & Lundstrom, M. Role of phonon scattering in carbon nanotube field-effect transistors. Applied Physics Letters 86, 193103 (2005).
Martin, A., Green, J. Z., Aihua Wang, Peter J. Reece. & Michael Gal. Efficient silicon light-emitting diodes. Nature 412, 805–808 (2001).
Frank Neubrech, Daniel Weber, Dominik Enders, Tadaaki Nagao & Annemarie Pucci. Antenna Sensing of Surface Phonon Polaritons. J. Phys. Chem. C 114, 7299–7301 (2010).
St-Gelais, R., Guha, B., Zhu, L., Fan, S. & Lipson, M. Demonstration of strong near-field radiative heat transfer between integrated nanostructures. Nano Lett 14, 6971–5 (2014).
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–7 (2011).
Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar Photonics with Metasurfaces. Science 339 (2013).
Meinzer, N., Barnes, W. L. & Hooper, I. R. Plasmonic meta-atoms and metasurfaces. Nat Photon 8, 889–898 (2014).
Aieta, F. et al. Out-of-Plane Reflection and Refraction of Light by Anisotropic Optical Antenna Metasurfaces with Phase Discontinuities. Nano Letters 12, 1702–1706 (2012).
Kang, M., Feng, T., Wang, H.-T. & Li, J. Wave front engineering from an array of thin aperture antennas. Optics Express 20, 15882–15890 (2012).
Pors, A., Albrektsen, O., Radko, I. P. & Bozhevolnyi, S. I. Gap plasmon-based metasurfaces for total control of reflected light. Scientific Reports 3, 2155 (2013).
Cai, X. et al. Integrated Compact Optical Vortex Beam Emitters. Science 338, 363–366 (2012).
Chen, X., Zhang, Y., Huang, L. & Zhang, S. Ultrathin Metasurface Laser Beam Shaper. Advanced Optical Materials 2, 978–982 (2014).
Cai, B. G., Li, Y. B., Jiang, W. X., Cheng, Q. & Cui, T. J. Generation of spatial Bessel beams using holographic metasurface. Optics Express 23, 7593–7601 (2015).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater 11, 426–431 (2012).
Lin, J. et al. Polarization-Controlled Tunable Directional Coupling of Surface Plasmon Polaritons. Science 340, 331–334 (2013).
Ni, X., Kildishev, A. V. & Shalaev, V. M. Metasurface holograms for visible light. Nat Commun 4 (2013).
Huang, L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun 4 (2013).
Pors, A. & Bozhevolnyi, S. I. Plasmonic metasurfaces for efficient phase control in reflection. Optics Express 21, 27438–27451 (2013).
Silva, A. et al. Performing Mathematical Operations with Metamaterials. Science 343, 160–163 (2014).
Zhao, Y., Belkin, M. A. & Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat Commun 3, 870 (2012).
Yu, N. et al. A Broadband, Background-Free Quarter-Wave Plate Based on Plasmonic Metasurfaces. Nano Letters 12, 6328–6333 (2012).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic Spin Hall Effect at Metasurfaces. Science 339, 1405–1407 (2013).
Li, G. X. et al. Spin-Enabled Plasmonic Metasurfaces for Manipulating Orbital Angular Momentum of Light. Nano Letters 13, 4148–4151 (2013).
Pfeiffer, C., Zhang, C., Ray, V., Guo, L. J. & Grbic, A. High Performance Bianisotropic Metasurfaces: Asymmetric Transmission of Light. Physical Review Letters 113, 023902 (2014).
Jiang, S.-C. et al. Controlling the Polarization State of Light with a Dispersion-Free Metastructure. Physical Review X 4, 021026 (2014).
Esfandyarpour, M., Garnett, E. C., Cui, Y., McGehee, M. D. & Brongersma, M. L. Metamaterial mirrors in optoelectronic devices. Nat Nano 9, 542–547 (2014).
Asadchy, V. S., Ra’di, Y., Vehmas, J. & Tretyakov, S. A. Functional Metamirrors Using Bianisotropic Elements. Physical Review Letters 114, 095503 (2015).
Lee, J. et al. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions. Nature 511, 65–69 (2014).
Li, G. et al. Continuous control of the nonlinearity phase for harmonic generations. Nat Mater 14, 607–612 (2015).
Ni, X., Wong, Z. J., Mrejen, M., Wang, Y. & Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 349, 1310–1314 (2015).
Khorasaninejad, M. et al. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016).
Pakizeh, T., Abrishamian, M. S., Granpayeh, N., Dmitriev, A. & Käll, M. Magnetic-field enhancement in gold nanosandwiches. Optics Express 14, 8240–8246 (2006).
Lu, D. Y. et al. Creation of a magnetic plasmon polariton through strong coupling between an artificial magnetic atom and the defect state in a defective multilayer microcavity. Physical Review B 77, 214302 (2008).
Wang, S. M. et al. Magnetic plasmon modes in periodic chains of nanosandwiches. Optics Express 16, 3560–3565 (2008).
Zhu, Z. H. et al. Optically pumped nanolaser based on two magnetic plasmon resonance modes. Applied Physics Letters 94, 103106 (2009).
Hao, J. et al. High performance optical absorber based on a plasmonic metamaterial. Applied Physics Letters 96, 251104 (2010).
Liu, N., Mesch, M., Weiss, T., Hentschel, M. & Giessen, H. Infrared Perfect Absorber and Its Application As Plasmonic Sensor. Nano Letters 10, 2342–2348 (2010).
Liu, H. et al. Linear and nonlinear Fano resonance on two-dimensional magnetic metamaterials. Physical Review B 84, 235437 (2011).
Liu, H. et al. Strong Light-Induced Negative Optical Pressure Arising from Kinetic Energy of Conduction Electrons in Plasmon-Type Cavities. Physical Review Letters 106, 087401 (2011).
Bao, Y., Zhu, X. & Fang, Z. Plasmonic Toroidal Dipolar Response under Radially Polarized Excitation. Scientific Reports 5, 11793 (2015).
Kirk, C. T. Quantitative analysis of the effect of disorder-induced mode coupling on infrared absorption in silica. Physical Review B 38, 1255–1273 (1988).
Tassin, P. et al. Electromagnetically Induced Transparency and Absorption in Metamaterials: The Radiating Two-Oscillator Model and Its Experimental Confirmation. Physical Review Letters 109, 187401 (2012).
Palik, E. D. Handbook of Optical Constants of Solids I (1985).
Berreman, D. W. Infrared Absorption at Longitudinal Optic Frequency in Cubic Crystal Films. Physical Review 130, 2193–2198 (1963).
Raizen, M. G., Thompson, R. J., Brecha, R. J., Kimble, H. J. & Carmichael, H. J. Normal-mode splitting and linewidth averaging for two-state atoms in an optical cavity. Physical Review Letters 63, 240–243 (1989).
Zhu, Y. et al. Vacuum Rabi splitting as a feature of linear-dispersion theory: Analysis and experimental observations. Physical Review Letters 64, 2499–2502 (1990).
V. Savona,, L. C. A., P. Schwendimann & A. Qua.ttropani. Quantum well excitons in semiconductor microcavities Unified treatment of weak and strong coupling regimes. Solid State Communications 93, 733–739 (1995).
Christ, A., Tikhodeev, S. G., Gippius, N. A., Kuhl, J. & Giessen, H. Waveguide-Plasmon Polaritons: Strong Coupling of Photonic and Electronic Resonances in a Metallic Photonic Crystal Slab. Physical Review Letters 91, 183901 (2003).
Ye, F., Burns, M. J. & Naughton, M. J. Symmetry-Broken Metamaterial Absorbers as Reflectionless Directional Couplers for Surface Plasmon Polaritons in the Visible Range. Advanced Optical Materials 2, 957–965 (2014).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No’s 11321063, 61425018 and 11374151), the National Key Projects for Basic Researches of China (No. 2012CB933501 and 2012CB921500).
Author information
Authors and Affiliations
Contributions
X. Zhang and Z.G. Zhang performed the sample fabrication and measurement, X. Zhang and Q. Wang performed numerical simulations. H. Liu and Q. Wang provided helpful discussions. X. Zhang and H. Liu wrote the manuscript. H. Liu and S.N. Zhu initiated the program and directed the research.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhang, X., Liu, H., Zhang, Z. et al. Controlling thermal emission of phonon by magnetic metasurfaces. Sci Rep 7, 41858 (2017). https://doi.org/10.1038/srep41858
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep41858
This article is cited by
-
Impact of the dielectric duty factor on magnetic resonance in Ag-SiO2-Ag magnetic absorber
Optoelectronics Letters (2021)
-
Thermal camouflage based on the phase-changing material GST
Light: Science & Applications (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.