Abstract
Locating influential nodes in temporal networks has attracted a lot of attention as data driven and diverse applications. Classic works either looked at analysing static networks or placed too much emphasis on the topological information but rarely highlighted the dynamics. In this paper, we take account the network dynamics and extend the concept of Dynamic-Sensitive centrality to temporal network. According to the empirical results on three real-world temporal networks and a theoretical temporal network for susceptible-infected-recovered (SIR) models, the temporal Dynamic-Sensitive centrality (TDC) is more accurate than both static versions and temporal versions of degree, closeness and betweenness centrality. As an application, we also use TDC to analyse the impact of time-order on spreading dynamics, we find that both topological structure and dynamics contribute the impact on the spreading influence of nodes, and the impact of time-order on spreading influence will be stronger when spreading rate b deviated from the epidemic threshold bc, especially for the temporal scale-free networks.
Similar content being viewed by others
Introduction
Centrality is a fundamental concept in network analysis, and how to measure the centrality of nodes has become an essential part of analysing and understanding networked systems including social networks1,2,3, biology networks4,5,6, Internet7,8, ecological networks9, traffic networks10. In networked system, some significant nodes are responsible for broadcasting information and therefore locating and protecting them are crucial for the whole information processing system11,12. The definition of centrality fails to reach an agreement, it leads to existing many methods to evaluate node importance. Most of conventional methods combine the definition of centrality closely with the networks topological structure13,14,15,16, these methods emphasize that the importance of nodes is related to the topological parameters, such as degree, closeness, betweenness, k-shell15, H-index16. Sometime these methods perform well while we are considering the structural importance of nodes, such as the path length and the number of paths. But they may not perform well in the processes like spreading which consider more about the dynamics of nodes17. As an extensive process, spreading can describe many important activities in the real-world, including the outbreak of epidemics18,19,20, the spread of news and ideas21,22, the rise of political movements23,24. The early method of describing the spreading process starts in the fields of epidemiology18,25. This years, at the core of all data-driven modeling approaches lies the structure of human interactions, mobility, and contact patterns that finds its best representation in the form of networks26,27,28, but the key problems that general solution of the master equation of the networked system is hardly achievable even for very simple dynamical processes29. The numerical simulation has been a good reference tool to find the approximate solutions of the spreading process, but when the scale of networks become large, numerical simulation may be ineffective. Recently, Morone and Makse developed the theory of influence maximization in complex networks and introduced a new method to find influencers via optimal percolation11, they found that some weakly connected nodes can become top influencers in large networks when they act as bridges among node clusters, the new method and its improved version make it possible to find influencers in large social media30.
Beside the topological features, recent studies indicate that the dynamics also play an important role in spreading process17,31,32,33. For example, if we change the spread rate in epidemic process, although the networks topological structure remain the same but the results of spreading may be totally different. There are few works taking into account the properties of the underlying spreading dynamics17,34,35. Klemm et al. suggested that the eigenvector centrality can be used in estimating dynamical influences of nodes in the susceptible-infected-recovered (SIR) spreading model34, and theoretical proof had been given to show that there exist a closed relation between the infection scale and eigenvector centrality in susceptible-infected-susceptible (SIS) model of the networks35. Liu et al.17 gave a definition of centrality (Dynamics-Sensitive centrality) of static networks while only use three parameters to describe the spreading influence, the numerical simulation shows that the new centrality performs much better than some topological structural centralities like degree, k-shell and also is of comparable with eigenvector centrality.
However, all above mentioned methods are restricted to static networks. In real life many networks are temporal36,37,38,39,40,41,42,43, namely the networks topological structure evolving with time, and many studies have shown that time-order have great influence not only on the topological structure but also the spreading dynamics of this kind of general networks41,44,45. There are many temporal versions of centrality which have been used to describe the structural importance of nodes44,46,47,48, but these methods only take into account the topological features. Since the dynamics are much more complicated in the networks with the variety of the topological structure, and more attention should be paid for this kind of general networks. It should be a significant work to investigate the dynamics on temporal networks.
In the past a few years, our group investigated the multifractal scaling properties of unweighted and weighted networks49,50,51,52. In this paper, we consider more about the spreading dynamics of nodes and extend the work of Liu et al.17 to a more general and more realistic model. According to the empirical results on three real-world temporal networks and a theoretical temporal network, the extended method performs much better than other six methods. As an application, we use it to analyse the influence of time-order in temporal networks.
Visualization model
A temporal network with N nodes and time length T is defined as a sequence of L time snapshots of equal size δ = T/L, we can use multilayer network structure53 to represent temporal networks, where each time snapshot can be treated as networks interaction inter-layer, and all nodes naturally connect themselves between layers. Fig. 1 is an example of temporal network represented by using a multilayer network structure, there are four nodes A, B, C, D with T = 3, L = 3,δ = 1. If node i has a connection with node j at time snapshots t, where t ∈ [1, …, L], then i and j are connected by undirected line at time layer t. In a temporal network with N nodes, the topological structure at time layer t can be described by the adjacency matrix A(t) = {a(t)}ij. As shown in Fig. 1:

As a tool to measure the influence of nodes, dynamics-sensitive centrality17 performs well in static networks. But for more general dynamical networked system, the use of it has been restricted. Now we use the above visualization model and extend dynamics-sensitive centrality to more general situation.
Temporal dynamics-sensitive centrality
We consider the susceptible-infected-recovered (SIR) model in discrete time, where individuals (i.e., the nodes of the network) can only be in one of three mutually exclusive states: susceptible (S), infectious (I), recovered (R). At each time step, a node in the state S will get infected with infection probability β when contacting one of its infected neighbors. And an infected node can be recovered with a probability μ. When we set μ = 0, the SIR model reduces to a standard SI model: nodes can only be susceptible or infected. We consider the temporal network forming the substrate of the spreading process to be a sequence of undirected and unweighted temporal networks, which has been described above. We used a Markov chain for the epidemic model and derive the analytical result of node influence. Denote x(t)(t ≥ 0) as an n × 1 vector whose components are the probabilities of nodes to be ever infected no later then the time step t, then P(t) = x(t) − x(t−1)(t ≥ 1) is the probabilities of nodes to be infected at time step t, and we denote P(0) = x(0) to represent the initial condition. If i is the only initially infected node, then xi(0) = 1. Notice that, x(t) is the cumulative probability that can be large than 1, and we use the term probability just for simplicity. In the first time step, x(1) = βA(1)x(0), and in the Methods Section, we prove that for t > 1 the following equation can be obtained:

So we have

where 
The probabilities of nodes to be ever infected no later than the time step t in temporal networks can be expressed by

where  , and we denote H(0) = 1. Aral and Walker54 showed that the attributes of nodes are highly correlated with influence of nodes and tendencies to be influenced, which indicates that we can use the sum of infected probabilities of all nodes to express the the spreading influence of nodes. Denote Si(t) to be the sum of infected probabilities of node i at time step t, then
, and we denote H(0) = 1. Aral and Walker54 showed that the attributes of nodes are highly correlated with influence of nodes and tendencies to be influenced, which indicates that we can use the sum of infected probabilities of all nodes to express the the spreading influence of nodes. Denote Si(t) to be the sum of infected probabilities of node i at time step t, then

where XT means the transpose of matrix X, V = (1, 1, …. 1)T is n × 1 vector whose components are all equal to 1. Obviously, A(t)T = A(t), so

then the spreading influence of all nodes can be described by the vector

If we let A = A(1) = A(2) = … = A(t), then the temporal networks are static. In this particular case,  is a symmetric matrix, then
is a symmetric matrix, then  , which is in accordance with the result obtained by Liu et al.17.
, which is in accordance with the result obtained by Liu et al.17.
Now we have established the method to measure the spreading influence of nodes in temporal networks. But there are three assumptions need to be explained. First, we follow Refs 17 and 55 and use a linear coupling instead of nonlinear coupling to calculate the probabilities of the nodes to be infected at time step t, namely, if a susceptible node has m infected neighbors, then the probability of the node to be infected is approximated as mβ, instead of 1 − (1 − β)m. Second, the cumulative probability x(t) can be larger than 1, which is not mathematically rigorous. As infected probability of every node is overestimated, here we take the cumulative probability x(t) just as a measure of influence. And we assume that x(t) is meaningful and has a closed relation with the spreading influence. The performance of the operation need to be tested in real networks, and this will be extended in the following section. Third, we assume periodic boundary conditions for the network dynamics, here we regard L as the total number of network time snapshots. i.e. A(L + 1) = A(1), where L is arbitrary and finite, this processing method causes no loss in generality and has been used by Valdano et al.56. With different recovery rate μ, the time-varying structure of temporal networks is able to alter the value of the epidemic threshold βc. We think the assumption is meaningful because when L → ∞ and β > βc, all nodes in the networks would be infected no matter which node is the source of the disease, in this special condition we could not distinguish the spreading influence between nodes. For a given recovery rate μ, Valdano et al.56 also tested that it would affect the epidemic threshold βc estimation only for rather small values of L, the asymptotic solutions of epidemic process are periodic of period L. From Eq. (2) and the same processing method56, we have the spectral radius of M meets:

Eq. (7) makes sure that  , this yields the threshold condition ρ(M) = 1, then the epidemic threshold βc can be calculated56,57.
, this yields the threshold condition ρ(M) = 1, then the epidemic threshold βc can be calculated56,57.
Results
Evaluating the spreading performance
In the following experimental results, we demonstrate the effectiveness of the method by comparing with the SIR model of varying spreading rate β. Three real-world temporal networks, including Email networks (EMA)58, High school friendship relations networks (FRI)59, University of California messages networks (UCM)60, and a theoretical temporal scale-free network (TSF) generated by Barabasi-Albert (BA) model61, are used in our empirical analysis, the data description can be found in Methods section. We calculated the spreading influence by both our method and SIR spreading model (see Methods section for the description of SIR spreading model). As shown in Fig. 2, we perform the method with β = 0.01, μ = 0.1, and the time step is set by t = 10 (t ≤ L, L has been given in Table 1), and a normalization can be performed without a loss of precision:

In order to compare between the results of the method and the results of SIR simulation but without a loss of precision, the simulation results use translation transform of S′ = normal(S) + 1 after the normalization. the Kendall’s Tau coefficients62 between the results of the method and the standard SIR model are 0.9265, 0.9443, 0.7866, 0.8514 respectively of the EMA, FRI, TSF, UCM which show a high effectiveness of the method.
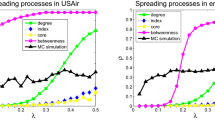
In addition, three well-known centrality measure methods degree centrality, closeness centrality, betweenness centrality, and their temporal version methods introduced by Kim et al.48 are considered, the details of these methods can be seen in the Methods section. We applied these six methods to the four temporal networks, both the results of above six methods and ours are compared with the simulation results of the standard SIR model. In the standard SIR model, the spreading rate β varies from 0.01 to 0.10 with a step of 0.01, the recovery rate μ is set by 0.1, and the time step is set as t = 10. As shown in Fig. 3, each data point is obtained by averaging over 104 independent runs, here SD, TD, SC, TC, SB, TB, TDC, SIR represent static degree, temporal degree, static closeness, temporal closeness, static betweenness, temporal betweenness, temporal dynamics-sensitive centrality, and simulation results of SIR model respectively. Temporal dynamics-sensitive centrality (TDC) proposed in this paper obtains much higher accuracy than other six methods through the Kendall’s Tau coefficient τ.
Moreover, we compare the consumed CPU time of the above eight methods in Table 2. All experiments are tested on a computer: Intel Core i3 2.53 G Hz with RAM DDR3 4 GB and 1.6 GHz. From Table 2, we can see that local centrality methods like static degree (SD) and temporal degree (TD) consumed least time, temporal dynamics-sensitive centrality (TDC) also performed well, and global centrality methods like static closeness (SC), temporal closeness (TC), static betweenness (SB), temporal betweenness (TB) consumed a substantial amount of computation time and memory resources. Although numerical simulation of SIR did not take a substantial amount of memory resources, it consumed too much time and sometime it was unbearable.
Dynamics of spreading analysis on null models
In the study of statistical properties of networks, it’s not enough to assess the importance, unexpectedness, or underrepresentation of topological features of empirical networks only by calculating the value of some topological statistics, a common way to deal with the problem is by comparing the features against some reference model where the network is randomized, and these randomized network models are called null models. More about null models, readers can refer to Refs 41 and 45.
Whether or not taking into consideration of the influence of time is the difference between statics networks and temporal networks. In temporal networks, time-order of the event sequences between nodes not only have influence on the networks topology structure, but also the spreading dynamics41,44,45. Tang et al.44 pointed out that a path is not reachable in temporal networks, but may be reachable when turning temporal networks into static networks. Karsai et al.45 showed that randomizing the time-order will slow down the spreading. In this paper, we care more about the effects of time-order on the spreading influence of nodes, we apply the above analysis to null models where the time-order of original event sequences are randomized. Algorithmically, the method of the model is defined as follows:
-
1
Step 1 Go over all edges sequentially.
-
2
Step 2 For every edge
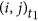 at time t1, randomly pick another time t2.
at time t1, randomly pick another time t2. -
3
Step 3 Replace the edge
 and
and 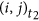 , namely only change the time-order of the events happen between the same two nodes.
, namely only change the time-order of the events happen between the same two nodes. -
4
Step 4 Repeat the above processes until the time orders are completely randomized.
Denoted E(i, j)t = 1 if i and j is connected at time t, or E(i, j)t = 0 means disconnected otherwise. It is easy to find that if  , then above randomly replace process between time t1 and t2 will be valid. This random method ensemble conserves the set of times of the original contact sequence, but destroys burstiness of events on individual vertices and edges as well as correlations between events such as triggered chains, the aggregated rate of events in the network is unchanged and will still follow the typical circadian and weekly patterns of human activity41,45. In the experiment, the temporal length of the four networks were chosen by t = L, we apply the null model to the spreading process while the recovery rate μ is set by 0.01, 0.04, 0.07, 0.10, and infection rate β is set by a range from 0.0025 to 0.1 with a step of 0.0025 respectively for each recovery rate μ. For every pair of (μ,β), the original networks are randomly reset 1000 times by using the null model algorithm, denoted S′(t) the mean of spreading influence of 1000 random networks, the Kendall’s Tau coefficients between the S(t) of the original networks and S′(t) are used to measure the the impact of the time-order, and larger the value of Kendall’s Tau coefficients, the impact of time-order is small. The epidemic threshold βc respectively for the four networks are shown in Table 3. As shown in Fig. 4, we are surprised to find that the impact of time-order on spreading influence will be stronger when β deviated from the epidemic threshold βc, especially for the temporal scale-free networks. When β is set by the epidemic threshold condition βc of the four networks, the Kendall’s Tau coefficients between S(t) of the original networks and S′(t) of the random networks can be larger than 0.84, which shows a small impact of time-order on spreading influence. The detailed results of Kendall’s Tau coefficients can be found in Supplementary Information.
, then above randomly replace process between time t1 and t2 will be valid. This random method ensemble conserves the set of times of the original contact sequence, but destroys burstiness of events on individual vertices and edges as well as correlations between events such as triggered chains, the aggregated rate of events in the network is unchanged and will still follow the typical circadian and weekly patterns of human activity41,45. In the experiment, the temporal length of the four networks were chosen by t = L, we apply the null model to the spreading process while the recovery rate μ is set by 0.01, 0.04, 0.07, 0.10, and infection rate β is set by a range from 0.0025 to 0.1 with a step of 0.0025 respectively for each recovery rate μ. For every pair of (μ,β), the original networks are randomly reset 1000 times by using the null model algorithm, denoted S′(t) the mean of spreading influence of 1000 random networks, the Kendall’s Tau coefficients between the S(t) of the original networks and S′(t) are used to measure the the impact of the time-order, and larger the value of Kendall’s Tau coefficients, the impact of time-order is small. The epidemic threshold βc respectively for the four networks are shown in Table 3. As shown in Fig. 4, we are surprised to find that the impact of time-order on spreading influence will be stronger when β deviated from the epidemic threshold βc, especially for the temporal scale-free networks. When β is set by the epidemic threshold condition βc of the four networks, the Kendall’s Tau coefficients between S(t) of the original networks and S′(t) of the random networks can be larger than 0.84, which shows a small impact of time-order on spreading influence. The detailed results of Kendall’s Tau coefficients can be found in Supplementary Information.
Here, black dotted line represent the epidemic threshold βc. The recovery rate μ was set by 0.01, 0.04, 0.07, 0.10, for each recovery rate, the spreading rate β varies from 0.0025 to 0.10 with a step of 0.0025, and the time step is set as t = L. Each data point is obtained by averaging over 103 independent runs. Each error bar covers two standard deviations for all the results.
Discussion
Centrality is a important topic with many diverse applications, and how to measure the centrality of nodes has become an essential part of analysing and understanding networked systems. As summarized in papers14,63,64, most of previous work concentrate on the topological information but rarely highlight the dynamics17. Liu et al.17 showed that dynamics-sensitive centrality in static networks performed much better than some topological structural centrality in spreading process, this inspire us to consider the problem in a more general dynamics networks, where networks topological structure evolving with time. In this paper, in addition to the topological information, we take the time into consideration and propose temporal centrality metrics based on the time-ordered graph. According to the empirical results on three real-world temporal networks and a theoretical temporal network, the extended method (TDC) perform much better than other six methods in the early stage of spreading. Although it is unfair to directly compare TDC with other six methods because TDC takes account more parameters, the method enables us to investigate the dynamics in spreading process while only use three parameters, we can use it to detect the potential super-spreaders for epidemic control in temporal networks. The method in this paper has advantage over the method proposed by Liu et al.17, it not only can be applied to static networks, but also can be used in more general networks.
The dynamics are much more complicated in temporal networks for the variety of the topological structure. To the best of our knowledge, there are few works had ever investigated the impact of time-order on the spreading influence of nodes. As an application, TDC enable us to analyse the impact of time-order on spreading dynamics, we are surprised to find that both topological structure and dynamics contribute the impact on the spreading influence of nodes, but the impact of time-order on spreading influence will be stronger when β deviated from the epidemic threshold βc. A direct application of this conclusion can be that when dynamics parameter β approach epidemic threshold βc, we can still find the super-spreaders for epidemic only rely on the static integrated networks and the number of each edge links. We think our method can be extend to more dynamics analyses such as the impact of edge sequences on spreading dynamics. All in all, there are many problem remain to be solved since we conclude that both topological structure and dynamics contribute the impact on the spreading influence of nodes, but the specific mechanisms involved remain to be explored.
Methods
Derivation of Eq. (1)

Proof: In the first time step, x(1) = βA(1)x(0), then when t = 1,

We assume that when t ≤ p, the following equation can be established

then for t = p + 1, we have

which completes the proof.
Benchmark methods
We consider two kinds of benchmark methods here, one type are static networks methods which have been widely used over last years, such as degree centrality, closeness centrality, and betweenness centrality. The other are temporal networks methods which have been developed these years, the representative are temporal type of degree centrality, closeness centrality, and betweenness centrality.
The degree centrality of node i is defined as the number of links incident upon it, namely

where aij is the element of matrix A. u(i) is the neighbor nodes of node i. Degree centrality is a local centrality, and works especially well in evaluating the spreading influence of nodes when the spreading rate β is small.
Closeness centrality65 of node i is defined by the reciprocal of sum of its distances from all other nodes.

where N is the total number of nodes, dij is the shortest path length between node i and node j. Closeness centrality is a global centrality and performs better in evaluating nodes’ spreading inflences when the spreading rate β is high.
Betweenness centrality65 of node i is defined by the number of shortest paths from all vertices to all others that pass through node i.

where σjk is the total number of shortest paths from node j to node k, and σjk(i) is the number of those paths that pass through node i. Betweenness centrality is also a global centrality and has been attached with wide application, including computer and social networks, biology, transport and scientific cooperation.
Tang et al.44 proposed a method to identify important nodes using temporal versions of conventional centrality metrics, Kim et al.48 extend Tang’s work to a more general and more realistic model. Readers can refer to Tang et al.44 or Kim et al.48 for the details of the temporal versions of conventional centrality. In this paper, we applied the above three conventional centrality metrics and the temporal version of these three centrality metrics proposed by Kim et al.48.
In fact the static networks can be regarded as a integrated process of temporal networks regardless of the influence of time-order42, and conventional centrality methods are no more suitable for this kind of general networks, in order to solve the problem and compare the performance of the conventional static methods with our methods, we first convert the temporal networks into static integrated networks (see Fig. 1), and then calculating the centrality by using the three conventional centrality methods. We also calculate the temporal versions of conventional centrality by using Kim’s methods, both of these results are considered as benchmark to be compared with the results of our method, and the results are shown in Results section.
SIR Spreading Model
Initially, we set one node to be in the initial infected state I, this node corresponds to our single spreader (in general, the initial node can be any node of the graph, here in the simulation we run over all nodes of networks; the same procedure is also performed for the baseline methods). The rest of the nodes are assigned to the susceptible state S. At each time step, the infected nodes can infect their susceptible neighbors with probability β (infection rate). Furthermore, the nodes that have been previously infected can recover from the disease with probability μ (recovery rate). The process is repeated within the given time step t(t ≤ L). We calculate the number of infected nodes Ni(t) after t steps the disease firstly spreads from the initial node i, and use Ni(t) to represent the simulation spreading influence of node i.
Data Sets
In order to demonstrate the effectiveness of the method, we performed the numerical analysis mainly using the following empirical networks.
-
Email networks(EMA)58. This network represented the history of internal e-mail communication between employees of a small-sized manufacturing.
-
High school friendship relations networks(FRI)59. This network was a medium-sized data set correspond to the contacts and friendship relations between students in a high school.
-
Temporal scale-free networks(TSF). This network was a combination of 100 snapshots, and each snapshots was generated by Barabasi-Albert BA model61.
-
University of California messages networks(UCM)60. This network contains sent messages between the users of an online community of students from the University of California, Irvine.
In Table 1, we provide some detailed statistical properties of the above networks. For our analyses, if not stated otherwise, these networks are both undirected and unweighted networks. EMA, FRI, UCM are real-world networks which represent human interactions in diverse social contexts and have different topological and temporal characteristics, TSF is a theoretical network generated by BA scale-free model.
Additional Information
How to cite this article: Huang, D.-W. and Yu, Z.-G. Dynamic-Sensitive centrality of nodes in temporal networks. Sci. Rep. 7, 41454; doi: 10.1038/srep41454 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Freeman, L. C. Centrality in social networks conceptual clarification. Social networks 1, 215–239 (1978).
Newman, M. E. J. Scientific collaboration networks. II. shortest paths, weighted networks, and centrality. Physical Review E 64, 016132 (2001).
Mislove, A., Marcon, M., Gummadi, K. P. & et al. Measurement and analysis of online social networks. In Acm Sigcomm Conference on Internet Measurement, 29–42 (2007).
Jeong, H., Mason, S. P., Barabási, A. L. & Oltvai, Z. N. Lethality and centrality in protein networks nature. Nature 411, 41–42 (2001).
Sporns, O., Honey, J., Christopher & Kötter, R. Identification and classification of hubs in brain networks. PLoS One 2, e1049 (2007).
Özgur, A., Vu, T. G. & Radev, D. R. Identifying gene-disease associations using centrality on a literature mined gene-interaction network. Bioinformatics 24, i277–i285 (2008).
Kleinberg & Jon, M. Authoritative sources in a hyperlinked environment. Journal of the Acm 46, 604–632 (1999).
Page, L., Brin, S., Motwani, R. & Winograd, T. The pagerank citation ranking: bringing order to the web. technical report, stanford infolab. (1999).
Jordán, F., Okey, T. A., Bauer, B. & Libralato, S. Identifying important species: Linking structure and function in ecological networks. Ecological Modelling 216, 75–80 (2008).
Holme, P. Congestion and centrality in traffic flow on complex networks. Advances in Complex Systems 6, 163–176 (2003).
Morone, F. & Makse, H. A. Influence maximization in complex networks through optimal percolation. Nature 524, 65–68 (2015).
Teng, X., Pei, S., Morone, F. & Makse, H. A. Collective influence of multiple spreaders evaluated by tracing real information flow in large-scale social networks. Scientific Reports 6, 36043 (2016).
Borgatti, S. P. Centrality and network flow. Social Networks 27, 55–71 (2005).
Borgatti, S. P. & Everett, M. G. A graph-theoretic perspective on centrality. Social Networks 28, 466–484 (2006).
Kitsak, M. et al. Identification of influential spreaders in complex networks. Nature Physics 6, 888–893 (2010).
Lü, L. Y., Zhou, T., Zhang, Q. M. & Stanley, H. E. The H-index of a network node and its relation to degree and coreness. Nature Communications 7 (2016).
Liu, J. G., Lin, J. H., Guo, Q. & Zhou, T. Locating influential nodes via dynamics-sensitive centrality. Scientific Reports 6, 21380 (2016).
Anderson, R. M. & May, R. M. Infectious diseases of humans: dynamics and control. Infectious Diseases of Humans Dynamics & Control 108, 174–175 (1992).
Keeling, M. J. & Rohani, P. Modeling infectious diseases in humans and animals (Princeton University Press, 2008).
Lloyd-Smith, J. O. & Grenfell, B. T. Epidemic dynamics at the human-animal interface. Science 326, 1362–1367 (2009).
Backstrom, L., Huttenlocher, D., Kleinberg, J. & Lan, X. Group formation in large social networks: membership, growth, and evolution. In Acm Knowledge Discovery & Data Mining, 44–54 (2006).
Leskovec, J., Backstrom, L. & Kleinberg, J. Meme-tracking and the dynamics of the news cycle. In Acm Knowledge Discovery & Data Mining, 497–506 (2009).
Polletta, F. & Jasper, J. M. Collective identity and social movements. Annual Review of Sociology 27, 283–305 (2001).
Diani, M. & McAdam, D. Social movements and networks: Relational approaches to collective action (Oxford University Press, 2003).
Kermack, W. O. & Mckendrick, A. G. Contributions to the mathematical theory of epidemics III. Further studies of the problem of endemicity. Bulletin of Mathematical Biology 53, 89–118 (1927).
Eubank, S. et al. Modelling disease outbreaks in realistic urban social networks. Nature 429, 180–184 (2004).
Ferguson, N. M. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 437, 209–214 (2005).
Jr, L. I. et al. Containing pandemic influenza at the source. Science 309, 1083–1087 (2005).
Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Review of Modern Physics 87, 925–979 (2015).
Morone, F., Min, B., Bo, L., Romain, M. & Makse, H. A. Collective influence algorithm to find influencers via optimal percolation in massively large social media. Scientific Reports 6, 30062 (2016).
Borge-Holthoefer, J. & Moreno, Y. Absence of influential spreaders in rumor dynamics. Physical Review E 85, 026116 (2012).
Borge-Holthoefer, J., Rivero, A. & Moreno, Y. Locating privileged spreaders on an online social network. Physical Review E 85, 066123 (2012).
Liu, Y., Tang, M., Zhou, T. & Do, Y. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition. Scientific Reports 5, 9602 (2015).
Klemm, K., Serrano, M. A., Eguluz, V. M. & Miguel, M. S. A measure of individual role in collective dynamics. Scientific Reports 2, 292 (2012).
Ping, L., Jie, Z., Xiao-Ke, X. & Michael, S. Dynamical influence of nodes revisited: A markov chain analysis of epidemic process on networks. Chinese Physics Letters 29, 048903 (2012).
Kossinets, G. & Watts, D. J. Empirical analysis of an evolving social network. Science 311, 88–90 (2006).
Onnela, J.-P. et al. Structure and tie strengths in mobile communication networks. Proceedings of the National Academy of Sciences of the United States of America 104, 7332–7336 (2007).
Palla, G. & Vicsek, T. Quantifying social group evolution. Nature 446, 664–667 (2007).
Iribarren, J. L. & Moro, E. Impact of human activity patterns on the dynamics of information diffusion. Physical Review Letters 103, 038702 (2009).
Taylor, I. W. et al. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nature Biotechnology 27, 199–204 (2009).
Holme, P. & Saramäki, J. Temporal networks. Physics reports 519, 97–125 (2012).
Perra, N., Gonçalves, B., Pastor Satorras, R. & Vespignani, A. Activity driven modeling of time varying networks. Scientific Reports 2, 469 (2012).
Wang, D., Yan, K.-K., Rozowsky, J., Pan, E. & Gerstein, M. Temporal dynamics of collaborative networks in large scientific consortia. Trends in Genetics 32, 251–253 (2016).
Tang, J., Musolesi, M., Mascolo, C., Latora, V. & Nicosia, V. Analysing information flows and key mediators through temporal centrality metrics. In The Workshop on Social Network Systems, 1–6 (2010).
Karsai, M., Kivelä, M. & Pan, R. K. et al. Small but slow world: How network topology and burstiness slow down spreading. Physical Review E 83, 025102 (2011).
Pan, R. K. & Saramäki, J. Path lengths, correlations, and centrality in temporal networks. Physical Review E 84, 016105 (2011).
Takaguchi, T., Sato, N., Yano, K. & Masuda, N. Importance of individual events in temporal networks. New Journal of Physics 14, 093003 (2012).
Kim, H. & Anderson, R. Temporal node centrality in complex networks. Physical Review E 85, 026107 (2012).
Liu, J.-L., Yu, Z.-G. & Anh, V. Topological properties and multifractal analysis of recurrence network constructed from fractional brownian motions. Physical Review E 89, 032814 (2014).
Liu, J.-L., Yu, Z.-G. & Anh, V. Determination of multifractal dimensions of complex networks by means of the sandbox algorithm. Chaos 25, 023103 (2015).
Song, Y.-Q., Liu, J.-L., Yu, Z.-G. & Li, B.-G. Multifractal analysis of weighted networks by a modified sandbox algorithm. Scientific Reports 5, 17628 (2015).
Yu, Z.-G., Zhang, H., Huang, D.-W., Lin, Y. & Anh, V. Multifractality and laplace spectrum of horizontal visibility graphs constructed from fractional brownian motions. Journal of Statistical Mechanics: Theory and Experiment 2016, 033206 (2016).
Boccaletti, S. et al. The structure and dynamics of multilayer networks. Physics Reports 544, 1–122 (2014).
Aral, S. & Walker, D. Identifying influential and susceptible members of social networks. Science 337, 337–41 (2012).
Gomez, S., Arenas, A., Borgeholthoefer, J., Meloni, S. & Moreno, Y. Discrete-time markov chain approach to contact-based disease spreading in complex networks. Europhysics Letters 89, 275–288 (2009).
Valdano, E., Ferreri, L., Poletto, C. & Colizza, V. Analytical computation of the epidemic threshold on temporal networks. Physical Review X 5, 021005 (2015).
Valdano, E., Poletto, C. & Colizza, V. Infection propagator approach to compute epidemic thresholds on temporal networks: impact of immunity and of limited temporal resolution. The European Physical Journal B 88, 1–11 (2015).
Michalski, R., Palus, S. & Kazienko, P. Matching organizational structure and social network extracted from email communication. In International Conference on Business Information Systems, 197–206 (Springer, 2011).
Mastrandrea, R., Fournet, J. & Barrat, A. Contact patterns in a high school: A comparison between data collected using wearable sensors, contact diaries and friendship surveys. PLoS One 10 (2015).
Opsahl, T. & Panzarasa, P. Clustering in weighted networks. Social Networks 31, 155–163 (2009).
Barabasi, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Kendall, M. G. A new measure of rank correlation. Biometrika 30, 81–93 (1938).
Pei, S. & Makse, H. A. Spreading dynamics in complex networks. Journal of Statistical Mechanics 2013, P12002 (2013).
Lü, L., Chen, D. & Ren, X.-L. et al. Vital nodes identification in complex networks. Physics Reports 650, 1–63 (2016).
Newman, M. E. J. Networks: An introduction (Oxford University Press: Oxford UK, 2010).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11371016), the Chinese Program for Changjiang Scholars and Innovative Research Team in University (PCSIRT) (Grant No. IRT_15R58)
Author information
Authors and Affiliations
Contributions
D.H. designed and performed research, analyzed data and wrote the paper; Z.Y. designed research, discussed the results and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Huang, DW., Yu, ZG. Dynamic-Sensitive centrality of nodes in temporal networks. Sci Rep 7, 41454 (2017). https://doi.org/10.1038/srep41454
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep41454
This article is cited by
-
A new causal centrality measure reveals the prominent role of subcortical structures in the causal architecture of the extended default mode network
Brain Structure and Function (2023)
-
Identifying critical nodes in temporal networks by network embedding
Scientific Reports (2020)
-
Fractal and multifractal analyses of bipartite networks
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





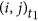 at time t1, randomly pick another time t2.
at time t1, randomly pick another time t2. and
and 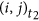 , namely only change the time-order of the events happen between the same two nodes.
, namely only change the time-order of the events happen between the same two nodes.