Enhanced thermoelectric performance of a chalcopyrite compound CuIn₃Se_5−xTe_x (x = 0~0.5) through crystal structure engineering

Abstract

In this work the chalcopyrite CuIn₃Se_5−xTe_x (x = 0~0.5) with space group through isoelectronic substitution of Te for Se have been prepared, and the crystal structure dilation has been observed with increasing Te content. This substitution allows the anion position displacement ∆u = 0.25-u to be zero at x ≈ 0.15. However, the material at x = 0.1 (∆u = 0.15 × 10⁻³), which is the critical Te content, presents the best thermoelectric (TE) performance with dimensionless figure of merit ZT = 0.4 at 930 K. As x value increases from 0.1, the quality factor B, which informs about how large a ZT can be expected for any given material, decreases, and the TE performance degrades gradually due to the reduction in n_H and enhancement in κ_L. Combining with the ZTs from several chalcopyrite compounds, it is believable that the best thermoelectric performance can be achieved at a certain ∆u value (∆u ≠ 0) for a specific space group if their crystal structures can be engineered.

Introduction

Thermoelectric (TE) materials have their potential applications in power generation and cooling systems, therefore, they have received great attention in recent decades. The TE performance of the materials is characterized by the dimensionless figure of merit (ZT), ZT = Tα²σ/κ = Tα²σ/ (κ_L + κ_e), here T is the absolute temperature, and α, σ, κ, κ_L and κ_e are the Seebeck coefficient, electrical conductivity, total thermal conductivity, lattice contribution and electronic part respectively. However, it is difficult to be improved as the α, σ and κ_e are usually coupled with each other strongly, which makes an independent property manipulation challenging for enhancing ZT.

In order to significantly improve the TE performance or ZT value, it is strongly necessary to explore effective strategies, in addition to those like nanostructure engineering^1,2,3 and band structure engineering^4,5,6. Under the guidance of such strategies, many new materials with high TE performance have been developed. The typical materials are those with high crystal symmetry structure like PbTe^4,5,6, SnSe^7,8, Mg₂Si_1−xSn_x solid solutions^9,10, and half-Heusler (HH) alloys¹¹.

Beyond those solid solutions, non-cubic diamond-like compounds, such as CuGa(In)Te₂, ZnSnP₂ and Cu₂ZnSnS₄, have also high power factors and ZTs if band convergence can be realized^12,13. The band converges only when the tetragonal deformation parameter η (η = c/2a, where c and a are the lattice parameters) becomes unity or the crystal field splitting Δ_CF approaches zero. However, deep investigations have revealed that as η approaches unity the chalcopyrite compounds often give low electrical conductivity and carrier concentration, due to the electrical inactivity caused by the attractive interaction between intrinsic donor-acceptor defect pairs^14,15,16. In addition, the cation–anion bond lengths in many chalcopyrite compounds are around 0.26–0.28 nm^17,18, a tiny disturbance of periodical crystal structure could have a profound impact on the phonon scattering mechanism. When η = 1 (Δ_CF = 0) non-cubic diamond-like compounds become pseudocubic ones^12,13. In this case, the least lattice distortion can be obtained and phonon scattering in point defect gets the minimum. As a result, the highest lattice part κ_L can be attained¹⁹.

The aforementioned different findings suggest that the impact of crystal structure on TE performance seems to be much more complex than what we anticipated. The origin might be the presence of different space groups for each compound caused by the vacancy that exists in some chalcopyrites with different site assignments²⁰. For example, in CuIn₃Se₅ the sum of cation atoms is less than that of anion atoms, therefore, the structure formula of CuIn₃Se₅ per unit cell is represented by Cu_1.6In_4.8□_1.6Se₈ where □ denotes structure vacancy²⁰. Therefore, the candidate space groups for CuIn₃Se₅ can be , , ,  ²⁰. Since different space group gives different chemical bonding, which gives rise to different physical properties, it is strongly necessary to tune the TE performance through engineering the crystal structure.

Although CuIn₃Se₅ have several space groups, the previous investigations have revealed that it still is a compound with defect non-cubic chalcopyrite structure^{21,22,23,24,25,26} with η = 0.997~1.013^27,28. Therefore, it is possible to engineer its crystal structure through manipulating its chemical compositions without changing its chalcopyrite structure. The tetragonal deformation parameter η is directly related to the anion position displacement u in chalcopyrites I_(m−3)III_(m+1)VI_2m, here m = 4, 5, 6, 7, 8, 9 …; I = Cu, Ag; III = Al, Ga, In; VI = Te, Se, S^29,30,31, u (or ∆u = 0.25-u) tends to be 0.25 (or zero) as η approaches unity³¹. In addition, the anion position displacement u in CuIn₃Se₅ fluctuates around 0.2435~0.2515^27,28, which facilitates us to examine the ∆u related TE performance as ∆u is around zero.

In this work, the CuIn₃Se₅-based compounds have been prepared, and their crystal structures through isoelectronic substitution of Te with lower electronegativity (2.1) for Se (2.55) have been engineered. It is believable that such an isoelectronic substitution is very important, because it tends to elongate the bond lengths d_Cu-Se and d_In-Se due to an increased repulsion between Cu- or In-Te bonds. Therefore, it has potential to manipulate the ∆u value, and optimize their TE performance.

Experimental

Sample preparations

Four elements Cu, In, Te and Se with a purity of 99.999% were loaded into different silica tubes in vacuum according to the formula CuIn₃Se_5−xTe_x (x = 0, 0.05, 0.1, 0.2, 0.5), and then melted at 1273 K for 24 h, followed by a rapid cooling to RT in water. The as-solidified ingots were pulverized and then ball milled in stainless steel bowls containing benzinum at a rotation rate of 350 rpm for 5 h. The dried powders were sintered using spark plasma sintering apparatus (SPS-1030) under a pressure of 60 MPa and at the highest temperature of ~950 K. The total sintering time is about 5 min. The densities (d) of the sintered samples (5.43~5.48 × 10³ kg/m³), which are more than 95% theoretical values²⁴, were measured using Archimedes’ method. The sintered block with the sizes of ϕ20 mm × 3.0 mm was cut into 3 mm-wide slices measuring 2.5 mm × 12 mm for electrical property measurement, and that with ϕ~10.0 mm × 2.0 mm was obtained for thermal diffusivity measurement.

Structural analyses

The structural analysis of the powders was made by powder X-ray diffractometer (D8 Advance) operating at 50 kV and 40 mA. Cu Ka radiation (λ = 0.15406 nm) and a scan rate of 4° min⁻¹ were used to record the patterns in the range from 10° to 140°.

In order to gain a deep understanding of the crystal structure, the microstructures of the samples (x = 0, 0.1) have been examined by using high resolution transmission electron microscopy (HRTEM), and pure CuIn₃Se₅ was examined for comparison. HRTEM images were obtained at 220 kV using JEM-2010F (Field emission TEM).

TE transport property measurements

The Hall coefficient (R_h) measurements at room temperature (RT) were conducted on a Physical Property Measurement System (PPMS, Model-9) using a four probe configuration with a magnetic field sweeping between ±2.0 T, and were performed on rectangular samples with size 2 × 2 × 7 mm³. The Hall carrier concentrations (n_H) and mobility μ were subsequently calculated based on the following formulae n_H = −1/(e|R_h|), μ = |R_h|σ, where e is the electron charge. The electrodes were fine copper wires for current and Hall voltage measurements, and the contacts were made of silver paste.

The Seebeck coefficients (α) and electrical conductivities (σ) were measured as a function of temperature using ULVAC ZEM-3 instrument under helium atmosphere from RT to ~930 K. A temperature difference of approximately 5 °C was applied between the two terminals of the sample in order to measure the Seebeck coefficient, whereas the electrical conductivity was measured using the four-probe method. The measurement uncertainties are 6% for both the electrical conductivity and Seebeck coefficient. The thermal conductivities (κ) at RT~930 K were calculated as the product of the material densities, specific heats and thermal diffusivities (with uncertainty below 10%), which was measured using TC-1200RH. The heat capacities (C_p) were estimated using Dulong–Petit rule, C_v = 3nR (where n is the number of atoms per formula unit, R is the gas constant). The total uncertainty for ZT is ~18%. The lattice contributions (κ_L) were obtained by subtracting the electronic part (κ_e) from the total κ, i.e., κ_L = κ − κ_e. Here κ_e is expressed by the Wiedemann–Franz law, κ_e = L₀σT, where L₀ is the Lorenz number, estimated at 1.5 × 10⁻⁸ WΩK⁻² for not fully degenerate environment of semiconductors¹².

The parameters were finalized after several repeated measurements using different samples.

Results and Discussion

Structural analyses

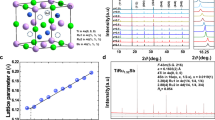
The x-ray diffraction patterns (Fig. S1) shows that the materials can be indexed as a tetragonal cell²⁰ (PDF:51-1221) with a = 5.7461~5.7709 and c = 11.4996~11.5340 Å, without any impurity phases identified in all the composition range (x = 0~0.5). In XRD patterns several diffraction peaks are apparent, namely: (110), (202) or (210) and (114), which are characteristic of the CuIn₃Se₅ phase with the space group  ^{20,32,33,34,35}. The lattice parameters a and c, which are in agreement with those reported^24,25,35, both increase linearly with Te content increasing, see Fig. 1a. indicating that the chalcopyrite lattice suffers dilation upon Te substitution for Se. Since the tetragonal deformation parameter η and u are also directly related to the mean cation-anion distances d_I–VI and d_III–VI in chalcopyrite compounds³¹, an equal d_I–VI and d_III–VI values can be obtained as η (or u) approaches unity (or 0.25)³¹. The calculated ∆u, d_Cu-Se and d_In-Se values are presented in Fig. 1b,c. With the Te content increasing, the ∆u decreases gradually from 0.32 × 10⁻³ to −0.34 × 10⁻³, and it approaches zero at x ≈ 0.15 (Fig. 1b), at which d_Cu-Se roughly equals to d_In-Se (Fig. 1c).

Figure 1

(a) Lattice constants a and c as a function of Te content (x value) in CuIn₃Se_5−xTe_x, they all increase linearly with x value; (b) Anion position displacement ∆u = 0.25−u, which decreases with x value. At x = 0.1, ∆u = 0.15 × 10⁻³, while at x ≈ 0.15, ∆u = 0; (c) Mean cation-Se distance d_Cu-Se and d_In-Se as a function of Te content (x value), at x ≈ 0.15, i.e. ∆u = 0, the difference between d_Cu-Se and d_In-Se gets the minimum.

In order to confirm the dilation of the crystal structure upon Te substitution, the microstructure analysis using HRTEM for the sample with x = 0.1 is shown in Fig. 2, while that for Te-free sample is shown in Fig. S2 for comparison. Figure 2a is the selected area electron diffraction (SAED) pattern, and Fig. 2b,c are the EDS measurement results and high resolution image respectively. It is apparent that the materials show a conventional polycrystalline structure consisting of many nano-domains. The boundaries between nano-domains are not coherent, and ambiguously terminate at a grown domain 15~20 nm in size. Fig. 2d is the magnified high resolution TEM image, which shows that the d spacing between (112) crystal planes is about 0.345 nm. Figure S2a is SAED pattern, and Fig. S2b,c are the EDS measurement results and high resolution image for Te-free sample. Figure S2d is the magnified high resolution TEM image, which shows that the d spacing between (112) crystal plane is about 0.335 nm. An increase in d spacing upon Te substitution is resulted from the dilation of the crystal lattice, and is in accordance with the elongated lattice constants from XRD analyses.

Figure 2

High resolution transmission electron microscopy (HRTEM) image observed in CuIn₃Se_4.9Te_0.1, (a) The selected area electron diffraction (SAED) pattern; (b) Chemical compositions analyses using EDS spectra; (c) High resolution TEM image, showing a conventional polycrystalline structure consisting of many nano-domains; (d) Magnified high resolution TEM image, which shows that the spacing between (112) crystal planes is about 0.345 nm.

Transport properties and TE performance

Although the isoelectronic substitution of Te for Se creates no extra electrons or holes, the dilation of the crystal structure upon such a substitution should have a profound impact on the structural and transport properties. In order to verify this conclusion, the Hall coefficients were measured at room temperature (RT), and the Hall carrier concentrations (n_H) and mobility (μ) were then calculated. The results are shown in Fig. 3. The measured n_H value, which is 4.11 × 10²¹ m⁻³ at x = 0, comparable to those from Jacob (3.40 × 10²¹ m⁻³)³⁶ and Ariswan (1.16 × 10²¹ m⁻³)³⁷, reaches the highest (6.27 × 10²³ m⁻³) at x = 0.1 and then reduces to 1.58 × 10²¹ m⁻³ at x = 0.5. While the mobility (μ) tends to increase from 1.62 cm² V⁻¹ s⁻¹, which is less than that from Jacob (12.8 cm² V⁻¹ s⁻¹)³⁶, to the highest 35.48 cm² V⁻¹ s⁻¹ at x = 0.5.

Figure 3: Measured Hall carrier concentration (n_H) and mobility (μ) against x value in CuIn₃Se_5−xTe _x .

The results from Jocob³⁶, Ariswan et al.³⁷ are presented for comparison.

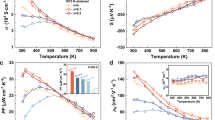
Since the carrier concentration is inversely related to the Seebeck coefficient (α), it is believed that there is a specific Te content at which the maximum α value can be attained. Surprisingly, in the present work the sample at x = 0.1 has the highest Seebeck coefficients among all samples below ~825 K (Fig. 4a), although the α values for different samples converge at high temperatures. The sample at x = 0.1 gives the highest σ value at ~930 K, at which the α and σ values are −292.58 μV.K⁻¹ and 2.05 × 10³ Ω⁻¹ m⁻¹ respectively (Fig. 4b). The lattice contribution κ_L as a function of temperature is shown in Fig. 4c, where the κ_L value reduces with temperature increasing for all the samples. The κ_L value at x = 0.1 is the lowest over the entire temperature range, and at T = 930 K it gives 0.37 WK⁻¹ m⁻¹. At x ≥ 0.1 the κ_L increases with κ_L = 0.61 WK⁻¹ m⁻¹ (x = 0.2) and 0.52 WK⁻¹ m⁻¹ (x = 0.5). An insert is the total thermal conductivity κ, which has a similar composition dependence with κ_L, suggesting the heat carrying by phonons dominates in these compounds.

Figure 4

TE properties as function of temperature, (a) Seebeck coefficient (α); (b) Electrical conductivity (σ); (c) lattice thermal conductivity (κ_L), where an inset is the total κ; (d) ZT values, an inset is the relation of ZT value with Te content (x value).

Combining the three physical parameters (α, σ and κ), the dimensionless figure of merit (ZT) is shown in Fig. 4d. The highest ZT value of the sample at x = 0.1 is 0.4 at 930 K. An insert is the plot of ZT against x value in CuIn₃Se_5−xTe_x. Although this ZT value is still lower than those of other chalcopyrites, such as CuGaTe₂-based (ZT = 1.22 at 850 K¹³; 0.91~1.07 at 703 K^17,19,38; 1.4 at 940 K³⁹), AgInSe₂-based alloys (1.05@815 K¹⁸, and CuInTe₂-based (0.69@737 K⁴⁰, 1.18 and 1.3 at 850 K^41,42), it is ~2.6 times that of intrinsic CuIn₃Se₅ (ZT = ~0.15).

Upon the substitution of element Te for Se, we engineer the crystal structure (Fig. 1). At x = 0.1, there is a relatively big difference between d_Cu-Se and d_In-Se, along with the highest carrier concentration. Therefore, the lowest κ_L values are mainly due to the heavy phonon scattering caused by the lattice distortion, coupled with the phonon-carrier interaction. However, the phonon-carrier scattering strength is relatively less important in the temperature range of the present study, therefore, the phonon scattering in the lattice defects plays a major role in reducing the κ_L value. Furthermore, both the Seebeck coefficient and carrier concentration reach the highest at x = 0.1 simultaneously, which is not consistent with the common relationship between the Seebeck coefficient and carrier concentration. We believe that the origin might be due to the alteration of the band structure.

In order to gain a deep understanding of the band structure upon Te incorporation, the Pisarenko plots are shown in Fig. S3, assuming m* = 0.006, 0.08, 0.11 and 0.34m_e at RT respectively. The data from Jocob³⁶ and Dejlle et al.²⁷ are plotted together for comparison. The α values for the Te-incorporated samples at RT slightly increase with n_H increasing, but the Pisarenko relations can exactly capture the measured values of Seebeck coefficient under assumed effective masses m*. In this sense, the alteration of the bandgap should be taken into consideration.

Figure 1c shows the simultaneous elongation of the bond lengths d_Cu-Se and d_In-Se. This elongation is mainly caused by the increased repulsion between cation and anion upon Te substitution for Se, due to the lower electronegativity of Te (2.1) than that of Se (2.5), thus increasing the covalency degree⁴³. In fact, the bond length d_Cu-Se increases more rapidly than d_In-Se with Te content increasing. As consequence, when x exceeds ~0.15 the bond length d_Cu-Se is longer than d_In-Se. This suggests that the hybridization (bonding) between Cu-d and Se-p near the bandgap region has been weakened, resulting in the increased bandgap energy^44,45,46. To confirm this result, the bandgap (E_g) is estimated as a function of x value using E_g = 2α_maxeT⁴⁷, here T is the temperature at which α appears with the maximum value. Although such an estimation could result in a large deviation of E_g⁴⁸, it can roughly estimate the variation tendency of the E_g value with chemical composition in some chalcopyrites, for example, the variation tendency of the E_g value with Mn content in Mn-incorporated Cu₃Ga₅Te₉ system⁴⁹. The results are shown in Fig. 5a. The E_g values obtained in this work are still less than reported by Ariswan (1.15 eV)³⁷ and Marín (1.23 eV)²⁴. However, it is observed that the bandgap (E_g) is rapidly enlarged with Te content increasing, and at x = 0.1 (∆u = 0.15 × 10⁻³) it reaches the highest value of 1.05 eV. Above x = 0.1 it is gradually reduced with Te content increasing. At x ≈ 0.15 (∆u = 0) the E_g value is estimated to be ~0.90 eV. The reduction in E_g above x ≥ 0.1 might be due to the reduced ionicity upon Te substitution for Se, proposed by Honeyman after he observed that energy gap increases with the crystalline ionicity increasing⁵⁰. Since the high energy gap could prevent the degradation of thermoelectric power through inhibiting the formation of the thermally activated minority carriers^6,51, that is why we have observed the highest Seebeck coefficients (Fig. 4a) and carrier concentration (Fig. 3) at x = 0.1. In addition, upon the substitution of Te for Se the relatively effective mass of the carrier (m*/m_e) increases rapidly with Te content from m*/m_e = 0.007 (x = 0) to m*/m_e = 0.342 (x = 0.1) (m_e: mass of the electron), and then decreases with Te content increasing at x ≥ 0.1, see Fig. 5b, which suggests that a proper substitution of Te could optimize the band structures.

Figure 5

(a) E_g value, roughly estimated using E_g = 2α_maxeT, against x value, which increases with x value increasing until at x = 0.1. At x ≈ 0.15 E_g ≈ 0.90 eV. The E_g values from Ariswan³⁷ and Marín et al.²⁴ are presented for comparison.; (b) The relatively effective mass (m*/m_e) as a function of Te content. At x = 0.1 the highest m*/m_e value is obtained; (c) The quality factor B at RT, defined by B = μ_H(m*/m_e)^3/2T^5/2/κ_L, as a function of x value. The B value increases until at x = 0.1, and then decreases with x increasing.

Since the chalcopyrite compound at x = 0.1 has the highest m*/m_e value, carrier concentration and lowest κ_L value, hence a highest quality factor B (B = μ_H(m*/m_e)^3/2T^5/2/κ_L)¹² can be anticipated. We therefore plot B value at near RT as a function of x, shown in Fig. 5c. In Fig. 5c we observed that the B value rapidly increases with x value increasing until x = 0.1, and then it decreases. Therefore, we consider that it is not necessary to let x > 0.1 (∆u = 0.15 × 10⁻³ at x = 0.1) in order to improve the TE performance. When x > 0.1 (for example: ∆u → 0 when x → 0.15), the TE performance may degrade owing to the enhanced lattice contribution κ_L. In fact, the ZT value reaches the highest at x = 0.1 (see the insert in Fig. 4d), corresponding to ∆u = 0.15 × 10⁻³. ZT value vs ∆u is plotted in Fig. 6, where the ZTs against ∆u in other chalcopyrite compounds, such as, CuGa_1−xIn_xTe₂³⁸, annealed CuGaTe₂¹⁹ and CuIn_1−xZn_xTe₂⁴⁰, are also presented for comparison. It is worth noting that at ∆u = 0, corresponding to x = 0.15, neither the E_g (E_g ≈ 0.90 eV) nor the ZT value reaches the highest, see Figs 5a and 6. The insert in Fig. 6 is close-up view of present relation between ZTs and ∆u in this work. These chalcopyrite compounds all show that they do not have the highest ZTs at ∆u = 0, but at a certain ∆u value, i.e. at a distance (∆δ) from ∆u = 0 they give the highest ZTs. This indicates that the best TE performance can be achieved with a certain crystal structure parameters for each chalcopyrite compound with a specific space group. This finding is in good agreement with the previous assumption that when ∆u = 0 or η = 1 it is difficulty to achieve the highest TE performance for some chalcopyrite compounds, due not only to electrical inactivity, but also a relatively high lattice part κ_L.

Figure 6: The ZTs against ∆u.

The maximum ZTs from different chalcopyrites, such as, CuGa_1−xIn_xTe₂³⁸, annealed CuGaTe₂¹⁹ and Cu_1−xIn_1−xZn_2xTe₂⁴⁰ are presented for comparison. These chalcopyrite compounds all show that they do not have the highest ZTs at ∆u = 0, but at a certain ∆u value. An insert is close-up view of present relation between ZTs and ∆u. The ZT value reaches the highest at ∆u = 0.15 × 10⁻³, rather than at ∆u = 0.

Conclusions

In this work the chalcopyrite compounds CuIn₃Se_5−xTe_x (x = 0~0.5) with space group have been prepared, and the dilation of the crystal structure as x value increases has been observed. At x = 0.15 the anion position displacement ∆u is tending to be zero. But at x = 0.1 (∆u = 0.15 × 10⁻³) both the band energy (E_g) and the Hall carrier concentration n_H reach the highest values, leading to the best thermoelectric performance with the ZT value of 0.4 at 930 K. Furthermore, at x = 0.1 it is the critical Te content in CuIn₃Se_5−xTe_x (x = 0~0.5), above which the quality factor B decreases, and lattice thermal conductivity κ_L are higher than those at x = 0.1, caused by reduced phonon scattering in lattice defects. We therefore conclude that the best thermoelectric performance can be achieved at a certain ∆u value (∆u ≠ 0) if one can engineer the crystal structures of the chalcopyrite with a specific space group.