Abstract
We propose and demonstrate a novel physical computing paradigm based on an engineered unipolar memristor that exhibits symmetric SET switching with respect to voltage polarity. A one-dimensional array of these devices was sufficient to demonstrate an efficient Hamming distance comparator for two strings of analog states represented by voltages from the physical world. The comparator first simultaneously applies the two sets of voltages to the array of memristors, each of which is initially in its high resistance state and switches to its low resistance state only if the two voltages applied on that memristor differ by more than the switching threshold. An accurate analog representation of the Hamming distance is then obtained by applying a reading voltage to the memristors and summing all the resultant currents. The comparator with a small footprint can directly process analog signals and store computation results without power, representing a promising application for analog computing based on memristor crossbar arrays.
Similar content being viewed by others
Introduction
Physical computing systems utilize physics laws (e.g., ohm’s law) to directly sense and respond to the analog world and most efficiently store and output the computing results1,2. Emerging devices, such as memristors, may be engineered to enable this attractive computing paradigm. An efficient analog Hamming distance comparator based on memristor arrays demonstrated in this study serves as a typical example of a physical computing system based on new devices. For any pair of strings or words of equal length, the Hamming distance is defined as the total number of positions where the symbols or characters of the pair are different from each other in the corresponding coordinate positions. In other words, the Hamming distance measures the minimum number of changes required to transform one string into the other. It is a widely used concept in information theory, with numerous applications in coding, error correction and cryptography3,4,5,6,7,8,9,10. One example of the use of the Hamming distance is an estimate of the transmitted signal quality through counting the number of flipped bits in a fixed-length binary word. The Hamming distance is also used in genetic mapping by the counting number of nucleotide differences between two gene sequences11.
Any strings or words can be converted into a sequence code based on binary bits. The task of a Hamming distance comparator in a digital system is to count the number of binary bit flips that occur in the corresponding digits of two sequences. Using two 8-bit-streams as an example, 01101001 and 10101000 have a Hamming distance of three, i.e., there are flips in the first, second, and eighth bits. Implementing the comparator logic in hardware usually requires an array of 1-bit cells. Traditionally, the Hamming distance is calculated in a digital circuit, for example, by Exclusive OR (XOR) gates performing a bit-wise comparison of the incoming bits followed by a corresponding decision logic. A full sequence-length comparator circuit can be significantly faster, but at the expense of a larger circuit area and more logic gates. Sequence processing with fewer logic gates is more efficient in circuit area but requires more clock cycles. For digital circuits, the power consumption is proportional to the circuit capacitance and the number of signal transitions, making the efficiency of the traditional Complementary Metal–Oxide–Semiconductor (CMOS) approach low. This is greatly exacerbated when the word or string comparison involves an analog input signal, which requires an analog-to-digital converter (ADC). In this paper, we present a simple yet efficient architecture to perform analog Hamming distance computation utilizing memristors, which are two-terminal passive devices that change resistance upon electrical stimulation and stay in a non-volatile state after the switching. Memristors have attracted significant attention as a potential next generation non-volatile memory12,13,14,15,16,17,18,19,20,21,22. Efforts have also been made recently to utilize these devices for data processing in new applications such as analog and neuromorphic computing23,24,25,26,27,28,29,30,31,32, pattern recognition33,34,35, security applications36,37 and so on. In one embodiment of these devices, the resistance can be electrically switched between two states: a high-resistance state (HRS) and a low-resistance state (LRS). The switching from the HRS to LRS is called “SET” or “ON” switching, and conversely from the LRS to HRS is called “RESET” or “OFF” switching. Nonvolatile memristors can be classified into two categories: bipolar and unipolar (or nonpolar). Bipolar switching refers to the case where one voltage polarity is used for SET while the opposite polarity is required for RESET. In contrast, the SET and RESET in unipolar switching can occur with the same polarity of the applied voltage38,39. Recently, in the newly developed diffusive memristors32, the OFF/ON ratio could be over 1E10. In addition, these diffusive memristors can relax back to the HRS under zero bias, which negates the process of resetting all the devices and can be favorable in some applications.
In this study, we designed unipolar memristors with an electrically symmetrical SET-switching and a large ON/OFF conductance ratio, as presented in Fig. 1. Figure 1(a) shows an optical microscopic image of a 32 × 32 memristor crossbar (MC) and the inset to Fig. 1(a) schematically illustrates the device structure. TiO2-based unipolar memristors were fabricated with symmetrical Pd electrodes. A thin Ta layer was deposited in order to enhance the adhesion of the bottom electrode to the SiO2/Si substrate. In addition, an Au layer was inserted between the Pd and the Ta layers in the bottom electrode and also deposited on the Pd layer in the top electrode to reduce the line resistance of the 32 × 32 MC. Figure 1(b) shows SET and RESET switching operations, which can be obtained with either positive or negative voltages (bottom electrode was grounded) with good symmetry and reproducibility in both voltage and current. In addition, by optimizing the thickness and fabrication conditions, an electroforming process was not needed to precondition the device for the subsequent SET and RESET switching operations. The SET was performed by using a quasi-DC voltage sweep with a current compliance, while no current compliance was used for RESET. The SET and RESET symmetries are important for a Hamming distance comparator because the voltage difference could be positive or negative depending on the amplitudes of the reference and input voltages. Figure 1(b) also shows the device has an ON/OFF conductance ratio of ~1000 at 0.2 V. The large ON/OFF conductance ratio increases the signal to noise ratio (SNR) by suppressing the background OFF current and enables a larger MC size for longer string comparison. Figure 1(c) and (d) present the measured variances of the operation voltages from cycle to cycle and from device to device, respectively. The average and standard deviation for the ON states of both polarities was 1.52905 ± 0.20446 V for positive and −1.59078 ± 0.19791 V for negative polarity. The uniform distributions of the SET and RESET threshold voltages demonstrated in the fabricated devices determined the accuracy of the Hamming distance comparator.
(a) Optical microscopic image of a 32 × 32 memristor crossbar. The inset is a schematic illustration of the device stack structure. (b) Semi-log plot of the I–V curves for switching. (c) Cycle-to-cycle variability of a single device. (d) Device-to-device variability for 32 memristors. The average and standard deviation for the ON states of both polarities was 1.52905 ± 0.20446 V for positive and −1.59078 ± 0.19791 V for negative polarity.
For digital circuits, the voltage level for the bit “1” or “0” is usually assigned a fixed value. For example, 3 V may be assigned to represent bit “1” and 0 V to represent bit “0”. There will always be DC voltage variations and AC fluctuations for analog signals. For our Hamming distance comparator, it is extremely valuable to perform direct analog comparisons without going through an ADC. This is important for applications in the internet of things (IoT) and wearable devices, since data gathered by sensors are usually in analog form and a Hamming distance needs to be computed against a known reference. For example, the outputs from temperature sensors and motion sensors are analog voltage levels within a predetermined range. If we compute the Hamming distance using the sum of currents via Kirchoff’s Laws, we want the total current to be linearly proportional to the number of different bits. In other words, we need the unipolar memristors to be always SET to the same level of resistance with input voltages of varying amplitudes (corresponding to different comparison codes), but over any SET switching threshold voltage. Two-wire electrical characterizations were carried out by applying defined voltages across the unipolar devices. Figure 2 shows the input switching voltage conditions and post switching current readings on the corresponding devices. As seen in Fig. 2(a), the 32 input voltages from 0 V to 5 V were applied to one electrode of each of the 32 diagonal devices, while the other electrode was grounded. A compliance current of 1 mA was enforced during the SET switching to limit over-switching and prevent permanent breakdown of a memristor. One of the key factors is to produce the same LRS in all the devices, which requires that the conduction channels in all the switched memristors to have similar sizes. Figure 2(b) shows the measured currents for all the memristors pre- and post-switching using a 0.2 V reading voltage. For any applied voltage amplitude below 1.5 V, a device remained in the HRS with a resistance of around 0.2 Mohm. Devices were switched to a LRS around 400 ohm for >2 V voltage amplitude difference (referenced from Ground). With a current compliance, the unipolar memristors exhibited nearly identical LRS and HRS after SET or RESET switching, respectively. This provides the required linear correlation between the summed current and the number of devices switched in the comparator circuit.
(a) With one electrode grounded, input voltages ranging from 0 V to 5 V were applied to the other electrode of each of the 32 devices. A compliance current of 1 mA was enforced to control the resistance level of the LRS. (b) Measured current through each memristor pre- and post-switching using a 0.2 V reading voltage.
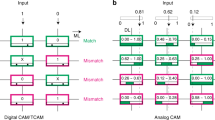
Using the unipolar memristor discussed above, a fully populated MC (i.e. a switch device in every row and column junction) was constructed for the demonstration of Fig. 3. Just a diagonal array of the devices was utilized, since only N diagonal memristors are needed for an N-bit comparison for this Hamming distance computation. More compact circuit geometries are possible in practical applications as shown in Fig. 3(d,e), but the experiments and measurements here took advantage of existing memristor crossbar fabrication procedures and electrical measurement facilities. The compact circuit will enjoy better accuracy since there will be essentially no sneak path current. There are three primary steps to compute the Hamming distance for N bit strings (An…A2A1) and (Bn…B2B1), as shown in Fig. 3(b):
(a) Schematic illustration of the core circuit architecture. (b) Steps for the comparator operation. (c) Active unipolar memristors on a full-populated crossbar with only diagonal devices utilized. The input and read conditions are indicated. The rest of the memristor devices highlighted in grey color are un-used devices and they will remain in the HRS all the time, which will have minimum impact to the circuit operation. (d) Unipolar memristors only exist on the diagonal line of a crossbar with the input and read conditions indicated for practical application. (d) Unipolar memristors on the in-line architecture with the input and read conditions indicated for practical application.
Step 1: All unipolar memristors are RESET to the HRS. This ensures the Hamming distance comparator operation is not affected by previous operations.
Step 2: The bit strings (An…A2A1 and Bn…B2B1) are input using their corresponding voltage levels (digital or analog values) to the rows and columns, respectively, as shown in Fig. 3(a). If bits Ai and Bi have the same voltage or the voltage difference between them is less than the threshold, the memristor at the cross-point of the ith Row and ith column will remain in the HRS. However, if bits Ai and Bi have a voltage difference greater than the threshold, the unipolar memristor will switch into the LRS state with the compliance current enforced on either the rows or columns.
Step 3: A small read voltage is subsequently applied to the columns (or rows) of the crossbar and the rows (or columns) are grounded. The summed current from the MC, which is an analog value for the Hamming distance, is measured and can be translated to a digital value using a trans-impedance amplifier (TIA) and an experimentally calibrated ADC.
Figure 4 shows two examples of analog string comparison. Figure 4(a)–(c) are case 1 with a Hamming distance of 15: Fig. 4(a) presents the actual voltages for the two strings to be compared; Fig. 4(b) shows the voltages applied on each device normalized by the corresponding reference voltage, which can be used to easily determine whether a device will be switched or not; Fig. 4(c) shows the pre-comparison validation (all devices in the HRS, black squares) and the post comparison devices (red dots) with high currents for those devices that switched to their LRS states. In this case, 15 devices were switched, yielding a Hamming distance of 15, which corresponds to a measured total current of 7.97 mA. Figure 4(d)–(f) provide another example with a Hamming distance of 13, corresponding to a current of 6.94 mA. Figure 5 shows a plot of the total measured current vs. the number of switched devices, which exhibits a fairly linear relationship. The current contribution from the unswitched devices is negligible because of the very large ON/OFF conductance ratio of the memristors. As an example, when the measured total current was 7.97 mA, the estimated number of switched memristors from the linear fit was 15.36 and the actual Hamming distance was 15. Thus, the Hamming distance comparator demonstrated reasonable accuracy even in the case of analog value comparison.
(a–c) Case 1 with Hamming distance = 15. (a) The actual voltages for the two strings to be compared; (b) the normalized voltage differences by setting reference voltages to 0 for each device; (c) pre-comparison validation (all devices are in the HRS) and current readings of post-comparison devices, some of which exhibit the LRS with a high current level. In this case, 15 devices have been switched, corresponding to a Hamming distance of 15. (d–f) Similarly for case 2 with a Hamming distance equal to 13.
In conclusion, we have constructed and demonstrated a new physical computing system, which directly senses analog inputs and performs computing within one step. The output results are stored in the computing system without requiring energy. Specially designed unipolar memristors are utilized for this demonstration. The results here provide an encouraging example and a pathway toward physical computing using emerging electronic devices.
Experimental Procedure
Pd/TiO2/Pd memristor device fabrication
Standard photolithography and lift-off processes for top and bottom Pd electrodes were used for the MC fabrication. The device area of an individual memristor was 5 μm × 5 μm. In an sputtering system (AJA international, Orion 8), around 20-nm-thick TiO2 layer was deposited on a 30-nm-thick Pd/Au(50 nm)/Ta(3 nm)/SiO2/Si substrate using a commercial TiO2 target under a 7 mtorr of Ar (20 sccm) and O2 (5 sccm) ambient. The Pd bottom electrode, Au and Ta layers were deposited by thermal evaporation system (CHA, SE-600). Finally, a 30-nm-thick Pd top electrode and then a 50-nm-thick Au were deposited by thermal evaporation system.
Electrical Measurements
DC electrical characterizations and MC switching operations were carried out using an Agilent B1500A Precision Semiconductor Parameter Analyzer.
Additional Information
How to cite this article: Ge, N. et al. An efficient analog Hamming distance comparator realized with a unipolar memristor array: a showcase of physical computing. Sci. Rep. 7, 40135; doi: 10.1038/srep40135 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
J. A. Stankovic, I. Lee, A. Mok & R. Rajkumar . Opportunities and obligations for physical computing systems. Computer 38(11), 23–31 (2005).
D. O’Sullivan & T. Igoe . Physical computing: sensing and controlling the physical world with computers. Course Technology Press (2004).
G. Forney . Generalized minimum distance decoding. Information Theory, IEEE Transactions on 12(2), 125–131 (1966).
A. Steane . Error correcting codes in quantum theory. Physical Review Letters 77(5), 793 (1996).
R. D’hulst & G. J. Rodgers . The hamming distance in the minority game. Physica A: Statistical Mechanics and its Applications 270(3), 514–525 (1999).
M. Fujino & V. G. Moshnyaga . An efficient Hamming distance comparator for low-power applications. In Electronics, Circuits and Systems 2, 641–644 (2002).
B. Parhami . Efficient Hamming Weight Comparators for Binary Vectors Based on Accumulative and Up/Down Parallel Counters. Ieee Transactions On Circuits And Systems 56(2), 167–171 (2009).
F. Kagan Gürkaynak, Y. Leblebici & D. Mlynek . A compact high-speed hamming distance comparator for pattern matching applications. Proc. 9th Eur. Signal Process. Conf 1–9 (1998).
H. J. Mattausch, N. Omori & S. Fukae . Fully-parallel pattern-matching engine with dynamic adaptability to Hamming or Manhattan distance. In VLSI Circuits Digest of Technical Papers 252–255 (2002).
H. Li et al. A learnable parallel processing architecture towards unity of memory and computing. Scientific Reports 5, 13330 (2015).
C. D. Pilcher, J. K. Wong & S. K. Pillai . Inferring HIV Transmission Dynamics from Phylogenetic Sequence Relationships. PLoS Med 5(3), 0350–0352 (2008).
D. B. Strukov, G. S. Snider, D. R. Stewart & R. S. Williams . The missing memristor found. Nature, 453(7191), 80–83, May (2008).
J. J. Yang et al. High switching endurance in TaOx memristive devices. Applied Physics Letters 97(23), 232102-232102-3, Dec (2010).
J. J. Yang et al. Memristive switching mechanism for metal/oxide/metal nanodevices. Nature Nanotechnology 3(7), 429–433 (2008).
M. J. Lee et al. A fast, high-endurance and scalable non-volatile memory device made from asymmetric Ta2O5-x/TaO2-x bilayer structures. Nature Materials 10(8), 625–630 (2011).
D. Kwon et al. Atomic structure of conducting nanofilaments in TiO2 resistive switching memory. Nature Nanotechnology 5(2), 148–453 (2010).
J. H. Yoon et al. Highly Uniform, Electroforming‐Free, and Self‐Rectifying Resistive Memory in the Pt/Ta2O5/HfO2‐x/TiN Structure. Advanced Functional Materials 24(32), 5086–5095 (2014).
J. H. Yoon et al. Pt/Ta2O5/HfO2− x/Ti resistive switching memory competing with multilevel NAND flash. Advanced Materials, 27(25), 3811–3816 (2015).
I. Valov, R. Waser, J. R. Jameson & M. N. Kozicki . Electrochemical metallization memories—fundamentals, applications, prospects. Nanotechonology 22(25), 254003 (2011).
I. Valov & M. N. Kozicki . Cation-based resistance change memory. Journal of Physics D: Applied Physics, 46(7), 074005 (2013).
A. Wedig et al. Nanoscale cation motion in TaOx, HfOx and TiOx memristive systems. Nature Nanotechonology, 11(1), 67–74 (2016).
H.-S. P. Wong et al. Metal–oxide RRAM. Proceedings of the IEEE 100(6), 1951–1970 (2012).
J. J. Yang, D. B. Strukov & D. R. Stewart . Memristive devices for computing. Nature Nanotechnology 8(1), 13–24 (2013).
S. H. Jo et al. Nanoscale Memristor Device as Synapse in Neuromorphic Systems. Nano Letters 10(4), 1297–1301 (2010).
K. Kim et al. A Functional Hybrid Memristor Crossbar-Array/CMOS System for Data Storage and Neuromorphic Applications. Nano Letters 12(1), 389 (2012).
L.-B. Bernabé & S.-G. Teresa . Memristance can explain spike-time-dependent-plasticity in neural synapses. Nature precedings 1 (2009).
M. Hu et al. Dot-product engine for neuromorphic computing: programming 1T1M crossbar to accelerate matrix-vector multiplication. In Proceedings of DAC 53 (2016).
M. Prezioso et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2015).
S. Gaba, P. Sheridan, J. T. Zhou, S. Choi & W. Lu . Stochastic memristive devices for computing and neuromorphic applications. Nanoscale 5(13), 5872–5878 (2013).
T. Ohno et al. Short-term plasticity and long-term potentiation mimicked in single inorganic synapses. Nature Materials 10(8), 591–595 (2011).
S. Yu, Y. Wu, R. Jeyasingh, D. Kuzum & H.-S. P. Wong . An Electronic Synapse Device Based on Metal Oxide Resistive Switching Memory for Neuromorphic Computation. Electron Devices, IEEE Transactions on 99, 1–9 (2011).
Z. R. Wang et al. Memristors with diffusive dynamics as synaptic emulators for neuromorphic computing. Nature materials, doi: 10.1038/nmat4756 (2016).
F. Corinto, A. Ascoli & M. Gilli . Analysis of current-voltage characteristics for memristive elements in pattern recognition systems. International Journal Of Circuit Theory And Applications 40(12), 1277–1320 (2012).
P. Sheridan, W. Ma & W. Lu . Pattern Recognition with Memristor Networks. IEEE ISCAS 1078–1081 (2014).
M. Chu, B. Kim & S. Park . Neuromorphic Hardware System for Visual Pattern Recognition With Memristor Array and CMOS Neuron. IEEE Transactions on Industrial Electronics 62(4), 2410–2419 (2015).
J. Rajendran, G. S. Rose, R. Karri & M. Potkonjak . Nano-PPUF: A Memristor-based Security Primitive. IEEE ISVLSI 84–87 (2012).
G. S. Rose, N. McDonald, L. K. Yan & B. Wysocki . A Write-Time Based Memristive PUF for Hardware Security Applications. IEEE ICCAD 830–833 (2013).
T. Yanagida et al. Scaling effect on unipolar and bipolar resistive switching of metal oxides. Scientific reports 3, 1657 (2013).
X. Sun et al. Unipolar memristors enable “stateful” logic operations via material implication. Applied Physics Letters 99(7), 072101 (2011).
Acknowledgements
This work was supported in part by the U.S. Air Force Research Laboratory (AFRL) (Grant No. FA8750-15-2-0044), U.S. Air Force Office for Scientific Research (AFOSR) (Grant No. FA9550-12-1-0038), and the National Science Foundation (NSF) (ECCS-1253073). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of AFRL. Part of the device fabrication was conducted in the clean room of the Center for Hierarchical Manufacturing (CHM), an NSF Nanoscale Science and Engineering Center (NSEC) located at the University of Massachusetts Amherst.
Author information
Authors and Affiliations
Contributions
N.G. conceived the concept. N.G., J.J.Y., and J.H.Y. designed the experiments. J.H.Y. fabricated the devices and performed electrical measurements. M.H., E.J.M., N.D., J.P.S., Z.L., H.H., Q.X. and R.S.W. helped with experiments and data analysis. N.G., J.H.Y., J.J.Y., Q.X. and R.S.W. wrote the paper. All authors discussed the results and implications and commented on the manuscript at all stages.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ge, N., Yoon, J., Hu, M. et al. An efficient analog Hamming distance comparator realized with a unipolar memristor array: a showcase of physical computing. Sci Rep 7, 40135 (2017). https://doi.org/10.1038/srep40135
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep40135
This article is cited by
-
An artificial nociceptor based on a diffusive memristor
Nature Communications (2018)
-
Analogue signal and image processing with large memristor crossbars
Nature Electronics (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.