Abstract
We analyze the process of strong field ionization using the Bohmian approach. This allows retention of the concept of electron trajectories. We consider the tunnelling regime of ionization. We show that, in this regime, the coordinate distribution for the ionized electron has peaks near the points in space that can be interpreted as exit points. The interval of time during which ionization occurs is marked by a quick broadening of the coordinate distribution. The concept of the exit point in the tunneling regime, which has long been assumed for the description of strong field ionization, is justified by our analysis.
Similar content being viewed by others
Introduction
An atom exposed to a strong laser field can be ionized. The Keldysh theory1 (also known as the strong field approximation or SFA theory) provides a basis for understanding this process and introduces the well-known classification of ionization phenomena based on the value of the Keldysh parameter  . (Here ω, E and |ε0| are the frequency, field strength and ionization potential of the target system, expressed in atomic units). The ionization regime corresponding to the values γ ≫ 1 is known as the multi-photon regime. The opposite limit, γ ≲ 1, is known as the tunnelling regime2. Depending on the ionization regimes, the ionization process is described in drastically different ways1,2.
. (Here ω, E and |ε0| are the frequency, field strength and ionization potential of the target system, expressed in atomic units). The ionization regime corresponding to the values γ ≫ 1 is known as the multi-photon regime. The opposite limit, γ ≲ 1, is known as the tunnelling regime2. Depending on the ionization regimes, the ionization process is described in drastically different ways1,2.
The tunnelling regime is particularly interesting since many features of tunnelling ionization and its accompanying phenomena are directly related to applications such as high harmonic generation (HHG), attosecond pulse generation and above-threshold ionization. Simple models based on the concept of electron trajectory have been developed in order to describe these phenomena. A well-known example demonstrating the great utility of such models is the famous simple man model (SMM)2,3,4,5,6, reproducing many qualitative features of strong field phenomena. The semiclassical TIPIS (tunnel ionization in parabolic coordinates with induced dipole and Stark shift) model5,7,8 is known to produce quite accurate quantitative results5,6,7,9,10.
In the TIPIS and similar approaches, the quantum-mechanical Keldysh theory and its modifications1,11,12,13,14,15 provide initial velocity distributions6,7,9 for the subsequent classical electron motion. The initial value of the coordinate is defined either by the Field Direction Model (FDM)10 or, in a more refined approach based on use of the parabolic coordinate system16, as a point at which electron emerges from under the barrier. This separation of the tunnelling ionization process in the quantum-mechanical part, describing the ionization event proper, and the classical part, describing subsequent motion, has been extremely fruitful, as it allows us to consider processes occurring in the strong laser field for systems that are too complex to allow an ab initio quantum mechanical (QM) treatment. It has been demonstrated17,18 that for small values of the Keldysh parameter, deep in the tunnelling regime, the results obtained using TIPIS agree very well quantitatively with the results of the Perelomov-Popov-Terentiev (PPT) theory13, which considers all stages of the electron motion fully quantum-mechanically. Despite this success, the concept of the electron exit point remains somewhat elusive. This is mainly due to the wave nature of QM.
In the present work we explore the view of the ionization process offered by the so-called Bohmian QM19. Bohmian QM introduces a well-defined notion of the electron trajectory. One need not be misled by the name into believing that Bohmian QM is something drastically different from orthodox QM. The difference between Bohmian and orthodox QM is, largely, only in the interpretation of the role of the wave-function. Bohmian mechanics reproduces exactly all the predictions of orthodox QM20. One does not need to subscribe to the Bohmian interpretation, moreover, to use its useful features, such as the concept of the electron trajectory. This feature has been exploited to describe ionization of atoms21,22 and molecules23,24 driven by strong laser fields, and for the description of the HHG process25,26. An approach to the problem of the tunnelling time, based on Bohmian QM, has been described recently in ref. 27. In the present work, we show that, by following the Bohmian trajectories, we can introduce the coordinate distributions describing ionized electrons. In particular, we can find a justification for the notion of the exit point.
Theory
We recapitulate briefly a few facts constituting the basis of the Bohmian approach to quantum mechanics19. Substituting the polar form of the wave function of a system (we consider for simplicity a one-electron system), Ψ( r , t) = R( r , t) exp {iS( r , t)} with R( r , t) = |Ψ( r , t)| and S( r , t) = arg(Ψ( r , t)), into the time-dependent Schrödinger equation and taking real and imaginary parts, one obtains:


where the quantum potential and the velocity field are respectively defined as:

and

The Bohmian interpretation involves assuming that the velocity field (4) generates a family of electron trajectories for an ensemble of particles. At the initial time, t = 0, the coordinates of the particles constituting the ensemble are distributed as prescribed by the usual R2( r , 0) rule of QM. Initial velocities of the particles of the ensemble are given by Eq. (4), evaluated at t = 0. Electron trajectories for t > 0 can be found by integrating Eq. (4) along each trajectory, provided that the velocity field, v ( r , t), is known as a function of coordinates and time. Alternatively, one may note that Eq. (1) is a Hamilton-Jacobi equation for a system described by the quantum potential (3). One may, therefore, find Bohmian trajectories by solving Newton’s equations of motion that are equivalent to the Hamilton-Jacobi equation (1), with the initial conditions specified above.
We consider a hydrogen atom in the field of a laser pulse Ez = E0f(t)cos ωt, polarized along the z-direction, which we use as a quantization axis. The pulse envelope function is f(t) = sin2 (πt/T1), where T1 is the total pulse duration. We performed calculations for pulses with T1 = 3T and T1 = 4T, where T = 2π/ω is an optical cycle (o.c.) of the field. We present results for various field strengths and frequencies, corresponding to the tunnelling regime of ionization. The initial state of the system is the ground state of the hydrogen atom. To solve the fully three-dimensional time-dependent Schrödinger equation (TDSE), we employed the procedure described in the works28,29. The atom-laser field interaction is described using the length gauge.
Using the time-dependent wave-function Ψ( r , t) provided by the TDSE, we can rewrite Eq. (4) in an equivalent way as:

where  is momentum operator. This equation gives us the velocity field as a function of spatial coordinates and time. Since the wave-function in our approach is defined on a spatial grid, we obtain the velocity field at the grid-points. The velocity field at other points is found by means of the Lagrange interpolation procedure. Due to the symmetry of the problem with respect to rotations around the z-axis, it is sufficient to compute the velocity field in any plane containing the z-axis. We choose the (x, z)- plane for this purpose. For the initial ground state of the hydrogen atom, all the Bohmian trajectories launched at t = 0 have zero velocities. It is a well-known feature of Bohmian QM19 that the velocity field in a state described by a real wave-function is zero. The physical possibility of this state of motion in the Bohmian picture is due to the fact that the force corresponding to the quantum potential (3) vanishes for such states, allowing particles to stay at rest.
is momentum operator. This equation gives us the velocity field as a function of spatial coordinates and time. Since the wave-function in our approach is defined on a spatial grid, we obtain the velocity field at the grid-points. The velocity field at other points is found by means of the Lagrange interpolation procedure. Due to the symmetry of the problem with respect to rotations around the z-axis, it is sufficient to compute the velocity field in any plane containing the z-axis. We choose the (x, z)- plane for this purpose. For the initial ground state of the hydrogen atom, all the Bohmian trajectories launched at t = 0 have zero velocities. It is a well-known feature of Bohmian QM19 that the velocity field in a state described by a real wave-function is zero. The physical possibility of this state of motion in the Bohmian picture is due to the fact that the force corresponding to the quantum potential (3) vanishes for such states, allowing particles to stay at rest.
Having obtained the velocity field v ( r , t) in the (x, z)- plane, we launch an ensemble (≈5 × 105 trajectories) of electron trajectories. The evolution of the trajectories in time is found by numerically integrating the system of differential equations  with the initial conditions x(0) = x0, z(0) = z0 in the (x, z)- plane.
with the initial conditions x(0) = x0, z(0) = z0 in the (x, z)- plane.
Some of the trajectories obtained in this way describe electrons remaining bound, while some describe ionized electrons. Two typical examples for different pairs of initial conditions, x0, z0, producing bound and ionized trajectories, are shown in Fig. 1.
(Red) solid line: bound trajectory zb(t) launched with initial conditions x0 = 0, z0 = 0.5 a.u. (Blue) dots: ‘ionized trajectories’ zi(t) with x0 = 0.3 a.u., z0 = 3.5 a.u. For better visibility, two vertical axes are used – the left vertical axis shows the range of the z-values for the bound trajectory zb(t), while the right vertical axis shows the range of z-values for the ionized trajectory zi(t). Inset shows dependence of the character of the electron trajectory on the initial coordinates in the (x, z)-plane. The initial values (x0, z0) corresponding to the ionized trajectories are in the (red) filled area.
The overall character of the trajectories can be inferred from the inset in Fig. 1, where we left uncolored the region in the (x, z)-plane from which bound trajectories originate. We define ‘ionized trajectories’ here as those trajectories for which the distance of the electron from the atomic core at the end of the pulse exceeds a threshold value Rmin. We found that the particular value of Rmin is not important, as long as the value of this parameter exceeds atomic dimensions. We use below Rmin = 10 a.u.
As in ordinary statistical mechanics, an ensemble of particles can be described using distribution functions. At any time t1 > 0, a distribution function ρ(Ω, t1) giving the probability of detecting an electron with coordinates r and velocity v , lying inside a region, Ω, of the electron’s phase-space can be found as:

where ϕ0( r ) is the initial ground state wave-function of the hydrogen atom, N is an overall normalization factor, and only trajectories ending in Ω at t = t1 are included in the sum. We impose one further restriction on the trajectories included into the sum (6). We are interested in those members of our ensemble for which ionization has occurred. This means that we must separate the distribution function describing the ionized subsystem from the total ensemble. This separation is necessary if the ionization probability is small and the contribution of the ionized electrons is difficult to see. To separate the ionized trajectories, we use the same criteria we employed above, including in the sum in Eq. (6) only those trajectories for which the distance of the electron from the atomic core at the end of the pulse exceeds the value Rmin. We should note that, with this choice of the parameter Rmin, the electrons which end up in the Rydberg atomic states after the end of the pulse are counted as ionized. This procedure agrees with the physical picture we are describing in the manuscript. Our aim is to follow the development of the ionization process in time. We must, therefore, take into account all the electron trajectories for which ionization event occurred at least once during the time interval of the pulse duration. It has been suggested30 that the dominant mechanism, leading to the population of the Rydberg states in the tunnelling regime, is the frustrated tunnelling ionization (FTI), a two-step process including tunnelling and subsequent rescattering. The majority of the electrons ending up in the Rydberg atomic states must, therefore, undergo ionization during the interval of the pulse duration.
For practical computation of the sum in Eq. (6), we launch the trajectories at time t = 0 with the initial conditions in phase-space region Ω0 = D0 × {0}, i.e. initial coordinates (x0, z0) in a region D0 of the (x, z)-plane, and zero velocities. For the region D0, we take a rectangle in the x, z-plane: |z| < 6 a.u., 0 < x < 6 a.u. The rectangle is divided into a number of squares, each with a side length of 0.01 a.u. Similarly, the phase-space volume at the time t = T1 at the end of the pulse is divided into a set of regions Ωi (with each Ωi being a direct product of squares with a side length of 0.01 a.u. in the momentum and coordinate spaces). With phase-space thus discretized, the discretized version of the distribution (6) can be obtained (apart from an overall normalization factor) as a number of trajectories arriving at the time t = T1 into a given region Ωi, weighted with the appropriate scaling factor, depending on the coordinate probability distribution in the initial state. We checked that the results we obtain are stable with respect to variations of the discretization parameters.
From the point of view of the statistical mechanics, the procedure encapsulated in Eq. (6) is equivalent to solving the Liouville equation for the distribution function describing the ensemble:

where {A, B} is a Poisson bracket,  , with a quantum potential defined in Eq. (3), and a distribution function describing the ensemble at the initial time t = 0 given by ρ( r, v , 0) = |ϕ0( r )|2δ( v ). We shall be interested not in the full distribution function, but in the reduced quantity W(z, t), describing the probability distribution for the electron coordinate along the laser polarization direction. This can be obtained by integrating ρ(Ω, t1) over all variables except z. A discretized version of this distribution function can be computed by including in the sum in Eq. (6) all the ionized trajectories having, at time t, a value of z-coordinate between z − Δ/2 and z + Δ/2. We use Δ = 0.01 a.u. in the calculation.
, with a quantum potential defined in Eq. (3), and a distribution function describing the ensemble at the initial time t = 0 given by ρ( r, v , 0) = |ϕ0( r )|2δ( v ). We shall be interested not in the full distribution function, but in the reduced quantity W(z, t), describing the probability distribution for the electron coordinate along the laser polarization direction. This can be obtained by integrating ρ(Ω, t1) over all variables except z. A discretized version of this distribution function can be computed by including in the sum in Eq. (6) all the ionized trajectories having, at time t, a value of z-coordinate between z − Δ/2 and z + Δ/2. We use Δ = 0.01 a.u. in the calculation.
Results and Discussion
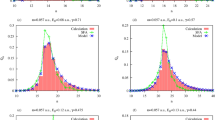
Distribution functions, W(z), calculated according to the recipe described above, are shown in Fig. 2 for the tunnelling regime of ionization (Keldysh parameter γ = 0.57 for the field parameters used to obtain the results presented in the Figure). One can clearly see that the distribution obtained in the tunneling regime has a double peak structure for small t, meaning that the ionization predominantly originates from two points along the polarization vector direction, which can be interpreted as exit points. This observation agrees with FDM.
To see how an ionized electron moves in the laser field, we follow the evolution of W(z) as time evolves. As the top panel of the Fig. 2 shows, in the case of tunneling ionization by a laser pulse with a total duration of 3 optical cycles, the distribution is a narrow-peaked function of z for all t except when the absolute value of the electric field of the pulse reaches a local maximum. In a narrow interval, including the local maximum at t ≈ 1.5T, W(z) undergoes a qualitative change. For this interval of time W(z) becomes a broad coordinate distribution, extending far into the region of large positive z-values. This long tail, which the distribution W(z) acquires, ensures that for a short period of time around the local field maximum, the probability to find an electron at the distances from the atom exceeding typical atomic dimensions increases dramatically. Natural interpretation of this behavior is to consider it as a signature of a burst of ionization in the Bohmian picture. This interpretation is further supported by the behavior of W(z) in the intervals of time containing secondary field maxima at t = T and t = 2T. In these intervals the distribution W(z) undergoes similar qualitative changes, developing tails extending far into the region of large negative z-values, with the implications that the probability to find an electron at large distances from the atom rises considerably. This behavior is consistent with the pulse shape shown in the inset in the top panel of the Fig. 2, electric field lowering the barrier in positive z-direction for t = 1.5T and negative z-direction for t = T and t = 2T, thus enabling electron to escape in these directions.
We have performed analogous calculations for other field parameters (different pulse strengths and pulse durations) and found that the described behavior is quite typical for the tunnelling regime of ionization, as evidenced by the results shown in Figs 2 and 3. In all cases, the tails in W(z) appear only in relatively short intervals of time, in agreement with the well-known fact that ionization predominantly occurs in short time intervals around the peak field strength. We may interpret the appearance of these tails in the coordinate distribution as a signature of ionization bursts in the Bohmian picture of ionization. The value of z immediately before the time when the tails appear may then be interpreted as the exit point, i.e. the z-value of the electron coordinate at the time when electron exits from under the barrier. This value is to be understood in the probabilistic sense, as the distribution W(z) at the time before the electron’s exit has finite width. This width is, however, relatively small, and this justifies the concept of a well-defined exit point that is often assumed in simulations5,7.
Top panel: distribution W(z) for E0 = 0.0534 a.u., ω = 0.057 a.u. Bottom panel: distribution W(z) for E0 = 0.12 a.u., ω = 0.057 a.u. Pulse duration 3 optical cycles (pulse shape shown in the inset in the top panel of Fig. 2).
Figure 4 gives a more detailed view of the process of the formation of the tails in the tunnelling regime, illustrating the evolution of the distribution W(z) for different times around the mid-point of the pulse shown in the inset in Fig. 2. One can observe the fast process of the development of a tail in the coordinate distribution, W(z) undergoing a change from a narrow to a broadly-peaked function of z in a short interval of time around the maximum peak field strength. This agrees with the probabilistic view of the exit time10. As present results show, the coordinate of the exit point should also be understood in a probabilistic sense.
The evolution of the distribution W(z) with time. E0 = 0.1 a.u., ω = 0.057 a.u., pulse duration 3 optical cycles (pulse shape shown in the inset in the top panel of Fig. 2).
To understand better the Bohmian perspective of the development of the ionization process in the tunnelling regime, let us consider in more detail the quantum potential given by the Eq. (3). The Bohmian trajectories are real for all the interval of the pulse duration. The tunnelling in the Bohmian picture occurs not because the trajectory at some point becomes complex (as in the quantum orbits31,32 approach), but because the quantum potential (3) effectively removes the barrier. For electric fields that are not too strong, when the depletion of the ground state can be neglected, the time-dependent wave-function of the system can be written as Ψ( r , t) = ϕ0e−iεt + ϕi( r , t), where ϕ0e−iεt is the time-evolved ground state wave-function and ϕi(t) describes the ionized wave-packet. The SFA ionization amplitudes, which are the Fourier transforms  of the ϕi(t), are essentially Gaussian functions of the velocity components14. The main dependence of the amplitude on the velocity in the polarization direction (which interests us presently) is given, for a hydrogen atom, by the factor14:
of the ϕi(t), are essentially Gaussian functions of the velocity components14. The main dependence of the amplitude on the velocity in the polarization direction (which interests us presently) is given, for a hydrogen atom, by the factor14:  , where h(γ) = arcsinhγ − γ(1 + γ2)−1/2, γ is the instantaneous value of the Keldysh parameter. The characteristic length on which
, where h(γ) = arcsinhγ − γ(1 + γ2)−1/2, γ is the instantaneous value of the Keldysh parameter. The characteristic length on which  changes appreciably in v-space is, therefore, a ≈ (2ω)1/2h(γ)−1/2. The characteristic length on which ϕi(z, t) changes in the coordinate space (assuming Gaussian character of
changes appreciably in v-space is, therefore, a ≈ (2ω)1/2h(γ)−1/2. The characteristic length on which ϕi(z, t) changes in the coordinate space (assuming Gaussian character of  ) is then 2/a. From this estimate and from the Eq. (3), defining the quantum potential, we may deduce that as long as we stay close to the atomic core, so that |ϕi( r , t)| ≪ |ϕ0( r )|, the contribution to the quantum potential due to the ionized wave-packet is confined to the region z ≲ 2a−1. This point is illustrated in Fig. 5, where the snapshots of the quantum potential computed according to Eq. (3), are given for several times around the maximum field strength for the pulse with shape shown in the inset in the top panel of Fig. 2. The quantum potential VQ( r , t) = VQ(0, 0, z, t), evaluated along the laser polarization axis, is shown.
) is then 2/a. From this estimate and from the Eq. (3), defining the quantum potential, we may deduce that as long as we stay close to the atomic core, so that |ϕi( r , t)| ≪ |ϕ0( r )|, the contribution to the quantum potential due to the ionized wave-packet is confined to the region z ≲ 2a−1. This point is illustrated in Fig. 5, where the snapshots of the quantum potential computed according to Eq. (3), are given for several times around the maximum field strength for the pulse with shape shown in the inset in the top panel of Fig. 2. The quantum potential VQ( r , t) = VQ(0, 0, z, t), evaluated along the laser polarization axis, is shown.
One can see that, at time t1 = 1.45T near the pulse midpoint, the quantum corrections effectively remove the barrier in the positive z–direction, so that a classical escape trajectory is possible. (This point is better illustrated in the bottom panel of Fig. 5, which shows potential curves under magnification). For times t2 = 1.6T, t3 = 1.35T, farther from the pulse midpoint, the barrier is closed. The quantum corrections to the potential are due to the part of the wave-function describing the ionized wave-packet, and using the estimate we made above, we find that these corrections manifest themselves close to the atomic core in the region z ≲ 3 a.u. for the field parameters in the Fig. 5. These corrections may become important again near the nodes of the wave-function, where the condition |ϕi( r , t)| ≪ |ϕ0( r )| is not satisfied. Figure 5 supports these assertions. For z-values outside the range of the quantum corrections due to the ionized wave-packet, VQ(z, t) is (up to an insignificant constant factor) just the potential E(t1)z describing the electron interaction with the instantaneous electric field of the pulse, provided the trajectory does not pass through a node of the wave-function. As Fig. 5 shows, this is the case for the trajectory escaping at t1 = 1.45T in the positive z-direction. The electron motion along this trajectory after the ionization event can be described considering only the laser field, which is a basic assumption made in the SMM.
The coordinate of the exit point can be estimated using a variant of the FDM formula obtained using parabolic coordinates to take full account of the Coulomb atomic potential:  10. Here I is the ionization potential and E- is the z– component of the electric field at the peak strength. This formula gives ze ≈ 3.6 a.u. for the field parameters in Fig. 4, in good agreement with the location of the peak of the distribution W(z) at the instant when it broadens and describes (in the picture we developed above) the time of ionization.
10. Here I is the ionization potential and E- is the z– component of the electric field at the peak strength. This formula gives ze ≈ 3.6 a.u. for the field parameters in Fig. 4, in good agreement with the location of the peak of the distribution W(z) at the instant when it broadens and describes (in the picture we developed above) the time of ionization.
To summarize, we have performed an analysis of the strong field ionization process based on the Bohmian approach. An advantage offered by the Bohmian approach, which we have exploited in the present work, is the possibility of using the well-defined notion of an electron trajectory that is valid on the whole interval of the duration of the laser-atom interaction, including the interval of the sub-barrier motion. After the ionization event, the Bohmian trajectories describing ionized electrons are essentially the classical trajectories describing electron motion in a laser field. This provides a connection between the Bohmian approach and the SMM. Using the Bohmian approach, we defined the notion of the distribution of the electron coordinate in the direction of the laser field, and this sets initial conditions for the subsequent classical motion. This distribution undergoes rapid changes at times when ionization occurs, remaining a sharply-peaked function of z for times immediately prior to the ionization event. This can be interpreted as a justification of the notion of the electron coordinate at the exit point.
A question arises: can the results presented above be obtained using prescriptions of the conventional QM? To answer this question, one should note that the statement that the Bohmian approach leads to the same predictions as conventional QM requires a qualification. This statement is literally true, i.e. there is a one-to-one correspondence between the predictions of the Bohmian and conventional QM only when the latter provides an unambiguous answer33. Consider, as an example, the tunnelling time problem, which has been discussed recently in ref. 27 or transmission time, discussed in ref. 33. One can propose several definitions of the tunnelling time (e.g., Larmor time, Büttiker-Landauer time, Eisenbud-Wigner time), based on various aspects of the description of the motion based on conventional QM27. Analogously, several plausible definitions for the transition time can be given within the framework of conventional QM33. The Bohmian approach, on the other hand, leads to definitions of these concepts that are based on the the so-called ‘dwell time’ (i.e. the time a particle spends inside a given region), which in the Bohmian picture is defined in a quite natural and essentially unique way. (For discussions of the relations between Bohmian time and tunnelling and transmission times, see refs 27 and 33, respectively.) This essential uniqueness is an attractive feature of the Bohmian approach. The situation with the exit point is similar, the Bohmian approach offers the possibility of defining this notion in a natural way.
Additional Information
How to cite this article: Ivanov, I. A. et al. Exit point in the strong field ionization process. Sci. Rep. 7, 39919; doi: 10.1038/srep39919 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Keldysh, L. V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. -JETP 20, 1307 (1965).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163 (2009).
Lewenstein, M., Balcou, P., Ivanov, M. Y., L’Huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117 (1994).
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994 (1993).
Shvetsov-Shilovski, N. I., Dimitrovski, D. & Madsen, L. B. Ionization in elliptically polarized pulses: Multielectron polarization effects and asymmetry of photoelectron momentum distributions. Phys. Rev. A 85, 023428 (2012).
Arbo, D. G. et al. Ionization of argon by two-color laser pulses with coherent phase control. Phys. Rev. A 92, 023402 (2015).
Pfeiffer, A. N. et al. Probing the longitudinal momentum spread of the electron wave packet at the tunnel exit. Phys. Rev. Lett. 109, 083002 (2012).
Hofmann, C., Landsman, A., Cirelli, C., Pfeiffer, A. & Keller, U. Comparison of different approaches to the longitudinal momentum spread after tunnel ionization. J. Phys. B 46, 125601 (2013).
Dimitrovski, D. & Madsen, L. B. Theory of low-energy photoelectrons in strong-field ionization by laser pulses with large ellipticity. Phys. Rev. A 91, 033409 (2015).
Landsman, A. S. & Keller, U. Attosecond science and the tunnelling time problem. Physics Reports 547, 1 (2015).
Faisal, F. H. M. Multiple absorption of laser photons by atoms. J. Phys. B 6, L89 (1973).
Reiss, H. R. Effect of an intense electromagnetic field on a weakly bound system. Phys. Rev. A 22, 1786 (1980).
Perelomov, A. M., Popov, V. S. & Terentiev, M. V. Ionization of atoms in an alternating electric field. Sov. Phys. -JETP 23, 924 (1966).
Popov, V. S. Tunnel and multiphoton ionization of atoms and ions in a strong laser field. Physics-Uspekhi 47, 855 (2004).
Ammosov, M. V., Delone, N. B. & Krainov, V. P. Tunnel ionization of complex atoms and of atomic ions in an alternating electromagnetic field. Sov. Phys. -JETP 64, 1191 (1986).
Hu, B., Liu, J. & Chen, S. G. Plateau in above-threshold-ionization spectra and chaotic behavior in rescattering processes. Phys. Lett. A 236, 533 (1997).
Hofmann, C., Landsman, A. S., Zielinski, A., Cirelli, C., Zimmermann, T., Scrinzi, A. & Keller, U. Interpreting electron-momentum distributions and nonadiabaticity in strong-field ionization. Phys. Rev. A 90, 043406 (2014).
Landsman, A. S. & Keller, U. Tunnelling time in strong field ionisation. J. Phys. B 47, 204024 (2014).
Bohm, D. A suggested interpretation of the quantum theory in terms of “hidden” variables. Physical Review 85, 166 (1952).
Bell, J. S. Speakable and Unspeakable in Quantum Mechanics (Cambridge University Press, Cambridge, 1987).
Botheron, P. & Pons, B. Self-consistent bohmian description of strong field-driven electron dynamics. Phys. Rev. A 82, 021404(R) (2010).
Jooya, H. Z., Telnov, D. A., Li, P.-C. & Chu, S.-I. Exploration of the subcycle multiphoton ionization dynamics and transient electron density structures with bohmian trajectories. Phys. Rev. A 91, 063412 (2015).
Sawada, R., Sato, T. & Ishikawa, K. L. Analysis of strong-field enhanced ionization of molecules using bohmian trajectories. Phys. Rev. A 90, 023404 (2014).
Takemoto, N. & Becker, A. Visualization and interpretation of attosecond electron dynamics in laser-driven hydrogen molecular ion using Bohmian trajectories. J. Chem. Phys. 134, 074309 (2011).
Wu, J., Augstein, B. B. & de Morisson Faria, C. F. Bohmian-trajectory analysis of high-order-harmonic generation: Ensemble averages, nonlocality, and quantitative aspects. Phys. Rev. A 88, 063416 (2013).
Jooya, H. Z., Telnov, D. A., Li, P.-C. & Chu, S.-I. Investigation of the characteristic properties of high-order harmonic spectrum in atoms using bohmian trajectories. J. Phys. B 48, 195401 (2015).
Zimmermann, T., Mishra, S., Doran, B. R., Gordon, D. F. & Landsman, A. S. Tunneling time and weak measurement in strong field ionization. Phys. Rev. Lett. 116, 233603 (2016).
Ivanov, I. A. Evolution of the transverse photoelectron-momentum distribution for atomic ionization driven by a laser pulse with varying ellipticity. Phys. Rev. A 90, 013418 (2014).
Ivanov, I. A. & Kheifets, A. S. Time delay in atomic photoionization with circularly polarized light. Phys. Rev. A 87, 033407 (2013).
Nubbemeyer, T., Gorling, K., Saenz, A., Eichmann, U. & Sandner, W. Strong-Field Tunneling without Ionization. Phys. Rev. Lett. 101, 233001 (2008).
Yan, T.-M., Popruzhenko, S. V., Vrakking, M. J. J. & Bauer, D. Low-energy structures in strong field ionization revealed by quantum orbits. Phys. Rev. Lett. 105, 253002 (2010).
Becker, W., Goreslavski, S. P., Milošević, D. B. & Paulus, G. G. Low-energy electron rescattering in laserinduced ionization. J. Phys. B 47, 204022 (2014).
Leavens, C. R. The “tunneling time problem”: fundamental incompatibility of the Bohm trajectory approach with the projector and conventional probability current approaches. Phys. Lett. A 197, 88 (1995).
Acknowledgements
This work was supported by IBS (Institute for Basic Science) under IBS-R012-D1 and the National Institute of Supercomputing and Network/Korea Institute of Science and Technology Information with supercomputing resources, including technical support (KSC-2015-C1-0005).
Author information
Authors and Affiliations
Contributions
All authors contributed to discussions and the preparation of the manuscript. I.A.I. performed the calculations.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ivanov, I., Nam, C. & Kim, K. Exit point in the strong field ionization process. Sci Rep 7, 39919 (2017). https://doi.org/10.1038/srep39919
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep39919
This article is cited by
-
Non-local temporal interference
Scientific Reports (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.