Abstract
A systematic study of the crystal structure of a layered iron oxypnictide LaFeAsO1−xHx as a function of pressure was performed using synchrotron X-ray diffraction. This compound exhibits a unique phase diagram of two superconducting phases and two parent phases. We established that the As–Fe–As angle of the FeAs4 tetrahedron widens on the application of pressure due to the interspace between the layers being nearly infilled by the large La and As atoms. Such rarely observed behaviour in iron pnictides implies that the FeAs4 coordination deviates from the regular tetrahedron in the present systems. This breaks a widely accepted structural guide that the superconductivity favours the regular tetrahedron, albeit the superconducting transition temperature (Tc) increases from 18 K at ambient pressure to 52 K at 6 GPa for x = 0.2. In the phase diagram, the second parent phase at x ~ 0.5 is suppressed by pressure as low as ~1.5 GPa in contrast to the first parent phase at x ~ 0, which is robust against pressure. We suggest that certain spin-fluctuation from the second parent phase is strongly related to high-Tc under pressure.
Similar content being viewed by others
Introduction
Iron pnictides are a new family of high-temperature superconductors, whose charge carriers located primarily in the two-dimensional iron plane play an active role in its superconductivity1,2,3,4. The supporting pnictide (Pn) atoms strongly perturb the 3d multi-orbital bands of Fe atoms through hybridization between Fe-3d and Pn-p electrons2,3,4. As a consequence, chemical substitution along with carrier-doping/chemical-pressure, or application of pressure on the crystal can drastically modify electronic properties, such as the superconducting transition temperature (Tc) of these materials2,3,4,5. Based on studies on chemical substitution in iron pnictides, an empirical guideline has been established that Tc is maximised when the geometry of the FePn4 unit approaches a regular tetrahedron6. The application of pressure is a direct and clean way to modify the local geometry of FePn4 without the degradation of the crystal in comparison to the chemical substitution; hence, the detailed crystal structure under pressure warrants further investigation.
One of the fascinating materials in iron pnictides is LaFeAsO1−xHx, which has a ZrCuSiAs-type structure with alternating stacks of conducting FeAs4 moieties and insulating (O, H)La4 layers (Fig. 1a) 7,8. LaFeAsO1−xHx exhibits a unique phase diagram on hydrogen anion substitution i.e. electron doping: two superconducting domes with Tc,max = 26 K at x ~ 0.08 (SC1) and Tc,max = 37 K at x ~ 0.35 (SC2), and two parent phases at x ~ 0 (PP1) and x ~ 0.5 (PP2)9,10,11,12. The SC2 and PP2 are rarely observed among high-Tc materials because they usually become normal metal in the heavily electron-doped region11. The resistivity behaviour changes from Fermi-liquid to non-Fermi liquid types with doping the electron, implying the electronic correlation developed in the higher x region7. Takahashi et al. have recently demonstrated that the application of pressure on LaFeAsO0.72H0.18 induced a notable enhancement of the Tc from 18 K at ambient pressure to 52 K at 6 GPa13. Interestingly, the maximum Tc of LaFeAsO0.72H0.18 under pressure was similar to that of Sm1111 (55 K), the highest known Tc among iron-based superconductors14.
Here, we examine the crystal structure of LaFeAsO1−xHx, (x = 0.0, 0.2, and 0.51), under pressure to analyse the relation between the FeAs4 geometry and the Tc. The results reveal that the FeAs4 unit deviates from regular tetrahedron on the application of pressure. This is an unexpected finding that breaks the hitherto believed guideline of approaching a regular FePn4 tetrahedron with an increase in Tc. Furthermore, we demonstrate that the peculiar PP2 is rapidly suppressed by pressure, while the conventional PP1 is robust against pressure15,16,17. We suggest that strong spin-fluctuations, originating from an orbital-selective Mott state in the PP2, is a key for enhancing the Tc under pressure. The pressure responses of the FeAs4 modification, the parent phases, and their correlation are previously unexplained peculiarities in 1111-type iron pnictides.
Results and Discussion
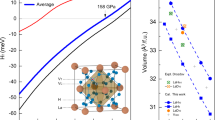
Figure 1b illustrates the lattice constants (a and c) of LaFeAsO1−xHx for x = 0, 0.20, and 0.51 as a function of pressure at room temperature (detailed experimental data in Supplementary Information, Table S1). No peak broadening was observed over the entire pressure range, indicating that the tetragonal systems are preserved (Supplementary information, Fig. S1a). For each value of x, the lattice parameters a and c decrease monotonically up to ~8 GPa with linear compressibilities of ka = 2.54–2.62 × 10−3 GPa−1 and kc = 5.50–5.64 × 10−3 GPa−1. These values agree with previously reported linear compressibilities of LaFeAsO0.72H0.18 and SmFeAsO13,18. ka and kc for all LaFeAsO1−xHx complexes are less than and similar to the respective corresponding values of 3.5 × 10−3 GPa−1 and 5.4 × 10−3 GPa−1 for BaFe2As219. The bulk moduli (B0) at all values of x are estimated as 100(1) GPa using the empirical Murnaghan equation of state (EOS): V/V0 = (1 + p(B’0/B0))−1/B’0, where V0 is the volume at ambient pressure and B0’ is fixed at 4.220.
The atomic positions are displayed in Fig. S1b (Supplementary Information). In Fig. 2a–c the Fe–As bond length (dFe−As), As–Fe–As bond angle (αAs-Fe-As), and As height from the Fe plane (hAs) are plotted as a function of pressure, where the parameters are described in the inset of Fig. 2a (detailed experimental data in Supplementary Information, Table S1). On the application of pressure, dFe-As and hAs decrease, while αAs-Fe-As increases i.e. opens up for all the compositions. The degree of pressure response of αAs-Fe-As is calculated to be +0.049, +0.18, and +0.24°/GPa for x = 0, 0.20, and 0.51, respectively. In contrast, that of αAs-Fe-As in BaFe2As2 and LiFe2As2 has been estimated at −0.48 and −0.29°/GPa, respectively, implying that their αAs-Fe-As bond-angles reduction with pressure21,22.
Pressure dependence of structural parameters for LaFeAsO1−xHx.
(a) Fe–As bond length (dFe-As). (b) As–Fe–As bond angle (αAs-Fe-As). (c) As height (hAs). (d) La–As distance (dLa-As). The inset in (a) describes the FeAs4 tetrahedron with the geometrical parameters. The marks are represented for x = 0 (red circles), 0.20 (green triangles), and 0.51 (blue squares). Almost all error bars are less than the size of the marks. (e) Modification of FeAs4 from ambient pressure (0 GPa) to 7.7 GPa for x = 0.20. The error bars represent the uncertainty in the least-squares fitting of the whole patterns in (a–d).
Pressure works primarily to infill the interspace between the FeAs4 conduction layer and the (O, H)La4 insulating layer. Figure 2d displays the La–As distances (dLa-As). Based on previous reports23,24, the sum of the radii of La and As ions was found to be 3.25 Å, which provides an estimate of the interspace distance. dLa-As and αAs-Fe-As change from 3.308(2) Å and 111.9(1)° at ambient pressure to 3.211(1) Å and 113.2(1)° at 7.7 GPa for x = 0.20, respectively (Fig. 2e). As dLa-As for x = 0.20 is close to the interspace filling limit, the pressure response of αAs-Fe-As results in a greater shift at higher x. Though the hard sphere perspective is simple, it can yield important findings with regard to superconductivity, but it has not been defined in explicit detail previously in the La1111 system17,25. Furthermore, as hAs can be calculated as: hAs = dFe-Ascos(αAs-Fe-As/2), it also responds to pressure and decreases significantly in the higher x region. On the other hand, in 122-type iron arsenides with a ThCr2Si2 structure, the drastic reduction of the As–As distance between the FeAs4 layers generally causes a structural collapse with the formation of an (As–As)4− molecule19,21, which possibly drives the reduction of αAs-Fe-As. This distinguishable response of 1111 and 122 compounds to pressure is attributed to the absence of an intervening blocking layer between two FeAs4 layers in the latter class of iron arsenides.
Figure 3 exhibits the contour plots of Tc against αAs-Fe-As and dFe-As under pressure, where the values of Tc in the whole map are interpolated from ref. 13. Since the thermal effect is small when compared to the pressure, it is valid to discuss the relation between the Tc and the structural parameters at room temperature. Pressure triggers the merge of the two SC domes at ambient pressure into a single SC dome along with an increase of Tc to 52 K at 6 GPa for x = 0.2. After the merge, the ridge line of Tc runs along the line for x = 0.20 as the pressure is increased.
In iron-based superconductors, the relation between the maximum Tc and structural parameters of FeAs4 has been proposed as follows: the highest Tc is achieved when αAs-Fe-As approaches 109.5° as in a regular tetrahedron of FeAs4 or when hAs ~ 1.38 Å6,26. Theoretical argument has been advanced that antiferromagnetic spin- or orbital-fluctuation is maximised as FeAs4 adopts a nearly regular tetrahedron geometry, leading to an optimum Tc27,28,29. The former is strongly related to the number and topology of Fermi surfaces, while the latter is due to the electron-phonon interaction. In agreement with the above rule, SmFeAsO0.78H0.22, which has the highest Tc of 55 K in iron pnictides, exhibits nearly ideal values of αAs-Fe-As (109.3°) and hAs (1.386 Å) at ambient pressure30. Moreover, the αAs-Fe-As for BaFe2As2 and LiFeAs act toward and away from the regular tetrahedron of FeAs4 along with increasing and decreasing the Tc, respectively21,22. However, our present results reveal that while αAs-Fe-As and hAs of LaFeAsO0.8H0.2 deviate from the optimum values with pressure (Fig. 3), there is a significant increase in Tc. Thus, this work highlights the inconsistencies in the guides for increasing the Tc. The electronic state calculations illustrate that the Fermi surface topologies of LaFeAsO0.8H0.2 are unaltered on the application of pressure (Supplementary Information, Fig. S2). Additionally, the band width of Fe-3d widens with pressure because of the shortening of dFe-As, resulting in a decrease of the spin-fluctuation that should cause Tc to decrease as well27. Thus, the properties examined so far fail to account for the increase of Tc under pressure.
In order to find the reason behind the enhancement of Tc, we next examined the parent phase under pressure. Both parent phases indicated tetragonal to orthorhombic (T–O) structural transitions (TS), and subsequently an antiferromagnetic ordering (TN). Figure 4a shows the temperature dependence of the full width at half maximum (FWHM) of the 220 reflection for x = 0.51, which is a good indicator of the T–O structural transition11. The transitions of TS2 are indicated by arrows and are estimated from the power law fitting. At 0.5 and 0.9 GPa, there is moderate broadening of the FWHM in the high-temperature region as extensive fluctuations occur in the vicinity of the structural transition. At 1.5 GPa, the FWHM exhibits slight broadening at low-temperature, not due to the structural transition but on account of the precursory phenomenon near the phase boundary. No broadening was observed at 3.2 GPa. Takahashi et al. demonstrated that an anomaly in resistivity, corresponding to TN2, for x = 0.51 was suppressed at ~2 GPa. This implies that the presence of TN2 as well as TS2, i.e. the PP2, vanished at low-pressure. Conversely, the PP1 could be seen up to 20 GPa (TN1) and 30 GPa (TS1) and was robust against pressure15,16,17. In Fig. 4b, we summarise the entire phase diagram of LaFeAsO1−xHx at ambient pressure and 6 GPa.
Full width at half maximum (FWHM) and electronic and structural phase diagram for LaFeAsO1−xHx.
(a) The FWHM of the 220 reflection at several pressures for x = 0.51 estimated by the single quasi-Voigt function. The arrows indicate the T–O structural transitions of TS2. The solid lines are guides to the eyes. Inset shows TS2 as a function of pressure. (b) The T vs x phase diagram of the parent phases (PP) with structural (TS) and magnetic (TN) transitions, and superconducting phases (SC) at 0 and 6 GPa. The PP1 and SC at 6 GPa are blue and red, respectively. The error bars represent the uncertainty in the least-squares fitting of the peaks in (a).
The distinct responses to pressure for both parent phases are unexpected and presumably arise due to their different origins. Since the origin of PP1 is interpreted as a spin density wave with Fermi surface nesting31,32, its robust behaviour of PP1 against pressure is consistent with insensitive change of the Fermi surface15,16,33. In contrast, the origin of PP2 is seemingly less relevant to the Fermi surface topology. Iimura et al. performed an electronic state calculation based on the molecular orbital concept for LaFeAsO1−xHx34. In the low x region, the bonding and antibonding states of the Fe-3d and As-4p orbitals give a large gap. This gap decreases rapidly with an increase in hAs, namely a decrease in the hybridization of Fe and As orbitals, making the non-bonding Fe-3dxy orbital the half-filled state. The resulting state implies that the orbital selective Mott state on Fe-3dxy is realised in the higher x region, i.e. in PP2, for LaFeAsO1−xHx35. Contrary to electron doping with increasing x, the pressure induces the rapid decrease of hAs as shown in Fig. 2c. Therefore, in contrast to PP1, PP2 can be easily broken by pressure.
Generally in high-Tc superconductors, the nature of the parent phase influences the superconducting state; that is, fluctuations derived from the parent phase may drive the pairing of the superconducting electrons. Thus, the origins of SC1 and SC2 adhering to PP1 and PP2, respectively, can be considered as fluctuations from PP1 and PP211. The former is the itinerant type spin-fluctuation32, and the latter is another type spin-fluctuation with a strongly localised character of the orbital selective Mott phase. Since PP2 disappears easily with pressure, the fluctuation from PP2 should also be sensitive to pressure. Thus, we suggest that the significant enhancement of Tc under pressure is mainly due to the favourable change of the latter fluctuation. The relation between the present results and the other mechanism of orbital- or charge-fluctuations remains unclear36,37,38,39. To identify the above suggestion, the further investigation on the spin/structural dynamics is required in this system.
Conclusion
We established that the FeAs4 tetrahedron in LaFeAsO1−xHx deviates from the regular one with applied pressure, which is inconsistent with the conventional believed structural guides for increasing the Tc. We found that the PP2 at x ~ 0.5 is lost under low-pressure, contrary to the sluggish pressure reaction of PP1 at x ~ 0. Pressure presumably suppresses the itinerant spin-fluctuation driving the superconductivity from PP1, but enhances another spin-fluctuation with the localised character from PP2 in 1111-type iron pnictides. These pressure responses of the FeAs4 modification and the parent phases are previously unexplained peculiarities in 1111-type. In future, we plan to further increase the Tc by combining the effects of the regular tetrahedron geometry of FeAs4 and the strong fluctuation state from PP2 under pressure in 1111 systems.
Methods
LaFeAsO1−xHx powder samples were prepared by a high-pressure solid-state reaction as reported in literature7. The hydrogen content in these systems was determined by thermal desorption spectroscopy. Synchrotron X-ray diffraction (sXRD) was performed at room temperature for pressures up to ~8 GPa at NE1A of PF-AR, KEK. Pressure was applied using a diamond anvil cell (DAC) with 600 μm culet diamond anvils and a gasket with a 300 μm hole. The DAC, in which the anvils are supported by the 45° tapered slit window without a backing plate, has the advantage of reducing the background scatter and simplifying the absorption correction of diamond (Supplementary Information, Fig. S3a). A very fine powder results in a perfect Debye ring of reflections on the two-dimensional image (Supplementary Information, Fig. S3b). The measured wavelength of λ = 0.4217 Å and the wide open angle of the DAC can approach a d-spacing of <0.7 Å, which enables accurate determination of atomic positions. The two-dimensional images collected using a RIGAKU R-AXIS on the curved imaging plate were integrated to yield 2θ-intensity data. Crystal structures were refined by the Rietveld method indexed to the space group of P4/nmm, and the reliable factors in the refinements were Rwp = 3.9–6.6% (Supplementary Information, Fig. S3c)40. Moreover, we traced the PP2 on the application of pressure by means of sXRD down to 8 K at BL-8B of PF, KEK, measured at λ = 0.8267 Å. A 4:1 methanol-ethanol mixture was used as a pressure transmitting medium in all the experiments.
Additional Information
How to cite this article: Kobayashi, K. et al. Pressure effect on iron-based superconductor LaFeAsO1−xHx: Peculiar response of 1111-type structure. Sci. Rep. 6, 39646; doi: 10.1038/srep39646 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-based layered superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 130, 3296 (2008).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645 (2010).
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589 (2011).
Hosono, H. & Kuroki, K. Iron-based superconductors: Current status of materials and pairing mechanism. Physica C 514, 399 (2015).
Sefat, A. S. Pressure effects on two superconducting iron-based families. Rep. Prog. Phys. 74, 124502 (2011).
Lee, C.-H. et al. Effect of Structural Parameters on Superconductivity in Fluorine-Free LnFeAsO1−y (Ln = La, Nd). J. Phys. Soc. Jpn. 77, 083704 (2008).
Iimura, S. et al. Two-dome structure in electron-doped iron arsenide superconductors. Nat. Commun. 3, 943 (2012).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272 (2011).
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899 (2008).
Qureshi, N. et al. Crystal and magnetic structure of the oxypnictide superconductor LaFeAsO1−xFx: A neutron-diffraction study. Phys. Rev. B 82, 184521 (2010).
Hiraishi, M. et al. Bipartite magnetic parent phases in the iron oxypnictide superconductor. Nat. Phys. 10, 300 (2014).
Fujiwara, N. et al. Detection of antiferromagnetic ordering in heavily doped LaFeAsO1−xHx pnictide superconductors using nuclear-magnetic-resonance techniques. Phys. Rev. Lett. 111, 097002 (2013).
Takahashi, H. et al. Superconductivity at 52 K in hydrogen-substituted LaFeAsO1−xHx under high pressure. Sci. Rep. 5, 7829 (2015).
Ren, Z.-A. et al. Superconductivity at 55 K in Iron-Based F-Doped Layered Quaternary Compound Sm[O1−xFx] FeAs. Chin. Phys. Lett. 25, 2215 (2008).
Okada, H. et al. Superconductivity under high pressure in LaFeAsO. J. Phys. Soc. Jpn 77, 113712 (2008).
Kawakami, T. et al. High-Pressure 57Fe Mössbauer Spectroscopy of LaFeAsO. J. Phys. Soc. Jpn. 78, 123703 (2009).
Kumar, R. S. et al. Pressure-induced superconductivity in LaFeAsO: The role of anionic height and magnetic ordering. Appl. Phys. Lett. 105, 251902 (2014).
Calamiotou, M. et al. Pressure and doping dependent anisotropic compressibility of the SmFeAsO1−xFx (x = 0.0–0.17) system. Physica C: Superconductivity 483, 136 (2012).
Mittal, R. et al. Ambient- and low-temperature synchrotron x-ray diffraction study of BaFe2As2 and CaFe2As2 at high pressures up to 56 GPa. Phys. Rev. B 83, 054503 (2011).
Garbarino, G. et al. Direct observation of the influence of the As-Fe-As angle on the Tc of superconducting SmFeAsO1−xFx . Phys. Rev. B 84, 024510 (2011).
Kimber, S. A. J. et al. Similarities between structural distortions under pressure and chemical doping in superconducting BaFe2As2 . Nat. Mater. 8, 471 (2009).
Mito, M. et al. Response of Superconductivity and Crystal Structure of LiFeAs to Hydrostatic Pressure. J. Am. Chem. Soc. 131, 2986 (2009).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr., Sect. A. 32, 751 (1976).
Nitsche, F., Jesche, A., Hieckmann, E., Doert, Th. & Ruck, M. Structural trends from a consistent set of single-crystal data of RFeAsO (R = La, Ce, Pr, Nd, Sm, Gd, and Tb). Phys. Rev. B 82, 134514 (2010).
Garbarino, G. et al. Correlated pressure effects on the structure and superconductivity of LaFeAsO0.9F0.1 . Phys. Rev. B 78, 100507(R) (2008).
Mizuguchi, Y. et al. Anion height dependence of Tc for the Fe-based superconductor. Supercond. Sci. Technol. 23, 054013 (2010).
Kuroki, K., Usui, H., Onari, S., Arita, R. & Aoki, H. Pnictogen height as a possible switch between high-Tc nodeless and low-Tc nodal pairings in the iron-based superconductors. Phys. Rev. B 79, 224511 (2009).
Usui, H. & Kuroki, K. Maximizing the Fermi-surface multiplicity optimizes the superconducting state of iron pnictide compounds. Phys. Rev. B 84, 024505 (2011).
Saito, T., Onari, S. & Kontani, H. Orbital fluctuation theory in iron pnictides: Effects of As-Fe-As bond angle, isotope substitution, and Z2-orbital pocket on superconductivity. Phys. Rev. B 82, 144510 (2010).
Matsuishi, S., Maruyama, T., Iimura, S. & Hosono, H. Controlling factors of Tc dome structure in 1111-type iron arsenide superconductors. Phys. Rev. B 89, 094510 (2014).
Klauss, H.-H. et al. Commensurate Spin Density Wave in LaFeAsO: A Local Probe Study. Phys. Rev. Lett. 101, 077005 (2008).
Kuroki, K. et al. Unconventional pairing originating from the disconnected fermi surfaces of superconducting LaFeAsO1−xFx . Phys. Rev. Lett. 101, 087004 (2008).
Opahle, I., Kandpal, H. C., Zhang, Y., Gros, C. & Valentí, R. Effect of external pressure on the Fe magnetic moment in undoped LaFeAsO from density functional theory: Proximity to a magnetic instability. Phys. Rev. B 79, 024509 (2009).
Iimura, S., Matsuishi, S. & Hosono, H. Heavy electron doping induced antiferromagnetic phase as the parent for the iron oxypnictide superconductor LaFeAsO1−xHx . Phys. Rev. B 94, 024512 (2016).
de’ Medici, L., Hassan, S. R., Capone, M. & Dai, X. Orbital-Selective Mott Transition out of Band Degeneracy Lifting. Phys. Rev. Lett. 102, 126401 (2009).
Kontani, H. & Onari, S. Orbital-Fluctuation-Mediated Superconductivity in Iron Pnictides: Analysis of the Five-Orbital Hubbard-Holstein Model. Phys. Rev. Lett. 104, 157001 (2010).
Yanagi, Y., Yamakawa, Y. & Ōno, Y. Two types of s-wave pairing due to magnetic and orbital fluctuations in the two-dimensional 16-band d-p model for iron-based superconductors. Phys. Rev. B 81, 054518 (2010).
Zhou, S., Kotliar, G. & Wang, Z. Extended Hubbard model of superconductivity driven by charge fluctuations in iron pnictides. Phys. Rev. B 84, 140505(R) (2011).
Thorsmølle, V. K., Khodas, M., Yin, Z. P., Zhang, Chenglin, Carr, V., Dai, Pengcheng & Blumberg, G. Critical quadrupole fluctuations and collective modes in iron pnictide superconductors. Phys. Rev. B 93, 054515 (2016).
Izumi, F. & Momma, K. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 130, 15 (2007).
Acknowledgements
We would like to thank K. Kuroki and Y. Kuramoto for their fruitful discussions. This work was supported by MEXT Elements Strategy Initiative to Form Core Research Centre and also by JSPS KAKENHI (No. 16K05434). This work is supported by approval of the Photon Factory Program Advisory Committee (Nos 2013S2-002, 2016S2-004, and 2015V002), and the Large Scale Simulation Program (No. 15/16-07 (FY2016)) at KEK.
Author information
Authors and Affiliations
Contributions
J.Y., Y.M., S.I., S. Matsuishi, H.H. conceived the study. K.K., J.Y., S. Maki, H.S. and R.K. measured the synchrotron X-ray diffraction. S.I. prepared the samples. H.T. supported the high-pressure experiments. K.K. and J.Y. co-wrote the manuscript. All the authors discussed the results and the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kobayashi, K., Yamaura, Ji., Iimura, S. et al. Pressure effect on iron-based superconductor LaFeAsO1−xHx: Peculiar response of 1111-type structure. Sci Rep 6, 39646 (2016). https://doi.org/10.1038/srep39646
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep39646
This article is cited by
-
Low Field Magnetic and Electric Transport Properties of LaFeAsO and Oxygen Deficiency of LaFeAsOx
Journal of Electronic Materials (2021)
-
Isovalent Substitution Effects of Arsenic on Structural and Electrical Properties of Iron-Based Superconductor NdFeAsO0.8F0.2
Journal of Superconductivity and Novel Magnetism (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.