Abstract
In the field of cardiac drug efficacy and safety assessment, information on drug concentration in heart tissue is desirable. Because measuring drug concentrations in human cardiac tissue is challenging in healthy volunteers, mathematical models are used to cope with such limitations. With a goal of predicting drug concentration in cardiac tissue, we have developed a whole-body PBPK model consisting of seventeen perfusion-limited compartments. The proposed PBPK heart model consisted of four compartments: the epicardium, midmyocardium, endocardium, and pericardial fluid, and accounted for cardiac metabolism using CYP450. The model was written in R. The plasma:tissues partition coefficients (Kp) were calculated in Simcyp Simulator. The model was fitted to the concentrations of amitriptyline in plasma and the heart. The estimated parameters were as follows: 0.80 for the absorption rate [h−1], 52.6 for Kprest, 0.01 for the blood flow through the pericardial fluid [L/h], and 0.78 for the P-parameter describing the diffusion between the pericardial fluid and epicardium [L/h]. The total cardiac clearance of amitriptyline was calculated as 0.316 L/h. Although the model needs further improvement, the results support its feasibility, and it is a first attempt to provide an active drug concentration in various locations within heart tissue using a PBPK approach.
Similar content being viewed by others
Introduction
According to current cardiac safety assessment guidelines, the focus is placed on in vitro hERG channel blockade1 as a predictive factor of in vivo QT interval prolongation1, which serves as a surrogate for torsades de pointes arrhythmia (TdP). However, the paradigm is shifting to other approaches. Among new recommended strategies are in silico mechanistic models of the human ventricular action potential and the assessment of drug effects on multiple cardiac currents in in vitro human models2,3.
The effect (extent of the delayed ventricular repolarization) should be related to the concentration of the test substance. The plasma concentration is most commonly used as the effective concentration surrogate due to the relatively high availability, yet it can be an imperfect substitute, especially for some types of chemical moieties (i.e., highly lipophilic). Drug concentration in heart tissue should be of particular interest regarding all possible sites where the drug might meet cardiac ion channels. It should gain even more prominence in light of reports that note that myocardial drug concentration better correlates with a change in QT length4,5 and that the tissue drug concentration profiles do not necessarily correlate with those in plasma6. Although measurements of drug concentration in human cardiac tissue seem impossible in patients not undergoing open heart surgery, the mathematical models do not face such limitations. A physiologically based pharmacokinetic (PBPK) modeling approach is considered a useful tool in tracking the concentration-time profiles of drugs in different tissues, based on in vitro data. Moreover, the mechanistic nature of PBPK allows for the creation of universal, drug-independent models7,8. The power of the idea lies in the fact that parameters describing PBPK models have their physiological meaning and that the compartments represent body’s organs and tissues. In recent years, there has been a significant rise in the interest of PBPK modeling by the pharmaceutical industry, impacting regulatory decision making. The models not only predict the pharmacokinetics but also can predict local drug concentrations to assess drug efficacy and safety7,9,10. A whole-body PBPK model usually treats tissues as homogeneous, ‘well-stirred’ compartments, not accounting for regional differences in drug concentrations within the tissue. Thus, Gaohua et al.11 proposed a multicompartment permeability-limited lung PBPK model applied to predict tuberculosis drug levels in the epithelial lining fluid and the lung tissue mass. Westerhout et al.12 developed a system-based pharmacokinetic model to describe the intra-brain drug distribution in rats. Neuhoff et al.13 built a PBPK kidney model under the name ‘MechKim’ to predict renal elimination. The model was also capable of simulating drug-drug interactions at the level of transporter inhibition14. According to our knowledge, there is a lack of such a detailed PBPK model for heart tissue. We aimed to fill the gap by providing a four-compartmental heart PBPK model structure as a basis for predicting drug distribution within cardiac tissue.
Materials and Methods
System-related input parameters
Whole-body PBPK model input parameters
The basic whole-body PBPK after Jones and Rowland-Yeo8 was implemented and used as a scaffold in which to nest the developed multicompartment heart model. The model assumed perfusion rate-limited kinetics, which means that the blood flow to the tissues (compartments) was the limiting process. The values of body weight-dependent fractional tissue volumes, fractional tissue blood flows, cardiac output and microsomal protein per gram of human liver (MPPGL) were from the provided code [Table 1]. The model assumed a reference human of 70 kg.
The perfusion rate-limited model works under the assumption that total drug concentrations in the tissue and in the plasma at steady state are in the equilibrium with each other. Tissue-to-plasma water partition coefficients (Kps), which define that concentration balance, were predicted in Simcyp Simulator v.14.1 using the Rodgers et al. method15,16. Kp defining the drug partition between plasma and the rest of the body (Kpre) was fitted. Non-linear hepatic metabolism according to Michaelis-Menten enzyme kinetics was incorporated into the model equations. The values of the maximal rate of saturating substrate concentrations (Vmax) in [mg/h] for each CYPs isoform considered in the model were calculated according to the Equations (1).

where:
Vmax_pmol-maximal rate of saturating substrate concentrations [pmol/min/pmol of CYP], CYP-CYP abundance in average human liver [pmol/mg of microsomal protein],
MPPGL - Microsomal protein per gram of human liver [mg/g]
Vli - total liver volume [L]. MW-molecular weight of the compound [g/mol],
Heart model input parameters
The physiological and anatomical data were derived from the literature to reflect the physiology of the normal human heart. They are presented in Table 2.
The parameter describing blood flow through the pericardium (Qpf) was unknown and fitted in the optimization process. It was subtracted from the Qhe to keep the sum of blood flow rates equal to cardiac output specified in the model. The Kps values between plasma and the epicardium (Kpepi), midmyocardium (Kpmid), and endocardium (Kpendo) were in the same ratio as those derived from Garcia et al.’s publication on saxitoxin poisoning17, i.e., 1:2.5:5, respectively. We took into account drug elimination in cardiac tissue as cytochrome P450 enzymes were detected in human cardiovascular tissue18,19,20. The values of mean microsomal fractions of the human heart for CYP enzymes (CYP2C8, CYP2C9, and CYP2J2) were used in computing total cardiac clearance in Equations (2) and (3). Heart muscle density was assumed to equal 1.0 g/mL21,22.

where:
CLint2C8_per_mg - intrinsic clearance per mg of protein [mcL/min/mg],
CLint2C8_per_pmol - intrinsic clearance per pmol of CYP2C8 isoform [mcL/min/pmol],
CYP2C8 - Mean CYP2C8 enzyme abundance in the human heart [pmol/mg],
CLint 2C8 - Intrinsic clearance for CYP2C8 in the human heart [L/h],
Whe - average heart weight [g],
CLuint 2C8 - intrinsic clearance for CYP2C8 based on unbound fraction of compound [L/h],
fumic - fraction of drug unbound in an in vitro microsomal preparation,
ISEF2C8 - Inter System Extrapolation Factor for CYP2C8.
Intrinsic clearances based on unbound fractions of amitriptyline for CYPs 2C9 (CLuint2C9) and 2J2 (CLuint2J2) were calculated analogically and added to calculate the total heart metabolic clearance according to Equation (3).


where:
CLuint - total unbound intrinsic clearance per heart [L/h],
CLmHT - total heart metabolic clearance [L/h],
Qhe - total heart blood flow [L/h],
fup - fraction of drug unbound in plasma,
BP - blood to plasma concentration ratio.
Drug-specific input parameters
The proposed PBPK model incorporating the permeability-limited (assuming the permeability across cell membranes being the limiting process) heart model was used to simulate plasma and cardiac concentrations of amitriptyline as an exemplary drug23. Physicochemical and PK parameters for amitriptyline used in a simulation scenario are listed in Table 3.
The oral bioavailability of amitriptyline is highly variable, ranging from 33 to 62%; thus, the fraction absorbed (Fabs) was fixed at 0.5 (50%)24,25. The value of the first order absorption rate (ka) could not be found in reports, so ka [h−1] was adjusted to the observed data. The percentage of unbound drug in the plasma (fup) differs between studies from 3% to 7.4%24,25,26,27,28,29,30, so the fup value was fixed at 0.05 (5% of the free fraction). Because of the lack of information regarding the amitriptyline free fraction in pericardial fluid (fupf), the fupf was assumed to equal fup. A blood to plasma ratio (BP) of 1.04 was derived from25. The utilized value is in the range of other measured values, i.e., 0.86–1.1324,31.
The fixed Kp values were 3.0 (Kpepi), 7.4 (Kpmid)32, and 14.0 (Kpendo). The Kp value between plasma and pericardial fluid was fixed at 2.633.
The liver metabolism considered amitriptyline biotransformation by CYP isoforms 1A2, 2B6, 2C8, 2C9, 2C19, 2D6, and 3A434,35. The values of the maximal rate of saturating substrate concentrations (Vmax), Michaelis constants (Km) and Inter System Extapolation Factors (ISEF) used in the model are reported in the Table (4). We used 0.014 as the value of unbound fraction in hepatocytes (fuh), which was reported to be the highest bound of the range of fuh studied for imipramine and propranolol by Hallifax and Houston36. The intrinsic clearances denoting amitriptyline N-demethylation by CYPs 2C8 and 2C9 were 0.072 and 0.079 mcL/min/pmol37. Amitriptyline does not undergo CYP 2J2 metabolism38. fumic and ISEF factors were assumed to equal 1. The literature value of octanol/water partition coefficient (Log P) was 4.6239.
Clinical and simulation data
The mean plasma concentrations of amitriptyline after administration of a single oral dose of 25 mg (as amitriptyline is taken as a hydrochloride salt, pure amitriptyline counts for 22 mg to which the model was fitted) were observed by Curry et al.40 in ten healthy men. The corresponding maximal concentration in heart tissue was set to 114.35 ng/mL at 3.5 h postdose based on pig data41. Two additional concentration values in heart tissue referring to the absorption phase and two in the elimination phase were set to make the fitting process feasible.
Software used
The model was written in R v.3.3.0. Numerical solutions were computed using deSolve library v.1.1342. The system of ordinary differential equations was integrated using the LSODA method43. Model fitting was performed with algorithms from FME package v.1.3.244. The weighted residuals (resi,l) of the model output versus any observed data point i, of observed variable l, were estimated by modCost function according to the Equation (4).

where Modi,l is the modeled value, Obsi,l is the observed value, and errori,l is a weighting factor. For errori,l the modCost default value, i.e. 1, was chosen.
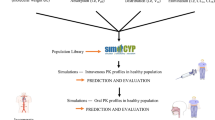
Simcyp Simulator45,46 v 14.1 (a Certara company) was used to predict Kp values for tissues represented in the full PBPK model. The diagram (Fig. 1) depicts the modeling workflow.
Results
Model structure
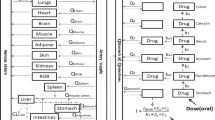
The structure of the final whole-body PBPK model is shown in Fig. 2.
The following is written as a set of ordinary differential equations (Equation 5 in the Appendix).
The model consisted of seventeen perfusion-limited compartments representing the following tissues: arterial blood, lung, adipose, bone, brain, kidney, spleen, gut, liver, muscle, skin, the rest of the body, venous blood, and the heart. Four compartments representing heart tissue were embedded into the whole-body PBPK structure. The added compartments stood for epicardium, midmyocardium, endocardium, and pericardial fluid, defined by the following volumes [L]: 0.0329, 0.0987, 0.1974, and 0.03, respectively. Epicardial, midmyocardial, and endocardial cells were set to constitute 10%, 30%, and 60% of the total heart tissue mass, according to Drouin et al.47.
The blood flow to the epicardium, midmyocardium, and endocardium was assumed to be equal, i.e., 4% of the cardiac output8. Arterial blood was assumed to perfuse the heart wall from the outward layer (epicardium), through the midmyocardium, to the most inner layer (endocardium). The blood left the cardiac tissue from the endocardium and returned to the venous blood compartment.
The pericardial fluid was perfused directly by arterial blood. Blood leaving the pericardial fluid entered the venous blood compartment directly.
The model also accounted for a drug disposition between the cardiac mass and pericardial fluid; it was described by passive disposition through the epicardial layer occurring in both directions. The parameters describing the permeability-limited process were grouped into one parameter (P) to simplify the model.
Physiological parameters describing the model structure were assumed to be constant, the compartments were homogeneous, and the equilibrium between the blood and tissues was reached immediately. The values of fup and fupf were assumed to be equal.
The proposed model assumed that the elimination occurred from the liver, kidney, and heart (tissue mass compartments). The implemented elimination clearances from the epicardium, midmyocardium, and endocardium contributed one-third each of the total cardiac metabolic clearance.
Modeling the PK of amitriptyline
The Kps predicted in Simcyp Simulator for the amitriptyline compound are presented in Table 5.
The calculated amitriptyline clearances was 0.316 L/h for total cardiac clearance. The renal clearance was set as 0.504 L/h according to Turner et al.37.
The first simulation was run to fit Kpre and ka [h−1] parameters to the observed amitriptyline concentration in plasma by Curry et al.40. Qpf [L/h] and P [L/h] were fixed at 0.01 and 0.40 as start parameters. The estimates (SD - standard error, p-value) are: ka = 0.80075 (0.03171, p = 4.33×10−11), and Kpre = 52.60950 (7.64768, p = 2.66×10-5). These values were used in the second simulation performed to estimate Qpf and P (the model was fitted to the set heart concentrations). The estimates (SD, p-value) are as follows: Qpf = 0.01193 (0.09783, p = 0.911), P = 0.78230 (5.76931, p = 0.901) (Table 6).
Simulated time-concentration profiles and observed/set data are presented in Figs 3, 4 and 5.
The time-amount of the amitriptyline profile (solid blue curve) resulted from fitting the model to values measured (solid black dots) by Curry et al.40.
Time-concentration profiles of amitriptyline in venous plasma (solid blue curve), pericardial fluid (solid green curve), and heart tissue in total (solid red curve) resulted from fitting the model to values measured by Curry et al. in healthy volunteers’ plasma40 (solid black dots) and to data set according to the amitriptyline concentration observed in pig heart41 (open black circles).
Time-concentration profiles of amitriptyline in heart tissue in total (solid green curve), in epicardium (solid blue curve), midmyocardium (solid violet curve), and the endocardium (solid red curve) data set according to the amitriptyline concentration observed in pig heart41 is depicted as open black circles.
The goodness of fit is depicted in Figs 6 and 7. There was good agreement between the observed data and model-predicted profiles. However, the highest observed value was not captured. The plots revealed no systemic bias.
Solid black dots refer to results from the 1st simulation run to fit the model to the observed concentration in plasma40 (fitting Kpre and ka parameters). Open black dots refer to results from the 2nd simulation run to fit the model to the data set on cardiac concentrations41 (fitting Qpf and P parameters).
Discussion
Regarding cardiovascular drug safety assessment and cardiac medication development, understanding active-site drug concentration is of great need. However, direct measurements pose problems, and prediction remains challenging. Because PBPK modeling makes predicting tissue concentration-time profiles possible, we focused on cardiac tissue and applied a PBPK quantitative mechanistic framework to develop a heart model structure.
Herein, the proposed heart model reflects a simplification of human cardiac anatomy and physiology. The assumption about equal blood perfusion throughout all three layers of the cardiac wall may be justified as it is claimed that “flow per gram of subendocardial myocardium is at least equal to flow per gram of subendocardial myocardium”48. The order of perfused compartments describes, in the simplest manner, the coronary tree that, arising from the right and left coronary arteries, forms a subepicardial system whose branches perforate more inner heart wall layers49. Pericardial fluid hypothetically forms in two ways, i.e., first by plasma ultrafiltration and secondly by the overflow of a small amount of interstitial fluid from the underlying myocardium50,51. Thus, blood flow and diffusion from a neighboring epicardial layer were applied in the model as possible routes for drug distribution within cardiac tissue. The estimate of Qpf at 0.01 L/h, which contributes 0.076% of total cardiac blood flow, seems realistic although there are no published measured results to support that value.
Amitriptyline was chosen as a subject of the simulation because tricyclic antidepressants are said to distribute within tissues extensively32,52 and to induce cardiotoxicity23. According to CredibleMeds classification53 supported by the published case reports of TdP54, amitriptyline poses a conditional risk of TdP arrhythmia. Thus, its concentration in cardiac tissue is worth being studied.
Regarding predicted amitriptyline absorption, the highest plasma concentration was achieved 1.3 h postdose whereas mean Tmax in the Curry et al.40 publication was 2.5 h. These differences most likely result from the oversimplified equation describing the absorption process. The estimated absorption rate constant being 0.80 [h−1] refers to the absorption of amitriptyline according to the first order kinetics. The more complex solution will be proposed in the next step of developing the model structure described herein.
The perfusion-limited distribution followed the Kps values predicted in Simcyp Simulator (Table 5). Kpre value defining the drug partition between plasma and the rest of the body was estimated as 52.6 suggesting a higher accumulation of amitriptyline in parts of the human body other than considered in our model, or the active transport being engaged in the disposition process. The model-predicted amitriptyline concentrations in the heart sub-model compartments, ranked in ascending order, are as follows: epicardium, midmyocardium, endocardium, and pericardial fluid. The maximal heart concentration is achieved at 1.7 h postdose. At that time point, the ratios of the concentrations in the sites in question to the concentration in venous blood are 2.89 for epicardium, 7.13 for midmyocardium, 13.41 for endocardium, 42.65 for pericardial fluid, and 10.47 for the total heart. All of these values (except for pericardial fluid, which is too high according to postmortem findings34 and pericardial fluid composition is similar to plasma55) are within the range of heart Kp values reported in the forensic and animal studies41,56,57, which supports the feasibility of the model and will be further tested to validate effective concentration surrogates. The disposition within the cardiac wall follows the assumed pattern after a postmortem study by Garcia et al.17; however, in animal studies, there were no appreciable gradients observed and homogeneous transmural drug distribution was described58,59. Therefore, investigating the disposition between cardiac mural layers requires more mechanistic insight, most likely with a permeability-limited kinetics assumption. The same case is with predicting drug concentration in the pericardial fluid compartment. Without the support of more mechanistic data allowing to describe the permeability process across the membrane of the epicardium, the P parameter, corresponding in fact to the clearance of interstitial fluid, was estimated to be 0.78 [L/h] leading to predict the concentration of amitriptyline in pericardial fluid higher than expected.
The model incorporates drug metabolism in cardiac tissue as some CYP450 enzymes are highly expressed in the heart20,60, and according to Michaud et al., “could be extremely relevant for the local clearance of drugs and metabolite formation in the heart.” Indeed, amitriptyline is metabolized to nortriptyline, which together with its metabolites (Z-10-hydroxy-nortriptyline, E-10-hydroxy-nortriptyline) can contribute to cardiotoxicity61. Therefore, its concentration in the heart should also be taken into account in assessing the cardiac effect of the parent drug. That will be done by expanding the current model with the sub-model for the metabolite.
In order to assess the drug triggered cardiac effect, in vitro – in vivo extrapolation approach will be utilized. The patient-specific parameters and the individual drug concentration simulated by the PBPK heart model will be combined with the in vitro measured ion channels inhibition. Translation to the human in vivo situation will be done with the use of the Cardiac Safety Simulator (CSS) and expressed as the pseudoECG signal62,63. The pharmacodynamic models built-in to CSS that can be used are O’Hara-Rudy64 and ten Tusscher65,66 models. The simulation results, namely parameters characterizing depolarization (QRS) and repolarization (QT), will be compared against the available clinical data taking into account intra- and inter-individual human variability67,68.
Conclusion
We described the development of a four-compartmental heart model and its nesting into a whole-body PBPK model. The model integrated literature-derived data on cardiac anatomy and physiology and was used to predict amitriptyline concentration in venous plasma, epicardium, midmyocardium, endocardium, and pericardial fluid. Our PBPK heart sub-model requires further development, but it represents a first attempt to provide an active drug concentration in various locations within heart tissue with the use of a PBPK approach.
Additional Information
How to cite this article: Tylutki, Z. and Polak, S. A four-compartment PBPK heart model accounting for cardiac metabolism - model development and application. Sci. Rep. 7, 39494; doi: 10.1038/srep39494 (2017).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
ICH. ICH E14 - CTs - Clinical Evaluation of QT/QTc Interval Prolongation and Proarrhythmic Potential for Non-Antiarrhythmic Drugs. Guideline 18 (2005).
Sager, P. T., Gintant, G., Turner, J. R., Pettit, S. & Stockbridge, N. Rechanneling the cardiac proarrhythmia safety paradigm: a meeting report from the Cardiac Safety Research Consortium. Am. Heart J. 167, 292–300 (2014).
Gintant, G., Sager, P. T. & Stockbridge, N. Evolution of strategies to improve preclinical cardiac safety testing. Nat. Rev. Drug Discov. 1–15, doi: 10.1038/nrd.2015.34 (2016).
Minematsu, T. et al. Quantitative relationship between myocardial concentration of tacrolimus and QT prolongation in guinea pigs: Pharmacokinetic/pharmacodynamic model incorporating a site of adverse effect. J. Pharmacokinet. Pharmacodyn. 28, 533–554 (2001).
Debbas, N. M. et al. The QT interval: a predictor of the plasma and myocardial concentrations of amiodarone. Br. Heart J. 51, 316–20 (1984).
Rostami-Hodjegan, A. Physiologically based pharmacokinetics joined with in vitro-in vivo extrapolation of ADME: a marriage under the arch of systems pharmacology. Clin. Pharmacol. Ther. 92, 50–61 (2012).
Jamei, M. Recent Advances in Development and Application of Physiologically-Based Pharmacokinetic (PBPK) Models: a Transition from Academic Curiosity to Regulatory Acceptance. Curr. Pharmacol. Reports, doi: 10.1007/s40495-016-0059-9 (2016).
Jones, H. & Rowland-Yeo, K. Basic concepts in physiologically based pharmacokinetic modeling in drug discovery and development. CPT pharmacometrics Syst. Pharmacol. 2, e63 (2013).
Wagner, C. et al. Application of Physiologically Based Pharmacokinetic (PBPK) Modeling to Support Dose Selection: Report of an FDA Public Workshop on PBPK. Clin. Pharmacol. Ther. 4, 226–230 (2015).
Rowland, M., Lesko, L. & Rostami-Hodjegan, A. Physiologically Based Pharmacokinetics Is Impacting Drug Development and Regulatory Decision Making. CPT Pharmacometrics Syst. Pharmacol 4, 313–315 (2015).
Gaohua, L. et al. Development of a Multicompartment Permeability-Limited Lung PBPK Model and Its Application in Predicting Pulmonary Pharmacokinetics of Antituberculosis Drugs. CPT Pharmacometrics Syst. Pharmacol. 4, 605–613 (2015).
Westerhout, J., Smeets, J., Danhof, M. & De Lange, E. C. M. The impact of P-gp functionality on non-steady state relationships between CSF and brain extracellular fluid. J. Pharmacokinet. Pharmacodyn. 40, 327–342 (2013).
Neuhoff, S. et al. Accounting for Transporters in Renal Clearance: Towards a Mechanistic Kidney Model (Mech KiM), in Transporters in Drug Development, eds. Sugiyama, Y. & Steffansen, B. Transp. Drug Dev. 7, 155–177 (2013).
Burt, H. J. et al. Metformin and cimetidine: Physiologically based pharmacokinetic modelling to investigate transporter mediated drug–drug interactions. Eur. J. Pharm. Sci. 88, 70–82 (2016).
Rodgers, T., Leahy, D. & Rowland, M. Physiologically based pharmacokinetic modeling 1: Predicting the tissue distribution of moderate-to-strong bases. J. Pharm. Sci. 94, 1259–1276 (2005).
Rodgers, T. & Rowland, M. Physiologically Based Pharmacokinetic Modelling 2: Predicting the Tissue Distribution of Acids, Very Weak Bases, Neutrals and Zwitterions. J. Pharm. Sci. 95, 1238–57 (2006).
Garcia, C., Bravo, M. D. C., Lagos, M. & Lagos, N. Paralytic shellfish poisoning: Post-mortem analysis of tissue and body fluid samples from human victims in the Patagonia fjords. Toxicon 43, 149–158 (2004).
Wu, S., Moomaw, C. R., Tomer, K. B., Falck, J. R. & Zeldin, D. C. Molecular cloning and expression of CYP2J2, a human cytochrome P450 arachisonic acid epoxygenase highly expressed in heart. J. Biol. Chem. 271, 3460–3468 (1996).
DeLozier, T. C. et al. Detection of human CYP2C8, CYP2C9, and CYP2J2 in cardiovascular tissues. Drug Metab. Dispos. 35, 682–688 (2007).
Thum, T. & Borlak, J. Gene expression in distinct regions of the heart. Lancet (London, England) 355, 979–83 (2000).
Kim, T. H. et al. Evaluation of right ventricular volume and mass using retrospective ECG-gated cardiac multidetector computed tomography: Comparison with first-pass radionuclide angiography. Eur. Radiol. 15, 1987–1993 (2005).
Yan, A. T. et al. Characterization of the peri-infarct zone by contrast-enhanced cardiac magnetic resonance imaging is a powerful predictor of post-myocardial infarction mortality. Circulation 114, 32–39 (2006).
Kerr, G. W., Mcgu, A. C. Y. & Wilkie, S. Tricyclic antidepressant overdose: a review. 18, 236–241 (2001).
Schulz, P., Turner-Tamiyasu, K., Smith, G., Giacomini, K. M. & Blaschke, T. F. Amitriptyline disposition in young and elderly normal men. Clin. Pharmacol. Ther. 33, 360–366 (1983).
Rollins, D. E. et al. Interindividual differences in amitriptyline demethylation. Clin. Pharmacol. Ther. 28, 121–129 (1980).
Burch, J., Roberts, S. & Raddats, M. Binding of amitriptyline and nortriptyline in plasma determined from their equilibrium distributions between red cells and plasma, and between red cells and buffer solution. Psychopharmacology (Berl). 75, 262–72 (1981).
Pike, E. & Skuterud, B. Plasma binding variations of amitriptyline and nortriptyline. Clin. Pharmacol. Ther. 32, 228–234 (1982).
Nyberg, G. & Mårtensson, E. Determination of free fractions of tricyclic antidepressants. Naunyn. Schmiedebergs. Arch. Pharmacol. 327, 260–5 (1984).
Baumann, P. et al. Amitriptyline Pharmacokinetics and Clinical Response: I. Free and Total Plasma Amitriptyline and Nortriptyline. Int. Clin. Psychopharmacol. 1, 89–101 (1986).
Brinkschulte, M., Gaertner, H. J. & Schied, H. W. Plasma Protein Binding of Perazine and Amitriptyline in Psychiatric Patients. 22, 367–373 (1982).
Maguire, K., Burrows, G., Norman, T. & Scoggins, B. Blood/plasma distribution ratios of psychotropic drugs. Clin. Chem. 26, 1624–1625 (1980).
Bynum, N. D., Poklis, J. L., Gaffney-Kraft, M., Garside, D. & Ropero-Miller, J. D. Postmortem distribution of tramadol, amitriptyline, and their metabolites in a suicidal overdose. J. Anal. Toxicol. 29, 401–6 (2005).
Moriya, F. & Hashimoto, Y. Pericardial fluid as an alternative specimen to blood for postmortem toxicological analyses. Leg. Med. 1, 86–94 (1999).
Venkatakrishnan, K., Schmider, J. & Mertzanis, P. Relative Contribution of CYP3A to Amitriptyline Clearance in Humans: In Vitro and In Vivo Studies. J. Clin. Pharmacol. 41, 1043–1054 (2001).
Ghahramani, P., Ellis, S. W., Lennard, M. S., Ramsay, L. E. & Tucker, G. T. Cytochromes P450 mediating the N-demethylation of amitriptyline. Br. J. Clin. Pharmacol. 43, 137–144 (1997).
Hallifax, D. & Houston, J. B. Uptake and intracellular binding of lipophilic amine drugs by isolated rat hepatocytes and implications for prediction of in vivo metabolic clearance. Drug Metab Dispos. 34, 1829–1836 (2006).
Turner, J. V., Maddalena, D. J. & Cutler, D. J. Pharmacokinetic parameter prediction from drug structure using artificial neural networks. Int. J. Pharm. 270, 209–219 (2004).
Lee, J. Y. et al. Impact of Pharmacometric Analyses on New Drug Approval and Labelling Decisions A Review of 198 Submissions Between 2000 and 2008. 50, 627–635 (2011).
Avdeef, A. Absorption and Drug Development: Solubility, Permeability, and Charge State. (John Wiley & Sons) (2003).
Curry, S. H., Devane, C. L. & Wolfe, M. M. Cimetidine Interaction with Amitriptyline. Eur. J. Clin. Pharmacol. 29, 429–433 (1985).
Heinonen, J. A., Litonius, E., Backman, J. T., Neuvonen, P. J. & Rosenberg, P. H. Intravenous Lipid Emulsion Entraps Amitriptyline into Plasma and Can Lower its Brain Concentration – An Experimental Intoxication Study in Pigs. Basic Clin. Pharmacol. Toxicol. 113, 193–200 (2013).
Soetaert, K., Petzoldt, T. & Setzer, R. W. Solving Differential Equations in R: Package deSolve. J. Stat. Softw. 33, 1–25 (2010).
Petzold, L. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 4, 136–148 (1983).
Soetaert, K. & Petzoldt, T. Inverse Modelling, Sensitivity and Monte Carlo Analysis in R Using Package FME. J. Stat. Softw. 33, 1–28 (2010).
Jamei, M. et al. The Simcyp Population-based ADME Simulator. Expert Opin. Drug Metab. Toxicol. 5, 211–223 (2009).
Jamei, M. et al. The Simcyp Population Based Simulator: Architecture, Implementation, and Quality Assurance. Silico Pharmacol. 1 (2013).
Drouin, E., Charpentier, F., Gauthier, C., Laurent, K. & Le Marec, H. Electrophysiologic Characteristics of Cells Spanning the Left Ventricular Wall of Human Heart: Evidence for Presence of M Cells. 26, 185–192 (1995).
Klocke, F. J. Coronary Blood Flow in Man. Prog. Cardiovasc. Dis. XIX, 117–166 (1976).
Fioranelli, M., Gonnella, C. & Tonioni, S. In CT Evaluation of Coronary Artery Disease 1–13 (Springer Milan, 2009).
Vogiatzidis, K. et al. Physiology of pericardial fluid production and drainage. Front. Physiol. 6, 1–6 (2015).
Shabetai, R. The Pericardium. (Kluwer Academic Publishers, 2003).
Langford, a M. & Pounder, D. J. Possible markers for postmortem drug redistribution. J. Forensic Sci. 42, 88–92 (1997).
CredibleMeds. CredibleMeds. at http://crediblemeds.org/.
Vieweg, W. & Wood, M. Tricyclic Antidepressants, QT Interval Prolongation, and Torsade de Pointes. Psychosomatics 45, 371–377 (2004).
Ben-Horin, S., Shinfeld, A., Kachel, E., Chetrit, A. & Livneh, A. The composition of normal pericardial fluid and its implications for diagnosing pericardial effusions. Am. J. Med. 118, 636–640 (2005).
Mikkelsen, C. R., Jornil, J. R., Andersen, L. V., Banner, J. & Hasselstrøm, J. B. Quantification of 16 QT-prolonging Drugs and Metabolites in Human Postmortem Blood and Cardiac Tissue Using UPLC–MS-MS. J. Anal. Toxicol. 40, 286–293 (2016).
Tylutki, Z. & Polak, S. Plasma vs heart tissue concentration in humans - literature data analysis of drugs distribution. Biopharm. Drug Dispos. 36, 337–51 (2015).
Bolderman, R. W. et al. Intrapericardial delivery of amiodarone and sotalol: atrial transmural drug distribution and electrophysiological effects. J. Cardiovasc. Pharmacol. 54, 355–63 (2009).
Maslov, M. Y. et al. Myocardial drug distribution generated from local epicardial application: Potential impact of cardiac capillary perfusion in a swine model using epinephrine. J. Control. Release 194, 257–265 (2014).
Michaud, V., Frappier, M., Dumas, M.-C. & Turgeon, J. Metabolic activity and mRNA levels of human cardiac CYP450s involved in drug metabolism. PLoS One 5, e15666 (2010).
Jornil, J., Jensen, K. G., Larsen, F. & Linnet, K. Risk assessment of accidental nortriptyline poisoning: The importance of cytochrome P450 for nortriptyline elimination investigated using a population-based pharmacokinetic simulator. Eur. J. Pharm. Sci. 44, 265–272 (2011).
Glinka, A. & Polak, S. QTc modification after risperidone administration – insight into the mechanism of action with use of the modeling and simulation at the population level approach. Toxicol. Mech. Methods 25, 279–286 (2015).
Wiśniowska, B. & Polak, S. Virtual clinical trial towards polytherapy safety assessment – combination of PBPK/PD based modelling and simulation approach with DDIs involving terfenadine as an example. J. Pharm. Sci. 105, 3415–3424 (2016).
O’Hara, T., Virág, L., Varró, A. & Rudy, Y. Simulation of the Undiseased Human Cardiac Ventricular Action Potential: Model Formulation and Experimental Validation. PloS Comput. Biol. 7, e1002061 (2011).
ten Tusscher, K. H. W. J., Noble, D., Noble, P. J. & Panfilov, A. V. A model for human ventricular tissue. AJP - Hear. Circ. Physiol. 286, H1573–H1589 (2004).
ten Tusscher, K. H. W. J. Ten & Panfilov, A. V. Cell model for efficient simulation of wave propagation in human ventricular tissue under normal and pathological conditions. Phys. Med. Biol. 51, 6141–6156 (2006).
Glinka, A. & Polak, S. The effects of six antipsychotic agents on QTc—An attempt to mimic clinical trial through simulation including variability in the population. Comput. Biol. Med. 47, 20–26 (2014).
Polak, S., Wiśniowska, B., Fijorek, K., Glinka, A. & Mendyk, A. In vitro–in vivo extrapolation of drug-induced proarrhythmia predictions at the population level. Drug Discov. Today 19, 275–281 (2014).
Acknowledgements
This project was financed by the National Science Centre, Poland, project number 2014/13/N/NZ7/00254.
Author information
Authors and Affiliations
Contributions
Z.T. - gathering the data, model development, running the simulations, writing the manuscript. S.P. - conception and design, writing the manuscript, critical revision.
Corresponding author
Ethics declarations
Competing interests
Z.T. declares no conflict of interest. S.P. is an employee of Certara.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tylutki, Z., Polak, S. A four-compartment PBPK heart model accounting for cardiac metabolism - model development and application. Sci Rep 7, 39494 (2017). https://doi.org/10.1038/srep39494
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep39494
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.