Abstract
Confining light into a sub-wavelength area has been challenging due to the natural phenomenon of diffraction. In this paper, we report deep sub-wavelength focusing via dispersion engineering based on hyperbolic metamaterials. Hyperbolic metamaterials, which can be realized by alternating layers of metal and dielectric, are materials showing opposite signs of effective permittivity along the radial and the tangential direction. They can be designed to exhibit a nearly-flat open isofrequency curve originated from the large-negative permittivity in the radial direction and small-positive one in the tangential direction. Thanks to the ultraflat dispersion relation and curved geometry of the multilayer stack, hyperlens can magnify or demagnify an incident beam without diffraction depending on the incident direction. We numerically show that hyperlens-based nanofocusing device can compress a Gaussian beam down to tens-of-nanometers of spot size in the ultraviolet (UV) and visible frequency range. We also report four types of hyperlenses using different material combinations to span the entire range of visible frequencies. The nanofocusing device based on the hyperlens, unlike conventional lithography, works under ordinary light source without complex optics system, giving rise to practical applications including truly nanoscale lithography and deep sub-wavelength scale confinement.
Similar content being viewed by others
Introduction
Recently, nanophotonics has opened new realm of science and technology, providing breakthrough in many different fields including data processing, optical communications and holography. As one critical step in controlling light wave, nanofocusing of light is fundamental and essential in a broad range of applications such as nanolithography, surface-enhanced Raman spectroscopy (SERS), enhancement of nonlinear effects and single molecule detection. However, the diffraction limit in classical optics makes it very challenging to confine light into a deep sub-wavelength dimension. To overcome such fundamental limit, there have been active researches on nanoscale focusing, most of which have been realized by utilizing tapered plasmonic waveguides1,2,3,4,5, structural designs such as curved geometry6,7 and channel plasmon-polariton modes8. The tapered waveguide systems ensure strong field confinement and nanometer scale resolution, but they are limited by the spatial dispersion and fabrication difficulty. Meanwhile, nanofocusing based on structural design relies on geometrical shaping of the surface in micro or nanoscale and hence it is very challenging for implementation. In this paper, we present a different approach where photons are guided by extreme anisotropy of the medium, not by physical barrier as in tapered waveguide approaches. Our system is based on hyperbolic metamaterials to achieve nanofocusing which enables confining light into a deep sub-wavelength scale as well as super-resolution imaging with an ordinary light source at the UV and visible wavelengths, which are important range in nanolithography and imaging applications.
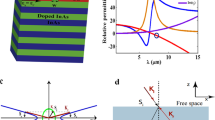
Metamaterials, artificial materials composed of the building blocks of deep sub-wavelength size and spacing, have been an intensive research subject. Metamaterials have shown various novel properties and applications such as negative refractive index9, cloaking10,11, sensing12, and imaging13,14,15 since Veselago first proposed the concept in 196816. Hyperbolic metamaterials, one intriguing and special kind of metamaterials, are a highly anisotropic material with different signs of permittivity along different axes17,18. Originated from the extreme anisotropy, hyperbolic metamaterials have shown exotic properties with various applications, including all-angle negative refraction19,20,21, sub-diffraction-limited imaging13,15,22, enhancement of spontaneous emission23,24,25, photonic spin Hall effect26,27 and sub-wavelength waveguiding28,29. To realize hyperbolic metamaterials, we can use metallic nanowires embedded in a dielectric matrix or metal-dielectric multilayer. In this paper, we will focus on the latter case. As schematically illustrated in Fig. 1(a), the hyperbolic metamaterial consists of alternating layers of metal and dielectric with thickness much smaller than the wavelength, and hence the medium can be approximated as a homogeneous medium with effective optical parameters. When wave propagates parallel to the anisotropy axis, the effective permittivity satisfies the relation as follows,

where d denotes thickness of each layer, the subscripts ⊥ and ∥ describe components perpendicular and parallel to the propagation directions, and the subscripts m and d indicate metal and dielectric, respectively. By adapting proper geometric parameters and materials, highly anisotropic permittivity can be achieved.
For transverse magnetic (TM) waves propagating in the multilayer metamaterials, the dispersion relation is given by

Here, the subscripts ⊥ and ‖ follow the same notation defined earlier. k is the wavevector, ε is the relative permittivity, ω is the angular frequency, and c is the speed of light in vacuum. At the frequency where the multilayer metamaterial has different signs of permittivity, the isofrequency surface exhibits hyperboloid shape as shown in Fig. 1(c) and (d), while naturally available anisotropic materials generally show ellipsoidal isofrequency surface (Fig. 1(b)).
Results
Thanks to this extraordinary dispersion relation, hyperbolic metamaterials support TM waves with transverse wave vector k‖ larger than k0 (wave vector in vacuum). Such waves are evanescent waves that cannot propagate in air, but they can be converted into propagating waves through a mechanism of angular momentum conservation in hyperlens30,31. Using these properties, super-resolution imaging has been achieved by using hyperlens, a cylindrical13,15,22 or a spherical32 multilayer hyperbolic metamaterials from many groups.
Since the effective permittivity depends on the optical properties of the metal and dielectrics components and their filling ratio as described in equation (1), different material compositions yield different working frequency ranges. One example is shown in Fig. 2 for silver and silicon. Metal and dielectrics are properly determined to provide hyperbolic dispersion as flat as possible and high transmission for nanofocusing and super-resolution applications. For flat dispersion, real part of effective permittivity should be highly negative in radial direction and slightly positive in tangential direction, as implied in equation (2). The effective permittivity should also have small imaginary part in both radial and tangential directions in order to allow high transmission. Although realizing hyperbolic dispersion using semiconductors instead of novel metals has been reported in infrared wavelength range19,33, material combinations conventionally used in visible frequency are limited to noble metals such as silver and gold and high index dielectrics because noble metals exhibit low losses whereas other metals such as aluminum are not used due to the relatively high losses.
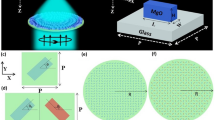
Figure 3(a) shows a schematic design where media marked by A, B and C are air, hyperlens and silicon dioxide, respectively. The hyperlens is composed of alternatively stacked metal and dielectric in which the thickness of the each layer is set to 15 nm and outer and inner radius is 750 nm and 60 nm, respectively. If the hyperlens has ultraflat iso-frequency curve for TM waves as shown in Fig. 3(b), it can support broad range of transverse component of the wave vector and compress or expand transverse wave vector without diffraction as beam passes the hyperlens depending on its propagation direction. As waves propagate along the radial direction from inner medium (A) to outer medium (C) (yellow arrow in Fig. 3(a)), the transverse wave vector decreases from the red arrow to the orange arrow in Fig. 3(b). Therefore, evanescent waves become propagating without diffraction or distortion of the original beam shape since the direction of the group velocities which are represented by the black arrows in Fig. 3(b) barely change. Moreover, because the group velocities in the hyperlens have nearly zero transverse components, the waves propagate along the radial direction, resulting magnification of the beam size. In other words, the role of the hyperlens is to convert evanescent waves into propagating waves and to magnify the image. However, if light passes the hyperlens inversely (purple arrow in Fig. 3(a)), radial propation direction leads to compression of the incoming waves, and the incident beam will be focused into an area below the diffraction limit34,35. Moreover, since the propagation of light depends on radial group velocity, highly anisotropic elliptical dispersion also supports nanofocusing with super-resolution.
Schematic and 2D simulation of the hyperlens-based nanofocusing.
(a) Schematic design. Media denoted by A, B and C are air, hyperlens and silicon dioxide, respectively. Yellow and purple arrows denote Poynting vector of outgoing and incoming TM waves, respectively. (b) Two-dimensional isofrequency curve for TM waves in hyperlens consisting of silver and silicon (blue), compared to the isofrequency curve of silicon dioxide (green) and air (black) at wavelength 560 nm. Red and orange arrows marked by A and C indicate wave vectors supported by the media of A and C in (a), and the black arrows indicate the direction of group velocities in the hyperlens. (c) and (d) Intensity profile in the hyperlens composed of silver and silicon with incident beam radius of (c) 900 nm and (d) 400 nm and white arrows denote Poynting vector. (e) Normalized intensity along red dotted line when the incident beam has radius of 400 nm.
Figure 3(c) and (d) are 2D simulation results of hyperlens-based nanofocusing using Finite Element Analysis since it has rotational symmetry. The incident beam is a TM-polarized Gaussian beam with beam radius of 900 nm in (c) and 400 nm in (d) both of which are easily achievable using conventional optical systems. While the incident beam exhitibits a full width at half maximum (FWHM) of 817 nm in free space, the beam in the hyperlens is compressed as it propagates, resulting in 34 nm FWHM which corresponds to 0.04 of that without hyperlens. Although the intensity, which corresponds to efficiency, is reduced to half, it is still relatively high compared to imaging application due to the localization of field.
This sub-wavelength focusing can be used in applications such as nanopatterning by adding a layer with slit to the inner surface (Fig. 4(a)). Light has been an attractive source of lithography for its easy accessibility and low cost, but diffraction is a natural and fundamental phenomenon obstructing nanoscale lithography. Utilizing hyperlens, which can confine light in sub-wavelength area, a new concept of nanoscale lithography under simple UV and visible light illumination beyond the current photolithography is achievable. Intensity along the line spaced 20 nm from the layer which is marked as red dotted line is shown in Fig. 4(b). Although intensity decreases rapidly as it goes away from the focal point since it is evanescent, it is still enough for lithography application. Therefore, hyperlens is a very promising candidate for deep sub-wavelength patterning of few nanometers scale without complicated optics systems, and it can be also integrated with more complex lithography system such as flying head lithography utilizing highly focused near-field focused light36.
Hyperlens-based nanofocusing where chrome layer with slit is added to the inner surface.
(a) Intensity profile in the hyperlens consisting of silver and silicon at wavelength of 560 nm. (b) Normalized intensity along the vertical line spaced 20 nm from the chrome layer which is indicated as red dotted line. The width of the slit is set to 20 nm.
Furthermore, this diffraction-unlimited focusing can be achieved in broad range of visible frequency by changing the materials. Figure 5 shows possible material combinations in the UV and visible range and its full-wave simulation where color map shows magnitude of Poynting vector. Here, metal filling ratio is fixed to 1/2 in all simulations. The wavelength, materials and their permittivities used in each simulation are specified under the simulation result. (The material properties are taken from literature37 for gold and experimentally measured value for the remaining.) Working frequency range can be, however, further expanded by diversifying the material combinations which has not been used widely such as conventional semiconductors. Also, hyperlens can have additional degrees of freedom by adapting graphene or phase change materials (PCM). High optical tunability of graphene-based hyperlens has been recently demonstrated in the mid-infrared region by controlling the applied voltage38,39, and PCM also proved characteristic optical properties which is tunable in the vicinity of the phase transition by tuning temperature in near-infrared regime40,41. If one can apply these schemes in the visible range, single material combination can cover whole range of optical frequencies by simply tuning voltage or temperature, opening new possibilities in both nanofocusing and imaging area.
In conclusion, hyperlens–based nanofocusing system provides both deep sub-wavelength confinement of light and super-resolution imaging by controlling the spot size in nanometer scale without complex optics system such as electron beam lithography, ion beam lithography and deep-UV photolithography. We have numerically showed light localization originated from nearly-flat hyperbolic dispersion and suggested various material combinations to cover parts of UV and whole visible range. Introducing tunable materials such as graphene and PCM will bring useful applications which remains as future works. Although fabrication of the hyperlens system is challenging because of their requirement of geometry definition and multi-level thin-film deposition process, it could be further improved with the on-going researches in scalable nanofabrication processes such as roll-to-roll system and pattern transfer techniques. Further, the proposed deep sub-wavelength nanofocusing property of hyperlens can be applied to not only low-cost and high-resolution nanoscale lithography, but also several other interesting applications such as SERS and single molecule level imaging with the extremely focused near-field light.
Methods
We used COMSOL Multiphysics 5.0 for numerical simulation.
Additional Information
How to cite this article: Kim, M. et al. Deep sub-wavelength nanofocusing of UV-visible light by hyperbolic metamaterials. Sci. Rep. 6, 38645; doi: 10.1038/srep38645 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Stockman, M. I. Nanofocusing of Optical Energy in Tapered Plasmonic Waveguides. Phys. Rev. Lett. 93, 137404 (2004).
Davoyan, A. R., Shadrivov, I. V., Zharov, A. A., Gramotnev, D. K. & Kivshar, Y. S. Nonlinear Nanofocusing in Tapered Plasmonic Waveguides. Phys. Rev. Lett. 105, 116804 (2010).
Verhagen, E., Polman, A. & Kuipers, L. Nanofocusing in laterally tapered plasmonic waveguides. Opt. Express 16, 45–57 (2008).
Choo, H. et al. Nanofocusing in a metal-insulator-metal gap plasmon waveguide with a three-dimensional linear taper. Nature Photon. 6, 838–844 (2012).
Lindquist, N. C., Nagpal, P., Lesuffleur, A., Norris, D. J. & Oh, S.-H. Three-Dimensional Plasmonic Nanofocusing. Nano Lett. 10, 1369–1373 (2010).
Ma, C. & Liu, Z. Focusing light into deep subwavelength using metamaterial immersion lenses. Opt. Express 18, 4838–4844 (2010).
Shi, H., Du, C. & Luo, X. Focal length modulation based on a metallic slit surrounded with grooves in curved depths. Appl. Phys. Lett. 91, 093111 (2007).
Volkov, V. S. et al. Nanofocusing with Channel Plasmon Polaritons. Nano Lett. 9, 1278–1282 (2009).
Shelby, R. A., Smith, D. R. & Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 292, 77–79 (2001).
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006).
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromangetic fields. Science 312, 1780–1782 (2006).
Kabashin, A. et al. Plasmonic nanorod metamaterials for biosensing. Nature Mater. 8, 867–871 (2009).
Jacob, Z., Alekseyev, L. V. & Narimanov, E. Optical Hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express 14, 8247–8256 (2006).
Pendry, J. B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969 (2000).
Salandrino, A. & Engheta, N. Far-field subdiffraction optical microscopy using metamaterial crystals: Theory and simulations. Phys. Rev. B 74, 075103 (2006).
Veselago, V. G. The electrodynamics of substances with simultaneously negative values of/epsilon and/mu. Sov. Phys. Usp. 10, 509–514 (1968).
Ferrari, L., Wu, C., Lepage, D., Zhang, X. & Liu, Z. Hyperbolic metamaterials and their applications. Prog. in Quant. Electron. 40, 1–40 (2015).
Guo, Y., Newman, W., Cortes, C. L. & Jacob, Z. Applications of Hyperbolic Metamaterial Substrates. Adv. in OptoElectron. 2012, 9 (2012).
Hoffman, A. J. et al. Negative refraction in semiconductor metamaterials. Nature Mater. 6, 946–950 (2007).
Liu, Y., Bartal, G. & Zhang, X. All-angle negative refraction and imaging in a bulk medium made of metallic nanowires in the visible region. Opt. Express 16, 15439–15448 (2008).
Yao, J. et al. Optical Negative Refraction in Bulk Metamaterials of Nanowires. Science 321, 930–930 (2008).
Liu, Z., Lee, H., Xiong, Y., Sun, C. & Zhang, X. Far-Field Optical Hyperlens Magnifying Sub-Diffraction-Limited Objects. Science 315, 1686–1686 (2007).
Lu, D., Kan, J. J., Fullerton, E. E. & Liu, Z. Enhancing spontaneous emission rates of molecules using nanopatterned multilayer hyperbolic metamaterials. Nature Nanotechnol. 9, 48–53 (2014).
Slobozhanyuk, A. P. et al. Purcell effect in hyperbolic metamaterial resonators. Phys. Rev. B 92, 195127 (2015).
Ferrari, L., Lu, D., Lepage, D. & Liu, Z. Enhanced spontaneous emission inside hyperbolic metamaterials. Opt. Express 22, 4301–4306 (2014).
Kapitanova, P. V. et al. Photonic spin Hall effect in hyperbolic metamaterials for polarization-controlled routing of subwavelength modes. Nature Commun. 5 (2014).
High, A. A. et al. Visible-frequency hyperbolic metasurface. Nature 522, 192–196 (2015).
Ishii, S., Shalaginov, M. Y., Babicheva, V. E., Boltasseva, A. & Kildishev, A. V. Plasmonic waveguides cladded by hyperbolic metamaterials. Opt. Lett. 39, 4663–4666 (2014).
He, Y., He, S. & Yang, X. Optical field enhancement in nanoscale slot waveguides of hyperbolic metamaterials. Opt. Lett. 37, 2907–2909 (2012).
Podolskiy, V. A. & Narimanov, E. E. Strongly anisotropic waveguide as a nonmagnetic left-handed system. Phys. Rev. B 71, 201101 (2005).
Govyadinov, A. A. & Podolskiy, V. A. Meta-material photonic funnels for sub-diffraction light compression and propagation. Phys. Rev. B 73, 155108 (2006).
Rho, J. et al. Spherical hyperlens for two-dimensional sub-diffractional imaging at visible frequencies. Nature Commun. 1, 143 (2010).
Naik, G. V., Liu, J., Kildishev, A. V., Shalaev, V. M. & Boltasseva, A. Demonstration of Al:ZnO as a plasmonic component for near-infrared metamaterials. Proc. Natl. Acad. Sci. USA 109, 8834–8838 (2012).
Xiong, Y., Liu, Z. & Zhang, X. A simple design of flat hyperlens for lithography and imaging with half-pitch resolution down to 20 nm. Appl. Phys. Lett. 94, 203108 (2009).
Wan, W., Ponsetto, J. L. & Liu, Z. Numerical study of hyperlenses for three-dimensional imaging and lithography. Opt. Express 23, 18501–18510 (2015).
Pan, L. et al. Maskless Plasmonic Lithography at 22|nm Resolution. Sci. Rep. 1, 175 (2011).
Rakić, A. D., Djurišić, A. B., Elazar, J. M. & Majewski, M. L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 37, 5271–5283 (1998).
Li, P. & Taubner, T. Broadband subwavelength imaging using a tunable graphene lens. ACS Nano 6, 10107–10114 (2012).
Zhang, T., Chen, L. & Li, X. Graphene-based tunable broadband hyperlens for far-field subdiffraction imaging at mid-infrared frequencies. Opt. Express 21, 20888–20889 (2013).
Qazilbash, M. M. et al. Mott Transition in VO2 Revealed by Infrared Spectroscopy and Nano-Imaging. Science 318, 1750–1753 (2007).
Shportko, K. et al. Resonant bonding in crystalline phase-change materials. Nature Mater. 7, 653–658 (2008).
Acknowledgements
The research was supported by Young Investigator Research program (NRF-2015R1C1A1A02036464), Engineering Research Center program (NRF-2015R1A5A1037668) and Global Frontier program (CAMM-2014M3A6B3063708) through the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science, ICT and Future Planning (MSIP) of Korean government.
Author information
Authors and Affiliations
Contributions
J.R. conceived the idea and guided the research. M.K. did numerical simulations. S.S., K.Y. and Y.L. suggested the idea of materials characterizations. M.K., S.S., K.Y., Y.L. and J.R. wrote the manuscript. All authors participated in the discussion and approved the final manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, M., So, S., Yao, K. et al. Deep sub-wavelength nanofocusing of UV-visible light by hyperbolic metamaterials. Sci Rep 6, 38645 (2016). https://doi.org/10.1038/srep38645
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38645
This article is cited by
-
Hyperbolic metamaterials: fusing artificial structures to natural 2D materials
eLight (2022)
-
Realization of broadband negative refraction in visible range using vertically stacked hyperbolic metamaterials
Scientific Reports (2019)
-
Demonstration of nanoimprinted hyperlens array for high-throughput sub-diffraction imaging
Scientific Reports (2017)
-
Selective dual-band metamaterial perfect absorber for infrared stealth technology
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.