Abstract
There are two ways to synchronize oscillators: by coupling and by common forcing, which can be pure noise. By virtue of the Ott-Antonsen ansatz for sine-coupled phase oscillators, we obtain analytically tractable equations for the case where both coupling and common noise are present. While noise always tends to synchronize the phase oscillators, the repulsive coupling can act against synchrony, and we focus on this nontrivial situation. For identical oscillators, the fully synchronous state remains stable for small repulsive coupling; moreover it is an absorbing state which always wins over the asynchronous regime. For oscillators with a distribution of natural frequencies, we report on a counter-intuitive effect of dispersion (instead of usual convergence) of the oscillators frequencies at synchrony; the latter effect disappears if noise vanishes.
Similar content being viewed by others
Introduction
Synchronization effects in ensembles of coupled oscillators are relevant for various physical systems, such as coupled lasers, spin-torque oscillators, and Josephson junctions1,2,3, as well as for diverse natural phenomena in life sciences4,5, and even for many social systems6,7. Synchronization caused by an attractive mean-field coupling, studied in pioneering works by Winfree and Kuramoto8,9, allows a two-fold characterization. On one hand, the synchronization transition can be described via the appearance of a macroscopic mean field, amplitude of which often serves as the order parameter of the transition. On the other hand, synchronization can be characterized via an adjustment of the frequencies of the oscillators in the ensemble (e. g., N. Wiener described synchronization10 as a “phenomenon of the pulling together of frequencies”). There is also a nontrivial way to synchronize oscillators without coupling by acting on them with a common external noise11,12,13,14,15,16. Weak noise can be treated in the phase approximation, and here only synchronization is possible. For strong noise, one has to go beyond the phase approximation, and here desynchronization can occur if the oscillators are strongly nonisochronous13,17. Remarkably, common noise synchronizes oscillators in the first meaning only. So, an ensemble of identical uncoupled oscillators under common noise forms a perfect cluster where all the states coincide and the value of the order parameter is the maximal possible. The phases of slightly different oscillators form an imperfect cluster; their frequencies are however not adjusted: their difference is preserved under common noise.
In this paper we study properties of synchronization and of the behavior of the frequencies if both coupling and common noise are present. We consider phase oscillators, what corresponds to the situation of small noise, so that noise always tends to synchronize the ensemble. This setup corresponds to experiments with metronomes on a common support18, if the latter is subject to a random force, and to experiments with coupled electronic oscillators19,20 with an additional driving noisy current. Our theory generalizes previous studies of noise-driven ensembles with21,22 and without coupling23 (dynamics of two oscillators with coupling and common and intrinsic noises has been studied in ref. 24). Similar to refs 22, 23 we use the Ott-Antonsen ansatz allowing one to get a closed stochastic equation for the order parameter of the ensemble. This ansatz is valid in the thermodynamic limit for coupled oscillators with a Lorenzian distribution of natural frequencies, and it can be generalized to include a common noisy driving. After averaging of the resulting equations over the fast basic frequency of oscillations, we get a tractable Langevin-type dynamics of the order parameter. We discuss in detail a nontrivial competition between the synchronizing action of noise and the desynchronizing action of the repulsive coupling. Here our study goes beyond that of ref. 22, which has been mainly focused on the effects of noise on the properties of the ensemble close to the transition to synchrony for attractive coupling. For nonidentical oscillators, where complete synchrony is impossible, we derive stationary distribution of the order parameter and describe a rather counter-intuitive dispersion of the frequencies at synchronization in presence of the repulsive coupling. This appears to be a surprising state where “phase locking” is accompanied by “frequency anti-entrainment”: although the oscillator phases are most of the time close to each other, their frequencies become more diverse compared to natural ones.
Results
Basic equations
We consider an ensemble of phase oscillators subject to a common Gaussian white noise with intensity σ2 and to a Kuramoto-type coupling with strength μ (the coupling is attractive for μ > 0 and repulsive otherwise). We consider the ensemble in the thermodynamic limit, suitable for the application of the Ott-Antonsen theory25:

Here the mean field is defined as

where g(Ω) is the distribution of the natural frequencies. According to the Ott-Antonsen ansatz25, the distribution function of the phases at given Ω can be represented as  and the mean field zΩ(t) of a subpopulation with frequency Ω obeys the equation
and the mean field zΩ(t) of a subpopulation with frequency Ω obeys the equation

For a Lorentzian distribution of frequencies g(Ω) = γ[π(γ2 + (Ω − Ω0)2)]−1, the integral in (2) can be calculated by virtue of the residual theorem, under assumption of analyticity of zΩ in the upper half-plane,  . As a result one obtains a closed equation for the mean field Z for coupled non-identical oscillators under common noise:
. As a result one obtains a closed equation for the mean field Z for coupled non-identical oscillators under common noise:

It contains four parameters: the basic frequency Ω0 (which, in contradistinction to the usual Kuramoto model, cannot be simply shifted to zero, because the noise term breaks the frequency-shift invariance), the noise intensity σ2, the coupling constant μ, and the width of the distribution of natural frequencies γ.
Generally, the common noise can not only synchronize identical oscillators, but also desynchronize them provided nonisochronicity inheres in the systems and the noise is strong enough to evoke significant perturbations of the amplitude degrees of freedom11,12,13. However, in the systems with purely phase dynamics, like equation (1) we consider in this paper, the noise can make only the synchronizing effect14,15; the effect of a weak noise is also generally synchronizing16.
For an analytical treatment below, it is convenient to use the real-valued variables (J, Φ), where J = R2/(1 − R2) is another order parameter characterizing the level of synchrony (closeness of the phases of oscillators in the ensemble): for J = 0 the mean field amplitude  vanishes, while the full synchrony with J = ∞ corresponds to R = 1. Equations for these variables read
vanishes, while the full synchrony with J = ∞ corresponds to R = 1. Equations for these variables read

and are complemented with the equation for the phase, relative to that of the mean field, θω = ϕΩ − Φ:

Here ω = Ω − Ω0 is the deviation of the natural frequency from the ensemble mean. For the sake of simplicity of notations we omit index ω below.
Averaged equations
As the first step, we employ the natural condition that the basic frequency of oscillations Ω0 is much larger than the parameters μ, γ, σ2 (which all have dimension of inverse time). This suggests averaging over the fast rotating phase Φ. One writes the Fokker-Planck equation corresponding to the Langevin equations (5, 6), and by virtue of the multiple scales expansion (see Section 1 of Supplementary material for a detailed derivation) obtains in the leading order in the small parameters μ, γ, σ2 the following equation for the probability density w(J, θ, t):

Here we defined the operators

The Fokker-Planck equations (7, 8) is equivalent to the following system of stochastic Langevin equations which can be interpreted as Eqs (5, 6) averaged over the fast oscillations with frequency Ω0:


The original noise ξ(t) generates two effective independent noise terms ζ1(t) and ζ2(t), which are Gaussian and delta-correlated, 〈ζn(t)ζl(t + t′)〉 = 2δn,lδ(t′), because the signals ξ(t) cos Ω0t and ξ(t) sin Ω0t are uncorrelated on time scales that are large compared to 2π/Ω0. The derived equations contain four parameters μ, γ, σ2, ω, and the properties of the stationary solutions depend on μ/σ2, γ/σ2, and ω/σ2 only.
Our first goal is to characterize the statistics of the order parameter J. One can see that, as it should be for any global coupling setup, the system (9,10) is a skew one, where the dynamics of the order parameter affects that of the phases, but not vice versa. Thus one obtains a closed Fokker-Planck equation (the corresponding Langevin equation is (9)) for the distribution of the order parameter

Identical oscillations
We start by considering the case of identical oscillators γ = 0. Here, the analysis of states close to full synchrony J → ∞ is simple, as ln J performs a biased random walk:

The quantity  is nothing else as the Lyapunov exponent determining stability of the full synchrony, the latter is stable if λ < 0, i.e. if μ > −σ2/2. Thus, the small enough repulsive coupling between the oscillators does not break stability of the full synchrony. Another important state is that of full asynchrony, J = 0. One can see however from Eq. (9) that this state is not invariant in presence of noise.
is nothing else as the Lyapunov exponent determining stability of the full synchrony, the latter is stable if λ < 0, i.e. if μ > −σ2/2. Thus, the small enough repulsive coupling between the oscillators does not break stability of the full synchrony. Another important state is that of full asynchrony, J = 0. One can see however from Eq. (9) that this state is not invariant in presence of noise.
In fact, here we meet a nontrivial situation where the states of full asynchrony (J = 0) and of full synchrony (J = ∞) are differently driven by noise. For the asynchronous state the driving is additive, therefore this state is not invariant and the order parameter experience fluctuations close to J = 0, even if this state is stable (i.e. for repulsive coupling μ < 0). In contradistinction, the noise is acting on the fully synchronous state in a multiplicative way, so that if this state is stable, noise does not kick the system out of it. Thus, the stable (λ < 0) fully synchronous state is an absorbing one. This means that also for a slightly repulsive coupling −σ2/2 < μ < 0, the asynchronous state J ≈ 0, although stable without noise, does not survive the competition with the fully synchronous state J = ∞ which is the global attractor.
In this “bistable” situation the nontrivial statistical characteristic is the mean first passage time  for the stochastic process (9,11), from asynchrony J(0) = 0 to synchrony
for the stochastic process (9,11), from asynchrony J(0) = 0 to synchrony  (here a cutoff is needed, because the approach to the full synchrony J = ∞ is exponential, formally the time to achieve it is infinite). The expression for T can be found via the standard first-passage time theory for one-dimensional stochastic processes26 (see Section 2 of Supplementary material for details):
(here a cutoff is needed, because the approach to the full synchrony J = ∞ is exponential, formally the time to achieve it is infinite). The expression for T can be found via the standard first-passage time theory for one-dimensional stochastic processes26 (see Section 2 of Supplementary material for details):

Depending on the value of μ/σ2, this time changes from a logarithmically large one  for 2μσ−2 + 3 > 0, to a time diverging as a power law of
for 2μσ−2 + 3 > 0, to a time diverging as a power law of  for 2μσ−2 + 3 < 0.
for 2μσ−2 + 3 < 0.
Nonidentical oscillators
For nonidentical oscillators, γ > 0, the fully synchronous state does not exist. In this situation the order parameter J fluctuates with the stationary distribution, which can be straightforwardly found from (11):

where Γ(m, x) is the upper incomplete Gamma function. The average value of the order parameter is

These expressions are valid for any γ > 0, however the limit γ → 0 is singular: a normalizable distribution for J at γ = 0

exists only if the synchronous state is unstable, i.e. μ < −σ2/2, and the average 〈J〉 = −(2μσ−2 + 2)−1 is finite only if μ < −σ−2. We present the dependencies of 〈J〉 on the parameters of the problem in Fig. 1.
For nonidentical oscillators we face a new problem of the behavior of the frequencies. The skew Langevin Eqs (9,10) appear to be analytically solvable only if we make another approximation: We neglect fluctuations of the order parameter (i.e. we assume J ≈ const, for large J this agrees with numerics) in the equations for the phases. In this approximation we obtain from Eq. (10) a closed Langevin equation for the phase dynamics:

where we denote  ,
,  . The stationary solution w(θ) of the corresponding Fokker-Planck equation with a constant flux
. The stationary solution w(θ) of the corresponding Fokker-Planck equation with a constant flux  obeys
obeys

(see Section 3 of Supplementary material for details). Solution of this equation reads

This rather lengthy exact solution can be simplified, for small ω, to include the first-order terms ~ω only. Here the expression for j reduces to  , and in the normalization factor C we can set ω = 0:
, and in the normalization factor C we can set ω = 0:

where Pλ(x) is the Legendre function. A rather simple expression appears for small μ, where an expansion of the Legendre function can be used. The final approximate formula for the observed frequencies of oscillators  reads
reads

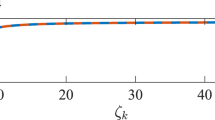
Noteworthy, for uncoupled oscillators (μ = 0) one obtains ν = ω. This means that common noise does not influence the average frequencies. In the presence of coupling, the observed frequencies ν are pulled together if the coupling is attractive, μ > 0, and are pushed apart if the coupling is repulsive, μ < 0. The effect depends on the level of synchrony, characterized by the value of the order parameter J. In fact, the limit J → ∞ is singular as here c → 1; as we show in Fig. 2, in this limit the dependence ν(ω) is not linear, but a power law one. Unfortunately, it is difficult to confirm these curves by direct simulations of the original system, because here we assume a definite value of the order parameter, which in a practical situation depends in a non-trivial way on the parameters of the problem – noise, coupling, and spread of natural frequencies.
Observed frequencies ν vs natural frequencies ω, obtained from (19).
We use here the continuous fraction expansion of the Fourier representation of w(θ), following27 (see Section 3 of Supplementary material for details). Solid lines: solutions for J = ∞, markers: solutions for 〈J〉 = 10. From top to bottom: μ/σ2 = −0.4, −0.2, 0, 0.2, 0.4. Dashed lines have slopes 1 + 2μ/σ2.
Formula (21) describes, in an approximate way, the main nontrivial effect that appears due to combined action of common noise and mean-field coupling on the ensemble of nonidentical oscillators. We first remind what happens to the frequencies in the absence of the common noise, i.e. for the standard Kuramoto model. In this case there is a critical value of the coupling constant, beyond which the order parameter is non-zero. In this synchronized state the frequencies are pulled together; moreover there appears a cluster of oscillators that have equal frequencies, the size of this cluster grows with the coupling constant. Below the critical coupling strength, the order parameter vanishes, so that there is no effect on the frequencies of the oscillators, and they remain the natural ones.
Common noise additionally influences the order parameter, which is non-vanishing and even large also when the mean-field coupling is repulsive (cf. Fig. 1). This leads to a surprising state of synchronization with dispersion of the frequencies: synchrony (in the sense of a large value of the order parameter) is in this case maintained by the common noise, while the repulsive coupling is responsible for the scattering of frequencies.
As this effect is notable, we characterize it below numerically on different levels. First, in Fig. 2 we show the solutions (19) for J = ∞ (perfect synchronization) and for a finite J. One can see that in the fully synchronous case J = ∞ the repulsion of frequencies is not linear as in Eq. (21), but follows a power law ν ∝ ωα, with an exponent that with high accuracy can be fitted as α = 1 + 2μ/σ2.
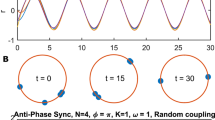
Next, we illustrate in Fig. 3 the effect of dispersion of the frequencies with the direct simulation of Langevin equations (1,4) describing the ensemble of coupled oscillators. One clearly sees dispersion of the frequencies for the repulsive coupling and their concentration for the attractive coupling, both for the cases of Ott-Antonsen equations (4) valid in the thermodynamic limit, and for a finite population governed by (1). This should be contrasted to the ensemble without noise (inset (a) in Fig. 3) where for repulsive coupling there is no repulsion of frequencies. Additionally, we confirm in inset (b) in Fig. 3 that the effect is valid not only for the Lorentzian distribution, but also for the Gaussian one.
Observed frequencies ν vs coupling strength μ, obtained from (1,4).
Parameters of simulations: Ω0 = 100, σ = 1, γ = 0.05. Markers: direct simulations of the population of 21 phase oscillators (1) (for better visibility, not all frequencies are depicted), solid lines: simulations of the Ott-Antonsen equations (4), valid in the thermodynamic limit, for the same individual frequencies. The inset (a) shows the case without noise σ = 0. The inset (b) shows the case of a Gaussian distribution of frequencies.
Discussion
To summarize, in this paper we have developed a theory for an ensemble of coupled oscillators driven by common noise. In the thermodynamic limit, by adopting the Ott-Antonsen ansatz and by averaging over the high basic frequency, we obtain analytically tractable equations for the order parameter and find the distribution of the order parameter in a closed form. As the common noise always fosters synchrony of oscillators, nontrivial features appear if the mean-field coupling acts in the opposite direction, i.e. is repulsive. For identical oscillators this competition results in the existence of the critical coupling strength μc = −σ2/2. For μ > μc the fully synchronous state where all the oscillators form a perfect cluster is stable, while for μ < μc it is not. Because, for vanishing noise, the splay state with a uniform distribution of phases is stable for all negative values of μ, one could expect bistability for μc < μ < 0. However, bistability does not happen, because the noise acts differently at the two states of interest: it is additive for the splay state with vanishing order parameter, and is multiplicative for the fully synchronous state. The latter is thus an absorbing state and the system never leaves it when the full synchrony is achieved. Therefore for μc < μ only the synchronous state is eventually observed, and the only nontrivial question is how fast it is reached—the answer to this question is given by Eq. (13).
Another quite counter-intuitive effect of the competition between the common noise and the coupling can be observed for non-identical oscillators. The order parameter is always non-vanishing in presence of common noise, and this leads to dispersion of the frequencies—their distribution is wider than in the coupling-free case. Here one should take into account that the common noise does not directly adjust the frequencies, although it pulls the phases together into a stochastic bunch. In presence of an additional repulsive coupling, the phases in the bunch repel each other (although synchrony is preserved) and as the result their frequencies diverge. This implies that in such a state, phase locking (characterized by large values of order parameter) is accompanied by frequency anti-entrainment (characterized by average frequencies). For example, many pendulum clocks (or metronomes) on a randomly forced platform will look like synchronous in snapshots of the pendula positions, while their average periods will differ stronger than without coupling and/or noise.
Methods
Numerical methods have been used to prepare Figs 2 and 3. Solution of the Fokker-Planck equation (18) was accomplished by virtue of an expansion of the solution in the Fourier series, and by solution of the resulting linear system of equation by virtue of the continuous fraction expansion method described in ref. 27. Results presented in Fig. 3 have been obtained by virtue of numerical simulation of stochastic differential equations using the stochastic Runge-Kutta method described in ref. 28; further details on the direct simulation can be found in Section 4 of Supplementary material.
Additional Information
How to cite this article: Pimenova, A. V. et al. Interplay of coupling and common noise at the transition to synchrony in oscillator populations. Sci. Rep. 6, 38518; doi: 10.1038/srep38518 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
23 May 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41598-023-35268-4
References
Nixon, M., Ronen, E., Friesem, A. A. & Davidson, N. Observing geometric frustration with thousands of coupled lasers. Phys. Rev. Lett. 110, 184102 (2013).
Grollier, J., Cros, V. & Fert, A. Synchronization of spin-transfer oscillators driven by stimulated microwave currents. Phys. Rev. B 73, 060409(R) (2006).
Cawthorne, A. B. et al. Synchronized oscillations in Josephson junction arrays: The role of distributed coupling. Phys. Rev. B 60, 7575–7578 (1999).
Richard, P., Bakker, B. M., Teusink, B., Dam, K. V. & Westerhoff, H. V. Acetaldehyde mediates the synchronization of sustained glycolytic oscillations in population of yeast cells. Eur. J. Biochem. 235, 238–241 (1996).
Prindle, A. et al. A sensing array of radically coupled genetic “biopixels”. Nature 481, 39–44 (2012).
Néda, Z., Ravasz, E., Vicsek, T., Brechet, Y. & Barabási, A. L. Physics of the rhythmic applause. Phys. Rev. E 61, 6987–6992 (2000).
Eckhardt, B., Ott, E., Strogatz, S. H., Abrams, D. M. & McRobie, A. Modeling walker synchronization on the Millennium Bridge. Phys. Rev. E 75, 021110 (2007).
Winfree, A. T. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16, 15–42 (1967).
Kuramoto, Y. Self-entrainment of a population of coupled nonlinear oscillators. In Araki, H. (ed.) International Symposium on Mathematical Problems in Theoretical Physics, 420 (Springer Lecture Notes Phys., v. 39, New York, 1975).
Wiener, N. Cybernetics Or Control and Communication in the Animal and the Machine (MIT Press, 2nd Ed., Cambridge, MA, 1965).
Pikovsky, A. Synchronization and stochastization of nonlinear oscillations by external noise. In Sagdeev, R. Z. (ed.) Nonlinear and Turbulent Processes in Physics vol. 3, 1601–1604 (Harwood Acad. Publ., 1984).
Pikovsky, A. S. Synchronization and stochastization of the ensemble of autogenerators by external noise. Radiophys. Quantum Electron. 27, 576–581 (1984).
Goldobin, D. S. & Pikovsky, A. Synchronization and desinchronization of self-sustained oscillators by common noise. Phys. Rev. E 71, 045201(R) (2005).
Teramae, J. & Tanaka, D. Robustness of the Noise-Induced Phase Synchronization in a General Class of Limit Cycle Oscillators. Phys. Rev. Lett. 93, 204103 (2004).
Goldobin, D. S. & Pikovsky, A. S. Synchronization of self-sustained oscillators by common white noise. Phys. A 351, 126–132 (2005).
Goldobin, D. S., Teramae, J.-N., Nakao, H. & Ermentrout, G.-B. Dynamics of Limit-Cycle Oscillators Subject to General Noise. Phys. Rev. Lett. 105, 154101 (2010).
Goldobin, D. S. & Pikovsky, A. Antireliability of noise-driven neurons. Phys. Rev. E 73, 061906 (2006).
Martens, E. A., Thutupalli, S., Fourrière, A. & Hallatschek, O. Chimera states in mechanical oscillator networks. Proc. Natl. Acad. Sci. 110, 10563–10567 (2013).
Temirbayev, A. A., Zhanabaev, Z. Z., Tarasov, S. B., Ponomarenko, V. I. & Rosenblum, M. Experiments on oscillator ensembles with global nonlinear coupling. Phys. Rev. E 85, 015204(R) (2012).
Temirbayev, A. A., Nalibayev, Y. D., Zhanabaev, Z. Z., Ponomarenko, V. I. & Rosenblum, M. Autonomous and forced dynamics of oscillator ensembles with global nonlinear coupling: An experimental study. Phys. Rev. E 87, 062917 (2013).
Gil, S., Kuramoto, Y. & Mikhailov, A. S. Common noise induces clustering in populations of globally coupled oscillators. EPL (Europhysics Letters) 88, 60005 (2009).
Nagai, K. H. & Kori, H. Noise-induced synchronization of a large population of globally coupled nonidentical oscillators. Phys. Rev. E 81, 065202 (2010).
Braun, W., Pikovsky, A., Matias, M. A. & Colet, P. Global dynamics of oscillator populations under common noise. EPL 99, 20006 (2012).
García-Álvarez, D., Bahraminasab, A., Stefanovska, A. & McClintock, P. V. E. Competition between noise and coupling in the induction of synchronisation. EPL (Europhysics Letters) 88, 30005 (2009).
Ott, E. & Antonsen, T. M. Low dimensional behavior of large systems of globally coupled oscillators. Chaos 18, 037113 (2008).
Gardiner, C. W. Handbook of Stochastic Methods (Springer, Berlin, 1996).
Risken, H. Z. The Fokker-Planck Equation (Springer, Berlin, 1989).
Burrage, P. M. Runge-Kutta methods for stochastic differential equations. PhD Thesis, The University of Queensland, Brisbane, Australia (1999).
Acknowledgements
We thank P. Collet and M. Matias for useful discussions. The work was supported by ITN COSMOS (funded by the European Union Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 642563). The paper was finalized during the visit supported by G-RISC (grant No. M-2016b-8). Numerical part of this work conducted by Ar.P. was supported by the Russian Science Foundation (Project No. 14-12-00811). The analytical calculations which led to Eqs (5)–(16), performed by An.P. and D.G. were supported by the Russian Science Foundation (Project No. 14-12-00090).
Author information
Authors and Affiliations
Contributions
D.G., M.R., and Ar.P. formulated the problem. An.P., D.G., and Ar.P. derived equations (5, 6). An.P. and D.G. performed the averaging and derived Eqs (9–11) and performed the analytical analysis of the statistics of identical oscillators (12, 13). An.P., D.G., and Ar.P. performed the analytical analysis of the statistics of non-identical oscillators. M.R. and Ar.P. performed numerical simulations. Ar.P., M.R., and D.G. wrote the main manuscript text. Ar.P. prepared Figures 1–3. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pimenova, A., Goldobin, D., Rosenblum, M. et al. Interplay of coupling and common noise at the transition to synchrony in oscillator populations. Sci Rep 6, 38518 (2016). https://doi.org/10.1038/srep38518
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38518
This article is cited by
-
Using noise to augment synchronization among oscillators
Scientific Reports (2021)
-
Coherence resonance in influencer networks
Nature Communications (2021)
-
Two-Bunch Solutions for the Dynamics of Ott–Antonsen Phase Ensembles
Radiophysics and Quantum Electronics (2019)
-
Correlations of the States of Non-Entrained Oscillators in the Kuramoto Ensemble with Noise in the Mean Field
Radiophysics and Quantum Electronics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.