Abstract
Dielectric resonators form the building blocks of nano-scale optical antennas and metamaterials. Due to their multipolar resonant response and low intrinsic losses they offer design flexibility and high-efficiency performance. These resonators are typically described in terms of a spherical harmonic decomposition with Mie theory. In experimental realizations however, a departure from spherical symmetry and the use of high-index substrates leads to new features appearing in the multipolar response. To clarify this behavior, we present a systematic experimental and numerical characterization of Silicon disk resonators. We demonstrate that for disk resonators on low-index quartz substrates, the electric and magnetic dipole modes are easily identifiable across a wide range of aspect-ratios, but that higher order peaks cannot be unambiguously associated with any specific multipolar mode. On high-index Silicon substrates, even the fundamental dipole modes do not have a clear association. When arranged into arrays, resonances are shifted and pronounced preferential forward and backward scattering conditions appear, which are not as apparent in individual resonators and may be associated with interference between multipolar modes. These findings present new opportunities for engineering the multipolar scattering response of dielectric optical antennas and metamaterials, and provide a strategy for designing nano-optical components with unique functionalities.
Similar content being viewed by others
Introduction
Dielectric resonators, first developed as radio-frequency antenna elements1, are now being used to develop high-performance nano-optical components. In particular, dielectric Mie resonators support a complete set of multipolar harmonics2, including magnetic dipole and quadrupolar modes. Due to their low intrinsic losses3,4, as compared to metal-based plasmonic antennas, dielectric resonators make attractive building blocks for metamaterial and metasurface based technologies. Recent demonstrations include ultra-thin lenses5,6,7,8,9,10,11, blazed gratings12,13, vector beam generators14,15, beam shaping16, fluorescence and nonlinearity enhancement17,18,19, optical antennas20,21,22,23,24,25, and reconfigurable metamaterials26,27.
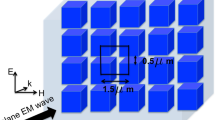
A common dielectric metasurface building block is a high-index sphere with a scattering response that can be decomposed into spherical harmonics (Fig. 1a) through Mie Theory28. Practical implementations favor easier to fabricate disk-shaped resonators, (Fig. 1b), which also provide additional design parameters: the aspect-ratio (AR) and substrate refractive index. When the aspect-ratio and substrate refractive index are close to unity, these disk-resonators may be considered a small perturbation29,30 of sphere resonators. However, when the aspect-ratio of the disk becomes large, or when a high-index substrate is introduced, the breaking of spherical symmetry introduces new features into the multipolar modes. It has been shown that for metallic nanostructures the presence of a dielectric substrate can couple and hybridize the resonator’s plasmonic modes31,32. When particles are arranged into arrays, inter-particle interference further modifies the optical response.
Multipolar response of dielectric resonators.
The simulated multipolar decomposition of the scattering-cross-section of an (a) individual Silicon sphere with diameter d = 660 nm in air, and (b) an individual Silicon disk with height h = 660 nm and diameter d = 660 nm in air. Simulation details are in the appendices. (c) SEM image of one of the fabricated Silicon disk arrays.
In this work, we systematically measure the dipolar and quadrupolar resonances of individual disks and disk arrays with varying aspect-ratio and substrate index. With standard cleanroom processes we fabricate Silicon disk resonators (Fig. 1c) and determine their resonance wavelengths through FTIR reflection and transmission measurements. With electromagnetics simulations, we then decompose the internal fields of the resonators into Cartesian multipole moments (Equations 1, 2, 3, 4), which include toroidal contributions (Equations 5 and 6). We neglect higher order mean-square radii correction terms, which represent a minor perturbation33. The approximate partial scattering-cross-sections (Equations 7, 8, 9, 10) are then calculated to track the dispersion of individual multipolar modes34,35. In doing so, we map the dispersion of multipolar resonances with respect to aspect ratio, demonstrate unique features of the multipolar response such as overlapping electric and magnetic modes36 and a frequency-shifted response in disk arrays, as compared to single resonators.










Individual Silicon Disks on Low-Index Substrates
In Fig. 2 we plot the simulated scattering-cross-section of varying aspect ratio (diameter/height) Silicon disk resonators in air (Fig. 2a), and on a quartz substrate (Fig. 2b). Resonances in the multipolar moments are determined by decomposing the fields internal to the disk according to equations 1, 2, 3, 4, 5, 6, 7, 8. Black lines are local maxima in the modal decompositions of the total multipole moments (i.e. including toroidal contributions). Consider Fig. 2c, the scattering cross-section of an AR = 1.2 disk on quartz (equivalent to a line-cut taken vertically through Fig. 2b). The breaking of spherical symmetry is evident in an additional peak in the electric dipole moment near 5000 cm−1, labeled ED”. There is also an additional, substrate-induced peak in the electric dipole moment at low frequencies, labeled ED’. This local peak becomes even more prevalent for disks on high-index substrates, and is discussed in more detail in the subsequent section. These ED, ED’, and ED” resonances are similar in that they all represent local maxima in the electric dipole moment. However the ED mode has a clear correspondence in spherical particles, whereas the ED’ and ED” resonances only appear due to symmetry breaking. To highlight this difference, they are represented as dashed lines in Fig. 2a and b. Similar to spheres, the modes disperse to lower frequencies with increasing radius. However, dispersion of the fundamental ED and MD modes flattens as the aspect ratio increases towards 2.0. Similar phenomena were recently observed in 0-D disk and 1-D rectangular Mie resonators of varying widths37,38. Additionally, the ED and MD resonances approach each other and overlap at an aspect ratio of ~2, a phenomenon that is particularly important for the design of transmissive metasurfaces39,40,41.
Individual Resonators on Low-Index Quartz Substrates.
The simulated scattering-cross-section of an individual Silicon resonator with height h = 660 nm, as a function of the aspect ratio (diameter/height) with (a) no substrate, and (b) a low-index quartz substrate. (c) A line-cut of the scattering cross section given in (b) at an aspect ratio AR = 1.2, with individual multipole contributions. (d) The experimentally measured transmission dips of Silicon resonators on a quartz substrate, compared to the simulated dispersion of the multipolar resonances. The height of each resonator is fixed at h = 660 nm and the aspect-ratio is varied by changing the diameter. Simulation and experimental details are in the Methods and Supplementary Material.
In Fig. 2d we plot experimentally measured dips (see Methods for optical characterization details) in the experimental transmission spectra (see supplementary material for experimental spectral line-shapes) of single resonators, along with their simulated dispersion curves. The lowest order MD and ED modes are easily identified and track the calculated dispersion of multipolar moments. However, higher order modes (i.e. ED”, MQ, and EQ resonances) do not appear as distinguishable features in the experimental spectra. At high frequencies, the observed transmission dips most closely track the ED” resonance, as expected from simulations (Fig. 2b). The interference of multipole resonances with each other, and with reflections off the substrate, leads to a broad scattering resonance whose maximum cannot be attributed to any individual multipole moment.
Individual Silicon Disks on High-Index Substrates
The substrate effects seen for resonators on quartz (n≈1.45) become far more prominent for resonators on higher index substrates. In Fig. 3a we plot the simulated scattering-cross-section of an individual Silicon resonator, on a high-index Silicon substrate (n≈3.4), as a function of the disk AR. Compared to the scattering response of identical resonators on low-index substrates, linewidths are substantially broadened and the fundamental ED and MD modes shift away from each other so that they no longer overlap. Additionally, each of the three lowest order scattering resonances exhibits substantial mode hybridization. Consider Fig. 3b, which shows a line-cut of Fig. 3a at AR = 1.2. The ED moment dominates over the competing multipoles. The origin of this behavior can be understood through examination of electromagnetic intensity plots. In Fig. 3c we plot the local electric and magnetic field intensities for the lowest order scattering resonance of Silicon disks on Quartz (top) and Silicon substrates (bottom). For the quartz substrate, a resonant magnetic field is positioned in the center of the disk. The electric fields are zero at the center and exhibit an approximately circular band of high intensity internal to the disk. These field patterns are quite similar to the MD modes of spheres, and the multipolar decomposition is dominated by the MD moment. On the high-index substrate, however, the field patterns are significantly altered. The peak magnetic field is pushed closer to the substrate and the dominant electric field intensity maxima are external to the disk. The multipolar decomposition is dominated instead by the ED moment42. It is important to note that multipolar decompositions are not unique, and will vary with choice of origin. We choose the disk center to facilitate comparison across different geometries. In any case, there is a significant perturbation of field profiles and multipolar moments for disks on high index substrates, and further work is needed to understand how this may affect, for example, the homogenized metamaterial response in such geometries. In Fig. 3d we compare the location of resonances in the multipolar moments with experimental measurements of reflection minima. We observe the dispersion of three clear sets of scattering peaks. In simulations however, each of these three clear curves does not have an obvious correspondence to a single multipolar mode. Unlike the previous case of resonators on a Quartz substrate, here even the fundamental mode appears to track the combined response of the MD and ED decomposition.
Individual Resonators on High-Index Silicon Substrates.
(a) The simulated scattering-cross-section of an individual Silicon resonator, with height h = 660 nm, as a function of the aspect ratio, on a high-index Silicon substrate. (b) A line-cut of the decomposed scattering cross section given in (a) at an aspect ratio AR = 1.2. (c) The local electric and magnetic field plots of Silicon resonators, with AR = 1, on Quartz and Silicon substrates. (d) The experimentally measured reflection peaks of individual Silicon resonators on a Silicon substrate, compared to the simulated dispersion of the multipolar resonances. The height of each resonator is fixed at h = 660 nm and the aspect-ratio is varied by changing the diameter. Simulation and experimental details are in the Methods and Supplementary Material.
Collective Interference in Silicon Disk Arrays
In arrays, inter-particle interference modifies the collective scattering response43,44,45,46. In Fig. 4a we plot the simulated transmission spectra of Silicon disk resonators, on a low-index quartz substrate, with sub-wavelength periodicity a = 1.55 μm and varying AR. Scattering resonances of disks now appear as minima in the transmission spectra. We see that the lowest order ED and MD modes are relatively narrow, as compared to the broader scattering response of individual resonators in Fig. 2b, and unlike individual resonators, can be independently resolved over a larger range of aspect-ratios. Due to near-field coupling, the fundamental MD mode is blue-shifted relative to the individual resonators in Fig. 2b. A narrow transmission peak appears at frequencies just above the ED mode due to the Kerker condition, in which the ED and MD modes interfere in-phase and enhance forward scattering. Although this Kerker condition is fulfilled in individual resonators as well47,48,49, it is much more apparent in the arrays. At frequencies above the Kerker condition, features in simulated (Fig. 4a) or experimental (Fig. 4b) transmission spectra can no longer be ascribed to individual multipolar resonances. In particular, the third set of experimentally observed peaks in Fig. 4b is substantially red-shifted relative to the peak of the ED” resonance. We speculate that this is due to the fulfillment of a preferentially backward scattering condition, or anti-Kerker condition, in which multipoles constructively interfere in the backward direction. Similar effects were recently observed in single dielectric spheres50. Furthermore, higher order quadrupole moments appear to be significantly suppressed, even at high frequencies near the MD2 peak.
Disk Resonators Arrays on Low- and High-Index Substrates.
(a) The simulated transmission spectra, as a function of disk aspect ratio, for an array of Silicon resonators on a Quartz substrate with period a = 1.55 μm. (b) The experimentally identified modal peaks and the simulated dispersion curves. (c) The simulated reflection spectra, as a function of disk aspect ratio, for an array of Silicon resonators on a Silicon substrate with period a = 1.55 μm. (d) The experimentally identified modal peaks and the simulated dispersion curves.
On high index substrates (Fig. 4c,d) the relationship between scattering and transmission is inverted—scattering resonances are correlated with peaks in transmission, or equivalently dips in reflection (see supplementary for experimental spectral line shapes). Due to its higher refractive index, and thus higher optical density of states, most of the scattered light is directed into the substrate51. Similar to individual resonators, we see that disk arrays on high-index substrates exhibit substantially broader ED and MD resonances compared to low-index substrates. Here however, in contrast to low-index Quartz substrates, the fundamental MD mode is red-shifted. We speculate that high-index substrates effectively reduce near-field coupling, due to reduced wavelengths, and that radiative interference leads to prominent red-shifting52.
Conclusion
In conclusion, we have elucidated the dependence of the multipolar scattering properties of dielectric disk-resonators, as a function of the disk aspect ratio and substrate refractive index. We demonstrate that changing the disk aspect-ratios or substrate refractive index can lead to overlapping electric and magnetic multipolar modes. For individual disks on Quartz substrates, dipolar modes are easily identified in numerical multipolar decompositions, but at higher frequencies broad scattering peaks cannot be easily attributed to any specific higher order multipole resonance. On high-index Silicon substrates, internal field patterns are significantly altered, and even the fundamental dipole modes cannot be unambiguously associated with an electric or magnetic type decomposition. When arranged into arrays, new effects arise due to interference between multipolar modes. On Quartz substrates the fundamental magnetic dipole mode is blue-shifted, and at higher frequencies there exist preferentially forward-scattering Kerker and preferentially backward-scattering anti-Kerker resonances. On high-index substrates however, the fundamental MD mode is strongly red-shifted, and highly directional scattering resonances are not apparent. These findings provide new insights into designing dielectric optical antennas, and will serve as guidelines for engineering metamaterials with novel functionalities.
Methods
Fabrication and Characterization
Prior to processing, substrates were ultrasonicated and cleaned with acetone, isopropanol, ‘nanostrip’ solution to remove organic contaminants, and HF to remove native oxide. Amorphous Silicon was deposited onto fused Quartz substrates with an Advanced Vacuum PECVD by decomposing silane with an electron plasma (650 mT, 2% SiH4 at 1500 sccm, high-frequency power 30 W, chuck temperature 300 C). Although there are differences in the optical constants of crystalline vs. amorphous Silicon in the visible spectrum, for the mid-infrared range examined in this work the difference in refractive index is negligible.
To compensate for stress-induced curvature across the sample, a film of SiO2 was deposited on the back-side. In preparation for deep ultraviolet photolithography with an ASML PAS 5500/300 DUV Stepper, an anti-reflective coating (AR15) and negative-type photoresist (UVN-2300) were spun onto the samples. The pattern was exposed with annular-type illumination with NA = 0.63, outer sigma = 0.8, inner sigma = 0.5, exposure dose = 109 mJ/cm2, and a focus offset −0.15 um, which enabled us to reliably achieve sub-150 nm feature sizes. After exposure, wafers were post-baked for 60 seconds at 105 C and develop with AZ300MIF for 30 seconds. Leftover AR and PR was removed in an O2 barrel asher for 30 seconds at 300 mT and 100 W.
Samples were etched with a deep reactive-ion-etching process using a PlasmaTherm 770 SLR system. Prior to etching the chamber was plasma cleaned for 30 minutes at 30 mT, 0 W substrate bias, 825 W ICP power, 20 sccm O2, and 10 sccm Ar. Etching was performed at 19 mT, 15 W substrate bias, 825 W ICP power, 26 sccm SF6, 54 sccm C4F8, 20 sccm Ar, with He backside cooling. Afterwards the photoresist was removed with an O2 plasma in a Gasonics ashing system at >350 C.
The reflection and transmission spectra of the Silicon disk resonators were measured with a Bruker Vertex FTIR and Hyperion Microscope. Simplified diagrams of the optical path in the reflection and transmission configurations are given in the supplementary material. Individual isolated resonators were identified and focused using visible light in the microscope. The infrared spectra were then measured with the MCT detector.
Simulation
All electromagnetic simulations were performed with the Lumerical FDTD Solver. Individual disk resonators were simulated with PML boundary conditions and boundaries at least 5 um away from the resonator. The resonator was excited with a total-field-scattered-field source. The total scattering cross section was measured using the built-in ‘cross-section’ analysis object. The forward and backward scattering cross sections are the field power transmitted through the forward and backward hemispheres of the ‘cross-section’ monitor respectively. The partial scattering cross sections were determined by performing a multipole decomposition based on the internal electric fields of the particle. Expressions for the multipolar moments were integrated across the volume of the disk, and the corresponding partial scattering cross section was subsequently calculated. The origin was taken to be at the center of the disk for all calculations. The Silicon and Quartz optical constants were modelled using a Lumerical fit to data collected by Palik. Convergence tests indicated a mesh size of less than 7.5 nm inside the disk resonator and a simulation time of at least 4,500 fs was needed.
Disk resonator arrays were simulated with PML boundary conditions in the z direction, and periodic boundary conditions along the x and y directions, and with an anti-symmetric condition applied along the x-direction and symmetric condition applied along the y-direction to improve computational efficiency. The disks were excited with a plane-wave source. The reflection and transmission scattering parameters were computed with the built-in ‘s_params’ analysis object.
Additional Information
How to cite this article: Butakov, N. A. and Schuller, J. A. Designing Multipolar Resonances in Dielectric Metamaterials. Sci. Rep. 6, 38487; doi: 10.1038/srep38487 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Mongia, R. K. & Bhartia, P. Dielectric resonator antennas—A review and general design relations for resonant frequency and bandwidth. International Journal of Microwave and Millimeter‐Wave Computer‐Aided Engineering 4, 230–247 (1994).
Das, T., Iyer, P. P., DeCrescent, R. A. & Schuller, J. A. Beam engineering for selective and enhanced coupling to multipolar resonances. Physical Review B 92, 241110 (2015).
Schuller, J. A., Zia, R., Taubner, T. & Brongersma, M. L. Dielectric metamaterials based on electric and magnetic resonances of silicon carbide particles. Physical Review Letters 99, 107401 (2007).
Huang, L., Yu, Y. & Cao, L. General modal properties of optical resonances in subwavelength nonspherical dielectric structures. Nano Letters 13, 3559–3565 (2013).
Arbabi, A., Briggs, R. M., Horie, Y., Bagheri, M. & Faraon, A. Efficient Dielectric Metasurface Collimating Lenses for Mid-Infrared Quantum Cascade Lasers. Optics Express 23, 33310–33317 (2015).
Lin, D., Fan, P., Hasman, E. & Brongersma, M. L. Dielectric gradient metasurface optical elements. Science 345, 298–302 (2014).
Khorasaninejad, M. et al. Achromatic metasurface lens at telecommunication wavelengths. Nano Letters 15, 5358–5362 (2015).
Kamali, S. M., Arbabi, A., Arbabi, E., Horie, Y. & Faraon, A. Decoupling optical function and geometrical form using conformal flexible dielectric metasurfaces. Nature Communications 7, 11618, doi: 10.1038/ncomms11618 (2016).
Arbabi, A., Briggs, R. M., Horie, Y., Bagheri, M. & Faraon, A. Efficient dielectric metasurface collimating lenses for mid-infrared quantum cascade lasers. Optics Express 23, 33310–33317 (2015).
Khorasaninejad, M. et al. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 352, 1190–1194 (2016).
Arbabi, A., Horie, Y., Ball, A. J., Bagheri, M. & Faraon, A. Subwavelength-thick lenses with high numerical apertures and large efficiency based on high-contrast transmitarrays. Nature Communications 6, 7069, doi: 10.1038/ncomms8069 (2015).
Khorasaninejad, M. & Capasso, F. Broadband Multifunctional Efficient Meta-Gratings Based on Dielectric Waveguide Phase Shifters. Nano Letters 15, 6709–6715 (2015).
Lalanne, P., Astilean, S., Cambril, E. & Launois, H. Blazed binary subwavelength gratings with efficiencies larger than those of conventional échelette gratings. Optics Letters 23, 1081–1083 (1998).
Yang, Y. et al. Dielectric meta-reflectarray for broadband linear polarization conversion and optical vortex generation. Nano Letters 14, 1394–1399 (2014).
Arbabi, A., Horie, Y., Bagheri, M. & Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nature Nanotechnology, 10, 937–943 (2015).
Desiatov, B., Mazurski, N., Fainman, Y. & Levy, U. Polarization selective beam shaping using nanoscale dielectric metasurfaces. Optics Express 23, 22611–22618 (2015).
Kruk, S. et al. Enhanced magnetic second-harmonic generation from resonant metasurfaces. ACS Photonics 2, 1007–1012 (2015).
Shcherbakov, M. R. et al. Enhanced third-harmonic generation in silicon nanoparticles driven by magnetic response. Nano Letters 14, 6488–6492 (2014).
Regmi, R. et al. All-Dielectric Silicon Nanogap Antennas to Enhance the Fluorescence of Single Molecules. Nano Letters 16(8), 5143–5151 (2016).
Albella, P. et al. Low-loss electric and magnetic field-enhanced spectroscopy with subwavelength silicon dimers. The Journal of Physical Chemistry C 117, 13573–13584 (2013).
Wells, S. M., Merkulov, I. A., Kravchenko, I. I., Lavrik, N. V. & Sepaniak, M. J. Silicon nanopillars for field-enhanced surface spectroscopy. ACS Nano 6, 2948–2959 (2012).
Zywietz, U. et al. Electromagnetic resonances of silicon nanoparticle dimers in the visible. ACS Photonics 2, 913–920 (2015).
Moitra, P. et al. Large-scale all-dielectric metamaterial perfect reflectors. ACS Photonics 2, 692–698 (2015).
Proust, J., Bedu, F., Gallas, B., Ozerov, I. & Bonod, N. All-Dielectric Colored Metasurfaces with Silicon Mie Resonators. ACS Nano 10(8), 7761–7767 (2016).
Shi, L., Tuzer, T. U., Fenollosa, R. & Meseguer, F. A New Dielectric Metamaterial Building Block with a Strong Magnetic Response in the Sub‐1.5‐Micrometer Region: Silicon Colloid Nanocavities. Advanced Materials 24, 5934–5938 (2012).
Shcherbakov, M. R. et al. Ultrafast all-optical switching with magnetic resonances in nonlinear dielectric nanostructures. Nano Letters 15, 6985–6990 (2015).
Lewi, T., Iyer, P. P., Butakov, N. A., Mikhailovsky, A. A. & Schuller, J. A. Widely tunable infrared antennas using free carrier refraction. Nano Letters 15(12), 8188–8193 (2015).
Zhao, Q., Zhou, J., Zhang, F. & Lippens, D. Mie resonance-based dielectric metamaterials. Materials Today 12, 60–69 (2009).
Coenen, T., van de Groep, J. & Polman, A. Resonant modes of single silicon nanocavities excited by electron irradiation. ACS Nano 7, 1689–1698 (2013).
Evlyukhin, A. B., Reinhardt, C. & Chichkov, B. N. Multipole light scattering by nonspherical nanoparticles in the discrete dipole approximation. Physical Review B 84, 235429 (2011).
Knight, M. W., Wu, Y., Lassiter, J. B., Nordlander, P. & Halas, N. J. Substrates matter: influence of an adjacent dielectric on an individual plasmonic nanoparticle. Nano letters 9, 2188–2192 (2009).
Zhang, S., Bao, K., Halas, N. J., Xu, H. & Nordlander, P. Substrate-induced Fano resonances of a plasmonic nanocube: a route to increased-sensitivity localized surface plasmon resonance sensors revealed. Nano letters 11, 1657–1663 (2011).
Radescu, E. & Vaman, G. Exact calculation of the angular momentum loss, recoil force, and radiation intensity for an arbitrary source in terms of electric, magnetic, and toroid multipoles. Physical Review E 65, 046609 (2002).
Paniagua-Domínguez, R. et al. Generalized Brewster effect in dielectric metasurfaces. Nature Communications 7(174), 93–102 (2016).
Miroshnichenko, A. E. et al. Nonradiating anapole modes in dielectric nanoparticles. Nature Communications 6, doi: 10.1038/ncomms9069 (2015).
Miroshnichenko, A. E., Evlyukhin, A. B., Kivshar, Y. S. & Chichkov, B. N. Substrate-induced resonant magnetoelectric effects for dielectric nanoparticles. ACS Photonics 2, 1423–1428 (2015).
Iyer, P. P., Pendharkar, M. & Schuller, J. A. Electrically Reconfigurable Metasurfaces Using Heterojunction Resonators. Advanced Optical Materials, doi: 10.1002/adom.201600297 (2016).
Van de Groep, J. & Polman, A. Designing dielectric resonators on substrates: Combining magnetic and electric resonances. Optics Express 21, 26285–26302 (2013).
Yu, Y. F. et al. High‐transmission dielectric metasurface with 2π phase control at visible wavelengths. Laser & Photonics Reviews 9, 412–418 (2015).
Iyer, P. P., Butakov, N. A. & Schuller, J. A. Reconfigurable Semiconductor Phased-Array Metasurfaces. ACS Photonics 2, 1077–1084 (2015).
Zhan, A. et al. Low-contrast dielectric metasurface optics. ACS Photonics 3, 209–214 (2016).
Evlyukhin, A. B., Reinhardt, C., Evlyukhin, E. & Chichkov, B. N. Multipole analysis of light scattering by arbitrary-shaped nanoparticles on a plane surface. JOSA B 30, 2589–2598 (2013).
Bezares, F. J. et al. Mie resonance-enhanced light absorption in periodic silicon nanopillar arrays. Optics Express 21, 27587–27601 (2013).
Evlyukhin, A. B., Reinhardt, C., Seidel, A., Luk’yanchuk, B. S. & Chichkov, B. N. Optical response features of Si-nanoparticle arrays. Physical Review B 82, 045404 (2010).
Evlyukhin, A. B., Reinhardt, C., Zywietz, U. & Chichkov, B. N. Collective resonances in metal nanoparticle arrays with dipole-quadrupole interactions. Physical Review B 85, 245411 (2012).
Butakov, N. & Schuller, J. Hybrid optical antennas with photonic resistors. Optics Express 23, 29698–29707 (2015).
Kerker, M., Wang, D.-S. & Giles, C. Electromagnetic scattering by magnetic spheres. JOSA 73, 765–767 (1983).
Person, S. et al. Demonstration of zero optical backscattering from single nanoparticles. Nano Letters 13, 1806–1809 (2013).
Luk’yanchuk, B. S., Voshchinnikov, N. V., Paniagua-Domínguez, R. & Kuznetsov, A. I. Optimum forward light scattering by spherical and spheroidal dielectric nanoparticles with high refractive index. ACS Photonics 2, 993–999 (2015).
Geffrin, J.-M. et al. Magnetic and electric coherence in forward-and back-scattered electromagnetic waves by a single dielectric subwavelength sphere. Nature Communications 3, 1171, doi: 10.1038/ncomms2167 (2012).
Spinelli, P., Verschuuren, M. & Polman, A. Broadband omnidirectional antireflection coating based on subwavelength surface Mie resonators. Nature Communications 3, 692, doi: 10.1038/ncomms1691 (2012).
Simpkins, B. et al. Pitch-dependent resonances and near-field coupling in infrared nanoantenna arrays. Optics express 20, 27725–27739 (2012).
Acknowledgements
This work was supported by the Air Force Office of Scientific Research Young Investigator Program (FA9550-13-1-0182) for the study of Infrared Semiconductor Metamaterials and by the UC Office of the President Multi-campus Research Programs and Initiatives (MR-15-328528). Numerical calculations were performed on the computing cluster at the Center for Scientific Computing from the California NanoSystems Institute at the University of California, Santa Barbara: an NSF MRSEC (DMR-1121053) and NSF CNS-0960316. Samples were fabricated at the UCSB Nanofabrication Facility. This research was conducted with government support under the DoD, Air Force Office of Scientific Research, National Defense Science and Engineering Graduate (NDSEG) Fellowship, 32 CFR 168a. We are grateful for discussions with Prasad Iyer, Tomer Lewi, Tanya Das, and Steven Brown.
Author information
Authors and Affiliations
Contributions
J.A.S. and N.A.B. conceived the ideas for the research project. N.A.B. performed the numerical simulations, sample fabrication, and optical characterization. N.A.B. and J.A.S. wrote the manuscript. J.A.S supervised the research project.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Butakov, N., Schuller, J. Designing Multipolar Resonances in Dielectric Metamaterials. Sci Rep 6, 38487 (2016). https://doi.org/10.1038/srep38487
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38487
This article is cited by
-
Mapping the refractive index with single plasmonic nanoantenna
Scientific Reports (2018)
-
Ultrawide thermal free-carrier tuning of dielectric antennas coupled to epsilon-near-zero substrates
Nature Communications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.