Abstract
Controlling the phase distributions on metasurfaces leads to fascinating effects such as anomalous light refraction/reflection, flat-lens focusing, and optics-vortex generation. However, metasurfaces realized so far largely reply on passive resonant meta-atoms, whose intrinsic dispersions limit such passive meta-devices’ performances at frequencies other than the target one. Here, based on tunable meta-atoms with varactor diodes involved, we establish a scheme to resolve these issues for microwave metasurfaces, in which the dispersive response of each meta-atom is precisely controlled by an external voltage imparted on the diode. We experimentally demonstrate two effects utilizing our scheme. First, we show that a tunable gradient metasurface exhibits single-mode high-efficiency operation within a wide frequency band, while its passive counterpart only works at a single frequency but exhibits deteriorated performances at other frequencies. Second, we demonstrate that the functionality of our metasurface can be dynamically switched from a specular reflector to a surface-wave convertor. Our approach paves the road to achieve dispersion-corrected and switchable manipulations of electromagnetic waves.
Similar content being viewed by others
Introduction
Metasurfaces1,2,3,4, planar metamaterials with tailored reflection/transmission phase profiles, attracted enormous interest recently5,6,7,8. Many fascinating effects were discovered based on metasurfaces in different frequency domains, such as anomalous light refraction/reflection9,10,11,12,13,14,15,16,17, surface wave (SW) couplers2,18, vortex beam generation19, flat lens20,21,22,23,24,25,26,27,28, polarization control29,30, holograms31,32,33,34, and photonic spin-Hall effect35,36. To design a metasurface with certain functionality, one typically combines a set of resonant meta-atoms with distinct electromagnetic (EM) responses to form a planar structure, such that the whole device exhibits the desired profiles of transmission/reflection amplitude/phase. Such a strategy has been successfully implemented in the past years to design various metasurfaces working for different purposes1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36.
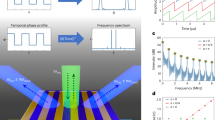
However, such a designing strategy only works for a single frequency, since the desired phase profile cannot maintain at other frequencies due to the intrinsic dispersions of passive resonant meta-atoms. Figure 1 schematically illustrates the underlying physics based on a reflective metasurface requiring a linear reflection-phase profile. Suppose a collection of meta-atoms have been chosen to form a device exhibiting an ideal linear phase profile at the frequency f0 (red line in Fig. 1a), such a strict linear relationship cannot be satisfied at other frequencies (blue lines) with the same device, since all resonant meta-atoms exhibit Lorenz-type phase dispersions (inset to Fig. 1a) and thus the phase difference between adjacent meta-atoms varies as a function of frequency. In particular, the phase gradient must decrease to zero at frequencies far away from f0 where all resonant behaviors die off. As a result, while at f0 the device can support single-mode anomalous reflection dictated by the generalized Snell’s law (Fig. 1e), at other frequencies, the device’s performance is significantly decreased with undesired modes appearing and deteriorated working efficiency (Fig. 1c). Such an issue seems inherent to all metasurfaces based on passive resonant meta-atoms, working in both reflection2,11,12,13,27,28,29,33,34,35 and transmission1,4,8,9,10,14,15,16,17,18,19,20,21,22,23,24,25,26,30,31,32,36 geometries and relying on either phase or amplitude modulations6,7. Although the phase profiles in geometric-phase-based metasurfaces can immune from the frequency change, the real performances of such devices are dictated by the EM responses of their basic meta-atoms, which are still strongly frequency dependent20,34,35,36. We emphasize that such “chromatic aberrations” cannot be solved by simply expanding the working bandwidths of metasurfaces11,12,13,14,15,16 using low-Q and/or multi-mode resonators, since the frequency dispersion is intrinsic to all passive resonators.
Tunable scheme to overcome the phase distortions in passive metasurfaces.
Typical phase responses of meta-atoms within a supercell in a (a) passive and (b) a tunable gradient metasurface, at working frequency f = f0 and non-working frequencies f ≠ f0. The nonlinear phase distributions at non-working frequencies in the passive device, caused by frequency dispersions of passive meta-atoms (see inset to Fig. 1a), can be rectified by active external controls in the tunable device. Typical scattering patterns of (c,e) passive or (d,f) tunable metasurfaces at (c,d) off-working frequencies and (e,f) working frequency.
In this paper, we experimentally demonstrate that such a limitation can be overcome by making tunable metasurfaces with meta-atoms controlled by external knobs (see inset to Fig. 1b). Borrowing similar technical ideas from previous studies on tunable reflectarrays/transmitarrays37,38,39,40,41 to involve varactor diodes into the meta-atom structures, we can individually control the reflection phase of each active unit by applying an appropriate voltage on the diode, so that the distorted phase profiles of the passive metasurface at off-working frequencies (f ≠ f0) can be rectified (see Fig. 1b). Consequently, our tunable metasurface can not only work well at the target frequency (Fig. 1f), but also works in the entire frequency band (Fig. 1d) with single-mode operation and high efficiency. We further experimentally demonstrate that the functionality of our device can be dynamically switched from a conventional reflector to a surface wave (SW) coupler, again based on the tunable and precise local-phase control. Such switchable functionality, not realized in previous SW couplers2,18, can be very useful in stealth applications where both normal detection and radar cross-section reduction are required. Our “tunable” approach, distinct from available strategies confined to homogenous metasurfaces and/or gradient-index materials with fabrication complexity and limited working frequencies42,43,44,45,46,47,48,49,50,51,52,53,54,55, opens the door to achieve dynamical control on the dispersions and functionalities of inhomogeneous metasurfaces, leading to many other exciting new applications such as aberration-free or functionality-switchable meta-lenses and tunable meta-devices including meta-holograms, flat sensors, etc.
Results
Dispersion issues in passive metasurfaces
To understand the dispersion issue in passive metasurfaces and lay a basis for designing our tunable structures, we first design a passive metasurface and analyze its wave-manipulation properties. Our meta-atom is a tri-layer structure, consisting of a composite planar resonator coupled with a metallic ground plane through a dielectric spacer (inset to Fig. 2a). To enlarge the working bandwidth of our device, we purposely design the meta-atom to contain two resonant modes, dictated by the metallic “H” structure and the metallic patch, respectively (Fig. 2a). The couplings between these planar structures and the ground plane generate two magnetic resonances, evidenced by the dips in the x-polarized reflectance spectra calculated by finite-difference-time-domain (FDTD) simulations, for two different systems with either only “H” or patch retained in the top layers (dashed and dotted lines in Fig. 2b). Detailed circuit-model analyses on these two modes can be found in Supplementary Information. With both “H” and patch present, our meta-atom can possess a much enlarged working bandwidth (~2–7 GHz) due to the coupling of two resonances (solid line in Fig. 2b). However, we will show that such bandwidth-enlargement cannot really improve the working performances of our metasurfaces, due to the intrinsic frequency dispersions of the passive resonant units.
Dispersion-induced functionality deteriorations in a typical passive metasurface.
(a) Geometry of the basic meta-atom and a gradient metasurface composed by six meta-atoms with parameter hi varying from 5.4 mm to 10.7 mm. (b) FDTD-simulated spectra of reflection amplitude (left axis) and phase (right axis) of three periodic metasurfaces with unit-cells being the second meta-atom as shown in the inset to (a) (solid lines), meta-atom with patch only (dotted lines), and meta-atom with “H” only (dashed lines). (c) FDTD simulated far-field scattering patterns of the gradient metasurface at three typical frequencies. (d) Calculated anomalous-reflection efficiency of the gradient metasurface as a function of frequency. The efficiency was defined as the ratio between anomalously reflected power  with θi0 and θi1 being the reflection angles of normal and anomalous modes, respectively) and the totally reflected power
with θi0 and θi1 being the reflection angles of normal and anomalous modes, respectively) and the totally reflected power  , calculated by integrating the scattered-field intensity based on the FDTD-simulated patterns. Inset depicts the phase profiles at three selected frequencies. Geometrical parameters of the meta-atoms: px = py = 12 mm, w1 = 0.8 mm, w2 = 0.5 mm, w3 = 5.1 mm, d1 = 0.25 mm, d2 = 0.5 mm. The spacer layer is assumed as the F4B dielectric board with εr = 2.65, h = 6 mm, tanδ = 0.001, and all metallic films are assumed of 36 μm thickness.
, calculated by integrating the scattered-field intensity based on the FDTD-simulated patterns. Inset depicts the phase profiles at three selected frequencies. Geometrical parameters of the meta-atoms: px = py = 12 mm, w1 = 0.8 mm, w2 = 0.5 mm, w3 = 5.1 mm, d1 = 0.25 mm, d2 = 0.5 mm. The spacer layer is assumed as the F4B dielectric board with εr = 2.65, h = 6 mm, tanδ = 0.001, and all metallic films are assumed of 36 μm thickness.
We now design a gradient reflective metasurface using the basic meta-atom structure. Set the target frequency at f0 = 5.7 GHz, we select six meta-atoms via carefully adjusting their structural details such that they exhibit the desired reflection phases following the relationship φ(x) ∼ ξ(x) with ξ ≈ 0.74k0 at this very frequency. Since the absorptions are generally weak due to low resonance quality factors of these structures (see Fig. 2b), we purposely adjusted the structures of six meta-atoms such that their reflection amplitudes are all nearly 1 (with fluctuations less than 0.1). The amplitude fluctuations over meta-atoms thus have much less pronounced effect on the device’s working efficiency than the corresponding phase variations. The six meta-atoms form a supercell of our passive metasurface, as shown in Fig. 2a. We then employed FDTD simulations to study the scattering patterns of such metasurface illuminated by x-polarized EM waves, at different frequencies. While the scattering pattern at f0 = 5.7 GHz (middle panel in Fig. 2c) does exhibit a single-mode reflection at the designed angle (θr ≈ 47°) with diffractions to other channels well suppressed, multi-mode diffractions are significant at other frequencies (upper and lower panels in Fig. 2c). As a result, the true working efficiency of our device drops dramatically as frequency leaves 5.7 GHz, as shown in Fig. 2d. The physics can be understood from the inset to Fig. 2d, where the phase profiles of our device are depicted at three typical frequencies. Whereas a prefect linear profile is found at 5.7 GHz, φ(x) are obviously distorted at 4.8 GHz and 7 GHz, due to the intrinsic dispersions of the meta-atoms. Such phase distortions are responsible for the appearances of diffractions to the wrong channels, which in turn, decrease the anomalous-mode conversion efficiency from 93.5% to 54.8% and 62.9%, respectively.
Designing tunable meta-atoms to compensate dispersions
We describe our strategy to design tunable meta-atoms to overcome the dispersion-induced phase distortions. As shown in Fig. 3a, our tunable meta-atoms are topologically equivalent to the passive one (Fig. 2a), only with the central bars of the “H” structures broken and then connected by varactor diodes (SMV1430-079LF, Skyworks Solutions Inc.56), which are, in turn, independently controlled by six external voltages Vi(i = 1, …, 6). Since the lumped-capacitance Ct of the diode depends sensitively on the voltage applied through it (see Supplementary Information), the resonance frequencies of our meta-atoms can be controlled by these external voltages. As a result, the reflection-phase spectra of six meta-atoms can be efficiently and independently controlled by Vi. Figure 3b depicts how the phase of the second meta-atom φ2(f) varies against V2. As V2 increases from 0 to 30 V, the lumped capacitance of the diode decreases from 1.2 to 0.3 pF, which shifts the relevant resonance from 4.7 to 6.6 GHz and thus generates dramatic modulations on φ2(f) (see Fig. 2b). Such modulation strongly depends on the structural details of the meta-atom. Detailed φi(f) ∼ Vi relationships for other five meta-atoms are presented in Supplementary Information.
Designs and tunabilities of tunable meta-atoms.
(a) Geometries of six tunable meta-atoms, each with a varactor diode loaded to connect the broken central line of the “H”. (b) Calculated reflection-phase spectra of a metasurface consisting of a periodic array of the second meta-atoms at different biasing voltages imparted on the diodes. (c) Retrieved values of the requested voltages imparted on six meta-atoms to maintain the linear phase distributions at every frequency within the band 4.1–6.6 GHz. Inset shows a zoom-in view of the retrieved voltages at frequencies from 6.3 to 6.5 GHz. (d) FDTD calculated reflection amplitudes and phases of six meta-atoms biased by the corresponding voltages as shown in (c). Inset plots the phase profile of the tunable metasurface at 6 GHz.
With all  relationships known, we can retrieve the voltage combinations
relationships known, we can retrieve the voltage combinations  imparted on six meta-atoms at every frequency (see Supplementary Information), which can yield a perfect linear phase profile for the metasurface constructed by these elements. We note that the solutions of
imparted on six meta-atoms at every frequency (see Supplementary Information), which can yield a perfect linear phase profile for the metasurface constructed by these elements. We note that the solutions of  may not be unique, since what we required is merely that the phase differences between adjacent elements are a constant (i.e.,φi+1−φi = π/3, i = 1, …, 5). Figure 3c depicts the retrieved
may not be unique, since what we required is merely that the phase differences between adjacent elements are a constant (i.e.,φi+1−φi = π/3, i = 1, …, 5). Figure 3c depicts the retrieved  varying against frequency, which is one particular set of solutions that we found by restricting on moderate values of voltages. We note that large fluctuations exist in V6 at high frequencies. This is because the resonance frequency of the sixth meta-atom is too low, and thus the meta-atom becomes quite inactive with respect to external control at high frequencies. To validate our solution, we plot in Fig. 3d the spectra of reflection amplitudes and phases for six meta-atoms controlled by the external voltages given in Fig. 3c. Perfect linear phase gradient is found for every frequency within the band 4.1–6.6 GHz (see inset for the phase profile at 6 GHz), with nearly uniform reflection amplitudes (|r| > 0.9). This is quite unusual since the original resonances of these meta-atoms are completely different. Yet, under appropriate biasing voltages, we can make their phase differences keeping constant within a very broad band, overcoming the intrinsic chromatic aberrations in passive meta-surfaces. In principle, one can use our strategy to make a meta-atom to exhibit arbitrary reflection phase φ, and thus the working bandwidth can be made as large as possible. However, this is practically impossible since any diode exhibits a limited tunable range and also the external voltage cannot be made too large. These factors collectively set an upper limit on the working bandwidth of a tunable metasurface. However, we emphasize here that within such a working bandwidth the tunable metasurface exhibits an ideal performance without chromatic aberrations. Therefore, our bandwidth is intrinsically different from conventional working bandwidth for a wideband passive device11,12,13 in which the device’s performance gets deteriorated at frequencies deviating from the central target one.
varying against frequency, which is one particular set of solutions that we found by restricting on moderate values of voltages. We note that large fluctuations exist in V6 at high frequencies. This is because the resonance frequency of the sixth meta-atom is too low, and thus the meta-atom becomes quite inactive with respect to external control at high frequencies. To validate our solution, we plot in Fig. 3d the spectra of reflection amplitudes and phases for six meta-atoms controlled by the external voltages given in Fig. 3c. Perfect linear phase gradient is found for every frequency within the band 4.1–6.6 GHz (see inset for the phase profile at 6 GHz), with nearly uniform reflection amplitudes (|r| > 0.9). This is quite unusual since the original resonances of these meta-atoms are completely different. Yet, under appropriate biasing voltages, we can make their phase differences keeping constant within a very broad band, overcoming the intrinsic chromatic aberrations in passive meta-surfaces. In principle, one can use our strategy to make a meta-atom to exhibit arbitrary reflection phase φ, and thus the working bandwidth can be made as large as possible. However, this is practically impossible since any diode exhibits a limited tunable range and also the external voltage cannot be made too large. These factors collectively set an upper limit on the working bandwidth of a tunable metasurface. However, we emphasize here that within such a working bandwidth the tunable metasurface exhibits an ideal performance without chromatic aberrations. Therefore, our bandwidth is intrinsically different from conventional working bandwidth for a wideband passive device11,12,13 in which the device’s performance gets deteriorated at frequencies deviating from the central target one.
Far-field characterizations on the tunable metasurface: Aberration corrections
We fabricated a tunable metasurface according to the design (Fig. 3a) and experimentally characterized its wave-manipulation performances. As shown in Fig. 4a, the fabricated sample contains 30 × 30 meta-atoms, with a total size of 360 × 360 mm2. Since the phase gradient is along the x direction, the meta-atoms in each vertical column are identical. Considering further the super-periodicity, we only need six independent constant-voltage sources to bias those diodes belonging to the same type of meta-atoms. According to ref. 2, we understand that our gradient metasurface functions as a SW convertor at frequencies below fc = 4.167 GHz when the phase gradient is larger than the free-space wave-vector, while it is an anomalous reflector at frequencies above fc. We first focus on the frequency region above fc in this subsection. Biasing the meta-atoms at their corresponding voltages as shown in Fig. 3c, we performed both microwave experiments and FDTD simulations to study the scattering patterns of our metasurface at different frequencies (see Methods section for microwave characterization details).
Far-field characterizations on the tunable metasurface.
(a) Photograph of the fabricated tunable metasurface, with inset depicting a supercell of the sample. Measured (symbols) and FDTD-simulated (line) scattering patterns of the tunable metasurface at 5 frequencies, when the sample is biased (b) at the required voltage combination corresponding to each frequency, (c) at 0 V voltage, and (d) at the fixed voltage combination (denoted by  ) corresponding to the frequency 5.5 GHz. (e) Frequency-dependent anomalous-reflection efficiency of our device for the cases studied in (b) (red), (c) (blue), and (d) (black), obtained by analyzing the measured (symbols) and FDTD simulated (lines) scattering patterns.
) corresponding to the frequency 5.5 GHz. (e) Frequency-dependent anomalous-reflection efficiency of our device for the cases studied in (b) (red), (c) (blue), and (d) (black), obtained by analyzing the measured (symbols) and FDTD simulated (lines) scattering patterns.
Figure 4b depicts the measured scattering patterns of the tunable metasurface under normal-incidence excitations at 5 frequencies (4.5, 5.0, 5.5, 6.0, 6.5 GHz). In all the cases studied, we found that the reflection beams only contain the desired anomalous mode with diffractions to the wrong channels fully suppressed. The experimentally identified anomalous reflection angle θr changes from 67.8ο to 39.9ο as frequency f increases from 4.5 GHz to 6.5 GHz, agreeing well with the generalized Snell’s law:  with
with  being the wave vector in free space and c the speed of light1 (see Fig. S7 in Supplementary Information). Since the phase gradient
being the wave vector in free space and c the speed of light1 (see Fig. S7 in Supplementary Information). Since the phase gradient  (L is the super periodicity) of our device is frequency independent, θr must be a decreasing function of f, which is verified experimentally (Fig. 4). We note that the anomalous-reflection beam becomes narrowed as f increases (Fig. 4b). This is again quite physical, since our metasurface becomes effectively enlarged in size (in term of wavelength) at higher frequencies, although its physical size remains unchanged. FDTD simulations match very well with the experimental data.
(L is the super periodicity) of our device is frequency independent, θr must be a decreasing function of f, which is verified experimentally (Fig. 4). We note that the anomalous-reflection beam becomes narrowed as f increases (Fig. 4b). This is again quite physical, since our metasurface becomes effectively enlarged in size (in term of wavelength) at higher frequencies, although its physical size remains unchanged. FDTD simulations match very well with the experimental data.
Figure 4b already indicates that our tunable metasurface exhibits nearly ideal functionalities, much more superior that its passive counterpart (see Fig. 2). Obviously, such improvement comes from the perfect linear phase gradient enabled by external controls. To further highlight the importance of the tunable phase control, we repeated all characterizations on the same device which is now under zero-voltage biasing. It is not surprising to see that the device does not show single-mode anomalous reflections at those frequencies selected (Fig. 4c). Instead, diffractions to the wrong channels are significant, similar to the passive device (Fig. 2). We note that zero-voltage-biased metasurface is not an ideal candidate to mimic a passive metasurface, since at this biasing condition the metasurface does not exhibit a good linear phase distribution at any frequency. Therefore, we further study the scattering properties of the same device under the biasing voltages designed for 5.5 GHz. Such a device can better mimic a passive system, since the effective lumped parameters of the diodes do not change with frequency. Figure 4d shows the measured/simulated reflection spectra of the device at the same 5 frequencies. As expected, the device works with ideal functionality only at the frequency 5.5 GHz, but the performance gets deteriorated significantly at other frequencies.
Such comparisons highlighted the key advantage of our tunable scheme — our device can work with the best functionality at any frequency within a broad band. Figure 4e compares the working efficiencies of three devices studied in Fig. 4b–d as functions of frequency. Whereas our tunable device (under appropriate biasing voltages) can always exhibit high anomalous-reflection efficiency (~90%) within 4.2–6.6 GHz, the fixed-voltage-biased device only works for a single frequency similar to a passive device, and the unbiased device exhibits poor efficiencies for all frequencies within the band.
Near-field characterizations on the tunable metasurface: Dynamical functionality switching
We now focus on another frequency domain (f < fc), and demonstrate a further important application of our tunable scheme, that is, dynamical functionality switching. The working principle can be understood as follows. At a frequency f < fc, our gradient metasurface can function as a propagating wave (PW) to SW convertor when its phase profile φ(x) exhibits a perfect linear relationship, but becomes a normal reflector when φ remains nearly a constant within a supercell. Therefore, engineering φ(x) in a designed manner can create two “states” between which the metasurface can switch.
We experimentally demonstrated this idea at 4.1 GHz. Following ref. 2, we first design and fabricate a mushroom structure (see inset for its unit-cell geometry) supporting spoof surface plasmon polariton (SPP) propagations at this frequency, and then place it at the right-hand side of the gradient metasurface (Fig. 5a). Such a device can guide out the SW generated on the metasurface, when the latter is shined by a normally incident PW. The real experimental sample and setup are shown in Fig. 5b. In our experiment, shining the metasurface alone by an x-polarized PW, we employed a monopole antenna to measure the distribution of local Re(Ez) fields generated on both the metasurface and the mushroom surface. To ensure a high conversion efficiency, the mushroom structure is carefully designed such that the wave vector of its spoof SPP is kspp ≈ 1.02k0 at 4.1 GHz (see Supplementary InformationM), which is matched to the wavevector of the “driven” SW generated on the metasurface.
Near-field characterizations on the tunable metasurface: Dynamical functionality switching.
(a) Schematics of the PW-SW conversion setup. Inset shows a unit cell of the mushroom structure, consisting of a metal bar (sized 3 mm × 8 mm) coupled with a continuous metal plate through a 6 mm – thick dielectric spacer (εr = 2.65). (b) Picture of the fabricated sample and the near-field probe. (c,d) FDTD simulated and (e,f) measured Re(Ez) distributions under (c,e) the voltage combination corresponding to frequency 4.1 GHz as shown in Fig. 3(c) and (d,f) Vi = 30 V for all elements. Insets in (c) and (d) depict the phase profiles under the specified external voltages. All fields in (c–f) share the same color bar shown in (d). FDTD simulated and measured far-field scattering patterns of the metasurface at 4.1 GHz under (g) the voltage combination corresponding to frequency 4.1 GHz and (h) Vi = 30 V for all elements.
We performed near-field (NF) measurements in two cases where the meta-atoms are biased at two different voltage combinations. In the “On”-state, the biasing voltages are chosen from Fig. 4c so that φ(x) exhibits perfect linear relationship (inset to Fig. 5c). In the “Off”-state where all voltages are set as 30 V, however, the φ(x) relation deviates significantly from a linear one and φ remains nearly unchanged in the large area of a supercell (inset to Fig. 5d). As expected, when the metasurface is set at the “On”-state, we do observe very strong spoof SPP signals and the simulated/measured NF patterns (Fig. 5c and e) exhibit a very well-defined kspp ≈ 1.02k0, indicating that our device is a very efficient SW convertor. On the other hand, when the metasurface is switched to the “Off”-state, we only detected negligible SPP signals on the mushroom structure with an On/Off power ratio 22.1, implying that the device now ceases to behave as a SW convertor (Fig. 5d and f). To further differentiate the functionalities of our device at two states, we performed far-field (FF) experiments to measure the scattering patterns (Fig. 5g and h) of our device at two different states. Combining experimental data from NF and FF measurements, we conclude that our device is mostly a SW convertor in the “On”-state, but dynamically changes to a conventional reflector in the “Off”-state.
Discussion
To summarize, we established a tunable scheme to overcome the dispersion-induced issues in microwave metasurfaces. Adding tunable elements to our meta-atoms, we can precisely control the phase response of each meta-atom via external knobs, thereby to rectify the inevitable phase distortions at arbitrary frequencies. Two distinct effects were experimentally demonstrated: (1) We can realize tunable metasurfaces exhibiting the best functionalities at every frequency within a broad band, overcoming the dispersion-induced phase distortions intrinsic to all passive devices; (2) We can dynamically switch the functionalities of metasurfaces via changing the external controls. Our findings pave the road to realize tunable meta-devices achieving dispersion-compensated and/or dynamically switchable high performances. Extensions to high-frequency domains are even more interesting, based on modern technologies such as optical pumping on semiconductors44 and gate-tunable dielectric materials57.
Methods
Simulations
All full-wave FDTD simulations were performed with a numerical solver (CONCERTO 7.0, Vector Fields Limited, UK (2008)). In the FDTD simulations, metals were treated as perfect electric conductors and the varactor was modeled by a series of RLC lumped elements containing an inductor (Ls = 0.7 nH), a resistor (Rt = 1.5 Ω) and a capacitor with Ct varying inside [0.3 pF, 1.2 pF] depending on the externally applied voltage (see Fig. S1b in Supplementary Information). In the simulation domains occupied by one of these lumped elements, the 4th Maxwell’s equation is modified as  , where, other than conventional free and displacement currents
, where, other than conventional free and displacement currents  , an additional term
, an additional term  is added to describe the responses of the lumped elements. These currents are determined by the voltages U applied across the lumped elements through the circuit equations
is added to describe the responses of the lumped elements. These currents are determined by the voltages U applied across the lumped elements through the circuit equations  ,
,  and
and  , which are in turn, related back to the electric fields defined in the corresponding meshes. By doing so, we can self-consistently incorporate the responses of the lumped elements in the FDTD simulations. In the calculations of reflection magnitudes/phases of meta-atoms, we studied a unit cell containing a single meta-atom with periodic conditions applied at its four boundaries and a floquet port assigned at a distance 15 mm away from the xy-plane where the meta-atom is placed. In the far-field calculations, we chose to study a line of meta-atoms belonging to five supercells arranged in the x direction, with open boundary conditions set as its two ends and periodic boundary conditions set at its two boundaries along the y direction. Similarly, in near-field calculations, the studied system contains five/three super cells along the y/x direction, again with periodic/open boundary conditions imposed at the boundaries. In all cases, the metasurface/meta-atom is shined by a normally incident x-polarized plane wave. The varactor SMV1430-079LF can only work well for frequencies below 10 GHz. Above 10 GHz, unreliable capacitance/inductance values and large self-resonant loss will be induced in the varactor, which is undesirable for our applications. The higher frequency micro-electromechanical system diode affords an extremely low loss strategy and thus would benefit much the high absolute efficiency.
, which are in turn, related back to the electric fields defined in the corresponding meshes. By doing so, we can self-consistently incorporate the responses of the lumped elements in the FDTD simulations. In the calculations of reflection magnitudes/phases of meta-atoms, we studied a unit cell containing a single meta-atom with periodic conditions applied at its four boundaries and a floquet port assigned at a distance 15 mm away from the xy-plane where the meta-atom is placed. In the far-field calculations, we chose to study a line of meta-atoms belonging to five supercells arranged in the x direction, with open boundary conditions set as its two ends and periodic boundary conditions set at its two boundaries along the y direction. Similarly, in near-field calculations, the studied system contains five/three super cells along the y/x direction, again with periodic/open boundary conditions imposed at the boundaries. In all cases, the metasurface/meta-atom is shined by a normally incident x-polarized plane wave. The varactor SMV1430-079LF can only work well for frequencies below 10 GHz. Above 10 GHz, unreliable capacitance/inductance values and large self-resonant loss will be induced in the varactor, which is undesirable for our applications. The higher frequency micro-electromechanical system diode affords an extremely low loss strategy and thus would benefit much the high absolute efficiency.
Sample fabrications
The active metasurfaces were fabricated using printed-circuit-board technique with all varactor diodes attached to the top metallic microstructure using surface-mount technology. To guarantee perfect electrical connections with correct electrodes, all varactors are checked by amultimeter of VICTOR VC9807A+. To control the capacitances of the varactor diodes, we connected constant-voltage sources (GPD4303S, GWINSTEK company, Taiwan) to their two ends by two thin wires. To suppress the leakage of microwave signals and thus enable a robust and reliable performance, the top and bottom horizontal bars functioning as zero- and reverse-biased line, respectively are engineered thinner than the perpendicular bar to provide a high reactance.
Microwave characterizations
In the far-field experiments, shining the metasurface by a microwave beam (with spot size ~250 mm at 6 GHz (E plane)) emitted from a linear-polarization horn antenna placed 1.2 m away, we measured the scattered-field intensity with another identical horn antenna, which can be freely rotated (with a step of 3°) on a circular track with 1.2 m radius. All scattered power was recorded by a vector network analyzer (Agilent E8362C PNA) and was normalized against a reference signal P0, obtained by measuring the specularly reflected signal with the metasurface replaced by a metallic plate with the same size. In measuring P0, two horn antennas were placed at the same side of the sample with a 10° angle separation. In the near-field experiments, we placed a 15 mm-long monopole antenna perpendicular to the metasurface, moving at a plane 3 mm above the metasurface, to measure the local Ez field (with both amplitude and phase). Absorbing materials are placed at the right side of the mushroom structure to prevent any reflected signals.
Additional Information
How to cite this article: Xu, H.-X. et al. Tunable microwave metasurfaces for high-performance operations: dispersion compensation and dynamical switch. Sci. Rep. 6, 38255; doi: 10.1038/srep38255 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science. 334, 333–337 (2011).
Sun, S. et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves. Nat Mater. 11, 426–431 (2012).
Engheta, N. Antenna-guided light. Science. 334, 317–318 (2011).
Ni, X., Emani, N. K., Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Broadband light bending with plasmonic nanoantennas. Science 335, 427 (2012).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat Mater. 13, 139–150 (2014).
Kim, M., Wong, A. M. & Eleftheriades, G. V. Optical huygens’ metasurfaces with independent control of the magnitude and phase of the local reflection coefficients. Phys Rev X. 4, 041042 (2014).
Liu, L. et al. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv Mater. 26, 5031–5036 (2014).
Aieta, F., Kats, M. A., Genevet, P. & Capasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science. 347, 1342–1345 (2015).
Aieta, F. et al. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities. Nano Lett. 12, 1702–1706 (2012).
Grady, N. K. et al. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science. 340, 1304–1307 (2013).
Sun, S. L. et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces. Nano Lett. 12, 6223–6229 (2012).
Pu, M. et al. Broadband anomalous reflection based on gradient low-Q meta-surface. Aip Adv. 3, 052136 (2013).
Li, Z., Palacios, E., Butun, S. & Aydin, K. Visible-frequency metasurfaces for broadband anomalous reflection and high-efficiency spectrum splitting. Nano Lett. 15, 1615–1621 (2015).
Zhang, X. et al. Broadband terahertz wave deflection based on c-shape complex metamaterials with phase discontinuities. Adv Mater. 25, 4567–4572 (2013).
Pfeiffer, C. et al. Efficient light bending with isotropic metamaterial Huygens’ surfaces. Nano Lett. 14, 2491–2497 (2014).
Liu, Z. et al. High-performance broadband circularly polarized beam deflector by mirror effect of multi-nano-rod metasurfaces. Adv Funct Mater. 25, 5428–5434 (2015).
Qin, F. et al. Hybrid bilayer plasmonic metasurface efficiently manipulates visible light, Sci. Adv. 2, e1501168 (2016).
Lin, J. et al. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science. 340, 331–334 (2013).
Genevet, P. et al. Ultra-thin plasmonic optical vortex plate based on phase discontinuities. Appl Phys Lett. 100, 013101 (2012).
Chen, X. et al. Dual-polarity plasmonic metalens for visible light. Nat Commun. 3, 1198 (2012).
Aieta, F. et al. Aberration-free ultrathin flat lenses and axicons at telecom wavelengths based on plasmonic metasurfaces. Nano Lett. 12, 4932–4936 (2012).
Ni, X., Ishii, S., Kildishev, A. V. & Shalaev, V. M. Ultra-thin, planar, babinet-inverted plasmonic metalenses. Light: Science & Applications. 2, e72 (2013).
Pfeiffer, C. & Grbic, A. Millimeter-wave transmitarrays for wavefront and polarization control. IEEETrans. Microw. Theory Tech. 61, 4407–4417 (2013).
Monticone, F., Estakhri, N. M. & Alù, A. Full control of nanoscale optical transmission with a composite metascreen. Phys Rev Lett. 110, 203903 (2013).
Spektor, G., David, A., Gjonaj, B., Bartal, G. & Orenstein, M. Metafocusing by a metaspiral plasmonic lens. Nano Lett. 15, 5739–5743 (2015).
Chen, X. et al. Longitudinal multifoci metalens for circularly polarized light. Adv Opt Mater. 3, 1201–1206 (2015).
Pors, A., Nielsen, M. G., Eriksen, R. L. & Bozhevolnyi, S. I. Broadband focusing flat mirrors based on plasmonic gradient metasurfaces. Nano Lett. 13, 829–834 (2013).
Farmahini-Farahani, M. & Mosallaei, H. Birefringent reflectarray metasurface for beam engineering in infrared. Opt Lett. 38, 462–464 (2013).
Ma, H. F., Wang, G. Z., Kong, G. S. & Cui, T. J. Independent controls of differently-polarized reflected waves by anisotropic metasurfaces. Sci Rep-Uk. 5, 9605 (2015).
Yu, N. et al. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 12, 6328–6333 (2012).
Ni, X., Kildishev, A. V. & Shalaev, V. M. Metasurface holograms for visible light. Nat Commun. 4, 2807 (2013).
Huang, L. et al. Three-dimensional optical holography using a plasmonic metasurface. Nat Commun. 4, 2808 (2013).
Huang, Y. et al. Aluminum plasmonic multicolor meta-hologram. Nano Lett. 15, 3122–3127 (2015).
Zheng, G. et al. Metasurface holograms reaching 80% efficiency. Nat Nanotechnol. 10, 308–312 (2015).
Luo, W., Xiao, S., He, Q., Sun, S. & Zhou, L. Photonic spin hall effect with nearly 100% efficiency. Adv Opt Mater. 3, 1102–1108 (2015).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin hall effect at metasurfaces. Science. 339, 1405–1407 (2013).
Hum, S. V., Okoniewski, M. & Davies, R. J. Modeling and design of electronically tunable reflectarrays. IEEE Trans. Antennas Propag. 55, 2200–2210 (2007).
Riel, M. & Laurin, J. Design of an electronically beam scanning reflectarray using aperture-coupled elements. IEEE Trans. Antennas Propag. 55, 1260–1266 (2007).
Kishor, K. K. & Hum, S. V. An amplifying reconfigurable reflectarray antenna. IEEE Trans. Antennas Propag. 60, 197–205 (2012).
Sazegar, M. et al. Beam steering transmitarray using tunable frequency selective surface with integrated ferroelectric varactors. IEEE Trans. Antennas Propag. 60, 5690–5699 (2012).
Clemente, A., Dussopt, L., Sauleau, R., Potier, P. & Pouliguen, P. Wideband 400-element electronically reconfigurable transmitarray in X band. IEEE Trans. Antennas Propag. 61, 5017–5027 (2013).
Jiang, S.-C. et al. Controlling the polarization state of light with a dispersion-free metastructure. Phys Rev X. 4, 021026 (2014).
R. Guzmán-Quirós, J. L. Gómez-Tornero, A. R. Weily & Y. J. Guo, Electronically steerable 1-D fabry-perot leaky-wave antenna employing a tunable high impedance, surface, IEEE Trans. Antennas Propagat. 60, 5046–5055 (2012).
Chen, H. et al. Active terahertz metamaterial devices. Nature. 444, 597–600 (2006).
Lee, J. et al. Ultrafast electrically tunable polaritonic metasurfaces. Adv Opt Mater. 2, 1057–1063 (2014).
Ma, F., Lin, Y., Zhang, X. & Lee, C. Tunable multiband terahertz metamaterials using a reconfigurable electric split-ring resonator array. Light: Science & Applications. 3, e171 (2014).
Jiang, T. et al. Low-DC voltage-controlled steering-antenna radome utilizing tunable active metamaterial. IEEE Trans. Microw. Theory Tech. 60, 170–178 (2012).
Hand, T. H. & Cummer, S. A. Reconfigurable reflectarray using addressable metamaterials. IEEE Antennas Wireless Propag. Lett 9, 70–74 (2010).
Chen, P. et al. Nanostructured graphene metasurface for tunable terahertz cloaking. New J. Phys. 15, 123029 (2013).
Wakatsuchi, H., Kim, S., Rushton, J. J. & Sievenpiper, D. F. Waveform-dependent absorbing metasurfaces. Phys Rev Lett. 111, 245501 (2013).
Chen, P., Argyropoulos, C. & Alù, A. Broadening the cloaking bandwidth with non-foster metasurfaces. Phys Rev Lett. 111, 233001 (2013).
Shadrivov, I. V., Kapitanova, P. V., Maslovski, S. I. & Kivshar, Y. S. Metamaterials controlled with light. Phys Rev Lett. 109, 083902 (2012).
Kaina, N., Dupré, M., Lerosey, G. & Fink, M. Shaping complex microwave fields in reverberating media with binary tunable metasurfaces. Sci Rep-Uk. 4, 6693 (2014).
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J. & Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Science & Applications. 3, e218 (2014).
Zhu, B. O. et al. Dynamic control of electromagnetic wave propagation with the equivalent principle inspired tunable metasurface. Sci Rep-Uk. 4, 4971 (2014).
SMV1405-SMV1430 series: plastic packaged abrupt junction tuning varactors. (Date of access: 10/05/2015) (2013).
Miao, Z. et al. Widely tunable terahertz phase modulation with gate-controlled graphene metasurfaces. Phys Rev X 5, 041027 (2015).
Acknowledgements
This work was supported by National Natural Science Foundation China (Grant Nos 61501499, 11474057, 11204040, and 11404063), China Postdoctoral Science Foundation under Grant Nos 2015M570323 and 2016T90337, MOE of China (Grant No. B06011), and Shanghai Science and Technology Committee (Grant No. 14PJ1401200) also Natural Science Foundation of Shaanxi Province under Grant No. 2016JQ6001.
Author information
Authors and Affiliations
Contributions
H.-X.X. and L.Z. proposed the idea. H.-X.X. designed the samples, conducted the numerical simulations and experiments, and interpreted the data. S.M. wrote the program for the CAD design. S.T., W.L., T.C. and Q.H. participated in the measurements. H.-X.X., Q.H., S.S. and L.Z. prepared the manuscript. L.Z. supervised the project. All authors commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Xu, HX., Tang, S., Ma, S. et al. Tunable microwave metasurfaces for high-performance operations: dispersion compensation and dynamical switch. Sci Rep 6, 38255 (2016). https://doi.org/10.1038/srep38255
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38255
This article is cited by
-
Design of a binary programmable transmitarray based on phase change material for beam steering applications in D-band
Scientific Reports (2024)
-
Ultra-low-loss tunable piezoelectric-actuated metasurfaces achieving 360° or 180° dynamic phase shift at millimeter-waves
Scientific Reports (2020)
-
Reconfigurable Antenna and Performance Optimization Approach
Wireless Personal Communications (2020)
-
Efficient visible light modulation based on electrically tunable all dielectric metasurfaces embedded in thin-layer nematic liquid crystals
Scientific Reports (2019)
-
High-efficiency dual-modes vortex beam generator with polarization-dependent transmission and reflection properties
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.