Abstract
We propose a theoretical protocol for preparing four-photon polarization entangled decoherence-free states, which are immune to the collective noise. With the assistance of the cross-Kerr nonlinearities, a two-photon spatial entanglement gate, two controlled-NOT gates, a four-photon polarization entanglement gate are inserted into the circuit, where X homodyne measurements are aptly applied. Combined with some swap gates and simple linear optical elements, four-photon polarization entangled decoherence-free states which can be utilized to represent two logical qubits, |0〉L and |1〉L are achieved at the output ports of the circuit. This generation scheme may be implemented with current experimental techniques.
Similar content being viewed by others
Introduction
Entanglement1,2,3 plays an important role in quantum information processing, mainly including quantum computation4 and quantum communication. It is the information carrier in some interesting branches of quantum communication, such as quantum key distribution5, quantum secret sharing6,7,8, quantum secure direct communication9,10,11, teleportation12, quantum dense coding13,14, and so on. Most of the above applications require maximally entangled states or noiseless quantum channels. However, in a realistic situation, decoherence, induced by uncontrolled coupling between a quantum system and the environment, is inevitable. When qubits are coupled to the environment, the quantum superposition and coherence are easily destructed, and as a result the maximally entangled state collapses into a non-maximally entangled one or even a mixed state. This will degrade the fidelity and security of quantum communication. To overcome this flaw, some specific entangled states, which are called decoherence-free states15,16,17, are proposed. Decoherence-free states, no matter how strong the qubit-environment interaction, exhibit some symmetry, so the quantum states are invariant under this interaction. Therefore, the decoherence-free states are very useful for long-distance quantum information transmission and storage.
Due to the fact that photons have the merits of higher speed, lower decoherence, easier manipulation, and lower energy cost compared with more massive qubits, polarization photons are destined to have a central role in long-distance communication. Recently, the encoding in decoherence-free states of polarization photons to overcome collective decoherence attracts the extensively attention. An optical experiment has been reported to overcome collective noise by encoding quantum information into the decoherence-free state18. For two qubits, there is only one decoherence-free singlet state, i.e.,  , where H and V denote horizontal and vertical linear polarizations respectively. Therefore, it is not sufficient to fully protect the quantum information of an arbitrary logical qubit against collective noise. Another nontrivial example is the four-photon polarization entangled decoherence-free state
, where H and V denote horizontal and vertical linear polarizations respectively. Therefore, it is not sufficient to fully protect the quantum information of an arbitrary logical qubit against collective noise. Another nontrivial example is the four-photon polarization entangled decoherence-free state

with


The dimension of the above four-qubit decoherence-free state in Eq. (1) is 2, and thus it is sufficient to fully protect an arbitrary logical qubit against collective noise in contrast to the two-qubit state. With its interesting applications, Bourennane et al.19 have generated four-photon polarization entangled decoherence-free states via a spontaneous parametric down-conversion source. Recently, Zou et al.20 and Gong et al.21 proposed two different schemes to generate four-photon polarization entangled decoherence-free states based on linear optical elements and postselection strategy. Subsequently, Xia et al.22 presented a protocol for the controlled generation of the four-photon polarization entangled decoherence-free state with conventional photon detectors. In 2010, Wang et al.23 proposed a probabilistic linear-optics-based scheme for local conversion of four Einstein-Podolsky-Rosen photon pairs into four-photon polarization entangled decoherence-free states. In 2013, Xia et al.24 also put forward a probabilistic protocol for preparation of four-photon polarization entangled decoherence-free states with the help of the cross-Kerr nonlinearity medium.
In this paper, we present an alternative scheme to generate the four-photon polarization entangled decoherence-free states with the assistance of the cross-Kerr nonlinearities. The states representing the logical qubits |0〉L and |1〉L can be achieved at different output ports of two beam splitters, combined with the output ports of the photon 3 and the photon 4. The rest of the paper is organized as follows. In Sec. II, we show how to generate these two logical qubits in the four-photon polarization entangled decoherence-free states based on the weak cross-Kerr nonlinearities. The discussion and conclusion are presented in Sec. III.
Generations of four-qubit entangled decoherence-free states
For the sake of the clearness, let us first introduce the cross-Kerr nonlinearity, which was first used by Chuang and Yamamoto to realize the simple optical quantum computation25. The interaction Hamiltonian has the form  , where
, where 
 is the photon-number operators of the signal (probe) mode, and κ is the strength of the nonlinearity. If the signal field contains n photons and the probe field is in an initial coherent state with amplitude α, the cross-Kerr nonlinearity interaction causes the combined signal-probe system to evolve as follows:
is the photon-number operators of the signal (probe) mode, and κ is the strength of the nonlinearity. If the signal field contains n photons and the probe field is in an initial coherent state with amplitude α, the cross-Kerr nonlinearity interaction causes the combined signal-probe system to evolve as follows:

where θ = κt with t being the interaction time. It is easy to observe that the Fock state is unaffected by the interaction but the coherent state picks up a phase shift nθ directly proportional to the number of photons n in the signal mode. One can exactly obtain the information of photons in the Fock state but not destroy them by detecting the probe mode with a general homodyne-heterodyne measurement. The cross-Kerr nonlinearity between photons offers an ideal playground for quantum state engineering, and a number of applications have been studied, such as constructing nondestructive quantum nondemoliton detectors (QND)26,27, deterministic entanglement distillation28, logic-qubit entanglement29,30, generation of multi-photon entangled states and decoherence-free states24,31,32,33,34,35,36.
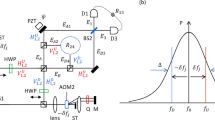
In what follows, we explain the detailed procedures for generating the four-photon polarization entangled docoherence-free states abided by the following processes, which is also illustrated in Fig. 1.
Illustration plot for generating four-photon polarization entangled decoherence-free state with the help of the cross-Kerr nonlinearities.
The symbol BS denotes the beam splitter which has equal probability (50:50) of transmission and reflection. HWP22.5, HWP45, and HWP denote half-wave plates which realize the Hadamard transformation operation, single photon σx operation, and single photon σz operation respectively. In the construction of the circuit, after two Controlled-Not gates, a polarization entanglement gate and two swap gates need to be performed, which can be seen in Figs 2 and 3 respectively. Before four photons leave the circuit, the four potential paths of the photon (1, 2) are coherently combined by BS3 and BS4 for obtaining the different four-photon polarization entanglement decoherence-free states.
Assume the four single photons are initially prepared in the state 
 , and let them enter into the circuit shown in Fig. 1 from the input ports. The first step is to create the spatial entanglement of the photons 1 and 2. Passing through beam splitters, BS1 and BS2, which have the following function between two input modes (a,b) and two output modes (c,d):
, and let them enter into the circuit shown in Fig. 1 from the input ports. The first step is to create the spatial entanglement of the photons 1 and 2. Passing through beam splitters, BS1 and BS2, which have the following function between two input modes (a,b) and two output modes (c,d):  ,
,  , the photons (1, 2) enter into the paths (S11, S12) and the paths (S21, S22) respectively. Accompanying with the coherent state, the photons (1, 2) enter into Kerr media. Then, the state of photons (1, 2) with the coherent state |α〉 evolves as
, the photons (1, 2) enter into the paths (S11, S12) and the paths (S21, S22) respectively. Accompanying with the coherent state, the photons (1, 2) enter into Kerr media. Then, the state of photons (1, 2) with the coherent state |α〉 evolves as

Performing an X homodyne measurement on the coherent state with α real, there are two measurement outcomes corresponding to scenarios of phase shift (0, ±θ). For the convenience of analysis, we expand the state in terms of the eigenstates of the X operator:

where the coefficients37 are

Explicitly, if zero phase shift occurs, the spatial entangled state of the photons (1, 2) is created and can be written as

Otherwise, another measurement outcome (nonzero phase shift) is obtained, a phase shift operation 2ϕ1(x) should be performed on the photon 2 passing through the path S21 to erase the phase difference between two terms of  and
and  . By omitting a global phase ϕ1(x), the photons (1, 2) are in the following spatial entangled state
. By omitting a global phase ϕ1(x), the photons (1, 2) are in the following spatial entangled state

Without considering other conditions, there is a small probability of error to distinguish the state in Eq. (8) and the state in Eq. (9) from each other due to the overlap of the measurement functions f(x, α) and f(x, α cos θ), which is given by  , xd = 2α(1 − cos θ). It is less than 10−5 when the distance xd ~ αθ2 > 926.
, xd = 2α(1 − cos θ). It is less than 10−5 when the distance xd ~ αθ2 > 926.
For simplifying description in the later processes, we take an example as the representative of two different scenarios of phase shift. If zero phase shift is witnessed by the X homodyne measurement, half wave plates, HWP22.5°s, are inserted into the paths S11, S22 at first, which function as Hadamard transformation operations to transform the state of the photons (1, 2) from  and
and  to
to  and
and  . Then two controlled-NOT (CNOT) gates are performed on two paths (S11, S21) (photon 1 as control photon and photon 2 as target photon), and paths (S22, S12) (photon 2 as control photon and photon 1 as target photon) respectively. The CNOT gate is important in the experimental realization. Knill et al.38 firstly proposed a probabilistic CNOT gate on two photonic qubits by using linear optical elements and postselection. The cross-Kerr nonlinearity has also been used to implement the CNOT gate26,39,40. After two CNOT gates, the four-photon system will evolve into
. Then two controlled-NOT (CNOT) gates are performed on two paths (S11, S21) (photon 1 as control photon and photon 2 as target photon), and paths (S22, S12) (photon 2 as control photon and photon 1 as target photon) respectively. The CNOT gate is important in the experimental realization. Knill et al.38 firstly proposed a probabilistic CNOT gate on two photonic qubits by using linear optical elements and postselection. The cross-Kerr nonlinearity has also been used to implement the CNOT gate26,39,40. After two CNOT gates, the four-photon system will evolve into

A polarization entanglement gate illustrated in Fig. 2 is put into the paths (S11, S12, S21, S22, S3, S4) of the photons (1, 2, 3, 4) to entangle them with the polarization degree of freedom. Affected by cross-Kerr nonlinearities, the horizontal polarization mode of photons (1, 2) via the paths S11, S12, S21, S22 will accumulate the phase shift θ, −θ respectively while the vertical polarization mode of photons (3, 4) will accumulate the phase shift θ, −θ respectively on the coherent state |α〉. As the consequence of the nonlinear interaction between photons and the coherent state, the state of the whole system can be expressed as
Illustration plot for depicting a polarization entanglement gate.
The polarization beam splitters (PBS) reflect the vertical polarization |V〉 mode and transmit the horizontal polarization |H〉 mode. Influenced by cross-Kerr nonlinearities, the photon 1 in the horizontal polarization state and the photon 3 in the vertical polarization state enable the coherent state |α〉 to pick up the phase shift θ, while the photon 2 in the horizontal polarization state and the photon 4 in the vertical polarization state enable the coherent state |α〉 to pick up the phase shift −θ.

After the photons leave Kerr media, the X homodyne measurement is performed on the coherent state. If zero phase shift occurs, no phase modulation is necessary. Otherwise, if nonzero phase shift of the coherent state presents on the measurement setup, a phase shift 2ϕ(x) operation should be performed on the photon 3 in the path S31. Moreover, a HWP45° should be inserted into the path S3 to perform σx operation on the photon 3. So the four-photon state can be denoted as

Here, two swap gates need to be performed on two photons in the paths (S21, S3) and (S22, S4) respectively to swap them. A swap gate is an important two-qubit logic gate. In terms of the basis of {|00〉, |01〉, |10〉, |11〉}, the swap gate can be represented as the following matrix:

In practice, the swap gate transformation can be yielded by the Hong-Ou-Mandel interference41 in the Mach-Zehnder interferometer39,42, illustrated in Fig. 3. Two beam splitters constitute a Mach-Zehnder interferometer. Additionally, the phase shifter PS π denotes the phase shift π executed on the photon passing through the line it is inserted.
After two swap gate operations, the state denoted in Eq. (12) is changed to

Then, a local unitary operation σy should be performed on photon 3 and 4, respectively, which can be realized by the combination of a HWP45° and a HWP. So the above state can be denoted as

Due to the presence of BS3 and BS4, the photons (1, 2) leave the paths (S11, S12) and the paths (S21, S22) to the paths  and the paths
and the paths  according to the following rules,
according to the following rules,  ,
,  ,
,  ,
,  . Correspondingly, at the output ports, the state of four photons expressed as Eq. (15) is transformed to
. Correspondingly, at the output ports, the state of four photons expressed as Eq. (15) is transformed to

From the above equation, we can see that by detecting the outputs of the four photons, the logical qubit |0〉L can be obtained with the total prabability of 25% at the output ports of  or
or  . As for the logical qubit |1〉L, it can be obtained with the total prabability of 75% at the output ports of
. As for the logical qubit |1〉L, it can be obtained with the total prabability of 75% at the output ports of  or
or  .
.
As for another scenario, if we obtain the spatial entangled state denoted as Eq. (9), with a similar process, we can also obtain the four-photon polarization entangled decoherence-free states. It is worth noting that the state denoted as Eq. (9) is the same as Eq. (8) when a swap gate is inserted into the path S21 and S22, so far, the preparation of four-photon polarization entangled decoherence-free states if fullfilled.
Discussion and Conclusion
We now give a brief discussion about the experimental feasibility of protocol with the current experimental technology. First of all, in the input ports, single-photon resources are used. The complete technology of these single photons is yet to be established43,44,45,46. Currently single-photon sources in signal modes can be achieved from the collinear type II spontaneous parametric down conversion47. As down conversion experiments are intrinsically probabilistic due to the statistical creation property of the photon pairs, the scheme will be in a sense probabilistic too in view of the usage of single-photon sources. Thus, more efficient ones are demanded for our setup. Second, in the present scheme, two CNOT gates are performed, which can be realized following the refs 26,38,39,40. However, these methods are at the best, nearly deterministic, so our scheme could be nearly deterministic. Third, in our protocol, we exploit the cross-Kerr nonlinearities medium in the spatial entanglement process and performing the polarization entanglement gate. It should be noted that in actual experiments, many factors will affect the perfect performance of cross-Kerr nonlinearities, such as dispersion, self-phase modulation, molecular vibrations in Kerr media, etc. Shapiro et al.48 analyzed the cross-Kerr nonlinear interaction and showed that single-mode cross-Kerr nonlinearities is not available for quantum information processing. Recently, Gea-Banacloche49 pointed out that the large phase shifts via the giant Kerr effect with single-photon wave packets is impossible at present. A proper physics systems providing larger strength of cross-Kerr nonlinearity should be atomic ensemble, and the fundamental problem with the cross-Kerr nonlinearity in atomic ensemble was discussed by Gea-Banacloche49, and He and Scherer50. Finally, the experiment feasibility of the present protocols also depends on the veracity of the X homodyne measurement. For the X homodyne measurement, we only consider the error chiefly coming from the overlap adjacent curves because of the fact that the coherent states of the probe beam with different phase shifts are not completely orthogonal. In fact, it is only one type of detection error in homodyne, other errors, such as the noises in detection, the reduced fidelity to the process in Eq. (4) due to multi-mode effect and decoherence, etc., also exist in a realistic implementation. Exploiting the appropriate measurement methods, the disadvantageous influence can be overcome or alleviated and the error probability will be decreased. In 2010, Wittmann et al.51 investigated quantum measurement strategies capable of discriminating two coherent states using a homodyne detector and a photon number resolving (PNR) detector. In order to lower the error probability, the postselection strategy is applied to the measurement data of homodyne detector as well as a PNR detector. They indicated that the performance of the new displacement controlled PNR is better than homodyne receiver.
To summarize, we have proposed a theoretical protocol for preparing four-photon polarization entangled decoherence-free states with the assistance of the cross-Kerr nonlinearity. In our protocol, combined with some swap gates and simple linear optical elements, a two-photon spatial entanglement gate, two CNOT gates, a four-photon polarization entanglement gate are applied. We hope our work will afford facilities for other practical implementations of quantum information processing based on optics.
Additional Information
How to cite this article: Wang, M. et al. Generation of four-photon polarization entangled decoherence-free states with cross-Kerr nonlinearity. Sci. Rep. 6, 38233; doi: 10.1038/srep38233 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Yan, F. L., Gao, T. & Chitambar, E. Two local observables are sufficient to characterize maximally entangled states of N qubits. Phys. Rev. A 83, 022319 (2011).
Gao, T., Yan, F. L. & van Enk, S. J. Permutationally invariant part of a density matrix and nonseparability of N-qubit states. Phys. Rev. Lett. 112, 180501 (2014).
DiVincenzo, D. P. Quantum gates and circuits. Proc. R. Soc. London A 454, 261–276 (1998).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999).
Deng, F. G. et al. Multiparty quantum-state sharing of an arbitrary two-particle state with Einstein-Podolsky-Rosen pairs. Phys. Rev. A 72, 044301 (2005).
Yan, F. L. & Gao, T. Quantum secret sharing between multiparty and multiparty without entanglement. Phys. Rev. A 72, 012304 (2005).
Deng, F. G., Long, G. L. & Liu, X. S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 68, 042317 (2003).
Gao, T., Yan, F. L. & Wang, Z. X. Deterministic secure direct communication using GHZ states and swapping quantum entanglement. J. Phys. A 38, 5761–5770 (2005).
Zhu, A. D., Xia, Y., Fan, Q. B. & Zhang, S. Secure direct communication based on secret transmitting order of particles. Phys. Rev. A 73, 022338 (2006).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Bennett, C. H. & Wiesner, S. J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992).
Liu, X. S., Long, G. L., Tong, D. M. & Feng, L. General scheme for superdense coding between multiparties. Phys. Rev. A 65, 022304 (2002).
Duan, L. M. & Guo, G. C. Preserving coherence in quantum computation by pairing quantum bits. Phys. Rev. Lett. 79, 1953–1956 (1997).
Zanardi, P. & Rasetti, M. Noiseless quantum codes. Phys. Rev. Lett. 79, 3306–3309 (1997).
Kempe, J., Bacon, D., Lidar, D. A. & Whaley, K. B. Theory of decoherence-free fault-tolerant universal quantum computation. Phys. Rev. A 63, 042307 (2001).
Altepeter, J. B. et al. Experimental investigation of a two-qubit decoherence-free subspace. Phys. Rev. Lett. 92, 147901 (2004).
Bourennane, M. et al. Decoherence-free quantum information processing with four-photon entangled states. Phys. Rev. Lett. 92, 107901 (2004).
Zou, X. B., Shu, J. & Guo, G. C. Simple scheme for generating four-photon polarization-entangled decoherence-free states using spontaneous parametric down-conversions. Phys. Rev. A 73, 054301 (2006).
Gong, Y. X. et al. Generation of arbitrary four-photon polarization-entangled decoherence-free states. Phys. Rev. A 77, 042317 (2008).
Xia, Y., Song, J., Song, H. S. & Zhang, S. Controlled generation of four-photon polarization-entangled decoherence-free states with conventional photon detectors. J. Opt. Soc. Am. B 26, 129–132 (2009).
Wang, H. F. et al. Local conversion of four Einstein-Podolsky-Rosen photon pairs into four-photon polarization-entangled decoherence-free states with non-photon-number-resolving detectors. Opt. Exp. 19, 25433–25440 (2011).
Xia, Y. et al. Effective protocol for preparation of four-photon polarization-entangled decoherence-free states with cross-Kerr nonlinearity. J. Opt. Soc. Am. B 30, 421–428 (2013).
Chuang, I. L. & Yamamoto, Y. Simple quantum computer. Phys. Rev. A 52, 3489–3496 (1995).
Nemoto, K. & Munro, W. J. Nearly deterministic linear optical controlled-NOT gate. Phys. Rev. Lett. 93, 250502 (2004).
Barrett, S. D. et al. Symmetry analyzer for nondestructive Bell-state detection using weak nonlinearities. Phys. Rev. A 71, 060302 (2005).
Sheng, Y. B. & Zhou, L. Deterministic entanglement distillation for secure double-server blind quantum computation. Sci. Rep. 5, 7815 (2015).
Ding, D., Yan, F. L. & Gao, T. Preparation of km-photon concatenated Greenberger-Horne-Zeilinger states for observing distinctive quantum effects at macroscopic scales. J. Opt. Soc. Am. B 30, 3075–3078 (2013).
Sheng, Y. B. & Zhou, L. Two-step complete polarization logic Bell-state analysis. Sci. Rep. 5, 13453 (2015).
He, Y. Q., Ding, D., Yan, F. L. & Gao, T. Exploration of multiphoton entangled states by using weak nonlinearities. Sci. Rep. 6, 19116 (2016).
Ding, D., Yan, F. L. & Gao, T. Entangler and analyzer for multiphoton Greenberger-Horne-Zeilinger states using weak nonlinearities. Sci. Chin. Phys. Mech. Astron. 57, 2098–2103 (2014).
He, Y. Q., Ding, D., Yan, F. L. & Gao, T. Exploration of photon-number entangled states using weak nonlinearities. Opt. Exp. 23, 21671 (2015).
Dong, L. et al. Nearly deterministic preparation of the perfect W state with weak cross-Kerr nonlinearities. Phys. Rev. A 93, 012308 (2016).
Lin, Q. & He, B. Highly efficient processing of multi-photon states. Sci. Rep. 5, 12792 (2015).
Dong, Li. et al. Generation of three-photon polarization-entangled decoherence-free states. Ann. Phys. 371, 287–295 (2016).
Gardiner, C. W. & Zoller, P. Quantum Noise, p. 113 (Springer, Berlin, 2000).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Lin, Q. & Li, J. Quantum control gates with weak cross-Kerr nonlinearity. Phys. Rev. A 79, 022301 (2009).
Beenakker, C. W. J., DiVincenzo, D. P., Emary, C. & Kindermann, M. Charge detection enables free-electron quantum computation. Phys. Rev. Lett. 93, 020501 (2004).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Milburn, G. J. Quantum optical fredkin gate. Phys. Rev. Lett. 62, 2124–2127 (1989).
Brunel, C., Lounis, B., Tamarat, P. & Orrit, M. Triggered source of single photons based on controlled single molecule fluorescence. Phys. Rev. Lett. 83, 2722–2725 (1999).
Michler, P. et al. A quantum dot single-photon turnstile device. Science 290, 2282–2285 (2000).
Santori, C. et al. Triggered single photons from a quantum dot. Phys. Rev. Lett. 86, 1502–1505 (2001).
Wang, S. M., Ma, H. Q. & Wu, L. A. A single photon source based on entangled photon pairs. Acta Phys. Sin. 58, 717–721 (2009).
Su, S. L., Cheng, L. Y., Wang, H. F. & Zhang, S. An economic and feasible scheme to generate the four-photon entangled state via weak cross-Kerr nonlinearity. Opt. Commun. 293, 172–176 (2013).
Shapiro, J. H. & Razavi, M. Continuous-time cross-phase modulation and quantum computation. New J. Phys. 9, 16 (2007).
Gea-Banacloche, J. Impossibility of large phase shifts via the giant Kerr effect with single-photon wave packets. Phys. Rev. A 81, 043823 (2010).
He, B. & Scherer, A. Continuous-mode effects and photon-photon phase gate performance. Phys. Rev. A 85, 033814 (2012).
Wittmann, C., Andersen, U. L., Takeoka, M. & Leuchs, G. Discrimination of binary coherent states using a homodyne detector and a photon number resolving detector. Phys. Rev. A 81, 062338 (2010).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant Nos: 11475054, 11371005, and Hebei Natural Science Foundation of China under Grant Nos: A2014205060, A2014205064 and A2016205145.
Author information
Authors and Affiliations
Contributions
M.Y.W., F.L.Y. and T.G. contributed equally to this work. All authors wrote the main manuscript text and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, M., Yan, F. & Gao, T. Generation of four-photon polarization entangled decoherence-free states with cross-Kerr nonlinearity. Sci Rep 6, 38233 (2016). https://doi.org/10.1038/srep38233
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38233
This article is cited by
-
Procedure via cross-Kerr nonlinearities for encoding single logical qubit information onto four-photon decoherence-free states
Scientific Reports (2021)
-
Encoding scheme using quantum dots for single logical qubit information onto four-photon decoherence-free states
Scientific Reports (2020)
-
Scheme for generation of three-photon entangled W state assisted by cross-Kerr nonlinearity and quantum dot
Scientific Reports (2019)
-
Quantum error rejection for faithful quantum communication over noise channels
Science China Physics, Mechanics & Astronomy (2019)
-
Scheme for encoding single logical qubit information into three-photon decoherence-free states assisted by quantum dots
Quantum Information Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





 ,
,  .
.