Abstract
New dual temperature and strain sensor has been designed using eccentric second-order fiber Bragg gratings produced in standard single-mode optical fiber by point-by-point direct writing technique with tight focusing of 800 nm femtosecond laser pulses. With thin gold coating at the grating location, we experimentally show that such gratings exhibit a transmitted amplitude spectrum composed by the Bragg and cladding modes resonances that extend in a wide spectral range exceeding one octave. An overlapping of the first order and second order spectrum is then observed. High-order cladding modes belonging to the first order Bragg resonance coupling are close to the second order Bragg resonance, they show a negative axial strain sensitivity (−0.55 pm/με) compared to the Bragg resonance (1.20 pm/με) and the same temperature sensitivity (10.6 pm/°C). With this well conditioned system, temperature and strain can be determined independently with high sensitivity, in a wavelength range limited to a few nanometers.
Similar content being viewed by others
Introduction
The use of femtosecond laser pulses has emerged as a competitive technology for Fiber Bragg Gratings (FBGs) inscription. The main advantage of this kind of lasers is the capability to engrave directly a variety of structures in almost all types of optical materials. Indeed, it has been demonstrated that femtosecond laser beam can be focused below the diffraction limit such that structures as small as 240 nm can be obtained1,2. With femtosecond pulses, the refractive index modulation is induced via a multi-photon transition process3. The latter does not require the presence of doping in the material such as germanium in silica matrix involved in traditional inscription methods based on continuous and nanosecond UV lasers. Thereby, the use of long working distance high numerical aperture microscope objective and subnanometric precision translation stages allow controlling the position of the inscribed grating in the core of the optical fiber4,5,6,7. Birefringent gratings can then be produced when the induced refractive index modulation is slightly shifted from the fiber core center, creating an asymmetry in the fiber cross section4,8,9. In these FBGs, also called eccentric gratings, both the Bragg and cladding modes are excited4,10. This is manifested by a transmission amplitude spectrum with the Bragg resonance at the right-hand side and several hundreds of narrowband dips (bandwidth ~200 pm) corresponding to the cladding modes at its left side. Their spectral range was estimated to one octave10, which is usually much more than tilted fiber Bragg gratings (TFBGs). Furthermore, these gratings can operate at very high temperature (more than 1000 °C) without any degradation of the FBGs performances, as it is the case for type II or type IIA FBGs11,12.
Beyond their use for lasers and telecommunication applications, the integration of FBGs as sensors has become almost a routine nowadays. Nevertheless, gratings that can be used in harsh environment with reliable self-compensation sensing solutions are still relevant to produce, especially for structural health monitoring, nuclear and oil & gas industries13,14. As FBGs in standard optical fibers are sensitive to both strain and temperature, different techniques have been set-up to discriminate between these two measurands. To cite but a few: FBGs in the same optical fiber where one is protected from thermal effect15, two gratings inscribed at two different wavelengths achieving different sensitivities16, a single FBG measured at its first and second order Bragg wavelength17, Bragg mode and cladding modes of standard tilted FBGs18, FBG in temperature insensitive specialty fibers19, among others13,20.
In this work, we demonstrate the production of first- and second-order eccentric FBGs with the 800 nm infrared (IR) femtosecond point-by-point (PbP) inscription technique. Our purpose is to study the sensing properties of the Bragg and cladding modes resonances in a wide spectral range (300 nm). These cladding modes are highly influenced by the surrounding medium. Hence, below the cut-off wavelength (corresponding to the resonance for which the effective refractive index matches the one of the surrounding medium), cladding modes are radiated21. They therefore disappear from the amplitude spectrum. In air, this phenomenon appears about 250 nm below the Bragg wavelength. In the following, we show that a thin gold coating deposited on the fiber surface at the grating location can prevent this radiation. Moreover, we demonstrate the existence of preserved cladding mode resonances over the predicted spectral range of one octave. Indeed, in the case of gold-coated second-order gratings, high-order resonances of the first-order grating overlap with the ones of the second-order grating. We experimentally demonstrate that while axial strain sensitivity of these cladding modes is mode-order dependent, temperature sensitivity is wavelength dependent, i.e. modes at the same wavelength range exhibit the same temperature sensitivity whatever they originate from first or second-order core mode coupling. However, they have totally different strain sensitivities.
As a result of these couplings, it is possible to monitor (in a short spectral range of several nanometers) both second order Bragg peak and high order cladding modes. While both kinds of peaks exhibit a similar temperature sensitivity (~10 pm/°C in the considered spectral window), their axial strain sensitivity is completely different (1.2 pm/με and −0.55 pm/με, respectively). These features yield one of the best-conditioned systems reported so far. Other important practical benefits result from the flexibility of production and the inherent grating resistance to high-temperature environments.
Experiments
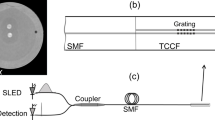
The production of eccentric FBGs is carried out with the direct PbP inscription technique and 800 nm femtosecond pulses delivered by Spitfire pro Spectra-Physics amplifier of 120 fs duration and 1 kHz repetition rate. The experimental setup and inscription process were described in previous works4,9. It consists in focusing the laser beam in the fiber core with high numerical aperture (0.65) microscope objective and without oil immersion (Fig. 1a). The fiber is then displaced along its z optical axis at a constant speed using a high precision air bearing translation stage to create a uniform modification over the required length. Each focused femtosecond pulse induces a refractive index modification in a point-like region of the fiber core, as shown in Fig. 1b.
The spacing between these points corresponds to the grating period, which can be controlled by correlating the speed of the translation stage to the repetition rate of the laser. To produce eccentric gratings, the fiber was first shifted 2 μm off-center in the horizontal direction (x direction as shown in Fig. 1), which was visually controlled in reflection using an infrared camera positioned above the microscope objective. The fiber was then translated with a constant speed along the fiber z axis up to a length of 1 cm. Figure 1b shows the transmission microscope image of 2 μm eccentricity second order FBG compared to 1 μm eccentricity first order FBG obtained by a high resolution (<300 nm) optical microscope (Zeiss Axio Imager.M2m). We have inscribed complementary gratings from the point of view of cladding modes orders beyond the cut-off wavelength (λC) in the spectral range [1300 nm–1600 nm] covered by the broadband optical source (Amonics Superluminescent Diode ASLD-CWDM-5-B-FA) and spectrum analyser (Yokogawa AQ6370) used in this work. In the following, we report the behaviour of 3 gratings inscribed in standard single mode optical fibre (Corning SMF28) with different periods 550 nm, 633 nm and 1096 nm and the same eccentricity (2 μm). Table 1 summarizes their main features, in terms of Bragg and cut-off wavelengths.
Figure 2a shows their transmitted amplitude spectra in air. For FBG1, we can see the first order Bragg resonance (λB) occurring at 1591 nm, and at its left side, in a very huge spectral range, cladding modes resonances, which are drastically attenuated around λC = 1345 nm (cut-off wavelength) indicted by a dashed line. In FBG2, we can only see cladding modes resonances down to λC = 1548 nm, because the Bragg resonance is out of the spectral range (1831 nm). FBG3 shows a similar transmitted amplitude spectrum as FBG1, with 1585 nm second order Bragg resonance and 1341 nm cut-off wavelength.
It is worth mentioning that the spectra are composed by four types of cladding modes TE0m, TM0m, HElm, and EHlm, where “l” is the azimuthal order and “m” is the order of a mode. The radial (Er) and azimuthal (Eϕ) electric fields are null for TE0m and TM0m modes so that they are polarization-independent. However, both HElm and EHlm modes are polarization-dependent since they combine axial and transverse components. As a result, a x-polarized core mode couples to the even HElm and TE0m modes while a y-polarized one couples to the odd EHlm and TM0m modes. Highest order modes EHlm and HElm are dominantly radially and azimuthally polarized, respectively22.
Each jth cladding mode resonance resulting from core mode coupling to cladding appears at a wavelength  given by:
given by:

Where m is the grating order, neff,core and  are, respectively, the effective refractive indices of the core and the jth cladding mode and
are, respectively, the effective refractive indices of the core and the jth cladding mode and  is the period of the grating.
is the period of the grating.
The cut-off wavelength can be easily calculated from Eq. (1). For silica fiber neff,core = 1.4467, the cut-off wavelength in air occurs around 1345 nm for FBG1, at 1545 nm for FBG2 and at 1340.7 nm for the second order grating FBG3. These values are in good agreement with the reported experimental results (Fig. 2). We must recall that within the framework of this study, sensing properties of the Bragg peak and cladding modes resonances have to be determined versus cladding modes order or more precisely the corresponding effective refractive index deduced from Eq. (1). In the considered spectral range (1300 nm, 1600 nm), if the cladding modes amplitudes are all maintained, FBG1 should give access to the core mode and cladding modes with neff,clad down to 0.9165. For FBG2 we can have cladding modes with neff,clad from 1.0732 down to 0.6007, and second order FBG3 will give rise to second order cladding modes with the same neff,clad as in FBG1. Therefore, so as to preserve cladding modes amplitudes below the cut-off wavelength, FBGs were shielded from the outer medium by a thin gold sheet (~50 nm) deposited on the fiber surface. A sputter coater was used for this purpose. The coated gratings were then cured at 200 °C during 6 hours for improved gold adhesion23.
Figure 2b shows the transmitted amplitude spectrum of these gold-coated eccentric gratings. Compared to Fig. 2a, we can clearly see that the gold sheet protection allows to recover cladding modes below the cut-off wavelength for the two first FBGs while for the third grating, two sets of modes become superimposed, the ones already present in Fig. 2 and others more spaced between each other.
According to other studies7 these modes can be identified as high order modes from the first order Bragg resonance coupling. From FBG1 and FBG2 spectra (Fig. 3), it appears that when the cladding modes are shielded from the outer medium influence, they can extend in very wide spectral range and even overlap on the second order spectrum. The advantage of having these high order cladding modes spectrally close to the Bragg resonance can be exploited to study simultaneously their sensitivities to axial strain and temperature.
It has been previously demonstrated that in tilted21,24,25 and highly tilted (80 degree) FBGs26, high order modes show differential strain sensitivity. Nevertheless, in these gratings Bragg resonance and high order modes that achieve the highest differential sensitivity are spectrally far (more than 100 nm). In this work, we have the opportunity with these special gratings to study the axial strain sensitivity for more extended mode-orders (FBG1 and FBG2) and even simultaneously with the Bragg reflection in FBG3.
Figure 3 illustrates the axial strain sensitivity versus the effective refractive index of the cladding modes deduced from Eq. (1) for the 3 investigated gratings. Eccentric gratings break the cylindrical symmetry of the fiber cross-section and locally creates a strong form birefringence4,10. For all the measurements, we have used a broadband source (Superluminescent Diodes Amonics ASLD-CWDM-5-B-FA) and spectrum analyser (Yokogawa AQ6370). A polarization controller was used to maintain the polarization of the light parallel to the fast mode of the grating. The plot shows a linear trend for the axial strain sensitivity versus neff,clad. We can see clearly an interval of neff,clad between 0.95 and 1.28 where the dispersion in the measurements increases for FBG1 and FBG3. In fact this region partly shown in the inset of Fig. 3, corresponds to high-order modes that display doublets. Indeed different families of cladding modes with different polarisation dependence compose the transmission amplitude spectrum of eccentric FBGs10. These families of modes may undergo different sensitivities as it was demonstrated in standard tilted FBGs for radially and azimuthally polarized modes24. Therefore, we assume that the peaks composing the doublets belong to two different families of modes with slightly different axial strain sensitivities. In the case of FBG2, the peaks are well defined (cf. upper inset of Fig. 4), yielding a linear dependence of the axial strain sensitivity versus neff,clad.
The linear regression of the experimental data for FBG2 yields:

where Kε is the strain sensitivity expressed in pm/με.
According to Eq. (1) and (2), one can assume that cladding modes with very low effective refractive index can achieve a negative axial strain sensitivity. Unfortunately, Eq. (1) is not sufficient to evaluate the effective refractive index overlapping on the second order Bragg spectrum. Numerical simulations conducted with the FimmWave complex mode solver for the optical fiber configuration used in this work confirm that hundreds of cladding modes can be supported with effective refractive indices ranging between 1.44 and 0.10. The spacing between neighbouring modes increases with the mode order. Considering that neff,clad = 0.1 in Eq. 2 yields a negative strain sensitivity of −0.66 pm/με. Such negative values for strain sensitivity have been already reported for high-order cladding modes in highly tilted (80 degree) FBGs26 and long period gratings27.
Therefore, gold-coated FBG3 is a perfect illustration of the presence of very high cladding modes (with very low neff,clad) coexisting with the Bragg resonance. In the following, we will study axial train and temperature sensitivities of this eccentric second-order grating.
Axial strain sensing properties
To decouple between temperature and strain effects, we propose to use here the second order Bragg resonance (Peak 1 at λ1) and the nearest high order cladding mode resonance (Peak2 at λ2) in the gold-coated eccentric second order FBG3. Figure 4a displays a close-up around the Bragg resonance of uncoated FBG3 transmission amplitude spectrum in air compared to the gold-coated one. It shows the selected two modes for temperature and strain characterization. The demodulation technique is based on the well-known matrix inversion approach28.
When axial strain and temperature are modified in an optical fiber, the wavelength shift is expressed as:

where Δλε and ΔλT are the wavelength changes under strain and temperature and Kε, KT are the strain and the temperature sensitivity coefficients, respectively.
Temperature and strain can be determined independently if their corresponding sensitivity coefficients of the considered peaks (1 and 2) satisfy the good conditioning of the matrix inversion:

The calibration curves for temperature and strain measurements of FBG3 allow extracting the sensitivities coefficients. In Fig. 4b we report the transmission amplitude spectrum of FBG3 around the Bragg resonance for different applied axial strains. It shows clearly that the Bragg peak at λB and cladding mode peak at λ2 undergo opposite shifts when the axial strain increases. The linear regression of the experimental data depicted in Fig. 5a gives a sensitivity of Kε1 = 1.20 pm/με for the Bragg peak whereas the one for high order cladding mode is Kε2 = −0.56 pm/με. This negative value is highly different from the Bragg peak sensitivity, which completely fulfill the condition of Eq. (4).
Axial strain (a) and temperature (b) dependence for the Bragg mode and one high order cladding mode (peak 2 Cf. Fig. 4).
For temperature calibration, the slope of the linear regression for the experimental wavelength shift versus temperature data (Fig. 5b) gives almost the same value (10.06 pm/°C and 10.05 pm/°C for KT1 and KT2, respectively).
For sensing application, a performance factor to compare the efficiency of decoupling methods is proposed in ref. 29. Accordingly, the experimentally determined sensitivities coefficients lead to a decoupling factor of 94%. This very high value places the proposed sensor among the most effective ones.
Conclusion
Eccentric FBGs were produced by point-by-point direct writing technique with femtosecond pulses. The flexibility and tunability of this inscription technique provide gratings with different pitches, which gives the possibility to study a very wide spectral range transmission amplitude spectrum providing access to different cladding mode orders. We experimentally demonstrate that the axial strain sensitivity of the cladding modes decreases linearly with the effective refractive index of the mode. For very high cladding mode orders that are kept in the amplitude spectrum thanks to a gold overlay, negative values can even be reached. This high differential strain sensitivity was exploited to implement a sensor for independent temperature and strain measurements from a single eccentric second-order grating. This sensor considers the sensing properties of the Bragg grating core mode and one very high-order cladding mode. We show that this cladding mode exhibits a similar temperature sensitivity (10.6 pm/°C) but a strongly different strain (−0.55 pm/με) sensitivity compared to the Bragg peak (10 pm/°C and 1.20 pm/με respectively). These properties are considered ideal for dual sensing purposes.
Additional Information
How to cite this article: Chah, K. et al. Negative axial strain sensitivity in gold-coated eccentric fiber Bragg gratings. Sci. Rep. 6, 38042; doi: 10.1038/srep38042 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Mezentsev, V. et al. Femtosecond laser microfabrication of subwavelength structures in photonics. Proc. SPIE 6459, 64590B (2007).
Nikogosyan, D. et al. Point-by-point inscription of 250-nm-period structure in bulk fused silica by tightly-focused femtosecond UV pulses: experiment and numerical modelling. Open Physics 8, 169–177 (2010).
Nikogosyan, D. N. Multi-photon high-excitation-energy approach to fibre grating inscription. Meas. Sci. Technol. 18, R1–R29 (2007).
Chah, K., Voisin, V., Kinet, D. & Caucheteur, C. Surface plasmon resonance in eccentric femtosecond-laser-induced fiber Bragg gratings. Opt. Lett. 39, 6887–6890 (2014).
Jovanovic, N. et al. Polarization-dependent effects in point-by-point fiber Bragg gratings enable simple, linearly polarized fiber lasers. Opt. Express 17, 6082–6095 (2009).
Martinez, A. et al. Direct writing of fibre Bragg gratings by femtosecond laser. Electron. Lett. 40 (19), 1170–1172 (2004)
Geernaert, T. et al. Point-by-point fiber Bragg grating inscription in free-standing step-index and photonic crystal fibers using near-IR femtosecond laser. Opt. Lett. 35, 1647–1649 (2010).
Koutsides, C. et al. Characterizing femtosecond laser inscribed Bragg grating spectra. Opt. Express. 19, 342–352 (2011).
Chah, K., Kinet, D., Wuilpart, M., Mégret, P. & Caucheteur, C. Femtosecond-laser-induced highly birefringent Bragg gratings in standard optical fiber. Opt. Lett. 38, 594–596 (2013).
Thomas, J. et al. Cladding mode coupling in highly localized fiber Bragg gratings: modal properties and transmission spectra. Opt. Express 19, 325–341 (2011).
Canning, J. Fibre gratings and devices for sensors and lasers. Laser Photon. Rev. 2, 275–289 (2008).
He, J. et al. Negative-index gratings formed by femtosecond laser overexposure and thermal regeneration. Sci. Rep. 6, 23379 (2016).
Kinet, D. et al. Fiber Bragg grating sensors towards structural health monitoring in composite materials: challenges and solutions. Sensors 2014, 7394–7419 (2014).
Mihailov, S. J., Grobnic, D., Walker, R. B., Lu, P. & Ding, H. Femtosecond laser induced fiber Bragg gratings for harsh environment sensing applications. Proc. SPIE 9288, 92880T (2014).
Rajan, G. Optical Fiber Sensors: Advanced Techniques and Applications. CRC Press, Taylor & Francis Group, 204–256 (2015).
Xu, M. G., Archambault, J. L., Reekie, L. & Dakin, J. P. Discrimination between strain and temperature effects using dual-wavelength fibre grating sensors. Electron. Lett. 30, 1085–1087 (1994).
Brady, G. P. et al. Simultaneous measurement of strain and temperature using the first- and second-order diffraction wavelengths of Bragg gratings. IEE Proc.-Optoelectron. 144, 156–161 (1997).
Caucheteur, C. & Mégret, P. Demodulation technique for weakly tilted fiber Bragg grating refractometer. IEEE Photon. Technol. Lett. 17, 2703–2705 (2005).
Geernaert, T. et al. Transversal load sensing with fiber Bragg gratings in microstructured optical fibers. IEEE Photon. Technol. Lett. 21, 6–8 (2009).
Ramakrishnan, M., Rajan, G., Semenova, Y. & Farrell, G. Overview of Fiber Optic Sensor Technologies for Strain/Temperature Sensing Applications in Composite Materials. Sensors 2016, 99–126 (2016).
Albert, J., Shao, L. Y. & Caucheteur, C. Tilted fiber Bragg grating sensors. Laser Photonics Rev. 7, 83 (2013).
Alam, M. Z. et al. Selective excitation of radially and azimuthally polarized optical fiber cladding modes. J. Lightwave Technol. 31, 3167 (2013).
Ribaut, C. et al. Small biomolecule immunosensing with plasmonic optical fiber grating sensor. Biosensors and Bioelectronics. 77, 315–322 (2016).
Voisin, V., Caucheteur, C., Mégret, P. & Albert, J. Anomalous effective strain-optic constants of nonparaxial optical fiber modes. Opt. Lett. 39, 578–581 (2014).
Chen, C. & Albert, J. Strain-optic coefficients of individual cladding modes of singlemode fibre: theory and experiment. Electron. Lett. 42, 18 (2006).
Zhou, K., Zhang, L., Chen, X. & Bennion, I. Optic sensors of high refractive-index responsivity and low thermal cross sensitivity that use fiber Bragg gratings of >80° tilted structures. Opt. Lett. 31, 1193–1195 (2006).
Zhang, Z. & Shi, W. Eigenvalue and field equations of three-layered uniaxial fibers and their applications to the characteristics of long-period fiber gratings with applied axial strain. J. Opt. Soc. Am. A 22, 2516–2526 (2005).
Xu, M. G., Archambault, J. L., Reekie, L. & Dakin, J. P. Discrimination between strain and temperature effects using dual-wavelength fibre grating sensors. Electron. Lett. 30, 1085–1087 (1994).
Triollet, S., Robert, L., Marin, E. & Ouerdane, Y. Discriminated measures of strain and temperature in metallic specimen with embedded superimposed long and short fibre Bragg gratings. Meas. Sci. Technol. 22, 015202 (2011).
Acknowledgements
This research has been conducted in the frame of the ERC (European Research Council) Starting Grant PROSPER (grant agreement N° 280161 – http://www.umons.ac.be/erc-prosper). C. Caucheteur is supported by the F.R.S.-FNRS.
Author information
Authors and Affiliations
Contributions
All authors have contributed equally to perform the experiments, to write and review this manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chah, K., Kinet, D. & Caucheteur, C. Negative axial strain sensitivity in gold-coated eccentric fiber Bragg gratings. Sci Rep 6, 38042 (2016). https://doi.org/10.1038/srep38042
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep38042
This article is cited by
-
Investigating the effect of modulation depth of refractive index in cascaded FBGs for dual sensing of strain and temperature
Optical and Quantum Electronics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.