Abstract
The discovery of the post-perovskite transition, which is the structural transition from the perovskite to post-perovskite structure in MgSiO3 under pressure, has aroused great interests in geosciences. Despite of previous extensive studies, key factors of the post-perovsktie transition are still under hot debate primarily due to the big difficulty in performing systematic experiments under extreme conditions. Hence, search for new materials showing the post-perovskite transition under ambient pressure has been highly expected. We here report a new-type of materials Cr3AX (A = Ga, Ge; X = C, N), which exhibits the post-perovskite transition as a function of “chemical pressure” at ambient physical pressure. The detailed structural analysis indicates that the tolerance factor, which is the measure of the ionic radius mismatch, plays the key role in the post-perovskite transition. Moreover, we found a tetragonal perovskite structure with loss of inversion symmetry between the cubic perovskite and orthorhombic post-perovskite structures. This finding stimulates a search for a ferroelectric state in MgSiO3.
Similar content being viewed by others
Introduction
The discovery of the post-perovskite phase transition, which is the structural transition from the perovskite (pv) to post-perovskite (ppv) structure on the application of pressure in MgSiO3, has aroused great interests in geosciences, because this transition can well explain the discontinuity in seismic wave velocities at the deeper mantle around the D” layer1,2,3,4,5. Since this discovery, various researches have been conducted for the ppv phase of MgSiO3; however, a simple question what is the driving force of the ppv transition has not yet be revealed6,7,8,9,10. The biggest difficulty in elucidating the mechanism is that the ppv phase of MgSiO3 is stable only under extreme high pressure of ~120 GPa and unquenchable to ambient pressure1,2,3,4,5. Thus, the related materials such as CaIrO3, CaRuO3, and NaMnF3, which exhibit the ppv transition under rather lower pressures, have been investigated7,8,9,10,11,12,13,14,15. However, the key factor of the ppv transition is still under hot debate.
We here demonstrate the ppv transition in anti-structure. The anti-structure is the structure where the positions occupied by the anions and cations are opposite to those in the original structure. We focus on a series of compounds M3AX (M = transition metal elements, A = main group elements, and X = C, N), which possess either anti-pv or anti-ppv structure, which are shown in Fig. 1(a–e), depending on the atomic species16,17,18,19. In these compounds, the Cr cations occupy the O2− sites in MgSiO3, and the A and X anions occupy the Mg2+ and Si4+ sites in MgSiO3, respectively. Even though these compounds have been investigated so far with special focus on novel electronic properties, these are also considered to be nice platforms to study the crystal chemistry concerning the ppv transition18,19. In this paper, we report the details of the structural data for two solid solutions Cr3Ga1−xGexN and Cr3GeN1−yCy, and give several insights on the ppv transition.
Crystal structures of the anti-perovskite and anti-post-perovskite M3AX.
(a) The ideal perovskite (pv) structure of the cubic Pm-3m symmetry, (b) the post-perovskite (ppv) structure of the orthorhombic Cmcm symmetry, (c) the perovskite structure of the tetragonal P4/mbm symmtery, (d) the perovskite structure of the tetragonal I4/mcm symmetry, and (e) the perovskite structure of the tetragonal P-421m symmetry. (f) The supergroup-subgroup relationships among 15 space groups, which are mathematically deduced from the assumption of rigid XCr6 octahedra20,21,22. The solid and dotted lines represent the second-order and first-order transitions, respectively. The space group inside the double line is the crystal structure discussed in this study.
We first summarize the crystal structures involved in this study. The ideal anti-pv structure has the cubic Pm-3m symmetry. The anti-pv structure is frequently distorted by the mismatch of the ionic radius between the cations and the anions. Assuming that the distortion is induced by the tilted XM6 octahedra in the rigid corner-sharing framework, we can mathematically derive 15 structures with the supergroup-subgroup relationship shown in Fig. 1(f)20,21,22. Among them, the crystal structures involved in this study are the cubic Pm-3m structure with the unit cell of a × a × a (a0a0a0 tilting) shown in Fig. 1(a), the tetragonal P4/mbm structure with the unit cell of ~ a ×
a ×  a × a (a0a0c+ tilting) shown in Fig. 1(c), and the tetragonal I4/mcm structure with the unit cell of ~
a × a (a0a0c+ tilting) shown in Fig. 1(c), and the tetragonal I4/mcm structure with the unit cell of ~ a ×
a ×  a × 2a (a0a0c− tilting) shown in Fig. 1(d)23. Whereas these 15 anti-pv structures are centrosymmetric, there can be also non-centrosymmetrically distorted anti-pv structures. One of them is the tetragonal P-421m structure with the unit cell of ~
a × 2a (a0a0c− tilting) shown in Fig. 1(d)23. Whereas these 15 anti-pv structures are centrosymmetric, there can be also non-centrosymmetrically distorted anti-pv structures. One of them is the tetragonal P-421m structure with the unit cell of ~ a ×
a ×  a × a shown in Fig. 1(e). In this structure, the XM6 octahedra are seemingly tilted in a similar manner as in the P4/mbm structure; however, in addition, the M atoms are shifted up and down along the c axis to form the elongated XM6 octahedra, resulting in the breakdown of the inversion symmetry. We note that this structure does not belong to the supergroup-subgroup relationship shown in Fig. 1(f). The anti-ppv structure possesses the two-dimensional character with the orthorhombic Cmcm symmetry as illustrated in Fig. 1(b), which differs from three-dimensional character of the anti-pv structure.
a × a shown in Fig. 1(e). In this structure, the XM6 octahedra are seemingly tilted in a similar manner as in the P4/mbm structure; however, in addition, the M atoms are shifted up and down along the c axis to form the elongated XM6 octahedra, resulting in the breakdown of the inversion symmetry. We note that this structure does not belong to the supergroup-subgroup relationship shown in Fig. 1(f). The anti-ppv structure possesses the two-dimensional character with the orthorhombic Cmcm symmetry as illustrated in Fig. 1(b), which differs from three-dimensional character of the anti-pv structure.
Results
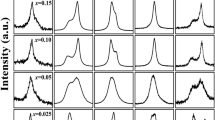
We present x-ray diffraction (XRD) patterns taken at room temperature for two solid solutions Cr3Ga1−xGexN and Cr3GeN1−yCy in Fig. 2(a). The XRD patterns can be divided into three regions: I. 0 ≤ x < 0.50 in Cr3Ga1−xGexN; II. 0.50 ≤ x ≤ 1 in Cr3Ga1−xGexN and 0 ≤ y < 0.20 in Cr3GeN1−yCy; and III. 0.20 ≤ y ≤ 1 in Cr3GeN1−yCy. The XRD patterns in region I can be well fitted by assuming the anti-pv structure with the cubic Pm-3m symmetry, confirming an earlier report on Cr3GaN23. In region II, a clear splitting of 0 0 2 reflection in the a × a × a notation into 0 0 2 and 2 2 0 reflections in the ~ a ×
a ×  a × a notation is observed, indicating the symmetry lowering from the cubic to tetragonal one. In addition, there appears new reflections including 1 2 0 and 1 2 1 in the ~
a × a notation is observed, indicating the symmetry lowering from the cubic to tetragonal one. In addition, there appears new reflections including 1 2 0 and 1 2 1 in the ~ a ×
a ×  a × a notations; and all of these reflections are well assigned by the P-421m space group in consistent with an earlier report on Cr3GeN24. In region III, the XRD patterns are different completely. All the peaks are well indexed by assuming the anti-ppv structure with the Cmcm space group, confirming an earlier report on Cr3GeC25. We can therefore see that the anti-pv structure in Cr3GaN changes to anti-ppv structure in Cr3GeC by the chemical substitution or the “chemical pressure”. This transition can be called as the post-pv transition in the anti-structure.
a × a notations; and all of these reflections are well assigned by the P-421m space group in consistent with an earlier report on Cr3GeN24. In region III, the XRD patterns are different completely. All the peaks are well indexed by assuming the anti-ppv structure with the Cmcm space group, confirming an earlier report on Cr3GeC25. We can therefore see that the anti-pv structure in Cr3GaN changes to anti-ppv structure in Cr3GeC by the chemical substitution or the “chemical pressure”. This transition can be called as the post-pv transition in the anti-structure.
The evolution of the crystal structure at room temperature for Cr3Ga1−xGexN and Cr3GeN1−yCy with the composition step of Δx = 0.1 and Δy = 0.1.
(a) The powder x-ray diffraction patterns in the selected 2θ regions. (b-e) Composition dependence of (b) the volume per a formula unit Cr3AX (V), (c) the lattice parameters, (d) the bond distance between X and Cr atoms (dX−Cr), and (e) the bond distance between A and Cr atoms (dA−Cr). The number in (d,e) corresponds to the number of bonds in XCr6 ocahedra and ACr12 polyhedra.
The crystal structures are refined by the Rietveld analysis as shown in Fig. S2, and the volume per unit formula (V), the lattice parameters (a, b, and c), and the bond distances are summarized in Fig. 2(b–e) and Table S1. With increasing x in Cr3Ga1−xGexN, the unit cell volume shrinks monotonously in both of the Pm-3m and P-421m phases owing to the smaller atomic radius of Ge than that of Ga. On the other hands, with increasing y in Cr3GeN1−yCy, the lattice has a general tendency to expand owing to the larger atomic radius of C than that of N. In the latter course, there is a discontinuous volume decrease by ~0.54% across the anti-ppv transition at y = 0.20. This indicates that the negative “chemical pressure” triggers the structural transition to the denser anti-ppv phase. The volume changes in a strong anisotropic manner with increasing x and y: the a axis decreases and the c axis increases in the P-421m phase; and the a and c axes increase and the b axis decreases in the Cmcm phase.
To understand the ppv transition from the microscopic viewpoint, we focus on the coordination environment around A and X atoms, and plot the A-Cr and X-Cr bond distances as a function of x and y in Fig. 2 (d,e). Across the transition from Pm-3m to P-421m in the anti-pv phases, the 6 X-Cr bonds in XCr6 octahedra of the Pm-3m phase are split into 2 longer bonds and 4 shorter bonds with large expansion of the averaged distance, resulting in the elongated XCr6 octahedara in the P-421m structure. In the anti-ppv phase with the Cmcm symmetry, on the other hand, the XCr6 octahedra are compressed; there are 4 longer bonds and 2 shorter bonds, keeping the similar averaged distances to those in the P-421m phase. Contrastively, the ACr12 polyhedron show more drastic change. The 12 A-Cr bonds in an ACr12 polyhedron of the Pm-3m structure are split into 5 groups in P-421m structure and 4 groups in the Cmcm structure. Among them, one group including 2 bonds in the P-421m structure and 4 bonds in the Cmcm structure have much longer bond distances than the other bonds. We can therefore say that the coordination numbers of A sites decreases from 12 in the Pm-3m structure to 10 in the P-421m structure and 8 in the Cmcm structure26. We here notice that, in the P-421m structure, the 2 longer bonds are expanding toward one side of ACr12 polyhedron as shown in Fig. S1(d), resulting in the local breakdown of the inversion symmetry. This feature is quite distinct from the centrosymmetrically distorted manner of ACr12 polyhedron in the Cmcm structure as shown in Fig. S1(e).
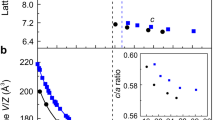
To investigate the crystal structure at high temperature, we have collected XRD patterns for Cr3GeN in the temperature (T) ranges of 25–800 °C; the warming process data are shown in Fig. 3(a). The XRD patterns qualitatively change around 150 and 650 °C, indicating the emergence of the successive structural transitions. The XRD patterns can be well fitted by assuming the P-421m structure for T < 150 °C24, the I4/mcm structure for 150 °C < T < 650 °C, the P4/mbm structure for 650 °C < T < 750 °C, and the Pm-3m structure for 750 °C < T. The results of XRD refinements are summarized in Fig. 3(b–e), Fig. S3, and Table S2. On warming, the lattice expands monotonously, and the tetragonal distortions characterized by the a/c ratio become smaller. In this course, the local environments around the A and X atoms change in a strange manner. The ratio between the shorter and longer X-Cr bonds in a XCr6 octahedra, which is the measure of the local tetragonal symmetry breakdown, exhibits anomalous sudden decrease across the P-421m to I4/mcm transition. Simultaneously, the ACr12 polyhedra change their local environment with 2 + 2 + 4 + 2 + 2 A-Cr bonds in the P-421m structure to that with 4 + 4 + 4 bonds in the I4/mcm structure in a discontinuous manner. We note that the I4/mcm structure has similar local environment in XCr6 octahedra and ACr12 polyhedra to that of the P4/mbm and Cmcm structures (Fig. S1(b), S1(c), and S1(e)), indicating the close connection among these three structures. We can therefore conclude that the P-421m structure is special among all the structures discussed in this study20,21,22.
The evolution of the crystal structure at high temperature for Cr3GeN.
(a) The powder x-ray diffraction patterns in the selected 2θ regions at 25–800 °C with the temperature step of 25 °C. Small impurities of Cr2O3, which appears above 700 °C, are marked by asterisk. (b–e) Temperature dependence of (b) the volume per a formula unit Cr3GeN (V), (c) the lattice parameters, (d) the bond distance between X and Cr atoms (dX−Cr), and (e) the bond distance between A and Cr atoms (dA−Cr). The number in (d) and (e) corresponds to the number of bonds in XCr6 ocahedra and ACr12 polyhedra.
To construct the precise phase diagram, we performed differential thermal analysis (DTA) and differential scanning calorimetry (DSC) for two solid solutions Cr3Ga1−xGexN and Cr3GeN1−yCy as shown in Fig. 4(a,b). In the DTA data on the warming process for Cr3GeN, there are three peaks at around 140, 590, and 690 °C, which correspond to the structural transitions observed in the XRD measurements. By changing compositions, the three structural transition temperatures shift systematically. Similar features are also discernible in the DSC data as shown in Fig. 4(b). Based on these data, the structural phase diagram shown in Fig. 5(b) was established. One can see that the crystal structure of Cr3AX develops from the cubic anti-pv structure to orthorhombic anti-ppv structure with the intermediate tetragonal anti-pv structure, and that the region of the intermediate tetragonal phase becomes narrower at higher temperature.
Thermal analysis for Cr3Ga1−xGexN and Cr3GeN1−yCy.
(a) The temperature dependence of the differential thermal analysis (DTA). (b) The temperature dependence of differential scanning calorimetry (DSC). The data are taken in the warming/cooling processes. Each curve is shifted by the offset for clarity. The symbols indicate the structural transition temperatures.
The phase diagram among the temperature-composition plane for Cr3Ga1−xGexN and Cr3GeN1−yCy.
(a) Tolerance factor (t) estimated by using the atomic radius. (b) Phase diagram constructed from the x-ray diffraction patterns, DTA, and DSC. The transition temperature estimated from the data taken on warming and cooling processes are indicated by closed and open symbols, respectively.
Discussions
We now discuss what the key factor of the ppv transition is. The most plausible candidate is the ionic radius mismatch between A and X ions, which is measured by the tolerance factor  , where dA−Cr and dX−Cr represents the average atomic distances between the A and Cr atoms, and the X and Cr atoms, respectively27. As shown in Fig. 5(a), the t factor calculated by using the atomic radius is 0.94, close to 1 for Cr3GaN, indicating the perfect matching of ionic radius and the stable cubic anti-pv structure28. With increasing x in Cr3Ga1−xGexN and y in Cr3GeN1−yCy, the t value becomes much smaller; and then the A atoms are not stable in the 12-fold coordination of Cr, destabilizing the anti-pv structure. As a consequence, the anti-ppv structure, in which the A atoms have 8 fold coordination of Cr, is stabilized. This is a rough sketch of the ppv transition in the anti-structure.
, where dA−Cr and dX−Cr represents the average atomic distances between the A and Cr atoms, and the X and Cr atoms, respectively27. As shown in Fig. 5(a), the t factor calculated by using the atomic radius is 0.94, close to 1 for Cr3GaN, indicating the perfect matching of ionic radius and the stable cubic anti-pv structure28. With increasing x in Cr3Ga1−xGexN and y in Cr3GeN1−yCy, the t value becomes much smaller; and then the A atoms are not stable in the 12-fold coordination of Cr, destabilizing the anti-pv structure. As a consequence, the anti-ppv structure, in which the A atoms have 8 fold coordination of Cr, is stabilized. This is a rough sketch of the ppv transition in the anti-structure.
In this respect, the three tetragonal anti-pv phases are considered to be the intermediate phases across the ppv transitions. Indeed, the resemblance of the local structure around the A atoms among the I4/mcm, P4/mbm, and Cmcm structures indicate that the tetragonal distortions in the I4/mcm and P4/mbm structures are the precursor of the ppv transition. However, this is not the case for the P-421m structure. The P-421m structure is different from the I4/mcm and P4/mbm structures in four respects: (1) the structure is not included in the subgroup-supergroup relationship shown in Fig. 1(f); (2) the inversion symmetry is broken; (3) the coordination number of A atoms is not 8 nor 12 but 10; and (4) the structural transition temperature is lowered with increasing y in Cr3GeN1−yCy. All of these facts indicate that the P-421m structure is not stabilized by the ionic radius mismatch between A and X atoms; instead, the structure is likely stabilized by the covalent nature of N-Cr and Ge-Cr bonds. Such a covalency driven structural phase transitions are discussed in ferroelectrics including PbTiO3 and BaTiO329, and ferroelectric-like metals including LiOsO3, Cd2Re2O7, and Pb2Ir2O730,31,32,33; in both class of materials, inversion symmetry is broken. Therefore, we can conclude that two driving forces of structural modifications, which are the ionic radius mismatch and covalency of chemical bonds, are competing and/or cooperating with each other in the present system. We also notice that the effect of these two driving forces becomes smaller at high-temperature, where thermal fluctuations prefer to high-symmetry structures, which well explains the experimentally observed narrower tetragonal phase at high temperature.
Finally, we discuss the resemblance and difference between the ppv transition in Cr3AX and that in MgSiO3. The ppv transition in Cr3AX is driven by the ionic radius mismatch between A and X atoms, which is in harmony with the several proposed scenario of the ppv transition in MgSiO3 focusing on the tolerance factor which decreases on the application of pressure11,34,35. Despite of this fundamental resemblance, there are several crucial differences. Firstly, whereas the application of the negative “chemical pressure” induces the ppv transition in Cr3AX, the application of positive physical pressure induces the ppv transition in MgSiO3. This means that the physical pressure is not the key factor of the ppv transition; instead, the tolerance factor is the fundamental factor. Secondly, whereas the pv structure adjacent to the ppv structure belongs to the tetragonal I4/mcm and P4/mbm symmetry in Cr3AX, it belong to the orthorhombic Pnma symmetry with the unit cell of ~ a × 2a ×
a × 2a ×  a (a+b−b− tilting) in MgSiO3. Thirdly, not only the structural instability toward to the ppv structure, but also the structural instability toward the inversion-broken state is present in Cr3AX. We are therefore tempted to imagine that there is a structural instability to the ferroelectric state in MgSiO3, in which the Si-O bonds are discussed to have the strong covalent characters36,37. Further experiments as well as computational simulations are required to clarify this issue. A possible interesting study is a search for new compounds with the anti-ilmenite and anti-LiNbO3 structures, which will highlight the important role of the tolerance factor as well as the covalent bonding38.
a (a+b−b− tilting) in MgSiO3. Thirdly, not only the structural instability toward to the ppv structure, but also the structural instability toward the inversion-broken state is present in Cr3AX. We are therefore tempted to imagine that there is a structural instability to the ferroelectric state in MgSiO3, in which the Si-O bonds are discussed to have the strong covalent characters36,37. Further experiments as well as computational simulations are required to clarify this issue. A possible interesting study is a search for new compounds with the anti-ilmenite and anti-LiNbO3 structures, which will highlight the important role of the tolerance factor as well as the covalent bonding38.
Methods
Polycrystalline samples were grown by the solid-state reaction. Powders of C (3 N), Cr (3 N), and Cr2N (2 N), and grains of Ga (4 N), and Ge (3 N) were mixed in a stoichiometric ratio in a N2-filled glove box, and then sealed in a quartz tube under 0.3 atm of Ar gas18. The quartz tube was heated to 1000 °C, held for 60 h, and quenched to room temperature. The product was pulverized, and pressed into pellets, which were annealed inside a quartz tube at 1000–1100 °C for 96 h. Then, the above annealing process was repeated. X-ray diffraction experiments were performed by utilizing Smartlab (Rigaku) and M21X (Mac science). Structural parameters were obtained by Rietveld refinement using Rietica software39. Differential thermal analysis (DTA) was measured continuously at 25–1000 °C with heating/cooling rates of 20 °C/min. by using the Al2O3 as the reference. The samples were put into a glass capillary with an inner diameter of 0.1 mm. Differential scanning calorimetry (DSC) was measured at −150–480 °C with heating/cooling rates of 20 °C/min.
Additional Information
How to cite this article: Wang, B. and Ohgushi, K. Post-perovskite Transition in Anti-structure. Sci. Rep. 6, 37896; doi: 10.1038/srep37896 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Murakami, M., Hirose, K., Kawamura, K., Sata, N. & Ohishi, Y. Post-Perovskite Phase Transition in MgSiO3 . Science 304, 855–858, doi: 10.1126/science.1095932 (2004).
Oganov, A. R. & Ono, S. Theoretical and experimental evidence for a post-perovskite phase of MgSiO3 in Earth’s D” layer. Nature 430, 445–448, doi: 10.1038/nature02701 (2004).
Iitaka, T., Hirose, K., Kawamura, K. & Murakami, M. The elasticity of the MgSiO3 post-perovskite phase in the Earth’s lowermost mantle. Nature 430, 442–445, doi: 10.1038/nature02702 (2004).
Tsuchiya, T., Tsuchiya, J., Umemoto, K. & Wentzcovitch, R. M. Phase transition in MgSiO3 perovskite in the earth’s lower mantle. Earth. Planet. Sci. Lett. 224, 241–248, doi: org/10.1016/j.epsl.2004.05.017 (2004).
Belonoshko, A. B. et al. High-Pressure Melting of MgSiO3 . Phys. Rev. Lett. 94, 195701, doi: 10.1103/PhysRevLett.94.195701 (2005).
Ohgushi, K. et al. Metal-insulator transition in Ca1−xNaxIrO3 with post-perovskite structure. Phys. Rev. B 74, 241104(R), doi: 10.1103/PhysRevB.74.241104 (2006).
Yamaura, K. et al. Synthesis and Magnetic and Charge-Transport Properties of the Correlated 4d Post-Perovskite CaRhO3 . J. Am. Chem. Soc. 131, 2722–2726, doi: 10.1021/ja8091906 (2009).
Cheng, J.-G., Zhou, J. S. & Goodenough, J. B. Stress-induced perovskite to post-perovskite transition in CaIrO3 at room temperature. Phys. Rev. B 82, 132103, doi: 10.1103/PhysRevB.82.132103 (2010).
Shirako, Y. et al. Integer spin-chain antiferromagnetism of the 4d oxide CaRuO3 with post-perovskite structure. Phys. Rev. B 83, 174411, doi: 10.1103/PhysRevB.83.174411 (2011).
Wang, B. S. & Ohgushi, K. Superconductivity in anti-post-perovskite vanadium compounds. Sci. Rep. 3, 3381, doi: 10.1038/srep03381 (2013).
Tateno, S., Hirose, K., Sata, N. & Ohishi, Y. High-pressure behavior of MnGeO3 and CdGeO3 perovskites and the post-perovskite phase transition. Phys. Chem. Minerals. 32, 721, doi: 10.1007/s00269-005-0049-7 (2006).
Xiao, P. H., Cheng, J.-G., Zhou, J. S., Goodenough, J. B. & Henkelman, G. Mechanism of the CaIrO3 post-perovskite phase transition under pressure. Phys. Rev. B 88, 144102, doi: 10.1103/PhysRevB.88.144102 (2013).
Bremholm, M., Dutton, S. E., Stephens, P. W. & Cava, R. J. NaIrO3-A pentavalent post-perovskite. J. Solid State Chem. 184, 601–607, doi: 10.1016/j.jssc.2011.01.028 (2011).
Yakovlev, S., Avdeev, M. & Mezouar, M. High-pressure structural behavior and equation of state of NaZnF3 . J. Solid State Chem. 182, 1545–1549, doi: 10.1016/j.jssc.2009.03.031 (2009).
Ijjaali, I., Mitchell, K., Huang, F. Q. & Ibers, J. A. Syntheses and characterization of the actinide manganese selenides ThMnSe3 and UMnSe3 . J. Solid State Chem. 177, 257–261, doi: 10.1016/j.jssc.2003.08.004 (2004).
He, T. et al. Superconductivity in the non-oxide perovskite MgCNi3 . Nature 411, 54–56, doi: 10.1038/35075014 (2001).
Takenaka, K. & Takagi, H. Giant negative thermal expansion in Ge-doped anti-perovskite manganese nitrides. Appl. Phys. Lett. 87, 261902, doi: 10.1063/1.2147726 (2005).
Boller, H. & Nowotny, H. Komplexcarbide und-nitride mit aufgefulltem Fe3B-type. Monatsh. Chem. 99, 721–725 (1968).
Umemoto, K. & Wentzcovitch, R. M. Phys. Rev. B 74, 224105, doi: 10.1103/PhysRevB.74.224105 (2006).
Glazer, A. M. The classification of tilted octahedra in perovskites. Acta Cryst. B 28, 3384, doi: 10.1107/S0567740872007976 (1972).
Glazer, A. M. Simple ways of determining perovskite structures. Acta Cryst. A 31, 756, doi: 10.1107/S0567739475001635 (1975).
Howard, C. J. & Stokes, H. T. Group-Theoretical Analysis of Octahedral Tilting in Perovskites. Acta Cryst. B 54, 782, doi: 10.1107/S0108768198004200 (1966).
Nardin, M. et al. Retude de cinq nouveaux nitrures MCr3N de type perovskite. Comptes Rendus Hebdomadaires des Seances des Sciences, Serie C,Sciences Chimiques 274, 2168–2171 (1972).
Bller, H. Die Kristallstruktur von Cr3GeN. Monatsh. Chem. 100, 1471–1476, doi: 10.1007/BF00900160 (1969).
Bller, H. Komplexcarbide und-nitride mit aufgefülltem U3Si-Typ. Monatsh. Chem. 99, 2444–2449, doi: 10.1007/BF01154362 (1968).
Nowotny, H. Crystal Chemistry of Complex Carbides and Related Compounds. Angew. Chem. Internat. Edit. 11, 906, doi: 10.1002/anie.197209061 (1972).
Tokura, Y. & Tomioka, Y. lossal magnetoresistive manganites. J. Magn. Magn. Mater. 200, 1–23, doi: 10.1016/S0304-8853(99)00352-2 (1999).
Slater, J. C. Atomic Radii in Crystals. J. Phys. Chem. 41, 3199, doi: 10.1063/1.1725697 (1964).
Millicent, B. S. et al. Crystal Structure and the Paraelectric-to-Ferroelectric Phase Transition of Nanoscale BaTiO3 . J. Am. Chem. Soc. 130, 6955–6963, doi: 10.1021/ja0758436 (2008).
Shi, Y. G. et al. A ferroelectric-like structural transition in a metal. Nature Mater. 12, 1024–1027, doi: 10.1038/nmat3754 (2013).
Samir, F. & Gerard, Demazeau Potential existence of post-perovskite nitrides; DFT studies of ThTaN3 . J. Solid State Chem. 183, 994–999, doi: 10.1016/j.jssc.2010.03.002 (2010).
Sergienko, I. A. et al. Metallic “Ferroelectricity” in the Pyrochlore Cd2Re2O7 . Phys. Rev. Lett. 92, 065501, doi: 10.1103/PhysRevLett.92.065501 (2004).
Hirata, Y. et al. Mechanism of Enhanced Optical Second-Harmonic Generation in the Conducting Pyrochlore-Type Pb2Ir2O7−x Oxide Compound. Phys. Rev. Lett. 110, 187402, doi: 10.1103/PhysRevLett.110.187402 (2013).
Sugahara, M. et al. Reinvestigation of the MgSiO3 perovskite structure at high pressure. Am. Mineral. 91, 533–536, doi: 10.2138/am.2006.1980 (2006).
Wu, X., Qin, S. & Wu, Z. Y. Generalized gradient approximation calculations of the pressure-induced phase transition of YAlO3 perovskite. J. Phys: Condens. Matter. 18, 3907–2916, doi: 10.1088/0953-8984/18/16/001 (2006).
Stixrude, L. & Bukowinski, M. S. T. Simple Covalent Potential Models of Tetrahedral SiO2: Applications to α-quartz and Coesite at Pressure. Phys. Chem. Minerals. 16, 199–206, doi: 10.1007/BF00203204 (1988).
Gillet, P., Guyot, F. & Wang, Y. B. Microscopic anharmonicity and equation of state of MgSiO3-perovskite. Geophys. Res. Lett. 23, 3043–3046, doi: 10.1029/96GL02771 (1996).
Inaguma, Y. et al. High-pressure synthesis of novel lithium niobate-type oxides. J. Phys: Conf. Ser. 215, 012131, doi: 10.1088/1742-6596/215/1/012131 (2010).
Rietveld, H. M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 2, 65–71, doi: 10.1107/S0021889869006558 (1969).
Acknowledgements
The authors acknowledge Prof. Y. Ueda, Prof. Y. Uwatoko, Prof. J. G. Cheng, Dr. M. Isobe, Dr. Y. Hirata, Dr. F. Du, Dr. Y. Q. Zhang, and T. Waki for their great support and useful discussions. This work was supported by JSPS KAKENHI Grant Number 26287073 and 16H01062.
Author information
Authors and Affiliations
Contributions
K.O. directed the research. B.W. carried out experiments and analyse the data. B.W. and K.O. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wang, B., Ohgushi, K. Post-perovskite Transition in Anti-structure. Sci Rep 6, 37896 (2016). https://doi.org/10.1038/srep37896
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37896
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.