Abstract
We study the ground-state behavior of a Bose-Einstein Condensate (BEC) in a Raman-laser-assisted one-dimensional (1D) optical lattice potential forming a multilayer system. We find that, such system can be described by an effective model with spin-orbit coupling (SOC) of pseudospin (N-1)/2, where N is the number of layers. Due to the intricate interplay between atomic interactions, SOC and laser-assisted tunnelings, the ground-state phase diagrams generally consist of three phases–a stripe, a plane wave and a normal phase with zero-momentum, touching at a quantum tricritical point. More important, even though the single-particle states only minimize at zero-momentum for odd N, the many-body ground states may still develop finite momenta. The underlying mechanisms are elucidated. Our results provide an alternative way to realize an effective spin-orbit coupling of Bose gas with the Raman-laser-assisted optical lattice, and would also be beneficial to the studies on SOC effects in spinor Bose systems with large spin.
Similar content being viewed by others
Introduction
The realization of Raman-induced artificial gauge fields in ultracold atomic gases1,2,3,4,5,6,7 provides a well-controllable way to investigate many fundamental phenomena induced by SOC8,9,10,11. Among these studies, the spin-orbit (SO) coupled Bose gases, which have no counterpart in conventional solid materials, are of particular interests in cold atom community. An important consequence brought by SOC is the degeneracy in the single-particle ground states, which play a centre role in determining the many-body ground states of BECs. Many new phases as well as phase transitions are predicted to appear in diverse Bose systems with different types of SOC12,13,14,15,16,17,18,19,20,21,22,23,24. For example, the stripe and plane wave phases12,13,14,15,16,17,18, half-vortex (meron) ground states19,20,21,22,23, and fractional skyrmion lattices24,25 may emerge in SO coupled BECs.
Despite of different proposals to generate SOC in ultracold atoms26,27,28,29,30,31,32,33,34,35,36, so far for Bose gases, the artificial SOC has been realized only in one dimension1,2,5 or in 2D lattices7. Recently, the technique of laser-assisted tunneling37,38,39 is developed to produce strong magnetic fields in optical lattices40,41,42,43. Such method provides a powerful and delicate way to manipulate atoms in lattice potential. Stimulated by these developments, some authors24,25 have proposed an alternative and realistic way to realize an effective 2D SOC in bilayer Bose systems based on the laser-assisted tunneling. In such schemes, the prerequisite “internal” states to fabricate SOC are essentially replaced by the Raman-assisted “external” motional states in each layer, providing a new system to investigate the SO coupled BECs.
Motivated by the above advances, in this paper, we consider a gas of ultracold scalar bosons subjected to a Raman-assisted 1D optical lattice potential forming a multilayer system. Within the lowest band of the lattice, the system can be mapped to an effective model with SOC, where N different layers play a role of a pseudospin (N − 1)/2 coupled to the intralayer motion via the laser-assisted tunneling of atoms between the layers. This scheme can avoid the using of near resonant light beams which cause heating in previous experiments1, and can be applied to a wide range of atom species including fermions. Recently, a related scheme has been experimentally implemented to realize the effective SOC with double well potential formed by an optical superlattice44. In such a scheme the double layer is in a direction of the atomic motion. On the other hand, we suggest to use a lattice with N sites in a direction perpendicular to the atomic motion. This resembles bosonic ladders43, but the atoms now undergo a planar rather than a one-dimensional motion.
We determine the ground states of the system in the presence of atomic interactions. Note that, the dynamics of a SO coupled BEC in a weakly tilted optical lattice has been studied45, where the correlated Bloch oscillations with spin Hall effect are revealed. Here, the one-dimensional optical lattice potential is sufficiently tilted and unlike the typical atom-atom interactions in conventional spinor BEC46, the special type of interactions from on-site repulsions in our system is quite different in the psuedospin representation, and can give rise to peculiar N-dependent phase diagrams with different behaviors: (1) For even N, by tuning the tunneling strength J, the single-particle ground state may change from a single minimal with zero-momentum to double minima with finite momentum, with the corresponding many-body ground states evolving from a normal phase to a robust stripe phase. (2) For odd N, the single-particle states only minimize at zero-momentum. However, when the interaction strength is increased, a stripe/plane wave phase with finite momentum can still emerge in the ground states. Such unique features reflect the competition and compromise between Raman-assisted tunneling and atomic interactions in this system.
Results
The model
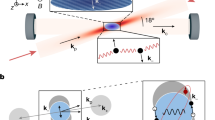
We consider a three-dimensional ultra-cold Bose gas (e.g. 87Rb) loaded into a one-dimensional optical lattice potential. Such potential are tight enough that the atoms only occupy the lowest energy band of the lattice potential (along z-axis), but move freely in the traverse xy-plane, forming a stacked-disk configuration. Furthermore, we apply a linear gradient potential in z-direction to tilt the lattice, as depicted in Fig. (1). Such global tilt can be achieved by implementing a frequency shift between the lasers for the creating of the lattice potential47,48, or by tilting the lattice along the direction of the gravitational field49,50. The single-particle Hamiltonian of this system reads:
Schematic diagram of the Raman-laser-assisted optical lattice.
The lattice potential is deep and tilted enough so that the tight-binding approximation can be applied but the direct tunnelings between adjacent sites can be neglected. Two Raman lasers (labeled as red and blue arrows) couple the internal electron ground state |g〉i to an excited state |e〉i and would induce an interlayer transition (see the context for detail). (a). Energy levels with Δ the energy difference between adjacent sites. (b) Momentum relations. k1,2 are the incident momenta of two Raman lasers, δk = k1 − k2 = δkz + δk⊥.

with

where Ψ(r) annihilates a boson at position r. U0 and F are the strengths of optical and linear gradient potential respectively, and  is a weak harmonic potential along z-axis with ωz the trapping frequency. P and m are the momentum and mass of atom, and ko is the wave-vector of laser to generate the lattice potential.
is a weak harmonic potential along z-axis with ωz the trapping frequency. P and m are the momentum and mass of atom, and ko is the wave-vector of laser to generate the lattice potential.
When the tilting is not too large, the atoms can still move in the lowest state of each well, forming the energy band of the lattice potential. We can expand the field operator  with the localized wannier function
with the localized wannier function  of the ith lattice, where N is the lattice number. The Hamiltonian. (1) then can be rewritten as:
of the ith lattice, where N is the lattice number. The Hamiltonian. (1) then can be rewritten as:

Here,  is the on-site energy and
is the on-site energy and  . When neglecting the small V(z), the energy differences between adjacent sites are mainly caused by the linear-tilted part, which is given by Δ ≡ Δij = |εi − εj|. Generally, there should also be a tunneling matrix element
. When neglecting the small V(z), the energy differences between adjacent sites are mainly caused by the linear-tilted part, which is given by Δ ≡ Δij = |εi − εj|. Generally, there should also be a tunneling matrix element  between adjacent sites <ij>. However, for a sufficiently tilted lattice potential, the inter-site tunneling is much smaller than the energy mismatch between two sites, i.e.
between adjacent sites <ij>. However, for a sufficiently tilted lattice potential, the inter-site tunneling is much smaller than the energy mismatch between two sites, i.e.  . For example,
. For example,  for Δ ≈ 8ER with ER the recoiling energy of the lattice39. As a result, the direct tunneling is inhibited and hence can be neglected. To restore the atomic hopping between adjacent wells, we resort to the newly developed laser-assisted process40,41,42,43.
for Δ ≈ 8ER with ER the recoiling energy of the lattice39. As a result, the direct tunneling is inhibited and hence can be neglected. To restore the atomic hopping between adjacent wells, we resort to the newly developed laser-assisted process40,41,42,43.
To this end, we implement two Raman lasers with wave-vector ki and frequency ωi (i = 1, 2), which couple to the atomic internal state via a two-photon transition. This gives rise to an time-dependent scalar potential VK = 1V0[ei(δk⋅r−δωt) + 1e−i(δk⋅r−δωt)], where V0 is controlled by the Raman beam intensities. δk = k1 − k2 and δω = ω1 − ω2 denotes the wave vector and frequency differences of the Raman lasers. Then along the z-direction, one has an additional overlap integral  , i.e.
, i.e.  , where we have assumed δω ~ Δ with the dominant contribution in K′ is from the overlap between adjacent sites <ij>, while other processes are far off-resonance and can be neglected. Then by introducing N-component spinor Φ = (ϕ1ϕ2 … ϕN)T, and applying a unitary transformation
, where we have assumed δω ~ Δ with the dominant contribution in K′ is from the overlap between adjacent sites <ij>, while other processes are far off-resonance and can be neglected. Then by introducing N-component spinor Φ = (ϕ1ϕ2 … ϕN)T, and applying a unitary transformation  , where
, where

and δk⊥ ⋅ r⊥ = δkxx + δkyy, the Hamiltonian is transformed as  (The definition of Fz is referred to Eq. 6). To write it explicitly, we have
(The definition of Fz is referred to Eq. 6). To write it explicitly, we have  , and
, and  with
with  being the laser-assisted tunneling strength. Notice that, it is the factor
being the laser-assisted tunneling strength. Notice that, it is the factor  due to the momentum transfer along the z-axis making the overlap integral J nonzero. Under the rotating-wave approximation, one can drop the counter-rotating terms and arrive at the following effective single-particle Hamiltonian
due to the momentum transfer along the z-axis making the overlap integral J nonzero. Under the rotating-wave approximation, one can drop the counter-rotating terms and arrive at the following effective single-particle Hamiltonian

Here,

and

is the z- component of angular momentum matrix with angular momentum  , δε = Δ − δω is the two-photon detuning. Furthermore, we have also included an additional harmonic trap V(z), which can be termed as an effective quadratic Zeeman energy
, δε = Δ − δω is the two-photon detuning. Furthermore, we have also included an additional harmonic trap V(z), which can be termed as an effective quadratic Zeeman energy  (a is the lattice spacing) by adjusting the trapping center. Due to
(a is the lattice spacing) by adjusting the trapping center. Due to  , Eq. (4) effectively describes a system with nontrivial spin-orbit coupling, which reduces to a familiar form with equal Rashba and Dresselhaus contributions13,14,15 for N = 2 and N = 3. The major difference is that the internal spin states now are played by atoms in different wells and the total pseudospin can be varied via the lattice number N.
, Eq. (4) effectively describes a system with nontrivial spin-orbit coupling, which reduces to a familiar form with equal Rashba and Dresselhaus contributions13,14,15 for N = 2 and N = 3. The major difference is that the internal spin states now are played by atoms in different wells and the total pseudospin can be varied via the lattice number N.
Before proceeding, we should mention that there are generally Bloch oscillations for atoms in a tilted optical lattice potential45,47,48,49,50. For sufficiently tilted lattice case as discussed above, the energy difference Δ between adjacent sites is much larger than the suppressed inter-site tunneling  . In this regime, the Bloch oscillation becomes a rapid shivering motion with frequency Δ/h and amplitude
. In this regime, the Bloch oscillation becomes a rapid shivering motion with frequency Δ/h and amplitude  . When the two-photon Raman transition is introduced, Δ reduces to a two-photon detuning δε, and a considerable effective tunneling J is induced. In this case, it was shown that the coherent Bloch oscillations of frequency δε/h would appear in the form of a periodic breathing dynamics51 or a periodic center of mass motion52. In the following, we mainly concentrate on the ground-state behaviors for the resonant case with δε = 0.
. When the two-photon Raman transition is introduced, Δ reduces to a two-photon detuning δε, and a considerable effective tunneling J is induced. In this case, it was shown that the coherent Bloch oscillations of frequency δε/h would appear in the form of a periodic breathing dynamics51 or a periodic center of mass motion52. In the following, we mainly concentrate on the ground-state behaviors for the resonant case with δε = 0.
Without loss of generality, in the following we assume that the traverse momentum transfer δk⊥ is along the x-axis, i.e.  with λ = |δk⊥|, and set m = ħ = 1 and energy unit Eλ = λ2/2 throughout the paper.
with λ = |δk⊥|, and set m = ħ = 1 and energy unit Eλ = λ2/2 throughout the paper.
Single particle spectrum
We first discuss the single particle states of this system. In the absence of effective Zeeman fields, Hamiltonian. (4) bears the time-reversal symmetry (TRS) with  , resulting in a symmetrical single-particle energy spectrum E(k) = E(−k). Due to the laser-assisted tunneling J, the atomic states in different wells get mixed, and hence the degeneracy of psuedospin components is lifted with N energy branches. We are interested in the lowest branch, which is responsible for the determining of bosonic ground states.
, resulting in a symmetrical single-particle energy spectrum E(k) = E(−k). Due to the laser-assisted tunneling J, the atomic states in different wells get mixed, and hence the degeneracy of psuedospin components is lifted with N energy branches. We are interested in the lowest branch, which is responsible for the determining of bosonic ground states.
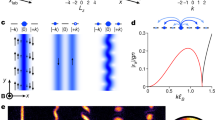
In general, the single-particle ground-state manifold can be classified into two categories: for even N, there may exist a two-fold degeneracy; while for odd N, there is only one state in the ground subspace. As shown in Fig. (2a), we plot the lowest energy spectrum by diagonalizing Hamiltonian. (4) for different N (= 2, 3, 4) with J/Eλ = 0.1. We can see that for odd N (= 3), there is only one minimum state at k = 0. On the other hand, for even N (= 2, 4), double minima at ±kmin can be identified. Here, we have also included a weak harmonic trap. As the quadratic Zeeman term does not break the TRS, it would just modify the ground state energy for small δz without destroying the double degeneracy. On the other hand, a nonzero linear term δε ≠ 0 would break the TRS and lead to asymmetric energy spectra. As a result, such possible degeneracy is lifted, with only one state left in the ground-state manifold.
(a) The lowest single-particle energy branch of N = 2 (blue solid), 3 (red dashed), 4 (green dash-dotted) for J/Eλ = 0.1. The curves have been shifted constantly for explicitness. Arrows label the energy minima. (b) Momentum evolution of the minimal states with the tunneling strength J for N = 2 (blue solid) and N = 4 (green dash-dotted). In both figures (a) and (b) the relative strength of the quadratic Zeeman shift is taken to be δz/Eλ = 0.1.
In Fig. (2b), we plot the momentum evolution of minimal states as a function of J for even N (= 2, 4). One can find that, when J surpasses a critical Jc, kmin would converge to 0, indicating a tunneling induced transition would happen in the single-particle ground state. As we will see below, above different behavior of the single-particle states would have dramatic effects on the many-body ground states when the atomic interactions are included.
Ground state phase diagram
We now turn to investigate the many-body ground states of this system in the presence of atom-atom interactions. Considering a short-ranged case, the interactions for atoms situated in the same well are much stronger than that in different wells. Then, one can neglect the contribution from the latter and write the Hamiltonian for interacting atoms as

where  denotes the atomic density in ith layer and
denotes the atomic density in ith layer and  with g0 the contact interaction strength. Notice that, the interactions here only happen in each pseudospin component, which keeps invariant under the unitary transformation U, and would play an important role in determining the ground-state configurations.
with g0 the contact interaction strength. Notice that, the interactions here only happen in each pseudospin component, which keeps invariant under the unitary transformation U, and would play an important role in determining the ground-state configurations.
In the following we will discuss independently the “even” and “odd” N cases, which exhibit different behavior in the single-particle spectra and the many-body ground states.
Even N
In this case, we find that for giving trapping potential δz, the phase diagrams in g2D − J plane for different N have similar structures, and three different phases may appear: (I) “Stripe” phase, where the wave-function is a superposition of two plane waves with opposite momenta ±km (km ≠ 0) and  (II) “Plane Wave” phase, where only one plane wave component with finite momentum km contributes to the ground state; (III) a “Normal” phase with bosons condensed in the zero-momentum state of k = 0.
(II) “Plane Wave” phase, where only one plane wave component with finite momentum km contributes to the ground state; (III) a “Normal” phase with bosons condensed in the zero-momentum state of k = 0.
To be more specific and without loss of generality, we choose the simplest N = 2 for illustrations. In Fig. (3), we give the ground-state phase diagram in the g2D − J plane for N = 2 by numerically minimizing the energy EG. Generally, due to the interplay between atomic tunneling and atom-atom interactions, above three phases may compete with each other and survive in three distinct regimes (labeled by colors), touching at a tricritical point.
Phase diagram in g2D − J plane for N = 2, consist of three phases: Stripe, Plane Wave and Normal phases (see the context for detail), touching at a tricritical point.
The color bar denotes the magnitude of ground state momentum. The green solid lines label the parameters we used in Fig. (4b).
In the dilute limit (g2D/Eλ ≪ 1), above a critical tunneling strength, i.e. J > Jc1 ≃ 0.5Eλ, the system is in the zero-momentum Normal phase. While for J < Jc2 ≃ 0.41Eλ, a Stripe phase is favored. Between them (Jc1 < J < Jc2), a Plane Wave phase is expected to have lower energy. The regime of such Plane Wave phase gets diminished with increasing of interaction g2D, and finally disappears at a tricritical point around (J/Eλ, g2D/Eλ) ≃ (0.38, 0.11), where three phases merge. Beyond the tricritical point, only Normal to Stripe phase transition survives (See Fig. (4b,d)). These features essentially reflect the competitions between kinetic and interaction energies of these states. In the weak interaction regime, the kinetic energy is dominant, and the system is always in a Normal phase when the single particle spectrum has only one minimum at k = 0. On the double minima side, the kinetic energies of Stripe and Plane Wave phases for the same km are degenerate, and would be further lifted by the atomic interactions.
In Fig. (4), we plot the ground-state momenta km and the interlayer polarization 〈Fz〉 as functions of tunneling J for two typical interaction strength. One can see that, the Plane Wave has homogeneous intralayer density  but finite interlayer polarization |〈Fz〉| > 0, while the Stripe phase has inhomogeneous density ni(r) with 〈Fz〉 = 0. On the other hand, since the atoms in the same layer repulse each other, the system tends to have both equal populations and homogeneous densities in each layer. Hence, close to the Normal phase, the Plane Wave phase with small |〈Fz〉| but homogeneous intralayer density is more favorable. While with decreasing of J, |〈Fz〉| becomes larger and larger, and the system transits into the Stripe phase. Moreover, the Plane Wave phase would be also suppressed by increasing of interactions and turn to a Normal phase continuously. Such two transitions finally meet at a quantum tricritical point.
but finite interlayer polarization |〈Fz〉| > 0, while the Stripe phase has inhomogeneous density ni(r) with 〈Fz〉 = 0. On the other hand, since the atoms in the same layer repulse each other, the system tends to have both equal populations and homogeneous densities in each layer. Hence, close to the Normal phase, the Plane Wave phase with small |〈Fz〉| but homogeneous intralayer density is more favorable. While with decreasing of J, |〈Fz〉| becomes larger and larger, and the system transits into the Stripe phase. Moreover, the Plane Wave phase would be also suppressed by increasing of interactions and turn to a Normal phase continuously. Such two transitions finally meet at a quantum tricritical point.
Several remarks are on hand: first, we have taken δz/Eλ = 0.01 in numerical calculations, which gives no physical effects for N = 2 and would modify the phase boundaries slightly for N > 2. Second, compared to the effective model in ref. 1, here the external states in different layers play the role of spin rather than the internal states. The corresponding effective spin-spin interaction takes the value c2/c0 = (g↑ − g↑↓)/(g↑ + g↑↓) = 1 with g↑↓ = 0, which is much larger than in the previous case, where c2 is very close to the degenerate point c2 = 01,24. This makes the Stripe phase in this system quite robust13. Third, for N > 2, the phase diagrams are qualitatively unchanged around tricritical regime and similar analysis can be applied.
Odd N
When N is odd, the situation changes a lot and the phase diagrams may exhibit different behaviors. To be specifc, in the following we take N = 3 as an example to address this problem. Similar results can be found for N > 3.
In Fig. (5), we give the phase diagram for N = 3. It is interesting to see that even though the single-particle spectrum is only minimized at the k = 0 state, the system can still be Plane Wave or Stripe phases carrying finite momenta in some regimes. In one hand, the zero-momentum Normal phase is predominant for small g2D. In the other hand, the interaction energy would become significant with the increasing of interactions. As shown in Fig. (6e,f), the density of Normal phase  in center layer is relative large. And for sufficient large g2D, an instability to Plane Wave/Stripe phases with more delocalized atomic distribution and finite km (Fig. (6a,b)) would happen, where the increasing of kinetic energies is compensated by the decreasing of interaction energies. Furthermore, similar to the even N case, the Plane Wave phase with a finite 〈Fz〉 ≠ 0 (Fig. (6c,d)) only survives for moderate tunneling strength J, between the Normal and Stripe phases, and ends at a tricritical point.
in center layer is relative large. And for sufficient large g2D, an instability to Plane Wave/Stripe phases with more delocalized atomic distribution and finite km (Fig. (6a,b)) would happen, where the increasing of kinetic energies is compensated by the decreasing of interaction energies. Furthermore, similar to the even N case, the Plane Wave phase with a finite 〈Fz〉 ≠ 0 (Fig. (6c,d)) only survives for moderate tunneling strength J, between the Normal and Stripe phases, and ends at a tricritical point.
Phase diagram in g2D − J plane for N = 3.
The color bar denotes the momentum magnitude of ground states. The green solid lines label the parameters we used in Fig. (6).
It is worthy to stress that, the emerging of Plane Wave/Stripe phases for odd N is mainly driven by atom-atom interactions, in a sharp contrast to the even N case, where the role is mainly played by atomic tunnelings. This may reflect the topological differences of single-particle ground-state manifolds between these two cases.
Discussions and Conclusions
We now discuss some experiment-related issues. First, our results are quite general and independent of specific atoms. Here, we take the 87Rb as an example. The simplest N = 2 case can be achieved by a similar scheme as the bilayer configurations24,25. For N > 2, one can resort to a superlattice potential with more than two nonequivalent sites39 or a linear tilt potential37. For a standing wave with wave-length λs and depth U0 ~ 15Er, where  is the recoil energy, the trapping frequency in each well is about
is the recoil energy, the trapping frequency in each well is about  . If one choose Δ ~ Er, the Raman-assisted tunneling
. If one choose Δ ~ Er, the Raman-assisted tunneling  with the bare tunneling Jz ≪ Δ, can be tuned up to J ~ 2π × 60 Hz by varying V0. Note that, V0 ≪ Δ ≪ ω0 can be satisfied to ensure the validity of tight-binding and the lowest band approximations. To reach the scope of the phase diagram, one need Eλ ~ J. This can be done by arranging the opening angles of two Raman lasers with
with the bare tunneling Jz ≪ Δ, can be tuned up to J ~ 2π × 60 Hz by varying V0. Note that, V0 ≪ Δ ≪ ω0 can be satisfied to ensure the validity of tight-binding and the lowest band approximations. To reach the scope of the phase diagram, one need Eλ ~ J. This can be done by arranging the opening angles of two Raman lasers with  . For a typical harmonic trap with frequency ωz ~ 2π × 10 Hz,
. For a typical harmonic trap with frequency ωz ~ 2π × 10 Hz,  is much smaller than Eλ. In the case of 87Rb, g0 ~ 7.8 × 10−12 Hz cm3, and the corresponding
is much smaller than Eλ. In the case of 87Rb, g0 ~ 7.8 × 10−12 Hz cm3, and the corresponding  with
with  , is limited to a weakly interacting regime.
, is limited to a weakly interacting regime.
Up to now, we have neglected the effects of effective Zeeman fields δε and δq. For not too large δε and/or δq, the phase boundaries would be modified quantitatively17 which are also confirmed in our case, while leaving the main results qualitatively unchanged. To detect these phases in experiments, one may implement the momentum-resolved time-of-flight measurements. The atom population in each well which characterizes 〈Fz〉 and  , can be measured via in-situ absorption imaging.
, can be measured via in-situ absorption imaging.
In conclusions, we have investigated the ground states and the associated phase diagrams of a BEC in a laser-assisted 1D optical lattice potential forming a multilayer system. The unique N-dependence of the single-particle spectra and the corresponding many-body ground-state configurations reflects the subtle competition between the effective SOC induced by laser-assisted interlayer tunneling and atom-atom interactions. Our results would have potential implications in searching new matter states in spin-orbit coupled Bose systems with a large spin. In future studies, one may consider the effects of interlayer long-range interactions, and the extensions to multicomponent BECs and Fermi gases.
Methods
For weakly interacting Bose gases, the quantum fluctuations can be neglected safely. And one can adopt the variational method13,24 to investigate the ground states of the system. In mean-field level, the variational Ansatz of the ground-state wave-function can be constructed as:

where Φ±k e±ikx are the eigenstates of the lowest energy branch with momentum ±k, determined by Eq. (4). a+ and a− are complex amplitudes with normalization condition |a+|2 + |a−|2 = 1. In the dilute limit, one has k = kmin for double minima case and k = 0 for single minimum. While in general, k is dependent on the interactions13. Minimizing the energy  with respect to variational parameters a+, a− and k, one can obtain the ground-state phases as well as the phase diagrams.
with respect to variational parameters a+, a− and k, one can obtain the ground-state phases as well as the phase diagrams.
Additional Information
How to cite this article: Sun, Q. et al. Ground states of a Bose-Einstein Condensate in a one-dimensional laser-assisted optical lattice. Sci. Rep. 6, 37679; doi: 10.1038/srep37679 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Lin, Y.-J., Jiménez-García, K. & Spielman, I. B. Spin-orbit-coupled Bose-Einstein condensates. Nature 471, 83 (2011).
Zhang, J.-Y. et al. Collective Dipole Oscillations of a Spin-Orbit Coupled Bose-Einstein Condensate. Phys. Rev. Lett. 109, 115301(2012).
Wang, P. J. et al. Spin-Orbit Coupled Degenerate Fermi Gases. Phys. Rev. Lett. 109, 095301 (2012).
Cheuk, L. W. et al. Spin-Injection Spectroscopy of a Spin-Orbit Coupled Fermi Gas. M. Phys. Rev. Lett. 109, 095302 (2012).
Qu, C., Hamner, C., Gong, M., Zhang, C. W. & Engels, P. Observation of Zitterbewegung in a spin-orbit-coupled Bose-Einstein condensate. Phys. Rev. A 88, 021604(R) (2013).
Huang, L. H. et al. Experimental realization of two-dimensional synthetic spin-orbit coupling in ultracold Fermi gases. Nat. Phys. 12, 540 (2016).
Wu, Z. et al. Realization of Two-Dimensional Spin-orbit Coupling for Bose-Einstein Condensates. Science354, 83 (2015).
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms Rev. Mod. Phys. 83, 1523 (2011).
Goldman, N., Juzeliūnas, G., Öhberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014).
Zhou, X. F., Li, Y., Cai, Z. & Wu, C. J. Unconventional States of Bosons with the Synthetic Spin-orbit Coupling. J. Phys. B: At. Mol. Opt. Phys. 46, 134001 (2013).
Zhai, H. Spin-Orbit Coupled Quantum Gases. Int. J. Mod. Phys. B 26, 1230001 (2012); Degenerate Quantum Gases with Spin-Orbit Coupling. Rep. Prog. Phys.78, 026001 (2015).
Wang, C. J., Gao, C., Jian, C.-M. & Zhai, H. Spin-Orbit Coupled Spinor Bose-Einstein Condensates. Phys. Rev. Lett. 105, 160403 (2010).
Li, Y., Pitaevskii, L. P. & Stringari, S. Quantum Tricriticality and Phase Transitions in Spin-Orbit Coupled Bose-Einstein Condensates. Phys. Rev. Lett. 108, 225301 (2012).
Martone, Giovanni I., Li, Y. & Stringari, S. Approach for making visible and stable stripes in a spin-orbit-coupled Bose-Einstein superfluid. Phys. Rev. A 90, 041604(R) (2014).
Ho T.-L. & Zhang, S. Z. Bose-Einstein Condensates with Spin-Orbit Interaction. Phys. Rev. Lett. 107, 150403 (2011).
Xu, Z. F., Lü, R. & You, L. Emergent patterns in a spin-orbit-coupled spin-2 Bose-Einstein condensate. Phys. Rev. A 83, 053602 (2011).
Wen, L., Sun, Q., Wang, H. Q., Ji, A. C. & Liu, W. M. Ground state of spin-1 Bose-Einstein condensates with spin-orbit coupling in a Zeeman field. Phys. Rev. A 86, 043602 (2012).
Zhang, Y. P., Mao, L. & Zhang, C. W. Mean-Field Dynamics of Spin-Orbit Coupled Bose-Einstein Condensates. Phys. Rev. Lett. 108, 035302 (2012).
Sinha, S., Nath, R. & Santos, L. Trapped Two-Dimensional Condensates with Synthetic Spin-Orbit Coupling. Phys. Rev. Lett. 107, 270401 (2011).
Hu, H., Ramachandhran, B., Pu, H. & Liu, X.-J. Spin-Orbit Coupled Weakly Interacting Bose-Einstein Condensates in Harmonic Traps. Phys. Rev. Lett. 108, 010402 (2012).
Wilson, R. M., Anderson, B. M. & Clark, C. W. Meron Ground State of Rashba Spin-Orbit-Coupled Dipolar Bosons. Phys. Rev. Lett. 111, 185303 (2013).
Kawakami, T., Mizushima, T., Nitta, M. & Machida, K. Stable Skyrmions in SU(2) Gauged Bose-Einstein Condensates. Phys. Rev. Lett. 109, 015301 (2012).
Chen, X., Rabinovic, M., Anderson, B. M. & Santos, L. Ring model for trapped condensates with synthetic spin-orbit coupling. Phys. Rev. A 90, 043632 (2014).
Sun, Q., Wen, L., Liu, W.-M., Juzeliūnas, G. & Ji, A.-C. Tunneling-assisted spin-orbit coupling in bilayer Bose-Einstein condensates. Phys. Rev. A 91, 033619 (2015).
Su, S.-W. et al. Rashba-type Spin-orbit Coupling in Bilayer Bose-Einstein Condensates. Phys. Rev. A 93, 053630 (2016).
Ruseckas, J., Juzeliūnas, G., Öhberg, P. & Fleischhauer, M. Non-Abelian Gauge Potentials for Ultracold Atoms with Degenerate Dark States. Phys. Rev. Lett. 95, 010404 (2005).
Stanescu, T. D. & Galitski, V. Spin relaxation in a generic two-dimensional spin-orbit coupled system. Phys. Rev. B 75, 125307 (2007).
Jacob, A., Öhberg, P., Juzeliūnas, G. & Santos, L. Cold atom dynamics in non-Abelian gauge fields. Appl. Phys. B 89, 439 (2007).
Juzeliūnas, G., Ruseckas, J., Lindberg, M., Santos, L. & Öhberg, P. Quasirelativistic behavior of cold atoms in light fields. Phys. Rev. A 77, 011802(R) (2008).
Juzeliūnas, G., Ruseckas, J. & Dalibard, J. Generalized Rashba-Dresselhaus spin-orbit coupling for cold atoms. Phys. Rev. A 81, 053403 (2010).
Campbell, D. L., Juzeliūnas, G. & Spielman, I. B. Realistic Rashba and Dresselhaus spin-orbit coupling for neutral atoms. Phys. Rev. A 84, 025602 (2011).
Xu, Z. F. & You, L. Dynamical generation of arbitrary spin-orbit couplings for neutral atoms. Phys. Rev. A 85, 043605 (2012).
Xu, Z. F., You, L. & Ueda, M. Atomic spin-orbit coupling synthesized with magnetic-field-gradient pulses. Phys. Rev. A 87, 063634 (2013).
Anderson, B. M., Juzeliūnas, G., Galitski, V. M. & Spielman, I. B. Synthetic 3D Spin-Orbit Coupling. Phys. Rev. Lett. 108, 235301 (2012).
Anderson, B. M., Spielman, I. B. & Juzeliūnas, G. Magnetically Generated Spin-Orbit Coupling for Ultracold Atoms. Phys. Rev. Lett. 111, 125301 (2013).
Liu, X.-J., Law, K. T. & Ng, T. K. Realization of 2D Spin-Orbit Interaction and Exotic Topological Orders in Cold Atoms. Phys. Rev. Lett. 112, 086401 (2014).
Jaksch D. & Zoller, P., Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. New J. Phys. 5, 56 (2003).
Mueller, E. J. Artificial electromagnetism for neutral atoms: Escher staircase and Laughlin liquids. Phys. Rev. A 70, 041603 (2004).
Gerbier, F. & Dalibard, J. Gauge fields for ultracold atoms in optical superlattices. New J. Phys. 12, 033007 (2010).
Aidelsburger, M. et al. Experimental Realization of Strong Effective Magnetic Fields in an Optical Lattice. Phys. Rev. Lett. 107, 255301 (2011).
Aidelsburger, M. et al. Realization of the Hofstadter Hamiltonian with Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 111, 185301 (2013).
Miyake, H., Siviloglou, G. A., Kennedy, C. J., Burton, W. C. & Ketterle, W. Realizing the Harper Hamiltonian with Laser-Assisted Tunneling in Optical Lattices. Phys. Rev. Lett. 111, 185302 (2013).
Atala, M. et al. Observation of chiral currents with ultracold atoms in bosonic ladders. Nat. Phys. 10, 588 (2014).
Li, J. et al. Spin-Orbit Coupling and Spin Textures in Optical Superlattices. Phys. Rev. Lett. 117, 185301 (2016).
Larson, J., Martikainen, J., Collin, A. & Sjöqvist, E. Spin-orbit-coupled Bose-Einstein condensate in a tilted optical lattice. Phys. Rev. A 82, 043620 (2010).
Stamper-Kurn, Dan M. & Ueda, M. Spinor Bose gases: Symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 85, 1191 (2013).
Dahan, M. Ben, Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch Oscillations of Atoms in an Optical Potential. Phys. Rev. Lett. 76, 4508 (1996).
Morsch, O., Müller, J. H., Cristiani, M., Ciampini, D. & Arimondo, E. Bloch Oscillations and Mean-Field Effects of Bose-Einstein Condensates in 1D Optical Lattices. Phys. Rev. Lett. 87, 140402 (2001).
Fattori, M. et al. Atom Interferometry with a Weakly Interacting Bose-Einstein Condensate. Phys. Rev. Lett. 100, 080405 (2008).
Gustavsson, M. et al. Control of Interaction-Induced Dephasing of Bloch Oscillations. Phys. Rev. Lett. 100, 080404 (2008).
Alberti, A., Ivanov, V. V., Tino, G. M. & Ferrari, G. Engineering the quantum transport of atomic wavefunctions over macroscopic distances. Nat. Phys. 5, 547 (2009).
Haller, E. et al. Inducing Transport in a Dissipation-Free Lattice with Super Bloch Oscillations. Phys. Rev. Lett. 104, 200403 (2010).
Acknowledgements
This work is supported by NSFC (Grants No. 11404225, No. 11474205, No. 21503138, No. 11504037 and No. 11434015), Foundation of Beijing/Chongqing Education Committees (Grants No. KM201510028005, KM201310028004, and No. KJ1500311), and CSTC under Grant No. cstc2015jcyjA50024. G. J. acknowledges a support by Lithuanian Research Council (Grant No. MIP- 086/2015).
Author information
Authors and Affiliations
Contributions
Qing Sun performed the theoretical as well as the numerical calculations. Qing Sun, Jie Hu, Lin Wen, W.-M. Liu, G. Juzeliūnas and An-Chun Ji wrote and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Sun, Q., Hu, J., Wen, L. et al. Ground states of a Bose-Einstein Condensate in a one-dimensional laser-assisted optical lattice. Sci Rep 6, 37679 (2016). https://doi.org/10.1038/srep37679
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37679
This article is cited by
-
Absence of Landau damping in driven three-component Bose–Einstein condensate in optical lattices
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.








 (e,f) as functions of tunneling J/Eλ for given interactions g2D/Eλ = 0.3 (left panel) and g2D/Eλ = 0.4 (right panel). Here, N = 3 and δz/Eλ = 0.01.
(e,f) as functions of tunneling J/Eλ for given interactions g2D/Eλ = 0.3 (left panel) and g2D/Eλ = 0.4 (right panel). Here, N = 3 and δz/Eλ = 0.01.