Abstract
The electronic structure and optical absorption spectrum of organometal halide perovskite compound CH3NH3BiI3 as a substituting candidate of well-concerned CH3NH3PbI3 not only for environmental friendly consideration are studied using the first principles calculations. It is revealed that a Bi replacement of Pb in CH3NH3PbI3 does not change seriously the band edge structure but the bandgap becomes narrow. Consequently, CH3NH3BiI3 exhibits not only stronger visible light absorption than CH3NH3PbI3 does but more strong absorption in the infrared region, which is however absent in CH3NH3PbI3. It is suggested that CH3NH3BiI3 may be one of even more promising alternatives to CH3NH3PbI3 for spectrum-broad and highly-efficient solar cells.
Similar content being viewed by others
Introduction
Photovoltaic (PV) effect is an ideal photoelectric energy conversion process1,2 and has been one of the major mechanisms for green energy utilization in past decades, benefiting to human life substantially. The photoelectric conversion efficiency and cost-competitive manufacturing represent two major issues for PV researches and industry. At present, the photoelectric conversion efficiency of solar cells based on semiconducting materials such as Si and GaAs et el is between 12~25%3, driving sustained search for additional PV materials which are more cost-competitive and more easily processed without much damage to environment. The emergency of organometal halide perovskite compound CH3NH3PbI3 as the absorbing layer in recent years seems to be a milestone-like breakthrough for solar cell materials researches4,5,6. Successively broken records in the photoelectric conversion efficiency as reported on CH3NH3PbI3 have been made. So far recorded efficiency has reached up to 20.2% from the original 3.8%. Moreover, the production cost of such perovskite-type compounds for solar cells is low, also stimulating development of a series of other organometal halide perovskites derivatives of CH3NH3PbI37,8,9 These events quickly have driven vigorous researches over the world.
Great amount of research in the past few years has comprehended several major issues. First, it is known that the diffusion lengths of electrons and holes in CH3NH3PbI3 and its derivatives are quite big10, thus establishing these compounds as high efficiency solar cell materials. For examples, Stranks et al.11 measured the electron and hole diffusion lengths using the photoluminescence quenching method, and found that the photon-generated carriers in CH3NH3PbI3 has ~100 nm in diffusion length. This length can be further enhanced for photon-generated carriers in CH3NH3PbI3-xClx, which is more than 1.0 μm, suggesting that the halogen family substitution or doping represents an effective and common strategy to improve the photoelectric performances. Second, the electronic structure of this compound family has been investigated. By using the light absorption test method, Grätzel et al. determined the binding energy to be ~30 meV for photon-generated carriers in CH3NH3PbI312, while the value determined by Sun et al. is ~19 meV13. Such a small binding energy allows the spontaneous separation of the carriers into free electrons and holes at room temperature. Third, the electrical transport behaviors of CH3NH3PbI3 were found to be sensitive to processing conditions, and the carriers can be dominated by electrons or holes, as predicted by the first principles calculations. Fourth, the defect states in CH3NH3PbI3 were identified to impose substantial influence on the materials performances. It was reported that the defect formation energy for shallow defect states can be relatively small, while those deep defect states can have very large defect formation energy. This big difference explains why CH3NH3PbI3 has a big electron-hole scattering length and high open circuit voltage14.
Here, element substitution of CH3NH3PbI3 has been highly concerned since this strategy allows additional opportunities via electronic structure modulation and carrier density control to improve practical performances of these compounds for solar cell applications. Along this line, halogen element replacement and partial substitution in CH3NH3PbI3, as described above, have been repeatedly tried. In fact, it was reported that a Cl substitution of I in CH3NH3PbI3 allows the formation of CH3NH3PbI3-xClx7,15, whose bandgap remains similar to that of CH3NH3PbI3 but the positions of conduction band and valence band are modulated, leading to great promotion of diffusion and transport of carriers and thus benefiting to conversion efficiency enhancement. By using light luminescence quenching experiment, Stranks et al. reported a diffusion length more than 1.0 μm for photon-generated carriers in CH3NH3PbI3-xClx10. In parallel to that, Xiao et al. replaced a replacement of I by Br to synthesize the CH3NH3PbBr38. It was found that the high conduction band energy level of CH3NH3PbBr3 can effectively enhance the open circuit voltage (Voc) of solar cells16, but the big bandgap of CH3NH3PbBr3 makes visible light absorption window narrow. At the same time, the large binding energy of photon-generated carriers of CH3NH3PbBr3 makes it difficult to spontaneously separate the carriers into free electrons and holes15.
In addition to the halogen substitution strategy, lattice reconstruction was believed to be effective too in improving the optical absorption properties of CH3NH3PbI3. Feng et al. successfully constructed the orthorhombic and tetragonal phases of CH3NH3PbI3, and calculated the optical absorptions of the two phases using the Heyd-Scuseria-Ernzerhof (HSE) screened hybrid functional (HSE06)8. Subsequently, the optical absorption spectra of the two phases were calculated using the quasi-particle GW correction method and multi-body interaction method17. Experimentally, substantial efforts have been made to probe the electronic structures and optical properties of CH3NH3PbX3 (X = I, Br, Cl)8,10.
Different from the above two approaches, the cationic Pb occupation in CH3NH3PbX3 (X = I, Cl, Br) has been thought to be irreplaceable, while the underlying reasons for this irreproducibility seems entangled to us. Either theoretical or experimental trial on replacement of Pb is still lacking. It is suggested that the upper valence band dispersion of CH3NH3PbI3 consists mainly of strong anti-bonding coupling of Pb-s and I-p orbitals. The strong s-p anti-bonding coupling makes the effective mass of holes close to that of electrons, enabling the quite big diffusion length for electron-hole pairs12, which is definitely unusual for solar cell applications. Nevertheless, Pb atom is a heavy metal which pollutes the environment and utilization of Pb is being strictly regulated world widely. It is immediately noted that the Bi-s orbital shows quite similar feature as that of the Pb-s orbital, making a replacement of Pb by Bi attractive for exploration. In such sense, CH3NH3BiI3 is likely to be a good candidate for solar cell devices, noting that Bi is non-toxic, abundant in earth, and has similar atomic properties as Pb.
In this work, our main motivation is to investigate the electronic structure and optical absorption of CH3NH3BiI3 as a generic substitute of CH3NH3PbI3 in terms of solar cell absorption properties. This motivation stems from two aspects. One is that CH3NH3BiI3 may exhibit broad optical absorption spectrum extending to infrared region. The other is that it is environment-friendly and cost-competitive. We employ the first-principles calculation based on the density functional theory (DFT) to study the band structure and optical absorption spectrum. The details for first-principles calculations are described in Sec. II, and the calculated results are presented and discussed in Sec. III. A brief conclusion is given in Sec. IV.
Models and Computation Details
All calculations are performed using the Vienna ab initio simulation package (VASP5.2) code based on the density functional theory (DFT)18,19. The exchange and correlation potential are modeled using the generalized gradient approximation (GGA) Perdew-Becke-Erzenhof (PBE) function20. In standard procedure, the interaction of valence electrons with ionic core is described using the projector augmented wave (PAW) method21, and the wave function of the valence electron is unfolded by plane wave basis using a cutoff energy of 400 eV14.
It is noted that CH3NH3BiI3 is yet a proposed compound and so far no data on its synthesis and lattice structure are available. It is noted that for a stable perovskite ABX3, the ion radius ratio ( ) is required to be close to 1 and thus the size of A atom is much larger than that of atom B. The large-size organic ion CH3NH3+ can effectively stabilize this perovskite structure but does not make considerable contribution to the electronic structure of CH3NH3PbI3 around the band edge. For CH3NH3BiI3, the large-size organic ion CH3NH3+ which can effectively stabilize this perovskite structures does not change. In this sense, CH3NH3BiI3 is the same as CH3NH3PbI3 and should have very stable crystal structure in ambient device processing conditions. So, our calculation then starts from the structural data on reference compound CH3NH3PbI3. CH3NH3PbI3 has the orthorhombic phase and tetragonal phase, while the structure data package was successfully constructed by Feng et al.8. The structures of the two phases are shown in Fig. 1 (for simplicity, herein we denote the orthorhombic and tetragonal CH3NH3XI3 as O-CH3NH3XI3 and T-CH3NH3XI3 respectively). Along this line, we start from experimentally given data on CH3NH3PbI3 and then Bi substitution of Pb is performed, followed by sufficient structural relaxation and optimization.
) is required to be close to 1 and thus the size of A atom is much larger than that of atom B. The large-size organic ion CH3NH3+ can effectively stabilize this perovskite structure but does not make considerable contribution to the electronic structure of CH3NH3PbI3 around the band edge. For CH3NH3BiI3, the large-size organic ion CH3NH3+ which can effectively stabilize this perovskite structures does not change. In this sense, CH3NH3BiI3 is the same as CH3NH3PbI3 and should have very stable crystal structure in ambient device processing conditions. So, our calculation then starts from the structural data on reference compound CH3NH3PbI3. CH3NH3PbI3 has the orthorhombic phase and tetragonal phase, while the structure data package was successfully constructed by Feng et al.8. The structures of the two phases are shown in Fig. 1 (for simplicity, herein we denote the orthorhombic and tetragonal CH3NH3XI3 as O-CH3NH3XI3 and T-CH3NH3XI3 respectively). Along this line, we start from experimentally given data on CH3NH3PbI3 and then Bi substitution of Pb is performed, followed by sufficient structural relaxation and optimization.
The two configurations of crystal cell both contain 48 atoms. For orthorhombic and tetragonal structures, the k-point grids are set to 5 × 5 × 5 and 7 × 7 × 5 for the Brillouin zones respectively using the Monkhorst-Pack scheme22. For the optimization, the structures are fully relaxed until the Hellmann-Feynman force acting on each atom is reduced down to 10 meV/Å, and the energy convergence threshold is set as 1.0 × 10−6 eV/atom. The normal generalized gradient approximation (GGA) is employed although CH3NH3PbI3 was reported to have the spin-orbital coupling (SOC) effect because of the strong relativistic effect of Pb23. However, it is known that the GGA method usually underestimates the band gap, which can offset exactly the ignored SOC effect with each other in occurrence24. This implies that the GGA method can give accurate bandgap of CH3NH3XI3, and thus the SOC will not be considered in our calculations.
Results
Structure optimization
In our calculations, we always take CH3NH3PbI3 as the reference for CH3NH3BiI3. The optimized structures of O-CH3NH3PbI3 and T-CH3NH3PbI3 respectively are obtained and the lattice constants are listed in Table 1, where measured and earlier predicted values on CH3NH3PbI3 are inserted too for comparison. It is seen that our calculated data are roughly consistent with those measured and earlier predicted values, indicating the reliability of the present computational scheme25,26. To the conventional stage, such differences are reasonably acceptable due to the relatively loose organic-inorganic hybrid structure. One sees that the Bi replacement of Pb does not induce remarkable variation of the lattice constants. The O-CH3NH3BiI3 has slightly tensioned a-axis and compressed b-axis with respect to the O-CH3NH3PbI3. For the t-CH3NH3BiI3, the a-axis is slightly tensioned but the c-axis is a little compressed. Considering the different definitions of lattice major axes for the two phases, the consequence of Bi replacement of Pb induces negligible variations of the lattice constants.
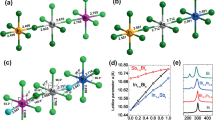
Nevertheless, no deterministic dependence of the three lattice constants on cation species at X site (Pb or Bi) can be evaluated from the data in Table 1. Alternatively, we consult to the six X-I bond lengths of the XI6 octahedra in order to see the differences between the two compounds and bond lengths of the XI6 octahedra are listed in Table 2. It is interested to notice that for O-CH3NH3BiI3 and T-CH3NH3BiI3, all the six Bi-I bonds are shorter than the corresponding Pb-I bonds of O-CH3NH3PbI3 and T-CH3NH3PbI3. In addition, the differences in XI6 octahedron distortion between the two compounds are distinct either. In order to see more clearly, we project the planar projections of the optimized structures (phases) and the results are presented in Fig. 2. First, the (010) plane projections of O-CH3NH3PbI3 and O-CH3NH3BiI3, presented in Fig. 2(a) and (b), respectively, show that the PbI6 octahedra rotate along the b-axis with serious distortion. The four octahedron centers within the projection plane constitute a diamond configuration. Very differently, O-CH3NH3BiI3 structure exhibits nearly no BiI6 octahedron distortion, and the four octahedron centers within the projection plane forms a square shape. The orientations of organic ion groups CH3NH3+ in the two compounds are different either.
The (001) plane projected configurations of T-CH3NH3PbI3 and T-CH3NH3BiI3 are plotted in Fig. 2(c) and (d) respectively. Again, the XI6 octahedra for both compounds have remarkable distortion which is more serious for T-CH3NH3PbI3. The significant difference is that the twists of the upper and lower PbI6 octahedra are not synchronous, but the BiI6 octahedra exhibit the synchronous twisting which leads to the coincidence of the upper and lower octahedron. At the same time, these octahedron distortion results in very different configurations of CH3NH3+ groups in the two structures, which certainly make the electronic structure quite different, to be shown below. Here, what should be mentioned here is that a more seriously distorted lattice usually favors stronger carrier localization and thus bigger bandgap. The charge transport in CH3NH3BiI3 is much easier due to the much weaker localization for charges in CH3NH3BiI3 than in CH3NH3PbI3. CH3NH3BiI3 would have better photoelectric properties than CH3NH3PbI3, which fits to our motivation on investigating CH3NH3BiI3 as a promising candidate for solar cell applications.
Electronic structure
Given the optimized lattice structure for CH3NH3BiI3, one is allowed to evaluate the band structure. First, the calculated band structures for the O-phase and T-phase are plotted in Fig. 3, where the red dashed lines represent the Fermi levels in each case. The presented results can be discussed from several aspects.
First, both compounds in the o-phase are direct band gap semiconductors as seen at the G points of the Brillouin zone. The bandgap of O-CH3NH3PbI3 is ~1.68 eV, similar to results obtained by previous theoretical predictions8, while measured gap values are smaller due to the inevitable defect states. The Fermi level locates at the valence band maximum (VBM), indicating the nature of p-type semiconductor, while experimental measurements often reported the n-type semiconducting behaviors, most likely due to the defect states in samples14. So, lead halide perovskite CH3NH3PbI3 can be tuned from good p-type to good n-type by controlling the growth conditions. The bandgap of O-CH3NH3BiI3 is ~1.05 eV. Since Bi atom has one more electron outermost than Pb atom, the Fermi level shifts into the conduction band minimum (CBM), which makes CH3NH3BiI3 metallized. It is noted that such a crossing of the Fermi level with the CBM does not imply real metallization, due to the fact that there still have the energy excitation greater than the band gap energy27,28,29. Therefore, O-CH3NH3BiI3 remains to be an n-type degenerate semiconductor. Same to CH3NH3PbI3, CH3NH3BiI3 might be tuned from n-type to p-type by controlling the growth conditions because the thermodynamic stable range for equilibrium growth of the material cover a long shape of chemical potential region14. Second, as shown in Fig. 3(c) and (d) respectively, the T-CH3NH3PbI3 is also a p-type direct bandgap semiconductor with gap of ~1.58 eV, similar to earlier predictions8. The band structure details are similar to those of the o-phase. For T-CH3NH3BiI3, a direct band gap of ~1.14 eV is identified, which is 0.09 eV smaller than that of the o-phase. The Fermi level is again above the CBM, exhibiting the n-type degenerate semiconducting behavior.
In the overall sense, both O-CH3NH3BiI3 and T-CH3NH3BiI3 have much less lattice distortion and smaller bandgap than O-CH3NH3PbI3 and T-CH3NH3PbI3 respectively. When the band gap becomes smaller, the charge recombination chances also increases. However, a smaller band gap either allows enhanced optical excitation. In the overall sense, the number of photo-generated electron-hole pairs still increase, benefiting to the photo-voltaic performance. A preliminary prediction, consistent with the analysis on lattice structure, is that CH3NH3BiI3 should have better optical absorption performance than CH3NH3PbI3. The n-type carriers in CH3NH3BiI3 also provide alternative choice for practical applications.
To further look into the details of electronic structure, we calculate the total density of states (TDOS) and projected density of states (PDOS) of CH3NH3PbI3 and CH3NH3BiI3 in the two phases respectively and the results are plotted in Fig. 4. The red vertical dashed line marks the Fermi level. For the o-phase, the two compounds exhibit similar TDOS profiles, as shown in Fig. 4(a). The main difference appears in the deep valence band ranging from −5.0 eV ~ −9.0 eV. It is generic to expect the similar photoelectric properties between the two compounds since electronic structure features around the conduction and valence bands are roughly the same. Figure 4(b) plots the PDOS profiles of the two compounds in the o-phase. Because the most important role of the big-size organic ion group CH3NH3+ is to stabilize the organic metal structure and denote an electron, one is allowed to argue nearly no contribution from the CH3NH3+ to the valence and conduction bands.
We first discuss the data on O-CH3NH3PbI3, as shown in Fig. 4(a), as a reference for subsequent discussion on O-CH3NH3PbI3. The O-CH3NH3PbI3 has a ~1.68 eV bandgap between empty Pb-p orbital and fully-occupied I-p orbital. The CBM mainly consists of Pb-p orbital which has nearly no coupling with I orbital, indicating the Pb-I ionic bond nature. The upper valence band mainly consists of fully-occupied Pb-s orbital with strong antibonding coupling with I-p orbital. Such band edge features were reported earlier14,30,31. The strong s-p antibonding coupling leads to very small effective mass of holes, comparable with electron effective mass. This is the reason why CH3NH3PbI3 is an ideal candidate for p-i-n configuration thin-film solar cells14.
For O-CH3NH3BiI3, the bandgap physics shows some similarities and differences. First, the gap appears between partially-occupied Bi-p orbital and fully-occupied I-p orbital, while the CBM mainly consists of Bi-p orbital. The Bi-p orbital has either nearly no coupling with I orbital, indicating the nature of Bi-I ionic bonding. The fully-occupied Bi-s orbital is coupled with the I-p orbital in strong-antibonding form, allowing small effective mass of holes which is comparable with that of electrons in O-CH3NH3PbI3. In this sense, O-CH3NH3BiI3 can be an ideal absorbing layer for thin-film solar cells alternative to O-CH3NH3PbI3. Furthermore, O-CH3NH3BiI3 has smaller bandgap and thus enables better optical absorption performance than O-CH3NH3PbI3. Finally, one comes to the TDOS and PDOS of T-CH3NH3BiI3 while those of T-CH3NH3PbI3 are inserted for comparison too, as shown in Fig. 5. While delicate difference in details of the TDOS and PDOS with the results of o-phases, highly similarity of major features between two T-phases is seen immediately.
We further consult to the calculated charge density and charge density difference for the two compounds, and the results for the O-phases are plotted in Fig. 6 illustrating the charge density on the equatorial plane of XI6 octahedron. First, clear octahedral distortion in O-CH3NH3PbI3 can be identified, consistent with earlier prediction25. The Pb-I ionic bonding feature is also significant. The octahedral distortion and ionic bonding in O-CH3NH3BiI3 are however relatively weaker. Second, the charge density in the region between Pb core and I core is less than that between Bi core and I core, and the reason is also obvious since Bi atom has one more outermost valence electron than Pb atom and the excess electron will mainly distribute on the I-p and Bi-p orbitals along the Bi-I direction. This feature enables the stronger covalent bonding character between Bi-I pair than that between Pb-I pair. Nevertheless, it should be mentioned that the Bi-I and Pb-I pair in these two materials are ionic bond dominant. A stronger covalent character between Bi-I pair only show more extensive charge spatial distribution rather than more electronic shackles. In this sense, the charges in CH3NH3BiI3 would show better transport performance. Third, a look at the charge density difference shown in Fig. 6(c) and (d) allows several more features. One sees that Pb loses electrons less along the Pb-I direction while the areas that Pb loses electrons most mainly appear in the four I-Pb-I sector regions divided by two neighboring I atoms and central Pb atom. I ion gets electrons most along the I-Pb direction. One also sees three strong gaining electronic regions around I ion on equatorial plane due to the torsion of PbI6 octahedron. Similarly, Bi loses electrons less along the Bi-I direction, and the areas that Bi loses electrons most mainly locate in the four I-Bi-I sector regions divided by two neighboring I atoms and central Bi atom. Although I atom gets electrons most along the I-Bi direction, here one sees four strong gaining electronic regions around I atom on equatorial plane, due to the fact that BiI6 octahedron has much less torsion.
Calculated electron density O-CH3NH3PbI3 (a), O-CH3NH3BiI3 (b); the electron density difference for O-CH3NH3PbI3 (c), O-CH3NH3BiI3 (d). Contours show the values in a slice of the (010) plane. The units are electrons Å−3. In panels (a,b), Color from blue to red represent electron density changes from low to high. In panels (c,d), Color red (blue) represent the electron density increased (decreased).
Optical properties
The major consequence to be expected from the above presented results is the much better optical absorption performance of CH3NH3BiI3 than CH3NH3PbI3. We use the linear response method to calculate the macroscopic optical response function described by complex dielectric function. The complex dielectric function ε(ω) = ε1(ω) + iε2(ω) contains real part ε1(ω) and imaginary part ε2(ω), where ε2(ω) can be obtained by calculating the momentum matrix elements between the occupied and unoccupied wave functions. Consequently, ε1(ω) is calculated from ε2(ω) using the Kramer–Kronig relationship32. It is noted that the optical absorption spectrum is characterized by the optical constant which is related with the dielectric function  , where α is the absorption coefficient, C the speed of light, ω the circular frequency.
, where α is the absorption coefficient, C the speed of light, ω the circular frequency.
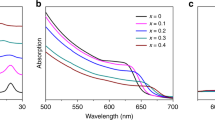
The calculated optical absorption spectrum for the O-phase and T-phase of CH3NH3PbI3 and CH3NH3BiI3 are plotted in Fig. 7(a) and (b), noting that visible light energy appears in 1.64 eV~3.19 eV, as marked out in the inset using green oblique lines. No matter what phase it is, one sees two major consequences. First, for CH3NH3BiI3, the long-wavelength boundary is substantially extended toward the infrared region, in which the optical absorption is significant as seen more clearly in the two insets. Second, CH3NH3BiI3 has even better absorption performance in the visible region than CH3NH3PbI3. The two characters of CH3NH3BiI3 suggest that using Bi to replace Pb in CH3NH3PbI3 would be a highly favored strategy, while CH3NH3BiI3 is expected to be a promising candidate for highly efficient absorption media for solar cell devices.
Discussions
In this paper, we have carefully calculated the electronic structures and optical properties of organometal halide perovskites materials CH3NH3XI3(X = Pb, Bi) using the first principle calculation. Our results indicate that CH3NH3PbI3 is a direct band gap semiconductor. The strong antibonding coupling state of Pb-s orbital and I-p orbital compose of the top of the valence band distribution. For CH3NH3BiI3, the band gap is narrow with respect to CH3NH3PbI3. The strong antibonding coupling states of Bi-s orbital and I-p orbital compose of the top of the valence band distribution of CH3NH3BiI3, and the band edge structure is similar to that of CH3NH3PbI3. The optical data show that CH3NH3BiI3 has stronger visible light absorption than CH3NH3PbI3 and infrared absorption is predicted. These similar electronic structures and better spectral absorption indicate that CH3NH3BiI3 system is likely to be a good candidate for solar battery.
Additional Information
How to cite this article: Zhu, H. X. and Liu, J.-M. Electronic structure of organometal halide perovskite CH3NH3BiI3 and optical absorption extending to infrared region. Sci. Rep. 6, 37425; doi: 10.1038/srep37425 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Kazim, S., Nazeeruddin, M. K., Grätzel, M. & Ahmad S. Perovskite as light harvester: a game changer in photovoltaics. Angew. Chem. Int. Ed. 53, 2812–2824 (2014).
Loi, M. A. & Hummelen, J. C. Hybrid solar cells: perovskites under the sun. Nat. Mater. 12, 1087–1089 (2013).
Kojima, A., Teshima, K., Shirai, Y. & Miyasaka, T. Organometalhalide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009).
Kim, H. S. et al. Lead Iodide Perovskite sensitized all-oslid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2, 591 (2012).
Burschka, J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–320 (2013).
Liu, M. Z., Johnston, M. B. & Snaith, H. J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 501, 395–398 (2013).
Wehrenfennig, C., Liu, M., Snaith, H. J., Johnston, M. B. & Herz, L. M. Homogeneous emission line broadening in the organo lead halide perovskite CH3NH3PbI3−xClx . J. Phys. Chem. Lett. 5, 1300–1306 (2014).
Feng, J. & Xiao, B. Crystal structures, optical properties, and effective mass tensors of CH3NH3PbX3 (X = I and Br) phases predicted from HSE06. J. Phys. Chem. Lett. 5, 1278–1282 (2014).
Mosconi, E., Ama, t A., Nazeeruddin, M. K., Gratzel, M. & Angelis, F. D. First principles modeling of mixed halide organometal perovskites for photovoltaic applications. J. Phys. Chem. C. 117, 13902–13913 (2013).
Xing, G. et al. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3 . Science 342, 344–347 (2013).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science, 342, 341–344 (2013).
Grätzel, M. The light and shade of perovskite solar cells. Nature Materials 13, 838–842 (2014).
Sun, S. et al. The origin of high efficiency in low-temperature solution-processable bilayer organometal halide hybrid solar cells. Energ. Environ. Sci. 7, 399–407 (2014).
Yin, W. J., Shi, T. & Yan, Y. Unusual defect physics in CH3NH3PbI3 perovskite solar cell absorber. Appl. Phys. Lett. 104, 063903 (2014).
Krüger, J., Plass, R., Grätzel, M., Cameron, P. & Peter, L. Charge transport and back reaction in solid-state dye-sensitized solar cells: a study using intensity-modulated photovoltage and photocurrent spectroscopy. J. Phys. Chem. B 107, 7536–7539 (2003).
Cai, B., Xing, Y., Yang, Z. & Zhang, W. & Qiu, High performance hybrid solar cells sensitized by organolead halide perovskites. J. Energy Environ. Sci. 6, 1480–1485 (2013).
Zhu, X., Su, H., Marcus, R. A. & Michel-Beyerle, M. E. Computed and experimental absorption spectra of the perovskite CH3NH3PbI3 . J. Phys. Chem. Lett. 5, 3061–3065 (2014).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, R558–R561 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Devi, L. G., Murthy, B. N. & Kumar, S. G. Photocatalytic activity of V5+, Mo6+ and Th4+ doped polycrystalline TiO2 for the degradation of chlorpyrifos under UV/solar light. J. Mol. Catal. A: Chem. 308, 174–181 (2009).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Even, L. P. J., Jancu, J.-M. & Katan, C. Importance of spin-orbit coupling in hybrid organic/inorganic perovskites for photovoltaic applications. J. Phys. Chem. Lett. 4, 2999–3005 (2013).
Mosconi, E., Amat, A., Nazeeruddin, M. K., Gratzel, M. & Angelis, F. D. First-Principles modeling of mixed halide organometal perovskites for photovoltaic applications. J. Phys. Chem. C 117, 13902–13913 (2013).
Kawamura, Y., Mashiyama, H. & Hasebe, K. Structural study on cubic-tetragonal transition of CH3NH3PbI3 . J. Phys. Soc. Jpn. 71, 1694–1697 (2002).
Maalej, A. et al. Phase transitions and crystal dynamics in the cubic perovskite CH3NH3PbCl3 . Solid State Commun. 103, 279–284 (1997).
Khan, M., Cao, W. B., Chen, N., Asadullah & Iqbal, M. Ab-initio calculations of synergistic chromium-nitrogen codoping effects on the electronic and optical properties of anatase TiO2 . Vacuum 92, 32–38 (2013).
Parks, C. C. et al. Origins of electronic band gap reduction in Cr-N codoped TiO2 . Phys. Rev. Lett. 112, 036404 (2014).
Yu, X. et al. First principles calculations of electronic and optical properties of Mo-doped rutile TiO2 . J. Alloys Compd. 507, 33–37 (2010).
Wang, Y. et al. Density functional theory analysis of structural and electronic properties of orthorhombic perovskite CH3NH3PbI3, Phys. Chem. Chem. Phys. 16, 1424–1429 (2014).
Brivio, F., Walker, A. B. & Walsh, A. Structural and electronic properties of hybrid perovskites for high-efficiency thin-film photovoltaics from first-principles. APL Mater. 1, 042111–042115 (2013).
Melrose, D. B. & Stoneham, R. J. Generalized kramers-kronig formula for spatially dispersive media. J. Phys. A: Math. Gen. 10, L17–L20 (1977).
Baikie, T. et al. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 1, 5628–5641 (2013).
Geng, W., Zhang, L., Zhang, Y. N., Lau, W. M. & Liu, L. M. First-principles study of lead iodide perovskite tetragonal and orthorhombic phases for photovoltaics. J. Phys. Chem. C 118, 19565–19571 (2014).
Acknowledgements
This work was supported by the National Key Research Programme of China (Grant No. 2016YFA0300101), the Natural Science Foundation of China (Grants No. 11234005 and No. 51431006).
Author information
Authors and Affiliations
Contributions
H.X.Z. and J.M.L. proposed the idea. H.X.Z. carried out the calculations under the guidance of J.M.L., H.X.Z. made numerical calculations and plotted the figures and wrote the paper. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhu, H., Liu, JM. Electronic structure of organometal halide perovskite CH3NH3BiI3 and optical absorption extending to infrared region. Sci Rep 6, 37425 (2016). https://doi.org/10.1038/srep37425
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep37425
This article is cited by
-
Focus on perovskite emitters in blue light-emitting diodes
Light: Science & Applications (2023)
-
Layer number dependent ferroelasticity in 2D Ruddlesden–Popper organic-inorganic hybrid perovskites
Nature Communications (2021)
-
Perovskite Solar Fibers: Current Status, Issues and Challenges
Advanced Fiber Materials (2019)
-
Electronic structure, magnetism properties and optical absorption of organometal halide perovskite CH3NH3XI3 (X = Fe, Mn)
Applied Physics A (2019)
-
Lead Iodide and Perovskite Films Obtained by Iodination of PbS Thin Films
Journal of Inorganic and Organometallic Polymers and Materials (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.