Abstract
Thermal transport of quantum magnets has elucidated the nature of low energy elementary excitations and complex interplay between those excited states via strong scattering of thermal carriers. BiCu2PO6 is a unique frustrated spin-ladder compound exhibiting highly anisotropic spin excitations that contain both itinerant and localized dispersion characters along the b- and a-axes respectively. Here, we investigate thermal conductivity κ of BiCu2PO6 under high magnetic fields (H) of up to 30 tesla. A dip-feature in κ, located at ~15 K at zero-H along all crystallographic directions, moves gradually toward lower temperature (T) with increasing H, thus resulting in giant suppression by a factor of ~30 near the critical magnetic field of Hc ≅ 23.5 tesla. The giant H- and T-dependent suppression of κ can be explained by the combined result of resonant scattering of phononic heat carriers with magnetic energy levels and increased phonon scattering due to enhanced spin fluctuation at Hc, unequivocally revealing the existence of strong spin-phonon coupling. Moreover, we find an experimental indication that the remaining magnetic heat transport along the b-axis becomes almost gapless at the magnetic quantum critical point realized at Hc.
Similar content being viewed by others
Introduction
Thermal transport of quasi low-dimensional (D) quantum spin systems has been widely investigated to uncover both the intriguing quantum mechanical nature of magnetism and the low dimensionality of spin networks. For instance, anisotropic thermal conductivity (κ) of quantum magnets along the chain, ladder leg or in-plane directions clearly reflects the kinetics of magnetic quasiparticles that is highly direction dependent1,2. Similar to other thermodynamic properties, κ also reflects low-energy quasiparticle excitations of the quantum magnets. The metallic power-law behavior observed in the temperature (T)-dependent thermal conductivity, κ(T), proximity to zero temperature indicates gapless spinon excitation in 1D spin chains3 or spinon Fermi surfaces in 2D quantum spin liquids4.
The magnetic field (H)-dependent behavior of κ, κ(H), further provides fruitful information on the evolution of spin excitations and their coupling with the lattice degree of freedom. H dependence of κ arises for various reasons, such as extra heat conduction due to magnetic quasiparticles or additional scattering of phononic heat carriers via strong spin-phonon coupling5,6,7,8,9,10,11. It is thus expected that the H dependence will be most pronounced near the magnetic quantum critical point (QCP) where the spin gap is closed to excite magnetic quasiparticles easily or spin fluctuation becomes maximized. In this respect, the investigations of magneto-thermal conductivity near the critical magnetic field (Hc) for a quantum phase transition can be a promising way to understand the spin-phonon interaction as well as the magnetism itself.
BiCu2PO6 is a new kind of spin-ladder compound that forms a unique spin ground state of a spin dimer crystal or valence bond solid. Its crystal structure inherently contains geometric spin frustration within the ladder (Fig. 1a); it is composed of distorted S = 1/2 (Cu2+ ions) spin chains with antiferromagnetic (AF) interactions Jleg (≈138 K) and JNNN (≈73 K) along the b axis, thereby having frustrated spin interactions. These chains are coupled to one another along the c axis through another AF interaction Jrung (≈58 K) to form a two-leg spin ladder in the bc plane12,13,14. Various thermodynamic, light scattering and nuclear magnetic resonance measurements have indicated anisotropic spin-gap with the excitation energy (Δ/kB) ranging from 32 to 45 K, without any long-range spin order down to 0.1 K12,13,14,15,16,17,18,19,20. The application of magnetic field then leads to reduction in the spin gap (Fig. 1b) and induces cascades of magnetic phase transitions above critical magnetic fields μ0Hc = 20–24 T, the values of which depend on the direction of the applied field21,22.
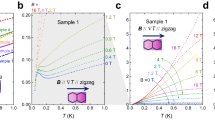
Crystal structure, magnetic energy levels and zero-field thermal conductivity of BiCu2PO6.
(a) The schematic crystal structure of the Cu2+ S = 1/2 frustrated two-leg ladder in BiCu2PO6. (b) Expected magnetic energy levels of BiCu2PO6 at H = 0 and H ~ Hc. Minima of the excitation branches satisfy Δ0 ≈ 19 K < Δ+1 ≈ 36 K < Δ−1 ≈ 45 K at H = 0 20. (c) Temperature-dependent thermal conductivity of BiCu2PO6 single crystals at 0 T and along each direction (κa, κb and κc). The solid black line represents the calculated phonon component along the a axis (κa,ph), and dashed black line represents κa,ph without resonant scattering processes. The inset shows the measured data divided by the boundary scattering limit of the phonon thermal conductivity (κ/κbd).
Inelastic neutron scattering studies on BiCu2PO6 have also uncovered intriguing spin excitations distinct from other conventional spin ladders. The spin excitation branches,  (i = 0, +1, −1), become split even at H = 0 because of giant anisotropic spin interactions originating from strong spin-orbit coupling, which can be described by antisymmetric Dzyaloshinskii-Moriya (D-M) and symmetric anisotropic spin exchange terms. Thus, the ground state can no longer be described as singlet only and the excited states exhibit the characteristics of mixed singlet and triplet states. It has thus resulted that spin excitations become highly dispersive particularly along the b* axis and almost dispersionless along the a* axis19. Naturally, the minima of the three excitation branches at H = 0 becomes different, giving rise to the three excitation gaps, Δ0/kB ≈ 19 K, Δ+1/kB ≈ 36 K and Δ−1/kB ≈ 45 K satisfying Δ0 < Δ+1 < Δ−1 (Fig. 1b)20. In the magnetic Raman spectra, in particular, the polarization dependency in the singlet bound modes has been observed, which constitutes a strong evidence of two-triplon bound states with the binding energy of approximately 33 K18. Furthermore, the observation of softening in the singlet modes suggested the melting of a spin dimer crystal (or valence bond solid) through the singlet fluctuations18. It has been also suggested that the triplons can even become fractionalized and reconstructed into a soliton lattice at higher magnetic fields above Hc17.
(i = 0, +1, −1), become split even at H = 0 because of giant anisotropic spin interactions originating from strong spin-orbit coupling, which can be described by antisymmetric Dzyaloshinskii-Moriya (D-M) and symmetric anisotropic spin exchange terms. Thus, the ground state can no longer be described as singlet only and the excited states exhibit the characteristics of mixed singlet and triplet states. It has thus resulted that spin excitations become highly dispersive particularly along the b* axis and almost dispersionless along the a* axis19. Naturally, the minima of the three excitation branches at H = 0 becomes different, giving rise to the three excitation gaps, Δ0/kB ≈ 19 K, Δ+1/kB ≈ 36 K and Δ−1/kB ≈ 45 K satisfying Δ0 < Δ+1 < Δ−1 (Fig. 1b)20. In the magnetic Raman spectra, in particular, the polarization dependency in the singlet bound modes has been observed, which constitutes a strong evidence of two-triplon bound states with the binding energy of approximately 33 K18. Furthermore, the observation of softening in the singlet modes suggested the melting of a spin dimer crystal (or valence bond solid) through the singlet fluctuations18. It has been also suggested that the triplons can even become fractionalized and reconstructed into a soliton lattice at higher magnetic fields above Hc17.
All those unusual spin excitation spectra and postulated high field phases suggest that study of thermal transport could be useful to understand the evolution of spin and phonon excitations of BiCu2PO6 in the high field region where conventional neutron scattering cannot be performed. In particular, it would be interesting to study how the geometrical frustration and strong D-M interaction can manifest themselves in the magnetic and phononic heat transport across the magnetic QCP. Indeed, a recent thermal transport study of BiCu2PO6 in a low-H region has found a pronounced suppression of κ at ~15 K, resulting in a double-peak feature in κ(T) along all crystallographic directions23. This behavior is highly unusual, as the double-peak feature has been found only along the leg direction in most other spin ladder compounds because of the separate contributions of phononic and magnetic heat carriers1,2. To shed light on the origin of this anomalous behavior, the application of high H across Hc should be also useful because it can provide information on the H-dependent variation of the double-peak feature and the intriguing nature of the strong spin-phonon coupling.
Here, we report an investigation of thermal conductivity in BiCu2PO6 single crystals under high magnetic fields up to 30 T. We found that the dip located between the double peaks in κ(T) moves systematically toward lower temperatures as H is increased to Hc, which result in the strongest field-induced suppression of κ known among the magnetic materials (by a factor of ~30). Such large T- and H-dependent variations in κ could be explained in terms of the resonant scattering of the phonons induced by magnetic transitions involving two-triplon bound states8,18. By developing a theoretical model for phononic κ having resonant scatterings with the three spin excitation branches, we could extract information on the evolution of those magnetic energy levels across Hc. Furthermore, κb(T) measured along the ladder leg direction revealed remnant magnetic contribution that scaled almost linearly in temperature at Hc., supporting that the magnetic heat transport nearly becomes gapless at the magnetic QCP.
Results
Zero-field thermal conductivity of BiCu2PO6
Figure 1c shows the κi(T) (i = a, b, c) of the BiCu2PO6 single crystals at μ0H = 0 T. Note that above 10 K, κb becomes clearly higher than κa and κc, thereby implying that the heat conduction along the leg (b) direction is higher than that along the interlayer (a) or rung (c) direction. The anisotropy observed in Fig. 1c does not appear to originate from the anisotropic phonon thermal conductivity (κph). To estimate the intrinsic anisotropy in κph, we rescaled κ in the low-temperature regime with respect to κbd, i.e., κ in the ‘boundary scattering limit’. From the kinetic theory, the boundary scattering limit of phononic thermal conductivity can be expressed as κbd = cphvphlbd/3, where cph is a phononic specific heat of a crystal approximately given as βT3, vph is an averaged sound velocity determined from the Debye temperature θD = v(ħ/kB)(6π2n/V)1/3 = 330 K 24 (n/V: number density of atoms), and lbd is the boundary scattering limit of the phonon mean free path determined from the sample geometry as  (S: cross section of the sample)25. The calculated κ/κbd values under the assumption of isotropic phonon dispersion thus reflect the intrinsic anisotropy in the phonon transport, independent of the crystal geometry. The κ/κbd curves in the inset of Fig. 1c exhibit anisotropy of less than 20%, which is not sufficient to explain the anisotropy in κ above 10 K, which shows a difference of more than 200%. Different strengths of umklapp scattering can also be ruled out as an explanation because it would lead to different peak positions in κph(T), which is inconsistent with the results shown in Fig. 1c 26. We therefore argue that the κph along the a axis (κa,ph) should be similar to the κph along the b axis (κb,ph), i.e., κa,ph ≈ κb,ph in BiCu2PO6, regardless of its crystallographic structure. Thus, the extra heat transport along the leg (b) direction could be magnetic in its origin, which indeed reflects the nature of anisotropic magnetic excitation of BiCu2PO6.
(S: cross section of the sample)25. The calculated κ/κbd values under the assumption of isotropic phonon dispersion thus reflect the intrinsic anisotropy in the phonon transport, independent of the crystal geometry. The κ/κbd curves in the inset of Fig. 1c exhibit anisotropy of less than 20%, which is not sufficient to explain the anisotropy in κ above 10 K, which shows a difference of more than 200%. Different strengths of umklapp scattering can also be ruled out as an explanation because it would lead to different peak positions in κph(T), which is inconsistent with the results shown in Fig. 1c 26. We therefore argue that the κph along the a axis (κa,ph) should be similar to the κph along the b axis (κb,ph), i.e., κa,ph ≈ κb,ph in BiCu2PO6, regardless of its crystallographic structure. Thus, the extra heat transport along the leg (b) direction could be magnetic in its origin, which indeed reflects the nature of anisotropic magnetic excitation of BiCu2PO6.
The most conspicuous feature in the shapes of κi(T), as shown in Fig. 1c, is the presence of a dip feature sandwiched by the double peak structure, which is observed for every crystallographic direction. Such a double-peak structure has been commonly observed in quasi low-dimensional magnets (spin chains or spin ladders), particularly in only one direction where the magnetic thermal transport reaches a maximum1,2. It is therefore anomalous to observe the double peaks along every direction in one of spin ladder compounds, BiCu2PO6. Moreover, none of the peaks in κ(T) appears to be either a solely phononic or a solely magnetic peak; because the magnetic excitation along the reciprocal a axis is known to be non-dispersive19 and the velocity of magnetic quasiparticles ( ) along the a axis should be much smaller than that along any other direction. Therefore, it is unlikely that magnetic thermal conductivity κmag can produce a separate peak along the a axis. In addition, attempts to estimate κph in every direction from the single peak only below 7 K (or above 20 K) resulted in extremely small κph at high (low) temperatures. Therefore, it is necessary to consider another mechanism for explaining the double peak feature in κph along every direction.
) along the a axis should be much smaller than that along any other direction. Therefore, it is unlikely that magnetic thermal conductivity κmag can produce a separate peak along the a axis. In addition, attempts to estimate κph in every direction from the single peak only below 7 K (or above 20 K) resulted in extremely small κph at high (low) temperatures. Therefore, it is necessary to consider another mechanism for explaining the double peak feature in κph along every direction.
Giant suppression of thermal conductivity under magnetic field
To better understand the origin of the double-peak feature, we performed κ(H) measurements along the a and b axes for fields of up to μ0H = 30 T (Fig. 2). As H is approached to Hc, the dip features in both directions systematically shift toward lower temperatures, resulting in very small κ at low temperatures. Above Hc where the spin-ordered phases appear, κ at low temperatures around 1.4 K is again enhanced. Figure 3a shows the magneto-thermal conductivity (κ(H)/κ(0)) at T = 1.4, 3 and 5 K, as summarized from the results in Fig. 2. At 1.4 K, it is clearly observed that κ(H)/κ(0) sharply decreases near Hc22. However, as temperature is increased, the decreasing region becomes widened and gradually shifts toward higher H. It is noteworthy that κ is suppressed by a factor of ~30 at T = 5 K and μ0H = 30 T, which is, to our knowledge, the largest magneto-thermal conductivity observed in magnetic materials. For example, SrCu2(BO3)2, Ba3Mn2O8, and hexagonal HoMnO3 showed similar field-induced κ suppression by a factor of ~4 at μ0H = 17 T 8, ~10 at 14 T 6, and ~9 at ~3 T 9, respectively. Therefore, the observation of such a large κ suppression under magnetic fields is a unique case. In comparison, such large suppression of κ has been also observed in the hexagonal HoMnO3 as a function of temperature near the Ho3+ spin ordering as compared with YMnO3. This has been attributed to the strong spin-phonon coupling and magnetic fluctuations arising from the spin frustration27.
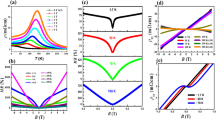
High-field thermal conductivity of BiCu2PO6.
Thermal conductivity of BiCu2PO6 single crystals under magnetic fields of up to 30 T is plotted (symbols), including a comparison with the calculated thermal conductivity from the transport theory for fields of up to 20 T (solid lines). In each case the thermal gradient was applied either along the (a) a or (b) b axis. The dashed lines represent the thermal conductivity along the a and b axes with a minimum Δ+1(H) ≈ 0, which represents the lowest limit on the thermal conductivity estimated from the resonant scattering model.
Magnetic field dependence of the thermal conductivity (κ(H)/κ(0)) and the magnetic excitation gaps.
(a) The magneto-thermal conductivity values at 1.4 K, 3 K and 5 K are extracted from κ(T) curves at fixed magnetic fields. The solid lines are guides for the eye. (b) Magnetic field dependence of the magnetic excitation gaps for fields of up to 25 T. The values were estimated from the analyses of the phonon and magnetic thermal conductivities (solid symbols). The minimum spin excitation energies determined from the inelastic neutron scattering results have been multiplied by a factor of 1.25 (small open symbols)20. The error bars represent typical uncertainties of the values estimated from the phonon thermal conductivity analysis. The dashed lines are guides for the eye.
Resonant scattering of phonon by magnetic excitations in BiCu2PO6
To understand the anomalous κ(T) behavior and strong H dependence of BiCu2PO6 in a quantitative level, we consider here the model of the resonant scattering of phonons by magnetic excitations, which has been formerly applied in SrCu2(BO3)2 to explain a similar dip feature8. SrCu2(BO3)2 represents an archetypal, exactly-solvable spin-frustrated networks, in which its ground state can be described as a bound two-dimer system having two S = 1/2 spins in each dimer28. Similarly, the frustrated spin interactions along the leg direction in BiCu2PO6 may provide a similar binding effect between adjacent dimers formed by the rung coupling as evidenced by a recent Raman scattering study18.
In such a bound two-dimer system, a phonon-assisted magnetic transition between the excited states with the same Sz value, i.e., one of the thermally excited S = 1 one-triplet, one-singlet states and S = 1 bound triplet states, having energy difference of Δs can be induced, accompanied by absorbing or emitting a phonon of energy ћω ≈ Δs due to the spin-phonon coupling. The entire two-step process, magnetic excitation and de-excitation, that restores the initial spin state can then be regarded as ω-dependent elastic scattering of the phonons, and the phonon relaxation rate τ−1 will be directly proportional to the transition rate of the magnetic excitation. In the isolated two-dimer system, there is no correlation between the momentum directions of the phonon at initial and final states. Although the original resonant scattering model8 assumed a flat dispersion of the magnetic excitation spectra, it is likely applicable to any spin-gapped system with dispersive excitations because most excitations appear within a narrow k region near the band minima. Furthermore, the evolution of the spin excitation gaps under H is likely to modify the transition rate, resulting in the strength change of the resonant phonon scattering (Fig. 1b).
Thermal transport by phonons or magnetic quasiparticles can be generally described by

where ck, vk, lk and nk represent the heat capacity, velocity, mean free path and statistical occupation of quasiparticles of wavevector k. Applying the Debye approximation to Eq. (1) leads to the Callaway model for κph, the temperature dependence of which is predominantly determined by the phonon relaxation rate 
 26,29.
26,29.
To calculate the relaxation rate by the resonant scattering ( ), we considered three nondegenerate excitation branches (Sz = 0, +1, −1), which are split even at zero field by the anisotropic spin interactions, and are subject to change under H by the Zeeman effect20. The phonon scattering rate due to such excited levels can be described as follows (Methods):
), we considered three nondegenerate excitation branches (Sz = 0, +1, −1), which are split even at zero field by the anisotropic spin interactions, and are subject to change under H by the Zeeman effect20. The phonon scattering rate due to such excited levels can be described as follows (Methods):

Here, Ci is the overall factor related to the strength of the spin-phonon coupling,  is the statistical occupation of thermally excited states with Sz = i (
is the statistical occupation of thermally excited states with Sz = i ( ), Δi is the H-dependent energy gap between the ground state (
), Δi is the H-dependent energy gap between the ground state ( ) and an excited state (
) and an excited state ( ), and Δs,i is the H-independent resonance energy determined by the energy difference between the magnetic excited states of the two-dimer system. In SrCu2(BO3)2 where degenerate triplet states are realized, Δs = Δ − B, where B is the binding energy of the two triplons. In addition,
), and Δs,i is the H-independent resonance energy determined by the energy difference between the magnetic excited states of the two-dimer system. In SrCu2(BO3)2 where degenerate triplet states are realized, Δs = Δ − B, where B is the binding energy of the two triplons. In addition,  and
and  are the probabilities of the excitation and de-excitation processes, respectively.
are the probabilities of the excitation and de-excitation processes, respectively.
The overall factors Ci are here assumed as magnetic field-independent parameters as long as H does not exceed Hc8. Although there is a possibility that strength of the elastic spin-phonon coupling decreases as the field-induced spin polarization appears even below Hc due to the D-M interactions and paramagnetic contributions14, its magnetic moment is sufficiently small (less than 0.005 μB/Cu2+ below Hc21) and thus the effect could be considered as higher-order terms.
Quantitative analyses of thermal transport with magnetic energy levels
The double-peak feature observed in the κ data (Fig. 1c) can be explained in terms of the resonant scattering model for κph described in Eqs (1) and (2), with the numerical parameters listed in Table 1. Because the dispersion of the magnetic excitation is nearly flat along the a axis19, we apply the resonant scattering model to κa. At μ0H = 0 T, the dip at ~15 K can be quantitatively explained as a consequence of the resonant scattering in κph; the calculated κ (solid line in Fig. 1c) shows good agreement with the experimental κa in the entire temperature range. In contrast, the predicted curve for κph without considering the resonant scattering (dashed line in Fig. 1c) exhibits a typical single-peak feature expected in nonmagnetic, insulating materials26. This observation supports the hypothesis that the resonant scattering in κph is the origin of the double peaks and the dip observed in Fig. 1c.
One of intriguing findings obtained from the best fit is that the overall constant related to the strength of the resonant scattering for Sz = 0 branch (C0) is at least one order of magnitude smaller than the constant for Sz = 1 (C1) or Sz = −1 (C−1) branches (Table 1). This indicates that the resonant scattering from the transition between S = 0 one-triplet, one-singlet and S = 0 bound triplet could be negligible as compared with other magnetic excitations, which may constitute a clue for developing further microscopic theories on the resonant scattering.
To understand the κ data under magnetic fields (Fig. 2), we apply the same resonant scattering model, assuming that the energy gaps are dependent on H (see Fig. 1b and Table 2). In a recent inelastic neutron scattering study20, each magnetic level exhibited the Zeeman splitting up to μ0H = 11 T such that the excitation gaps could be roughly described as follows: Δ0(H) = Δ0(0), Δ+1(H) = Δ+1(0) − Δ(H) and Δ−1(H) = Δ−1(0) + Δ(H). Here, Δ(H) is an H-dependent parameter. The κa curves calculated for different Δ(H) (solid lines in Fig. 2a) are in good agreement with the experimental data, particularly for temperatures above 5 K and fields of up to 20 T. This finding clearly indicates that the double-peak feature in κa(T) and the suppression of the peak at low temperatures can be mostly explained by κph based on the resonant scattering model.
The filled squares in Fig. 3b summarize the H dependence of the three energy gaps, Δi(H), for fields of up to 20 T, as obtained from the best fits to the results presented in Fig. 2a and Table 2. For example, the energy gaps of the three excitation branches at μ0H = 0 T were found to be Δ0/kB ≈ 25 K, Δ+1/kB ≈ 42 K and Δ−1/kB ≈ 57 K. All the H-dependent energy gaps Δi(H) obtained by fitting κa(T) (filled squares) are qualitatively consistent with the recent neutron scattering results (open symbols), although they are larger by ~25% than those obtained from the minimum energies of the magnetic excitation spectra20. Because magnetic excitations involving phonon scattering are not confined only to the minima of these dispersive branches, it seems reasonable that the effective gap values estimated from the κph fits are higher.
Based on the three excitation gaps obtained from our fit (see Table 2), the averaged gap value becomes Δ~41 K. As the resonance energy (Δs) obtained from our fit was approximately 32 K, the triplon binding energy B is then roughly estimated to be B = Δ − Δs ≈ 9 K. Recent Raman scattering result18 pointed that the binding energy of the bound singlet is 2B ≈ 33 K and thus B ≈ 16 K, which is rather close to the B from our fits although it is a rough estimation based on the averaged spin gap value. Such agreement supports the presence of the triplon bound state in the resonant phonon scattering processes, and justifies the application of the above model into the BiCu2PO6 system.
Along the b axis, however, the experimental κb data cannot be explained solely by the resonant scattering model in κph. Figure 1c shows that the experimental κb data are overall larger than κa,ph (≈κb,ph). To better fit the experimental κb data, an additional contribution from κmag was indeed essential. This seems consistent with the fact that the inelastic neutron scattering studies found most dispersive spin excitation branches along the reciprocal b* axis19. To calculate κmag explicitly, we have extended Eq. (1) to derive new formula for κmag when the excited triplet states are nondegenerate (Methods). The result is

Here, β = 1/kBT, and lmag,i is the magnetic mean free path of the i-th branch. The solid lines in Fig. 2b show the calculated κb ( = κb,ph + κb,mag) results for fields of up to μ0H = 20 T, in which κb,ph is assumed to be the same as κa,ph. As a result of including the additional κmag, we could achieve good agreement between the experimental κb data and the calculated ones, particularly at temperatures above 5 K and fields of up to μ0H = 20 T. The excitation gap values obtained from the fit are also plotted in Fig. 3b as filled circles, which overall show good agreement with the excitation gaps obtained from the fit along the a axis.
However, when 20 T < H < Hc, the theoretically predicted values of both κa (=κa,ph) and κb (=κb,ph + κb,mag) clearly overestimated the experimental data in a wide temperature window below 10 K. For example, the experimental data at μ0H = 22 T are far more suppressed below ~10 K than the theoretically predicted κa and κb, even after applying a minimum Δ+1(H) ≈ 0, which yields the most significant suppression of κph in the resonant scattering model (dashed lines in Fig. 2). This observation directly points out that the additional scattering of heat carriers, beyond the resonant scattering model adopted here, should exist particularly near Hc. Two possible origins could be postulated. First, when the spin energy gap becomes sufficiently small, the resonant scattering model, which assumes flat dispersion, may not fully account for the effect of dispersion in the magnetic energy levels. However, it is unlikely that the dispersion effect will bring up enhanced resonant scattering at H ≈ Hc. More importantly, beyond the resonant scattering, the additional nonresonant scattering of phononic heat carriers due to the spin fluctuation seems to play a role because the spin fluctuation most likely increases at the magnetic quantum critical point.
Field dependence of magnetic thermal conductivity near the critical magnetic field
The very large suppression of κph at H ≤ Hc in both directions suggests the possibility that κb,mag can be extracted approximately at low temperatures and at H ≈ Hc where κph becomes sufficiently small due to the enhanced phonon scattering30. Assuming that the relation κa,ph ≈ κb,ph is valid at T > 7 K or H ≈ Hc, we subtracted the κa from the κb data to plot (κb − κa)/T, as shown in Fig. 4. The (κb − κa)/T at T > 7 K, μ0H = 0 T shows a clear peak at T~13 K, which is a typical feature of κmag in the gapped spin ladder systems1,30. The κmag peak is almost insensitive to the magnetic field, suggesting that Δ0 is indeed magnetic field-independent and magnetic mean free path is not strongly subject to the resonant phonon scattering. Interestingly, the most constant behavior is observed at μ0Hc = 23.5 T in the low-temperature limit down to 0.8 K, whereas the neighboring data at 23 T or 24 T show clear decreases. This observation implies that the magnetic thermal conductivity becomes nearly linear in the low-temperature limit at the critical field μ0Hc = 23.5 T.
High-field magnetic thermal conductivity divided by temperature, as estimated from the difference between the b axis and a axis components.
The thick solid lines are theoretical curves calculated based on the transport theory with Δ0/kB ≈ 25 K, Δ+1/kB ≈ 0 K and Δ−1/kB ≈ 99 K (H = Hc, black) and Δ0/kB ≈ 25 K, Δ+1/kB ≈ 42 K and Δ−1/kB ≈ 57 K (Δi at 0 T, gray). The calculated magnetic components at H = Hc from the Sz = 0 (dotted line) and Sz = +1 (dashed line) branches are individually plotted. The calculated magnetic thermal conductivity curves with finite spin gaps (Δ+1/kB = 1 K and 2 K) are also included (thin solid lines).
However, it was difficult to analyze the experimental data at μ0H ≤ 22 T and ~1 K < T < 7 K in a more quantitative level because anomalous peak- or dip-like structures were superimposed on top of the exponential tail of κmag (e.g. gray solid line in Fig. 4). Although the anisotropy ratio between κa,ph and κb,ph (=κa,ph/κb,ph) is expected to be less than 20%, the anisotropy of κph that is presumably related to the sample geometry and/or directional dependence of the spin-phonon coupling could be still non-negligible to produce such additional peak- or dip-like structures in the (κb − κa)/T data.
With the caveat of having such additional structures, to understand whether κmag can still explain the low temperature experimental data of the (κb − κa)/T near H ≈ Hc, we calculated κmag,i/T (i = 0, +1, −1) individually with fitted parameters listed in Tables 1 and 3 and plotted κmag/T ≡ ∑i = 0,±1κmag,i/T, κmag,0/T and κmag,+1/T in Fig. 4. Here, the energy gaps were assumed to be Δ0/kB ≈ 25 K, Δ+1/kB ≈ 0 K and Δ−1/kB ≈ 99 K. The calculated κmag/T results well reproduced the overall shape of (κb − κa)/T at μ0H = 0 T and 23.5 T, including the magnetic field-independent broad peak at 11 K~13 K. [The hump at ~3 K may be attributable to the anisotropic phonon component that does not exactly cancel out in the (κb − κa)/T plot.] Moreover, the results for κmag,+1/T with Δ+1/kB ≈ 0 K (at H = Hc) can explain the constant behavior observed in the low-temperature limit, whereas the κmag,−1/T data contribute only very little. This finding indicates that a gapped magnetic excitation to the Sz = 0 branch and a nearly-gapless magnetic excitation to Sz = +1 coexist at H = Hc. When a finite energy gap of Δ+1/kB = 1 K or 2 K is used, the calculated κmag/T results decrease at low temperatures, showing a clear deviation from the constant κmag/T behavior. Therefore, the energy gap Δ+1/kB at μ0Hc = 23.5 T, if any, could be less than 1 K to reproduce constant κmag/T behavior for temperatures down to 0.8 K. Moreover, the energy gap Δ+1/kB at 23 T is expected to be approximately 2 K. Based on the experimental data in this work, we estimate that the excitation gaps are close to Δ0/kB ≈ 25 K, Δ+1/kB ≈ 0 K and Δ−1/kB ≈ 99 K at H = Hc. Triangles in Fig. 3b and Table 2 summarize those estimated gap values around Hc. The results in Fig. 3b exhibiting the continuous evolution of the three excited levels corroborates that a magnetic quantum phase transition indeed occurs at H = Hc due to the crossing of the energy levels between the Sz = +1 excited state and the magnetic ground state.
Almost negligible energy gap in the Sz = +1 branch around Hc expected from the T dependence of the magnetic thermal conductivity is rather peculiar, because the spin gap in the spin-dimer systems with strong D-M interaction is not expected to be closed completely even at Hc due to the mixing of singlet and triplet states. It may indicate that opening of the spin gap by the anisotropic D-M interaction is comparable or less than the energy scale of ~0.8 K17, or the D-M interaction is strong enough so that it cannot be treated as a higher-order effect and different physics might be need to understand our observation. Investigations of the critical behavior of BiCu2PO6 at lower temperatures and related theoretical works will be necessary for understanding its magnetism around the critical field.
Discussion
One fundamentally interesting question is why the phonon transport in BiCu2PO6 is subject to strong resonant and nonresonant scatterings with the magnetic energy levels and then result in giant magneto-thermal conductivity. A common feature in SrCu2(BO3)2 and BiCu2PO6 where the resonant scattering process becomes conspicuous, is the existence of spin frustration and anisotropic spin interaction described by the Dzyaloshinskii-Moriya interaction20,31. Hence, the spin-orbit coupling represented by the Dzyaloshinskii-Moriya interaction in the frustrated spin network might be one of necessary conditions for having the dominant resonant phonon scattering. Moreover, the conventional phonon scattering due to spin fluctuation effect, beyond the level described by the resonant scattering model, seems to be also significant particularly near Hc and at low temperatures in BiCu2PO6. It gives rise to the additional suppression of κ by a factor of ~3 while the resonant scattering leads to the κ suppression typically by a factor of ~10 according to our fit results. Similar kinds of large κ suppression have been observed in multiferroics with strong magnetoelectric (or spin-phonon) coupling and attributed to the enhanced spin-phonon scattering near the magnetic phase transitions9,10,11.
Related to this, it is noteworthy that the spin dimer (valence bond solid) state in BiCu2PO6 lies in the distorted, non-coplanar network of CuO4 squares that share their edges and corners along the rung and leg directions of the ladders, respectively. Hence, both spin couplings along the rung and leg directions should be greatly affected by the Cu-O-Cu superexchange interaction, which is inherently sensitive to the local Cu-O-Cu boding angle. This structural characteristic seems to provide one natural route to favor strong spin-phonon coupling in BiCu2PO6. It is further noteworthy that the field-induced electric polarization and magnetoelectric effect have been recently found in the magnetically-ordered, high-field phases of BiCu2PO6, clearly supporting the existence of strong spin-phonon coupling (B.-G. Jeon et al., unpublished data). Therefore, the presence of both resonant and nonresonant phonon-scattering processes via the strong spin-orbit and spin-phonon coupling in frustrated spin networks seems to be the salient feature for causing the giant suppression of κ near the magnetic quantum phase transition in BiCu2PO6.
In summary, we have observed the unprecedentedly large suppression of the phononic thermal conductivity in the vicinity of magnetic quantum critical point in BiCu2PO6 single crystals. In contrast to other quasi-low-dimensional magnets, in which both phononic and magnetic heat conduction exist almost independently, both resonant scattering of phononic heat carriers with the magnetic excitation levels and the additional phonon scattering due to the magnetic fluctuation were found to be dominant sources of the κ suppression. We claim the importance of spin-orbit and spin-phonon coupling in the frustrated spin network to boost up such resonant and nonresonant scatterings of phononic heat carriers with the spin degree of freedom. Finally, our work also points to an interesting possibility of using the quantum magnet as a field-tunable thermal insulator under high magnetic field environment while superconducting materials have often been used as a thermal insulator at low field regions below their upper critical fields.
Methods
Sample preparation
High-quality single crystalline BiCu2PO6 samples were grown using the floating zone method. After the crystallographic axes had been aligned using a Laue camera, the single crystals were carefully cut into three small pieces with typical dimensions of 1.2 × 0.2 × 0.2 mm3 to have the longest directions parallel to a, b, and c axes. The sample size was kept nearly constant to ensure that the boundary scattering effect was similar for all samples. We note that the chemical formula for this compound should be BiCu2(PO4)O2, in which (PO4)3− acts as a polyatomic ion group, while the notation in this manuscript was used to follow the former literature.
Thermal conductivity measurements in high magnetic fields
A one-heater, two-thermometer configuration was used to measure κ in a Physical Property Measurement System (PPMSTM) for fields of up to 14 T. The calibration curves of the CernoxTM thermometers at each magnetic field were measured in prior to the κ(T) measurement. A similar configuration with custom-made, vacuum-sealed 3He probe was inserted in a resistive magnet for fields of up to 35 T at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, USA. The magnetic field dependence of the CernoxTM thermometers used in here has been calibrated at fixed temperatures down to 0.6 K and up to 50 T, by using a 65 T short-pulse magnet at NHMFL in Los Alamos, USA. The resistance change of the resistance thermometers due to the temperature gradient inside the sample was measured with the lock-in amplifiers (Stanford Research SR830), while applying the heat with the dc current source (Keithley 6221) and measuring the voltage difference of the heater with the nanovoltmeter (Keithley 2182). A high vacuum of well below 10−5 mbar was maintained throughout the measurements. For these measurements of κ under high magnetic fields, H was applied along the a axis.
Kinetic theory of phonon thermal conductivity with resonant scattering
The phonon thermal conductivity of an insulating system can be explained with the equation derived from the transport theory26

with the phonon scattering rate of

Here, θD is the Debye temperature of the crystal (θD = v(ħ/kB)(6π2n/V)1/3 where n/V is number density of atoms), v is averaged sound velocity of phonon, ω = xkBT/ħ and  is the resonant scattering rate. L, A, A’, B and b are the adjustable parameters related to the strength of the phonon scattering.
is the resonant scattering rate. L, A, A’, B and b are the adjustable parameters related to the strength of the phonon scattering.
Calculation based on the concept of the resonant scattering in the isolated S = 1/2 dimer system described above shows that the resonant scattering rate is8

In this equation, C is related to the overall strength of the spin-phonon coupling, N0 is the probability of excitation process starting from one of the one-triplet, one-singlet states ( ), N1 is the probability of de-excitation process starting from one of the bound triplet states (
), N1 is the probability of de-excitation process starting from one of the bound triplet states ( ) and ci is the probability of the thermal excitation (
) and ci is the probability of the thermal excitation ( ). Δs is the resonance energy.
). Δs is the resonance energy.
When the energy gap between the ground state and three excited states are split, the resonant scattering process for each excited configuration should be considered separately. This can be achieved phenomenologically by decomposing the Eq. (6) into three different terms.

Here, ,
,  and
and
 . Δi is the energy gap between
. Δi is the energy gap between  and
and  and Δs,i is the resonance energy of each excitation.
and Δs,i is the resonance energy of each excitation.
Although the Shastry-Sutherland lattice is considered while establishing details of this model8, any kind of the spin gap system can be applicable in principle since the model does not require direct information about geometry of the Shastry-Sutherland system.
Theory of magnetic thermal conductivity
The calculation for magnetic thermal conductivity also starts from the kinetic theory of the thermal conductivity given in Eq. (1). Now we need to consider the one-dimensional dispersion of the magnetic excitations in BiCu2PO6. As we mentioned above, the energy gap between ground state ( ) and excited states (
) and excited states ( ) are split due to the anisotropic interactions20. Thus, one should rewrite the Eq. (1) for three different branches (εk,0, εk,+1 and εk,−1).
) are split due to the anisotropic interactions20. Thus, one should rewrite the Eq. (1) for three different branches (εk,0, εk,+1 and εk,−1).

The overall constant Cm,i is related to the relative weight of each branch ( ). The statistical occupation for the excitation to
). The statistical occupation for the excitation to  can be written as
can be written as

Now the formula for the magnetic thermal conductivity can be calculated as follows. For simplicity, one can assume that dispersion of the energy bands εk,i are same except constant shift (i.e. εk,1 = εk,0 + (Δ1 − Δ0) and εk,−1 = εk,0 + (Δ−1 − Δ0)). Then nk,i become an explicit function of εk,i. We also assume one-dimensional heat conduction along the N ladders in a unit area. By considering vk = ħ−1dε/dk, the summation over k can be replaced to the integration with respect to ε. The integral range for each excitation branch is from Δi (band minima) to  (band maxima). Further approximation such as a constant mean free path lk = lmag can be possible since the quasiparticle excitation for magnetic heat conduction dominates just close to the band minima at k = k0 1. By considering all of above, the formula for magnetic thermal conductivity will be
(band maxima). Further approximation such as a constant mean free path lk = lmag can be possible since the quasiparticle excitation for magnetic heat conduction dominates just close to the band minima at k = k0 1. By considering all of above, the formula for magnetic thermal conductivity will be

One can check that this equation reduces to

when there is no energy split among the magnetic excitations30.
Magnitude of the magnetic thermal conductivity is usually limited by the magnetic mean free path lmag. Various sources such as defect and spin-lattice interaction determine the magnetic mean free path. The temperature dependence of the magnetic mean free path can be given as  , where Asp is strength of spin-lattice interaction (interaction between phonon and magnetic quasiparticle),
, where Asp is strength of spin-lattice interaction (interaction between phonon and magnetic quasiparticle),  is an adjustable parameter related to the energy scale of thermal excitation and Lsd is mean distance between magnetic defects25,32. Unfortunately, this is too much simplified model to describe the magnetic mean free path, and in reality other scattering sources such as the scattering among the magnetic quasiparticles might be included as well.
is an adjustable parameter related to the energy scale of thermal excitation and Lsd is mean distance between magnetic defects25,32. Unfortunately, this is too much simplified model to describe the magnetic mean free path, and in reality other scattering sources such as the scattering among the magnetic quasiparticles might be included as well.
Additional Information
How to cite this article: Jeon, B.-G. et al. Giant suppression of phononic heat transport in a quantum magnet BiCu2PO6. Sci. Rep. 6, 36970; doi: 10.1038/srep36970 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Hess, C. Heat conduction in low-dimensional quantum magnets. Eur. Phys. J. Special Topics 151, 73–83 (2007).
Sologubenko, A. V., Lorenz, T., Ott, H. R. & Freimuth, A. Thermal Conductivity via Magnetic Excitations in Spin-Chain Materials. J. Low Temp. Phys. 147, 387–403 (2007).
Hess, C. et al. Linear Temperature Dependence of the Magnetic Heat Conductivity in CaCu2O3 . Phys. Rev. Lett. 98, 027201 (2007).
Yamashita, M. et al. Highly Mobile Gapless Excitations in a Two-Dimensional Candidate Quantum Spin Liquid. Science 328, 1246–1248 (2010).
Sun, X. F., Tao, W., Wang, X. M. & Fan, C. Low-Temperature Heat Transport in the Low-Dimensional Quantum Magnet NiCl2-4SC(NH2)2 . Phys. Rev. Lett. 102, 167202 (2009).
Ke, W. P. et al. Low-temperature heat transport in the layered spin-dimer compound Ba3Mn2O8 . Phys. Rev. B 84, 094440 (2011).
Kohama, Y. et al. Thermal Transport and Strong Mass Renormalization in NiCl2-4SC(NH2)2 . Phys. Rev. Lett. 106, 037203 (2011).
Hofmann, M. et al. Strong Damping of Phononic Heat Current by Magnetic Excitations in SrCu2(BO3)2 . Phys. Rev. Lett. 87, 047202 (2001).
Wang, X. M. et al. Large magnetothermal conductivity of HoMnO3 single crystals and its relation to the magnetic-field-induced transitions of magnetic structure. Phys. Rev. B 82, 094405 (2010).
Zhao, Z. Y. et al. Magnetic phase transitions and magnetoelectric coupling of GdFeO3 single crystals probed by low-temperature heat transport. Phys. Rev. B 83, 014414 (2011).
Zhao, Z. Y. et al. Ground state and magnetic phase transitions of orthoferrite DyFeO3 . Phys. Rev. B 89, 224405 (2014).
Koteswararao, B., Salunke, S., Mahajan, A. V., Dasgupta, I. & Bobroff, J. Spin-gap behavior in the two-leg spin-ladder BiCu2PO6 . Phys. Rev. B 76, 052402 (2007).
Mentré, O. et al. Incommensurate spin correlation driven by frustration in BiCu2PO6 . Phys. Rev. B 80, 180413(R) (2009).
Tsirlin, A. A. et al. Bridging frustrated-spin-chain and spin-ladder physics: Quasi-one-dimensional magnetism of BiCu2PO6 . Phys. Rev. B 82, 144426 (2010).
Alexander, L. K. et al. Impurity effects in coupled-ladder BiCu2PO6 studied by NMR and quantum Monte Carlo simulations. Phys. Rev. B 81, 054438 (2010).
Casola, F. et al. Direct Observation of Impurity-Induced Magnetism in a Spin-1/2 Antiferromagnetic Heisenberg Two-Leg Spin Ladder. Phys. Rev. Lett. 105, 067203 (2010).
Casola, F. et al. Field-Induced Quantum Soliton Lattice in a Frustrated Two-Leg Spin-1/2 Ladder. Phys. Rev. Lett. 110, 187201 (2013).
Choi, K.-Y. et al. Evidence for Dimer Crystal Melting in the Frustrated Spin-Ladder System BiCu2PO6 . Phys. Rev. Lett. 110, 117204 (2013).
Plumb, K. W. et al. Incommensurate dynamic correlations in the quasi-two-dimensional spin liquid BiCu2PO6 . Phys. Rev. B 88, 024402 (2013).
Plumb, K. W. et al. Quasiparticle-continuum level repulsion in a quantum magnet. Nat. Phys. 12, 224–229 (2016).
Kohama, Y. et al. Anisotropic Cascade of Field-Induced Phase Transitions in the Frustrated Spin-Ladder System BiCu2PO6 . Phys. Rev. Lett. 109, 167204 (2012).
Kohama, Y. et al. Entropy of the quantum soliton lattice and multiple magnetization steps in BiCu2PO6 . Phys. Rev. B 90, 060408(R) (2014).
Nagasawa, H. et al. Thermal Conductivity in the Frustrated Two-Leg Spin-Ladder System BiCu2PO6 . J. Phys.: Conf. Ser. 568, 042012 (2014).
Koteswararao, B., Mahajan, A. V., Alexander, L. K. & Bobroff, J. Doping effects in the coupled, two-leg spin ladder BiCu2PO6 . J. Phys.: Condens. Matter 22, 035601 (2010).
Sologubenko, A. V., Giannò, K., Ott, H. R., Vietkine, A. & Revcolevschi, A. Heat transport by lattice and spin excitations in the spin-chain compounds SrCuO2 and Sr2CuO3 . Phys. Rev. B 64, 054412 (2001).
Berman, R. Thermal Conduction in Solids (Clarendon, Oxford, 1976).
Sharma, P. A. et al. Thermal Conductivity of Geometrically Frustrated, Ferroelectric YMnO3: Extraordinary Spin-Phonon Interactions. Phys. Rev. Lett. 93, 177202 (2004).
Kageyama, H. et al. Exact Dimer Ground State and Quantized Magnetization Plateaus in the Two-Dimensional Spin System SrCu2(BO3)2 . Phys. Rev. Lett. 82, 3168–3171 (1999).
Callaway, J. Model for Lattice Thermal Conductivity at Low Temperatures. Phys. Rev. 113, 1046–1051 (1959).
Hess, C. et al. Magnon heat transport in (Sr,Ca,La)14Cu24O41 . Phys. Rev. B. 64, 184305 (2001).
Cépas, O. et al. Dzyaloshinski-Moriya Interaction in the 2D Spin Gap System SrCu2(BO3)2 . Phys. Rev. Lett. 87, 167205 (2001).
Sologubenko, A. V. et al. Thermal conductivity and specific heat of the linear chain cuprate Sr2CuO3: Evidence for thermal transport via spinons. Phys. Rev. B 62, 6108(R) (2000).
Acknowledgements
We thank M. Jaime, N. Harrison and F. F. Balakirev for the assistance of the thermometer calibrations in the pulsed field. This work has been supported by the NRF grants funded by the Korean government (MSIP) with the grant numbers 2010-0018300 and 2016K1A4A3914691. Work at NHMFL Pulsed Field Facility at LANL and NHMFL DC Field facility was supported by the NSF grant DMR-0654118, the State of Florida, and the US DOE-BES project ‘Science at 100 tesla’ BES FWP LANLF100. F.C.C. acknowledges the support from the National Science council of Taiwan under project number NSC-102-2119-M-002-004. S.B.C is supported by IBS-R009-Y1.
Author information
Authors and Affiliations
Contributions
B.-G.J., B.K. and K.H.K. initiated the project. G.J.S. and F.C.C. synthesized the sample. B.-G.J., C.B.P., S.C.R. and K.H.K. performed the experiments. B.-G.J., E.G.M. and S.B.C. conceived the theoretical models. B.-G.J., B.K. and K.H.K. analyzed the data. B.-G.J. and K.H.K. wrote the manuscript with input from all other authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Jeon, BG., Koteswararao, B., Park, C. et al. Giant suppression of phononic heat transport in a quantum magnet BiCu2PO6. Sci Rep 6, 36970 (2016). https://doi.org/10.1038/srep36970
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36970
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.