Abstract
We demonstrate that the giant magnetoresistance can be switched off (on) in even- (odd-) width zigzag graphene-like nanoribbons by an atomistic gate potential or edge disorder inside the domain wall in the antiparallel (ap) magnetic configuration. A strong magneto-thermopower effect is also predicted that the spin thermopower can be greatly enhanced in the ap configuration while the charge thermopower remains low. The results extracted from the tight-binding model agree well with those obtained by first-principles simulations for edge doped graphene nanoribbons. Analytical expressions in the simplest case are obtained to facilitate qualitative analyses in general contexts.
Similar content being viewed by others
Introduction
The giant magnetoresistance (GMR) effect, which is discovered in sandwiched structures of magnetic and nonmagnetic materials in 19881,2, means that a large conductance difference turns up when the relative spin orientation in adjacent magnetic materials change from parallel (p) to antiparallel (ap). GMR is essential in some spintronic devices that manipulate electron spin rather than charge3 and has led to the explosive enlargement of storage capability on hard disk in the last decades, reflecting its important value in commercial applications.
Charge and spin thermopower of a material describes the ability to produce charge and spin current, respectively, from a temperature gradient rather than a voltage one. Charge thermopower devices such as thermocouple have been widely used in our daily life. Spin thermopower has been observed in magnetic4 and nonmagnetic5 materials and should have application potential in spintronics. Similar to the GMR effect, the thermopower in magnetic junctions can change when the magnetic configuration changes from p to ap and lead to the magneto-thermopower phenomena6. The GMR and thermopower effects are both intrinsically relevant to the transmission spectrum in tunneling junctions. Recently, magnetoresistance7,8,9,10,11,12,13 and spin thermopower13,14,15,16 in graphene-like nanoribbons have become one of the focuses.
The discovery of graphene and its many outstanding properties17 has inspired enormous attentionon on graphene-like two-dimensional (2D) materials. The long spin relaxation time and length in graphene indicates it a prospective material for spintronics18. Specially, experimental observations have confirmed the existence of magnetism on zigzag edges of graphene19,20. Both theoretical models20,21,22 and computational simulations based on ab initio density functional theory23,24 have shown that the magnetism origins from the spin polarized edge atoms. Zigzag graphene nanoribbons (ZGNRs) have two zigzag edges and can be in ferromagnetic (FM) or antiferromagnetic (AFM) state classified by the relative spin orientations on the two edges20,24. External magnetic field can convert a ZGNR from its ground insulator AFM state to its metallic FM state. The consequent large colossal magnetoresistance was observed persistent up to room temperature7. In addition, GMR in FM ZGNRs of even width has been predicted very high10 as well as the colossal magnetoresistance8. ZGNR based GMR devices are believed very useful based on the fact that ZGNRs can be synthesized and relevant devices fabricated in atomic precision with the state-of-the-art technology19,20. Traditional chemical and physical edge functionalizations in atomistic scale such as atom adsorption, doping, vacancy and local lattice distortion have been proposed to manipulate further the properties and design diversified devices25,26. Specifically, the edge disorders or defects can break geometry symmetry of ZGNRs and enhance the spin thermopower effect. In addition, scanning tunneling microscopy (STM) tip and atomic force microscopic techniques can be used as atomistic gate to apply local electrostatic potential for graphene transistors and manually introduce and control the disorders27,28. In this work, based on the tight-binding model and the first-principles simulations, we propose a mechanism to switch on and off GMR and spin thermopower by applying an atomistic extrinsic potential on edge of FM zigzag nanoribbons (ZNRs) of two-dimensional (2D) graphene-like honeycomb lattice. Our prediction may be confirmed via an experimental setup schemed in Fig. 1 by combining the techniques for measuring the current-voltage curve of narrow nanoribbons7,29,30 with the STM techniques for controlling the potential in atomistic scale27,28. In addition, the effects discussed in the following for single local potential or impurity might be enhanced in disordered systems31.
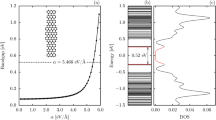
(a) Schematic structure of a FM n-ZNR two-probe junction with a central region of length 2 m. A third probe, the STM tip, can apply a local potential Ui at an edge site i ∈ [−m, m] to manipulate the magnetoresistance RM and spin Seebeck coefficient SS. Edge site 0 (in red) has the minimal magnetization in the ap configuration. The colored arrow indicates the spin orientation of the electrodes. (b,c) Edge magnetization profile along the x direction in the ap and p configurations, respectively, for up (red) and down (blue) spins. (d,e) A possible variation set of  , RM, and SS with a square-wave signal Ui applied by the STM tip for even and odd n, respectively. (f) Zero temperature RM versus U0 in a 4-ZNR (red) and a 20-ZNR (blue) with m = 5 and M = 0.1 t. The left inset shows the transmission spectra
, RM, and SS with a square-wave signal Ui applied by the STM tip for even and odd n, respectively. (f) Zero temperature RM versus U0 in a 4-ZNR (red) and a 20-ZNR (blue) with m = 5 and M = 0.1 t. The left inset shows the transmission spectra  (red) and
(red) and  (blue) under U0 = 0, 0.1, 0.2, 0.5, 1.0 t (upward) in a 4-ZNR and the right shows
(blue) under U0 = 0, 0.1, 0.2, 0.5, 1.0 t (upward) in a 4-ZNR and the right shows  . (g) Same as (f) for odd n = 5 (red) and 21 (blue) and the insets for n = 5. Note that the spectra for U0 ≠ 0 in the insets of (f,g) have been shifted upward for clearness and the vertical value of their fact parts is equal to 1.
. (g) Same as (f) for odd n = 5 (red) and 21 (blue) and the insets for n = 5. Note that the spectra for U0 ≠ 0 in the insets of (f,g) have been shifted upward for clearness and the vertical value of their fact parts is equal to 1.
Models and Methods
As schemed in Fig. 1(a), we partition a FM ZNR into two-probe devices with left (L) and right (R) electrodes and a central (C) device region (domain wall in the ap configuration). A simplified tight-binding Hamiltonian can be used to describe the system9

here  (ci,σ) is the creation (annihilation) operator of spin σ (↑ or ↓) on site i. t is the nearest-neighbor hopping integral and is chosen as the unit of energy throughout the paper. The uniform on-site energy of the corresponding pristine 2D materials gives the Dirac point energy and is set to zero. Ui and λσMi (λ↑ = −1 and λ↓ = +1) are the on-site extrinsic potential energy from gate or disorder and the local magnetization, respectively. The magnetizations on the two edges are in parallel and linearly decay to zero from the edges to the center along the y direction. Along the x direction, λσMi is constant λσM (full magnetization) in the electrodes and varies linearly in region C as depicted in Fig. 1(b,c) for the ap and p magnetic configurations of electrodes, respectively.
(ci,σ) is the creation (annihilation) operator of spin σ (↑ or ↓) on site i. t is the nearest-neighbor hopping integral and is chosen as the unit of energy throughout the paper. The uniform on-site energy of the corresponding pristine 2D materials gives the Dirac point energy and is set to zero. Ui and λσMi (λ↑ = −1 and λ↓ = +1) are the on-site extrinsic potential energy from gate or disorder and the local magnetization, respectively. The magnetizations on the two edges are in parallel and linearly decay to zero from the edges to the center along the y direction. Along the x direction, λσMi is constant λσM (full magnetization) in the electrodes and varies linearly in region C as depicted in Fig. 1(b,c) for the ap and p magnetic configurations of electrodes, respectively.
In the Landauer-Buttiker formalism with non-coherent effects neglected, the current of spin σ read  where
where  is the Fermi-Dirac distribution function
is the Fermi-Dirac distribution function  in electrode L (R). T and μσ are the electron temperature and the Fermi energy. τσ(ε) = Tr[ΓL(ε)Gr(ε)ΓR(ε)Ga(ε)]σ is the electron transmission calculated by nonequilibrium Green’s function (NEGF) method32. Here Gr(ε) = [Ga(ε)]+ = [ε − hC − ∑L − ∑R]−1 is the retarded Green’s function corresponding to the Hamiltonian hC in region C and
in electrode L (R). T and μσ are the electron temperature and the Fermi energy. τσ(ε) = Tr[ΓL(ε)Gr(ε)ΓR(ε)Ga(ε)]σ is the electron transmission calculated by nonequilibrium Green’s function (NEGF) method32. Here Gr(ε) = [Ga(ε)]+ = [ε − hC − ∑L − ∑R]−1 is the retarded Green’s function corresponding to the Hamiltonian hC in region C and  is the broadening function. The self-energy function ∑L(R) due to the coupling between the device and electrode L (R) is obtained via the iterative procedure.
is the broadening function. The self-energy function ∑L(R) due to the coupling between the device and electrode L (R) is obtained via the iterative procedure.
In the linear response regime of small voltage bias ΔVσ and temperature difference ΔT between the electrodes, we express  in Taylor expansion33 and have Iσ = G0K0σ(μσ, T)ΔVσ + G0K1σ(μσ, T)ΔT/(eT) with Kνσ = ∫dε(ε − μσ)ντσ(ε)(∂fσ/∂ε) for ν = 0, 1 and the conductance quantum G0 = e2/h. The tunneling magnetoresistance
in Taylor expansion33 and have Iσ = G0K0σ(μσ, T)ΔVσ + G0K1σ(μσ, T)ΔT/(eT) with Kνσ = ∫dε(ε − μσ)ντσ(ε)(∂fσ/∂ε) for ν = 0, 1 and the conductance quantum G0 = e2/h. The tunneling magnetoresistance  of the device is then evaluated34 from the total linear conductance
of the device is then evaluated34 from the total linear conductance  in the p (ap) configuration. The charge and spin Seebeck coefficients are defined by SC(S) = (S↑ ± S↓)/2 with
in the p (ap) configuration. The charge and spin Seebeck coefficients are defined by SC(S) = (S↑ ± S↓)/2 with  when Iσ = 035,36,37,38. At low temperature the Mott formula35,36
when Iσ = 035,36,37,38. At low temperature the Mott formula35,36  applies and analytical results can be obtained in simple cases.
applies and analytical results can be obtained in simple cases.
More realistic Hamiltonians for ZNRs of specific materials can be obtained from the density functional theory (DFT) based on first-principles. As an example, we have carried out simulations on magnetoresistance and thermopower for doped n-ZGNRs with width n employing the Atomistic Toolkits (ATK) package39,40. The double-ζ plus polarization (DZP) basis set and an energy cutoff of 150 Ry within the local spin density approximation (LSDA) are used in the DFT simulation and a force tolerance of 0.03 eV/Å is set on each atom during the geometry relaxation. We find good agreement between results from the tight-binding model and from the first-principles simulations.
Results and Discussion
We consider ZNR systems of m = 5 in the linear response regime with the Fermi energy at the neutral point, i.e. μσ = 0 throughout the manuscript. The effect of one single impurity on the Fermi energy is assumed negligible. For systems with Fermi energy away from the neutral point, the conductance of the system can be estimated from the energy dependence of transmission. In the p configuration, perfect ZNRs are uniformly magnetized and translationally symmetric along the x direction. The extended edge states have flat bands at the full magnetization energy λσM near the boundary of the first Brillouin zone. There is one transport channel for each spin σ at ε = 09 so  for both even and odd n at zero temperature. In the presence of a local extrinsic potential Ui at any edge site i, a bound state of energy
for both even and odd n at zero temperature. In the presence of a local extrinsic potential Ui at any edge site i, a bound state of energy  appears around the site with
appears around the site with  . The bound state can slightly reduce
. The bound state can slightly reduce  if
if  is close to zero41 as illustrated by the transmission spectra
is close to zero41 as illustrated by the transmission spectra  in the left insets of Fig. 1(f,g) where Ui > 0. The charge and spin thermopower are both very limited according to the Mott formula.
in the left insets of Fig. 1(f,g) where Ui > 0. The charge and spin thermopower are both very limited according to the Mott formula.
In the ap configuration the conductance becomes much more sensitive to Ui and n. We define the site i = 0 as the edge site where the magnetization reverses direction in the domain wall. For a geometrically left-right symmetric junction as schemed in Fig. 1(a), the residual magnetization vanishes at site 0, i.e. M0 = 0. In the absence of extrinsic potential Ui, we have  for even n and
for even n and  for odd n at zero temperature due to geometry symmetry as indicated in the right insets of Fig. 1(f,g). The corresponding magnetoresistance RM is about 100% for even n and very small for odd n10,11,12,13,17. In the presence of Ui, we will present the results for Ui > 0 in two typical cases, i = 0 and i > 0 in the following since those for Ui < 0 or i < 0 can be then deduced based on the symmetry of the systems.
for odd n at zero temperature due to geometry symmetry as indicated in the right insets of Fig. 1(f,g). The corresponding magnetoresistance RM is about 100% for even n and very small for odd n10,11,12,13,17. In the presence of Ui, we will present the results for Ui > 0 in two typical cases, i = 0 and i > 0 in the following since those for Ui < 0 or i < 0 can be then deduced based on the symmetry of the systems.
At first we apply a local potential U0 only at edge site 0 of an n-ZNR. For even n, as shown in the right inset of Fig. 1(f), a transmission peak emerges at ε = 0 with  approaching to unit as U0 increases. The corresponding RM, as plotted in Fig. 1(f), then decreases from 100% to near zero and can become negative if
approaching to unit as U0 increases. The corresponding RM, as plotted in Fig. 1(f), then decreases from 100% to near zero and can become negative if  is reduced to
is reduced to  by the bound state. In contrast, for odd n as illustrated in Fig. 1(g),
by the bound state. In contrast, for odd n as illustrated in Fig. 1(g),  decreases inversely with U0 from unit and approaches to zero, which leads to a jump of RM from zero to near 100%. When the dip bottom of
decreases inversely with U0 from unit and approaches to zero, which leads to a jump of RM from zero to near 100%. When the dip bottom of  due to the bound state passes through the Fermi energy near U0 = 0.5 t, a RM minimum appears for both even and odd n.
due to the bound state passes through the Fermi energy near U0 = 0.5 t, a RM minimum appears for both even and odd n.
The conductance and magnetoresistance are also relevant to the full magnetization M which can vary for different materials and/or substrates. In Fig. 2(a,b), we plot  versus M under U0 = t for various even and odd n, respectively. In nonmagnetic ZNRs (M = 0),
versus M under U0 = t for various even and odd n, respectively. In nonmagnetic ZNRs (M = 0),  or RM = 0. As M increases,
or RM = 0. As M increases,  decreases gradually from 2G0 but remains high for even n. In contrast, for odd n,
decreases gradually from 2G0 but remains high for even n. In contrast, for odd n,  is very sensitive to M and jumps down to zero once M becomes finite, similar to the behavior of perfect even-width ZNRs10 as shown in the inset of Fig. 2(a). It then increases monotonically with M but remains in low values. In the range of M ∈ [0, 0.2]t,
is very sensitive to M and jumps down to zero once M becomes finite, similar to the behavior of perfect even-width ZNRs10 as shown in the inset of Fig. 2(a). It then increases monotonically with M but remains in low values. In the range of M ∈ [0, 0.2]t,  in 2-ZNRs while
in 2-ZNRs while  in 3-ZNRs and the difference between
in 3-ZNRs and the difference between  of even- and odd-width ZNRs enlarges as the width increases. In the insets of Fig. 2(a,b), we plot also the variation of
of even- and odd-width ZNRs enlarges as the width increases. In the insets of Fig. 2(a,b), we plot also the variation of  versus M under U0 of different strengths to show its dependence. At any finite M,
versus M under U0 of different strengths to show its dependence. At any finite M,  increases (decreases) from zero (2G0) and saturates to 2G0 (zero) for even (odd) n as U0 increases (see also the insets of Fig. 1(f,g) and Figure S1).
increases (decreases) from zero (2G0) and saturates to 2G0 (zero) for even (odd) n as U0 increases (see also the insets of Fig. 1(f,g) and Figure S1).
(a,b) Show the total zero-temperature conductance  versus the edge magnetization M in the presence of potential U0 = t at edge site 0 of n-ZNRs for even n (2, 4, 10, 20) and odd n (3, 5, 11, 21), respectively. The corresponding magnetoresistance RM is illustrated in (c,d).
versus the edge magnetization M in the presence of potential U0 = t at edge site 0 of n-ZNRs for even n (2, 4, 10, 20) and odd n (3, 5, 11, 21), respectively. The corresponding magnetoresistance RM is illustrated in (c,d).  versus M and RM versus T at M = 0.1 t are plotted in the insets of the upper and lower panels, respectively, for 4-ZNRs and 5-ZNRs under different U0. Note that results of M = 0 are not shown.
versus M and RM versus T at M = 0.1 t are plotted in the insets of the upper and lower panels, respectively, for 4-ZNRs and 5-ZNRs under different U0. Note that results of M = 0 are not shown.
The corresponding magnetoresistances RM versus M are shown in Fig. 2(c,d) for even and odd n, respectively. Under U0 = t, RM is well below 10% for all even n and above 60% for all odd n in the range M ∈ [0, 0.2]t. When the energy of the bound state confined by U0 in the p configuration is close to the Fermi energy, RM can be negative for even n and shows an extra dip for odd n.
Using the density functional theory combined with the nonequilibrium Green’s function implemented in the ATK package39,40, we have simulated the transmission spectrum of hydrogen-passivated 4-ZGNRs and 5-ZGNRs substitutionally doped by a boron atom at edge site 0. The result agrees well with that from the tight-binding model of parameters M = 0.07 t, U0 = 1.15 t for 4-ZGNR and M = 0.08 t, U0 = 1.20 t for 5-ZGNR with t = 2.7 eV as shown in Figure S2. The magnetoresistance switch effect can be quite robust in real materials like ZGNRs. In the insets of Fig. 2(c,d), we plot RM versus the temperature T for 4-ZNRs and 5-ZNRs with parameters close to those of the above boron doped ZGNRs, i.e. U0 = t and M = 0.1 t. The behaviors of perfect/doped and even/odd ZNRs remains well distinguished from each other up to the room temperature T = 0.01 t/kB.
In the simplest case of 2-ZNR structure with m = 0, we have the analytical transmission expressions  and
and  with
with  and
and  . They may be helpful for qualitative analysis in more general contexts. For M = 0.1 t, the zero temperature magnetoresistance decreases from RM = 100% at Ui = 0 to RM = −22.1% at U0 = t similar to the result presented in Fig. 2(c) with m = 5 (see Figure S3 for the details).
. They may be helpful for qualitative analysis in more general contexts. For M = 0.1 t, the zero temperature magnetoresistance decreases from RM = 100% at Ui = 0 to RM = −22.1% at U0 = t similar to the result presented in Fig. 2(c) with m = 5 (see Figure S3 for the details).
If the potential shifts from site 0 to a site i > 0 where a downward residual magnetization Mi exists, the two-fold rotation symmetry of the system is broken and the transmission becomes spin dependent. The spin thermopower in the ap configuration can be greatly enhanced and shows strong even-odd effects on the nanoribbon width.
In even-width nanoribbons the spin-up (down) transmission peak shifts accordingly from  to
to 
 as shown in Fig. 3(a) for U2 = t, n = 4, i = 2, and M2 = iM/(m + 1) = 0.033 t with M = 0.1 t and m = 5. The transmission spectrum then has a positive
as shown in Fig. 3(a) for U2 = t, n = 4, i = 2, and M2 = iM/(m + 1) = 0.033 t with M = 0.1 t and m = 5. The transmission spectrum then has a positive  (negative
(negative  ) which results in a negative S↑ (positive S↓) at low temperature according to the Mott formula. Interestingly, the spin Seebeck coefficient appears usually much greater than the charge one, i.e. |SS| ≫ |SC|, because the transmission peaks of up and down spins are located almost symmetrically beside the Fermi energy, i.e.
) which results in a negative S↑ (positive S↓) at low temperature according to the Mott formula. Interestingly, the spin Seebeck coefficient appears usually much greater than the charge one, i.e. |SS| ≫ |SC|, because the transmission peaks of up and down spins are located almost symmetrically beside the Fermi energy, i.e.  and τ↑(0) ≈ τ↓(0). SS can be further enhanced in wider nanoribbons where the transmission peaks become sharper with bigger |τ′(0)| and smaller τ(0).
and τ↑(0) ≈ τ↓(0). SS can be further enhanced in wider nanoribbons where the transmission peaks become sharper with bigger |τ′(0)| and smaller τ(0).
(a)  (solid) and
(solid) and  (dotted) of a 4-ZNR under a potential U2 = t at edge site 2. (b,c) SS and SC versus the temperature T, respectively, of n-ZNRs for even n = 4 (thin), 10 (medium), and 20 (thick) at U2 = t and M = 0.1 t. (d)
(dotted) of a 4-ZNR under a potential U2 = t at edge site 2. (b,c) SS and SC versus the temperature T, respectively, of n-ZNRs for even n = 4 (thin), 10 (medium), and 20 (thick) at U2 = t and M = 0.1 t. (d)  and (e) τσ(0)/τ′σ(0) of up (solid) and down (dotted) spins are plotted versus the local edge magnetization M2 for n = 4 (thin), 10 (medium), and 20 (thick) as M varies. (f–j) The same as in (a–e) for odd n = 5, 11, 21 with
and (e) τσ(0)/τ′σ(0) of up (solid) and down (dotted) spins are plotted versus the local edge magnetization M2 for n = 4 (thin), 10 (medium), and 20 (thick) as M varies. (f–j) The same as in (a–e) for odd n = 5, 11, 21 with  replaced by
replaced by  .
.
The temperature dependent SS and SC plotted in Fig. 3(b,c), respectively, indicate that the Mott formula is valid below the critical temperature Tc = τ(1−τ )/τ′kB|ε=0 which is determined by the width Δσ and the position  of the transmission peak. At high temperature the Seebeck coefficients decay gradually with the temperature due to the nonlinearity of the transmission spectrum.
of the transmission peak. At high temperature the Seebeck coefficients decay gradually with the temperature due to the nonlinearity of the transmission spectrum.
The Seebeck coefficients can also be manipulated by the full magnetization M since both  and Δσ increase with M. As illustrated in Fig. 3(d,e) for i = 2, the variation of τ(0) is limited due to the opposite effects from increase of
and Δσ increase with M. As illustrated in Fig. 3(d,e) for i = 2, the variation of τ(0) is limited due to the opposite effects from increase of  and Δσ but |τ′(0)| decreases quickly and results in the decrease of Sσ. On the other hand, if the potential shifts from site 2 to site 3 while M remains fixed,
and Δσ but |τ′(0)| decreases quickly and results in the decrease of Sσ. On the other hand, if the potential shifts from site 2 to site 3 while M remains fixed,  increases since M3 > M2, SS then increases with the decrease of τ(0).
increases since M3 > M2, SS then increases with the decrease of τ(0).
In odd-width nanoribbons, the spin-up (down) transmission dip shifts from  to
to 
 when the potential moves from site 0 to a site i > 0 as shown in Fig. 3(f) for n = 5. The dip width Δσ increases with
when the potential moves from site 0 to a site i > 0 as shown in Fig. 3(f) for n = 5. The dip width Δσ increases with  but decreases with n. We have
but decreases with n. We have  and then a positive SS rather than the negative one in even-width nanoribbons. SS decreases with i since the corresponding increase of
and then a positive SS rather than the negative one in even-width nanoribbons. SS decreases with i since the corresponding increase of  enhances τ(0). SS decreases also with M because the increase of both Δσ and
enhances τ(0). SS decreases also with M because the increase of both Δσ and  reduces τ′(0) as shown in Fig. 3(j). If n increases, SS becomes weaker further as illustrated in Fig. 3(g) when the decrease of Δσ leads to competing larger τ′(0) and larger τ(0). Different from the cases in even-width ZNRs, as shown in Fig. 3(i,j),
reduces τ′(0) as shown in Fig. 3(j). If n increases, SS becomes weaker further as illustrated in Fig. 3(g) when the decrease of Δσ leads to competing larger τ′(0) and larger τ(0). Different from the cases in even-width ZNRs, as shown in Fig. 3(i,j),  and
and  are more sensitive to n in odd-width ZNRs.
are more sensitive to n in odd-width ZNRs.
Summary
Zigzag nanoribbons of graphene-like materials are expected very useful for spintronics due to their edge spin polarization or magnetism. Giant magnetoresistance exists in pristine even-width ferromagnetic nanoribbons. With the help of an atomistic gate potential or edge disorder, the giant magnetoresistance can be switched off (on) in even- (odd-) width nanoribbons. This originates from the jump of electronic transmission at the Fermi energy from zero to near 100% or verse vise in the antiparallel magnetic configuration if the potential is located at the transition interface of magnetization. If the potential shifts from the interface, the transmission peaks or dips of opposite spins split symmetrically beside the Fermi energy. The spin thermopower then becomes very large according to the Mott formula showing strong magneto-thermopower effect. This suggests that spin current can be produced from temperature gradient in the material.
Additional Information
How to cite this article: Zhai, M.-X. and Wang, X.-F. Atomistic switch of giant magnetoresistance and spin thermopower in graphene-like nanoribbons. Sci. Rep. 6, 36762; doi: 10.1038/srep36762 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Baibich, M. N., Broto, J. M., Fert, A., Nguyen Van Dau, F. & Petroff, F. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 61, 2472–2475 (1988).
Binasch, G., Grunberg, P., Saurenbach, F. & Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828–4830 (1989).
Prinz, G. A. Magnetoelectronics. Science 282, 1660–1663 (1998).
Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).
Jaworski, C. M., Myers, R. C., Johnston-Halperin, E. & Heremans, J. P. Giant spin Seebeck effect in a non-magneticmaterial. Nature 487, 210–213 (2012).
Walter, M. et al. Seebeck effect in magnetic tunnel junctions. Nature Mater. 10, 742–746 (2011).
Bai, J. et al. Very large magnetoresistance in graphene nanoribbons. Nature Nanotech. 5, 655–659 (2010).
Muñoz-Rojas, F., Fernández-Rossier, J. & Palacios, J. J. Giant Magnetoresistance in Ultrasmall Graphene Based Devices. Phys. Rev. Lett. 102, 136810-1-4 (2009).
Zhang, Y. T., Jiang, H., Sun, Q. F. & Xie, X. C. Spin polarization and giant magnetoresistance effect induced by magnetization in zigzag graphene nanoribbons. Phys. Rev. B 81, 165404-1-6 (2010).
Kim, W. Y. & Kim, K. S. Prediction of very large values of magnetoresistance in a graphene nanoribbon device. Nature Nanotech. 3, 408–412 (2008).
Wang, Z. F. & Liu, F. Giant magnetoresistance in zigzag graphene nanoribbon. Appl. Phys. Lett. 99, 042110-1-3 (2011).
Xu, C. et al. Giant magnetoresistance in silicene nanoribbons. Nanoscale 4, 3111–3117 (2012).
Zhai, M. X. et al. Giant magnetoresistance and spin Seebeck coefficient in zigzag a-graphyne nanoribbons. Nanoscale 6, 11121–11129 (2014).
Chen, A. B. et al. Spin-dependent ballistic transport properties and electronic structures of pristine and edge-doped zigzag silicene nanoribbons: large magnetoresistance. Phys. Chem. Chem. Phys. 16, 5113–5118 (2014).
Zeng, M., Huang, W. & Liang, G. Spin-dependent thermoelectric effects in graphene based spin valves. Nanoscale 5, 200–208 (2013).
Liu, Y. S., Wang, X. F. & Chi, F. Non-magnetic doping induced a high spin-filter efficiency and large spin Seebeck effect in zigzag graphene nanoribbons. J. Mater. Chem. C 1, 8046–8051 (2013).
Novoselov, K. S. et al. Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669 (2004).
Tombros, N., Jozsa, C., Popinciuc, M., Jonkman, H. T. & van Wees, B. J. Electronic spin transport and spin precession in single graphene layers at room temperature. Nature 448, 571–574 (2007).
Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).
Magda, G. Z. et al. Room-temperature magnetic order on zigzag edgesof narrow graphene nanoribbons. Nature 514, 608–611 (2014).
Fujita, M., Wakabayashi, K., Nakada, K. & Kusakabe, K. J. Peculiar localized state at zigzag graphite edge. Phys. Soc. Jap. 65, 1920–1923 (1996).
Fernández-Rossier, J. Prediction of hidden multiferroic order in graphene zigzag ribbons. Phys. Rev. B 77, 075430-1-5 (2008).
Son, Y. W., Cohen, M. L. & Louie, S. G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 97, 216803-1-4 (2006).
Pisani, L., Chan, J. A., Montanari, B. & Harrison, N. M. Electronic structure and magnetic properties of graphitic ribbons. Phys. Rev. B 75, 064418-1-9 (2007).
Georgakilas, V. et al. Functionalization of graphene: covalent and non-covalent approaches, derivatives and applications. Chem. Rev. 112, 6156–6214 (2012).
Martins, T. B., Miwa, R. H., da Silva, A. J. R. & Fazzio, A. Electronic and transport properties of boron-doped graphene nanoribbons. Phys. Rev. Lett. 98, 196803-1-4 (2007).
Wong, D. et al. Characterization and manipulation of individual defects in insulating hexagonal boron nitride using scanning tunneling microscopy. Nature Nanotech. 10, 949–953 (2015).
Stroscio, J. A. & Eigler, D. M. Atomic and molecular manipulation with the scanning tunneling microscope. Science 254, 1319–1326 (1991).
Díez-Pérez, I. et al. Rectification and stability of a single molecular diode with controlled orientation. Nature Chem. 1, 635–641 (2009).
Cretu, O. et al. Electrical Transport Measured in Atomic Carbon Chains. Nano Lett. 13, 3487–3493 (2013).
Rocha, A. R., Martins, T. B., Fazzio, A. & da Silva, A. J. R. Disorder-based graphene spintronics. Nanotechnology 21, 345202-1-6 (2010).
Datta, S. Quantum Transport: Atom to transistor. (England: Cambridge University Press 2005).
Rejec, T., Ramšak, A. & Jefferson, J. Spin-dependent thermoelectric transport coefficients in near perfect quantum wires. Phys. Rev. B 65, 235301-1-5 (2002).
Heiliger, C., Zahn, P. & Mertig, I. Microscopic origin of magnetoresistance. Mat. Today 9, 46–54 (2006).
Cutler, M. & Mott, N. F. Observation of Anderson Localization in an Electron Gas. Phys. Rev. 181, 1336–1340 (1969).
Mott, N. F. & Davis, E. A. Electronic Processes in Non-Crystalline Materials. (New York: Oxford University Press 2012).
Sivan, U. & Imry, Y. Multichannel Landauer formula for thermoelectric transport with application to thermopower near the mobility edge. Phys. Rev. B 33, 551–558 (1986).
Paulsson, M. & Datta, S. Thermoelectric effect in molecular electronics. Phys. Rev. B 67, 241403-1-4 (2003).
Taylor, J., Guo, H. & Wang, J. Ab initio modeling of open systems: Charge transfer, electron conduction, and molecular switching of a C60 device. Phys. Rev. B 63, 121104-1-4 (2001).
Brandbyge, M., Mozos, J. L., Ordejón, P., Taylor, J. & Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 65, 165401-1-17 (2002).
Li, T. C. & Lu, S. P. Quantum conductance of graphene nanoribbons with edge defects. Phys. Rev. B 77, 085408-1-8 (2008).
Acknowledgements
We appreciate Hong Guo and Yu-Shen Liu for helpful discussion. This work was supported by National Natural Science Foundation of China (Grant Nos 61674110 and 91121021).
Author information
Authors and Affiliations
Contributions
M.-X.Z. and X.-F.W. designed research, performed research, analyzed data, and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Zhai, MX., Wang, XF. Atomistic switch of giant magnetoresistance and spin thermopower in graphene-like nanoribbons. Sci Rep 6, 36762 (2016). https://doi.org/10.1038/srep36762
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36762
This article is cited by
-
Thermoelectric properties of graphene-like nanoribbon studied from the perspective of symmetry
Scientific Reports (2020)
-
The magnetism enhancement and spin transport in zigzag borophene nanoribbons edge-passivated by N atoms
Applied Nanoscience (2020)
-
Electronic Structure and I-V Characteristics of InSe Nanoribbons
Nanoscale Research Letters (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.