Abstract
In this paper, we present a protocol to generate a W state of three superconducting qubits (SQs) by using multiple Schrödinger dynamics. The three SQs are respective embedded in three different coplanar waveguide resonators (CPWRs), which are coupled to a superconducting coupler (SCC) qubit at the center of the setups. With the multiple Schrödinger dynamics, we build a shortcuts to adiabaticity (STA), which greatly accelerates the evolution of the system. The Rabi frequencies of the laser pulses being designed can be expressed by the superpositions of Gaussian functions via the curves fitting, so that they can be realized easily in experiments. What is more, numerical simulation result shows that the protocol is robust against control parameters variations and decoherence mechanisms, such as the dissipations from the CPWRs and the energy relaxation. In addition, the influences of the dephasing are also resisted on account of the accelerating for the dynamics. Thus, the performance of the protocol is much better than that with the conventional adiabatic passage techniques when the dephasing is taken into account. We hope the protocol could be implemented easily in experiments with current technology.
Similar content being viewed by others
Introduction
Entanglement plays a significant role in quantum information processing (QIP)1,2,3,4,5,6,7,8,9,10,11,12. Therefore, the generation of entangled states for two or more particles is not only fundamental for showing quantum nonlocality13,14,15, but also useful in many research fields in QIP, such as, quantum secure direct communication16,17, quantum secret sharing18,19, quantum teleportation20,21, quantum cloning machine22,23 and so on. For multi-qubit entanglement, there are two major types of entangled states, the W states14 and the Greenberger-Horne-Zeilinger (GHZ) states15, which can not be converted to each other by local operations and classical communications. The GHZ states are usually called as “maximally entangle” in several senses, e.g., the GHZ state violates Bell inequalities maximally. But a particle trace of a GHZ state results in a maximally mixed state compared with a nonmaximally mixed result for a W state, i.e., the W states show perfect correlations. Therefore, in past several years, the W states have attracted more attentions because of their robustness against qubit loss and advantages in quantum teleportation20.
Till now, the generation of the W states has been studied in numerous systems24,25,26,27,28,29,30,31,32,33,34,35, such as the atom-cavity coupled systems24,25,26, electronic spin qubits inside the quantum dots systems27, photons and linear optical systems28,29, superconducting qubits (SQs) systems30,31,32,33,34,35,36, etc. Among of these protocols24,25,26,27,28,29,30,31,32,33,34,35,36, the generation of W states with SQs has shown fantastic advantages, since new progress in circuit cavity quantum electrodynamics makes it a standout performance among the most promising candidates for implementing QIP37,38. It has been shown that, the SQs (e.g., flux, phase and charge qubits) and microwave resonators can be manufactured using modern integrated circuit technology, their features can be characterized and adjusted in situ. Moreover, the SQs have relatively long decoherence times39, and various single and multiple qubits operations with state readout have been shown40,41,42,43. Furthermore, a superconducting resonator can provide a quantized cavity field, in order that the fast and long-range interaction between distant SQs could be mediated44,45,46. What is more, it has been proved by both a lot of theoretical researches47,48 and experiments49,50 that, the strong-coupling limit can be easily realized with SQs. Therefore, creating W states with SQs is a wise choice.
On the other hand, if one decides to generate W states with SQs, another question is how to accurately controlling the system with high fidelity. Many previous researches have indicated that the adiabatic passages, especially the stimulated Raman scattering involving adiabatic passage (STIRAP) and its variants51,52,53,54 hold robustness against variations of the controlled parameters. Generally speaking, if the system remains in the instantaneous ground state of its time-dependent Hamiltonian during the whole evolution process under an adiabatic control, the dissipations caused by decoherence, noise and losses may be repressed. However, we all know that, to prevent the transition between each instantaneous eigenstate, the adiabatic condition is required, which will badly limit the evolution speed of the system. During a long evolution, the dissipations may accumulate and finally destroy the intended dynamics. For example, refs 31 and 36 has shown that, the fidelity for generating of the W state by using adiabatic passage is quite sensitive to the dephasing, which is an ineluctable element of the decoherence mechanisms in the superconducting systems, i.e., a small increase of the dephasing rates causes a large decrease of the fidelity; this will also bring challenges to the experiments. Therefore, to overcome the problem causing by the long evolution time of the adiabatic passage, one should speed up the evolution by using some other techniques. To speed up the evolution, using resonant interaction is a choice. But unfortunately, using resonant interaction will make the system quite sensitive to the variations of experimental parameters. For example, if there are a little variations of the evolution time or Rabi frequencies of laser pulses, the fidelity will decrease a lot. It is also proved in ref. 32 that, with resonant interaction, the population of each state changes rapidly when the evolution time increases, and a high fidelity of the target state only appears in very narrow ranges around some certain moments. Therefore, methods with both robustness and high speed are desired, and consequently, a new technique called “Shortcuts to adiabatic passage” (STAP) has been proposed55,56,57,58,59,60,61,62,63.
The STAP is closely related to adiabatic passage but totally breaks the limit of the adiabatic condition. It depicts a rapid adiabatic-like process which is not really adiabatic but leading to the same goals with adiabatic process. With these advantages, the STAP has attracted a lot of interests and been used in many research fields including “fast cold-atom”, “fast ion transport”, “fast quantum information processing”, “fast wave-packet splitting”, “fast expansion”, and so on refs 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93. Among of these protocols55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93, the method named “Transitionless quantum driving” (TQD)58,59,60,61 has shown its power to construct the STAP. However, when we accelerate adiabatic protocols using TQD, the structure or the values of the shortcut-driving Hamiltonian might not exist in practice. For example, in refs 24,80,94, 95, 96, the authors did a lot to design Hamiltonians to overcome the problem caused by the problematic terms which are actually equivalent to the special one-photon 1–3 pulse (the microwave field). Nevertheless, the operations usually cause some other problems or make some other limiting conditions to the protocols, for examples, there will be a limiting condition for the total operation time to generate the entangled states. Therefore, numerous protocols with different methods97,98,99,100,101,102,103,104,105,106,107 have been further presented to avoid the problematic terms of the system’s Hamiltonian which is designed by TQD. Among of these methods97,98,99,100,101,102,103,104,105,106,107, the multiple Schrödinger dynamics104,105 is a very interesting method. It exploits iterative interaction pictures to obtain Hamiltonians with physically feasible structure for quantum systems. Moreover, by choosing suitable boundary conditions, it enables the designed interaction picture to reproduce the same final population (or state) as those in the original Schrödinger picture. In 2012, Ibáñez et al.105 have adopted some Schrödinger pictures and dynamics to design alternative and feasible STAP for harmonic transport, trap expansions and trap compressions. Subsequently, in 2013, Ibáñez et al.104 have studied the capabilities and limitations of superadiabatic iterations to construct a sequence of shortcuts to adiabaticity by iterative interaction pictures. Afterwards, Song et al.106 have investigated the physical feasibility of the multiple Schrödinger dynamics in a three-level systems, and obtained very interesting results in 2016. They have shown that the Hamiltonian of the interaction picture in the second iteration has the same form as the Hamiltonian in the original Schrödinger picture. This makes the multiple Schrödinger dynamics useful in three-level systems.
Inspired by the protocols in refs 104, 105, 106, as well as considering the advantages of the superconducting systems, we come up with a protocol for generating a W state of three SQs by using multiple Schrödinger dynamics. With the help of the multiple Schrödinger dynamics, a STAP is constructed, which greatly speeds up the evolution of the system. The Hamiltonian being designed in this protocol has the same form as the system’s original Hamiltonian. Moreover, the Rabi frequencies of the laser pulses being designed can be expressed by the superpositions of Gaussian functions assisted by the curves fitting, so that they can be realized in experiments. Numerical simulation demonstrates that the protocol is robust against control parameters variations and decoherence mechanisms, such as the dissipations from the coplanar waveguide resonators (CPWRs) and the energy relaxation of SQs. What is more, the influences of the dephasing are also resisted because of the accelerating for the dynamics. Therefore, the performance of the protocol is much better comparing with the conventional adiabatic passage techniques when the dephasing is taken into account. Based on a circuit quantum electrodynamics system, the protocol could be controlled and implemented readily in experiments.
The article is organized as follows. In the section of “The multiple Schrödinger dynamics”, we will introduce the method of the multiple Schrödinger dynamics. In the section of “Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics”, we will describe the generation of a W state of three SQs in detail. In the section of “Numerical simulations and discussions”, we will investigate the performance of the protocol when the control parameters variations and decoherence mechanisms are considered. Finally, the conclusions will be given in the section of “Conclusions”.
The multiple Schrödinger dynamics
In this section, we would like to review the multiple Schrödinger dynamics104,105,106 firstly. Assume that the original Hamiltonian of the system is H0(t). We perform a picture transformation as  , where
, where  and |n0(t)〉 is the n-th instantaneous eigenstate of H0(t). So, the Hamiltonian in the 1-st interaction picture is
and |n0(t)〉 is the n-th instantaneous eigenstate of H0(t). So, the Hamiltonian in the 1-st interaction picture is  with
with  . Suppose that the 1-st modified Schrödinger Hamiltonian is
. Suppose that the 1-st modified Schrödinger Hamiltonian is  . If one hopes the transitions between instantaneous eigenstates {|n0(t)〉} are all forbidden, the simplest choice is
. If one hopes the transitions between instantaneous eigenstates {|n0(t)〉} are all forbidden, the simplest choice is  , so that the Hamiltonian in the 1-st interaction picture is diagonal. If the 1-st modified Hamiltonian
, so that the Hamiltonian in the 1-st interaction picture is diagonal. If the 1-st modified Hamiltonian  is difficult to be realized, the 2-nd interaction picture should be introduced. Assume that {|n1(t)〉} are the eigenstates of H1(t). We perform a picture transformation as
is difficult to be realized, the 2-nd interaction picture should be introduced. Assume that {|n1(t)〉} are the eigenstates of H1(t). We perform a picture transformation as  with
with  . Then, we obtain the Hamiltonian in the 2-nd interaction picture as
. Then, we obtain the Hamiltonian in the 2-nd interaction picture as  with
with  . Suppose that the 2-nd modified Schrödinger Hamiltonian is
. Suppose that the 2-nd modified Schrödinger Hamiltonian is  . To forbid the transitions between {|n1(t)〉} and diagonalize the Hamiltonian in the 2-nd interaction picture,
. To forbid the transitions between {|n1(t)〉} and diagonalize the Hamiltonian in the 2-nd interaction picture,  can be calculated as
can be calculated as  . Repeating the processing as the 1-st and the 2-nd iterations, according to the Hamiltonian in the j-th (
. Repeating the processing as the 1-st and the 2-nd iterations, according to the Hamiltonian in the j-th ( ) interaction picture (Hj(t)), one can obtain the j-th modified Schrödinger Hamiltonian as
) interaction picture (Hj(t)), one can obtain the j-th modified Schrödinger Hamiltonian as

where  and
and  with {|nj(t)〉} being the instantaneous eigenstates of Hj(t). Governed by the Hamiltonian
with {|nj(t)〉} being the instantaneous eigenstates of Hj(t). Governed by the Hamiltonian  , the transitions between instantaneous eigenstates {|nj(t)〉} of Hj are forbidden.
, the transitions between instantaneous eigenstates {|nj(t)〉} of Hj are forbidden.
Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics
In this section, we will show how to generate a W state of three SQs with multiple Schrödinger dynamics. Consider a system composed of a superconducting coupler (SCC) qubit and three CPWRs (CPWR1, CPWR2 and CPWR3). As shown in Fig. 1(a), the SCC qubit in the center of the devices is coupled to CPWRk through capacitor Ck (k ∈ {1, 2, 3}). There is a SQ named SQk in the CPWRk, which has an excited state |e〉k and two ground states |g〉k and |f〉k. As shown in Fig. 1(b) the transition |e〉k ↔ |f〉k is driven by the laser pulse with Rabi frequency Ωk(t), and the transition |e〉k ↔ |g〉k is coupled to CPWRk with coupling constant λk. As for the SCC qubit, it has an excited state |e〉c and two ground states |g〉c and |f〉c, which has similar structure as the three SQs. The transition |e〉c ↔ |f〉c is driven by the laser pulse with Rabi frequency Ωc(t). Different from the three SQs, the transition |e〉c ↔ |g〉c may couple to three CPWRs with different coupling constants. We assume that the coupling constant for the transition |e〉c ↔ |g〉c coupled to CPWRk is νk. Therefore, in the interaction picture, the Hamiltonian for the system can be written by

For simplicity of calculations, we adopt λk = λ and νk = ν in the following. Assuming that the initial state of the system is  , where, |0〉k and |1〉k are the vacuum state and one-photon state of the cavity mode in k-th CPWR, respectively. The excited number operator of the system is defined by
, where, |0〉k and |1〉k are the vacuum state and one-photon state of the cavity mode in k-th CPWR, respectively. The excited number operator of the system is defined by  . As [Ne, HI] = 0, and
. As [Ne, HI] = 0, and  , the system will remain in the one-excited subspace spanned by
, the system will remain in the one-excited subspace spanned by

Moreover, the eigenstates of Hc can be described as

with corresponding eigenvalues ε0 = 0, ε1 = λ, ε2 = λ, ε3 = −λ, ε4 = −λ,  and
and  , respectively.
, respectively.
For simplicity, we set  and
and  . Under the condition Ωa(t),
. Under the condition Ωa(t),  , ν, we can obtain the effective Hamiltonian of the system as
, ν, we can obtain the effective Hamiltonian of the system as

where  ,
,  ,
,  . Without loss the generality, we assume α = π/4. We also assume
. Without loss the generality, we assume α = π/4. We also assume  and
and  . Then, the system’s effective Hamiltonian can written by
. Then, the system’s effective Hamiltonian can written by

Afterwards, the instantaneous eigenstates of Heff(t) can be solved as

with corresponding eigenvalues ϵ0 = 0, ϵ+ = Ω and ϵ− = −Ω, respectively. Therefore, the picture transformation for the 1-st iteration in basis  is
is

By calculating  , in basis
, in basis  , we obtain
, we obtain

If we add  to modify the Hamiltonian Heff(t) in Eq. (6), the structure of the system is also required to be adjusted. Therefore, we consider the 2-nd iteration picture to find another shortcut. Then, the Hamiltonian in the 1-st iteration picture can be solved in basis
to modify the Hamiltonian Heff(t) in Eq. (6), the structure of the system is also required to be adjusted. Therefore, we consider the 2-nd iteration picture to find another shortcut. Then, the Hamiltonian in the 1-st iteration picture can be solved in basis  as
as

Defining  ,
,  and
and  , the eigenstates of H1(t) can be described as
, the eigenstates of H1(t) can be described as

corresponding to the eigenvalues η0 = 0,  and
and  , respectively. Therefore, the picture transformation for the 2-nd iteration in basis
, respectively. Therefore, the picture transformation for the 2-nd iteration in basis  can be given by
can be given by

Submitting j = 2, Eqs (6) and (12) into Eq. (1), one can obtain the 2-nd modified Hamiltonian for Heff(t) in basis  as
as

where  ,
,  ,
,  ,
,  and
and  . We find that
. We find that  has the same form as Heff(t). Therefore, using
has the same form as Heff(t). Therefore, using  instead of Heff(t), we only need to adjust the Rabi frequencies Ωb(t) and Ωa(t).
instead of Heff(t), we only need to adjust the Rabi frequencies Ωb(t) and Ωa(t).
Now, let us design the frequencies Ωb(t) and Ωa(t) so that the system governed by  can be driven from its initial state
can be driven from its initial state  to the target state |W〉. Firstly, when the system is governed by
to the target state |W〉. Firstly, when the system is governed by  , the transitions between instantaneous eigenstates
, the transitions between instantaneous eigenstates  of H1(t) are forbidden. Assuming that the initial time is ti = 0 and the final time is tf = T, we find that if the boundary condition
of H1(t) are forbidden. Assuming that the initial time is ti = 0 and the final time is tf = T, we find that if the boundary condition  is satisfy, the instantaneous eigenstate
is satisfy, the instantaneous eigenstate  of H1 will coincide with the dark state
of H1 will coincide with the dark state  of Heff(t) at t = 0 and t = T. Therefore, we adopt the boundary condition
of Heff(t) at t = 0 and t = T. Therefore, we adopt the boundary condition  , and we set θ(0) = 0 and θ(T) = π/2. Then, we will have the following results
, and we set θ(0) = 0 and θ(T) = π/2. Then, we will have the following results

So, the system will evolve along the instantaneous eigenstate  of H1 and finally at t = T, we can obtain the target state
of H1 and finally at t = T, we can obtain the target state  . After the boundary conditions of θ and
. After the boundary conditions of θ and  are set, in the second step, let us design the Rabi frequencies of the laser pulses. To satisfy the boundary conditions of θ and
are set, in the second step, let us design the Rabi frequencies of the laser pulses. To satisfy the boundary conditions of θ and  mentioned above, we firstly design the Ωb and Ωa via STIRAP. Ωb and Ωa can be expressed as
mentioned above, we firstly design the Ωb and Ωa via STIRAP. Ωb and Ωa can be expressed as

where Ω0 is the pulse amplitude, t0 = 0.16T and tc = 0.25T are two related parameters. By calculating  and
and  , one can obtain the Rabi frequencies
, one can obtain the Rabi frequencies  and
and  of laser pulses for the modified Hamiltonian
of laser pulses for the modified Hamiltonian  . However, the forms of
. However, the forms of  and
and  are too complex to be realized in experiments. For the sake of making the protocol more feasible in experiments, the Rabi frequencies of laser pulses should be expressed by some frequently used functions (e.g. Gaussian functions and sine function), or their superpositions. Fortunately, by using curves fitting,
are too complex to be realized in experiments. For the sake of making the protocol more feasible in experiments, the Rabi frequencies of laser pulses should be expressed by some frequently used functions (e.g. Gaussian functions and sine function), or their superpositions. Fortunately, by using curves fitting,  and
and  can be replaced respectively with
can be replaced respectively with  and
and  , whose expressions can be written by
, whose expressions can be written by
where,

when Ω0 = 8/T. As a comparison, we plot  and
and  versus t/T in Fig. 2(a) and
versus t/T in Fig. 2(a) and  and
and  versus t/T in Fig. 2(b). As shown in Fig. 2, the curve for
versus t/T in Fig. 2(b). As shown in Fig. 2, the curve for  (
( ) is very close to that for
) is very close to that for  (
( ). In the next section, we will show that the laser pulses with Rabi frequencies
). In the next section, we will show that the laser pulses with Rabi frequencies  ,
,  ,
,  and
and  can drive the system from its initial state
can drive the system from its initial state  to the target state
to the target state  with a high fidelity, so, the replacements here for the Rabi frequencies of the laser pulses are effective.
with a high fidelity, so, the replacements here for the Rabi frequencies of the laser pulses are effective.
Numerical Simulations and Discussions
In this section, various numerical simulations will be performed to demonstrate the effective of the present protocol. The fidelity of the target state |W〉 is defined as  , where ρ(t) is the density operator of the system. Firstly, let us choose suitable coupling constants λ and ν. As we adopted α = π/4, the relation between λ and ν is
, where ρ(t) is the density operator of the system. Firstly, let us choose suitable coupling constants λ and ν. As we adopted α = π/4, the relation between λ and ν is  . And the Rabi frequencies of laser pulses satisfy
. And the Rabi frequencies of laser pulses satisfy  . We plot the final fidelity F(T) versus λ in Fig. 3. As shown in Fig. 3, F(T) is near 1 around λ = 10/T. Moreover, F(t) is close to 1 when λ > 20/T. One can easily find that even when the condition
. We plot the final fidelity F(T) versus λ in Fig. 3. As shown in Fig. 3, F(T) is near 1 around λ = 10/T. Moreover, F(t) is close to 1 when λ > 20/T. One can easily find that even when the condition  ,
,  , ν is not satisfied well, the target state |W〉 can also be obtained. This can also easily be understood, as the evolution of the system, between the initial state
, ν is not satisfied well, the target state |W〉 can also be obtained. This can also easily be understood, as the evolution of the system, between the initial state  and the target state |W〉, may move along different medium states, and it is not governed by the effective Hamiltonian Heff(t), which guides the system moving through the dark state
and the target state |W〉, may move along different medium states, and it is not governed by the effective Hamiltonian Heff(t), which guides the system moving through the dark state  of Hc as the only medium state. However, when the condition
of Hc as the only medium state. However, when the condition  ,
,  , ν is broken, the system may move through a medium state with higher energy. That will make the evolution of the system suffers more from dissipations. On the other hand, for a relative higher evolution speed, the value of λT should not be too large, as λ has a upper limit in a real experiment. Therefore, to make the protocol with both high speed and robustness against dissipations, we choose λ = 35/T, slightly larger than
, ν is broken, the system may move through a medium state with higher energy. That will make the evolution of the system suffers more from dissipations. On the other hand, for a relative higher evolution speed, the value of λT should not be too large, as λ has a upper limit in a real experiment. Therefore, to make the protocol with both high speed and robustness against dissipations, we choose λ = 35/T, slightly larger than  (
( ).
).
Secondly, since we have adopted a suitable value of the coupling constant λ, we would like to examine the fidelity F(t) and the population 
 of state
of state  during the evolution. The fidelity F(t) versus t/T is plotted in Fig. 4(a). And the the population Pm of each state is shown in Fig. 4(b). As shown in Fig. 4(a), the fidelity F(t) keeps steady during time intervals [0, 0.3T] and [0.8T, T], and increases rapidly to approach 1 during time interval [0.3T, 0.8T]. As shown in Fig. 4(b), P1 falls from 1 to 0 during evolution; P9, P10 and P11 are initial 0 and final 1/3 at time t = T as our expectation.
during the evolution. The fidelity F(t) versus t/T is plotted in Fig. 4(a). And the the population Pm of each state is shown in Fig. 4(b). As shown in Fig. 4(a), the fidelity F(t) keeps steady during time intervals [0, 0.3T] and [0.8T, T], and increases rapidly to approach 1 during time interval [0.3T, 0.8T]. As shown in Fig. 4(b), P1 falls from 1 to 0 during evolution; P9, P10 and P11 are initial 0 and final 1/3 at time t = T as our expectation.
Thirdly, to show that the present protocol is faster than the adiabatic protocol, we plot the fidelity of the target state |W〉 with different methods versus t/T in Fig. 5. The Rabi frequencies of laser pulses for the STIPAP method can be set as  and
and  , where Ωa(t) and Ωb(t) are shown in Eq. (15). And it is easy to obtain that
, where Ωa(t) and Ωb(t) are shown in Eq. (15). And it is easy to obtain that  . As shown in Fig. 5, the curve of “STAP” describes the change of the fidelity versus t/T of the present protocol, and the curves of “STIRAP” describe the changes of fidelities versus t/T of the STIRAP method under some different conditions. Seen from blue line of Fig. 5, if one use STIRAP method with the same condition as the present protocol (
. As shown in Fig. 5, the curve of “STAP” describes the change of the fidelity versus t/T of the present protocol, and the curves of “STIRAP” describe the changes of fidelities versus t/T of the STIRAP method under some different conditions. Seen from blue line of Fig. 5, if one use STIRAP method with the same condition as the present protocol ( , λ = 35/T), the final fidelity is only about 0.55 due to the greatly violation of the adiabatic condition. Even when
, λ = 35/T), the final fidelity is only about 0.55 due to the greatly violation of the adiabatic condition. Even when  , λ = 100/T (see the pink line of Fig. 5) for the STIRAP method, the fidelity can get close to 1, but the result is still a little unsatisfactory. When
, λ = 100/T (see the pink line of Fig. 5) for the STIRAP method, the fidelity can get close to 1, but the result is still a little unsatisfactory. When  , λ = 150/T (see the green line of Fig. 5) for the STIRAP method, the fidelity can approach 1. However, in this case, the laser amplitude
, λ = 150/T (see the green line of Fig. 5) for the STIRAP method, the fidelity can approach 1. However, in this case, the laser amplitude  is much larger than the one (
is much larger than the one ( ) of the present protocol. If one desire a relative high evolution speed, the product (denotes by μ) of laser amplitude and the evolution time is the smaller the better. Because when two persons have the same value of the laser amplitudes, the one with smaller μ will have less evolution time. Therefore, comparing with the STIRAP method, the present protocol to obtain a W state is much faster by using multiple Schrödinger dynamics. In addition, it is also been shown in ref. 31 that, to obtain a W state with the adiabatic passage with a fidelity larger that 0.99, the authors should chose λ > 100/T and Ω0 = 0.35λ. That supports the discussion here as well.
) of the present protocol. If one desire a relative high evolution speed, the product (denotes by μ) of laser amplitude and the evolution time is the smaller the better. Because when two persons have the same value of the laser amplitudes, the one with smaller μ will have less evolution time. Therefore, comparing with the STIRAP method, the present protocol to obtain a W state is much faster by using multiple Schrödinger dynamics. In addition, it is also been shown in ref. 31 that, to obtain a W state with the adiabatic passage with a fidelity larger that 0.99, the authors should chose λ > 100/T and Ω0 = 0.35λ. That supports the discussion here as well.
Fourthly, since the dissipations caused by decoherence mechanisms are ineluctable in real experiments, it is worthwhile to discuss the fidelity F(t) when different kinds of decoherence factors are considered. In the present protocol, the decay of the cavity mode in each CPWR, the energy relaxation and the dephasing of every SQ play the major roles. The evolution of the system can be described by a master equation in Lindblad form as following

where, Ll (l = 1, 2, 3, …, 19) is the Lindblad operator. There are nineteen Lindblad operators

in which γks and  (k = 1, 2, 3, s = f, g) are the energy relaxation rate and dephasing rate of the k-th SQ for decay path |e〉k → |s〉k, respectively. And γcs and
(k = 1, 2, 3, s = f, g) are the energy relaxation rate and dephasing rate of the k-th SQ for decay path |e〉k → |s〉k, respectively. And γcs and  (s = f, g) are the energy relaxation rate and dephasing rate of the SCC qubit for decay path |e〉c → |s〉c, respectively.
(s = f, g) are the energy relaxation rate and dephasing rate of the SCC qubit for decay path |e〉c → |s〉c, respectively.  (k = 1, 2, 3) is the decay rate of the k-th cavity mode in CPWRk. We suppose γks = γ,
(k = 1, 2, 3) is the decay rate of the k-th cavity mode in CPWRk. We suppose γks = γ,  (k = 1, 2, 3, s = f, g) and
(k = 1, 2, 3, s = f, g) and  (k = 1, 2, 3) for simplicity. We plot the final fidelity F(T) versus
(k = 1, 2, 3) for simplicity. We plot the final fidelity F(T) versus  and γ/λ in Fig. 6(a), versus
and γ/λ in Fig. 6(a), versus  and
and  in Fig. 6(b) and versus γ/λ and γ/λ in Fig. 6(c). And we also examine some samples of the final fidelities F(T) with corresponding
in Fig. 6(b) and versus γ/λ and γ/λ in Fig. 6(c). And we also examine some samples of the final fidelities F(T) with corresponding  , γ/λ and
, γ/λ and  and give them in Table 1. As shown in Fig. 6 and Table 1, we can obtain following results. (i) F(T) is insensitive to decays of the cavity modes in CPWRs. This is easy to be understood by seeing Fig. 4(b). Because the populations of
and give them in Table 1. As shown in Fig. 6 and Table 1, we can obtain following results. (i) F(T) is insensitive to decays of the cavity modes in CPWRs. This is easy to be understood by seeing Fig. 4(b). Because the populations of  ,
,  and
and  are all almost zero during the whole evolution, the influences from decays of the cavity modes in CPWRs will be greatly resisted. (ii) The fidelity suffers more influence from the energy relaxations of SQs comparing with the influences from decays of the cavity modes in CPWRs. However, F(T) is 0.9502 when γ/λ = 0.01,
are all almost zero during the whole evolution, the influences from decays of the cavity modes in CPWRs will be greatly resisted. (ii) The fidelity suffers more influence from the energy relaxations of SQs comparing with the influences from decays of the cavity modes in CPWRs. However, F(T) is 0.9502 when γ/λ = 0.01,  and
and  , i.e., the decreasing of F(T) caused by the increasing of γ is only about 0.05. Therefore, the present protocol is also robust against the energy relaxations of SQs. (iii) The dephasing plays a significant role here. When
, i.e., the decreasing of F(T) caused by the increasing of γ is only about 0.05. Therefore, the present protocol is also robust against the energy relaxations of SQs. (iii) The dephasing plays a significant role here. When  increases from 0 to 0.001, F(T) decreases from 1 to 0.9824. However, in ref. 31, with the adiabatic passages, the fidelity of the target W state deceases from 1 to 0.85 when
increases from 0 to 0.001, F(T) decreases from 1 to 0.9824. However, in ref. 31, with the adiabatic passages, the fidelity of the target W state deceases from 1 to 0.85 when  increases only from 0 to 0.0001. This shows that the present protocol is more robust against the dephasing comparing with the adiabatic passages. According to ref. 107, in experiments, parameters λ = 2π × 300 MHz, γ = 6π MHZ,
increases only from 0 to 0.0001. This shows that the present protocol is more robust against the dephasing comparing with the adiabatic passages. According to ref. 107, in experiments, parameters λ = 2π × 300 MHz, γ = 6π MHZ,  and
and  can be realized. By submitting these parameters, we have F(T) = 0.9484.
can be realized. By submitting these parameters, we have F(T) = 0.9484.
 , γ/λ and
, γ/λ and  .
.Fifthly, since most of the parameters are hard to faultlessly achieve in experiments, it is necessary to investigate the variations of the parameters caused by the experimental imperfection. Here, we discuss the variation δT of the evolution time T, the variation  of the laser amplitude
of the laser amplitude  and the variation δλ of the coupling constant λ. We plot F(T′) versus δT/T and δλ/λ in Fig. 7(a), F(T′) versus δT/T and
and the variation δλ of the coupling constant λ. We plot F(T′) versus δT/T and δλ/λ in Fig. 7(a), F(T′) versus δT/T and  in Fig. 7(b) and F(T) versus δλ/λ and
in Fig. 7(b) and F(T) versus δλ/λ and  in Fig. 7(c), where T′ = T + δT is the real evolution time when the variation of the evolution time is taken into account. Seen from Fig. 7(a,c), the final fidelity is quite insensitive to the variation δλ. This results has also been announced in Fig. 3. Moreover, according to Fig. 7(a,b), the final fidelity F(T′) is very robust against the variation δT. The final fidelity almost unchanged when both δT/T, δλ/λ ≤ 10%. As shown in Fig. 7(b,c), variation
in Fig. 7(c), where T′ = T + δT is the real evolution time when the variation of the evolution time is taken into account. Seen from Fig. 7(a,c), the final fidelity is quite insensitive to the variation δλ. This results has also been announced in Fig. 3. Moreover, according to Fig. 7(a,b), the final fidelity F(T′) is very robust against the variation δT. The final fidelity almost unchanged when both δT/T, δλ/λ ≤ 10%. As shown in Fig. 7(b,c), variation  influences the final fidelity mainly. However, even when
influences the final fidelity mainly. However, even when  , the final fidelity is still higher than 0.95. Therefore, we conclude that the present protocol for generating a W state of three SQs is robust against the variations δT,
, the final fidelity is still higher than 0.95. Therefore, we conclude that the present protocol for generating a W state of three SQs is robust against the variations δT,  and δλ.
and δλ.
Sixthly, in experiments, the protocol can be realized in charge qubits and CPWR coupling system. In other words, all the superconducting qubits including the SCC qubit can be chosen to be charge qubits. The structure of the a charge qubit is shown in Fig. 8. As shown in Fig. 8, the charge qubit contains a gate capacitance and two Josephson junctions with Josephson energy EJ. The charge qubit can be manipulated by controlling the gate voltage Vg and the magnetic flux  threading the loop. It was pointed out in previous protocols108,109 that, for a charge qubit with energy structure as Fig. 1(b), when an external applied magnetic flux
threading the loop. It was pointed out in previous protocols108,109 that, for a charge qubit with energy structure as Fig. 1(b), when an external applied magnetic flux  of a pulse threads the ring, it can driven the transition between |e〉 ↔ |f〉, and the Rabi frequency can be given by
of a pulse threads the ring, it can driven the transition between |e〉 ↔ |f〉, and the Rabi frequency can be given by

where, L is the loop inductance, S is surface bounded by the loop of the charge qubit, Bx (r, t) is the magnetic components of the pulse in the superconducting loop of the charge qubit. For the SQs inside the CPWR, the cavity mode with frequency  can couples resonantly to the levels |g〉 and |e〉 and gives the coupling constant as
can couples resonantly to the levels |g〉 and |e〉 and gives the coupling constant as

where, Bg (r) is the magnetic components of the cavity mode109,110. For the SCC qubits placed in the center of the devices, it can couple capacitively to three different CPWR directly. This kind of directly coupling has been shown in many previous protocols both in theory38,111. For example, Yang et al.38 have used these kind of coupling to generate entanglement between microwave photons and qubits in multiple cavities coupled by a superconducting qubit. Moreover, to improve the efficiency of the coupling between SCC qubit and each CPWR, one can chose SCC qubit to be a transmon112 or a phase qubit113 as well.
Conclusions
In conclusion, we have proposed a protocol to generate a W state of three SQs by using multiple Schrödinger dynamics to construct a shortcut to adiabaticity, so that the evolution of the system has been greatly accelerated. Interestingly, the form of the Hamiltonian being designed by the multiple Schrödinger dynamics was the same as that of the system’s original Hamiltonian. Therefore, we only need to adjust the Rabi frequencies of laser pulses. In this protocol, the Rabi frequencies of the laser pulses can be expressed by the superpositions of Gaussian functions via the curves fitting. So, the laser pulses can be realized easily in experiments. One the other hand, numerical simulations results have demonstrated that the protocol is robust against different kinds of control parameters variations and decoherence mechanisms. Notably, the present protocol is more robust against the dephasing, comparing with adiabatic passages. Therefore, we hope the protocol could be controlled and implemented easily in experiments based on a circuit quantum electrodynamics system.
Additional Information
How to cite this article: Kang, Y.-H. et al. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Sci. Rep. 6, 36737; doi: 10.1038/srep36737 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Barrett, S. D. & Kok, P. Efficient high-fidelity quantum computation using matter qubits and linear optics. Phys. Rev. A. 71, 060310(R) (2005).
Lim, Y. L., Barrett, S. D., Beige, A., Kok, P. & Kwek, L. C. Repeat-until-success quantum computing using stationary and flying qubits. Phys. Rev. A. 73, 012304 (2006).
Zhou, D. L., Sun, B. & You, L. Generating entangled photon pairs from a cavity-QED system. Phys. Rev. A 72, 040302 (2005).
Bennett, C. H. & DiVincenzo, D. P. Quantum information and computation. Nature (London) 404, 247 (2000).
Braunstein, S. L. & Kimble, H. J. Teleportation of continuous quantum variables. Phys. Rev. Lett. 80, 869 (1998).
Bennett, C. H. & Wiesner, S. J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 69, 2881 (1992).
Ekert, A. K. Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 67, 661 (1991).
Divincenzo, D. P. Quantum Computation. Science 270, 255 (1995).
Bennett, C. H., Brassard, G., Popescu, S., Schumacher, B., Smolin, J. A. & Wootters, W. K. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722 (1996).
Sheng, Y. B. & Zhou, L. Two-step complete polarization logic Bell-state analysis. Sci. Rep. 5, 13453 (2016).
Zhou, L. & Sheng, Y. B. Complete logic Bell-state analysis assisted with photonic Faraday rotation. Phys. Rev. A 92, 042314 (2015).
Zhou, L. & Sheng, Y. B. Feasible logic Bell-state analysis with linear optics. Sci. Rep. 6, 20901 (2016).
Bell, J. S. On the einstein podolsky rosen paradox. Physics (Long Island City, NY) 1, 195 (1965).
Dür, W., Vidal, G. & Cirac, J. I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 62, 062314 (2000).
Greenberger, D. M., Horne, M. A. & Zeilinger, A. Going beyond Bell’s theorem. In Bell’s theorem, quantum theory, and conceptions of the universe, edited by Kafatos, M. (Kluwer, Dordrecht) p. 69 (1989).
Li, X. H., Deng, F. G. & Zhou, H. Y. Improving the security of secure direct communication based on the secret transmitting order of particles. Phys. Rev. A 74, 054302 (2006).
Wang, C., Deng, F. G., Li, Y. S., Liu, X. S. & Long, G. L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 71, 044305 (2005).
Xiao, L., Long, G. L., Deng, F. G. & Pan, J. W. Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 69, 052307 (2004).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829 (1999).
Bennett, C. H., Brassard, G., Crepeau, C., Jozsa, R., Peres, A. & Wootters, W. K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Karlsson, A. & Bourennane, M. Quantum teleportation using three-particle entanglement. Phys. Rev. A 58, 4394 (1998).
Bužek, V. & Hillery, M. Crossed-field hydrogen atom and the three-body Sun-Earth-Moon problem. Phys. Rev. A 54, 1884 (1996).
Gisin, N. & Massar, S. Optimal quantum cloning machines. Phys. Rev. Lett. 79, 2153 (1997).
Chen, Y. H., Huang, B. H., Song, J. & Xia, Y. Transitionless-based shortcuts for the fast and robust generation of W states. Opt. Comm. 380, 140 (2016).
An, N. B. Cavity-catalyzed deterministic generation of maximal entanglement between nonidentical atoms. Phys. Lett. A 344, 77 (2005).
Zheng, S. B. Scalable generation of multi-atom W states with a single resonant interaction. J. Opt. B 7, 10 (2005).
Kang, Y. H., Xia, Y. & Lu, P. M. Effective scheme for preparation of a spin-qubit Greenberger-Horne-Zeilinger state and W state in a quantum-dot-microcavity system. J. Opt. Soc. Am. B 32, 1323 (2015).
Eibl, M., Kiesel, N., Bourennane, M., Kurtsiefer, C. & Weinfurter, H. Experimental Realization of a Three-Qubit Entangled W State. Phys. Rev. Lett. 92, 077901 (2004).
Zou, X. B., Pahlke, K. & Mathis, W. Generation of an entangled four-photon W state. Phys. Rev. A 66, 044302 (2002).
Neeley, M., Bialczak, R. C., Lenander, M. & Lucero, E. Generation of three-qubit entangled states using superconducting phase qubits. Nature (London) 467, 570 (2010).
Wei, X. & Chen, M. F. Preparation of multi-qubit W states in multiple resonators coupled by a superconducting qubit via adiabatic passage. Quantum Inf. Process. 14, 2419 (2015).
Wei, X. & Chen, M. F. Generation of N-qubit W state in N separated resonators via resonant interaction. Int. J. Theor. Phys. 54, 812 (2015).
Helmer, F. & Marquardt, F. Measurement-based synthesis of multiqubit entangled states in superconducting cavity QED. Phys. Rev. A 79, 052328 (2009).
Song, K. H., Zhou, Z. W. & Guo, G. C. Quantum logic gate operation and entanglement with superconducting quantum interference devices in a cavity via a Raman transition. Phys. Rev. A 71, 052310 (2005).
Deng, Z. J., Gao, K. L. & Feng, M. Generation of N-qubit W states with rf SQUID qubits by adiabatic passage. Phys. Rev. A 74, 064303 (2006).
Wu, J. L., Song, C., Xu, J., Yu, L., Ji, X. & Zhang, S. Adiabatic passage for one-step generation of n-qubit Greenberger-Horne-Zeilinger states of superconducting qubits via quantum Zeno dynamics. Quantum Inf. Process., doi: 10.1007/s11128-016-1366-0.
You, J. Q. & Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature (London) 474, 589 (2011).
Yang, C. P., Su, Q. P., Zheng, S. B. & Han, S. Generating entanglement between microwave photons and qubits in multiple cavities coupled by a superconducting qutrit. Phys. Rev. A 87, 022320 (2013).
Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. Nature (London) 453, 1031 (2008).
Filipp, S., Maurer, P., Leek, P. J., Baur, M., Bianchetti, R., Fink, J. M., Göppl, M., Steffen, L., Gambetta, J. M., Blais, A. & Wallraff, A. Two-qubit state tomography using a joint dispersive readout. Phys. Rev. Lett. 102, 200402 (2009).
Bialczak, R. C., Ansmann, M., Hofheinz, M., Lucero, E., Neeley, M., O’Connell, A. D., Sank, D., Wang, H., Wenner, J., Steffen, M., Cleland, A. N. & Martinis, J. M. Quantum process tomography of a universal entangling gate implemented with Josephson phase qubits. Nat. Phys. 6, 409 (2010).
Yamamoto, T., Neeley, M., Lucero, E., Bialczak, R. C., Kelly, J., Lenander, M., Mariantoni, M., O’Connell, A. D., Sank, D., Wang, H., Weides, M., Wenner, J., Yin, Y., Cleland, A. N. & Martinis, J. M. Quantum process tomography of two-qubit controlled-Z and controlled-NOT gates using superconducting phase qubits. Phys. Rev. B 82, 184515 (2010).
Reed, M. D., DiCarlo, L., Johnson, B. R., Sun, L., Schuster, D. I., Frunzio, L. & Schoelkopf, R. J. High-fidelity readout in circuit quantum electrodynamics using the Jaynes-Cummings nonlinearity. Phys. Rev. Lett. 105, 173601 (2010).
Yang, C. P., Chu, S. I. & Han, S. Possible realization of entanglement, logical gates, and quantum-information transfer with superconducting-quantum-interference-device qubits in cavity QED. Phys. Rev. A 67, 042311 (2003).
Majer, J., Chow, J. M., Gambetta, J. M., Koch, J., Johnson, B. R., Schreier, J. A., Frunzio, L., Schuster, D. I., Houck, A. A., Wallraff, A., Blais, A., Devoret, M. H., Girvin, S. M. & Schoelkopf, R. J. Coupling superconducting qubits via a cavity bus. Nature (London) 449, 443 (2007).
DiCarlo, L., Chow, J. M., Gambetta, J. M., Bishop, L. S., Johnson, B. R., Schuster, D. I., Majer, J., Blais, A., Frunzio, L., Girvin, S. M. & Schoelkopf, R. J. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature (London) 460, 240 (2009).
Blais, A., Huang, R. S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Yang, C. P., Chu, S. I. & Han, S. Quantum information transfer and entanglement with SQUID qubits in cavity QED: a dark-state scheme with tolerance for nonuniform device parameter. Phys. Rev. Lett. 92, 117902 (2004).
Wallraff, A., Schuster, D. I., Blais, A., Frunzio, L., Huang, R. S., Majer, J., Kumar, S., Girvin, S. M. & Schoelkopf, R. J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature (London) 431, 162 (2004).
Chiorescu, I., Bertet, P., Semba, K., Nakamura, Y., Harmans, C. J. P. M. & Mooij, J. E. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature (London) 431, 159 (2004).
Fewell, M. P., Shore, B. W. & Bergmann, K. Coherent population transfer among three states: full algebraic solutions and the relevance of non adiabatic processes to transfer by delayed pulses. Aust. J. Phys. 50, 281 (1997).
Bergmann, K., Theuer, H. & Shore, B. W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 70, 1003 (1998).
Vitanov, N. V., Halfmann, T., Shore, B. W. & Bergmann, K. Laser-induced population transfer by adiabatic passage techniques. Annu. Rev. Phys. Chem. 52, 763 (2001).
Král, P., Thanopulos, I. & Shapiro, M. Coherently controlled adiabatic passage. Rev. Mod. Phys. 79, 53 (2007).
Demirplak, M. & Rice, S. A. Adiabatic population transfer with control fields. J. Phys. Chem. A 107, 9937 (2003).
Demirplak, M. & Rice, S. A. On the consistency, extremal, and global properties of counterdiabatic fields. J. Chem. Phys. 129, 154111 (2008).
Torrontegui, E., Ibáñez, S., Martnez-Garaot, S., Modugno, M., del Campo, A., Gué-Odelin, D., Ruschhaupt, A., Chen, X. & Muga, J. G. Shortcuts to adiabaticity. Adv. Atom. Mol. Opt. Phys. 62, 117 (2013).
Berry, M. V. Transitionless quantum driving. J. Phys. A 42, 365303 (2009).
Chen, X., Lizuain, I., Ruschhaupt, A., Guéry-Odelin, D. & Muga, J. G. Shortcut to adiabatic passage in two- and three-level atoms. Phys. Rev. Lett. 105 123003 (2010).
del Campo, A. Shortcuts to adiabaticity by counterdiabatic driving. Phys. Rev. Lett. 111, 100502 (2013).
Chen, X., Torrontegui, E. & Muga, J. G. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys. Rev. A 83, 062116 (2011).
Muga, J. G., Chen, X., Ruschhaup, A. & Guéry-Odelin, D. Frictionless dynamics of Bose-Einstein condensates under fast trap variations. J. Phys. B 42, 241001 (2009).
Chen, X. et al. Fast optimal frictionless atom cooling in harmonic traps: shortcut to adiabaticity. Phys. Rev. Lett. 104, 063002 (2010).
Torrontegui, E., Ibáñez, S., Chen, X., Ruschhaupt, A., Guéry-Odelin, D. & Muga, J. G. Fast atomic transport without vibrational heating. Phys. Rev. A 83, 013415 (2011).
Muga, J. G., Chen, X., Ibáñez, S., Lizuain, I. & Ruschhaupt, A. Transitionless quantum drivings for the harmonic oscillator. J. Phys. B 43, 085509 (2010).
Torrontegui, E., Chen, X., Modugno, M., Ruschhaupt, A., Guéry-Odelin, D. & Muga, J. G. Fast transitionless expansion of cold atoms in optical Gaussian-beam traps. Phys. Rev. A 85, 033605 (2012).
Masuda, S. & Nakamura, K. Acceleration of adiabatic quantum dynamics in electromagnetic fields. Phys. Rev. A 84, 043434 (2011).
Masuda, S. & Rice, S. A. Fast-Forward Assisted. STIRAP. J. Phys. Chem. A. 199, 3479 (2015).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Fast and noise-resistant implementation of quantum phase gates and creation of quantum entangled states. Phys. Rev. A 91, 012325 (2015).
Chen, X. & Muga, J. G. Transient energy excitation in shortcuts to adiabaticity for the time-dependent harmonic oscillator. Phys. Rev. A 82, 053403 (2010).
Schaff, J. F., Capuzzi, P., Labeyrie, G. & Vignolo, P. Shortcuts to adiabaticity for trapped ultracold gases. New J. Phys. 13, 113017 (2011).
Chen, X., Torrontegui, E., Stefanatos, D., Li, J. S. & Muga, J. G. Optimal trajectories for efficient atomic transport without final excitation. Phys. Rev. A 84, 043415 (2011).
Torrontegui, E., Chen, X., Modugno, M., Schmidt, S., Ruschhaupt, A. & Muga, J. G. Fast transport of Bose-Einstein condensates. New J. Phys. 14, 013031 (2012).
del Campo, A. Frictionless quantum quenches in ultracold gases: A quantum-dynamical microscope. Phys. Rev. A 84, 031606(R) (2011).
del Campo, A. Fast frictionless dynamics as a toolbox for low-dimensional Bose-Einstein condensates. Eur. Phys. Lett. 96, 60005 (2011).
Ruschhaupt, A., Chen, X., Alonso, D. & Muga, J. G. Optimally robust shortcuts to population inversion in two-level quantum systems. New J. Phys. 14, 093040 (2012).
Schaff, J. F., Song, X. L., Vignolo, P. & Labeyrie, G. Fast optimal transition between two equilibrium states. Phys. Rev. A 82, 033430 (2010).
Schaff, J. F., Song, X. L., Capuzzi, P., Vignolo, P. & Labeyrie, G. Shortcut to adiabaticity for an interacting Bose-Einstein condensate. Eur. Phys. Lett. 93, 23001 (2011).
Chen, X. & Muga, J. G. Engineering of fast population transfer in three-level systems. Phys. Rev. A 86, 033405 (2012).
Chen, Z., Chen, Y. H., Xia, Y., Song, J. & Huang, B. H. Fast generation of three-atom singlet state by transitionless quantum driving. Sci. Rep. 6, 22202 (2016).
Lu, M., Xia, Y., Shen, L. T., Song, J. & An, N. B. Shortcuts to adiabatic passage for population transfer and maximum entanglement creation between two atoms in a cavity. Phys. Rev. A 89, 012326 (2014).
Chen, Y. H., Xia, Y., Chen, Q. Q. & Song, J. Efficient shortcuts to adiabatic passage for fast population transfer in multiparticle systems. Phys. Rev. A 89, 033856 (2014).
Song, X. K., Zhang, H., Ai, Q., Qiu, J. & Deng, F. G. Shortcuts to adiabatic holonomic quantum computation in decoherence-free subspace with transitionless quantum driving algorithm. New J. Phys. 18, 023001 (2016).
Vacanti, G., Fazio, R., Montangero, S., Palma, G. M., Paternostro, M. & Vedral, V. Transitionless quantum driving in open quantum systems. New J. Phys. 16, 053017 (2016).
Santos, A. C. & Sarandy, M. S. Superadiabatic controlled evolutions and universal quantum computation. Sci. Rep. 5, 15775 (2015).
Santos, A. C., Silva, R. D. & Sarandy, M. S. Shortcut to adiabatic gate teleportation. Phys. Rev. A 93, 012311 (2016).
Hen, I. Quantum gates with controlled adiabatic evolutions. Phys. Rev. A 91, 022309 (2015).
Sarandy, M. S., Wu, L. A. & Lidar, D. Consistency of the adiabatic theorem. Quantum Inf. Process 3, 331 (2004).
Coulamy, I. B., Santos, A. C., Hen, I. & Sarandy, M. S. Energetic cost of superadiabatic quantum computation. arXiv:1603.07778.
Rams, M. M., Mohseni, M. & del Campo, A. Inhomogeneous quasi-adiabatic driving of quantum critical dynamics in weakly disordered spin chains. arXiv:1606.07740.
Deffner, S., Jarzynski, C. & del Campo, A. Classical and quantum shortcuts to adiabaticity for scale-invariant driving. Phys. Rev. X 4, 021013 (2014).
del Campo, A. Shortcuts to adiabaticity in quantum many-body systems: a quantum dynamical microscope. Aps March Meeting (2014).
Huang, B. H., Chen, Y. H., Wu, Q. C., Song, J. & Xia, Y. Fast generating Greenberger-Horne-Zeilinger state via iterative interaction pictures. Laser Phys. Lett. 13, 105202 (2016).
Chen, Y. H., Xia, Y., Song, J. & Chen, Q. Q. Shortcuts to adiabatic passage for fast generation of Greenberger-Horne-Zeilinger states by transitionless quantum driving. Sci. Rep. 5, 15616 (2016).
Huang, X. B., Zhong, Z. R. & Chen, Y. H. Generation of multi-atom entangled states in coupled cavities via transitionless quantum driving. Quantum Inf. Process. 14, 4775 (2015).
Shan, W. J., Xia, Y., Chen, Y. H. & Song, J. Fast generation of N-atom Greenberger-Horne-Zeilinger state in separate coupled cavities via transitionless quantum driving. Quantum Inf. Process. 15, 2359 (2016).
Martnez-Garaot, S., Torrontegui, E., Chen, X. & Muga, J. G. Shortcuts to adiabaticity in three-level systems using Lie transforms. Phys. Rev. A 89, 053408 (2014).
Opatrný, T. & Mømer, K. Partial suppression of nonadiabatic transitions. New J. Phys. 16, 015025 (2014).
Saberi, H., Opatrny, T., Mømer, K. & del Campo, A. Adiabatic tracking of quantum many-body dynamics. Phys. Rev. A 90, 060301(R) (2014).
Torrontegui, E., Martnez-Garaot, S. & Muga, J. G. Hamiltonian engineering via invariants and dynamical algebra. Phys. Rev. A 89, 043408 (2014).
Torosov, B. T., Valle, G. D. & Longhi, S. Non-Hermitian shortcut to adiabaticity. Phys. Rev. A 87, 052502 (2013).
Torosov, B. T., Valle, G. D. & Longhi, S. Non-Hermitian shortcut to stimulated Raman adiabatic passage. Phys. Rev. A 89, 063412 (2014).
Chen, Y. H., Wu, Q. C., Huang, B. H., Xia, Y. & Song, J. Method for constructing shortcuts to adiabaticity by a substitute of counterdiabatic driving terms. Phys. Rev. A 93, 052109 (2016).
Ibáñez, S., Chen, X. & Muga, J. G. Improving shortcuts to adiabaticity by iterative interaction pictures. Phys. Rev. A 87, 043402 (2013).
Ibáñez, S., Chen, X., Torrontegui, E., Muga, J. G. & Ruschhaupt, A. Multiple Schrödinger pictures and dynamics in shortcuts to adiabaticity. Phys. Rev. Lett. 109, 100403 (2012).
Song, X. K., Ai, Q., Qiu, J. & Deng, F. G. Physically feasible three-level transitionless quantum driving with multiple Schröodinger dynamics. Phys. Rev. A 93, 052324 (2016).
Kang, Y. H., Chen, Y. H., Wu, Q. C., Huang, B. H., Xia, Y. & Song, J. Reverse engineering of a Hamiltonian by designing the evolution operators. Sci. Rep. 6, 30151 (2016).
Xiang, Z. L., Ashhab, S., You, J. Q. & Nori, F. Hybrid quantum circuits: superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623 (2013).
Siewert, J., Brandes, T. & Falci, G. Adiabatic passage with superconducting nanocircuits. Opt. Commun. 264, 435 (2006).
Feng, Z. B. Coupling charge qubits via Raman transitions in circuit QED. Phys. Rev. A 78, 032325 (2008).
Strauch, F. W., Jacobs, K. & Simmonds, R. W. Arbitrary Control of Entanglement between two Superconducting Resonators. Phys. Rev. Lett. 105, 050501 (2010).
Koch, J., Yu, T. M., Gambetta, J., Houck, A. A., Schuster, D. I., Majer, J., Blais, A., Devoret, M. H., Girvin, S. M. & Schoelkopf, R. J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Mariantoni, M., Wang, H., Bialczak, R. C., Lenander, M., Lucero, E., Neeley, M., O’Connell, A. D., Sank, D., Weides, M., Wenner, J., Yamamoto, T., Yin, Y., Zhao, J., Martinis, J. M. & Cleland, A. N. Photon shell game in three-resonator circuit quantum electrodynamics. Nature Physics 7, 287 (2011).
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grants No. 11575045 and No. 11374054, and the Major State Basic Research Development Program of China under Grant No. 2012CB921601.
Author information
Authors and Affiliations
Contributions
Y.X. and Y.H.K. came up with the initial idea for the work and performed the simulations for the model. Y.H.C., Q.C.W., J.S. and B.H.H. performed the calculations for the model. Y.X., Y.H.K. and Y.H.C. performed all the data analysis and the initial draft of the manuscript. All authors participated in the writing and revising of the text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kang, YH., Chen, YH., Wu, QC. et al. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Sci Rep 6, 36737 (2016). https://doi.org/10.1038/srep36737
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36737
This article is cited by
-
Efficient Generation of W Entangled States Among Superconducting Qubits via Lie-Algebra–Based Transforms
International Journal of Theoretical Physics (2023)
-
Non-locality Correlation in Two Driven Qubits Inside an Open Coherent Cavity: Trace Norm Distance and Maximum Bell Function
Scientific Reports (2019)
-
Fast and robust generation of singlet state via shortcuts to adiabatic passage
Quantum Information Processing (2019)
-
Non-Classical Correlations and Transfer of Quantum Information in a Superconducting Qubit System with Dynamical Decoupling Pulses
International Journal of Theoretical Physics (2019)
-
Fast preparing W state via a chosen path shortcut in circuit QED
Quantum Information Processing (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


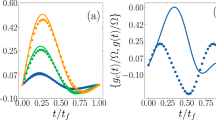


 and
and  (versus t/T). (b) Comparison between
(versus t/T). (b) Comparison between  and
and  (versus t/T).
(versus t/T).

 versus t/T.
versus t/T.

 and γ/λ. (b) The final fidelity F(T) versus
and γ/λ. (b) The final fidelity F(T) versus  and
and  . (c) The final fidelity F(T) versus γ/λ and
. (c) The final fidelity F(T) versus γ/λ and  .
.
 . (c) The final fidelity F(T) versus
. (c) The final fidelity F(T) versus  and δλ/λ.
and δλ/λ.