Abstract
We report the discovery of a new fluoride-arsenide bulk diluted magnetic semiconductor (Ba,K)F(Zn,Mn)As with the tetragonal ZrCuSiAs-type structure which is identical to that of the “1111” iron-based superconductors. The joint hole doping via (Ba,K) substitution & spin doping via (Zn,Mn) substitution results in ferromagnetic order with Curie temperature up to 30 K and demonstrates that the ferromagnetic interactions between the localized spins are mediated by the carriers. Muon spin relaxation measurements confirm the intrinsic nature of the long range magnetic order in the entire volume in the ferromagnetic phase. This is the first time that a diluted magnetic semiconductor with decoupled spin and charge doping is achieved in a fluoride compound. Comparing to the isostructure oxide counterpart of LaOZnSb, the fluoride DMS (Ba,K)F(Zn,Mn)As shows much improved semiconductive behavior that would be benefit for further application developments.
Similar content being viewed by others
Introduction
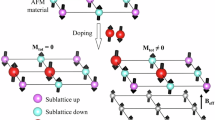
Diluted magnetic semiconductors (DMSs) are semiconductors where a small part of the component ions are substituted by magnetic ions, leading to a variety of cooperative effects and exhibiting outstanding properties and functionalities1,2,3,4,5,6. For example, a carrier-mediated magnetism in a DMS can be tuned by the carrier density through an applied electric field2,3. The discovery of Mn-doped III-V ferromagnetic semiconductors, such as (In,Mn)As4, (Ga,Mn)N5 and (Ga,Mn)As6, has triggered extensive research with the intention of exploring new DMSs and enables examination of collective magnetic phenomena in a well-controlled environment7,8,9,10. At the same time, applications in sensors and memory devices as well as for computing with electronic spins can be envisaged2,11,12,13.
However, the typical systems based on III-V semiconductors face serious challenges. In (Ga,Mn)As, for example, substitution of divalent Mn2+ into trivalent Ga3+ sites has severely limited chemical solubility, resulting in metastable specimens only available as epitaxial thin films, which has led to considerable controversy about mechanisms of ferromagnetism in (Ga,Mn)As. Therefore, seeking decoupled of spin and charge injections with bulk DMSs become one of major missions for DMS materials14. Recently, a new type of DMS Li(Zn,Mn)As was reported to be a bulk DMS material with a ferromagnetic Curie temperature (TC) up to 50 K15. In this material, spins are doped via isovalent (Zn2+, Mn2+) substitution, while charges are provided by off-stoichiometry of the Li concentrations. Shortly after, another new type of bulk ferromagnetic DMS (Ba,K)(Zn,Mn)2As2 was synthesized with much higher TC up to 230 K16,17. More recently, several types of bulk DMSs with decoupled spin & charge doping have been successfully fabricated, including Li(Zn,Mn)P18, (La,Ca)(Zn,Mn)SbO19, (La,Ba)(Zn,Mn)AsO20, (La,Sr)(Cu,Mn)SO21, (Sr,Na)(Cd,Mn)2As222, and (A,Na)(Zn,Mn)2As2 (A = Ca, Sr,)23,24.
The successful discovery of superconductivity in the F doped LaFeAsO has aroused extensively studies on the compounds with the ZrCuSiAs-type structure and the relationship with other structures19,20,25. In this article, we report a new fluoride-arsenide ferromagnetic semiconductor (Ba,K)F(Zn,Mn)As, which shares the same structure as that of “1111” iron-based superconductor Sr1−xSmxFFeAs25 and Ba1−xSmxFFeAs26 (the tetragonal ZrCuSiAs-type structure). The compound of (Ba,K)F(Zn,Mn)As is isostructural to its variants, i.e., antiferromagnets and superconductors with lattice matching within 5%26,27, which could provide the possibility to make junction devices with these materials. Compared to BaZn2As228 (the parent compound of the high TC DMS (Ba,K)(Zn,Mn)2As2) and the isostructure oxide counterpart of LaOZnSb29, the fluoride-based parent compound BaFZnAs is more ionic hence semiconductive. Via (Ba,K) substitution to dope hole carriers and (Zn,Mn) substitution to supply local spins, this system reaches decoupled spin & charge doping exhibiting ferromagnetic order with TC up to 30 K and related negative magnetoresistance. Compared to the oxides compounds, fluoride compounds are able to form mostly ionic bonds, resulting in fluorines’s high electronegativity30. Hence, DMS achieved in fluoride compound seem to provide materials with several useful properties and promote the development of new materials for modern applications.
Results and Discussion
Crystal Structure of (Ba1−xKx)F(Zn1−yMny)As
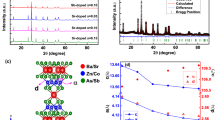
The structure of (Ba,K)F(Zn,Mn)As, as shown in Fig. 1a, is the same as that of the parent compound BaFZnAs31. It is found that the majority of peaks in the XRD pattern can be well indexed to main phase, except for some tiny peaks from the nonmagnetic impurity phase of BaF2. The unit cell of BaFZnAs is composed of two different layers: ZnAs-layer with [ZnAs4] tetrahedron and BaF-layer with [BaF4] tetrahedron. The two different layers are stacked in an AB AB sequence along the c-axis, resulting in the compound’s quasi two-dimensional nature. The lattice parameters were calculated to be a = 4.2380 Å and c = 9.5284 Å, which are similar with that of LaOZnSb (a = 4.2267 Å and c = 9.538 Å), the parent compound for “1111” oxide-arsenide diluted magnetic semiconductors19. This is caused by big size difference between La3+ (1.061 Å) and Ba2+ (1.35 Å) as well as between Sb3− (0.76 Å) and As3− (0.58 Å). Figure 1b shows the X-ray diffraction patterns of (Ba1−xKx)F(Zn0.9Mn0.1)As for x = 0, 0.025, 0.05, 0.075, 0.1 and 0.15, respectively. The lattice parameters monotonically increase with the increase of K doping, as shown in Fig. 1c, due to the slightly larger ionic radius of K+ (1.38 Å) compared with that of Ba2+ (1.35 Å). However, the deviation from the linear relation is likely from the incorporation of defects such as antisites, interstitials etc that are common in these type of compounds. These results indicate the successful chemical doping of K.
Magnetic Properties of (Ba1−xKx)F(Zn1−yMny)As
In DMSs, competing interactions between ferromagnetic and anti-ferromagnetic along with the spin-exchange interactions between local magnetic moments and carriers in magnetic systems could contribute to a variety of magnetic structures and critical phenomena12. Particularly, the long-range magnetic order nature of the magnetic interactions mediated by the conduction carriers leads to a diversity of cooperative effects. Figure 2a shows the temperature dependence of the magnetization M(T) in zero-field-cooling (ZFC) and field-cooling (FC) procedures under H = 1000 G for BaF(Zn0.9Mn0.1)As. No ferromagnetic order is observed when only doping Mn. BaF(Zn0.9Mn0.1)As is paramagnetic from room temperature down to 2 K. Inset of Fig. 2a shows the magnetization curve of (Ba1−xKx)F(Zn0.9Mn0.1)As specimens with x = 0.025, 0.05, 0.1 and 0.2, respectively. Signatures of ferromagnetic order are seen in the curves at temperatures of 20 K ~30 K. TC monotonously increases with the increase of K doping. These results indicate that only joint carrier doping via (Ba,K) substitution with spin doping arising from (Zn,Mn) substitution can give rise to the ferromagnetic order. Hole doping drives the system toward ferromagnetism32,33,34,35. Meanwhile, the ferromagnetic order is tuned by carrier concentration x and the spin level y, which is consistent with the carrier-mediated mechanism of the ferromagnetism as described by the Rudermann-Kittel-Kasuya-Yosida (RKKY) model or the Zener model12,36. Figure 2b shows the M(T) in ZFC and FC procedures under H = 500 G for the (Ba0.8K0.2)F(Zn1−yMny)As samples with y = 0.025, 0.05, 0.075, 0.1 and 0.15, respectively. The maximum TC is 30 K for optimal Mn doping (y = 0.1). Further Mn doping results in TCgradually decreasing, as shown in Fig. 2b. Above TC, the susceptibility χ can be fit to Curie-Weiss formula,
(a) DC M(T) measurements measured in H = 1000 G for BaF(Zn0.9Mn0.1)As without charge doping. Inset shows the magnetization curve of (Ba1−xKx)F(Zn0.9Mn0.1)As specimens with several charge doping. (b) M(T) measured in H = 500 G for (Ba0.8K0.2)F(Zn1−yMny)As with ZFC and FC procedures. Inset shows the temperature dependence of the inverse susceptibility for (Ba0.8K0.2)F(Zn0.925Mn0.075)As. (c) M(H) curves of (Ba0.8K0.2)F(Zn1−yMny)As samples at temperature T = 5 K.

where χ0 is a temperature-independent paramagnetic term, C is the Curie constant, and θ is the Weiss temperature. The positive value of θ found for (Ba0.8K0.2)F(Zn0.925Mn0.075)As [inset of Fig. 2(b)] indicates a ferromagnetic interaction between Mn2+ ions.
Figure 2c shows the field dependence of magnetization M(H) curves of (Ba0.8K0.2)F(Zn1−yMny)As with y = 0.05, 0.1 and 0.15 at T = 5 K with corrections by subtracting the small H-linear component presumably from remaining paramagnetic spins and/or field-induced polarization17. For x fixed to 20%, the maximum saturation magnetization (Msat) is 0.9 μB when y = 5%. However, upon further increasing Mn concentration, Msat of the samples decreases to 0.6 μB with the increasing Mn doping. These decreasing trends of Msat probably reflect the competition between the short-range antiferromagnetic superexchange of nearest-neighbor Mn moments and a longer-range ferromagnetic interaction of distant Mn moments regulated by hole carriers32, i.e. the RKKY-like interaction. The direct antiferromagnetic coupling between the Mn-Mn pairs causes G-type antiferromagnetic order in BaFMnAs at TN = 338 K27. A similar trend was found in other magnetic ion doped systems15,18,23,37.
Muon spin relaxation (μSR) measurements
The ability of μSR to determine the temperature dependence of the magnetically ordered volume fraction and the magnetic order parameter has made it a valuable tool for studying many other DMS materials15,17,20,23,24,38,39,40,41,42. The availability of bulk specimens allowed us to perform conventional μSR on (Ba1−xKx)F(Zn1−yMny)As. To further probe the magnetic order in this system, we performed μSR measurements on a sample of (Ba0.85K0.15)F(Zn0.9Mn0.1)As. Zero-field (ZF) μSR spectra taken at various temperatures are displayed in Fig. 3a. The development of rapid relaxation indicates the presence of magnetic order starting around 40 K and below. When a longitudinal field (LF) of 300 G is applied parallel to the initial muon spin direction, nearly the full asymmetry is recovered, confirming that the relaxation in ZF is due primarily to static magnetic order rather than dynamically fluctuating magnetic moments. The LF spectrum taken at 2 K is shown as blue diamonds in Fig. 3a.
Results of μSR measurements of (Ba0.85K0.15)F(Zn0.9Mn0.1)As.
(a) Zero-field μSR spectra at various temperatures. The colored points represent the experimental data, and the solid curves represent the fits described in the text. A longitudinal-field measurement taken at 2 K is shown by the blue diamonds. (b) Fast relaxation rate Λ obtained from fits described in the text. The error bars represent the estimated standard deviations of the refined parameters. (c) Weak-transverse-field measurements at various temperatures, offset vertically for clarity. (d) Low-temperature relaxation rate Λ plotted against the ferromagnetic ordering temperature TC for various DMS systems, including the present work, exhibiting a linear relationship with a common slope. The gray dashed line is the best linear fit.
The ZF spectra can be well fit by a sum of two exponential functions, a “fast” component whose rate is proportional to the magnetic order parameter, and a “slow” component capturing the relaxation from the paramagnetic regions of the sample and the “1/3 tail” of the ordered regions. The lack of coherent oscillations in the ZF spectra reflect the spatial disorder of the magnetic moments due to the random distribution of the magnetic dopants, and has also been observed in other DMS systems23. The temperature dependence of the fast relaxation rate Λ is displayed in Fig. 3b, exhibiting a monotonic increase as the temperature is lowered below 40 K and reaching a maximum value of 11.5+/− 0.7 μs−1 at the lowest measurement temperature (2 K). From these results, we assign the onset transition temperature (TC°) to be around 40 K ~ 50 K, but slightly higher than TC = 30 K determined from magnetization measurements. This suggests a rather broad transition, with the higher μSR onset temperature corresponding to a partial volume fraction that orders first, while the lower TC from bulk magnetization reflects the point where the majority of the sample becomes ordered.
To verify that the full sample volume orders magnetically at low temperature, we performed weak-transverse field (WTF) μSR measurements. Representative WTF spectra are shown in Fig. 3c, offset vertically for clarity. The oscillating amplitude, which is proportional to the non-magnetically ordered volume fraction, is gradually reduced as the temperature is lowered, again pointing to a broad magnetic transition and confirming the presence of magnetic order in a large majority of the sample volume. From the ratio of the oscillating amplitude at 2 K and 50 K, we estimate the magnetically ordered volume fraction to be 0.85+/− 0.1 at 2 K. Background contributions and minor phase impurities may contribute to the non-magnetically-ordered volume fraction, but these results nevertheless confirm the intrinsic nature of the magnetic order in this material.
The magnetically ordered volume fraction reaches 50% at approximately 30 K, coinciding with the transition temperature determined by magnetization. Broadly assigning the transition temperature to be TC = 30 K+/− 5 K, the low-temperature ZF relaxation rate Λ (T → 0) = 11.5+/− 0.7 μs−1 can be plotted against TC, as shown in Fig. 3d. We compare the present result on (Ba0.85K0.15)F(Zn0.9Mn0.1)As with the earlier DMS systems of the (Ga,Mn)As41 system, Li(Zn,Mn)As15 system, (Ba,K)(Zn,Mn)2As217 system, and (La,Ba)(Zn,Mn)AsO20 system in a plot of the low temperature relaxation rate Λ and the Curie temperature TC. This system lies quite close to the roughly linear relationship between Λ (T → 0) and TC exhibited by the other systems, which suggests that exchange interaction supporting ferromagnetic coupling in these systems has a common mechanism for the ferromagnetism in all of these materials.
Bandgap and Electronic Structure of parent compound BaFZnAs
High quality polycrystalline BaFZnAs was reported to be a semiconductor in our previous work31. Figure 4 shows the temperature dependence of resistivity of BaFZnAs, indicating a semiconductor behavior. Inset shows the lnρ vs. 1/T plot of BaFZnAs. The red curve is the fit by the formula,

where ρ0 is the preexponential constant, kB is the Boltzmann constant, and Ea is the activation energy, at high-temperature region (300 to and 400 K). The high-T linear region should be attributed to the intrinsic region of ρ. The fit gave an intrinsic Ea value of 0.43 eV, i.e. the bandgap Eg = 2Ea = 0.86 eV, which is slightly larger than that of BaFMnAs (0.73 eV)27. The band gap of BaFeAsZn is much larger than that of BaZn2As2 (0.23 eV)28 and the isostructure oxide counterpart of LaOZnSb29, suggesting the larger ionicity of fluoride counterpart than that of BaZn2As2 and LaOZnSb.
To understand the electronic structure of the host semiconductor BaFZnAs, we also calculated the bandgap of BaFZnAs by first-principles calculations. The underestimated value of bandgap from GGA results happened in LaOZnAs28, but a reasonable result was obtained with modified Becke-Johnson local density approximation (MBJLAD). Here we apply the same approach, i.e. the MBJLAD to estimate the band gap of BaFZnAs. The calculation gives rise to a gap of 1.2 eV, as shown in Fig. 5a, which is a little larger than the value from transport experiments. Taking the improved conductivity caused by crystal defects into consideration, the bandgap (0.86 eV) of BaFZnAs from transport may be smaller than that of real value. We conclude that the value estimated from MBJLDA calculation provide a reasonable bandgap for BaFZnAs.
(a) Band structure of BaFZnAs: the weight of As (Zn) p (s)-orbitals is in blue (red). (b) Band gaps with different heights of As for hAs = 0.6755, hAs = 0.6655 and hAs = 0.6455, respectively, which reveals that the band gap of BaFZnAs will increase (decrease) if the As is slightly moved to the BaF-(Zn) layer.
In Fig. 5a, both As 4p (in blue) and Zn 4s states (in red) are located around the Fermi level (−2.0 to 2.0 eV) in BaFZnAs. The topmost valence bands and the lowest conducting band are dominated by the As 4p-orbitals and the Zn 4s-orbitals, respectively. The bandwidth of Zn 4s is determined by two kinds of 4s-4s hybridization, i.e., direct 4s-4s hybridization in the Zn plane and indirect 4s-4s hybridization mediated by the As 4p-orbitals. The indirect 4s-4s hybridization mediated by As 4p-orbitals is proportional to

where (sρσ) is the two-center integral of Zn 4s and As 4p-orbitals, θ is the As-Zn-Zn angle in yz/xz plane, and Δ is single particle energy difference of Zn 4s and As 4p-orbitals. Our calculated band gaps with different heights reveal that the band gap of BaFZnAs will increase (decrease) if the As is slightly moved to the BaF- (Zn) layer, as clearly shown in Fig. 5b. The As height dependent evolution of band gap can be interpreted by the competition of direct and indirect 4s-4s hybridization. The indirect 4s-4s hybridization will enhanced when the As is moved to the Zn layer, and the bandwidth of Zn 4s will increase leading to smaller band gap. The band gap will be dominated by the direct 4s-4s hybridization if the As is moved to the BaF-layer, leading to larger band gap. The delicate band gap of BaFZnAs and its analogies is determined by the completion of direct 4s-4s hybridization and indirect hybridization mediated by As 4p-orbitasl. The absence of dispersion along R-X line also suggests quasi two dimensional character of the band structure in BaFZnAs (Fig. 5a).
Transport Properties of (Ba1−xKx)F(Zn1−yMny)As
The temperature dependence of electrical resistivity ρ(T) of (Ba1−xKx)FZnAs for x = 0, 0.1, and 0.2 is shown in Fig. 6a. All the specimens exhibit typical semiconducting behavior over the entire temperature range. For the x = 0 specimen, ρ(T) is on the order of 106 Ω cm at room temperature, much larger than that of BaZn2As2, another parent compound of diluted magnetic semiconductor17. Doping K atoms into Ba sites introduces hole carriers, leading to the much smaller resistivity in (Ba,K)FZnAs than that of BaFZnAs. Figure 6b shows the resistivity ρ(T) for (Ba0.925K0.075)F(Zn0.9Mn0.1)As under various magnetic field. The ρH(T) diverges from each other under different fields and increases drastically below TC. Resistivity was beyond our measurement limitation below 20 K that is primarily caused by the more ionic nature of fluorides in sharp contrast to low resistance oxide counterparts wherein more covalence chemical bonding is expected20. The extremely large resistivity precluded Hall effect measurements on the polycrystalline specimens at low temperature. However, the Hall effect can be measured at high temperature (T = 250 K), as shown in Fig. 6c. The positive Hall coefficient demonstrates dominated hole type carriers by 10% K-substitution in the system. In a single-band model, the Hall coefficient RH is associated with carrier density (p) as RH = 1/pe. Therefore, we calculate the hole concentration to be 1.21 × 1017 cm−3. The Zener model description of ferromagnetism in Ga1−xMnxAs reveals that the higher values of TC are predicted for materials containing larger concentrations of holes and magnetic ions12, which suggests that a higher TC could be achieved in the present system if further charging doping could be accompanied by a corresponding increase in hole concentrations32. Figure 6d compares the hole concentrations and ferromagnetic transition temperatures of (Ba,K)F(Zn,Mn)As) to those of other DMS systems. The hole concentration of (Ba0.8K0.2)F(Zn0.95Mn0.05)As is comparable with that of Li(Zn,Mn)P system, while is more than two order of magnitude smaller than that of typical metallic DMS ferromagnets15,17,23,43. It is interesting to noticed that the present work and Li(Zn,Mn)P18 system both exhibit ferromagnetism with relatively high TC while the carriers still remain semiconducting. The relationship between TC and hole concentration exhibited by (Ga,Mn)As37, (In,Mn)As4,43, Li(Zn,Mn)As15 and (Ba,K)(Zn,Mn)2As217 systems suggests that further charge and spin doping would cause (Ba,K)F(Zn,Mn)As to be metallic and achieve magnetically order at a higher TC3,9,12,15,17,18,44. The parallel expectations are valid to the present fluoride DMS.
(a) Resistivity of Ba1−xKxFZnAs for x = 0, 0.1, 0.2 samples. (b) ρ(T) of (Ba0.925K0.075)F(Zn0.9Mn0.1)As under various fields. Inset shows the enlarged ρ(T) curve for (Ba0.925K0.075)F(Zn0.9Mn0.1)As under various fields at low temperatures. (c) Hall effect measurements of (Ba0.1K0.1)F(Zn0.9Mn0.1)As specimen at T = 250 K. (d) Correlation between TC and the hole concentration for various DMS systems. The blue stars represent the present work. (e) Negative magnetoresistance of (Ba0.8K0.2)F(Zn0.95Mn0.05)As at different temperatures, which can be defined as [ρ(H) − ρ(0)]/ρ(0).
There are many factors in magnetic semiconductors that can produce a sizable magnetoresistance. Under many conditions, the reduction of spin-dependent scattering by aligning the spins in an applied field leads to negative magnetoresistance2,37. The resistivity dependence of magnetic field ρ(H) for (Ba0.8K0.2)F(Zn0.95Mn0.05)As at several temperatures is shown in Fig. 6e. Negative magnetoresistance is observed in the whole temperature range of (Ba0.8K0.2)F(Zn0.95Mn0.05)As. The negative magnetoresistance is far from saturation even in rather high magnetic field, at which spin orientation is fully aligned. In this condition, an orbital effect resulting from the destructive influence of the magnetic field on the interference of scattered waves prevents the negative magnetoresistance from saturating even in low temperatures and rather strong magnetic fields.
Conclusion
We presented the successful synthesis of a new fluoride-arsenide ferromagnetic DMS (Ba,K)F(Zn,Mn)As via decoupled charge and spin doping. It is the first time that ferromagnetic ordering has been observed in a fluoride-arsenide semiconductor with Mn doping. The ferromagnetism of this system is mediated with decoupled spin & charge doping. The magnetization showed bulk ferromagnetism with TC around 15 K ~30 K for various composition of (Ba,K)F(Zn,Mn)As. The μSR measurements confirmed the intrinsic nature of the long range magnetic order in the entire volume at low temperature. Compared to parent compounds of (Ba,K)(Zn,Mn)2As2 and (La,Ca)O(Zn,Mn)Sb, i.e., BaZn2As2 and LaOZnSb, the fluoride-based parent compound BaFZnAs is more ionic and semiconductive, which would be benefit for further application developments.
Our results suggest that further studies of transition-metal-based ZrCuSiAs type structure of DMS materials in general, and other members of the fluoride-arsenide family in particular, are warranted.
Methods
Synthesis of Polycrystalline Samples
Polycrystalline (Ba,K)F(Zn,Mn)As specimens were synthesized via conventional solid-state reactions, a procedure similar to that employed for (Sr,Na)(Zn,Mn)2As223. Firstly, potassium arsenide and barium arsenide precursors were synthesized from stoichiometric mixtures of potassium pieces, arsenide powders and barium pieces in evacuated silica-glass ampules at 500 °C and 700 °C for 20 h, respectively. Secondly, powders of potassium arsenide, barium arsenide, barium fluoride, and high-purity zinc and manganese were mixed and ground in stoichiometric quantities, and pressed into pellets. The pellets were loaded into tantalum tubes filled with high-purity Ar gas, and then were sealed in evacuated quartz tubes. The mixtures were sintered at 750 °C for 20 h before they were slowly decreased to room temperature. All the synthesis processes were carried out in high-purity Ar atmosphere (O2 < 0.1 ppm, H2O < 0.01 ppm).
Structural, Magnetic and Electronic Measurements
The phase purity of the resulting powers was examined by powder X-ray diffraction (XRD; Philips X’pert diffractometer) using Cu-Kα radiation at room temperature. The crystal structure and lattice constants were calculated by Rietveld refinement using the GSAS software package. The DC magnetic susceptibility measurements were performed with a superconducting quantum interference device (SQUID-VSM; Quantum Design). The electronic transport measurements were measured by the four-probe technique using silver paste electrodes on a Quantum Design PPMS. Muon spin relaxation (μSR) measurements were performed at TRIUMF in Vancouver, Canada.
Band Structure Calculations
The first-principle electronic structure calculations were performed using experimental crystallographic parameters31 and the full-potential linearized augmented plane wave (LAPW) method implemented in the WIEN2k package45. The general gradient approximation (GGA)46 was used for the exchange-correlation potential. However, we found it underestimated the bandgaps of BaFZnAs. We then examined with modified Becke-Johnson local density approximation (MBJLAD) provided better results. The LAPW sphere radius was set to 2.40, 1.00, 2.49 and 2.37 Bohr for Ba, F, Zn and As, respectively. The energy cut-off was set to RminKmax = 8.0 and the k-point sample was set to 40 × 40 × 18.
Additional Information
How to cite this article: Chen, B. et al. New Fluoride-arsenide Diluted Magnetic Semiconductor (Ba,K)F(Zn,Mn)As with Independent Spin and Charge Doping. Sci. Rep. 6, 36578; doi: 10.1038/srep36578 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Žutić, I., Fabian, J. & Sarma, S. D. Spintronics fundamentals and applications. Rev.Mod. Phys. 76, 323–410 (2004).
Ohno, H. Making nonmagnetic semiconductors ferromagnetic. Science 281, 951–956 (1998).
Dietl, T. A ten-year perspective on dilute magnetic semiconductors and oxides. Nat. Mater. 9, 965–974 (2010).
Ohno, H., Munekata, H., Penney, T., Von Molnár, S. & Chang, L. L. Magnetotransport properties of p-type (In,Mn)As diluted magnetic III-V semiconductors. Phys. Rev. Lett. 68, 2664–2667 (1992).
Reed, M. L. et al. Room temperature ferromagnetic properties of (Ga,Mn)N. Appl. Phys. Lett. 79, 3473–3475 (2001).
Ohno, H. et al. (Ga,Mn)As: A new diluted magnetic semiconductor based on GaAs. Appl. Phys. Lett. 69, 363–365 (1996).
Samarth, N. A model ferromagnetic semiconductor. Nat. Mater. 9, 955–956 (2010).
Chambers, S. Is it really Intrinsic Ferromagnetism? Nat. Mater. 9, 956–957 (2010).
Jungwirth, T., Sinova, J., Mašek, J., Kučera, J. & MacDonald, A. H. Theory of ferromagnetic (III,Mn)V semiconductors. Rev. Mod. Phys. 78, 809–864 (2006).
Novák, V. et al. Curie point singularity in the temperature derivative of resistivity in (Ga, Mn)As. Phys. Rev. Lett. 101, 077201 (2008).
Shi, J., Gider, S., Babcock, K. & Awschalom, D. D. Magnetic clusters in molecular beams, metals, and semiconductor. Science 271, 937–941 (1996).
Dietl, T., Ohno, H., Matsukura, F., Cibert, J. & Ferrand, D. Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science 287, 1019–1022 (2000).
Hirohata, A. et al. Roadmap for emerging materials for spintronic device applications[J]. IEEE Transactions on Magnetics, 51, 1–11 (2015).
Mašek, J. et al. Dilute moment n-type ferromagnetic semiconductor Li(Zn,Mn)As. Phys. Rev. Lett. 98, 067202 (2007).
Deng, Z. et al. Li(Zn,Mn)As as a New generation ferromagnet based on a I-II-V Semiconductor. Nat. Commun. 2, 422 (2011).
Zhao, K. et al. Ferromagnetism at 230 K in (Ba0.7K0.3)(Zn0.85Mn0.15)2As2 diluted magnetic semiconductor. Chin. Sci. Bull. 59, 2524–2527 (2014).
Zhao, K. et al. New diluted ferromagnetic semiconductor with curie temperature up to 180 K and isostructural to the “122” iron-based superconductors. Nat. Commun. 4, 1442 (2013).
Deng, Z. et al. Diluted ferromagnetic semiconductor Li(Zn,Mn)P with decoupled charge and spin doping. Phys. Rev. B 88, 081203(R) (2013).
Han, W. et al. Diluted ferromagnetic semiconductor (LaCa)(ZnMn)SbO isostructural to “1111” type iron pnictide superconductors. Sci. China-Phys., Mech. Astron. 56, 2026–2030 (2013).
Ding, C. et al. (La1−xBax)(Zn1−xMnx)AsO: A two-dimensional 1111-type diluted magnetic semiconductor in bulk form. Phys. Rev. B 88, 041102 (2013).
Yang, X. J. et al. Sr and Mn co-doped LaCuSO: a wide band gap oxide diluted magnetic semiconductor with TC around 200 K. Appl. Phys. Lett. 103, 022410 (2013).
Chen, B. J. et al. (Sr1−xNax)(Cd1−xMnx)2As2:a new charge and spin doping decoupled diluted magnetic semiconductors with CaAl2Si2-type structure. Appl. Phys. Lett. 120, 083902 (2016).
Chen, B. J. et al. (Sr,Na)(Zn,Mn)2As2: a diluted ferromagnetic semiconductor with the hexagonal CaAl2Si2 type structure. Phys. Rev. B 90, 155202 (2014).
Zhao, K. et al. (Ca,Na)(Zn,Mn)2As2: a new spin and charge doping decoupled diluted ferromagnetic semiconductor. J. Appl. Phys. 116, 163906 (2014).
Wu, G. et al. Superconductivity at 56 K in samarium-doped SrFeAsF. J. Phys.: Condens. Matter. 21, 142203 (2009).
Wu, G. et al. Superconductivity in Ba1−xSmxFFeAs and Eu1−xSmxFFeAs systems. Chin. Sci. Bull. 54, 1872 (2009).
Saparov, B., Singh, D. J., Garlea, V. O. & Sefat, A. S. Crystal, magnetic, and electronic structures, and properties of new BaMnPnF (Pn = As, Sb, Bi). Sci. Rep. 3, 2154 (2013).
Xiao, Z. et al. Narrow bandgap in β-BaZn2As2 and its chemical origins. J. Am. Chem. Soc. 136, 14959 (2014).
Takano, Y. et al. Electrical and magnetic properties of LnOZnPn (Ln = rare earths; Pn = P, As, Sb). J. Alloys Comp. 451, 467–469 (2008).
Agulyansky, A. Chemistry of tantalum and niobium fluoride compounds, Elsevier (2004).
Chen, B. J. et al. Structural stability at high pressure, electronic and magnetic properties of BaFZnAs: A new candidate of host material of DMS. Chin. Rev. B 25, 077503 (2016).
Glasbrenner, J. K., Žutić, I. & Mazin, I. I. Theory of Mn-doped II-II-V semiconductors. Phys.Rev.B 90, 140403(R) (2014).
Suzuki, H. et al. Fermi surfaces and p-d hybridization in the diluted magnetic semiconductor Ba1−xKx(Zn1−yMny)2As2 studied by soft x-ray angle-resolved photoemission spectroscopy. Phys. Rev. B 92, 235120 (2015).
Sun, F. et al. Pressure effect on the magnetism of the diluted magnetic semiconductor (Ba1−xKx)(Zn1−yMny)2As2 with independent spin and charge doping. Phys. Rev. B 93, 224403 (2016)
Suzuki, H. et al. Photoemission and x-ray absorption studies of the isostructural to Fe-based superconductors diluted magnetic semiconductor Ba1−xKx(Zn1−yMny)2As2 . Phys. Rev. B 91, 140401(R) (2015).
Ferrand, D. et al. Carrier-induced ferromagnetism in p-Zn1−xMnxTe. Phys. Rev. B 63, 085201 (2001).
Matsukura, F., Ohno, H., Shen, A. & Sugawara, Y. Transport properties and origin of ferromagnetism in (Ga,Mn)As. Phys. Rev. B 57, R2037 (1998).
Uemura, Y. J., Yamazaki, T., Harshmann, D. R., Senba, M. & Ansaldo, E. J. Muon spin relaxation in AuFe and CuMn spin glasses. Phys. Rev. B 31, 546–563 (1985).
Uemura, Y. J. et al. Phase separation and suppression of critical dynamics at quantum phase transitions of MnSi and (Sr1−xCax)RuO3 . Nat. Phys. 3, 29–35 (2007).
Uemura, Y. J. et al. Quantum evolution from spin-gap to antiferromagnetic state in the frustrated J1–J2 system Cu(Cl,Br)La(Nb,Ta)2O7 . Phys. Rev. B 80, 174408 (2009).
Dunsiger, S. et al. Spatially homogeneous ferromagnetism of (Ga,Mn)As. Nat. Mater. 9, 299–303 (2010).
Ning, F. L. et al. Suppression of TC by overdoped Li in the diluted ferromagnetic semiconductor Li1+y(Zn1−xMnx)P: a μSR investigation. Phys. Rev. B 90, 085123 (2014).
Ohno, H. et al. Electric-field control of ferromagnetism. Nature 408, 944–946 (2000).
Dietl, T., Ohno, H. & Matsukura, F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors. Phys. Rev. B 63, 195205 (2001).
Schwarz, K. & Blaha, P. Solid state calculations using WIEN2k. Computational Mater. Sci. 28, 259 (2003).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This research at IOP in Beijing was supported by NSF, MOST & CAS(112111KYS820150017) of China through research Projects; at Columbia and TRIUMF by NSF grants DMR-1105961, OISE-0968226 (PIRE) and DMR-1436095 (DMREF), REIMEI project from JAEA, Japan, and the Friends of Todai Inc. Foundation.
Author information
Authors and Affiliations
Contributions
C.Q.J. conceived & coordinated the work; B.J.C. grown the polycrystalline (Ba,K)F(Zn,Mn)As crystals with preliminary characterizations and conducted the magnetic susceptibility measurements and electronic transport measurements with the help of Z.D., M.R.G., W.M.L.; B.F., S.C., L.L., Y.J.U., C.D., S.L.G., F.L.N., T.J.S.M., M.N.W., Y.P.C., G.M.L., Z.G., S.Y. and B.J.C. contributed to the muon spin relaxation measurements; C.Q.J., B.J.C., B.F. and S.C. analyzed the data; C.Q.J., B.J.C. and B.F. wrote the paper. C.Z.G., Q.Q.L., F.X.H., B.G.S. and Z.L contributed to the discussions of the work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, B., Deng, Z., Li, W. et al. New Fluoride-arsenide Diluted Magnetic Semiconductor (Ba,K)F(Zn,Mn)As with Independent Spin and Charge Doping. Sci Rep 6, 36578 (2016). https://doi.org/10.1038/srep36578
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36578
This article is cited by
-
Comparison of Fourier-transformed and Wavelet-transformed EXAFS
Journal of the Korean Physical Society (2024)
-
Single Crystal Growth and Spin Polarization Measurements of Diluted Magnetic Semiconductor (BaK)(ZnMn)2As2
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.