Abstract
Structural changes induced by radiation damage in X-ray crystallography hinder the ability to understand the structure/function relationship in chemical reactions. Serial femtosecond crystallography overcomes this problem by exposing the sample to very short and intense laser pulse leading to measurement before destruction. Here we use molecular modeling to map the radiation damage during the 10–50 fs to the intensity, the energy and the time duration of the laser pulse on the oxygen-evolving complex (OEC) of photosystem II. In the model, the nuclei move classically in a fully quantum potential created by electron density under the effect of strong laser pulse in the Ehrenfest dynamics regime. The results show that the Mn-Mn and Mn-Ca distances are less affected by radiation damage due to the their heavy masses, while one μ-oxo bridge (O5) moves significantly. The radiation damage may induce conformational changes of the water ligands but only bond elongation for the amino acids ligands. These effects are relatively intensity independent from 1016 to 1017 W/cm2, but changes increase dramatically if the beam intensity is increased to 1018 W/cm2. In addition, the self amplified spontaneous emission (SASE) nature of the laser beam does not affect the dynamics of the ions.
Similar content being viewed by others
Introduction
In serial femtosecond crystallography randomly oriented crystals are exposed to very intense, ultra short laser pulses that produce one diffraction pattern in the tens of femtoseconds before it destroys the crystal1. One of the main advantages of this technique is that it is proposed to overcome the problem of radiation damage, which is caused by the interactions between the X-ray photons and the atoms in the sample. These interactions are statistical events dominated by the photoelectric effect2. Thus, it has been assumed that the atoms have little time to move during the brief time of the measurement.
The radiation damage induced by X-ray photons was studied as a stochastic process in which the probability of the photoelectric effect and inelastic events are measured as a function of the interaction cross section2. However, some quantum effects such as femtosecond collisional electron transfer and trapping of electrons due to the accumulated positive charges in the system were ignored. Because the geometrical structures of the atoms cannot change as fast as the electronic structure, Neutze and coworkers concluded that the obtained structures using this method may be considered radiation damage free structures2.
The structure of the oxygen-evolving center (OEC) of Photosystem II (PSII) that catalyzes the water splitting reaction has been studied intensively3,4,5,6,7,8,9. The OEC uses light energy to photo-oxidize water in a series of oxidation steps in the catalytic S-state cycle10. The first crystal structure of PSII at 3.1 Å resolution3 revealed that the OEC contains four Mn atoms, in addition to calcium atom. Due to the limited resolution the electron densities of the bridging oxygens that connect the Mn centers were not resolved. However, combining the lower resolution structural information with other data and computational studies provided good working models of the basic OEC structure11,12,13,14,15. The lowest catalytically active OEC (in the S0 state) has 3 Mn(III) and 1 Mn(IV).
However, the reported Mn-Mn distances in the 3.1 Å structure were not fully consistence with those found via Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy and the differences were attributed to the radiation damage, which reduced the Mn in the OEC distorting the cluster16. In 2011, Umena and coworkers solved the PSII structure at 1.90 Å resolution and five bridging oxygens and all Mn ligands were identified8. However, the Mn-O distances remained longer than the bond distances measured by EXAFS or calculated using ab-initio calculations, which suggested that the Mn centers are reduced because of the free electrons generated due to the radiation damage17.
Serial femtosecond crystallography has been employed in the hope of obtaining a structure of the OEC free of radiation damage18,19. However, due to the limited resolution, the detailed structure of the OEC could not be resolved. Recently, Suga and coworkers obtained a radiation-damage-free structure by collecting still diffraction images of highly isomorphous crystals using the 10 KeV XFEL beam at a cryogenic temperature20.
Here, we study the radiation damage that might be expected in the intense XFEL beam using computer simulation. First, we optimized the geometry obtained from the crystal structure using localized orbital Density Functional Theory (DFT)21. Then, we applied an intense 10 KeV laser pulse for 50 femtoseconds and used Time Dependent Density Functional Theory (TDDFT) for the electrons to generate “on-the fly” potential that is applied on the classically moving ions in Ehrenfest Dynamics framework22,23. In addition, we have added absorption boundaries using a mask wavefunction to allow electrons to leave the system as will occur in the real reaction.
The deviation of each atom coordinates from the starting ground state position is evaluated by calculating the root mean square deviation (RMSD) for each atom type at each 0.15 femtosecond to map the radiation damage to the pulse duration. In addition, we study the evolution of the ion’s kinetic and potential energy, the total electronic energy and the total number of electrons lost through the exposure to the laser pulse.
Furthermore, we study how the beam intensity and energy correlate with the evolution of the RMSD of the nuclei and the energy of the system by applying laser pulses at different intensities and energies for 10 femtoseconds. Then we apply a combination of laser pulses that span a frequency band of 40 eV at different intensities to mimic the self-amplified spontaneous emission (SASE) spectrum and study its effect on the behavior of the system.
Results and Discussions
In the “diffraction before destruction” XFEL experiment, an intense, ultra short laser pulse is applied to a sample, which produces a diffraction pattern recorded on the detector. The intense high-energy laser beam destroys the sample as it causes the electrons to be ejected from their orbitals and leave the system. The strong electrostatic repulsion between newly created ionic atoms stimulates them to move further from each other. The open question is; at which point of the destruction reaction is the diffraction pattern recorded?
The evolution of the structure in time under the effect of laser field
A laser flash interacts with the PSII crystals in a nonadiabatic electronic process, which cannot be described in the Born-Oppenheimer regime. Ehrenfest dynamics can be used to model nonadiabatic interactions given that the time step is on the scale of the motion of electrons, which is order of magnitude faster than the nuclei. Thus, Ehrenfest dynamics is ideal for studying the effect of the short laser field on the OEC for times on the order of 50 fs. However, it should be noted that this method cannot describe the process in which, excited electrons dissipate energy into ionic vibrations known as Joule heating24.
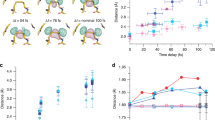
The optimized X-ray structure is exposed to 50 fs laser pulse of 1.2 × 1016 W/cm2 intensity and 10 KeV photon energy; then the system is propagated in time using Approximated Enforced Time-Reversal Symmetry (AETRS) operator25 with a time step of 0.0015 fs (see supplementary information for simulation movie). The calculated RMSD from the initial position at t = 0 shows that the atoms are clustered in three groups (Fig. 1A); group 1 contains the hydrogen atoms, which have high kinetic energy due to their light mass; group 2 contains carbon, nitrogen and oxygen atoms where these atoms have similar masses and moves much slower than hydrogens; group 3 which contains manganese and calcium ions, which are the slowest moving ions due to their heavy masses. Thus, the Mn-Mn and Mn-Ca distances are expected to be more accurate and less affected by radiation damage.
The ion motion here is driven by a Coulomb explosion, that is to say as high energy photons are absorbed by the electrons, they gain enough energy to escape from their hosting atoms (Fig. 1B). The electrons disappear when they reach the boundary of the simulation box and the number of electrons in the system decreases rapidly in the first 5 fs. Then, the accumulated positive charges pose a potential barrier keeping the electrons from leaving the system (Fig. 1C). However, because the system is positively charged, the individual ions repel each other. Thus, the Coulomb electrostatic potential energy is converted to kinetic energy that induces the ionic motion (Fig. 1D).
To study the effect of the intensity of the laser field on the reaction, we applied laser pulses of intensities 1.2 × 1016, 1.2 × 1017 and 1.2 × 1018 W/cm2 in three independent runs at energy of 10 KeV. The runs with intensities 1016 and 1017 W/cm2 yielded very similar results as shown in Fig. 2. However, if the intensity increased to 1018 W/cm2, the number of electrons that leave the system increases dramatically (Fig. 2A), which in turn increases the kinetic energy (and decreases the potential energy) of the ions (Fig. 2B,C) and causes severe radiation damage in very short time even for the heaviest ions (Fig. 2D). In contrast, increasing the energy of the beam to 15 KeV with the intensity fixed at 1.2 × 1016 for 10 fs does not produce any significant change in the RMSD of the ions or in the number of electrons lost.
The X-ray laser is often generated by Self-Amplified Spontaneous Emission, where free electrons are the lasing source. Due to the stochastic nature of the lasing electrons, the generated beam is not monochromatic and has a bandwidth of approximately 40 eV. Here, we model the effect of the SASE spectrum by applying 5 laser pulses of different frequencies and intensities simultaneously (Fig. 3A). The five pulses spans an energy range of 40 eV and the peak intensity is 1.2 × 1016 W/cm2. The results show that the SASE spectrum yields ion behavior that is identical to the case where a smooth Gaussian shape pulse with the same peak intensity is applied. The only observed difference is the temporal behavior of the electronic energy, which is driven by the applied spectrum (Fig. 3B).
(A) The intensity profile of the applied laser pulse represented as the square of the amplitude of the electric field. The intensity is a superposition of 5 Gaussian pulses. The energies of the pulses are 10, 9.98, 9.993, 10.02 and 10.008 KeV. The intensities of the pulses are 1.2, 0.97, 0.01, 0.43 and 0.11 × 1016 W/cm2 respectively. (B) The evolution of electronic energy of the system in time.
Insights on the radiation damage free structure of the OEC
The XFEL radiation damage free structure was obtained by applying a 10 fs laser pulse on highly isomorphous crystals20. The reported bond lengths differ significantly from the structure obtained from the traditional X-ray crystallography8 (Table 1a). These differences were attributed to the bond elongation resulting from reducing the Mn centers induced by radiation damage.
The geometry optimization of the X-ray or XFEL structures using DFT leads to structures with good agreement with EXAFS17,26. However, the calculated Mn-O5 distances do not match the measured values (Table 1b DFT column). To test if these structural changes are resulting from the radiation damage, we expose the DFT optimized structure to a laser pulse of 10 KeV energy and 1.2 × 1016 W/cm2 intensity for 10 fs (Table 1b 10 fs column). The elongated bonds due to the exposure to the laser filed are slightly in better agreement with XFEL measurements. However, the Mn4-O5 and Mn3-O5 distances are 0.40 and 0.28 Å shorter than the measured bond lengths respectively. Batista and coworkers suggested the structure is a mixture of the S0 and S1 states due to the dark adaptation prior to data collection26.
To further examine the structure, we exposed the DFT structure to a laser pulse of 50 fs to check if the structure will converge at any point to the XFEL structure (Table 1b 50 fs column). Although the Mn-O5 and Ca-O5 distances agree better with the XFEL structure, the Mn-Mn distances are longer and diverging from the measured bond lengths. Thus, our simulation suggests that the Mn-O5 bonds elongation in the XFEL structure is not caused by radiation damage.
Methods
TDDFT and Ehrenfest dynamics
Starting from the DFT optimized structure in the localized orbital framework; the ground state wavefunction is obtained in the real space grid representation in OCTOPUS27,28 with 0.18 Å grid spacing. Then, the time propagation method is used to evolve the ground state wavefunction in time with 0.0015 fs time step in the existence of Gaussian shape laser field of 1.2 × 1016, 1.2 × 1017 or 1.2 × 1018 W/cm2. In addition, a mask wavefunction is applied on the borders of the simulation box to absorb the electrons reaching there to mimic the real reaction27,28. The ions are allowed to move in Ehrenfest dynamics framework. The beam energy operated on PSII crystals at Stanford Linear Accelerator Center (SLAC) is less than 10 KeV19,29. However, to study the extreme case the input laser energy in our calculations was set to 10 KeV and 15 KeV to study the effect of energy increase.
Geometry optimization
Because OCTOPUS27,28 is not designed for geometry optimization, the structure is optimized with localized orbitals DFT using the B3LYP density functional in Gaussian0921 starting from the 1.9 Å structure of PSII (PDB ID 3ARC)8. The LANL2DZ basis sets with effective core potentials are used for Mn and Ca, while 6-31G* is used for the other atoms. The model includes the four terminal waters bound to Mn4 and Ca2+, the side chains of the amino-acid ligands to each Mn (D170, E189, H332, E333, D342, A344, and CP43-E354), as well as the side chains hydrogen bonded to the bridging and terminal oxygens (D61, H337, and CP43-R357). In addition, 5 crystallographic waters are included in the model (Fig. 4). All Mn centers are fixed in the high spin states.
Additional Information
How to cite this article: Amin, M. et al. Radiation Damage in XFEL: Case study from the oxygen-evolving complex of Photosystem II. Sci. Rep. 6, 36492; doi: 10.1038/srep36492 (2016).
References
Schlichting, I. Serial femtosecond crystallography: the first five years. IUCrJ 2, 246–255, doi: 10.1107/S205225251402702X (2015).
Neutze, R., Wouts, R., van der Spoel, D., Weckert, E. & Hajdu, J. Potential for biomolecular imaging with femtosecond X-ray pulses. Nature 406, 752–757, doi: 10.1038/35021099 (2000).
Zouni, A. et al. Crystal structure of photosystem II from Synechococcus elongatus at 3.8 Å resolution. Nature 409, 739–743 (2001).
Sproviero, E. M., Gascon, J. A., McEvoy, J. P., Brudvig, G. W. & Batista, V. S. QM/MM models of the O-2-evolving complex of photosystem II. Journal of Chemical Theory and Computation 2, 1119–1134, doi: Doi 10.1021/Ct060018l (2006).
Barber, J. & Murray, J. W. The structure of the Mn4Ca2+ cluster of photosystem II and its protein environment as revealed by X-ray crystallography. Philosophical Transactions of the Royal Society B-Biological Sciences 363, 1129–1137, doi: 10.1098/rstb.2007.2208 (2008).
Murray, J. W. et al. X-ray crystallography identifies two chloride binding sites in the oxygen evolving centre of Photosystem II. Energy & Environmental Science 1, 161–166, doi: Doi 10.1039/B810067p (2008).
Guskov, A. et al. Photosystem II at 2.9 Angstrom resolution: role of quinones, lipids, channels and chloride. Structure 3BZI released Jan 20th, 2009 (2009).
Umena, Y., Kawakami, K., Shen, J.-R. & Kamiya, N. Crystal structure of oxygen-evolving photosystem II at 1.9 A resolution. Nature 473, 55–60 (2011).
Amin, M., Pokhrel, R., Brudvig, G. W., Badawi, A. & Obayya, S. S. A. Effect of Chloride Depletion on the Magnetic Properties and the Redox Leveling of the Oxygen-Evolving Complex in Photosystem II. The journal of physical chemistry. B 120, 4243–4248 (2016).
Kok, B., Forbush, B. & McGloin, M. Cooperation of charges in photosynthetic O2 evolution-I. A linear four step mechanism. Photochem Photobiol 11, 457–475 (1970).
Hasegawa, K., Ono, T., Inoue, Y. & Kusunoki, M. How to evaluate the structure of a tetranuclear Mn cluster from magnetic and EXAFS data: Case of the S-2-state Mn-cluster in photosystem II. Bull. Chem. Soc. Jpn. 72, 1013–1023 (1999).
Robblee, J. et al. The Mn cluster in the S-0 state of the oxygen-evolving complex of photosystem II studied by EXAFS spectroscopy: Are there three di-mu-oxo-bridged Mn-2 moieties in the tetranuclear Mn complex? J. Am. Chem. Soc. 124, 7459–7471 (2002).
Dau, H., Liebisch, P. & Haumann, M. The structure of the manganese complex of Photosystem II in its dark-stable S-1-state-EXAFS results in relation to recent crystallographic data. Phys. Chem. Chem. Phys. 6, 4781–4792 (2004).
Yano, J. et al. High-resolution Mn EXAFS of the oxygen-evolving complex in photosystem II: Structural implications for the Mn4Ca cluster. J. Am. Chem. Soc. 127, 14974–14975 (2005).
Sproviero, E. M., Gascon, J. A., McEvoy, J. P., Brudvig, G. W. & Batista, V. S. A model of the oxygen-evolving center of photosystem II predicted by structural refinement based on EXAFS simulations. Journal of the American Chemical Society 130, 6728–6730, doi: 10.1021/ja801979n (2008).
Baxter, R. H. G., Seagle, B. L., Ponomarenko, N. & Norris, J. R. Specific radiation damage illustrates light-induced structural changes in photosynthetic reaction centers. J. Am. Chem. Soc. 126, 16728–16729 (2004).
Luber, S. et al. S1-state model of the O2-evolving complex of photosystem II. Biochemistry 50, 6308–6311, doi: 10.1021/bi200681q (2011).
Kern, J. et al. Room temperature femtosecond X-ray diffraction of photosystem II microcrystals. Proceedings of the National Academy of Sciences of the United States of America 109, 9721–9726, doi: 10.1073/pnas.1204598109 (2012).
Kupitz, C. et al. Serial time-resolved crystallography of photosystem II using a femtosecond X-ray laser. Nature 513, 261–265, doi: 10.1038/nature13453 (2014).
Suga, M. et al. Native structure of photosystem II at 1.95 A resolution viewed by femtosecond X-ray pulses. Nature 517, 99–103, doi: 10.1038/nature13991 (2015).
Frisch, M. J. et al. Gaussian 09, Revision A.1. Gaussian 09 (2009).
Li, X., Tully, J. C., Schlegel, H. B. & Frisch, M. J. Ab initio Ehrenfest dynamics. The Journal of chemical physics 123, 084106, doi: 10.1063/1.2008258 (2005).
Wang, F., Yam, C. Y., Hu, L. & Chen, G. Time-dependent density functional theory based Ehrenfest dynamics. The Journal of chemical physics 135, 044126, doi: 10.1063/1.3615958 (2011).
Horsfield, A. P., Bowler, D. R., Fisher, A. J., Todorov, T. N. & Sánchez, C. G. Beyond Ehrenfest: correlated non-adiabatic molecular dynamics. J. Phys.: Condens. Matter 16, 8251–8266 (2004).
Castro, A., Marques, M. A. & Rubio, A. Propagators for the time-dependent Kohn-Sham equations. The Journal of chemical physics 121, 3425–3433, doi: 10.1063/1.1774980 (2004).
Askerka, M., Vinyard, D. J., Wang, J., Brudvig, G. W. & Batista, V. S. Analysis of the radiation-damage-free X-ray structure of photosystem II in light of EXAFS and QM/MM data. Biochemistry 54, 1713–1716, doi: 10.1021/acs.biochem.5b00089 (2015).
Andrade, X. et al. Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems. Phys Chem Chem Phys 17, 31371–31396, doi: 10.1039/c5cp00351b (2015).
Andrade, X. et al. Time-dependent density-functional theory in massively parallel computer architectures: the OCTOPUS project. Journal of physics. Condensed matter: an Institute of Physics journal 24, 233202, doi: 10.1088/0953-8984/24/23/233202 (2012).
Kern, J. et al. Simultaneous femtosecond X-ray spectroscopy and diffraction of photosystem II at room temperature. Science 340, 491–495, doi: 10.1126/science.1234273 (2013).
Acknowledgements
We would like to thank Dr. Marilyn Gunner, Dr. Gary Brudvig, Dr. Jimin Wang, Dr. Nicholas Sauter, Dr. Junko Yano and Dr. Vittal Yachandra for the useful discussion. We acknowledge financial support from the Division of Chemical Sciences, Geosciences, and Biosciences, Office of Basic Energy Sciences, U.S. Department of Energy (DE-SC0001423).
Author information
Authors and Affiliations
Contributions
Muhamed Amin, proposed the idea, created the simulation model, and prepared the manuscript. Ashraf Badawi, wrote part of the manuscript and analyzed the data. S.S. Obayya, wrote part of the manuscript and analyzed the data.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Amin, M., Badawi, A. & Obayya, S. Radiation Damage in XFEL: Case study from the oxygen-evolving complex of Photosystem II. Sci Rep 6, 36492 (2016). https://doi.org/10.1038/srep36492
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36492
This article is cited by
-
Megahertz pulse trains enable multi-hit serial femtosecond crystallography experiments at X-ray free electron lasers
Nature Communications (2022)
-
Structural dynamics in proteins induced by and probed with X-ray free-electron laser pulses
Nature Communications (2020)
-
Serial femtosecond crystallography structure of cytochrome c oxidase at room temperature
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.