Abstract
Semiconductor-based quantum dot single-electron pumps are currently the most promising candidates for the direct realization of the emerging quantum standard of the ampere in the International System of Units. Here, we discuss a silicon quantum dot single-electron pump with radio frequency control over the transparencies of entrance and exit barriers as well as the dot potential. We show that our driving protocol leads to robust bidirectional pumping: one can conveniently reverse the direction of the quantized current by changing only the phase shift of one driving waveform with respect to the others. We anticipate that this pumping technique may be used in the future to perform error counting experiments by pumping the electrons into and out of a reservoir island monitored by a charge sensor.
Similar content being viewed by others
Introduction
After a quarter of a century of development of charge pumps, we are close to redefining the International System of Units (SI) standard for the electrical current, the ampere, such that it would be based on a fixed value of the elementary charge1,2. The direct experimental realization of such a quantum ampere standard is based on charge pumps which transfer accurately an integer n number of electrons per cycle from the source to the drain at frequency f, yielding direct current I = nef. The parameter region where the pumped current is quantized in such a way and where it is insensitive to changes in the system parameters is referred to as a plateau. For practical realizations of the current standard and for the closure of the so-called quantum metrology triangle, it is sufficient that the pump yields a current of hundreds of picoamperes with relative error of 10−8 3,4,5.
The very first charge pumps were able to produce currents of a few picoamperes with uncertainties of a few per cent6,7,8,9. After this, several different implementations of charge pumps have been proposed and tested: normal-metal tunnel junction devices10,11, superconducting devices12,13,14, superconductor–normal-metal hybrid turnstiles15,16,17,18,19,20, and surface acoustic wave devices21,22. At the moment, the most promising candidates for the emerging quantum ampere are semiconductor quantum dots23,24,25,26,27,28,29,30,31,32,33,34,35,36 and single-atom impurities in semiconductors37,38,39,40, the state of the art being, a current of 87 pA in a GaAs/AlGaAs quantum dot with an uncertainty of less than 0.2 parts per million (ppm)26. Silicon single-electron pumps have also been studied widely31,32,33,34,35,36,37,38,41,42,43,44. Benefits of silicon pumps are that they are based on technologies well-known by the industry and they may exhibit suppressed 1/f noise and the absence of large random charge jumps45,46,47,48,49.
The accuracy of a charge pump can be determined with a charge sensor that monitors the charge state of a reservoir island into which electrons are pumped. Several different charge sensing schemes have been demonstrated: pumping electrons into and out of the reservoir10,41,42,50, pumping a number of electrons into the reservoir and cyclically emptying it51, monitoring multiple reservoirs interleaved with pumps in a series configuration20,52,53, and monitoring the pump dot without any storage node27. In general, pumping electrons into and out of a reservoir in semiconductor devices is highly nontrivial due to the asymmetry of the devices and pumping protocols.
In this paper, we demonstrate bidirectional electron pumping in a silicon-based quantum dot by employing a three-waveform protocol, thus offering a step towards error counting based on a reservoir dot. Our technology allows simultaneous control over both barriers and the dot potential, enabling convenient switching between the pumping by changing only the phase of one driving signal. This kind of switching between the directions has been demonstrated before in silicon devices32,24 with two driving waveforms to the barrier gates8 and in metallic pumps with three waveforms9,14.
Results
Pumping with three waveforms
A scanning electron microscope image of our quantum dot device and a schematic measurement set-up are presented in Fig. 1(a). The details of forming a two-dimensional electron gas (2DEG) and a single-electron dot isolated from the leads are discussed in refs 34, 51 and 54. Initially, we pump with sinusoidal radio frequency (rf) waveforms applied to the plunger gate (PL) and to the barrier right gate (BR) with a phase difference of PL with respect to BR, ϕBR-PL = 95° at 800 mK temperature. We electrically confine the dot by setting negative bias on the confining gates C1 and C2, with gate voltages VC1 and VC2, respectively34,55. Then we search in the dc parameter space for a stable pumping plateau in the positive current direction, i.e., BR corresponds to the entrance barrier and the barrier left gate (BL) to the exit barrier. Here, we define the first plateau as the parameter region for which the normalized pumped current, I/ef is within 5% of unity. Subsequently, we decrease the dc potential on BL, VBL, i.e., we make the exit barrier more opaque, until we measure only a narrow pumping plateau as a function of PL and BR dc voltages, VPL and VBR respectively. At this point, our pumping process is limited by the unloading process. Then we drive BL a sinusoidal waveform 180° phase-shifted with respect to BR so that all the waveforms are sines by  ,
,  , and
, and  . We determine the cross talks between the barriers to the dot by measuring the shift of the pumping plateau due to dc barrier voltages and find CBL-dot/CPL-dot ≈ 0.1 and CBR-dot/CPL-dot ≈ 0.2.
. We determine the cross talks between the barriers to the dot by measuring the shift of the pumping plateau due to dc barrier voltages and find CBL-dot/CPL-dot ≈ 0.1 and CBR-dot/CPL-dot ≈ 0.2.
Sample and pumping protocol.
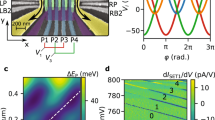
(a) Scanning electron microscope image of a sample similar to the one used in the experiments together with the schematic measurement setup. The lateral position of the quantum dot is indicated by an orange oval. Blue squares indicate the ohmic contacts of source and drain to the two-dimensional electron gas. (b) Schematic potential landscapes for an electron along the red line in (a) at different stages of the pumping process for two different phases of plunger drive leading to either positive (left) or negative (right) pumped current. The whole process consists of electron loading (I), trapping (II), and unloading (III). (c) Temporal dependence of the potentials below the barriers and at the dot (blue, red, and green lines as indicated) in the three-waveform driving scheme with two different phases (solid and dashed lines) of the plunger drive with respect to BR drive. The Fermi level of the leads is shown by the black dashed line. The gray lines indicate the time instants visualized in (b). (d) Pumped current as a function of plunger gate voltage, VPL, with different amplitudes of the driving voltage on the left barrier, ABL, at 200 MHz frequency. Inset: The pumped current from the main panel in the vicinity of plateau I/ef = 1. The dc gate voltages defined in (a) assume the following values: VSL = 3.5 V, VDL = 1.8 V, VC1 = −0.40 V, VC2 = −0.50 V, VBL = 0.80 V, and VBR = 0.72 V. The rf driving amplitudes are ABR = 158 mV, and APL = 79 mV with a phase difference ϕBR-PL = 95°.
A schematic illustration of the pumping process with three pulses is presented in Fig. 1(b). First (I) we lower the entrance barrier and the potential of the dot such that an electron tunnels into the dot. In the second phase, (II) the entrance barrier is raised and the electron is trapped in the dot. Then the electron is unloaded (III) by lowering the exit barrier and raising the dot potential. Depending on the phase of PL it is possible that electrons exit at energies above the Fermi level of the leads. Hence it is possible that the electron escapes to the source but such process is unlikely due to the high opacity of the entrance barrier. The time dependence of the estimated potential heights of the barriers and of the dot with two different phases on PL is presented in Fig. 1(c). Here, we have taken into account the estimated cross couplings of the gates to the potential barriers and to the dot. The normalized pumped current, I/ef, at f = 200 MHz is shown as a function of VPL with varying ABL in Fig. 1(d). The length of the first plateau increases significantly with higher ABL. Note also that with low amplitudes there is no second plateau, but with high amplitudes the second plateau corresponding to transfer of two electrons per cycle is clearly visible. Even with low amplitudes we load two electrons in this VPL region but the out tunneling is unlikely to happen due to too high left potential barrier. The tiny plateaus at the rise to the first plateau arise owing to excited states, a phenomenon also observed in other quantum dot pumps34,56.
Not only does the length of the plateaus increase with increasing ABL but the current quantization becomes more accurate, i.e., the pumped current is closer to the expected value. The inset of Fig. 1(d) shows that with low amplitude, the normalized pumped current at the first plateau is below unity by a few per cent. However, with high amplitudes the normalized current reaches unity more precisely which indicates a more precise unloading process.
In order to find a good working point for bidirectional pumping, we study the pumping process by measuring the pumped current as a function of VPL, VBR, and VBL. We begin by pumping with PL and BR as described above, but decrease ABR until we measure only a narrow plateau region in terms of VPL, VBR, and VBL. We measure the pumped current as a function of VPL and VBR and as a function of VPL and VBL. We repeat these scans with different ABL values. The results are shown in Fig. 2(a). We observe that the plateau enlarges in the parameter space (VPL, VBR, and VBL) with increasing ABL. The maximum length of the plateau in terms of VPL increases from 14 to 52 mV as ABL increases from 0 to 123 mV.
Stability of the pumped current.
Pumped current as a function of the plunger gate voltage, VPL, and the barrier right gate voltage, VBR, (left columns) and of the plunger gate voltage and the barrier left gate voltage, VBL, (right columns) with different amplitudes on BL (a) and BR (b). The frequencies are 200 MHz in (a) and 100 MHz in (b). Magenta (a) and cyan (b) color indicate pumping regions where I/ef = ±1 within 5%. The parameter values used in (a) are the same as in Fig. 1(d) except for VBL = 0.9 V in the left column, VBR = 0.725 V in the right column, and ABR = 123 mV in both columns. In (b) the values are the same as in (a) except for VBL = 0.814 V in left column, VBR = 0.85 V in the right column, ABL = 112 mV and APL = 205 mV in both columns, and ϕBL-PL = 120°. (c) Maximum plateau length in the plunger dc voltage as a function of the exit barrier amplitude extracted from (a) for BL (black squares) and from (b) for BR (red circles) as the exit barrier.
This experiment is repeated in the case where the exit barrier is BR, i.e., the opposite pumping direction. We pump initially with PL and BL using PL phase difference w.r.t. BL as ϕBL-PL = 120° at 100 MHz. A third waveform (complement waveform to that of BL) is applied to BR. The waveforms are:  ,
,  , and
, and  . We observe a similar widening of the plateau in Fig. 2(b) as in Fig. 2(a). However, in this case the length of the plateau in VPL reaches a maximum around ABR = 79 mV, suggesting that BR couples to the quantum dot more strongly than BL. For simplicity, we do not compensate this coupling in the experiment. Therefore the increased amplitude in BR interferes with the pumping process more than that in BL, restricting our ability to improve the pumping process beyond the observed optimal point. The maximum length of the plateau in terms of VPL increases from 12 mV to 25 mV as ABR increases from 0 to 79 mV. The slopes of the contours at the rising edges of the plateaus observed in Fig. 2(a,b) are caused by the cross coupling of the barrier gates to the dot.
. We observe a similar widening of the plateau in Fig. 2(b) as in Fig. 2(a). However, in this case the length of the plateau in VPL reaches a maximum around ABR = 79 mV, suggesting that BR couples to the quantum dot more strongly than BL. For simplicity, we do not compensate this coupling in the experiment. Therefore the increased amplitude in BR interferes with the pumping process more than that in BL, restricting our ability to improve the pumping process beyond the observed optimal point. The maximum length of the plateau in terms of VPL increases from 12 mV to 25 mV as ABR increases from 0 to 79 mV. The slopes of the contours at the rising edges of the plateaus observed in Fig. 2(a,b) are caused by the cross coupling of the barrier gates to the dot.
The maximum length of the plateau in VPL as a function of the exit barrier amplitude extracted from the data of Fig. 2(a,b) is presented in Fig. 2(c). In both scenarios, the length increases rather linearly as we increase the amplitude of the exit barrier, but in the case of BR, we observe a maximum.
Bidirectional pumping
Let us choose the values of all experimentally controllable parameters such that they correspond to the maximum plateau length in Fig. 2(b). Then we measure the pumped current as a function of VPL and ϕBL-PL with the results shown in Fig. 3(a). The pumping plateaus in both directions have the same midpoint, VPL = 0.823 V. Thus in comparison to bidirectional pumping observed with two rf waveform in a similar sample34, the advantage is that we can pump in both directions with a fixed VPL value. With only two rf waveforms we also needed to change VPL to reverse the pumping direction.
Bidirectional pumping.
(a) Pumped direct current as a function of the plunger dc voltage and the phase difference of plunger rf driving voltage with respect to the barrier left rf drive. Magenta and cyan color indicate the regions where I/ef = ±1 within 5%, i.e., where one electron is pumped per cycle in the positive and negative directions, respectively. The parameter values are the same as in Fig. 2(b) with the choice VBL = 0.814 V, VBR = 0.850 V, and ABR = 79 mV. (b) Absolute values of the cross sections along VPL in (a) at ϕBL-PL = 120° (blue) and 240° (red) with 95% confidence intervals indicated. (c) Cross section of the pumped current along ϕBL-PL at VPL = 0.823 V indicated by the green dashed line in (a).
We examine the cross sections along VPL with two phase differences, ϕBL-PL = 120° and ϕBL-PL = 240°. The absolute value of the pumped current in both cases is shown in Fig. 3(b). In the region where VPL = 0.820–0.826 V, the absolute magnitude of current in each direction is the same within the experimental uncertainty. In the middle of this region (at VPL = 0.823 V), we study the cross section of Fig. 3(a) along the phase difference ϕBL-PL, as shown in Fig. 3(c). We clearly observe that the pumping plateau appears in the negative direction in the range ϕBL-PL = 40–160° and in the positive direction in the range ϕBL-PL = 200–290°.
Discussion
We have demonstrated robust bidirectional pumping with convenient switching between the pumping directions in a silicon single-electron pump with independent rf control over both barriers and the dot potential. Initially, we pump with the entrance barrier and PL, and then we introduce a third rf waveform to the exit barrier. We study the effect of the amplitude of the exit barrier waveform on the pumped current and observe that it can increase the length of the current plateau in the parameter space of applied gate potentials without the need to increase the amplitudes of the other drives. Subsequently, we studied the pumped current as a function of the plunger gate voltage and the phase difference of the plunger drive with respect to the barrier drives. We find a parameter region where we can perform pumping in positive and negative directions simply by changing the phase of the plunger drive. Furthermore, there is a parameter region where the magnitudes of the pumped currents in different directions are equal within experimental accuracy.
Our architecture, which incorporates individual control over both barriers and the quantum dot is highly flexible. It allows convenient switching between the pumping directions simply by changing the phase of the plunger gate rf drive. This property can potentially be used to extend the basic electron counting scheme demonstrated in ref. 51, to a more sophisticated error counting protocol10, where single electrons are pumped back and forth between a source and a reservoir, without accumulating electrons in the reservoir. Different pumping directions may also be used to improve the signal–to–noise ratio in the current measurement by averaging over +I and −I rather than +I and zero. A pumping scheme with three rf drives may also be beneficial in increasing the accuracy of unidirectional output current of semiconductor quantum dot pumps owing to relaxed requirements on the amplitudes of the waveforms.
Methods
Sample fabrication
Our quantum dot is based on a three-layer gate-stack silicon metal–oxide–semiconductor (MOS) technology. The sample is fabricated on a high-purity intrinsic silicon wafer. A 8-nm thick SiO2 layer is thermally grown in the active region to form the gate–channel oxide. Three layers of aluminum gates with thicknesses 30, 55, and 80 nm are fabricated on top of the wafer with electron beam lithography. Polymethyl methacrylate (PMMA 950k) A4 resist is used as a mask material. After patterning the mask, we develop it in a mixture of methyl isobutyl ketone and isopropanol (MIBK:IPA 1:3) solution. Each layer of Al gates is deposited with a thermal evaporator, followed by a lift-off process. The gates are oxidized on a hot plate in an ambient environment. This process is repeated in total three times to realize all the layers. The source and drain electrodes are connected to the 2DEG with phosphorus-doped regions which form the ohmic contacts. Further details of the fabrication process are discussed elsewhere54.
Measurement set-up
All the experiments are performed in a self-made, torlon-based, plastic dilution refrigerator with a base temperature of 100 mK submerged in a 4-K helium bath. The device is cooled down to the base temperature but due to the dissipation in the coaxial cables delivering the rf waveforms, the mixing chamber temperature increases during the experiments up to 800 mK. The device is mounted on a sample holder including a printed circuit board (PCB) with integrated bias tees with capacitance of 10 nF and resistance of 100 kΩ. This allows simultaneous application of rf and dc voltages on the desired gates. Our silicon chip is attached to the sample stage with vacuum grease and wedge bonded to the PCB with Al bond wires. For the rf driving voltages, we employ a 10-dB attenuator at the 4-K bath. The dc voltages are connected to the PCB with twisted-pair loom lines. The wiring of the sample and the cryostat is discussed in more detail in ref. 54.
A 2DEG is induced at the interface between Si and SiO2 by applying positive voltage to the Al gates. All dc gate voltages are generated by floating dc voltage sources connected to 1:5 voltage dividers. The rf waveforms are generated by an arbitrary waveform generator and synchronized with a rubidium frequency standard. These waveforms are attenuated at room temperature depending on the experiment. The pumped current is amplified by 1010 V/A with a transimpedance amplifier powered by a regulated battery pack. The amplified signal is optoisolated to eliminate ground loops and subsequently recorded by a digital multimeter.
Additional Information
How to cite this article: Tanttu, T. et al. Three-waveform bidirectional pumping of single electrons with a silicon quantum dot. Sci. Rep. 6, 36381; doi: 10.1038/srep36381 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Pekola, J. et al. Single-electron current sources: Toward a refined definition of the ampere. Rev. Mod. Phys. 86, 1421 (2013).
Kaestner, B. & Kashcheyevs, V. Non-adiabatic quantized charge pumping with tunable-barrier quantum dots: a review of current progress. Reports on Progress in Physics 78, 103901 (2015).
Feltin, N. & Piquemal, F. Determination of the elementary charge and the quantum metrological triangle experiment. Eur. Phys. J. Spec. Top. 172, 267 (2009).
Drung, D., Krause, C., Becker, U., Scherer, H. & Ahlers, F. J. Ultrastable low-noise current amplifier: A novel device for measuring small electric currents with high accuracy. Review of Scientific Instruments 86, 024703 (2015).
Drung, D., Götz, M., Pesel, E. & Scherer, H. Improving the traceable measurement and generation of small direct currents. Instrumentation and Measurement, IEEE Transactions on 64, 3021 (2015).
Geerligs, L. J. et al. Frequency-locked turnstile device for single electrons. Phys. Rev. Lett. 64, 2691–2694 (1990).
Geerligs, L. J. et al. Single cooper pair pump. Z. Phys. B 85, 349 (1991).
Kouwenhoven, L. P., Johnson, A. T., van der Vaart, N. C., Harmans, C. J. P. M. & Foxon, C. T. Quantized current in a quantum-dot turnstile using oscillating tunnel barriers. Phys. Rev. Lett. 67, 1626 (1991).
Pothier, H., Lafarge, P., Urbina, C., Esteve, D. & Devoret, M. H. Single-electron pump based on charging effects. Europhys. Lett. 17, 249 (1992).
Keller, M. W., Martinis, J. M., Zimmerman, N. M. & Steinbach, A. H. Accuracy of electron counting using a 7-junction electron pump. Appl. Phys. Lett. 69, 1804 (1996).
Keller, M. W., Eichenberger, A. L., Martinis, J. M. & Zimmerman, N. M. A capacitance standard based on counting electrons. Science 285, 1706 (1999).
Niskanen, A. O., Kivioja, J. M., Seppä, H. & Pekola, J. P. Evidence of cooper-pair pumping with combined flux and voltage control. Phys. Rev. B 71, 012513 (2005).
Vartiainen, J. J., Möttönen, M., Pekola, J. P. & Kemppinen, A. Nanoampere pumping of cooper pairs. Appl. Phys. Lett. 90, 082102 (2007).
Möttönen, M., Vartiainen, J. J. & Pekola, J. P. Experimental determination of the berry phase in a superconducting charge pump. Phys. Rev. Lett. 100, 177201 (2008).
Pekola, J. P. et al. Hybrid single-electron transistor as a source of quantized electric current. Nat. Phys. 4, 120 (2008).
Maisi, V. F., Pashkin, Y. A., Kafanov, S., Tsai, J. S. & Pekola, J. P. Parallel pumping of electrons. New J. Phys. 11, 113057 (2009).
Kemppinen, A. et al. Experimental investigation of hybrid single-electron turnstiles with high charging energy. Appl. Phys. Lett. 94, 172108 (2009).
Kemppinen, A., Meschke, M., Möttönen, M., Averin, D. V. & Pekola, J. P. Quantized current of a hybrid single-electron transistor with superconducting leads and a normal-metal island. Eur. Phys. J. Spec. Top. 172, 311 (2009).
Maisi, V. F. et al. Real-time observation of discrete andreev tunneling events. Phys. Rev. Lett. 106, 217003 (2011).
Peltonen, J. T., Maisi, V. F., Singh, S., Mannila, E. & Pekola, J. P. On-chip error counting for hybrid metallic single-electron turnstiles. ArXiv, 1512.00374 (2015).
Shilton, J. M. et al. High-frequency single-electron transport in a quasi-one-dimensional GaAs channel induced by surface acoustic waves. J. Phys. Condens. Matter 8, L531 (1996).
Talyanskii, V. I. et al. Single-electron transport in a one-dimensional channel by high-frequency surface acoustic waves. Phys. Rev. B 56, 15180 (1997).
Blumenthal, M. D. et al. Gigahertz quantized charge pumping. Nat. Phys. 3, 343 (2007).
Jehl, X. et al. Hybrid metal-semiconductor electron pump for quantum metrology. Phys. Rev. X 3, 021012 (2013).
Giblin, S. P. et al. Towards a quantum representation of the ampere using single electron pumps. Nat. Commun. 3, 930 (2012).
Stein, F. et al. Validation of a quantized-current source with 0.2 ppm uncertainty. Appl. Phys. Lett. 107, 103501 (2015).
Giblin, S. P. et al. High-resolution error detection in the capture process of a single-electron pump. Appl. Phys. Lett. 108, 023502 (2016).
Connolly, M. R. et al. Gigahertz quantized charge pumping in graphene quantum dots. Nat. Nanotech. 8, 417 (2013).
Fujiwara, A., Zimmerman, N. M., Ono, Y. & Takahashi, Y. Current quantization due to single-electron transfer in Si-wire charge-coupled devices. Appl. Phys. Lett. 84, 1323 (2004).
Fujiwara, A., Nishiguchi, K. & Ono, Y. Nanoampere charge pump by single-electron ratchet using silicon nanowire metal-oxide-semiconductor field-effect transistor. Appl. Phys. Lett. 92, 042102 (2008).
Fujiwara, A. & Takahashi, Y. Manipulation of elementary charge in a silicon charge-coupled device. Nature 410, 560 (2001).
Ono, Y. & Takahashi, Y. Electron pump by a combined single-electron/field-effect-transistor structure. Appl. Phys. Lett. 82, 1221 (2003).
Chan, K. W. et al. Single-electron shuttle based on a silicon quantum dot. Appl. Phys. Lett. 98, 212103 (2011).
Rossi, A. et al. An accurate single-electron pump based on a highly tunable silicon quantum dot. Nano Lett. 14, 3405 (2014).
Jo, M. et al. Fabrication and single-electron-transfer operation of a triple-dot single-electron transistor. J. Appl. Phys. 118, 214305 (2015).
Yamahata, G., Giblin, S. P., Kataoka, M., Karasawa, T. & Fujiwara, A. Gigahertz single-electron pumping in silicon with accuracy better than 9.2 parts in 107. Appl. Phys. Lett. 109, 013101 (2016).
Yamahata, G., Nishiguchi, K. & Fujiwara, A. Gigahertz single-trap electron pumps in silicon. Nat. Commun. 5, 5038 (2014).
Tettamanzi, G. C., Wacquez, R. & Rogge, S. Charge pumping through a single donor atom. New J. Phys. 16, 063036 (2014).
Lansbergen, G. P., Ono, Y. & Fujiwara, A. Donor-based single electron pumps with tunable donor binding energy. Nano Lett. 12, 763 (2012).
Roche, B. et al. A two-atom electron pump. Nat. Commun. 4, 1581 (2013).
Yamahata, G., Nishiguchi, K. & Fujiwara, A. Accuracy evaluation of single-electron shuttle transfer in Si nanowire metal-oxide-semiconductor field-effect transistors. Appl. Phys. Lett. 98, 222104 (2011).
Yamahata, G., Nishiguchi, K. & Fujiwara, A. Accuracy evaluation and mechanism crossover of single-electron transfer in Si tunable-barrier turnstiles. Phys. Rev. B 89, 165302 (2014).
Yamahata, G., Karasawa, T. & Fujiwara, A. Gigahertz single-hole transfer in Si tunable-barrier pumps. Appl. Phys. Lett. 106, 023112 (2015).
d’Hollosy, S. et al. Gigahertz quantized charge pumping in bottom-gate-defined InAs nanowire quantum dots. Nano Letters 15, 4585 (2015).
Zimmerman, N. M. et al. Charge offset stability in tunable-barrier Si single-electron tunneling devices. Appl. Phys. Lett. 90, 033507 (2007).
Hourdakis, E., Wahl, J. A. & Zimmerman, N. M. Lack of charge offset drift is a robust property of Si single electron transistors. Appl. Phys. Lett. 92, 062102 (2008).
Zimmerman, N. M. et al. Why the long-term charge offset drift in Si single-electron tunneling transistors is much smaller (better) than in metal-based ones: Two-level fluctuator stability. J. Appl. Phys. 104, 033710 (2008).
Koppinen, P. J., Stewart, M. D. J. & Zimmerman, N. M. Fabrication and electrical characterization of fully cmos-compatible Si single-electron devices. IEEE Trans. Electron Devices 60, 78 (2013).
Zimmerman, N., Yang, C.-H., Lai, N. S., Lim, W. H. & Dzurak, A. S. Charge offset stability in Si single electron devices with al gates. Nanotechnology 25, 405201 (2014).
Kautz, R. L., Keller, M. W. & Martinis, J. M. Leakage and counting errors in a seven-junction electron pump. Phys. Rev. B 60, 8199 (1999).
Tanttu, T. et al. Electron counting in a silicon single-electron pump. New J. Phys. 17, 103030 (2015).
Fricke, L. et al. Counting statistics for electron capture in a dynamic quantum dot. Phys. Rev. Lett. 110, 126803 (2013).
Fricke, L. et al. Self-referenced single-electron quantized current source. Phys. Rev. Lett. 112, 226803 (2014).
Rossi, A. et al. Silicon metal-oxide-semiconductor quantum dots for single-electron pump. J. Vis. Exp. 100, e52852 (2015).
Seo, M. et al. Improvement of electron pump accuracy by a potential-shape-tunable quantum dot pump. Phys. Rev. B 90, 085307 (2014).
Kataoka, M. et al. Tunable nonadiabatic excitation in a single-electron quantum dot. Phys. Rev. Lett. 106, 126801 (2011).
Acknowledgements
We thank Y. Sun, M. Jenei, G. C. Tettamanzi, I. Iisakka, A. Kemppinen, J. Lehtinen, and E. Mykkänen for fruitful discussions, and M. Meschke and J. Pekola for their design and help in building the cryostat used in the experiments. The financial support from the Centre of Excellence in Computational Nanoscience (project 284621 and 251748) by the Academy of Finland (Grant Nos 251748, 135794, 272806, and 276528), the Australian Research Council (Grant Nos DP120104710 and DP160104923), Jenny and Antti Wihuri Foundation, The Finnish Cultural Foundation, and the Australian National Fabrication Facility are acknowledged. A. R. thanks the University of New South Wales Early Career Research Grant scheme for financial support. We acknowledge the provision of facilities and technical support by Aalto University at Micronova Nanofabrication Centre.
Author information
Authors and Affiliations
Contributions
T.T. and A.M. conducted the experiments with support from A.R. and K.Y.T. T.T. wrote the manuscript with input from all authors. A.R. fabricated the sample. K.W.C. prepared the silicon substrates. A.S.D. and M.M. provided project guidance and supervision.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Tanttu, T., Rossi, A., Tan, K. et al. Three-waveform bidirectional pumping of single electrons with a silicon quantum dot. Sci Rep 6, 36381 (2016). https://doi.org/10.1038/srep36381
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36381
This article is cited by
-
Zero-average Bias Bidirectional Single-electron Current Generation in a Hybrid Turnstile
Journal of Low Temperature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.