Abstract
Over the years, there has been increasing interest in the integration of metal hole array (MHA) with optoelectronic devices, as a result of enhanced coupling of incident light into the active layer of devices via surface plasmon polariton (SPP) resonances. However, not all incident light contributes to the SPP resonances due to significant reflection loss at the interface between incident medium and MHA. Conventional thin-film antireflection (AR) coating typically does not work well due to non-existing material satisfying the AR condition with strong dispersion of MHA’s effective impedances. We demonstrate a single-layer metasurface AR coating that completely eliminates the refection and significantly increases the transmission at the SPP resonances. Operating at off-resonance wavelengths, the metasurface exhibits extremely low loss and does not show resonant coupling with the MHA layer. The SPP resonance wavelengths of MHA layer are unaffected whereas the surface wave is significantly increased, thereby paving the way for improved performance of optoelectronic devices. With an improved retrieval method, the metasurface is proved to exhibit a high effective permittivity ( ) and extremely low loss (tan δ ~ 0.005). A classical thin-film AR coating mechanism is identified through analytical derivations and numerical simulations.
) and extremely low loss (tan δ ~ 0.005). A classical thin-film AR coating mechanism is identified through analytical derivations and numerical simulations.
Similar content being viewed by others
Introduction
When electromagnetic waves encounter the interface between two media with different refractive indices, the energy of incident light is partially reflected while the rest propagates into the second medium. The undesired reflection can severely limit the performance of modern optoelectronic devices, such as photovoltaic cells, light-emitting diodes, and infrared detectors, etc. Extensive efforts have been made to develop antireflection (AR) techniques to reduce the amount of reflective losses. Conventionally, a layer of quarter-wavelength-thick dielectric coating has been used to suppress the reflection at certain wavelength owing to the destructive interference. To completely eliminate the reflection, the dielectric coating has to satisfy the AR condition,  and tc = λ/4, where tc is the thickness of the coating layer, λ is the wavelength in the coating material,
and tc = λ/4, where tc is the thickness of the coating layer, λ is the wavelength in the coating material,  and
and  are the impedances,
are the impedances,  and
and  are permittivities, and μc and μs are permeabilities of the coating material and substrate, respectively. However, due to the lack of coating material with accurate impedance at wavelengths of practical applications, a perfect elimination of reflection is usually unachievable. Metamaterials (MMs) are artificially structured materials that provide the tunable effective permittivity and effective permeability by varying their geometric design, thereby enabling to achieve the required AR impedance matching conditions. Recent progress in MMs has demonstrated AR coating on non-dispersive semiconductor surfaces1,2,3. It has been shown that a metallic-resonator/dielectric/metallic-mesh sandwich-type MM can be used as AR coating on a gallium arsenide (GaAs) substrate1. In this work, destructive interference of light reflected by two metallic structure layers eliminates the overall reflection within certain wavelength range in the THz regime. A more recent work has demonstrated that an array of metallic nanoantenna buried between an amorphous silicon (α-Si) film and crystalline silicon substrate can effectively reduce the reflection between air and silicon substrate2. An array of metallic cross-wires on top of a low refractive index magnesium fluoride (MgF2) dielectric film can also dramatically reduce the reflection from germanium (Ge) substrate3. In these reports, MM based AR coatings were applied to homogenous material (GaAs, Si or Ge) with nearly constant impedance. However, it has not been clarified to date whether MM based AR coating can be applicable to the resonant metallic structures fabricated on substrate and by extension, integrated with optoelectronic devices4,5,6,7. MMs are typically made from metallic resonators. Accordingly, MM based AR coating may cause the AR impedance matching to malfunction due to unwanted resonance coupling8 with metallic structures underneath. In addition, the expected functionality resulting from metallic structures on substrate or devices (e.g. extraordinary optical transmission (EOT), improved device performance) may be affected.
are permittivities, and μc and μs are permeabilities of the coating material and substrate, respectively. However, due to the lack of coating material with accurate impedance at wavelengths of practical applications, a perfect elimination of reflection is usually unachievable. Metamaterials (MMs) are artificially structured materials that provide the tunable effective permittivity and effective permeability by varying their geometric design, thereby enabling to achieve the required AR impedance matching conditions. Recent progress in MMs has demonstrated AR coating on non-dispersive semiconductor surfaces1,2,3. It has been shown that a metallic-resonator/dielectric/metallic-mesh sandwich-type MM can be used as AR coating on a gallium arsenide (GaAs) substrate1. In this work, destructive interference of light reflected by two metallic structure layers eliminates the overall reflection within certain wavelength range in the THz regime. A more recent work has demonstrated that an array of metallic nanoantenna buried between an amorphous silicon (α-Si) film and crystalline silicon substrate can effectively reduce the reflection between air and silicon substrate2. An array of metallic cross-wires on top of a low refractive index magnesium fluoride (MgF2) dielectric film can also dramatically reduce the reflection from germanium (Ge) substrate3. In these reports, MM based AR coatings were applied to homogenous material (GaAs, Si or Ge) with nearly constant impedance. However, it has not been clarified to date whether MM based AR coating can be applicable to the resonant metallic structures fabricated on substrate and by extension, integrated with optoelectronic devices4,5,6,7. MMs are typically made from metallic resonators. Accordingly, MM based AR coating may cause the AR impedance matching to malfunction due to unwanted resonance coupling8 with metallic structures underneath. In addition, the expected functionality resulting from metallic structures on substrate or devices (e.g. extraordinary optical transmission (EOT), improved device performance) may be affected.
One example of metallic structures integrated with substrate or optoelectronic devices4,5,6,7 is a metallic hole array (MHA) which exhibits strong surface plasmon polarition (SPP) resonances. SPPs are the collective oscillations of electron plasma in the metallic structure excited by electromagnetic (EM) radiation9. The SPP resonances occurring on various types of periodic arrays of subwavelength holes in the metallic film lead to EOT10. At the resonance wavelengths, SPPs help to concentrate light into subwavelength scale beyond the diffraction limit and also assist in significantly enhancing the EM field. These characteristic features have been utilized in many applications including surface-enhanced Raman spectroscopy11, bio- or chemical-sensors12, photonic circuits13,14 and photovoltaic devices15. In particular, for MHA structure on a dielectric substrate, when the wave vector of normally incident light matches the reciprocal lattice of the array, strong SPP resonances occur and produce evanescent waves that tunnel through subwavelength apertures, resulting in extraordinary transmission of light on the other side10,16. However, not all incident light contribute to the SPP resonances due to the impedance mismatch at the air-MHA interface (i.e. a part of incident light can be reflected). It has been recently demonstrated that a thin dielectric film used as an AR coating can effectively improve the transmission through MHA at the resonant wavelengths17. Another recent study shows that with proper thin dielectric film AR coating, a gold (Au) MHA’s grating layer can effectively enhance the absorption of light in the underneath active quantum well device region by 13 times18. However, the resonance wavelength is tunable with MHA geometry (e.g. periodicity or aperture size), so it is impossible to find a common material with appropriate impedance that matches the AR condition, , for different wavelengths in various applications. Furthermore, the effective impedance of MHA, zMHA, exhibits strong dispersion around the SPP resonance wavelength. As previously stated, MM based AR coating can provide great flexibility to solve these challenges, but the resonance of MM may be able to generate the interaction with the SPP resonance of MHA, leading to the shift of SPP resonance wavelength and damping or degradation of surface wave8.
, for different wavelengths in various applications. Furthermore, the effective impedance of MHA, zMHA, exhibits strong dispersion around the SPP resonance wavelength. As previously stated, MM based AR coating can provide great flexibility to solve these challenges, but the resonance of MM may be able to generate the interaction with the SPP resonance of MHA, leading to the shift of SPP resonance wavelength and damping or degradation of surface wave8.
In this paper, we demonstrate an off-resonance, disk-type MM operating as the AR (Meta-AR) coating for a MHA layer fabricated on a GaAs substrate. The Meta-AR coating can effectively reduce the reflection at both first-order and second-order SPP resonances, thereby increasing the transmission. Additionally, our results do not show the resonance shift or damping of the SPP because MM does not couple with SPP resonance. Instead, the surface wave is enhanced as compared to the uncoated MHA (no AR coating atop MHA). Furthermore, we demonstrate that MM layer works as a homogenous thin film with high dielectric constant (~30) and extremely low loss (loss tangent ~0.005). Thus the Meta-AR coating can be understood as well-known thin-film AR coating, which provides an intuitive purely optical model compared to the electrical transmission-line model used in previous work2. We also validate through simulation that such thin-film model can be generally applicable to other MM-based AR coating structures1,2.
Results
Metasurface antireflection coating
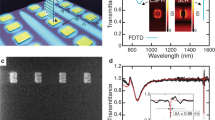
Our metamaterial based antireflection (Meta-AR) coating consists of a planar metallic disk array (MDA) on the top of a cured layer of benzencyclobutene (BCB). For comparison of Meta-AR coating with conventional AR coating (a BCB layer only), we designed three types of samples, namely the uncoated MHA, a BCB layer coated MHA and MHA coated with an array of circular Au disks (MDA) atop the BCB layer. Figure 1a–c illustrate three structures on GaAs substrates, respectively. In all structures, the orthogonal pitches of MHA, Px (pitch along x-axis) and py (pitch along y-axis), are both fixed at 1.8 μm (px = py = p) and the diameter of the circular aperture (dMHA) and thickness of Au (tAu) are 0.9 μm (a half of pitch, 0.5∙p) and 0.05 μm, respectively. We performed numerical simulations using CST Microwave Studio19, which utilizes a finite integration technique to obtain the solutions of Maxwell’s equations. In our simulation, the dielectric constant for GaAs and BCB are εGaAs = 11.56 and εBCB = 2.37, respectively. Au is described by a Drude model with plasma frequency, ωp = 9.02 eV and collision frequency, ωc = 0.038 eV20. Figure 1d–f show the simulated z component-electric field (Ez) distribution in a plane parallel to yz-plane through the center of the unit cell (the distance between the parallel planes is 0.36 μm) when x-polarized light is incident along the normal direction. The surface waves are observed in all three structures, evidenced by the exponential decay of Ez along z-direction. This indicates that the SPP waves are confined to MHA-GaAs interface and propagate along the lateral direction. As compared with uncoated MHA (Fig. 1d: p = 1.8 μm, dMHA = 0.9 μm), Ez of the SPP waves for BCB coated MHA (Fig. 1e: tBCB = 0.95 μm) and Meta-AR coated MHA (Fig. 1f: tBCB = 0.5 μm, p = 1.8 μm, dMDA = 1.4 μm) are enhanced by ~20% and ~33%, respectively. The intensity of surface wave, I ∝ |Ez|2, are remarkably increased by ~44% and ~77%, respectively. Without AR coating, the reflection of MHA at the first-order (λ1 = 6.25 μm) and the second-order (λ2 = 4.38 μm) SPP resonances are R1 ≈ 0.45 and R2 ≈ 0.67, respectively. This indicates that ~45% and ~67% of incident light do not contribute to the surface waves at the two lowest-order SPP resonances.
Illustrations of (a) MHA, (b) BCB layer coated MHA and (c) MHA coated with MDA atop the BCB layer. (d–f) Ez distribution at the first-order SPP resonance λ1 = 6.25 μm in x = 0.36 μm plane of a unit cell (x = 0 at the center of the unit cell) for structures shown in (a–c), respectively. The interface between MHA and GaAs substrate is set to zero in z-axis (z = 0). (g) Simulated reflection colormap for structure displayed in (b) as a function of wavelength and the BCB thickness tBCB. Colormaps of simulated reflection at (h) the first-order and (i) the second-order SPP resonance wavelengths for structure as shown in (c) as a function of BCB thickness tBCB and the ratio dMDA/p.
Figure 1g shows the simulated reflection of a BCB layer coated MHA sample (Fig. 1b) with thickness tBCB varying from 0.35 μm to 1.55 μm. In the region enclosed by black curves, the reflection is reduced as compared with the uncoated MHA. However, reflection cannot be completely eliminated with only BCB coating because the impedance of the BCB (ZBCB = 1/nBCB) does not match the AR condition ( ) at these resonance wavelengths. The minimum values of reflection for the first-order and the second-order SPP resonances, min(R1) and min(R2) reach 0.136 and 0.388 with tBCB = 0.95 μm and 0.75 μm, respectively. These optimal thicknesses can be well explained by the destructive interference of light reflected at the top (air-BCB interface) and bottom (BCB-MHA interface) surfaces of BCB layer. At the resonance wavelengths, the impedance of BCB layer is smaller than the impedance of air but larger than the effective impedance of MHA structure17, i.e. Zair (=1) > ZBCB > ZMHA. So both the lights reflected at the air-BCB and the BCB-MHA interfaces exhibit a phase shift of π with respect to the corresponding incident light at each interface. This leads to the condition for destructive interference, tBCB = λ/4nBCB = ~1.02 μm and ~0.71 μm, at the first and the second-order SPP resonances, respectively. With a properly designed MDA on the top of the BCB layer, the reflection can be further reduced and reach nearly zero at SPP resonance wavelengths. Figure 1h,i show the reflections taken at the SPP resonance wavelengths (λ1 and λ2) for the MHA structures with a MDA layer added on top of the BCB layer. In order to investigate the geometry dependence, tBCB and dMDA are varied from 0.35 μm to 1.55 μm and from 0.5∙p to 0.8∙p, respectively. The contour lines in black show the minimum reflection of only BCB layer coated MHA (min (R1) = 0.136 and min (R2) = 0.388). In between these lines shows a large region that the Meta-AR coating outperforms the BCB coating. For the first SPP resonance (Fig. 1h), the white contour line shows a wide range of 0.35 μm < tBCB < 0.55 μm and 0.65 · p < dMDA < 0.8 · p that reduces the reflection below 0.01 (R1 < 0.01). This shows that our Meta-AR (MDA atop BCB layer) coating is robust against possible fabrication tolerance, i.e. variations of BCB thickness (tBCB) and MDA size (dMDA). Reflections reach the minimum values, min(R1) = 1.21 × 10−4 and min(R2) = 3.16 × 10−3 when tBCB = 0.55 μm and dMDA = 0.75 · p and tBCB = 0.35 μm and dMDA = 0.65 · p at two resonance wavelengths, respectively. Two regions of minimum values of R1 and R2 do not overlap perfectly. For this reason, we mainly focus on AR coating designs that eliminate the reflection at the first-order SPP resonance (R1), which can also substantially reduce the reflection at the second-order SPP resonance (R2). Based on the simulation results, three type of structures illustrated in Fig. 1a–c have been fabricated.
) at these resonance wavelengths. The minimum values of reflection for the first-order and the second-order SPP resonances, min(R1) and min(R2) reach 0.136 and 0.388 with tBCB = 0.95 μm and 0.75 μm, respectively. These optimal thicknesses can be well explained by the destructive interference of light reflected at the top (air-BCB interface) and bottom (BCB-MHA interface) surfaces of BCB layer. At the resonance wavelengths, the impedance of BCB layer is smaller than the impedance of air but larger than the effective impedance of MHA structure17, i.e. Zair (=1) > ZBCB > ZMHA. So both the lights reflected at the air-BCB and the BCB-MHA interfaces exhibit a phase shift of π with respect to the corresponding incident light at each interface. This leads to the condition for destructive interference, tBCB = λ/4nBCB = ~1.02 μm and ~0.71 μm, at the first and the second-order SPP resonances, respectively. With a properly designed MDA on the top of the BCB layer, the reflection can be further reduced and reach nearly zero at SPP resonance wavelengths. Figure 1h,i show the reflections taken at the SPP resonance wavelengths (λ1 and λ2) for the MHA structures with a MDA layer added on top of the BCB layer. In order to investigate the geometry dependence, tBCB and dMDA are varied from 0.35 μm to 1.55 μm and from 0.5∙p to 0.8∙p, respectively. The contour lines in black show the minimum reflection of only BCB layer coated MHA (min (R1) = 0.136 and min (R2) = 0.388). In between these lines shows a large region that the Meta-AR coating outperforms the BCB coating. For the first SPP resonance (Fig. 1h), the white contour line shows a wide range of 0.35 μm < tBCB < 0.55 μm and 0.65 · p < dMDA < 0.8 · p that reduces the reflection below 0.01 (R1 < 0.01). This shows that our Meta-AR (MDA atop BCB layer) coating is robust against possible fabrication tolerance, i.e. variations of BCB thickness (tBCB) and MDA size (dMDA). Reflections reach the minimum values, min(R1) = 1.21 × 10−4 and min(R2) = 3.16 × 10−3 when tBCB = 0.55 μm and dMDA = 0.75 · p and tBCB = 0.35 μm and dMDA = 0.65 · p at two resonance wavelengths, respectively. Two regions of minimum values of R1 and R2 do not overlap perfectly. For this reason, we mainly focus on AR coating designs that eliminate the reflection at the first-order SPP resonance (R1), which can also substantially reduce the reflection at the second-order SPP resonance (R2). Based on the simulation results, three type of structures illustrated in Fig. 1a–c have been fabricated.
The structure of all samples discussed here consists of a semi-insulating double-polished GaAs (100) substrate with MHA, BCB layer coated MHA, or Meta-AR (MDA atop BCB layer) coated MHA. In brief, the processing steps to fabricate the aforementioned samples are as follows. (i) Conventional photolithography was used to produce periodic circular post arrays in the photoresist (PR) layer (Fig. 2a). (ii) 5-nm-thick adhesion layer of titanium and 50-nm-thick layer of Au were deposited using e-beam evaporation and a liftoff processing, resulting in MHA structure (Fig. 2b). (iii) Based on the colormap of measured BCB film thickness (Fig. 2c) depending on spin-coating speed and dilution ratio between BCB and rinse solvent (Cyclotene 3022-35 and T1100, The Dow Chemical Company), BCB was spin-coated on MHA, whose top-surface is flat and smooth (Fig. 2d). (iv) A periodic circular hole pattern in the PR layer was defined by photolithography once again (Fig. 2e), followed by e-beam deposition of a 50-nm-thick layer of Au. (v) After the lift-off processing to remove the PR layer, the Meta-AR coated MHA was finally obtained as shown in Fig. 2f. The detailed fabrication is included in Supporting Information.
Scanning electron microscope (SEM) images of three samples (MHA, a BCB layer coated MHA, MHA coated with an array of circular metal disks atop the BCB layer) and BCB coating condition.
(a) A periodic circular post photoresist (PR) pattern defined by standard photolithography. (b) E-beam deposition (5 nm of Ti and 50 nm of Au in sequence) and a liftoff processing, which leads to MHA structure. (c) Measured BCB thickness as a function of spin-coating speed and dilution ratio between BCB and rinse solvent. (d) BCB coated on MHA sample showing the flat-top surface. (e) A periodic circular hole PR pattern on the BCB layer shown in (d). Consecutive e-beam evaporations were used to deposit Ti (5 nm)/Au (50 nm) after (e), followed by a lift-off step. (f) Completed Meta-AR coated MHA (an array of circular metal disks atop the BCB coated MHA). Insets display the magnified MHA and MDA in Meta-AR coating.
Transmission enhancement due to Meta-AR coating
As discussed in Fig. 1, the Meta-AR coating can effectively reduce the reflection at SPP resonance wavelengths, which leads to significant increase of transmission. The uncoated MHA (no AR coating atop MHA) exhibits low transmission where T1 ≈ 0.39 and T2 ≈ 0.12, at the first-order and second-order SPP resonances, respectively. Figure 3a–c show the simulated transmission of MHA with the BCB coating (Fig. 3a) and Meta-AR coating (Fig. 3b,c) as tBCB and dMDA vary within the range of 0.35 μm ≤ tBCB ≤ 1.55 μm and 0.5 · p ≤ dMDA ≤ 0.8 · p. Note that the maximum values of transmission are achieved with identical tBCB and dMDA to the minimum values of reflection as shown in Fig. 1g–i. Specifically, the regions enclosed by the black contour lines in Fig. 3a indicate the enhanced transmission due to BCB coating. Within these regions, transmission reaches the maximum values, T1 = 0.618 when tBCB = 0.95 μm and T2 = 0.208 when tBCB = 0.75 μm at the first-order and second-order SPP resonances, respectively. Owing to additional MDA design on top of the BCB layer, the transmission can further be improved up to T1 = 0.717 and T2 = 0.318 when tBCB = 0.35 μm and dMDA = 0.7 · p, as shown in Fig. 3b,c. The regions where the Meta-AR coating (MDA-BCB coating) outperforms the BCB coating are enclosed by black contour lines (Fig. 3b,c). The measured transmission spectra (Fig. 3d) show excellent agreement with simulations (Fig. 3e). In Fig. 3d, we also observe that the MDA+BCB coating significantly increases the transmission at SPP resonances. Figure 3f,g show the measured and simulated enhancement ratio (ER) of transmission for seven samples with various thickness of BCB layer (tBCB is varied from 0.35 μm to 1.55 μm with a step of 0.2 μm), however pitch p and disk size dMDA are fixed at p = 1.8 μm and 1.26 μm (0.7∙p), respectively. Here the ER is calculated by ER = (Ti − TMHA)/TMHA, where i’s are the BCB and Meta-AR (MDA+BCB). The overall agreement between experimental (solid lines) and simulated (dashed lines) ERs at the first-order SPP resonance is apparent from Fig. 3f. We find the maxima of measured ERs for BCB and Meta-AR coating are obtained with 58% and 88% when tBCB = 0.95 μm and 0.55 μm, respectively. Remarkably, with the Meta-AR coating, the ER is improved by 30% as compared with only BCB coating, but on the contrary the thickness of BCB is reduced by 42%. The significant reduction of the thickness is beneficial in the low frequency regime (e.g. THz), where the thickness of AR coating is normally in the order of ~50 μm, which gives rise to great challenge in film deposition. The transmission at the second-order SPP resonance exhibits even higher ER with both BCB and Meta-AR coating due to the relatively low transmission for the bare MHA structure (as compared with TMHA at the first-order SPP resonance). Accordingly, the maximum ERs are found to be 106% for BCB (tBCB = 0.75 μm) coating and 99% for Meta-AR (tBCB = 0.35 μm) coating (Fig. 3g). Note that the discrepancy between experiment and simulation for Meta-AR coating is probably due to the imperfections in the fabrication, specifically the misalignment between MDA and MHA (Discussions are provided in the Supporting Information).
(a) Colormap of simulated transmission for BCB layer coated MHA as tBCB increases from 0.35 μm to 1.55 μm with 0.2 μm step. Simulated transmission for MHA with Meta-AR coating at (b) the first-order and (c) second-order SPP resonance wavelengths when dMDA is varied from 0.9 μm (0.5 · p) to 1.44 μm (0.8 · p) with a step of 0.09 μm (0.05 · p) and tBCB is changed in the same manner as (a). (d) Measured and (e) simulated transmission for MHA, MHA with BCB coating and MHA with MDA+BCB coating when tBCB = 0.55 μm. Experimental (sphere) and simulated (cross) transmission enhancement ratio for BCB (blue) and Meta-AR (red) coating at (f) the first-order and (g) second-order SPP resonance wavelengths.
AR condition at SPP resonances
To understand the underlying mechanism of our Meta-AR coating, we developed a multiple-layer model based on a transfer matrix method21. Our Meta-AR coated MHA structure is composed of three layers: MDA, BCB and MHA on a GaAs substrate. Using a transfer matrix method, the overall reflection coefficient r of the three-layer structure can be obtained by multiplying the transfer matrix of each layer, M = M1 · M2 · M3, as given below and further details on the derivation are presented in the Supporting Information.

The transmission and reflection coefficients involved in Eq. 1 can be obtained through numerical simulaitons. In particular, r12 and r21 are the reflection coefficients of MDA from front (air) and back (BCB) side, respectively. r23 is the reflection coefficient of the MHA. β = nBCB · k · tBCB is the propagating phase term in the BCB layer, where nBCB, tBCB and k are the refractive index, the BCB thickness, and the wave vector in vacuum, respectively. α = t21t12 − r21r12, where t12 and t21 are the transmission coefficients through MDA along forward (air-MDA-BCB) and backward (BCB-MDA-air) directions, respectively. Although α is strictly equal to 1 at the interface between two homogenous media, α ≠ 1 for the MDA around the resonance wavelengths because of the structural asymmetry in forward and backward directions (air-MDA-BCB structure). In order to achieve perfect antireflection, r = 0 (Eq. 1) requires the following conditions for amplitude and phase:


where the coefficients r12, r21, t21 and t12 are obtained from numerical simualtion of the air-MDA-BCB structure and r23 is obtained from the simulation of the BCB-MHA-GaAs structure. To find the appropriate geometric paramters of MDA that simultaneously satisfy amplitude (Eq. 2) and phase (Eq. 3) conditions, we carried out a series of simulations by varying the BCB thickness, tBCB and the diameter for MDA, dMDA. Specifically, the complex reflection coefficients, r12 and r23, are obtained from simulations of two different configurations, air-MDA-BCB and BCB-MHA-GaAs, respectively. For the variation of BCB thickness, dMDA is fixed at 0.7 · p (1.26 μm) and tBCB is changed from 0.35 μm to 1.55 μm. For the variation of MDA size, tBCB is fixed at 0.5 μm and dMDA is changed from 0.3 · p (0.54 μm) to 0.8 · p (1.44 μm). The circular aperture size of MHA, dMHA is kept at 0.5 · p (0.9 μm). Figure 4 shows the difference of amplutides,  (Fig. 4a,c) and the phase term θ (Fig. 4b,d) for wavelengths around the first-order SPP resoannce. The regions enclosed by black rectangles represent the minimum value of Δ|r| and satisfaction of the phase condition (i.e. θ = π). Figure 4a suggests that the amplitudes of reflection coefficients, |r12| and |r23|, are independent of the BCB thickness for all tBCB values in the range of 0.35 μm to 1.55 μm, so that Δ|r| can always reach the minimum value of Δ|r|, min (Δ|r|) = 0.081 at the first-order SPP resonance wavelength λ1 = 6.25 μm. The phase condition is satisfied when the BCB thickness is within a range of 0.35 μm < tBCB < 0.6 μm around the white dash line as indicated in Fig. 4b. In combination, we find the amplitude and phase conditions are satisfied simultaneously when tBCB ≈ 0.5 μm at the first-order SPP resonance wavelength λ1 = 6.25 μm. In contrast, the size of the MDA is strongly correlated to both the amplitude and phase as shown in Fig. 4c,d. In the region of 0.75 · p < dMDA < 0.8 · p, both the amplitude Δ|r| ≈ 0 and the phase θ ≈ π conditions are satisfied simultaneously. Using the strategy of geometric parameter (tBCB, dMDA) sweep, we find the optimal AR coating structure with tBCB = 0.5 μm and dMDA = 0.78 · p (1.4 μm) that is able to completely eliminate the reflection at the first SPP resonance λ1 = 6.25 μm, and furthermore is capable of greatly reducing the reflection R at the second-order resonance λ2 = 4.38 μm. The optimized Meta-AR coating design (via our strategy) agrees well with the experimental results shown in Fig. 3; the fabricated sample with tBCB = 0.55 μm and dMDA = 0.7 · p shows the best transmission enhancement among all samples.
(Fig. 4a,c) and the phase term θ (Fig. 4b,d) for wavelengths around the first-order SPP resoannce. The regions enclosed by black rectangles represent the minimum value of Δ|r| and satisfaction of the phase condition (i.e. θ = π). Figure 4a suggests that the amplitudes of reflection coefficients, |r12| and |r23|, are independent of the BCB thickness for all tBCB values in the range of 0.35 μm to 1.55 μm, so that Δ|r| can always reach the minimum value of Δ|r|, min (Δ|r|) = 0.081 at the first-order SPP resonance wavelength λ1 = 6.25 μm. The phase condition is satisfied when the BCB thickness is within a range of 0.35 μm < tBCB < 0.6 μm around the white dash line as indicated in Fig. 4b. In combination, we find the amplitude and phase conditions are satisfied simultaneously when tBCB ≈ 0.5 μm at the first-order SPP resonance wavelength λ1 = 6.25 μm. In contrast, the size of the MDA is strongly correlated to both the amplitude and phase as shown in Fig. 4c,d. In the region of 0.75 · p < dMDA < 0.8 · p, both the amplitude Δ|r| ≈ 0 and the phase θ ≈ π conditions are satisfied simultaneously. Using the strategy of geometric parameter (tBCB, dMDA) sweep, we find the optimal AR coating structure with tBCB = 0.5 μm and dMDA = 0.78 · p (1.4 μm) that is able to completely eliminate the reflection at the first SPP resonance λ1 = 6.25 μm, and furthermore is capable of greatly reducing the reflection R at the second-order resonance λ2 = 4.38 μm. The optimized Meta-AR coating design (via our strategy) agrees well with the experimental results shown in Fig. 3; the fabricated sample with tBCB = 0.55 μm and dMDA = 0.7 · p shows the best transmission enhancement among all samples.
Designer Metasurface (εeff and μeff) using thin-film AR coating mechanism
Due to the small size-to-wavelength ratio, dMDA/λ ~ 0.1667, the role of MDA in the Meta-AR coating can be understood by using the effective medium theory. The MDA exhibits localized surface plasmon resonances at wavelengths determined by its geometric size and the refractive indices of surrounding materials14. The plasmon resonances induce abrupt amplitude and phase changes to the light reflected by or transmitted through the MDA layer. Such phase and amplitude discontinuities have been used to reshape the beam profile to achieve negative refraction and beam steering22,23. These single layers of plasmonic resonator arrays are typically regarded as two-dimensional metasurfaces instead of bulk metamaterial since they only consist of single “meta-atom” layer. The electromagnetic properties of the metasurface can be described by the effective surface electric susceptibility χse and the effective surface magnetic susceptibility χsm, which are calculated from the transmission and reflection coefficients24,25. Due to the skin effect, the induced electric current in the plasmonic resonators only flows within extreme thin region under the surface of the structure (in the order of the skin depth  , where σ is the conductivity of metal). Therefore, χse and χsm are typically independent of the physical thickness of the resonators. However, at infrared regime, the conductivity of metal decreases dramatically, so that the skin effect is less pronounced and the electric current distributes throughout an entire volume of the resonator. As a results, we observe that the surface susceptibilities χse and χsm increase as the thickness of the MDA increases (see Supporting Information). To address the thickness dependence, in this work we model the MDA metasurface as a thin film (metafilm) with the same thickness as the MDA (tMDA). The effective permittivity εeff and effective permeability μeff of the metafilm can be calculated from simulated transmission and reflection coefficients of an air-MDA-BCB configuration by using a well-known retrieval method26 or alternatively by
, where σ is the conductivity of metal). Therefore, χse and χsm are typically independent of the physical thickness of the resonators. However, at infrared regime, the conductivity of metal decreases dramatically, so that the skin effect is less pronounced and the electric current distributes throughout an entire volume of the resonator. As a results, we observe that the surface susceptibilities χse and χsm increase as the thickness of the MDA increases (see Supporting Information). To address the thickness dependence, in this work we model the MDA metasurface as a thin film (metafilm) with the same thickness as the MDA (tMDA). The effective permittivity εeff and effective permeability μeff of the metafilm can be calculated from simulated transmission and reflection coefficients of an air-MDA-BCB configuration by using a well-known retrieval method26 or alternatively by  and
and  24,25. With εeff and μeff, the metafilm model considers the MDA layer as an effective thin film, which provides a more intuitive description compared to effective surface susceptibilities χse and χsm. It can be shown that the phase of EM waves transmitted through and reflected by the metafilm is exactly equal to the abrupt phase changes of the corresponding transmission and refleciton coefficients of the actual MDA metasurface (see Supporting Information). Using the metafilm model, the meta-AR coating can be understood intuitively as the classical thin-film AR coating that consists of two thin flims, i.e. MDA metafilm and BCB layer.
24,25. With εeff and μeff, the metafilm model considers the MDA layer as an effective thin film, which provides a more intuitive description compared to effective surface susceptibilities χse and χsm. It can be shown that the phase of EM waves transmitted through and reflected by the metafilm is exactly equal to the abrupt phase changes of the corresponding transmission and refleciton coefficients of the actual MDA metasurface (see Supporting Information). Using the metafilm model, the meta-AR coating can be understood intuitively as the classical thin-film AR coating that consists of two thin flims, i.e. MDA metafilm and BCB layer.
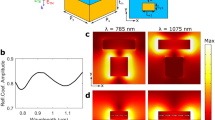
Both the effective surface susceptibilities, χse and χsm in the metasurface model24,25 and εeff and μeff in the retrieval method26 are calculated using the transmission and reflection coefficients of an air-MM-air configuratoin. In reality, MM structures are usually made on a dielectric substrate, so the transmission and reflection coefficients are obtained at the interfaces of an air-MM-dielectric configuration. To the best of our knowledge, many MM related works use the transmission and reflection coefficients of air-MM-dielectric configuration directly to extract εeff and μeff, which cause inaccurate values. In our structure, the metasurface is modeled as a metafilm with thickness tMDA = 50 nm. The extremely thin thickness magnifies the error greatly because the effective refractive index of the metafilm, neff, is inversely proportional to tMDA. To obtain correct effective parameters of the metafilm, we develop a method to obtain the transmission and reflection coefficients of the air-MM-air configuraiton from that of the air-MM-dielectric configuation. The resutlsing transmission and reflection coefficients produce accurate χse, χsm, εeff and μeff. Details of this improved retrieval method are elucidated in the Supporting Information. Figure 5a,b show εeff and μeff of MDA structure calculated from simulation data of an air-MDA-BCB configuration with tBCB = 0.5 μm and dMDA = 0.78 · p, where solid lines show εeff and μeff calculated by the retrieval method and dash lines show  and
and  . It can be seen that two methods give nearly identical values except minor deviation at the resonance wavelength λr = 2.92 μm, where the thin-film retrieval shows typical antiresonance in μeff due to the periodicity effects27. The strong Lorentzian line shaped resonance in εeff indicates an electric response, where the electric field of the incident light induces resonant electric current in the disk. μeff is nearly constant (μeff ≈ 0.86) within the entire wavelength range from 2.5 μm to 7.0 μm. The resonance wavelength (λr = 2.92 μm) of MDA is much shorter than the operating wavelengths of our Meta-AR coating, i.e. the first-order (λ1 = 6.25 μm) and second-order (λ2 = 4.38 μm) SPP resonances of MHA. Therefore, the imaginary parts (blue lines) of εeff and μeff at these wavelengths are nearly zero, and hence the loss in MDA is neglegible. Specifically, as shown in the inset of Fig. 5a, the real part of εeff gradually decreases from 40.25 to 30.52 in the wavelength range from 4.2 μm to 6.4 μm. The loss tangent, defined as the ratio between the imaginary and the real parts of the permittivity (tan δ = ε′′/ε′), also decreases from 0.0097 to 0.0046. The effective permittivity reads values of
. It can be seen that two methods give nearly identical values except minor deviation at the resonance wavelength λr = 2.92 μm, where the thin-film retrieval shows typical antiresonance in μeff due to the periodicity effects27. The strong Lorentzian line shaped resonance in εeff indicates an electric response, where the electric field of the incident light induces resonant electric current in the disk. μeff is nearly constant (μeff ≈ 0.86) within the entire wavelength range from 2.5 μm to 7.0 μm. The resonance wavelength (λr = 2.92 μm) of MDA is much shorter than the operating wavelengths of our Meta-AR coating, i.e. the first-order (λ1 = 6.25 μm) and second-order (λ2 = 4.38 μm) SPP resonances of MHA. Therefore, the imaginary parts (blue lines) of εeff and μeff at these wavelengths are nearly zero, and hence the loss in MDA is neglegible. Specifically, as shown in the inset of Fig. 5a, the real part of εeff gradually decreases from 40.25 to 30.52 in the wavelength range from 4.2 μm to 6.4 μm. The loss tangent, defined as the ratio between the imaginary and the real parts of the permittivity (tan δ = ε′′/ε′), also decreases from 0.0097 to 0.0046. The effective permittivity reads values of  and
and  at the first-order and second-order SPP resonance wavelengths (λ1, λ2), respectively. Note that the loss tangents,
at the first-order and second-order SPP resonance wavelengths (λ1, λ2), respectively. Note that the loss tangents,  and
and , have the same order of magnitude of commonly used low-loss dielectric coating materials such as polyimide (tan δ~0.005) and BCB (tan δ~0.001).
, have the same order of magnitude of commonly used low-loss dielectric coating materials such as polyimide (tan δ~0.005) and BCB (tan δ~0.001).
The real (red) and imaginary (blue) parts of (a) effective permittivity εeff and (b) permeability μeff of the MDA metasurface. Inset shows the real part of effective permittivity, Re(εeff) (red) and the loss tangent, tan δ (green). (c) Diagram of the reflection and transmission coefficients of MDA and MHA. (d) Reflections obtained by full-wave simulation of actual MDA-BCB-MHA (black line), analytical calculation (blue line) using Eq. 1 and full-wave simulation of metafilm-BCB-MHA structure with wavelength-dependent (red dash line) and wavelength-independent (green dash-dot line) effective parameters. (e) The amplitude and phase (f) terms in the AR conditions (Eqs 2 and 3).
With the calculated εeff and μeff, we can replace the MDA layer as a thin film of thickness t = tMDA. As illustrated in Fig. 5c, the AR coating on the MHA comprises two layers of homogenous films: a MDA metasurface with εeff and μeff and a BCB layer. The numerically calculated (blue line: using Eq. 1) and simulated reflections (black line: using actual MDA structure; red dash and green dash-dot lines: using homogeneous film with wavelength-dependent (ε = εeff(λ), μ = μeff(λ) as shown in Fig. 5a,b) and wavelength-independent ( ,
,  ) effective parameters, respectively) are shown in Fig. 5d. At the first-order SPP resonance (λ1 = 6.25 μm), all four curves are matched very well and perfect antireflection is achieved with nearly zero reflection (R ≈ 0). Such perfect match is attributed to the fact of λ1 ≫ λr, so that the MDA operates at off-resonance wavelengths. In this region, the MDA layer only transmits/reflects light without any resonant coupling with MHA layer. Therefore, the calculation (blue) based on the transfer matrix method (Eq. 1) can perfectly reproduce the full-wave simulation of actual MDA-Spacer-MHA structure (black). The simulations using metafilms with dispersive (red dash) and constant (green dash-dot) εeff and μeff show that these effective parameters correctly discribe the EM property of MDA layer in the MDA-spacer-MHA system. However, at the second-order SPP resonance, the simulated reflection using effective medium model does not match with using actual MDA structure. The discrepancy attributes to the resonance coupling between the MHA and the MDA (Supporting Information) because the second-order SPP resonance (λ2 = 4.38 μm) is much closer to the resonance wavelength (λr = 2.92 μm) of the MDA (Note: the effective permittivity and permeability of MDA are obtained from simulation of the air-MDA-BCB configuration, where the coupling between the MDA and the MHA resonances is absent). The phase and amplitude conditions given in Eqs 2 and 3 reveal the underlying mechanism of AR as the destructive interference of light reflected at the MDA-BCB and BCB-MHA interfaces. In Fig. 5e, we can clearly see that the amplitudes of r12 and α · r23 are equal at the first-order SPP resonance wavelength λ1 = 6.25 μm (i.e. the amplitude condition is satisfied). Simultaneously, as shown in Fig. 5f, the phase term, θ = ϕ(r12) − ϕ(α · r23) − 2β crosses π (gray line), as predicted in the phase condition. At the second-order SPP resonance λ2 = 4.38 μm, the reflection is reduced but does not reach zero because only the amplitude condition is satisfied.
) effective parameters, respectively) are shown in Fig. 5d. At the first-order SPP resonance (λ1 = 6.25 μm), all four curves are matched very well and perfect antireflection is achieved with nearly zero reflection (R ≈ 0). Such perfect match is attributed to the fact of λ1 ≫ λr, so that the MDA operates at off-resonance wavelengths. In this region, the MDA layer only transmits/reflects light without any resonant coupling with MHA layer. Therefore, the calculation (blue) based on the transfer matrix method (Eq. 1) can perfectly reproduce the full-wave simulation of actual MDA-Spacer-MHA structure (black). The simulations using metafilms with dispersive (red dash) and constant (green dash-dot) εeff and μeff show that these effective parameters correctly discribe the EM property of MDA layer in the MDA-spacer-MHA system. However, at the second-order SPP resonance, the simulated reflection using effective medium model does not match with using actual MDA structure. The discrepancy attributes to the resonance coupling between the MHA and the MDA (Supporting Information) because the second-order SPP resonance (λ2 = 4.38 μm) is much closer to the resonance wavelength (λr = 2.92 μm) of the MDA (Note: the effective permittivity and permeability of MDA are obtained from simulation of the air-MDA-BCB configuration, where the coupling between the MDA and the MHA resonances is absent). The phase and amplitude conditions given in Eqs 2 and 3 reveal the underlying mechanism of AR as the destructive interference of light reflected at the MDA-BCB and BCB-MHA interfaces. In Fig. 5e, we can clearly see that the amplitudes of r12 and α · r23 are equal at the first-order SPP resonance wavelength λ1 = 6.25 μm (i.e. the amplitude condition is satisfied). Simultaneously, as shown in Fig. 5f, the phase term, θ = ϕ(r12) − ϕ(α · r23) − 2β crosses π (gray line), as predicted in the phase condition. At the second-order SPP resonance λ2 = 4.38 μm, the reflection is reduced but does not reach zero because only the amplitude condition is satisfied.
Discussion
In summary, we have experimentally, numerically and analytically investigated the enhanced transmission due to a metasurface antireflection (AR) coating on a dispersive surface plasmon (SP) structure in the mid-infrared regime. Our metasurface AR coating (based on MDA) works at off-resonance wavelengths and can be modeled as a metafilm with high effective permittivity ( ). The extremely low loss tangent,
). The extremely low loss tangent,  , is comparable to low-loss films used in AR coating such as polyimide (tan δ~0.005) and BCB (tan δ ~ 0.001). In addition, the effective permittivity εeff is easily tunable by changing the geometric size of the MDA, which provides unprecedented flexibility to fit the different wavelengths for a variety of applications. With the metasurface coating, the measured transmission through the dispersive SP structure is greatly increased at both the first-order (58% for tBCB = 0.35 μm; 88% for tBCB = 0.55 μm) and second-order (99% for tBCB = 0.35 μm; 80% for tBCB = 0.55 μm) SP resonances. The electric field and the intensity of surface wave are also enhanced by ~33% and ~77%, respectively, for the first-order SP resonance. The enhanced electric field of surface wave will benefit to applications where the local field engineering (strong local field) is demanded, e.g. improving the performance of optoelectronic devices. Moreover, the metafilm model, transfer matrix analysis and improved retrieval method developed in our work are generally applicable to multi-layered metasurface system including antireflection coating and plasmonic perfect absorbers21,28,29.
, is comparable to low-loss films used in AR coating such as polyimide (tan δ~0.005) and BCB (tan δ ~ 0.001). In addition, the effective permittivity εeff is easily tunable by changing the geometric size of the MDA, which provides unprecedented flexibility to fit the different wavelengths for a variety of applications. With the metasurface coating, the measured transmission through the dispersive SP structure is greatly increased at both the first-order (58% for tBCB = 0.35 μm; 88% for tBCB = 0.55 μm) and second-order (99% for tBCB = 0.35 μm; 80% for tBCB = 0.55 μm) SP resonances. The electric field and the intensity of surface wave are also enhanced by ~33% and ~77%, respectively, for the first-order SP resonance. The enhanced electric field of surface wave will benefit to applications where the local field engineering (strong local field) is demanded, e.g. improving the performance of optoelectronic devices. Moreover, the metafilm model, transfer matrix analysis and improved retrieval method developed in our work are generally applicable to multi-layered metasurface system including antireflection coating and plasmonic perfect absorbers21,28,29.
Additional Information
How to cite this article: Jeon, J. et al. A Low-loss Metasurface Antireflection Coating on Dispersive Surface Plasmon Structure. Sci. Rep. 6, 36190; doi: 10.1038/srep36190 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Chen, H. T. et al. Antireflection Coating Using Metamaterials and Identification of Its Mechanism. Physical Review Letters 105, 073901 (2010).
Kabiri, A., Girgis, E. & Capasso, F. Buried Nanoantenna Arrays: Versatile Antireflection Coating. Nano Letters 13, 6040–6047 (2013).
Zhang, B., Hendrickson, J., Nader, N., Chen, H.-T. & Guo, J. Metasurface optical antireflection coating. Applied Physics Letters 105, 241113 (2014).
Lee, S. J. et al. A monolithically integrated plasmonic infrared quantum dot camera. Nat Commun 2, 286 (2011).
Chang, C.-C. et al. A Surface Plasmon Enhanced Infrared Photodetector Based on InAs Quantum Dots. Nano Letters 10, 1704–1709 (2010).
Lee, S. C., Krishna, S. & Brueck, S. R. J. Quantum dot infrared photodetector enhanced by surface plasma wave excitation. Optics Express 17, 23160–23168 (2009).
Zhao, F., Zhang, C., Chang, H. & Hu, X. Design of Plasmonic Perfect Absorbers for Quantum-well Infrared Photodetection. Plasmonics 9, 1397–1400 (2014).
Clausen, J. S. et al. Plasmonic Metasurfaces for Coloration of Plastic Consumer Products. Nano Letters 14, 4499–4504 (2014).
Raether, H. Surface plasmons on smooth and rough surfaces and on gratings. (Springer-Verlag, 1988).
Ebbesen, T. W., Lezec, H. J., Ghaemi, H. F., Thio, T. & Wolff, P. A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 391, 667–669 (1998).
Nie, S. & Emory, S. R. Probing Single Molecules and Single Nanoparticles by Surface-Enhanced Raman Scattering. Science 275, 1102–1106 (1997).
Homola, J., Yee, S. S. & Gauglitz, G. Surface plasmon resonance sensors: review. Sensors and Actuators B: Chemical 54, 3–15 (1999).
Gramotnev, D. K. & Bozhevolnyi, S. I. Plasmonics beyond the diffraction limit. Nature Photonics 4, 83–91 (2010).
Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 311, 189–193 (2006).
Atwater, H. A. & Polman, A. Plasmonics for improved photovoltaic devices. Nature Materials 9, 205–213 (2010).
Ghaemi, H. F., Thio, T., Grupp, D. E., Ebbesen, T. W. & Lezec, H. J. Surface plasmons enhance optical transmission through subwavelength holes. Physical Review B 58, 6779–6782 (1998).
Park, M. S. et al. Enhanced transmission due to antireflection coating layer at surface plasmon resonance wavelengths. Optics Express 22, 30161–30169 (2014).
Chang, H., Zhang, C., Zhao, F. & Hu, X. Antireflection Coatings on Au Plasmonic Gratings for Infrared Photodetection. Plasmonics 10, 1519–1524 (2015).
CST Micwave Studio: A numerical simualtion software for electromagnetic computing, Computer Simulation Technology GmbH, Darmstadt, Germany. URL https://www.cst.com/.
Ordal, M. A., Bell, R. J., Alexander, R. W. Jr., Long, L. L. & Querry, M. R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Applied optics 24, 4493 (1985).
Bhattarai, K. et al. A Large-Area, Mushroom-Capped Plasmonic Perfect Absorber: Refractive Index Sensing and Fabry–Perot Cavity Mechanism. Advanced Optical Materials 3, 1779–1786 (2015).
Kildishev, A. V., Boltasseva, A. & Shalaev, V. M. Planar Photonics with Metasurfaces. Science 339 (2013).
Yu, N. et al. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337 (2011).
Holloway, C. L. et al. A discussion on the interpretation and characterization of metafilms/metasurfaces: The Two-Dimensional Equivalent of Metamaterials. Metamaterials 3, 100 (2009).
Zhou, J. et al. Application of metasurface description for multilayered metamaterials and an alternative theory for metamaterial perfect absorber. arXiv:1111.0343v1 (2011).
Smith, D. R., Schultz, S., Markos, P. & Soukoulis, C. M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Physical Review B 65, 195104 (2002).
Koschny, T., Markos, P., Smith, D. R. & Soukoulis, C. M. Resonant and antiresonant frequency dependence of the effective parameters of metamaterials. Physical review. E, Statistical, nonlinear, and soft matter physics 68, 065602 (2003).
Watts, C. M., Liu, X. L. & Padilla, W. J. Metamaterial Electromagnetic Wave Absorbers. Advanced Materials 24, 98–120 (2012).
Landy, N. I., Sajuyigbe, S., Mock, J. J., Smith, D. R. & Padilla, W. J. Perfect metamaterial absorber. Physical Review Letters 100, 207402 (2008).
Acknowledgements
The USF portion of this work was supported by the Alfred P. Sloan Research Fellow grant BR2013-123 and by KRISS grant GP2016-034. The KRISS portion of this work was supported by the KRISS grant GP2016-034 and the AOARD grant FA2386-14-1-4094 funded by the U.S. government (AFOSR/AOARD).
Author information
Authors and Affiliations
Contributions
J.J., D.-K.K., J.O.K. and S.J.L. fabricated and measured the metasurface ARC samples. K.B., Z.K. and J.Z. developed the multiple layer model and retrieval method, and performed the analysis of the ARC mechanism. J.Z., Z.K., J.J. and K.B. wrote the manuscript. S.J.L., A.U., Z.K. and J.Z. supervised the work.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Jeon, J., Bhattarai, K., Kim, DK. et al. A Low-loss Metasurface Antireflection Coating on Dispersive Surface Plasmon Structure. Sci Rep 6, 36190 (2016). https://doi.org/10.1038/srep36190
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36190
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






 and the phase term, θ = ϕ(r12) − ϕ(α · r23) − 2β with (a,b) various BCB thicknesses and (c,d) MDA sizes, respectively.
and the phase term, θ = ϕ(r12) − ϕ(α · r23) − 2β with (a,b) various BCB thicknesses and (c,d) MDA sizes, respectively.