Abstract
Current closed-loop insulin delivery methods stem from sophisticated models of the glucose-insulin (G/I) system, mostly based on complex studies employing glucose tracer technology. We tested the performance of a new minimal model (GLUKINSLOOP 2.0) of the G/I system to characterize the glucose and insulin dynamics during multiple mixed meal tests (MMT) of different sizes in patients with type 1 diabetes (T1D) on insulin pump therapy (continuous subcutaneous insulin infusion, CSII). The GLUKINSLOOP 2.0 identified the G/I system, provided a close fit of the G/I time-courses and showed acceptable reproducibility of the G/I system parameters in repeated studies of identical and double-sized MMTs. This model can provide a fairly good and reproducible description of the G/I system in T1D patients on CSII, and it may be applied to create a bank of “virtual” patients. Our results might be relevant at improving the architecture of upcoming closed-loop CSII systems.
Similar content being viewed by others
Introduction
The glucose-insulin (G/I) system is a physiological closed-loop, which is able to maintain the plasma glucose levels within a narrow physiological range, as a result of a complex interaction among many components1,2. Of them, only a limited number (namely, plasma glucose, insulin and C-peptide levels) is directly accessible for measurement in the bloodstream. Thus, either the closed-loop is experimentally interrupted under strictly controlled conditions, i.e. by the glucose clamp technique3, or dedicated mathematical models4,5 are needed to estimate the intimate components of the G/I system6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22.
Over the past four decades a number of experimental protocols have been developed to assess the dynamics of the G/I system in vivo3,6,7,12,15,20,23,24, often analyzed by multi-compartmental modeling techniques9,22,25. In such models the G/I dynamics are described through a set of ordinary differential equations (ODEs) according to well validated modeling strategies, which often require complex experimental settings, including the use of a variable number of glucose tracers to exactly track the glucose dynamics12,26,27. In order to mitigate the burden of both experimental and modeling complexity, more parsimonious models, i.e. with a lower number of ODEs and of parameters, have been proposed and successfully employed6,15,23,28,29,30,31,32,33. These “minimal models” have been thus far applied most frequently to the intravenous glucose tolerance tests (IVGTT) with the primary aim of measuring insulin sensitivity6,14,33. Their extension to more physiological settings, such as oral glucose tolerance tests (OGTT)17,23 and mixed meal tests (MTT)30,34, although feasible and widely in use, relies, when no glucose tracer(s) is (are) used, on an additional number of assumptions, especially regarding the dynamics of oral glucose appearance into the peripheral circulation31, plus glucose effectiveness, volume of distribution26,35 and splanchnic extraction31,36. Although the insulin sensitivities yielded by the oral models are well correlated to those obtained by the IVGTTs, they may overestimate insulin sensitivity, as assessed by the IVGTT26,28,31,37. Furthermore, insulin sensitivity provided by the OGTT model is lower than insulin sensitivity measured by the insulin clamp38 and higher than insulin sensitivity estimated by the MTT model39. Current evidence, however, indicates that, when measured with appropriate tools, i.e. tracer aided models of glucose dynamics, insulin sensitivity is relatively constant, regardless of the route of glucose/carbohydrate entry in the body26,38. Thus, current minimal modeling of glucose/carbohydrate meals with no tracer(s) aid, even though calibrated to successfully handle the oral glucose rate of appearance with a set of constrained parameters31,36, provides estimates of insulin sensitivity which, albeit correlated to those obtained with reference methods, display significant deviations from all other methods for somewhat unclear reasons26,28,31,37,38,39.
Modeling the G/I system is particularly relevant nowadays in the therapeutic area of type 1 diabetes (T1D), specifically in those patients treated with continuous subcutaneous insulin infusions (CSII) coupled with continuous glucose monitoring (CGM). A considerable research effort has resulted in G/I models based on the results of complex tracer studies40,41 and growing experience has been accrued to successfully close the loop with control algorithms of the G/I system derived from them7,42. Recent real-life clinical trials have reported very promising results towards the development of a reliable, wearable closed-loop insulin delivery system43,44,45.
For the reasons described above, published parsimonious models may be of limited help for these specific applications. We reasoned that some limitations of the most parsimonious G/I models (e.g. inaccurate estimation of insulin sensitivity, multiple assumptions in key parameters of the G/I system) could be overcome by combining the assessment of insulin sensitivity yielded by a gold standard technique, i.e. the hyperinsulinemic euglycemic clamp (HEC), with minimal modeling previously applied by us to unlabeled IVGTTs46 with slight modifications inspired by our experience with labeled IVGTT22.
This paper presents a novel mathematical model (GLUKINSLOOP 2.0) aimed at characterizing the G/I time-courses and quantitating the components of the G/I system during a standardized meal test. The GLUKINSLOOP 2.0 model builds on previous experience in our lab22,46 and provides a comprehensive description of the G/I system by introducing an original solution to model glucose dynamics after meals, which is usually accommodated with either a piecewise linear continuous function, partial differential equations, or delay compartments, or a combination of them16,17,28,31.
Owing to the potential applicability of this work in the field of T1D, the GLUKINSLOOP 2.0 model has been used to describe the G/I system during a mixed meal test (MMT) in patients with T1D on insulin pump therapy. Among the ten patients considered, six were studied twice in separate days with MMTs of variable size in order to explore both the performance and the reproducibility of GLUKINSLOOP 2.0. Our results might be relevant to strategies aimed at improving the architecture of upcoming closed-loop insulin delivery systems.
Results
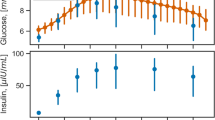
The main clinical and metabolic features of the study patients are shown in Table 1. A quite large heterogeneity was evident in terms of age, body size, glucose control, duration of diabetes and time since the initiation of CSII therapy. When compared to historical healthy controls, the study patients had somewhat lower insulin sensitivity47. Figure 1 shows the time courses of plasma insulin and glucose concentrations during the 292 Kcal MTTs and during the 600 Kcal MTT, calculated as the average (±SEM) of the insulin and glucose concentrations at each time point during the MMTs for each group of patients undergoing the metabolic studies. As expected, plasma glucose/insulin time-series were higher in the latter (panels E-F) than in the former (panels A-D) set of MTTs. Figure 2 provides a simplified description of the GLUKINSLOOP 2.0 model herein applied to describe the G/I system and to identify its (unknown) parameters. The figure highlights the inherent conciseness of this new modeling solution, which is based on a parsimonious core set of ordinary differential equations (ODEs), as further detailed in the Methods section. A more detailed scheme and an accompanying thorough explanation of the GLUKINSLOOP 2.0 model equations are provided in the Supplementary Material (Figure S1 and Supplementary Note).
Time courses of plasma insulin and glucose levels during the 292 Kcal and 600 Kcal MMTs.
Panels A,B: mean (±SEM) plasma insulin and glucose concentrations at each time point during the 292 Kcal MMT (MMT1) in the 10 study participants. Panels C,D: MMT2, n = 3, MMT = 292 Kcal. Panels E-F: MMT2, n = 3, MMT = 600 Kcal.
The GLUKINSLOOP 2.0 model.
In this schematic representation57 of the model continuous arrows indicate transformations and dashed ones indicate regulations. Arrows pointing towards grey dots indicate degradation. A more detailed figure and an accompanying thorough explanation of the model are provided in the Supplementary Material (Figure S1).
Visual inspection of weighted residuals indicates a good fit of the model to the experimental data (Fig. 3). The simulation outputs, expressed as model fits to the insulin and glucose curves, are provided in Figures S2-S11. In Figures S2-S7 the curves for each repeated study patient, during the 292 Kcal and 600 Kcal meals, are labeled as MMT1 and MMT2, respectively.
Mean weighted residuals of the model fit to experimental insulin and glucose time courses during MMT1 and MMT2.
The weighted residuals are a quantitative point-by-point assessment of the goodness-of-fit of the model to the experimental data: a theoretically perfect fit should generate weighted residuals with mean 0 and SD of 1, reflecting the distribution of errors during the experimental sampling. Panels A,B: mean ± SD of weighted residuals at each time point during the 292 Kcal MMT (MMT1) in all 10 study participants. Panels C,D: MMT2, n = 3, MMT = 292 Kcal. Panels E,F: MMT2, n = 3, MMT = 600 Kcal.
Figure 4 shows the mean behavior (mean ± SEM) of the Oral Glucose Input function (OGI), among the patients for the different meals. The shape and the peak of the curve agree with existing literature26.
The Oral Glucose Input function.
Panels (A–C) show the output of the OGI function layered by different MMTs. The OGI function, i.e. the predicted glucose rate of appearance in the bloodstream at each time point after the MMT ingestion, is provided as mean ± SEM of the individual OGI values for the study patients undergoing the MMT1 and MMT2 and is expressed as mg/Kg/min (see Figure S12 for the same panels expressed as μmol/min). Curves’ shapes and peaks are consistent with literature’s analogous functions26. Detailed description of the function can be found in Supplementary Material.
Repeated MMTs showed a good degree of reproducibility of the key physiological parameters (Table 2 and Supplementary Table S4). Importantly, reproducibility was fairly good even when comparing meals of different sizes (Table 2 and Supplementary Table S4, patients 4, 5 and 6). Mean transit time of insulin (Insulin MTT) in the s.c. deposit were 112 ± 56 (min) for MMT1 and 131 ± 66 (min) for MMT2, respectively (Table 2); its within-subject coefficient of variation (±SD) was 28 ± 18% (Table 3). The apparent mean transit time of the oral glucose load from ingestion to the appearance in the accessible glucose pool (Glucose MTT) were 117 ± 35 (min) for MMT1 and 109 ± 35 (min) for MMT2, respectively (Table 2); its within-subject coefficient of variation (±SD) was 11 ± 6% (Table 3).
Discussion
In this study, we successfully tested the hypothesis that, with the aid of the “external” assessment of insulin sensitivity by the HEC, the G/I system would be amenable to be successfully reconstructed in T1D patients, in whom modeling of the G/I system has become a key component of therapeutic innovative strategies43,44,45. Differently from previous models, which need to fix a number of parameters (glucose effectiveness, volume of distribution, fractional splanchnic extraction of glucose) to estimate meal insulin sensitivity, we exploit clamp-derived insulin sensitivity and parameters to reconstruct the G/I system during a mixed meal.
The novelty of our approach lies primarily in parsimony. Published models for OGTTs or meal tests were first based on more complex structures of the glucose system (typically two compartments were needed to accommodate glucose dynamics) and this, at variance with our proposal, entailed the need of tracer technology to identify the parameters governing the glucose system7,8,9,12,26,48. In the last 15 years, single compartment models were introduced, both without and with the aid of tracer technology11,17,23,28,29,30,31,34,49. Single compartment models with no tracer aid require a number of assumptions to reconstruct a reliable estimate of the rate of appearance of oral glucose, but they may provide somewhat variable estimates of insulin sensitivity26,28,31,37,38. The single compartment model with oral tracer glucose performs better than in the absence of a glucose tracer; however, its estimate of endogenous glucose production is good when expressed as the ratio of basal endogenous glucose production, but it may be inaccurate in absolute terms35. Increasing the number of tracers to two or three yields the best available estimates of endogenous glucose production, insulin sensitivity and glucose disposal, but it considerably increases study complexity and costs27.
Our approach transfers the single glucose compartment description of the time honored minimal model from the IVGTT6 to the MMT7. So far, a parsimonious description of the OGTT23,30 was focused only on the use of the OGTT as a test to assess insulin sensitivity23,30,32, at the cost of embodying a number of assumptions, of fixing numerical values for some parameters and of eventually providing insulin sensitivity values, which may be somewhat inaccurate.
These limitations are overcome by the herein presented GLUKINSLOOP 2.0 model of the G/I system. The performance of our model, however, does not contradict the extensive previous experience with the single compartment OGTT (and MTT) models with no glucose tracer(s)23,28,30,31,32. Early experience taught us that, when insulin sensitivity is unknown, it can be estimated from the oral tests at the cost of several approximations and assumptions in the parameters governing glucose dynamics23,30,31,32. Our present experience is logically coherent and complementary to the previous one, in that, if insulin sensitivity is known with the low uncertainty provided by the hyperinsulinemic euglycemic clamp (HEC), the key parameters of the G/I system can be safely estimated and a parsimonious description of the system can provide a good description of the glucose dynamics.
As an added value, this evidence is obtained in patients with T1D, in whom new, parsimonious models of the G/I system may improve current efforts in building algorithms capable to safely and precisely deliver insulin in the context of closed-loop devices42. From this viewpoint, our model has the attractive feature of showing a good degree of reproducibility of its key physiological parameters from day to day, and also with different meal sizes (Table 2). Of note, both the performance and robustness of the G/I dynamics estimates yielded by the GLUKINSLOOP 2.0 model were quite satisfactory despite the wide clinical heterogeneity of the study patients in terms of age, sex, diabetes duration and glycemic control.
Some specific characteristics of our model are different from the original minimal models and need to be discussed in some detail. First, in contrast with some previous single-compartment models with no tracer(s), we explicitly deal with glucose fluxes, and not concentrations32. The latter ones may be more convenient to handle, at least for the sake of simplicity. For instance, we are forced to know exactly the amount of glucose equivalents ingested. On the other hand, working with extensive properties of the G/I system (fluxes, volumes) is unavoidable, if one wants to obtain a complete description of the system and of its capability to cope with meal challenges, as well as to predict its behavior in response to meals of different size. Second, we introduced a fixed flux of glucose utilization, which primarily reflects brain glucose utilization, in agreement with the two-compartment minimal models proposed for studies with glucose tracer22,25, but not for single compartment models, such as the present one. In our opinion, the assumption of fixed glucose utilization (by the brain) is a perfectly tenable assumption and it is one of the improvements brought about by two-compartment minimal models for tracer glucose25 over the minimal models for unlabeled glucose50. In our experience, there is no reason why this improvement in the description of the system should not be implemented also in the models for unlabeled glucose. Third, the combined presence of a fixed glucose utilization and glucose effectiveness (SG) forced the need of a glucose input in the basal, un-stimulated state, which exactly matches the combined effect of brain glucose utilization and SG and ensures the attainment of a steady state at baseline. Although it would be tempting to label this glucose input as endogenous glucose production - and its order of magnitude in our patients is indeed in the expected range - no measure of endogenous glucose production is available in our work and this glucose input should be considered as instrumental to the attainment of a steady state in the post-absorptive state. Fourth, as in all minimal models in which no glucose tracers are used, insulin sensitivity combines the net effect of insulin on glucose utilization and on glucose production6,28,30,32. Fifth, since no explicit endogenous glucose production is included in our model, the glucose input after meal ingestion should not be considered as a pure estimate of the appearance of oral glucose, because we cannot rule out the possibility that a minor fraction of it actually is due to an amount of residual endogenous glucose production, which is not captured by the insulin sensitivity parameter.
Some limitations of our study should be recognized. First, only patients with T1D are presented in this study; hence, the performance of our approach in normal individuals or in other pathologic conditions currently remains unexplored. However, the class of patients included in this study is expected to directly benefit most from novel simplified glucose models. Secondly, the number of studies herein presented is somewhat limited; however, this paper primarily aims at presenting the new GLUKINSLOOP 2.0 model, and it is not concerned with the report of novel pathophysiological insights. To this regard, it should be noted that the presentation of repeat studies with the same modeling methodology is a somewhat rare occurrence in this field and, as such, accounts for the stringent sensitivity analysis we applied to our data. Third, a separate insulin clamp (HEC) needs be performed to measure insulin sensitivity, thereby adding to the experimental burden one additional study day.
In summary, we have introduced a HEC-supported minimal model of glucose dynamics after a mixed meal in patients with T1D. The GLUKINSLOOP 2.0 model apparently performs reasonably well and shows a good degree of reproducibility without employing labeled tracers. Hence, given the relevance of in vivo characterization of the G/I system dynamics, this model timely proposes itself as a useful step towards better algorithms to control glucose dynamics after meal ingestion in patients with T1D on sensor-augmented insulin pump therapy.
Methods
Subjects
Ten (7 men/3 women) adult patients with C-peptide negative type 1 diabetes (T1D) on insulin pump therapy were recruited for the study among those regularly attending the Diabetes Center of the Verona City Hospital. Eligible patients included those 18–65 years old, on insulin pump therapy for at least 1 year, with HbA1c between 6.0 and 9.0%. Other inclusion/exclusion criteria can be found at the ClinicalTrials.gov website (https://clinicaltrials.gov/ct2/show/NCT02003274?term=NCT02003274&rank=1). Their main clinical characteristics are shown in Table 1. All patients were on isocaloric dietitian prescribed diet and were free from any other disease except diabetes (only Patient #3 had autoimmune hypothyroidism and was euthyroid on 150 μg/day levothyroxine p.o. at the time of study enrollment). After a thorough explanation of the procedures and purposes of the study, a written informed consent was obtained from all patients to be included in the study. The study protocol (registered as NCT01800734 on February 8th, 2013 and NCT02003274 on December 3rd, 2013) was approved by the local Institutional Review Board (Comitato etico per la sperimentazione clinica delle Provincie di Verona e Rovigo) and was carried out according to the International Conference on Harmonisation Good Clinical Practice guidelines.
Phenotyping
Standard clinical parameters were assessed in all study patients. Metabolic tests were carried out at the Division of Endocrinology, Diabetes and Metabolism of the University of Verona Medical School (Verona, Italy), on three separate days, each test starting at 08:00 a.m., after a 10–12-h overnight fast. All patients were on CGM; the device had been in place and properly working (calibration with capillary blood glucose as measured by glucometer at pre-established hours of the day) for at least two days before metabolic studies. CGM data were collected for a companion experiment. During the entire study duration patients lay recumbent in bed. Two of the three studies were performed in random order. Study 1 - On one day, all patients underwent a hyperinsulinemic euglycemic insulin clamp (HEC). Study 2 - On a second occasion, all patients were studied with a standardized mixed meal test (MMT1) of 292 Kcal. Study 3 - The third study (MMT2) was in 3 patients the repetition of the 292 Kcal MMT, whereas in other 3 patients it consisted of a 600 Kcal MMT, with the same relative macronutrient composition of the 292 Kcal MTT.
Assessment of Insulin Sensitivity (Study 1)
A standard HEC was carried out to assess insulin sensitivity, which was computed with standard formulae3,51, and expressed as the amount of glucose metabolized during the last 60 min of the clamp.
Subjects were instructed to use their usual nocturnal fast insulin analogue basal rate, to be left unchanged for at least five hours before the beginning of the test. Human insulin concentration was raised with an intravenous prime (0.8 U/m2 BSA) and maintained constant by a constant intravenous infusion (40 mU/min·m2 BSA). Plasma glucose was allowed to fall until it reached the physiologic range (i.e. <5.6 mmol/l), after which it was clamped at 5.0 mmol/l for at least 60 min by appropriately changing an intravenous infusion of 20% dextrose.
Mixed-Meal Tests (Study 2 and 3)
The MMTs were performed to determine the time courses of plasma glucose and insulin during a mixed meal and to assess the pathophysiology of glucose control during a standardized physiological challenge. Subjects were instructed to be on an Indian corn free and cane sugar free diet for at least one week before each study and were instructed to use their usual nocturnal fast insulin analogue basal rate, to be left unchanged for at least five hours before the beginning of the test. A standardized mixed meal of maize polenta plus seasoned Italian Parmesan cheese (292 Kcal, 38.9 g carbohydrates, 8.9 g fats and 14 g proteins) was ingested by all study participants, and patients were monitored for 300 minutes thereafter. The time taken by the patients to ingest the meal was recorded. Right before meal ingestion, a fast subcutaneous insulin analogue bolus was administered through the pump, according to the individual insulin-to-carbohydrate ratio and correction dose.
On a separate day, a MMT of the same size was repeated in three patients, while a MMT with the same composition, but of double caloric size, was administered in the other three patients. In both cases, the experimental procedures were identical to the first MMT.
In all studies, blood samples were drawn at time intervals, put in ice and quickly spun at 1500 g at +4 °C. Plasma/serum specimens were stored at −80 °C.
Measurements
Plasma glucose was measured in duplicate with an YSI 2300 Stat Plus Glucose&Lactate Analyzer (YSI Inc., Yellow Springs, OH, USA), at bedside. Blood samples were collected at timed intervals to measure plasma insulin. Interstitial glucose monitoring was performed by the CGM device throughout the entire duration of insulin clamp for a companion experiment. Serum insulin concentrations were measured by ELISA (Mercodia, Sweden)51, which can detect also lispro, aspart and glulisine insulin. Standard curves for each analog were used to measure accurately circulating insulin levels. To calculate the total insulin concentration achieved during the HEC, it was assumed that the insulin analog infused through the pump would generate the same concentration observed at baseline also throughout the entire clamp procedure. Glycosylated hemoglobin was measured by standard in-house methods. GAD-65 antibodies were measured by immunoradiometry (CentAK, Medipan, Germany), according to manufacturer’s instructions (detection limit >1 KU/l).
Models
The MMT experiment, described in detail above, is modeled starting from the Minimal Model6,50 ideas and its further refinements7,22,25,28,31,33,49,50. Figure 2 and Figure S1 present a schematic representation of the model, which is tailored to consider T1D patients’ conditions and presents an original and physiologically plausible function, called Oral Glucose Input (OGI), to model the glucose appearance in the plasma. The MMT model is used to reproduce the insulin-glucose time series obtained during two different MMT experiments, as explained in Mixed-Meal Tests (Study 2 and 3). Parameters are estimated by fitting experimental data using non-linear least squares and a multi-start approach to ensure a global optimum. To reduce the uncertainty of parameter estimates, a combination of clamp-derived, patient-specific and literature-based prior information have been considered to drive the optimization process (see Technologies section and Supplementary Material). The robustness of the model has been also confirmed by the good reproducibility of parameter estimates on the two MMT experiments for all the physiological parameters (Table 2).
To simplify the description, the MMT model has been conceptually designed as being composed by two submodels (the “insulin” and the “glucose” submodel), which interact as shown in Figure S1. Since we are dealing here with T1D patients, the insulin submodel has been developed as a mono-compartmental model, where the beta-cell contribution to insulin secretion15,20,52,53 is removed. It describes the dynamics of the insulin deposit in tissues, due to the insulin injection, and the insulin concentration in the volume where insulin sampling takes place.
The glucose submodel is realized through a mono-compartmental model as well, where insulin action regulates glucose metabolism according to the minimal model principles6,7. The appearance of the ingested glucose in the system is obtained through the Oral Glucose Input function (OGI, see Supplementary Material). Such a function is the output of two chains of compartments, representing fast and slow glucose absorption during the digestion, which produces exponential-shaped outputs combined into a one/two peak(s) shape with exponential decay, as depicted in Fig. 4. This function integrates and extends previous observations17,31,54, by modeling the processes of digestion/absorption with just three parameters.
For a more detailed description of the model, we refer to the Supplementary Material. We refer to the Technologies section for further details on the implementation and parameter estimation procedures.
Technologies
We implemented the GLUKINSLOOP 2.0 model in MATLAB v. R2016a (The MathWorks Inc., Natick, MA, USA) using ordinary differential equations (ODEs) simulated according to a Runge-Kutta algorithm. Model equations include sixteen unknown parameters. We carried out parameter estimation by non-linear least squares using the lsqnonlin function (MATLAB Optimization Toolbox v. R2016a, trust-region-reflective algorithm55,56) with a 1e-10 tolerance and a multi-start approach to ensure a global optimum (MATLAB Global Optimization Toolbox v. R2016a). To take into account the differences in concentration of insulin and glucose without introducing a bias in the fitting procedure, squared-relative-errors weighted on experimental standard deviations have been considered for parameter estimation. In addition, for each parameter whose prior information was available, a penalty term proportional to the distance of the current parameter estimate from the prior has been added to drive the optimization process.
Additional Information
How to cite this article: Marchetti, L. et al. A Novel Insulin/Glucose Model after a Mixed-Meal Test in Patients with Type 1 Diabetes on Insulin Pump Therapy. Sci. Rep. 6, 36029; doi: 10.1038/srep36029 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Ferrannini, E. & DeFronzo, R. A. In International Textbook of Diabetes Mellitus Vol. 1 (eds R. A. DeFronzo, E. Ferrannini, P. Zimmet & K. G. M. M. Alberti ) Ch. 14, 211–233 (John Wiley & Sons, Ltd, Chichester, UK, 2015).
Natali, A., Prato, S. D. & Mari, A. In International Textbook of Diabetes Mellitus Vol. 1 (eds R. A. DeFronzo, E. Ferrannini, P. Zimmet & K. G. M. M. Alberti ) Ch. 8, 108–124 (John Wiley & Sons, Ltd, Chichester, UK, 2015).
DeFronzo, R. A., Tobin, J. D. & Andres, R. Glucose clamp technique: a method for quantifying insulin secretion and resistance. The American journal of physiology 237, E214–E223 (1979).
Priami, C. M. M. J. Analysis of biological systems. (Imperial College Press, 2015).
Priami, C. Algorithmic Systems Biology. Communications of the Acm 52, 80–88, doi: 10.1145/1506409.1506427 (2009).
Bergman, R. N., Phillips, L. S. & Cobelli, C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J Clin Invest 68, 1456–1467 (1981).
Cobelli, C. et al. The oral minimal model method. Diabetes 63, 1203–1213, doi: 10.2337/db13-1198 (2014).
Cobelli, C., Man, C. D., Pedersen, M. G., Bertoldo, A. & Toffolo, G. Advancing our understanding of the glucose system via modeling: a perspective. IEEE Trans Biomed Eng 61, 1577–1592, doi: 10.1109/TBME.2014.2310514 (2014).
Cobelli, C. et al. Assessment of beta-cell function in humans, simultaneously with insulin sensitivity and hepatic extraction, from intravenous and oral glucose tests. American journal of physiology. Endocrinology and metabolism 293, E1–E15 (2007).
Dalla Man, C., Raimondo, D. M., Rizza, R. A. & Cobelli, C. GIM, simulation software of meal glucose-insulin model. J Diabetes Sci Technol 1, 323–330 (2007).
Dalla Man, C., Rizza, R. A. & Cobelli, C. Meal simulation model of the glucose-insulin system. IEEE Trans Biomed Eng 54, 1740–1749, doi: 10.1109/TBME.2007.893506 (2007).
Insel, P. A. et al. Insulin control of glucose metabolism in man: a new kinetic analysis. J Clin Invest 55, 1057–1066, doi: 10.1172/JCI108006 (1975).
Manca, V., M. L. & Pagliarini, R. MP Modelling of Glucose-Insulin Interactions in the Intravenous Glucose Tolerance Test. International Journal of Natural Computing Research (IJNCR) 2, 13–24, doi: 10.4018/jncr.2011070102 (2011).
Mari, A. Mathematical modeling in glucose metabolism and insulin secretion. Curr Opin Clin Nutr Metab Care 5, 495–501 (2002).
Mari, A. et al. Meal and oral glucose tests for assessment of beta -cell function: modeling analysis in normal subjects. Am J Physiol Endocrinol Metab 283, E1159–E1166, doi: 10.1152/ajpendo.00093.2002 (2002).
Palumbo, P., Ditlevsen, S., Bertuzzi, A. & De Gaetano, A. Mathematical modeling of the glucose-insulin system: a review. Math Biosci 244, 69–81, doi: 10.1016/j.mbs.2013.05.006 (2013).
Salinari, S., Bertuzzi, A. & Mingrone, G. Intestinal transit of a glucose bolus and incretin kinetics: a mathematical model with application to the oral glucose tolerance test. Am J Physiol Endocrinol Metab 300, E955–E965, doi: 10.1152/ajpendo.00451.2010 (2011).
Silber, H. E., Jauslin, P. M., Frey, N. & Karlsson, M. O. An integrated model for the glucose-insulin system. Basic Clin Pharmacol Toxicol 106, 189–194, doi: 10.1111/j.1742-7843.2009.00510.x (2010).
Toffolo, G., Bergman, R. N., Finegood, D. T., Bowden, C. R. & Cobelli, C. Quantitative estimation of beta cell sensitivity to glucose in the intact organism: a minimal model of insulin kinetics in the dog. Diabetes 29, 979–990 (1980).
Toffolo, G., De Grandi, F. & Cobelli, C. Estimation of beta-cell sensitivity from intravenous glucose tolerance test C-peptide data. Knowledge of the kinetics avoids errors in modeling the secretion. Diabetes 44, 845–854 (1995).
Tura, A., Muscelli, E., Gastaldelli, A., Ferrannini, E. & Mari, A. Altered pattern of the incretin effect as assessed by modelling in individuals with glucose tolerance ranging from normal to diabetic. Diabetologia 57, 1199–1203, doi: 10.1007/s00125-014-3219-7 (2014).
Trombetta, M. et al. Type 2 diabetes mellitus: a disease of the governance of the glucose-insulin system: an experimental metabolic control analysis study. Nutr Metab Cardiovasc Dis 23, 23–30, doi: 10.1016/j.numecd.2011.05.006 (2013).
Mari, A., Pacini, G., Murphy, E., Ludvik, B. & Nolan, J. J. A model-based method for assessing insulin sensitivity from the oral glucose tolerance test. Diabetes Care 24, 539–548 (2001).
Man, C. D. et al. The UVA/PADOVA Type 1 Diabetes Simulator: New Features. J Diabetes Sci Technol 8, 26–34, doi: 10.1177/1932296813514502 (2014).
Vicini, P., Caumo, A. & Cobelli, C. The hot IVGTT two-compartment minimal model: indexes of glucose effectiveness and insulin sensitivity. The American journal of physiology 273, E1024–E1032 (1997).
Dalla Man, C. et al. Measurement of selective effect of insulin on glucose disposal from labeled glucose oral test minimal model. Am J Physiol Endocrinol Metab 289, E909–E914, doi: 10.1152/ajpendo.00299.2004 (2005).
Basu, R. et al. Use of a novel triple-tracer approach to assess postprandial glucose metabolism. Am J Physiol Endocrinol Metab 284, E55–E69, doi: 10.1152/ajpendo.00190.2001 (2003).
Caumo, A., Bergman, R. N. & Cobelli, C. Insulin sensitivity from meal tolerance tests in normal subjects: a minimal model index. The Journal of clinical endocrinology and metabolism 85, 4396–4402, doi: 10.1210/jcem.85.11.6982 (2000).
Greenbaum, C. J. et al. Mixed-meal tolerance test versus glucagon stimulation test for the assessment of beta-cell function in therapeutic trials in type 1 diabetes. Diabetes Care 31, 1966–1971, doi: 10.2337/dc07-2451 (2008).
Dalla Man, C. et al. Two-hour seven-sample oral glucose tolerance test and meal protocol: minimal model assessment of beta-cell responsivity and insulin sensitivity in nondiabetic individuals. Diabetes 54, 3265–3273 (2005).
Dalla Man, C., Caumo, A. & Cobelli, C. The oral glucose minimal model: estimation of insulin sensitivity from a meal test. IEEE Trans Biomed Eng 49, 419–429, doi: 10.1109/10.995680 (2002).
Breda, E., Cavaghan, M. K., Toffolo, G., Polonsky, K. S. & Cobelli, C. Oral glucose tolerance test minimal model indexes of beta-cell function and insulin sensitivity. Diabetes 50, 150–158 (2001).
De Gaetano, A. & Arino, O. Mathematical modelling of the intravenous glucose tolerance test. J Math Biol 40, 136–168, doi: 10.1007/s002850050007 (2000).
Dalla Man, C. et al. Modeling hepatic insulin sensitivity during a meal: validation against the euglycemic hyperinsulinemic clamp. Am J Physiol Endocrinol Metab 304, E819–E825, doi: 10.1152/ajpendo.00482.2012 (2013).
Visentin, R. et al. Hepatic insulin sensitivity in healthy and prediabetic subjects: from a dual- to a single-tracer oral minimal model. Am J Physiol Endocrinol Metab 309, E161–E167, doi: 10.1152/ajpendo.00358.2014 (2015).
Dalla Man, C. et al. Minimal model estimation of glucose absorption and insulin sensitivity from oral test: validation with a tracer method. Am J Physiol Endocrinol Metab 287, E637–E643, doi: 10.1152/ajpendo.00319.2003 (2004).
Steil, G. M. et al. Evaluation of insulin sensitivity and beta-cell function indexes obtained from minimal model analysis of a meal tolerance test. Diabetes 53, 1201–1207 (2004).
Dalla Man, C. et al. Insulin sensitivity by oral glucose minimal models: validation against clamp. Am J Physiol Endocrinol Metab 289, E954–E959, doi: 10.1152/ajpendo.00076.2005 (2005).
Bock, G. et al. Effects of nonglucose nutrients on insulin secretion and action in people with pre-diabetes. Diabetes 56, 1113–1119, doi: 10.2337/db06-1272 (2007).
Mallad, A. et al. Nocturnal Glucose Metabolism in Type 1 Diabetes: A Study Comparing Single Versus Dual Tracer Approaches. Diabetes Technol Ther 17, 587–595, doi: 10.1089/dia.2015.0011 (2015).
Mallad, A. et al. Exercise effects on postprandial glucose metabolism in type 1 diabetes: a triple-tracer approach. Am J Physiol Endocrinol Metab 308, E1106–E1115, doi: 10.1152/ajpendo.00014.2015 (2015).
Steil, G. M. Algorithms for a closed-loop artificial pancreas: the case for proportional-integral-derivative control. J Diabetes Sci Technol 7, 1621–1631 (2013).
Russell, S. J. et al. Outpatient glycemic control with a bionic pancreas in type 1 diabetes. N Engl J Med 371, 313–325, doi: 10.1056/NEJMoa1314474 (2014).
Thabit, H. et al. Home Use of an Artificial Beta Cell in Type 1 Diabetes. N Engl J Med 373, 2129–2140, doi: 10.1056/NEJMoa1509351 (2015).
Kropff, J. et al. 2 month evening and night closed-loop glucose control in patients with type 1 diabetes under free-living conditions: a randomised crossover trial. Lancet Diabetes Endocrinol 3, 939–947, doi: 10.1016/S2213-8587(15)00335-6 (2015).
Maffeis, C. et al. Ghrelin, insulin sensitivity and postprandial glucose disposal in overweight and obese children. Eur J Endocrinol 154, 61–68, doi: 10.1530/eje.1.02055 (2006).
Bonora, E. et al. Hyperinsulinemia and insulin resistance are independently associated with plasma lipids, uric acid and blood pressure in non-diabetic subjects. The GISIR database. Nutr Metab Cardiovasc Dis 18, 624–631, doi: 10.1016/j.numecd.2007.05.002 (2008).
Cobelli, C., Pacini, G., Toffolo, G. & Sacca, L. Estimation of insulin sensitivity and glucose clearance from minimal model: new insights from labeled IVGTT. The American journal of physiology 250, E591–E598 (1986).
Man, C. D., Toffolo, G., Basu, R., Rizza, R. A. & Cobelli, C. Use of labeled oral minimal model to measure hepatic insulin sensitivity. American journal of physiology. Endocrinology and metabolism 295, E1152–E1159, doi: 10.1152/ajpendo.00486.2007 (2008).
Bergman, R. N., Ider, Y. Z., Bowden, C. R. & Cobelli, C. Quantitative estimation of insulin sensitivity. The American journal of physiology 236, E667–E677 (1979).
Bonetti, S. et al. Variants of GCKR affect both beta-cell and kidney function in patients with newly diagnosed type 2 diabetes: the Verona newly diagnosed type 2 diabetes study 2. Diabetes Care 34, 1205–1210, doi: 10.2337/dc10-2218 (2011).
Bertuzzi, A., Salinari, S. & Mingrone, G. Insulin granule trafficking in beta-cells: mathematical model of glucose-induced insulin secretion. Am J Physiol Endocrinol Metab 293, E396–E409, doi: 10.1152/ajpendo.00647.2006 (2007).
Cobelli, C. & Pacini, G. Insulin secretion and hepatic extraction in humans by minimal modeling of C-peptide and insulin kinetics. Diabetes 37, 223–231 (1988).
De Gaetano, A. et al. Routine OGTT: a robust model including incretin effect for precise identification of insulin sensitivity and secretion in a single individual. PLoS One 8, e70875, doi: 10.1371/journal.pone.0070875 (2013).
Coleman, T. F. Y. L. On the convergence of interior-reflective Newton methods for nonlinear minimization subject to bounds. Mathematical Programming 67, 189–224, doi: 10.1007/BF01582221 (1994).
Coleman, T. F. Y. L. An Interior Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM Journal on Optimization 6, 418–445, doi: 0.1137/0806023 (1996).
Gostner, R., Baldacci, B., Morine, M. J. & Priami, C. Graphical Modeling Tools for Systems Biology. Acm Computing Surveys 47, 16, doi: 10.1145/2633461 (2015).
Acknowledgements
Federica Moschetta and Monica Zardini provided superb technical help. Fabio Favaretto, Rosanna Tinelli, Paola Girardi and Nicoletta Francesconi carried out the insulin clamps and provided expert nursing assistance to the patients. Ilaria Rubbo, MD, contributed to supervise the meal tolerance tests. Paola Branzi provided excellent dietary counseling to the study patients. This study was supported in part by a grant of the European Foundation for the Study of Diabetes/Novartis and by a research contribution of University of Parma, both to RCB, and partly by research grants of the University of Verona to RCB and EB. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
L.M. and F.R. under the supervision of C.P. and R.C.B. participated in the development of the mathematical model, computed parameter estimates and model dynamics and contributed to the writing of the paper. M.D. discussed the results and wrote the first draft of the manuscript. E.B. and R.C.B. designed the study and wrote and edited the manuscript. C.B. and G.C. supervised and carried out the experimental studies, and revised the first draft of the manuscript. L.B. and R.C.B. developed a preliminary version of the mathematical model, applied it in a preliminary analysis of the experimental studies, revised the final version of the mathematical model and edited the Supplementary Material of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Marchetti, L., Reali, F., Dauriz, M. et al. A Novel Insulin/Glucose Model after a Mixed-Meal Test in Patients with Type 1 Diabetes on Insulin Pump Therapy. Sci Rep 6, 36029 (2016). https://doi.org/10.1038/srep36029
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep36029
This article is cited by
-
A QSP model of prostate cancer immunotherapy to identify effective combination therapies
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.