Abstract
When CO2 is injected in saline aquifers, dissolution causes a local increase in brine density that can cause Rayleigh-Taylor-type gravitational instabilities. Depending on the Rayleigh number, density-driven flow may mix dissolved CO2 throughout the aquifer at fast advective time-scales through convective mixing. Heterogeneity can impact density-driven flow to different degrees. Zones with low effective vertical permeability may suppress fingering and reduce vertical spreading, while potentially increasing transverse mixing. In more complex heterogeneity, arising from the spatial organization of sedimentary facies, finger propagation is reduced in low permeability facies, but may be enhanced through more permeable facies. The connectivity of facies is critical in determining the large-scale transport of CO2-rich brine. We perform high-resolution finite element simulations of advection-diffusion transport of CO2 with a focus on facies-based bimodal heterogeneity. Permeability fields are generated by a Markov Chain approach, which represent facies architecture by commonly observed characteristics such as volume fractions. CO2 dissolution and phase behavior are modeled with the cubic-plus-association equation-of-state. Our results show that the organization of high-permeability facies and their connectivity control the dynamics of gravitationally unstable flow. We discover new flow regimes in both homogeneous and heterogeneous media and present quantitative scaling relations for their temporal evolution.
Similar content being viewed by others
Introduction
Geological sequestration of carbon dioxide (CO2) has been proposed as a technology to reduce the amount of CO2 emitted into the atmosphere1,2,3,4,5,6. The main processes controlling the trapping of CO2 during geological sequestration are storage of supercritical CO2 in a gas cap, CO2 dissolution in brine, known as solubility trapping7,8, residual trapping due to hysteresis9,10, and mineral trapping by CO2 precipitation as secondary carbonates11. In this work, we focus on solubility trapping, which can be enhanced when gravitational instabilities (fingering) are triggered by a local increase in brine density as CO2 dissolves into brine in the top of an aquifer. This Rayleigh-Taylor-type instability12 is sometimes referred to as gravito-convective mixing and involves both diffusive and advective motion of dissolved CO2, with advection being the dominant driving force. Whether the interface between CO2-bearing brine and fresh brine becomes gravitationally unstable depends on the ratio of advection to molecular diffusion (Rayleigh or Péclet numbers). When a fingering instability is triggered, dissolved CO2 is mixed throughout the aquifer at advective time-scales, which can be much faster than diffusive transport12,13,14. This improves the storage capacity of a given aquifer and decreases the leakage risk in case of cap rock failure.
There is extensive literature on gravitational instabilities14,15,16,17,18. Stability analyses and numerical simulations predict a critical wavelength for the instability that depends on fluid and reservoir properties as13,14,15,16,17,18,19:

with brine viscosity, μ, porosity, ϕ, CO2 diffusion coefficient, D, permeability, k, maximum density increase of the aqueous phase upon CO2 dissolution, Δρ, and gravitational acceleration, g. A critical onset time is predicted by:

Different proportionality constants c1 and c2 have been obtained by the different authors cited above.
It is evident from Eq. (1) and Eq. (2) that the critical wavelength and onset time depend on porosity and permeability. Since the spatial variability of porosity is much smaller than that of permeability, the latter is often used to represent the heterogeneity of porous media20,21,22.
Various studies have characterized the transport of CO2-rich brine through heterogeneous systems. Using numerical simulations, Farajzadeh et al.23 studied the influence of spatial heterogeneity in permeability on gravitational fingering, and explained three different flow regimes for stable trapping of dissolved CO2: fingering, dispersion, and channeling. Different models of permeability heterogeneity have been tested by previous authors24,25. These studies concluded that permeability heterogeneity could have a significant impact on the onset, rate, and characteristic behavior of density-driven flow of CO2. On the other hand, theoretical26, numerical27, and experimental6 results suggest that density-driven flow may not always lead to significant convective mixing especially in layered systems containing low-permeability zones; CO2 may actually become immobilized in these zones. In order to quantify the effects of vertical heterogeneity, Green and Ennis-King28 developed a simple model consisting of a random and uncorrelated distribution of horizontal, impermeable barriers with a given overall volume fraction (0.04% and 0.15%). They found that in a homogeneous medium with equivalent effective vertical permeability, compared to heterogeneous medium, convection begins at later onset times.
In reality, geological heterogeneity is controlled by the spatial organization of sedimentary facies with different physical attributes, such as permeability29. Facies distributions therefore affect species transport through a formation9. Architectures of sedimentary facies can exhibit sharp discontinuities across boundaries between depositional features, for instance across the sandstone-shale contacts that are common in fluvial deposits. The complex patterns in such fluvial architectures30 exist in many candidate aquifers for CO2 sequestration9,31,32 and result in variable connectivity and tortuous flow pathways33. Representing such discontinuous, correlated heterogeneity in reservoir simulations is non-trivial34, and its influence on the characteristics of density-driven flow has not been studied in detail. In this work, we generate many volume-preserving realizations of bimodal facies architectures using a Markov Chain approach combined with an indicator simulation with quenching. For comparison, homogeneous domains are defined by the equivalent geometric mean permeability for each realization. We then perform high-resolution two-dimensional simulations of gravitational fingering in both homogeneous and heterogeneous media to investigate the influence of facies-based heterogeneity and connectivity on the transport of dissolved CO2.
For accurate numerical simulations of gravitational fingering, the physics of fluid flow and thermodynamics have to be represented rigorously. High-resolution numerical discretizations are required to minimize numerical dispersion which can obscure the onset of small-scale fingers. We adopt a combination of the mixed hybrid finite element (MHFE) method –to simultaneously solve for continuous pressure and velocity fields– and a higher-order discontinuous Galerkin (DG) method for the species transport. Phase behavior is described by the cubic-plus-association (CPA) equation of state (EOS). CPA-EOS has been shown to accurately reproduce measured densities of CO2-brine mixtures and the volume swelling due to CO2 dissolution1,35,36. Volume swelling and the associated movement of the interface between free CO2 in a gas cap and the underlying brine, cannot be modeled by considering only the aqueous phase15 and replacing the gas cap with a constant-CO2-composition Dirichlet boundary condition37. In this work, we inject CO2 from the upper boundary at a sufficiently low rate that the simulated domain remains a single aqueous phase (i.e., without a capillary transition zone22). We do not adopt the Boussinesq approximation in order to fully study the effects of fluid compressibility and the pressure response due to swelling effect when increasing volumes of CO2 are injected in a confined domain (impermeable boundaries) and subsequently dissolve in the brine1,18.
Numerical Experiments
We consider CO2 sequestration in saline aquifers by injecting CO2 uniformly from the top without production of brine (alternatively, this can be interpreted as a CO2 dissolution rate from an overlying CO2-gas cap). The rate is kept sufficiently low (0.1% pore volume (PV) per year) to insure that brine is nearly CO2-saturated in the top but without forming a gas phase in the computational domain. Because saline aquifers are large, injection of 1–2% PV in 10–20 years is sufficient, and higher injection volumes result in excessive pressure increases. We model a 12 m × 30 m subdomain, discretized by a fine 240 × 300 grid and with a uniform (or heterogeneous average) porosity of 10%. The constant temperature is 77 °C and the initial pressure is 100 bar at the bottom. At these conditions, the pure and CO2-saturated brine densities are ρw = 978 kg/m3 and ρ = 978 kg/m3, with Δρ = (ρ−ρw)/ρw = 0.9%, for a CO2 solubility of 1.7 mol%. The diffusion coefficient is D = 1.33 × 10−8 m2 s−1.
Whether spatial heterogeneity of an aquifer enhances density-driven flow of CO2-rich brine depends on the volume fraction of high-permeability facies and their connectivity. Our long-term goal is to perform large two- and three-dimensional simulations with multiple facies types. In this preliminary study we show the fundamental importance of heterogeneities arising from facies architecture. We choose a parsimonious set of two facies types representing a bimodal architecture29,38. Different structures are created using a Markov Chain model and indicator simulation with quenching in TPROGS39. Rather than focusing on any single site or data set, we represent general permeability distributions consisting of high- and low-permeability facies. The high-permeability facies volume fraction is increased from 10% to 90% in increments of 10% (Fig. 1), which also increases the facies connectivity29,40. In all cases, the mean length of the less abundant facies are 2 m in both horizontal and vertical directions representative of meter-scale sedimentary features. For each volume fraction, we generate five realizations of facies structures and for each realization we superimpose a lognormal permeability distribution with a variance of 0.1 within each facies. The geometric mean of high and low-permeability facies are 8.5 (5,000 md) and 4.6 (100 md), respectively29. For comparison, we create homogeneous domains with the same mean permeabilities (Table 1).
Results and Discussions
To characterize density-driven flow of CO2, we use the method from a seminal paper by Sudicky41. The spatial moments of the CO2 distribution provide an insightful measure for the transport of CO2 at various time-scales. The first three central moments of the distribution are employed to define the spatial variance,  , of the CO2 molar density as an indicator of vertical spreading (dispersion) and a reasonable proxy to mixing. The square root of spatial variance, σz, is defined as the dispersion-width (scale) to determine the extent to which the descending plume of CO2 has stretched (i.e., the volume of CO2-enriched brine). These definitions are in line with models developed for flow and transport in systems having complex spatial variability in physical and chemical properties42,43, but also take into account the density change due to dissolution and compressibility. In our analyses, we consider the dynamics from the first contact of CO2 with brine until
, of the CO2 molar density as an indicator of vertical spreading (dispersion) and a reasonable proxy to mixing. The square root of spatial variance, σz, is defined as the dispersion-width (scale) to determine the extent to which the descending plume of CO2 has stretched (i.e., the volume of CO2-enriched brine). These definitions are in line with models developed for flow and transport in systems having complex spatial variability in physical and chemical properties42,43, but also take into account the density change due to dissolution and compressibility. In our analyses, we consider the dynamics from the first contact of CO2 with brine until  or σz reach their maximum values –determined by domain dimensions– above which they plateau (see Methods). Next, we study the temporal evolution of
or σz reach their maximum values –determined by domain dimensions– above which they plateau (see Methods). Next, we study the temporal evolution of  and note that faster vertical motion implies reaching the maximum variance in a shorter amount of time (Eq. (7)). Fast mixing and spreading towards higher depths improve the long-term storage of dissolved CO2 throughout the aquifer6, because CO2 is likely to remain in aquifer due to residual and mineral trapping even if the pressure were to drop due to a failure of the cap rock.
and note that faster vertical motion implies reaching the maximum variance in a shorter amount of time (Eq. (7)). Fast mixing and spreading towards higher depths improve the long-term storage of dissolved CO2 throughout the aquifer6, because CO2 is likely to remain in aquifer due to residual and mineral trapping even if the pressure were to drop due to a failure of the cap rock.
We summarize our main findings in Figs 2 and 3, which show the molar density of dissolved CO2 at 2, 6, 12, 15, and 25 years for heterogeneous media and their homogeneous equivalents. Density-driven flow in homogeneous domains has been extensively studied before, though with simplifying assumptions in terms of boundary conditions and phase behavior. Phase behavior is critical because the driving force for gravitational instabilities is the density contrast, Δρ, upon CO2 dissolution. From our scaling analyses (Fig. 4) for fully compositional EOS-based simulations of compressible flow, we observe new flow regimes even for homogeneous domains due to the non-trivial evolution of maximum Δρ over time (Fig. 5). In the following, we first discuss these results for homogeneous media and then for different bimodal heterogeneous facies architectures.
Natural log of molar density of CO2 after 2, 6, 12, 15, and 25 years for bimodal heterogeneous domains (for the realizations shown in Fig. 1).
(a)
Spatial variance of molar density of CO2 ( ) for all homogeneous and ensemble (i.e., averaged over 5 realizations) heterogeneous cases. (b) Dispersion-width of molar density of CO2 (σz) for homogeneous domains. (c) Ensemble σz for heterogeneous cases. (d) Dispersion coefficient, defined as
) for all homogeneous and ensemble (i.e., averaged over 5 realizations) heterogeneous cases. (b) Dispersion-width of molar density of CO2 (σz) for homogeneous domains. (c) Ensemble σz for heterogeneous cases. (d) Dispersion coefficient, defined as  , and tip velocity of the most advanced finger, defined as U tip = dztip/dt where ztip is the tip vertical depth, for one homogeneous domain corresponding to 10% of the high-permeability facies (initial fluctuations of tip velocity are of order Δz/Δt due to the numerical differentiation of tip location with respect to time). Onset of different regimes and critical features correlate well with each other through different measurements of σz, Dz, U tip, and the maximum Δρ (see Fig. 5 for global scaling of the latter).
, and tip velocity of the most advanced finger, defined as U tip = dztip/dt where ztip is the tip vertical depth, for one homogeneous domain corresponding to 10% of the high-permeability facies (initial fluctuations of tip velocity are of order Δz/Δt due to the numerical differentiation of tip location with respect to time). Onset of different regimes and critical features correlate well with each other through different measurements of σz, Dz, U tip, and the maximum Δρ (see Fig. 5 for global scaling of the latter).
Mass density difference between fresh brine and partially-saturated brine at top boundary, i.e. the maximum Δρ, for homogeneous media.
Results are shown for 4 different geometric mean permeabilities equivalent to 10, 40, 60, and 90% volume fractions of high-permeability facies. Visualizations of the 60% case illustrate universal features revealed by this analysis. The onset of various regimes seen in the spatial variance of CO2 can be understood by variations in the driving force. In addition, a consistent relation is obtained between critical onset time of the instability, geometric mean permeability, and maximum Δρ at the onset, which also satisfies the traditional scaling of Eq. (2). Panels in Fig. 3 corresponding to these different flow regimes are discussed in the text.
Homogeneous media
We observe four distinct flow regimes in all simulations for homogeneous media, but most clearly identifiable at low mean permeabilities (Fig. 4a,b). Dependencies on the mean formation permeability can be related to the Rayleigh number, which is the ratio of buoyancy to diffusive flux: Ra = kgΔρH/μϕD, with H the depth of the domain44. In this study, the Rayleigh number is equivalent to the Péclet number because the advective Darcy flux is predominantly gravity-driven.
Traditionally, a constant pressure and CO2-composition are assumed at the top boundary of a brine-saturated subdomain. Consequently, the density contrast between pure and CO2-saturated brine in the top remains at a constant, maximum value Δρmax, which has been used to estimate tc, λc, and Ra15. For a nearly constant brine viscosity and CO2 diffusion coefficient, the critical wavelength and time only depend on rock properties k and ϕ. In our work, we continuously inject CO2 and the composition in the top depends both on the injection rate, and on the downward transport rate of dissolved CO2. The latter also depends on permeability: for low permeabilities, buoyancy-driven Darcy fluxes are slower and more injected CO2 accumulates in the top. This gradually increases the brine density and makes the dissolution front increasingly unstable (positive feedback). Conversely, for high permeabilities, downward transport of dissolved CO2 is faster, which decreases the CO2 composition and thus the unstable density-contrast in the top (negative feedback). Swelling, and the associated pressure response, due to different rates of CO2 dissolution further complicate the evolution of Δρmax. These different feedbacks between transport dynamics and the buoyant driving force result in the four flow regimes (Figs 4 and 5) that we discuss in the next paragraphs.
-
1
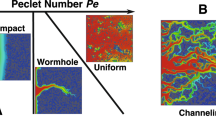
Initially, CO2 transport is controlled by diffusion as long as the CO2-front remains stable and advective flow is less than the diffusive flux (with small Δρmax resulting in low Rayleigh/Péclet numbers). Molecular diffusion involves low dissolution and mixing rates. The front travels to a ‘diffusion penetration depth’ which obeys a ~(Dt)0.5 Einstein-type scaling45. Likewise, the dispersion-width shows a classical Fickian scaling of σz ∝ t0.5 in Fig. 4b. We also keep track of the vertical propagation speed of the most advanced finger tip, which is shown in Fig. 4d for one case. The tip velocities are consistent with our measure of the dispersion coefficient (
 ). This first flow regime is observed in all homogeneous cases and as long as Rayleigh numbers are small, diffusion-dominated transport is insensitive to permeability (and for nearly constant μ and D and small Δρmax, also independent of Ra). Interestingly, while the total amount of introduced CO2 increases linearly with time (due to constant injection rate), the driver for advective buoyant flow, Δρmax, also follows Fickian ~t0.5 scaling until it has increased sufficiently to trigger gravitational instabilities (Fig. 5). The onset time, tc, of this next flow regime does depend on permeability (and Ra). The instability onset for the 60% volume fraction can also be observed in Fig. 3 after 2 years.
). This first flow regime is observed in all homogeneous cases and as long as Rayleigh numbers are small, diffusion-dominated transport is insensitive to permeability (and for nearly constant μ and D and small Δρmax, also independent of Ra). Interestingly, while the total amount of introduced CO2 increases linearly with time (due to constant injection rate), the driver for advective buoyant flow, Δρmax, also follows Fickian ~t0.5 scaling until it has increased sufficiently to trigger gravitational instabilities (Fig. 5). The onset time, tc, of this next flow regime does depend on permeability (and Ra). The instability onset for the 60% volume fraction can also be observed in Fig. 3 after 2 years. -
2
The onset of fingering can be recognized as the transition to a convection-dominated regime15 (high Rayleigh numbers), which manifests itself as a sharp increase in
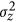 and σz (Fig. 4). This regime occurs after ~6 years in Fig. 3 for the 40% volume fraction. Table 1 summarizes the critical times from stability analysis13,14,19,46 as well as the critical times derived from the deviation of σz from Fickian scaling (inset of Fig. 4b). It has been recognized that the initial exponential growth of a dominant harmonic perturbation, as predicted by linear stability analyses, may not necessarily be apparent in numerical simulations or even in experiments. Observed tc are generally higher by at least an order of magnitude1,14. As discussed above, Eq. (2) also does not fully take into account the non-linear evolution of Δρmax. The dependence of critical times and wavelengths on permeability (Eqs (1)–(2), and Table 1) imply that higher permeabilities result in an earlier onset time with a larger number of small-scale fingers, illustrated in Fig. 3. However, Fig. 4b shows a new scaling relation of tc ∝ k−1, rather than the tc ∝ k−2 from stability analyses in Eq. (2). This is because Δρmax itself evolves. Since Δρmax(t) ∝ t0.5 in the first regime (Fig. 5), we find that Δρmax(t) ∝ k−0.5. Using this scaling of Δρmax in Eq. (2) is consistent with our independent finding for the scaling of tc with k.
and σz (Fig. 4). This regime occurs after ~6 years in Fig. 3 for the 40% volume fraction. Table 1 summarizes the critical times from stability analysis13,14,19,46 as well as the critical times derived from the deviation of σz from Fickian scaling (inset of Fig. 4b). It has been recognized that the initial exponential growth of a dominant harmonic perturbation, as predicted by linear stability analyses, may not necessarily be apparent in numerical simulations or even in experiments. Observed tc are generally higher by at least an order of magnitude1,14. As discussed above, Eq. (2) also does not fully take into account the non-linear evolution of Δρmax. The dependence of critical times and wavelengths on permeability (Eqs (1)–(2), and Table 1) imply that higher permeabilities result in an earlier onset time with a larger number of small-scale fingers, illustrated in Fig. 3. However, Fig. 4b shows a new scaling relation of tc ∝ k−1, rather than the tc ∝ k−2 from stability analyses in Eq. (2). This is because Δρmax itself evolves. Since Δρmax(t) ∝ t0.5 in the first regime (Fig. 5), we find that Δρmax(t) ∝ k−0.5. Using this scaling of Δρmax in Eq. (2) is consistent with our independent finding for the scaling of tc with k.A second interesting new finding is that the initial scaling of the dispersion-width in the fingering regime is σz ∝ t3.5 for all permeabilities. This is comparable to the Rayleigh-independent convective mixing rate found in Hidalgo et al.12. We argue that this independence from Rayleigh number is because
 , and the critical time tc in Eq. (2) is related to a Rayleigh number in which H is the thickness of the propagating diffusive layer before the onset of instabilities47, rather than the domain height. Because the initial diffusive layer grows as t0.5, Δρmax(tc) × H(tc) ∝ tc ~ k−5 and the Rayleigh number at the onset of fingering (Ra(tc) ∝ kΔρmaxH) becomes insensitive to permeability.
, and the critical time tc in Eq. (2) is related to a Rayleigh number in which H is the thickness of the propagating diffusive layer before the onset of instabilities47, rather than the domain height. Because the initial diffusive layer grows as t0.5, Δρmax(tc) × H(tc) ∝ tc ~ k−5 and the Rayleigh number at the onset of fingering (Ra(tc) ∝ kΔρmaxH) becomes insensitive to permeability. -
3
We observe a third flow regime that has not been clearly recognized in the literature before. Figure 4 shows an inflection point in the spatial variance curves, followed by another regime of diffusion-type scaling. This regime can be seen in Fig. 3 for a volume fraction of 10% after 25 years. The cause of this diffusive regime is three-fold. First, persistent coalescence and merging of growing fingers involve lateral diffusion, which result in coarsened fingers. Second, as the fingers stretch, the compositional gradients across the finger surface become steeper due to compression, which enhances diffusive fluxes across the finger boundaries48. Third, diffusion is further promoted by the nature of Rayleigh-Taylor fluid dynamics: downward motion of (growing) dense fingers and subsequent upwards displacement of fresh lighter brine increase the surface area of the CO2 dissolution front. The evolution of mixing rates is controlled by the competition between the advective stretching mechanism and such lateral compositional diffusion12. Following the onset of the previous regime, fast advective downward transport of fingers exceeds the diffusive rate of CO2 dissolution at the top. This depletion of CO2 concentrations in the fingers causes Δρmax to drop soon after the fingering onset (Fig. 5). As the driving force for advection/buoyancy (Δρmax) weakens, an inflection point is reached where diffusion exceeds advection and stretching stops. The inflection point corresponds to the local minimum of Δρmax and to the onset of a diffusion-dominated restoration regime (Figs 4d and 5), after which the dispersion-width returns to diffusive scaling as well (Fig. 4b). This third regime is comparable to a stagnation point in the advective flow where the rate of compression balances the rate of diffusive expansion49. During this transition period, CO2 transport is slower, concentrations are replenished (owing to the constant injection rate), and Δρmax increases, similar to the first regime, until the dissolution front becomes gravitationally unstable once again.
-
4
The fourth regime is again convection-dominated and shows a sharp increase in the growth rates of the CO2 spatial variance and dispersion-widths. The duration of the first convective regime is shorter for high-permeability cases and the reduction in Δρmax is smaller (Fig. 5). This regime occurs after 2 years for the 90% volume fraction in Fig. 3. This is in line with experimental results17 that show a reduced Δρ scaling as ~Ra−0.2 rather than a Rayleigh-independent constant dissolution flux14,50. Likewise, the third transition periods are shorter in high-permeability domains with less replenishment with CO2. Counterintuitively, this results in finger growth rates that are slower for the highest permeabilities (σz ∝ t1.5) than for the lowest permeability cases (σz ∝ t4) in this regime. This suggests that while Rayleigh and Péclet numbers are in the convection-dominated range for all permeabilities, they are lower for the high-permeability than for the low-permeability domains, due to the complex finger-brine interface at the end of the previous regime and the different depletion-replenishment histories of CO2 concentrations (and densities) inside the fingers.
Heterogeneous media
In the previous section, we considered density-driven flow in homogeneous aquifers and found four alternating diffusion- and convection-dominated flow regimes, the extent of which depends on Rayleigh numbers. Next, we investigate whether similar behavior persists in realistic heterogeneous media that have regions of different facies with tortuous and potentially connected pathways. We expect that our global measures of CO2 spreading will be a mixture of the flow regimes observed for a range of homogeneous mean permeabilities. How the gravito-convective mixing of dissolved CO2 is controlled by realistic permeability fields may dramatically affect the long-term CO2 storage efficiency.
Comparing Figs 2 and 3 shows that fingering is more pronounced in the heterogeneous media. This is different from flow in unimodal heterogeneous media, characterized by (pressure-driven) permeability-channeling that dominates (gravity-driven) hydrodynamic fingering. The reason for this is the spatial organization of facies: for a given mean permeability, the corresponding bimodal facies distribution has both regions with much higher and with much lower permeabilities. In large connected regions of the high-permeability facies, the critical time and wavelength are shorter than those for the mean permeability, and fingering is more pronounced. In addition, small-scale fingers may survive longer without merging because they are shielded from each other by low-permeability facies.
In terms of our quantitative measures, Fig. 4a exhibits a higher degree of CO2 spreading throughout the domain at early times in heterogeneous compared to homogeneous cases. At later times (during the fourth regime in homogeneous domains), we observe a crossover after which CO2 spreading in heterogeneous media is no longer higher than that in homogeneous domains. The reason is that for all heterogeneous cases the onset of convective fingering (first deviation from Fickian scaling: σz ∝ tβ>0.5) is almost instant, leading to more initial spreading but with a lower growth rate than for the homogeneous cases (Fig. 4c). Higher initial spreading ends in an earlier convective-shutdown regime in bimodal heterogeneities once the fingers reach the lower boundary and the domain starts to be saturated with CO2. This phenomenon has been studied in both numerical simulations and experiments as a late-time reduction of mixing rates12,51.
At late times, there is a delay in reaching the maximum spreading and a slower growth of σz for heterogeneous domains. This sub-convective behavior is caused partly by slow diffusion of CO2 into isolated low-permeability islands that locally impede the vertical propagation of descending fingers. More tortuous flow-paths can also be a factor, resulting in either a longer transit time of CO2-rich brine or favorable channeling of flow depending on the facies structure. Blockage of flow may also happen in bimodal structures, especially in aquifers with lower volume fractions of high-permeability facies.
The global measure of CO2 spreading is a superposition of fast convective (albeit tortuous) flow of CO2-rich fingers through high-permeability pathways and slower diffusive transport of CO2 through the lower-permeability facies. The former explains the higher initial mixing, while the latter causes the delay in reaching the maximum spreading. This phenomenon can be clearly seen in the 30% case (Figs 2 and 4a). For larger high-permeability volume fractions (above 50%), the delay in the spatial variance of CO2 over time is reduced. This is because we exceed the percolation threshold above which high-permeability clusters form large and connected preferential pathways that span the full extent of the domain52.
Scaling of the dispersion-width with time in Fig. 4c provides further insight into the complex flow dynamics of bimodal architectures. The four distinct flow regimes observed in homogeneous domains are smoothed out in heterogeneous formations. We find that CO2 transport in architectures below the percolation threshold scales from a diffusion-dominated Fickian regime (~t0.5) at early time, associated with flow through low-permeability facies, to a subsequent ballistic regime (~t) within high-permeability facies, and eventually to a sub-diffusive non-Fickian regime (~tβ<0.5). The latter is due to a contribution from diffusive transport through low-permeability facies in a subset of the domain at late times. The ballistic regime is due to advective flow through connected high-permeability pathways with a linear growth rate of fingers13. Similar regimes of dispersion-widths have been observed in viscously unstable solute transport through heterogeneous porous media, in which flow starts ballistically and reaches a Fickian scaling in the late-time asymptotic stage, but showing no sub-diffusive spreading48,53.
We note that for facies architectures below the percolation threshold, the chronological order of Fickian and ballistic flow regimes are realization dependent: when high-permeability facies are concentrated at top of the domain, a ballistic period is likely to precede a Fickian diffusive regime and vice versa. Above the percolation threshold, we see predominantly ballistic flow through fully connected clusters, followed by sub-diffusive scaling in a final delay period that is shorter than that below the percolation threshold. For the high-permeability heterogeneous simulations, σz reaches the maximum spreading at comparable times as the equivalent homogeneous cases, because its temporal scaling is similar (t1 versus t1.5).
We also model gravitational fingering in heterogeneous media at infinite Rayleigh numbers (D = 0) to isolate the predominantly advective flow (channeling) through high-permeability facies (for 30% and 90% volume fractions). Diffusive effects are generally more pronounced in heterogeneous (particularly, layered or fractured) aquifers in which compositional gradients tend to occur across interfaces between different permeabilities54. Expectedly, in the absence of diffusion as a restoring force, we see more dramatic fingering throughout the high-permeability facies (Fig. 6a). Our quantitative spreading measures show correspondingly higher values of σz and  in Fig. 6b. Comparing the evolution of the spatial variance and dispersion-widths for simulations with and without diffusion, we see that diffusion has little impact on the global mixing rates in the 90% case because the flow is advection-dominated from the start. For the 30% case, diffusion causes more stagnation at early times and mainly delays the onset of ballistic regime. This suggests that while bimodal formations with low proportions of high-permeability facies may show less vertical spreading of CO2-rich brine, they can promote more lateral mixing due to diffusion into low-permeability zones at early times compared to those with higher volume fractions of such facies. For both the 30% and 90% facies distributions, maximum spreading is achieved at similar times with or without diffusion, confirming that the transport of CO2 is ultimately driven by advection-dominated, unstable, gravito-convective mixing.
in Fig. 6b. Comparing the evolution of the spatial variance and dispersion-widths for simulations with and without diffusion, we see that diffusion has little impact on the global mixing rates in the 90% case because the flow is advection-dominated from the start. For the 30% case, diffusion causes more stagnation at early times and mainly delays the onset of ballistic regime. This suggests that while bimodal formations with low proportions of high-permeability facies may show less vertical spreading of CO2-rich brine, they can promote more lateral mixing due to diffusion into low-permeability zones at early times compared to those with higher volume fractions of such facies. For both the 30% and 90% facies distributions, maximum spreading is achieved at similar times with or without diffusion, confirming that the transport of CO2 is ultimately driven by advection-dominated, unstable, gravito-convective mixing.
(a) Natural log of molar density of CO2 for simulations without Fickian diffusion for two heterogeneous cases with volume fractions of 30% and 90% of the high-permeability facies. (b) Dispersion-width for simulations with and without Fickian diffusion. Inset: temporal evolution of spatial variance for the same problems in linear scale.
Finally we study the impact of heterogeneous porosity distributions on density-driven CO2 mixing (Fig. 7). We select one realization each of the 10%, 40%, and 90% volume fractions. A ratio of 10 is assigned between the porosities of the two facies while keeping the average porosity at 10% to allow comparison to homogeneous media and to keep the injection rates the same. This means that the bimodal porosities for the low- and high-permeability facies are 5.3% and 53% for the 10% case, 2.7% and 27% for the 40% case, and 1% and 10% for the 90% case. Lower porosities formally reduce λc, tc, and the diffusive flux (see Eq. (4)) and also affect CO2 transport (Eq. (3)) and its spatial variance (Eq. (7)). Lower permeability-porosity facies become saturated with CO2 earlier on, which increases the density contrast and triggers instabilities. As a result, while the advective flux is lower in low-permeability facies, the finger growth rates can be comparable to that in the higher permeability regions. This effect becomes more pronounced as the volume fraction of low-permeability facies increases. Figure 7b,c compare the temporal evolution of  and σz for these cases. We observe a diffusion-dominated initial regime, followed by a ballistic regime for all bimodal porosity distributions, with flow in the low porosity facies more unstable than in the corresponding uniform porosities of 10%.
and σz for these cases. We observe a diffusion-dominated initial regime, followed by a ballistic regime for all bimodal porosity distributions, with flow in the low porosity facies more unstable than in the corresponding uniform porosities of 10%.
(a) Natural log of molar density of CO2 for simulations with homogeneous and heterogeneous porosity for three cases with volume fractions of 10%, 40%, and 90% of the high-permeability facies. Low-permeability facies are illustrated in white. (b) Spatial variance of molar density of CO2 ( ). (c) Dispersion-width of molar density of CO2 (σz).
). (c) Dispersion-width of molar density of CO2 (σz).
Conclusions
We perform physically robust simulations of gravito-convective mixing of CO2 in saline aquifers without the limiting assumptions of prior studies. CO2 is injected into a confined domain and phase behavior is described by the cubic-plus-association EOS. CPA provides accurate densities, and accounts for both volume swelling due to CO2-dissolution, and compressibility due to injection-induced pressure increases. Heterogeneity, typical of fluvial deposits, is represented by bimodal facies architectures (e.g., shale and sandstone). To quantify the spreading of dissolved CO2 during the complex gravito-convective mixing, we evaluate global measures for the spatial variance and dispersion-width of CO2 as well as the evolution of a dispersion coefficient, the maximum density contrast Δρmax, and the velocity of the fastest growing unstable finger. From these measures, new flow regimes emerge at all Rayleigh numbers, caused by changes in Δρmax, the driving force for fast advective mixing. Due to competing diffusive and advective processes, we find in homogeneous media that for a constant dissolution rate in the top, Δρmax initially scales as k−0.5. Moreover, the critical onset time of fingering scales as k−1, rather than the k−2 found from stability analyses that assume a constant Δρmax. Topological structures of sedimentary facies and their connectivity are responsible for additional complexities. Fingering is enhanced in connected high-permeability facies (especially above the percolation threshold). Low-permeability regions can delay downward advective transport, but diffusion through such regions results in a longer mixing tail. Solubility trapping is an important process in predicting the fate of injected CO2 in feasibility studies of carbon storage, and the subsurface distribution of CO2 is critical when evaluating, e.g., the risk of leakage through nearby abandoned wells. A promising result is that in bimodal facies architectures, convective mixing of dissolved CO2 starts much earlier leading to higher degrees of mixing than predictions for equivalent homogeneous media. Our detailed analyses of the scaling relations of various global measures of the flow dynamics can be used to upscale the computationally expensive fine-grid simulations to the large dimensions of saline aquifers.
Methods
Governing equations: species transport and pressure equations
We consider a fluid mixture consisting of 2 components, labeled by index i with i = 1 for brine and i = 2 for CO2. The advection-diffusion transport equation is represented in terms of each component’s molar density (czi) as follows:

where c is the molar density, zi the mole fraction of component i with z1 + z2 = 1, Fi [mol/m3s] a source term of component i, ϕ the porosity, t the time,  the advective flux and
the advective flux and  the diffusive flux, given by55:
the diffusive flux, given by55:

Velocities follow from Darcy’s law as:

with ρ[kg/m3] the brine mass density, which is related to the molar density through the molecular weight of each component, Mi, as ρ = c(M1z1 + M2z2).
Most studies of carbon sequestration assume an incompressible aqueous phase, while we allow for both fluid compression due to the pressure build-up during CO2 injection into an aquifer with impermeable boundaries, and volume swelling of brine due to CO2 dissolution. The pressure response is computed from56:

where Cf is the brine compressibility and  is the total partial molar volume of each component in the mixture.
is the total partial molar volume of each component in the mixture.
Numerical framework: higher-order finite element methods for flow and transport
We use numerical methods presented in earlier works1,18,55,57. A second-order discontinuous Galerkin (DG) method is used to update the transport equations. This approach has been demonstrated to reliably capture the small-scale onset of viscous and gravitational fingers on relatively coarse grids by reducing numerical dispersion54. Shahraeeni et al.18 showed that the higher-order mass transport update can resolve the critical wavelength with only a few elements. A Mixed Hybrid Finite Element (MHFE) method is used to solve the Darcy and pressure equations simultaneously, which provides accurate velocity and pressure fields. MHFE is particularly useful in the simulations presented in this article due to the sharp contrasts in the heterogeneous permeability fields.
Phase behavior is based on the cubic-plus-association (CPA) EOS. The CPA-EOS is suitable for water-containing mixtures and takes into account the hydrogen bonding of water molecules by thermodynamic perturbation theory. The physical interactions follow from the Peng-Robinson EOS. In addition, the CPA-EOS allows for cross-association of CO2 with water, which is induced by polar-polar interactions1,35,36. This approach is an improvement over previous studies that relied on Henry’s law for CO2 solubilities and empirical correlations for the brine density.
Characterization of CO2 spreading: spatial variance and dispersion-width of CO2 molar density
In order to quantify the degree of mixing due to density-driven flow of CO2, we compute the spatial variance  of the molar density of CO2 and the dispersion-width σz41. The choice of CO2 molar density, rather than composition, accounts for both the density change due to CO2 dissolution and the compressibility of the aqueous phase.
of the molar density of CO2 and the dispersion-width σz41. The choice of CO2 molar density, rather than composition, accounts for both the density change due to CO2 dissolution and the compressibility of the aqueous phase.
The first three central moments of the distribution define the spatial variance  of the molar density of CO2 (
of the molar density of CO2 ( ):
):

where N01/N00 expresses the coordinate location of the center of mole in the vertical (z) direction. The Nik is the ik-th moment of the CO2 molar density distribution in space, analogous to the moment of concentration distribution58, defined here as:

with Lx and Lz the domain size in x- and z-directions, respectively. The zeroth moment, N00, physically represents the total number of moles of CO2 in the domain. The N00 does not remain constant over time because CO2 is continuously injected into the domain, unlike previous studies involving a pulse input of a solute in solution59. However, by normalizing the first and second moments by N00, the spatial variance becomes insensitive to increasing N00. The variance in the x-direction is assumed to be negligible due to the dominant downward migration of CO2-rich brine. As a result, i equals to 0 in the ik-th moments.
While spreading and dispersion can fundamentally differ from mixing and dilution, especially in highly heterogeneous media48, it is a reasonable proxy to mixing, especially when there is a variable total volume of the dissolving solute in the system, because more spreading usually leads to more dilution and mixing60. The  or σz reach their maximum values, above which they plateau, shortly after entering a convection-shutdown regime. During this period, it can be concluded that spatial fluctuations of CO2 concentration about its mean value will gradually vanish as CO2 begins to saturate the entire domain. This implies a mixing degree that will finally increase to unity at the perfect mixing state, though with dissipative rates. To obtain an estimate of the maximum value of
or σz reach their maximum values, above which they plateau, shortly after entering a convection-shutdown regime. During this period, it can be concluded that spatial fluctuations of CO2 concentration about its mean value will gradually vanish as CO2 begins to saturate the entire domain. This implies a mixing degree that will finally increase to unity at the perfect mixing state, though with dissipative rates. To obtain an estimate of the maximum value of  , we can assume a constant and spatially invariant non-zero C(x, z, t) throughout the domain and analytically solve the integral in Eq. (8). This results in
, we can assume a constant and spatially invariant non-zero C(x, z, t) throughout the domain and analytically solve the integral in Eq. (8). This results in  m2, i.e. close to the values observed in Fig. 4a (higher values are partly due to compressibility as the pressure increases).
m2, i.e. close to the values observed in Fig. 4a (higher values are partly due to compressibility as the pressure increases).
Additional Information
How to cite this article: Soltanian, M. R. et al. Critical Dynamics of Gravito-Convective Mixing in Geological Carbon Sequestration. Sci. Rep. 6, 35921; doi: 10.1038/srep35921 (2016).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Moortgat, J., Li, Z. & Firoozabadi, A. Three-phase compositional modeling of CO2 injection by higher-order finite element methods with CPA equation of state for aqueous phase. Water Resour. Res. 48 (2012).
Bachu, S., Gunter, W. & Perkins, E. Aquifer disposal of CO2: hydrodynamic and mineral trapping. Energ. Convers. and Manage. 35, 269–279 (1994).
Deng, H., Stauffer, P. H., Dai, Z., Jiao, Z. & Surdam, R. C. Simulation of industrial-scale CO2 storage: Multi-scale heterogeneity and its impacts on storage capacity, injectivity and leakage. Int. J. Greenh. Gas Control. 10, 397–418 (2012).
Dai, Z. et al. Pre-site characterization risk analysis for commercial-scale carbon sequestration. Environ. Sci. Technol. 48, 3908–3915 (2014).
Dai, Z. et al. An integrated framework for optimizing CO2 sequestration and enhanced oil recovery. Environ. Sci. Technol. Lett . 1, 49–54 (2013).
Agartan, E. et al. Experimental study on effects of geologic heterogeneity in enhancing dissolution trapping of supercritical CO2 . Water Resour. Res. 51, 1635–1648 (2015).
Islam, A., Sun, A. Y. & Yang, C. Reactive transport modeling of the enhancement of density-driven CO2 convective mixing in carbonate aquifers and its potential implication on geological carbon sequestration. Sci. Rep. 6 (2016).
Yang, C. et al. Regional assessment of CO2–solubility trapping potential: A case study of the coastal and offshore Texas Miocene Interval. Environ. Sci. Technol. 48, 8275–8282 (2014).
Gershenzon, N. I. et al. Influence of small-scale fluvial architecture on CO2 trapping processes in deep brine reservoirs. Water Resour. Res. 51, 8240–8256 (2015).
Juanes, R., Spiteri, E., Orr, F. & Blunt, M. Impact of relative permeability hysteresis on geological CO2 storage. Water Resour. Res. 42 (2006).
Lichtner, P. & Karra, S. Modeling multiscale-multiphase-multicomponent reactive flows in porous media: Application to CO2 sequestration and enhanced geothermal energy using PFLOTRAN. Computational Models for CO2 Geo-sequestration & Compressed Air Energy Storage 81–136 (2014).
Hidalgo, J. J., Dentz, M., Cabeza, Y. & Carrera, J. Dissolution patterns and mixing dynamics in unstable reactive flow. Geophys. Res. Lett. 42, 6357–6364 (2015).
Riaz, A., Hesse, M., Tchelepi, H. & Orr, F. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111 (2006).
Pau, G. S. et al. High-resolution simulation and characterization of density-driven flow in CO2 storage in saline aquifers. Adv. Water Resour. 33, 443–455 (2010).
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. Scaling behavior of convective mixing, with application to geological storage of CO2 . AlChE J. 53, 1121–1131 (2007).
Lu, C. & Lichtner, P. C. High resolution numerical investigation on the effect of convective instability on long term CO2 storage in saline aquifers. In JPCS, vol. 78 (IOP Publishing, 2007).
Neufeld, J. A. et al. Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37 (2010).
Shahraeeni, E., Moortgat, J. & Firoozabadi, A. High-resolution finite element methods for 3D simulation of compositionally triggered instabilities in porous media. Comput. Geosci. 19, 899–920 (2015).
Pruess, K. Numerical modeling studies of the dissolution-diffusion-convection process during CO2 storage in saline aquifers. LBNL (2008).
Ambrose, W. et al. Geologic factors controlling CO2 storage capacity and permanence: case studies based on experience with heterogeneity in oil and gas reservoirs applied to CO2 storage. Environ. Geol. 54, 1619–1633 (2008).
Jensen, J. L. & Lake, L. W. The influence of sample size and permeability distribution on heterogeneity measures. SPE Reservoir Eng. 3, 629–637 (1988).
Emami-Meybodi, H., Hassanzadeh, H., Green, C. P. & Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control. 40, 238–266 (2015).
Farajzadeh, R., Ranganathan, P., Zitha, P. L. J. & Bruining, J. The effect of heterogeneity on the character of density-driven natural convection of CO2 overlying a brine layer. Adv. Water Resour. 34, 327–339 (2011).
Ranganathan, P., Farajzadeh, R., Bruining, H. & Zitha, P. L. Numerical simulation of natural convection in heterogeneous porous media for CO2 geological storage. Transport Porous Med. 95, 25–54 (2012).
Kong, X.-Z. & Saar, M. O. Numerical study of the effects of permeability heterogeneity on density-driven convective mixing during CO2 dissolution storage. Int. J. Greenh. Gas Control. 19, 160–173 (2013).
Daniel, D., Riaz, A. & Tchelepi, H. A. Onset of natural convection in layered aquifers. J. Fluid Mech. 767, 763–781 (2015).
Frykman, P. & Wessel-Berg, D. Dissolution trapping-convection enhancement limited by geology. Energy Procedia. 63, 5467–5478 (2014).
Green, C. P. & Ennis-King, J. Effect of vertical heterogeneity on long-term migration of CO2 in saline formations. Transport Porous Med. 82, 31–47 (2010).
Gershenzon, N., Soltanian, M., Ritzi, R. W. & Dominic, D. F. Understanding the impact of open-framework conglomerates on water–oil displacements: the Victor interval of the Ivishak Reservoir, Prudhoe Bay Field, Alaska. Pet. Geosci. 21, 43–54 (2015).
Lunt, I., Bridge, J. & Tye, R. A quantitative, three-dimensional depositional model of gravelly braided rivers. Sedimentology 51, 377–414 (2004).
Lu, J. et al. Complex fluid flow revealed by monitoring CO2 injection in a fluvial formation. J. Geophys. Res. 117 (2012).
Gershenzon, N. I., Soltanian, M. R., Ritzi, R. W. & Dominic, D. F. Influence of small scale heterogeneity on CO2 trapping processes in deep saline aquifers. Energy Procedia. 59, 166–173 (2014).
Willis, B. J. & White, C. D. Quantitative outcrop data for flow simulation. J. Sediment. Res. 70, 788–802 (2000).
Koltermann, C. E. & Gorelick, S. M. Heterogeneity in sedimentary deposits: A review of structure-imitating, process-imitating, and descriptive approaches. Water Resour. Res. 32, 2617–2658 (1996).
Li, Z. & Firoozabadi, A. Cubic-plus-association equation of state for water-containing mixtures: Is “cross association” necessary? AIChE J. 55, 1803–1813 (2009).
Li, Z. & Firoozabadi, A. General strategy for stability testing and phase-split calculation in two and three phases. SPE J. 17, 1–096 (2012).
Hidalgo, J. J., Carrera, J. & Medina, A. Role of salt sources in density-dependent flow. Water Resour. Res. 45 (2009).
Massabó, M., Bellin, A. & Valocchi, A. Spatial moments analysis of kinetically sorbing solutes in aquifer with bimodal permeability distribution. Water Resour. Res. 44 (2008).
Carle, S. F. T-PROGS: Transition probability geostatistical software. University of California, Davis, CA (1999).
Stauffer, D. & Aharony, A. Introduction to percolation theory (CRC press, 1994).
Sudicky, E. A. A natural gradient experiment on solute transport in a sand aquifer: Spatial variability of hydraulic conductivity and its role in the dispersion process. Water Resour. Res. 22, 2069–2082 (1986).
Dagan, G. Flow and transport in porous formations (Springer Science & Business Media, 1989).
Soltanian, M. R., Ritzi, R. W., Huang, C. C. & Dai, Z. Relating reactive solute transport to hierarchical and multiscale sedimentary architecture in a Lagrangian-based transport model: 2. Particle displacement variance. Water Resour. Res. 51, 1601–1618 (2015).
Lapwood, E. R. Convection of a fluid in a porous medium. Math. Proc. Cambridge Philos. Soc. 44, 508–521 (1948).
Einstein, A. Über die von der molekularkinetischen theorie der wärme geforderte bewegung von in ruhenden flüssigkeiten suspendierten teilchen. Annalen der physik 322, 549–560 (1905).
Slim, A. C. & Ramakrishnan, T. Onset and cessation of time-dependent, dissolution-driven convection in porous media. Phys. Fluids. 22, 124103 (2010).
Ennis-King, J. P. & Paterson, L. Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. SPE J. 10, 349–356 (2005).
Le Borgne, T. et al. Persistence of incomplete mixing: A key to anomalous transport. Phys. Rev. E. 84, 015301 (2011).
Batchelor, G. K. An Introduction to Fluid Dynamics (Cambridge University Press, 2000).
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. Scaling of Convective Mixing in Porous Media. Phys. Rev. Lett. 109, 264503 (2012).
Szulczewski, M., Hesse, M. & Juanes, R. Carbon dioxide dissolution in structural and stratigraphic traps. J. Fluid Mech. 736, 287–315 (2013).
Renard, P. & Allard, D. Connectivity metrics for subsurface flow and transport. Adv. Water Resour. 51, 168–196 (2013).
Le Borgne, T., Dentz, M. & Carrera, J. Lagrangian statistical model for transport in highly heterogeneous velocity fields. Phys. Rev. Lett. 101, 090601 (2008).
Moortgat, J. Viscous and gravitational fingering in multiphase compositional and compressible flow. Adv. Water Resour. (2016).
Moortgat, J. & Firoozabadi, A. Fickian diffusion in discrete-fractured media from chemical potential gradients and comparison to experiment. Energy Fuels. 27, 5793–5805 (2013).
Acs, G., Doleschall, S. & Farkas, E. General purpose compositional model. SPE J. 25, 543–553 (1985).
Moortgat, J. B. & Firoozabadi, A. Three-phase compositional modeling with capillarity in heterogeneous and fractured media. SPE J. 18, 1–150 (2013).
Aris, R. On the dispersion of a solute in a fluid flowing through a tube. In Proc. Math. Phys. Eng. Sci., vol. 235, 67–77 (The Royal Society, 1956).
Freyberg, D. A natural gradient experiment on solute transport in a sand aquifer: 2. Spatial moments and the advection and dispersion of nonreactive tracers. Water Resour. Res. 22, 2031–2046 (1986).
Kitanidis, P. K. The concept of the Dilution index. Water Resour. Res. 30, 2011–2026 (1994).
Acknowledgements
The first author was supported by the U.S. Department of Energy’s (DOE) Office of Fossil Energy funding to Oak Ridge National Laboratory (ORNL) under project FEAA-045. ORNL is managed by UT-Battelle for the U.S. DOE under Contract DE-AC05-00OR22725.
Author information
Authors and Affiliations
Contributions
M.R.S. designed and carried out the simulations, performed data analysis. M.R.S. and M.A.A. wrote the draft manuscript. M.A.A. and J.M. helped on model development and parameter characterization. D.C. and Z.D. helped in manuscript preparation. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Soltanian, M., Amooie, M., Dai, Z. et al. Critical Dynamics of Gravito-Convective Mixing in Geological Carbon Sequestration. Sci Rep 6, 35921 (2016). https://doi.org/10.1038/srep35921
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep35921
This article is cited by
-
Carbon dioxide sequestration in underground formations: review of experimental, modeling, and field studies
Journal of Petroleum Exploration and Production Technology (2021)
-
Potential of \(\hbox {CO}_{2}\) based geothermal energy extraction from hot sedimentary and dry rock reservoirs, and enabling carbon geo-sequestration
Geomechanics and Geophysics for Geo-Energy and Geo-Resources (2020)
-
Assessment of Trapping Mechanisms of CO2 Sequestration and Optimization of Key Process Parameters in a Deep Saline Aquifer Using Reservoir Simulation and Response Surface Methodology
Arabian Journal for Science and Engineering (2019)
-
Hydro-dynamic Solute Transport under Two-Phase Flow Conditions
Scientific Reports (2017)
-
A method to generate small-scale, high-resolution sedimentary bedform architecture models representing realistic geologic facies
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.








 ). This first flow regime is observed in all homogeneous cases and as long as Rayleigh numbers are small, diffusion-dominated transport is insensitive to permeability (and for nearly constant μ and D and small Δρmax, also independent of Ra). Interestingly, while the total amount of introduced CO2 increases linearly with time (due to constant injection rate), the driver for advective buoyant flow, Δρmax, also follows Fickian ~t0.5 scaling until it has increased sufficiently to trigger gravitational instabilities (
). This first flow regime is observed in all homogeneous cases and as long as Rayleigh numbers are small, diffusion-dominated transport is insensitive to permeability (and for nearly constant μ and D and small Δρmax, also independent of Ra). Interestingly, while the total amount of introduced CO2 increases linearly with time (due to constant injection rate), the driver for advective buoyant flow, Δρmax, also follows Fickian ~t0.5 scaling until it has increased sufficiently to trigger gravitational instabilities (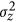 and σz (
and σz ( , and the critical time tc in
, and the critical time tc in 
