Abstract
Galaxy mergers produce supermassive black hole binaries, which emit gravitational waves prior to their coalescence. We perform three-dimensional hydrodynamic simulations to study the tidal disruption of stars by such a binary in the final centuries of its life. We find that the gas stream of the stellar debris moves chaotically in the binary potential and forms accretion disks around both black holes. The accretion light curve is modulated over the binary orbital period owing to relativistic beaming. This periodic signal allows to detect the decay of the binary orbit due to gravitational wave emission by observing two tidal disruption events that are separated by more than a decade.
Similar content being viewed by others
Introduction
Most galaxies are inferred to harbor supermassive black holes (SMBHs) with masses in the range of  at their centers1,2, based on observations of stellar proper motion3, stellar velocity dispersion4 or accretion luminosity5. Most of time, their nuclei do not exhibit significant activities6, but in a small fraction of all galaxies the inflow of cold gas triggers active galactic nuclei (AGNs) which produce intense radiation and powerful outflows. Tidal disruption events (TDEs) provide a distinct opportunity to probe dormant SMBHs in inactive galaxies (see a recent general review7).
at their centers1,2, based on observations of stellar proper motion3, stellar velocity dispersion4 or accretion luminosity5. Most of time, their nuclei do not exhibit significant activities6, but in a small fraction of all galaxies the inflow of cold gas triggers active galactic nuclei (AGNs) which produce intense radiation and powerful outflows. Tidal disruption events (TDEs) provide a distinct opportunity to probe dormant SMBHs in inactive galaxies (see a recent general review7).
SMBH binaries with a sub-parsec ( ) separation are considered to be the end product of a galaxy merger before two black holes finally coalesce8,9. The merger of two SMBHs goes through the following processes10: first, the SMBHs sink towards each other via dynamical friction on the surrounding stars and gas. Once their separation drops below a parsec, a hard binary forms11 and tightens further due to other mechanisms12,13 until gravitational wave emission takes over at the final stage14.
) separation are considered to be the end product of a galaxy merger before two black holes finally coalesce8,9. The merger of two SMBHs goes through the following processes10: first, the SMBHs sink towards each other via dynamical friction on the surrounding stars and gas. Once their separation drops below a parsec, a hard binary forms11 and tightens further due to other mechanisms12,13 until gravitational wave emission takes over at the final stage14.
The observed TDE rate on single SMBHs is ~10−5 yr−1 per galaxy15,16, although another recent survey suggests that the rate could be one-order of magnitude higher17. This higher rate has been implied by the recent theoretical works based on two-body relaxation18,19. However, SMBH binaries are expected to exhibit an enhanced TDE rate of up to 10−1 yr−1 from chaotic orbital evolution and the Kozai-Lidov effect20,21,22. Recent work suggests that multiple TDEs may occur in merging SMBH binaries with a rate of up to a few times over an observing period of five years with the Large Synoptic Survey Telescope (LSST, http://www.lsst.org)23. It is less clear what characteristic flares such TDEs would exhibit, although interruptions in the light curve are likely if the orbital period of SMBH binaries is less than the period of an observable emission24,25,26.
If the binding energy of the approaching star relative to either component of the binary is negative inside the tidal disruption radius, the star should be finally tidally disrupted. Here, we study how stars migrating through the binary Lagrange points are tidally disrupted by the SMBHs. In Section 2, we describe the numerical method used in our simulations of these TDEs. We then analyze our numerical results in Section 3. Finally, we summarize our main conclusions in Section 4.
Methods
Test-particle limit
We consider a system composed of a star orbiting around a circular SMBH binary with mass ratio q = M2/M1 = 0.1. The initial position and velocity in our simulation are correspondingly the Lagrange point L2 and the Keplerian velocity there. This situation would be, for example, realized in the case of a massive circumbinary disk27, where the disk makes stars migrate inwards and approach the Lagrange points around the binary (L2 or L3) via a mass stream from the disk’s inner edge28. The dynamics of the star can be treated as a restricted three-body problem. We solve numerically the motion of the star as a test particle in the binary potential.
In the test-particle limit, the star is initially located just inside the L2 point with a Keplerian velocity, and then is trapped by the binary potential and freely moves between two black holes inside the inner Roche-lobe of the binary. The outside of the inner lobe is marked by the shaded area of Fig. 1 as the forbidden zone29. The star is tidally disrupted once it enters the tidal disruption radius:
Orbit of a test particle in a co-rotating frame around a circular binary with M2/M1 = 0.1.
The red and blue circles shows the tidal disruption radii around the primary and secondary black holes, respectively. The three black crosses mark the Lagrange points, L1, L2, and L3. Both axes are normalized by the binary semi-major axis. The black solid line shows the motion of a test particle inside the zero-velocity curve for a Jacobi constant CJ = 3.45, and the shaded area outside the curve denotes the forbidden zone29.

where MBH is the SMBH mass, m* and r* are the star’s mass and radius, and rS = 2GMBH/c2 is the Schwarzschild radius. The corresponding orbit is depicted in Fig. 1. The fate of the tidally disrupted star is similar to that of an eccentric TDE30, in which the TDE accretion rate deviates significantly from the standard t−5/3 time evolution31,32.
SPH simulations
Our simulations are performed with a three-dimensional Smoothed Particle Hydrodynamics (SPH) code33. The hydrodynamic equations are integrated using a second-order Runge-Kutta-Fehlberg integrator with individual time steps for each particle, leading to substantial savings in time for a large dynamic range of timescales. We also use a variable smoothing length scheme to find the relevant spatial resolution in our code, but ignore the term proportional to the gradient of the smoothing length. We adopt standard the SPH artificial viscosity parameters αSPH = 1 and βSPH = 2.
The photon diffusion timescale of the stellar debris is given by

where H is the debris scale height and τ = κesΣ ~ 2.6 × 106 (Σ/Σ0) is the optical depth for electron scattering with κes = 0.4 cm2 g−1, and Σ is surface density of the stellar debris with the fiducial value of

where r and Δr are the radius and width of the debris ring. Recent three-dimensional radiation magneto-hydrodynamic simulations showed that the magnetic buoyancy induced through the magneto-rotational instability (MRI)34 provides an efficient radiative cooling mechanism for super-Eddington accretion flows35. In this regime, their preliminary simulations indicate that the radiative cooling speed is determined by the sound speed of the radiation. In our simulation, the stellar debris loses its orbital energy and then circularizes via a shock into an accretion flow at a super-Eddington rate at ~rt. The initial radiation energy density is  , where ρ0 = Σ0/rt and
, where ρ0 = Σ0/rt and  , and so the radiation sound speed is estimated to be
, and so the radiation sound speed is estimated to be  . Thus, the resulting cooling timescale rt/cs,rad is estimated to be ~2.8 × 103 s, shorter than the heating timescale by the shock
. Thus, the resulting cooling timescale rt/cs,rad is estimated to be ~2.8 × 103 s, shorter than the heating timescale by the shock  . It takes several dynamical times for the magnetic field to grow via the MRI, after which the efficient cooling reduces the thickness of the debris streams. Thus, we use a simple polytropic equation of state: P = Kργ, where P and ρ are the gas pressure and density, γ = 5/3 and K is a constant. This ensures that the radiative cooling is efficient throughout our simulation.
. It takes several dynamical times for the magnetic field to grow via the MRI, after which the efficient cooling reduces the thickness of the debris streams. Thus, we use a simple polytropic equation of state: P = Kργ, where P and ρ are the gas pressure and density, γ = 5/3 and K is a constant. This ensures that the radiative cooling is efficient throughout our simulation.
We model the initial star as a polytrope with the polytrope index n = 1.5 in hydrostatic equilibrium. The star is set in motion through the gravitational field of the SMBH binary with the following parameters:  ,
,  ,
,  , a = 100rS, and q = 0.1. The simulations follow 0.5 million SPH particles for 14 binary orbital periods, where a single period Porb ~ 1 day.
, a = 100rS, and q = 0.1. The simulations follow 0.5 million SPH particles for 14 binary orbital periods, where a single period Porb ~ 1 day.
Results
Tidal disruption of a star
Figure 2 shows the evolutionary sequence of density maps for the stellar debris of a TDE around the SMBH binary. A star approaching the binary from the L2 point is tidally disrupted by the secondary black hole. Part of the stellar debris is not gravitationally bound, while the rest accretes onto the secondary SMBH. The unbound debris moves chaotically in the binary potential and forms accretion disks around both black holes by transferring mass along the potential valley through the L1 point.
Gas density maps, projected on the orbital (x-y) plane, during a tidal disruption event in a circular SMBH binary with  , a = 100rS, and q = 0.1. The run time t is in units of Porb as labeled in the top-right corner of each panel. The number of SPH particles is indicated at the bottom-right corner. The panels are shown in chronological order. The coloration indicates the density in five orders of magnitude on a logarithmic scale normalized by Σ0 = 6.5 × 106 g cm−2. The dashed circles indicate the tidal disruption radii for the primary and secondary SMBHs.
, a = 100rS, and q = 0.1. The run time t is in units of Porb as labeled in the top-right corner of each panel. The number of SPH particles is indicated at the bottom-right corner. The panels are shown in chronological order. The coloration indicates the density in five orders of magnitude on a logarithmic scale normalized by Σ0 = 6.5 × 106 g cm−2. The dashed circles indicate the tidal disruption radii for the primary and secondary SMBHs.
The resulting mass accretion rates are shown in Fig. 3A. The green and red dotted lines show the bolometric light curves of the primary and secondary black holes, respectively. The luminosities are derived as  with i = 1, 2, where
with i = 1, 2, where  and
and  are the mass accretion rates of the primary and secondary black holes based on the simulation. The accretion rates are estimated at the radius of the innermost stable circular orbit of a Schwarzschild black hole, 3rS. The black and blue lines show the bolometric light curves, including the relativistic doppler beaming effect due to the orbital motion of the binary36,
are the mass accretion rates of the primary and secondary black holes based on the simulation. The accretion rates are estimated at the radius of the innermost stable circular orbit of a Schwarzschild black hole, 3rS. The black and blue lines show the bolometric light curves, including the relativistic doppler beaming effect due to the orbital motion of the binary36,
(A) Bolometric luminosity of the primary (black and green) and secondary (red and blue) black holes normalized by its maximum value Lmax = max{Lo,1 + Lo,2}. The black and blue lines include relativistic beaming. (B) Power Spectrum of the bolometric light curves with relativistic beaming as a function of frequency ω in units of Ωorb = 2π/Porb. The blue solid line shows the power spectrum of the first TDE, and the red dashed line shows that of the second TDE 50 years later. The half maximum full-width are given by 0.05240 ± 0.000563 with a fixed peak position 0.99027. If the two peaks are sampled by N data points, it should be possible to separate them even after a time interval of  years. (C) Inclination angle dependence of the maximum value of L2/Lo,2. The dashed, dot-dashed, dotted lines are the ones corresponding to 1 to 3 σ of the fluctuations in Lo,2.
years. (C) Inclination angle dependence of the maximum value of L2/Lo,2. The dashed, dot-dashed, dotted lines are the ones corresponding to 1 to 3 σ of the fluctuations in Lo,2.

where  and
and  are the Lorentz factor and the orbital speed, respectively, and
are the Lorentz factor and the orbital speed, respectively, and

with  being the orbital frequency and θ being the inclination angle between the line-of-sight and the binary orbital plane, which is assumed to be π/2 in the current simulation. Note that
being the orbital frequency and θ being the inclination angle between the line-of-sight and the binary orbital plane, which is assumed to be π/2 in the current simulation. Note that  intrinsically shows the bursty nature and is more than one order of magnitude smaller than
intrinsically shows the bursty nature and is more than one order of magnitude smaller than  , since the angular momentum of the stellar debris relative to the primary black hole is much larger than that of the secondary black hole. In addition, the periodicity of the bolometric light curves of the secondary black hole is enhanced by relativistic beaming.
, since the angular momentum of the stellar debris relative to the primary black hole is much larger than that of the secondary black hole. In addition, the periodicity of the bolometric light curves of the secondary black hole is enhanced by relativistic beaming.
Figure 3B shows the power spectrum of the total light curve with relativistic beaming. The blue solid and red dashed lines mark the simulated and predicted power spectra, respectively. The blue line indicates a sharp peak at the binary orbital frequency. Since the full-width at half maximum of the peak is ~0.052Ωorb, the shift of the peak over time due to orbital decay should be larger than ±0.052Ωorb in order to be easily noticeable. For a fiducial TDE rate of ~0.02 per year, a second TDE would likely occur 50 years after the first TDE, and the shift in the power spectrum due to the orbital decay by gravitational wave emission will be noticeable, as shown by the red dashed line of the figure. If the peak is sampled by N data points, then the shift in the peak would be detectable over a period shorter by  . Our simulation implies that it would be possible to measure the orbital decay by gravitational wave emission through the shift of the peak in the power spectrum.
. Our simulation implies that it would be possible to measure the orbital decay by gravitational wave emission through the shift of the peak in the power spectrum.
Figure 3C shows the dependence on the inclination angle, θ, of the amplitude of relativistic doppler boosting relative to the amplitude of the original bolometric light variation emitted from the secondary black hole. The black line represents L2/Lo,2 (see equation 4), whereas the dashed, dash-dotted, and dotted lines represent the amplitudes corresponding to 3σ, 2σ, and 1σ of the fluctuating Lo,2, respectively. The panel indicates that the periodic signal corresponds to 3σ detection if  .
.
Shift in the binary orbital period
The feasibility of detecting the shift in the peak of the power spectrum depends primarily on the semi-major axis of the binary at the first TDE. We consider a circular binary whose coalescence timescale due to gravitational wave emission is given by37,

Setting a0 and a as the semi-major axes of the binary at the first and second TDEs, respectively, the time difference between two TDEs, Δtgw, needs to satisfy the condition that the normalized frequency is significantly increased, namely

Thus, the upper limit on a value of semi-major axis a0 is,

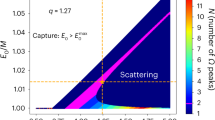
Figure 4A shows the dependence of a0 on Ωorb/Ωorb,0. The blue and red solid lines denote a0 if Δtgw is given by 10 and 50 years, respectively. The black dashed line shows the tidal disruption radius rt below which the binary can be regarded as a single black hole (see equation 1). The range of the semi-major axis at the first TDE, which is detectable, is shown by the shaded area.
(A) Dependence of the semi-major axis at the first TDE, a0, on the orbital frequency at the second TDE, normalized by the orbital frequency at the first TDE, for  . The blue and red solid lines show a0 if the time difference between the first and second TDEs is given by 10 and 50 years, respectively (see equation 8). The black dashed line shows the tidal disruption radius rt below which the binary can be regarded as a single black hole (see equation 1). (B) Dependence of the decoupling radius on black hole mass. The red, blue and black dashed lines show the decoupling radius, fiducial semi-major axis, and tidal disruption radius, respectively.
. The blue and red solid lines show a0 if the time difference between the first and second TDEs is given by 10 and 50 years, respectively (see equation 8). The black dashed line shows the tidal disruption radius rt below which the binary can be regarded as a single black hole (see equation 1). (B) Dependence of the decoupling radius on black hole mass. The red, blue and black dashed lines show the decoupling radius, fiducial semi-major axis, and tidal disruption radius, respectively.
Summary and Discussion
We have simulated the tidal disruption of a star by a circular SMBH binary with a 1:10 mass ratio. Our simulation indicates that the mass accretion rate of the secondary black hole is higher than that of the primary black hole. The resulting total bolometric luminosity shows a strong relativistic beaming effect due to the enhanced line-of-sight velocity of the secondary black hole. Therefore, the power spectrum naturally shows a sharp peak at the orbital frequency (see Fig. 3B).
Interaction with a circumbinary disk
If the SMBH binaries are located in a gas-rich environment, a circumbinary disk can be the agent supplying the stars. Accretion disks around SMBHs are predicted to be gravitationally unstable at large radii where they fragment into stars or planets owing to their self-gravity38,39,40. Similarly, a circumbinary disk could form stars in its outskirts. Hence, a self-gravitating circumbinary disk would naturally lead to be an enhanced TDE rate27. In addition, a circumbinary disk could grind the orbits of background stars and trigger additional TDEs41,42. Through both mechanisms, stars would migrate to the inner edge of the circumbinary disk, and subsequently approach both black holes through the Lagrange points (L2 or L3) of the binary.
When tgw is shorter than the viscous timescale evaluated at the inner edge of the circumbinary disk, the binary is viscously decoupled from the circumbinary disk43. The viscous timescale measured at the inner edge of the circumbinary disk is given by tvis = r2/ν with the inner radius being ~2a44, where the disk viscosity ν = αSScsH, expressed in terms of the sound speed cs and the Shakura-Sunyaev viscosity parameter αSS. Based on the assumption that the circumbinary disk is a standard disk, the decoupling radius is obtained by equating tvis to tgw, giving

where cs,0 ~ 1.7 × 108 cm s−1 is the sound speed for typical parameters. Figure 4B shows the black-hole mass dependence of the decoupling radius. The decoupling radius is clearly larger than the fiducial semi-major axis afid = 100rS of our simulation for  .
.
Recent numerical simulations show that the rate of gas accretion from the circumbinary disk is modulated by the orbital period45,46. Detection of the orbital decay based on the shift in the power spectrum of the light curves can also, in principle, be inferred in such a system. However, if the semi-major axis of the binary is larger than the decoupling radius, the shift of power spectrum is undetectable because it is too small to be identified observationally (Ωorb/Ωorb,0 < 1.01 in Fig. 4A). This implies that only periodic signals caused by tidal disruption events around the SMBH binaries with the semi-major axis shorter than the decoupling radius can provide a detectable shift in the power spectrum.
The TDE flares are attributed to super-Eddington accretion phases of short duration47,48. They differ from a sub-Eddington accretion mode which may last much longer, as illustrated in Fig. 3 of Farris et al.49. The surface density of the stellar debris in our simulations is many orders of magnitude higher than that of a sub-Eddington accretion flow. We therefore expect that any pre-existing accretion disk would not affect significantly the dynamics of the debris.
The TDE rate for a binary SMBH system is dictated by the supply rate of stars from the outer region of the circumbinary disk to the inner cavity. The formation rate of the solar mass stars is estimated to be of order  in the self-gravitating accretion disk40. If the stars can induce gap formation in the disk, they would migrate on a timescale that cannot be shorter than the Eddington accretion timescale as they are coupled to the viscous evolution of the disk. In this case, the expected TDE rate ranges between 0.01 yr−1 and the Eddington rate,
in the self-gravitating accretion disk40. If the stars can induce gap formation in the disk, they would migrate on a timescale that cannot be shorter than the Eddington accretion timescale as they are coupled to the viscous evolution of the disk. In this case, the expected TDE rate ranges between 0.01 yr−1 and the Eddington rate,  , where
, where  is the mass-to-radiation conversion efficiency. On the other hand, the rate at which the orbits of disk-crossing stars are brought into the inner cavity could also be controlled by the hydrodynamic drag force acting on the trapping stars42,50. In this case, stars of a solar mass should migrate to the inner cavity on the radial drift timescale
is the mass-to-radiation conversion efficiency. On the other hand, the rate at which the orbits of disk-crossing stars are brought into the inner cavity could also be controlled by the hydrodynamic drag force acting on the trapping stars42,50. In this case, stars of a solar mass should migrate to the inner cavity on the radial drift timescale  for the relatively massive, geometrically thin disk, where Rd and H are the disk radius and scale-height50. Therefore, the expected TDE rate is suppressed by the radial drift timescale down to
for the relatively massive, geometrically thin disk, where Rd and H are the disk radius and scale-height50. Therefore, the expected TDE rate is suppressed by the radial drift timescale down to  .
.
Detectability of the events
The light curve of the radiation emitted by the jet, whose flux is proportional to the mass accretion rate obtained in our simulation, would make it possible to distinguish a binary TDE from the usual emission in AGNs based on the following characteristics: 1. the angle between the line of sight and jet direction should change transiently for a TDE, even if there is steady feeding of the black hole. 2. the jetted emission shows clear periodicity during several tens of binary orbital periods.
LSST would be ideally suited for identifying candidate source for follow-up monitoring that will seek our predicted periodic signal. Given that a typical galaxy undergoes a merger with a mass ratio 1:10 once every ~1 Gyr51, the probability for finding a corresponding SMBH binary in the last century of its life before coalescence is ~(102 yr/109 yr) ~ 10−7. Since the LSST will survey 3.7 × 1010 galaxies for variability during its 10 year operation (http://www.lsst.org), it is expected to find  events. In order to obtain the 3 sigma detection of the periodicity by relativistic doppler boosting, we multiply the above number by the factor
events. In order to obtain the 3 sigma detection of the periodicity by relativistic doppler boosting, we multiply the above number by the factor  , where dS = 2π sin θdθ is the differential solid angle for θ direction, from Fig. 4C. Therefore, we expect to detect
, where dS = 2π sin θdθ is the differential solid angle for θ direction, from Fig. 4C. Therefore, we expect to detect  signals from the SMBH binaries with a detectable shift over a period of 10 year.
signals from the SMBH binaries with a detectable shift over a period of 10 year.
Additional Information
How to cite this article: Hayasaki, K. and Loeb, A. Detection of Gravitational Wave Emission by Supermassive Black Hole Binaries Through Tidal Disruption Flares. Sci. Rep. 6, 35629; doi: 10.1038/srep35629 (2016).
References
Kormendy, J. & Richstone, D. Inward bound—the search for supermassive black holes in galactic nuclei. Annu. Rev. Astron. Astrophys. 33, 581–624 (1995).
Kormendy, J. & Ho, L. C. Coevolution (or not) of supermassive black holes and host galaxies. Annu. Rev. Astron. Astrophys. 51, 511–653 (2013).
Schödel, R. et al. A star in a 15.2 year orbit around the supermassive black hole at the centre of the Milky Way. Nature 419, 694–696 (2002).
Magorrian, J. et al. The demography of massive dark objects in galaxy centers. Astron. J. 115, 2285–2305 (1998).
Miyoshi, M. et al. Evidence for a black hole from high rotation velocities in a sub-parsec region of NGC4258. Nature 373, 127–129 (1995).
Genzel, R. et al. Near-infrared flares from accreting gas around the supermassive black hole at the galactic centre. Nature 425, 934–937 (2003).
Komossa, S. Tidal disruption of stars by supermassive black holes: Status of observations. arXiv:1505.01093 (2015).
Sillanpää, A. et al. OJ 287 - Binary pair of supermassive black holes. Astrophys. J. 325, 628–634 (1988).
Graham, M. J. et al. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 518, 74–76 (2015).
Begelman, M. C., Blandford, R. D. & Rees, M. J. Massive black hole binaries in active galactic nuclei. Nature, 287, 307–309 (1980).
Mayer, L. et al. Rapid formation of supermassive black hole binaries in galaxy mergers with gas. Science 316, 1874–1877 (2007).
Ivanov P. B., Papaloizou J. C. B. & Polnarev A. G. The evolution of a supermassive binary caused by an accretion disc. Mon. Not. R. Astron. Soc. 307, 79 (1999).
Hayasaki, K. A new mechanism for massive binary black-hole evolution. Publ. Astron. Soc. J. 61, 65–74 (2009).
Colpi, M. & Dotti, M. Massive binary black holes in the cosmic landscape. Advanced Science Letters 4, 181–203 (2011).
Donley, J. L., Brandt, W. N., Eracleous, M. & Boller, T. Large-amplitude X-ray outbursts from galactic nuclei: a systematic survey using ROSAT archival data. Astron. J. 124, 1308–1321 (2002).
Velzen, S. & Farrar, G. R. Measurement of the rate of stellar tidal disruption flares. Astrophys. J. 792, 53–62 (2014).
Holoien, T. W.-S. et al. Six months of multi-wavelength follow-up of the tidal disruption candidate ASASSN-14li and implied TDE rates from ASAS-SN. arXiv:1507.01598 (2015).
Stone, N. C. & Metzger, B. D. Rates of stellar tidal disruption as probes of the supermassive black hole mass function. arXiv:1410.7772 (2014).
Wang, J. & Merritt, D. Revised rates of stellar disruption in galactic nuclei. Astrophys. J. 600, 149–161 (2004).
Ivanov, P. B., Polnarev, A. G. & Saha, P. The tidal disruption rate in dense galactic cusps containing a supermassive binary black hole. Mon. Not. R. Astron. Soc. 358, 1361–1378 (2005).
Chen, X., Madau, P., Sesana, A. & Liu, F. K. Enhanced tidal disruption rates from massive black hole binaries. Astrophys. J. 697, L149–L152 (2009).
Gongjie, L., Smadar, N., Kocsis, B. & Loeb, A. Implications of the eccentric Kozai-Lidov mechanism for stars surrounding supermassive black hole binaries. Mon. Not. R. Astron. Soc. 451, 1341–1349 (2015).
Wegg, C. & Bode, J. N. Multiple tidal disruptions as an Indicator of binary supermassive black hole systems. Astrophys. J. 738, L8–L14 (2011).
Liu, F. K., Li, S. & Chen, X. Interruption of tidal-disruption flares by supermassive black hole binaries. Astrophys. J. 706, L133–L137, (2009).
Liu, F. K., Li, S. & Komossa, S. A Milliparsec supermassive black hole binary candidate in the galaxy SDSS J120136.02 + 300305.5. Astrophys. J., 786, 103–117 (2014).
Ricarte, A., Natarajan, P., Dai, L. & Coppi, P. Tidal disruption events by a massive black hole binary. arXiv:1510.04693 (2015).
Amaro-Seoane, P., Brem, P. & Cuadra, J. Tidal disruptions in circumbinary disks. I. star formation, dynamics, and binary evolution. Astrophys. J. 764, 14–23 (2013).
Hayasaki, K., Mineshige, S. & Sudou, H. Binary black hole accretion flows in merged galactic nuclei. Publ. Astron. Soc. J. 59, 427–441 (2007).
Murray, D. C. & Dermott, S. F. Solar System Dynamics (Cambridge: Cambridge University Press), ch. 3, 70 (1999).
Hayasaki, K., Stone, N. & Loeb, A. Finite, intense accretion bursts from tidal disruption of stars on bound orbits. Mon. Not. R. Astron. Soc. 434, 909–924 (2013).
Bonnerot, C., Rossi, E. M., Lodato, G. & Price, D. J. Disc formation from stellar tidal disruptions, arXiv:1501.04635 (2015).
Hayasaki, K., Stone, N. C. & Loeb, A. Circularization of tidally disrupted stars around spinning supermassive black holes. arXiv:1501.05207 (2015).
Bate, M. R., Bonnell, I. A. & Price, N. M. Modelling accretion in protobinary systems. Mon. Not. R. Astron. Soc. 277, 362–376 (1995).
Balbus, S. A. & Hawley, J. F. A powerful local shear instability in weakly magnetized disks. I - Linear analysis. II - Nonlinear evolution. Astrophys. J. 376, 214–233 (1991).
Jiang, Y., Stone, J. M. & Davis, S. W. A global three-dimensional radiation magneto-hydrodynamic simulation of super-Eddington accretion disks. Astrophys. J. 796, 106–120 (2014).
D’Orazio, D. J., Haiman, Z. & Schiminovich, D. Relativistic boost as the cause of periodicity in a massive black-hole binary candidate. Nature 525, 351–353 (2015).
Peters, P. C. Gravitational Radiation and the Motion of Two Point Masses. Phys. Rev. D. 136, 1224–1232 (1964).
Gammie, C. F. Nonlinear outcome of gravitational instability in cooling, gaseous disks. Astrophys. J. 553, 174–183 (2001).
Paczynśki, B. A model of selfgravitating accretion disk. Acta Astron. 28, 91–109 (1978).
Nayakshin, S., Cuadra, J. & Volker, S. Simulations of star formation in a gaseous disc around Sgr A* - a failed active galactic nucleus. Mon. Not. R. Astron. Soc. 379, 21–33 (2007).
Syer, D., Clarke, C. J. & Rees, M. J. Star-disc interactions near a massive black hole. Mon. Not. R. Astron. Soc. 250, 505–512 (1991).
Miralda-Escudé, J. & Kollmeier, J. A. Star captures by quasar accretion disks: a possible explanation of the M-σ relation. Astrophys. J. 619, 30–40 (2005).
Milosavljevic, M. & Phinney, E. S. The afterglow of massive black hole coalescence. Astrophys. J. 622, L93–L96 (2005).
Artymowicz, P. & Lubow, S. H., Dynamics of binary-disk interaction. 1: resonances and disk gap sizes, Astrophys. J. 421, 651–667 (1994).
MacFadyen, A. I. & Milosavljević, M. An eccentric circumbinary accretion disk and the detection of binary massive black holes. Astrophys. J. 672, 83–93 (2008).
D’Orazio, J. D., Haiman, Z. & MacFadyen, A. Accretion into the central cavity of a circumbinary disk. Mon. Not. R. Astron. Soc. 436, 2997–3020 (2013).
Rees, M. J. Tidal disruption of stars by black holes of 10 to the 6th-10 to the 8th solar masses in nearby galaxies. Nature 333, 523–528 (1988).
Evans, C. R. & Kochanek, C. S. The tidal disruption of a star by a massive black hole. Astrophys. J. 346, L13–L16 (1989).
Farris, B. D., Duffell, P., MacFadyen, A. I. & Haiman, Z., Binary black hole accretion during inspiral and merger, Mon. Not. R. Astron. Soc. 447, L80–L84 (2015).
Lin, D. N. C., Artymowicz, P. & Wampler, J. Star-disk interaction in quasars and AGNs in Theory of Accretion Disks: 2, ed. W. J. Duschl et al. (Dordrecht: Kluwer) 235 (1994).
Wetzel, A. R., Cohn, J. D. & White, M. Simulating subhaloes at high redshift: merger rates, counts and types Mon. Not. R. Astron. Soc. 395, 1376–1390 (2009).
Acknowledgements
The authors thank to the anonymous referee for fruitful comments and suggestions. The numerical simulations were performed using a high performance computing cluster at the Korea Astronomy and Space Science Institute. This work was supported in part by the research grant of the Chungbuk National University in 2015 [K.H.] and by NSF grant AST-1312034 [A.L.].
Author information
Authors and Affiliations
Contributions
Both authors originated the idea for the project and worked out collaboratively its general details. K.H. performed the SPH simulation described in the Method. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Hayasaki, K., Loeb, A. Detection of Gravitational Wave Emission by Supermassive Black Hole Binaries Through Tidal Disruption Flares. Sci Rep 6, 35629 (2016). https://doi.org/10.1038/srep35629
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep35629
This article is cited by
-
The Process of Stellar Tidal Disruption by Supermassive Black Holes
Space Science Reviews (2021)
-
X-ray flares from the stellar tidal disruption by a candidate supermassive black hole binary
Nature Communications (2020)
-
The X-ray Chirp of a Compact Black Hole Binary
Foundations of Physics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.