Introduction

QKD is a real-time art of generating secure key bit string between remote partners1,2,3. Its security is not based on the computational complexity, but on the correctness of physical principles4,5,6,7. In practical conditions where imperfectly experimental devices are used, it is proven that secure key bit string can still be generated when the tagged key bits are well restricted8. For example, phase-randomized weaken coherent sources are used in practical QKD. There are multi-photon pulses emitted from the source. Eve can launch the photon-number-splitting (PNS) to tag the multi-photon events9,10. If the amount of the tagged event can be well bounded, with decoy state technology for example, secure key bits can be generated between remote partners11,12,13,14.

Recently, the detector side channel attacks have attracted great attention. Eve exploits the drawbacks of the detectors to control the detections. Moreover, the photons registered by the detectors may be not the ones expected by Bob, but well devised by Eve to obtained illegal information. In the fake state attack, Eve intercepts the photons from Alice and reads out the bit values on them. According to her measurement outcomes, she exploits the detection efficiency mismatches and prepares a fake state to be detected by Bob15. The time-shift attack uses the detection efficiency mismatches to eavesdrop on the communication without intercepting on Alice’s photons16,17. Furthermore, the problem of information leaking from the detector side channels also exists in the blinding attack18,19,20 and the phase re-mapping attack21,22.

The detector side channel attacks do great harm to the security of QKD because Eve’s illegal information gain obtained in the attacks cannot be well bounded8. Great improvement must be made on the detectors to avoid the detector side channel attacks19,23,24,25. It has been shown that alternative ways of measurements can be used to beat these attacks26,27,28,29,30,31,32. In this case, the security of the measurement outcomes relies on the monogamy of entanglement33,34. Accordingly, the experimental realization is more complex and the key generation rate is lower when compared with the prepare-and-measure QKD. An easy way to beat the detector side channel attack from the physics principle is expected.

Quantum theory is exclusive with the local hidden variable (lhv) theory35,36,37. Loophole-free Bell violation means that the lhv theory can be excluded. Or else, if no Bell violation can be obtained in the loophole-free Bell test, the quantum theory is incorrect. Recently, Bell violation is experimentally obtained with all loopholes are closed38,39,40. These significant results mean the lhvs do not exist. Based on this fact, the detector side channel attack in the prepare-and-measure QKD can be beat with a simple but efficient way. Random Bell test is required to be carried out at Bob’s side to check the quantum correlations between Alice and Bob. Though this protocol is devised for the BB84 protocol1, it is applicable to any prepare-and-measure QKD.

The prepare-and-measure Bell test

In the Bell test, a parametric-down-conversion (PDC) source is set between Alice and Bob. Entangled photon pairs are generated and distributed to them. Alice has two sets of two-channel measurement devices, A1 and A2. Similarly, Bob has two sets of two-channel measurement settings, B1 and B2. Alice and Bob randomly choose their measurement settings to measure their incoming photons. The binarily possible measurement outcomes obtained from the measurement settings are assigned with −1 and 1. Alice and Bob use their basis choices and measurement outcomes to calculate the CHSH polynomial37

Here 〈Ai〉, 〈Bj〉 are the average values generated on Ai and Bj, with i, j ∈ {1, 2}.

In local hidden variable theory and classical physics, the measurement outcomes at Alice’s side cannot be affected by those at Bob’s side. Similarly, the measurement outcomes at Bob’s side cannot be affected by those at Alice’s side, namely, the relation 〈AiBj〉 = 〈Ai〉 〈Bj〉 obeys41. Because −1 ≤ 〈Ai〉 ≤ 1 and −1 ≤ 〈Bj〉 ≤ 1 should be satisfied, SCHSH varies from −2 to 2. Quantum-mechanically, its lower bound and upper bound are and , respectively42. Now that the Bell violation has been obtained with loophole-free Bell test38,39,40, the lhv theory does not need to be considered. If the experiment is not artificially controlled, Bell violation certifies the existence of entanglement.

Suppose that the entangled photon pair generated from the PDC source is encoded with , where the subscripts A and B denote Photon A and Photon B, respectively. After the photon pairs generated from the PDC source, Photon A is distributed to Alice, while Photon B is sent to Bob. In order to maximize the Bell violation, confinements are put on their basis choices. Without loss of any generality, one can assume that , , , and , where and are the Pauli operators. Because the state is rotationally invariant in the X − Z plane, one can obtain that , with and . In this case, it is easy to verify that .

Traditionally, the PDC source is usually set between Alice and Bob to exclude the locality loophole. Because the lhv theory is refuted, it is not necessary to care about this loophole. Alice can set the PDC source in her laboratory. When the entangled photon pair is generated, she keeps one of them and transfers the other to Bob. As there is no need to care about the locality loophole, the measurement sequences of Alice and Bob do not affect their experimental results. Alice’s measurement can be implemented before that of Bob, and vise versa. If Eve does not intervene, Bell violation must be obtained.

The moment Alice measures on Photon A, the state on Photon B collapses accordingly. It means that Alice prepares the state on Photon B the moment she measures on Photon A. Because the photon pair is prepared with the state , the state on Photon B should correlate with what Alice obtains in her measurement. The same correlation can also be obtained with prepare-and-measure procedure: Suppose that single photon is generated from Alice’s source. She randomly chooses the rectilinear basis or the diagonal basis , together with random bit value −1 or 1, to prepare Photon B. Before Photon B is measured, its state correlates with the state chosen by Alice.

If Alice’s basis choices and bit value choices on Photon B are totally random, the item 〈A1B1〉 in (1) can be calculated as

Similarly, one can obtain

Substituting B1 and B2 with and , one can obtain that , , , and . The value of the CHSH polynomial is calculated to be . It is the same as that when the entangled state is used. This is because the correlations between the state on Photon B and that of Alice are the same in these two cases.

BB84 protocol with the prepare-and-measure Bell test

The BB84 protocol is a prepare-and-measure QKD protocol. Alice prepares the state on Photon B and transfers it to Bob. Bob measures it in randomly chosen basis to read its state. The states |0〉B and |+〉B are used to encode the bit value 0, while the states |1〉B and |−〉B are used to encode the bit value 1 (Here the definitions of the bit values in the quantum key distribution and those of the Bell test are different).

The prepare-and-measure BB84 protocol is characterized as follows:

(a) N single photons are generated in Alice’s laboratory. She randomly chooses between the diagonal basis and rectilinear basis and the random bit values 0 and 1 to prepare her state on the photon. Then the photon is transferred to Bob.

(b) Bob has two modes: with probability p he chooses the signal mode and with probability 1 − p he chooses the test mode (Only Bob himself is aware of the value of p). In the signal mode, Bob’s measurement bases are randomly chosen from and . In the test mode, his measurement bases are randomly chosen between , and .

(b′) When Bob chooses the signal mode, Alice and Bob publish their measurement bases through the public channel. They keep their measurement outcomes in the same bases as the sifted key bits.

(b″) When Bob chooses the test mode, Alice and Bob announce their basis choices and measurement outcomes through the public channel to calculate the value of SCHSH.

(c) After the key distribution, Alice and Bob implement error correction (EC) and privacy amplification (PA) on their sift key bits. If secure key bits can be generated, their key distribution task is fulfilled. Or else, their task is failed.

Because Alice randomly chooses her basis and bit values on Photon B, the state on it is for any third party. The state is uniformly prepared in the conjugated bases. Eve cannot differentiate which state is prepared. If she carries out state distinguishing task on the photon, disturbance must be introduced43,44. Without loss of any generality, one can assume that Eve interacts on Photon B with a probe. If the interaction between the probe and Photon B can be characterized as a unitary process, one can obtain

Here |E〉 is the blank state on Eve’s probe. f and e correspond to the probability that the state on Photon B is intact and the probability that the state on Photon B is changed, respectively. It means that Eve’s intervention introduces quantum bit error rate (QBER) with probability e. The amount of information for Alice and Bob used to correct the errors on their bit string is h(e), with h(x) = −xlog2x − (1 − x)log2x the binary entropy. In the prepare-and-measure QKD, Eve’s ability to attack on the communication can be bounded with the collective attack3,45. In this case, the rate for Eve to tag Bob’s key bits is upper bounded with46,47

After Eve’s intervention, 〈A1B1〉 is recalculated to be

Similarly, one has

It means Alice’s and Bob’s states are correlated with probability f, and anti-correlated with probability e that is also known as the QBER. After Eve’s intervention, is obtained.

Refute the detector side channel attack

In the BB84 protocol, Eve’s illegal information is also bounded as3,4,7

Here e is the phase error rate gained on Bob’s state. Strictly speaking, phase error rate is the concept of entangled states. Because of the symmetry of BB84 protocol, however, the phase error rate is estimated from the bit error rate on the results generated from the conjugated bases4,7. Within the process of Eve’s attack, if she can hide the bit error rates of both bases, Alice and Bob cannot find her existence. In the detector side channel attack, for instance, it is possible for Eve to intervene without introducing any bit error rate.

If Bob’s detectors are imperfect, the detector side channel information leaking problem may exist. Eve can exploit the flaws of Bob’s detectors to carry out the detector side channel attacks.

Theorem 1 The detector side channel attacks can be successfully carried out if and only if Eve’s information of Alice’s bit value conditioned on Bob’s measurement outcome is partially or totally certain. Proof: In the BB84 protocol, Eve interacts with Photon B to extract Alice’s state on it. After Bob measuring on the incoming photons, he and Alice declare their basis choices. When considering the individual attack, Eve’s information gain from Alice is bounded by her entropy decrease on her state3

In the detector side channel attack, though drawbacks exist on Bob’s detectors, it is indispensable to assume that no unwanted information can leak out of his laboratory. Or else, the security of QKD cannot be ensured. It means that Eve should control the information leaking from the detectors indirectly. If Alice’s state on Photon B is uniformly prepared, Ha priori = 1 is obtained.

Consider that Ha posteriori = ∑rP(r)H(i|r), with P(r) the probability Eve obtains the measurement result r, and H(i|r) the information gain of i conditioned on r. If Eve does not interact with Photon B, Ha posteriori = 1 after Bob declaring his basis choices. Thus IE = 0 and Eve cannot obtain any illegal information on Alice’s state. In the detector side channel attack, r has two possible values: the registered and the unregistered, and ∑rP(r) = 1 is satisfied. Whether for the registered pulses or for the unregistered pulses, Bob’s measurement outcomes are controlled to be bit value biased. Bob announces Alice the values of r after his measurements. The bias of Bob’s measurement outcomes is known to Eve in the detector side channel attack and H(i|r) should be less than 1. Correspondingly, Ha posteriori < 1 and IE > 0 are satisfied. In some detector side channel attacks, Eve’s uncertainty on Alice’s states is eliminated with the intercept-resend attack. However, only the pulses encoded with Eve’s expected bit values and expected bases are forced to be detected by Bob. Or else, Alice and Bob can find Eve’s presentence according to the correlations between them. In any case, Bob’s measurement outcomes are partially or totally certain to Eve. Thus we end the proof.

In order to refute the detector side channel attack, Alice and Bob should estimate Eve’s information gain from the attack. In practical QKD, time-windows is set for the detectors so that their dark count rate can be decreased. Thus their detection efficiencies are time-dependent. If the time windows of the two detectors are not the same, there are detection mismatches between them. This can be exploited by Eve to launch the so-called time-shift attack. Furthermore, the detector flaws may also be used by Eve to control the detectors to detect unwanted signals. Taking the blinding attack for instance, the detectors can be blinded with strong illuminations so that they are insensitive to single-photon pulses but to strong pulses. Both in the time-shift attack and in the blinding attack, Eve’s a posteriori information on Alice’s bit value is partially or even totally deterministic.

In practical Bell test with EPR pairs, the quantum channel is lossy and one has to consider the detection loophole. It means that any pulse in quantum channel cannot represent the others in violating the CHSH inequality. If the devices are inefficient, fair-sampling assumption must be made to obtain the Bell violation. If Alice and Bob can implement quantum non-demolition measurement on the photon number, they differentiate the vacuum pulses from the non-vacuum pulses. With this technique, they can remove the channel loss. Now that the lhv theory has be excluded by recent experiments, it is reasonable to assume that the movements all pulses obey the quantum principles and all photon pulses experience the same transmission situation. Thus one can sample the behaviors of some of the incoming pulses on the behalf of those of the others.

We consider the QKD with active basis choice. Bob has two detectors D0 and D1 to decode the key bits 0 and 1 encoded on Alice’s pulses. Their detection efficiencies are assumed to be η0 and η1, respectively. D0 and D1 are manufactured to be the same so that η0 = η1 = η is satisfied when there is no detector side channel attack. We assume that Bob has another detector Dt whose detection efficiency is ηt. Dt is also the same as D0 and D1 apart from its big time window. The time window of Dt is big enough so that its detection efficiency is stably kept within the whole time windows of both D0 and D1. This can be realized by keeping Dt switched on within this period of time. When Bob receives the pulses from Alice, she randomly detect them directly with Dt or decode their key bits with D0 and D1 in randomly chosen bases. When detector side channel attacks randomly happen on D0 and D1, η0 and η1 decrease. For Bob, the detection efficiency he can observe for D0 and D1 is . According to Eqs (2) and (3), the value of the CHSH polynomial should be normalized as

This relation can also be explained with the theory raised by Garg and Mermin where the photons that can be detected by Dt but are missed by D0 and D1 can only be assigned with the bit value 048. Accordingly, the illegal information gain Eve obtained within her detector side channel attack is calculated to be

The performance of the present protocol

In practical QKD, instead of single-photon source, weaken coherent sources are used for Alice to encode her key bits. Compared with single-photon source, multi-photon pulses exist. It is proven that Eve can exploit the multi-photon pulses to launch the so-called PNS attack. Thus decoy states are usually added in practical QKD protocol to beat this attack12,13,14. We consider the practical decoy state protocol raised by Ma et al. where a signal source, a weaker decoy source and a vacuum decoy source are used14. The intensities of the signal source and the weaker decoy source are μ and ν, respectively. After randomization of the phase, the photon number distributions of the sources obey

Here i is the photon number in the pulses.

Alice randomly chooses the signal source and the decoy sources to encode her bit values and transfers them to Bob. When Bob takes the pulses from Alice, with probability p he chooses the signal mode that he measures the incoming pulses randomly in and to extract the key bits on them. With probability p′, he chooses the test mode that his measurement bases are randomly chosen between , and . With probability 1 − p − p′, however, Bob directly measures Alice’s pulses in his detector Dt. The gains on the detectors D0/D1, and Dt write

Here Y0 and are the dark counts on D0/D1 and Dt that can be estimated from the vacuum decoy state. After Bob’s measurements, Alice announces Bob her state choices with which Bob can calculate the values of η and ηt.

After the EC and PA, the final key generation rate is

where is the gain on the untagged pulses of the weaker decoy source, f(Eν) is error correction efficiency, and Eν is the total QBER on the sifted key bits generated from the decoy source. Here we choose the weaker decoy source for key generation because the multi-photon pulses affect the value of the CHSH polynomial greatly. Numerical results shows that no Bell violation can be obtained when the intensity of the signal source is greater than 0.659 even if D0 and D1 have perfect detection efficiency. The fraction of the multi-photon pulses in the decoy source is comparably small, however, thus we assume Alice and Bob use it to generate the key bits.

We will give some numerical simulations on the performance of the QKD with prepare-and-measure Bell test. We will use the setup parameters from the QKD experiment completed by Gobby, Yuan and Shields (GYS)49 that has also been taken used for numerical simulation in ref. 14. Namely, the transferring coefficient is β = 0.21dB/km, the detector’s detection efficiency is ηB = 4.5%, the misalignment coefficient is ed = 3.3%, and the dark count rate Y0 = 1.7 × 10−6. The intensities of the signal pulses, weaker decoy pulses and vacuum pulses are 0.48, 0.1 and 0, respectively. One thing should be pointed out that we will not consider the contribution of the misalignment to the value of the CHSH polynomial.

Firstly, we want to show the performances of the present protocol under the blinding attack and the time-shift attack. For blinding attack, Eve controls the basis of Bob. When Bob’s basis choices coincide with hers, there are efficient registers on his measurement settings. Or else, no clicking event happens. Thus one can obtain ηt = 2η, and the value of CHSH polynomial is for perfect single-photon source. It means that no secure key bits can be generated between Alice and Bob. For the time-shift attack, the CHSH inequality after the time-shift attack is calculated to be . In this attack, however, Eve’s illegal information gain is calculated to be , with . For simplicity of discussion, one can assume that η0 < η1. It is apparent that the big the value is, the more key bits should be sacrificed for PA. The amount of information Alice and Bob should sacrifice for PA is .

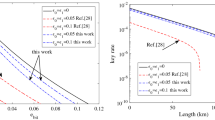
From Fig. 1, it is apparent that the amount of information (dash line) Alice and Bob sacrificed for PA is greater than that (solid line) Eve obtained in her time-shift attack. Thus the present protocol is secure under the time-shift attack. The value of r begins from 0.414 because required that . When , however, one can obtain SCHSH ≤ 2. It means that the classical bound of the CHSH inequality cannot be violated and no secure key bit can be generated. We can also compare the key generation rate of the present protocol with that of the practical decoy state QKD14. In Fig. 2, one can see that the key generation rate of the present protocol is small than that in ref. 14. This is because we generate the key bits from the weaker decoy state whose intensity is smaller than that of the signal state. Furthermore, the transmission distance of the present protocol can reach about 103 km (solid line). This distance is also shorter than that in ref. 14 (dash line).

Figure 1
figure 1

The solid line represents Eve’s information gain within her time-shift attack.

The dash line represents the amount of information Alice and Bob should sacrifice for PA after Eve’s time-shift attack.

Full size image
Figure 2
figure 2

The solid line represents the relation between the key generation rate and the transmission distance of the present protocol.

The dash line characterize the relation between the key generation rate and the transmission distance in ref. 14.

Full size image

Discussion and Conclusion

In this paper, the QKD protocol with prepare-and-measure Bell test has been proposed. Though the security of the present protocol is based on Bell’s theorem, it is different with the DI-QKD protocol46,47 and the Ekert91 protocol2. First, there is no need to care about the detection efficiency. In the present protocol, only the registered photons are used to calculate the CHSH polynomial. Second, entanglement is not required in the present protocol. The protocol is implemented in a prepare-and-measure way. Furthermore, the Bell test in the present protocol is only carried out at Bob’s side. Our protocol is also different with the detection device-independent QKD protocols of the ref. 50. In the detection device-independent protocols, Alice and Bob have characterized sources but uncharacterized detectors. In the present protocol, however, Bob’s detectors are partially characterized. We assume that the detectors have the same attributions. Furthermore, Bob can control the time window of the testing detector.

Additional Information

How to cite this article: Tan, Y.-g. Quantum key distribution with prepare-and-measure Bell test. Sci. Rep. 6, 35032; doi: 10.1038/srep35032 (2016).