Abstract
The general and practical inversion of diffraction data–producing a computer model correctly representing the material explored–is an important unsolved problem for disordered materials. Such modeling should proceed by using our full knowledge base, both from experiment and theory. In this paper, we describe a robust method to jointly exploit the power of ab initio atomistic simulation along with the information carried by diffraction data. The method is applied to two very different systems: amorphous silicon and two compositions of a solid electrolyte memory material silver-doped GeSe3. The technique is easy to implement, is faster and yields results much improved over conventional simulation methods for the materials explored. By direct calculation, we show that the method works for both poor and excellent glass forming materials. It offers a means to add a priori information in first-principles modeling of materials and represents a significant step toward the computational design of non-crystalline materials using accurate interatomic interactions and experimental information.
Similar content being viewed by others
Introduction
On the eve of the First World War, William Lawrence Bragg and his father, William Henry Bragg, exposed crystalline solids to X-rays and discovered what we now call “Bragg diffraction”, strong reflection at particular incident angles and wavelengths. These “Bragg peaks” were sharply defined and, when analyzed with a wave theory of the X-rays, led to clear evidence of order in the crystalline state1. By analyzing the diffraction angles at which the peaks appeared and the wavelength of the X-rays, the full structure of the crystal could be ascertained. In the language of modern solid state physics, the X-ray structure factor of a single crystal consists of a sequence of sharp spikes, which are broadened in a minor way by thermal effects. The information obtained from this palisade of delta functions, arising from a crystal, is sufficient for the determination of lattice structure. The rapid development of X-ray Crystallography in the past several decades had made it possible to successfully determine the structure of complex protein molecules, with more than 105 atoms, leading to the formation of a new branch of protein crystallography in structural biology2.
In contrast with crystals, amorphous materials and liquids have structure factors that are smooth and thus contain far less specific information about structure. The lack of sharp peaks principally originates from the presence of local atomic ordering in varying length scales and no long-range order in the amorphous state. The resulting structure factor is one-dimensional and is effectively a sum rule that must be satisfied by the three-dimensional amorphous solids. This presents a far more difficult problem of structural determination of amorphous solids that requires the development of new tools and reasoning. A natural approach to address the problem is to carry out computer simulations, either employing molecular dynamics or Monte Carlo, with suitable interatomic potentials. We have called this approach the “simulation paradigm”3 elsewhere. By contrast, the other limit is to attempt to invert the diffraction data by “Reverse Monte Carlo” (RMC) or otherwise without using any interatomic potential but information only4,5. This we have called the “information paradigm”3. The information paradigm in its purest form produces models reproducing the data using a random process. These models tend to be maximally disordered and chemically unrealistic. The information paradigm is closely related to the challenge of Materials by Design6,7, for which one imposes external constraints to incorporate additional information on a model to enable a set of preferred physical properties that are of technological utility.
Neither paradigm is ideal, or even adequate. The simulation paradigm is plagued by severe size and time-scale limitations that misrepresent the real process of forming a glass, not to mention imperfect interatomic interactions. For amorphous materials with no or weak glass-forming ability, either approach is rather desperate and leads to the formation of unrealistic models with too many structural defects in the networks. In this paper we introduce ab initio Force Enhanced Atomic Refinement (AIFEAR). A preliminary trial of the algorithm using only empirical potentials recently appeared8.
Others have undertaken related approaches9,10,11,12,13,14,15,16,17. By including ‘uniformity’ as a constraint for the refinement of models, Goodwin and coworkers showed their Invariant Environment Refinement Technique11 to produce improved models of a-Si and other systems. A liquid-quench procedure, combined with a hybrid Reverse Monte Carlo approach, which incorporates both experimental and energy-based constraints has been employed by Opletal and coworkers12. A similar approach via hybrid RMC with empirical bonded and non-bonded forces was used by Gereben and Pusztai to study liquid dimethyl trisulfide18. Likewise, by refining the initial interatomic empirical potential-energy function and fitting the input experimental structure-factor data, empirical potential structure refinement has been quite successful in predicting liquid structures14. An alternative approach, experimentally constrained molecular relaxation, which incorporates experimental information in first-principles modeling of materials in a ‘self-consistent’ manner16 was discussed in refs 15 and 16. Recently, a means for including electronic a priori information has also appeared17. These methods have all contributed significantly to the field, yet they have limitations such as employing empirical potentials of limited reliability8,12, or unacceptable convergence properties1516. A general and successful framework for inverting solid state diffraction data does not exist. AIFEAR is a major step toward this important goal.
We begin with some definitions. If V(X1 … Xn) is the energy functional for atomic coordinates {Xi} and χ2 measures the discrepancy between diffraction experiment and theory, we seek to find a set of atomic coordinates {Xi} with the property that V = minimum and χ2 is within experimental error. AIFEAR is a simple iterative process consisting of (i) producing a structural model at random (at a sensible but not necessarily exact density, which may not be available), (ii) invoking N accepted moves within conventional RMC19 followed by M conjugate-gradient (CG) steps using ab initio interactions. We then iterate (ii) until convergence. The final results do not depend heavily on the numerical values of N and M, which were chosen to be 1000 and 10, respectively, for the present work. For the examples discussed here, we find that significantly fewer ab initio force calls are needed for AIFEAR than for an ab initio ‘melt-quench’ simulation. In addition, AIFEAR avoids the problem of relative weighting of V and χ2 in a penalty or target energy functional as in hybrid approaches developed elsewhere12,20. If the density of the material is unknown, it is straightforward to carry out the simulation at zero pressure (with variable cell geometries) in the CG loop and simply pass the modified supercell vectors back to the RMC loop.
To illustrate the efficacy of this new approach, we begin with a persistently vexing problem: the structure of amorphous Si which is particularly difficult because the network is over-constrained21,22 and it is not a glass former. The only methods that yield really satisfactory results are the Wooten-Weaire-Winer (WWW)23 and Activation Relaxation Technique24 methods. Structural and electronic experiments reveal that coordination defects in good quality material have a concentration less than a part in 1000. As such, a satisfactory model should have at most a few percent (or less) defects. Inversion methods like RMC and ab initio melt-quench both produce unsatisfactory models with far too many coordination defects compared to experiments. In this illustration, we employ the local-orbital-based density functional code SIESTA for the calculation of ab initio forces, but the approach is easily implemented with ab initio total-energy plane-wave codes as we show in the next example.
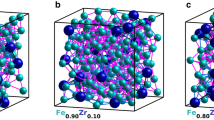
We began by preparing three 216-atom models of a-Si, at the experimental density25 of 2.33 g.cm−3 , using (1) RMC, (2) melt-quench and (3) AIFEAR. The starting atomic configurations were chosen to be random and the diffraction data from ref. 23 were employed in RMC and AIFEAR. The structural properties of a-Si, obtained from these models, are summarized in Fig. 1. For a discussion on convergence and comparisons to other calculations, see the Methods section. RMC produces a highly unrealistic model, far from the accepted tetrahedral network topology, as seen in Fig. 1. Melt-quench, while better, still produces far too many coordination defects. By contrast, AIFEAR produces a nearly perfect tetrahedral structure, with 99.07% fourfold coordination and a bond-angle distribution close to that of a WWW model. In comparing the bond-angle distributions (from AIFEAR with that of from WWW), one must take into account the fact that ab initio interactions tend to produce a slightly wider bond-angle distribution than the highly artificial WWW (Keating spring) interactions.
Top: A 216-atom model of a-Si obtained from (a) RMC, (b) melt-quench and (c) AIFEAR simulations. Silicon atoms with a coordination number of 3, 4 and 5 are shown in green, blue and red colors, respectively. Center: The radial distribution function (RDF) for the (d) RMC, (e) melt-quench and (f) AIFEAR models. Bottom: The bond-angle distributions for the models as indicated in the figure. See supplementary materials for animations showing the formation of three-dimensional network structure and the corresponding evolution of the radial and coordination-number distributions.
We wish to emphasize that the starting configuration used in AIFEAR was random, so that one can logically infer that a combination of atomic-radial-correlation data and DFT interactions leads to an almost perfect tetrahedral network as illustrated in Fig. 1. Table 1 lists the key structural properties of the model, along with the total energy per atom. In the Methods section, we report the detailed convergence of total energy E and χ2. In the Supplementary Materials, we also offer an animation of the convergence of AIFEAR by showing the formation of a tetrahedral network as the simulation proceeds with the disappearance of coordination defects.
For a challenging and timely example, we have also studied the solid electrolyte material Agx(GeSe3)1−x. This is a chemically complex system with important applications to conducting bridge computer FLASH memory devices, which are of considerable fundamental and technological interest. We employ the same scheme as for a-Si, but with ab initio interactions from the plane-wave DFT code VASP26,27,28, with 135 and 108 atoms in a unit cell of length 15.923 Å and 15.230 Å for x = 0.05 and x = 0.077, respectively. These values correspond to the densities of 4.38 g.cm−3 and 4.04 g.cm−3 for the models with 5% and 7.7% Ag, respectively. For x = 0.05, both the structure-factor data and density of 4.38 g.cm−3 are taken from the work of Piarristeguy and Pradel29. For x = 0.07, we have used the RDF data provided by Zeidler and Salmon30 and a density of 4.04 g.cm−3 was obtained from a zero-pressure conjugate-gradient relaxation using VASP. For completeness, we have also studied a melt-quench model of x = 0.077 as described in the Methods section. The melt-quench model (in Fig. 2a) shows significant discrepancies with experiments: the first sharp diffraction peak (FSDP) near 1 Å−1 is absent and there are significant inconsistencies in the structure factor at high k values. The FSDP is an indicator of medium range order, a signature of structural correlations between the tetrahedral GeSe structural building blocks of the glass. By contrast, the AIFEAR model captures all the basic characteristics of the structure factor, including the FSDP (in fact, it slightly overfits the FSDP). We show that the method has similar utility in either real or k space, using S(k) for the first composition and g(r) for the second. Figure 2 shows the structure factors and radial distribution functions obtained from AIFEAR and melt-quench simulations and compares with the experimental data from neutron diffraction measurements29,30.
(a) Structure factors of (GeSe3)1−xAgx [x = 0.05] from AIFEAR. Experimental data, from neutron diffraction measurements, are shown for comparison29. Melt-quench data are from Pradel et al.29 (b) The radial distribution function of (GeSe3)1−xAgx [x = 0.077] from AIFEAR and melt-quench simulations. Experimental RDF shown here are from Zeidler et al.30.
The GeSeAg systems are of basic interest as solid electrolytes. One of the most interesting questions pertains to the dynamics of Ag atoms, which are sufficiently rapid that they can be tracked even in first-principles molecular-dynamics simulations31. The fast Ag dynamics have led to the invention of conducting bridge Random Access Memory32,33. As this dynamics appears to be of trap-release form31, the structure, including features like medium range order and associated energetics may be expected to play a key role in the silver hopping. The 7.7% Ag composition is near to a remarkable and abrupt ionic mobility transition34,35. Dynamical simulations are currently underway to determine the role of the structure in this dynamics.
The following features of Agx(GeSe3)1−x glasses have been observed in the AIFEAR model: 1) the Ge-Se correlation is not affected by an increase in Ag content: Ge(Se1/2)4 tetrahedra remain the fundamental structural units in the network. 2) Ge-Ge correlations, greatly affected by Ag doping, are revealed by the shift in Ge-Ge nearest-neighbor distance from 3.81 Å in Ag = 0%29 to 2.64 Å and 2.56 Å in Ag = 5% and Ag = 7.7%, respectively 3) the Ag-Se correlation peak is near 2.66 Å for both the systems, which is consistent with the experimental work of Zeidler30 and others29. 4) The Se-Se coordination number for 5% and 7.7% Ag are 1.12 and 0.83 (0.81 from experimental data30), respectively. This is consistent with the observed phenomena of decrease in Se coordination with the increase in Ag concentration29.
Beside retaining the important chemical features of the network, the AIFEAR model is superior to the melt-quench model by the manifestation of a prominent FSDP (cf. Fig. 2a), a signature of medium range order in these materials. Absence of the FSDP indicates the lack of structural correlations in the Ge(Se1/2)4 tetrahedra, which is less prominent for low Ag concentration. Also, the energy of the AIFEAR model for x = 0.077 is 0.02 eV/atom less than the melt-quench model (see Fig. 3b).
It is important and promising that in the GeSeAg systems, as in a-Si, AIFEAR is not a greedy optimization scheme, as it is evidently able to unstick itself (for example in Fig. 3b) near 400 steps, there is a dramatic and temporary increase in χ2, which then enabled the system to find a new topology which produced further reduction of both χ2 and energy. A similar, if less dramatic, event is indicated in Fig. 3a around step 1100. The Monte-Carlo moves robustly explore the configuration space and are not so prone to getting trapped as in MD simulations and yet the chemistry is properly included in the ab initio relaxation loop.
In conclusion, we have introduced a new and practical method that enables the joint exploitation of experimental information and the information inherent to ab initio total-energy calculations and a powerful new approach, to the century-old problem of structural inversion of diffraction data. The method is simple and robust and independent of the systems, the convergence of which has been readily obtained in two highly distinct systems, both known to be challenging and technologically useful. By direct calculation, we show the network topology of a-Si, implied by the atomic pair correlations and accurate total energies, is: structurally similar to WWW models, including the bond-angle distribution. Using only the total structure-factor (or pair-correlation) data and SIESTA/VASP, we obtain models of unprecedented accuracy for a difficult test case (a-Si) and a technologically important memory material (GeSe3Ag). The inclusion of a priori experimental information emphasized here may also be developed into a scheme to include other information for materials optimization. It is easily utilized with any interatomic potentials, including promising current developments in “machine learning”36. The method is unbiased in the sense that it starts from a completely random configuration and explore the configuration space of a total-energy functional aided by additional experimental information to arrive at a stable amorphous state. Beside these attributes, it requires fewer force calls to the expensive ab initio interactions.
Methods
As described in the main text, AIFEAR jointly minimizes the configurational energy V and the cost function (see refs 4 and 37)

where FE/M(ki) is the experimental/model structure factor and σ (ki) is the error associated with the experimental data for wave vector ki. To undertake this program, (i) we begin with a random model, (ii) invoke M RMC accepted moves followed by N conjugate-gradient steps to optimize the total energy. We have found M = 1000 and N = 10 to be satisfactory for the materials of this paper. The process (ii) is repeated until the desired accuracy of δχ2 ≈ 0.1 and a force tolerance of δf ≈ 0.02 eV/Å is attained. All that is required are RMC and total-energy codes and an appropriate driver program connecting them.
Amorphous Si
Initially, conventional RMC (i.e. without any constraint) runs were performed using the RMCProfile software19 for a random starting configuration of 216-atom a-Si with a cubic box of side 16.281 Å corresponding to the density 2.33 g.cm−3. The maximum step length of the RMC moves for Si atoms is chosen to be 0.05 Å. In a parallel simulation, the same starting configuration is taken through a process of melt-quench using the density-functional code SIESTA38 with single-ζ basis under Harris functional scheme38 within the local density approximation. The total-energy and force calculations are restricted to the Γ point of the supercell Brillouin zone. After melting at 2300 K, the liquid structure was quenched to 300 K at a rate of 240 K/ps. Each step was followed by the equilibration of the system for 2000 time steps. To ensure the reproducibility of the FEAR method, we have generated 10 a-Si models starting from random configurations and the models yielded 4-fold coordination always exceeding 96%. Details of convergence and comparison to the best available WWW model is provided in Fig. 4. The elimination of defects is chronicled in an animation provided in the Supplementary Materials.
Results for 216-atom a-Si: (a) The variation of cost function and total energy with the number of AIFEAR steps. (b) Electronic density of states (EDOS) for RMC, melt-quench and AIFEAR models with the Fermi level at 0 eV. (c) The bond-angle distribution from AIFEAR compared to that of WWW (see Table 1 for details).
Chalcogenide glasses
The experimental structure factors data taken from the work of Piarristeguy et al.29 for 5% Ag and the pair distribution function (PDF) was obtained from the work of Zeidler and Salmon30 for 7.7% Ag. For ab initio interactions, we used the plane-wave DFT code VASP26,27,28 using projected augmented plane waves (PAW)39 with Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional40 and a plane-wave cutoff of 312.3 eV. All calculations were carried out at Γ point. The random starting configurations of 5% and 7.7% Ag-doped GeSe3Ag were subjected to ab initio FEAR. The 5% Ag-doped GeSe3Ag ab initio FEAR model is compared to the melt-quench model of the identical system of Piarristeguy and co-workers29. The melt-quench model of 7.7% Ag-doped GeSe3 is prepared by melting the same starting configuration at 1400 K for 10,000 steps, followed by a quenching to 300 K at the rate of 100 K/ps and then by equilibrating at 300 K for another 5000 steps. To estimate the density of the equilibrated system, the volume of the simulation cell was relaxed. A final relaxation at zero pressure was employed, which yielded a density of 4.04 g.cm−3. A time step of 1.5 fs was used for the production of melt-quenched models in MD simulations.
We have included a comparison of the number of force calls in the various simulations in Fig. 5. It is evident from Fig. 5 that AIFEAR offers a significant computational advantage, with fewer force calls to the expensive ab initio codes.
Additional Information
How to cite this article: Pandey, A. et al. Inversion of diffraction data for amorphous materials. Sci. Rep. 6, 33731; doi: 10.1038/srep33731 (2016).
References
Bragg, W. H. & Bragg, W. L. The Reflexion of X-Rays by Crystals. Proceedings of the Physical Society of London A 88(605), 428–438 (1913).
Kendrew, J. C. et al. A three dimensional Model of the Myoglobin Molecule obtained by X-Ray Analysis. Nature 181(4610), 662–666 (1958).
Drabold, D. A. Topics in the theory of amorphous materials. The European Physical Journal B 68(1), 1–21 (2009).
McGreevy, R. L. Reverse monte carlo modelling. Journal of Physics: Condensed Matter 13(46), R877 (2001).
Biswas, P., Atta-Fynn, R. & Drabold, D. A. Reverse Monte Carlo modeling of amorphous silicon. Physical Review B 69(19), 195207 (2004).
Eberhart, M. E. & Clougherty, D. P. Looking for design in materials design. Nature Materials 3(10), 659–661 (2004).
Carter, E. A. Challenges in modeling materials properties without experimental input. Science 321(5890), 800–803 (2008).
Pandey, A., Biswas, P. & Drabold, D. A. Force-enhanced atomic refinement: Structural modeling with interatomic forces in a reverse Monte Carlo approach applied to amorphous Si and SiO2 . Phys. Rev. B 92, 155205 (2015).
Timilsina, R. & Biswas, P. A study of hydrogen microstructure in amorphous silicon via inversion of nuclear magnetic resonance spectra. Journal of Physics: Condensed Matter 25(16), 165801 (2013).
Meredig, B. & Wolverton, C. A hybrid computational-experimental approach for automated crystal structure solution. Nature materials 12(2), 123–127 (2013).
Cliffe, M. J., Dove, M. T., Drabold, D. A. & Goodwin, A. L. Structure determination of disordered materials from diffraction data. Phys. Rev. Lett. 104, 125501 (2010).
Opletal, G. et al. The structure of disordered carbon solids studied using a hybrid reverse Monte Carlo algorithm. Journal of Physics: Condens. Matt. 17(17), 2605 (2005).
Pickard, C. J. & Needs, R. J. Ab initio random structure searching. Journal of Physics: Condensed Matter 23(5), 053201 (2011).
Soper, A. K. Tests of the empirical potential structure refinement method and a new method of application to neutron diffraction data on water. Molecular Physics 99(17), 1503–1516 (2001).
Biswas, P., Atta-Fynn, R. & Drabold, D. The inclusion of experimental information in first principles modelling of materials. Journal of Physics: Condensed Matter 16(44), S5173 (2004).
Biswas, P., Tafen, D. & Drabold, D. A. Experimentally constrained molecular relaxation: the case of GeSe2, Phys. Rev. B 71 054204 (2005).
Prasai, K., Biswas, P. & Drabold, D. A. Sculpting the band gap: a computational approach. Scientific reports 5, 15522 (2015).
Gereben, O. & Pusztai, L. RMC-POT: a computer code for reverse Monte Carlo modeling the structure of disordered systems containing molecules of arbitrary complexity. Journal of computational chemistry 33(29), 2285–2291 (2012).
Tucker, M. G. et al. RMCProfile: reverse Monte Carlo for polycrystalline materials. Journal of Physics: Condensed Matter 19(33), 335218 (2007).
Rieping, W., Habeck, M. & Nilges, M. Inferential structure determination. Science 309, 303306 (2005).
Phillips, J. C., Bean, J. C., Wilson, B. A. & Ourmazd, A. Bragg diffraction by amorphous silicon. Nature 325, 121–125 (1987).
Beeman, D., Tsu, R. & Thorpe, M. F. Structural information from the Raman spectrum of amorphous silicon. Physical Review B 32(2), 874 (1985).
Wooten, F., Winer, K. & Weaire, D. Computer generation of structural models of amorphous Si and Ge. Phys. Rev. Lett. 54, 1392 (1985).
Mousseau, N. & Barkema, G. T. Traveling through potential energy landscapes of disordered materials: The activation-relaxation technique. Physical Review E 57(2), 2419 (1998).
McGuire, G. E. Semiconductor materials and process technology handbook. William Andrew (1988).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558 (1993).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 1116986 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science 6, 15 (1996).
Piarristeguy, A. A. et al. Short range order and Ag diffusion threshold in Agx(Ge0.25Se0.75)100−x glasses. Physica Status Solidi B 249(10), 2028–2033 (2012).
Zeidler, A., Salmon, P. S., Piarristeguy, A., Pradel, A. & Fischer, H. E. Structure of Glassy Ag-Ge-Se by Neutron Diffraction with Isotope Substitution. Zeitschrift fur Physikalische Chemie. (2016).
Tafen, D. N., Drabold, D. A. & Mitkova, M. Silver transport in GexSe1−x:Ag materials: Ab initio simulation of a solid electrolyte. Phys. Rev. B 72, 054206 (2005).
Kozicki, M. N. & West, W. C. Programmable metallization cell structure and method of making same. US Patent 5, 761, 115 (1998).
Waser, R. & Aono, M. Nanoionics-based resistive switching memories. Nature Materials 6(11) 833–840 (2007).
Kawasaki, M., Kawamura, J., Nakamura, Y. & Aniya, M. Ionic conductivity of Agx(GeSe3)1−x(0 ≤ x ≤ 0.571) glasses. Solid State Ionics. 123(1), 259–269 (1999).
Urena, M. A., Piarristeguy, A. A., Fontana, M. & Arcondo, B. Ionic conductivity (Ag+) in AgGeSe glasses. Solid state ionics 176(5), 505–512 (2005).
Nosengo, N. The Material Code: Machine-learning techniques could revolutionize how materials science is done. Nature 533(22) (2016).
McGreevy, R. L. & Pusztai, L. Reverse Monte Carlo simulation: a new technique for the determination of disordered structures. Molecular Simulation 1(6), 359–367 (1988).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. Journal of Physics: Condensed Matter 14(11), 2745 (2002).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Acknowledgements
We thank the US NSF under the grants DMR 150683, 1507166 and 1507670 for supporting this work and the Ohio Supercomputer Center for computer time. We thank Dr. Anita Zeidler and coworkers for providing us with their experimental data.
Author information
Authors and Affiliations
Contributions
All the authors (A.P., P.B. and D.A.D.) wrote the manuscript and planned the research. Pandey carried out most of the calculations.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pandey, A., Biswas, P. & Drabold, D. Inversion of diffraction data for amorphous materials. Sci Rep 6, 33731 (2016). https://doi.org/10.1038/srep33731
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33731
This article is cited by
-
Comprehensive characterization of the structure of Zr-based metallic glasses
Scientific Reports (2024)
-
Characterizing MRO in atomistic models of vitreous SiO2 generated using ab-initio molecular dynamics
Applied Physics A (2023)
-
Connecting theory and simulation with experiment for the study of diffusion in nanoporous solids
Adsorption (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.