Abstract
Dengue viruses, which infect millions of people per year worldwide, cause large epidemics that strain healthcare systems. Despite diverse efforts to develop forecasting tools including autoregressive time series, climate-driven statistical and mechanistic biological models, little work has been done to understand the contribution of different components to improved prediction. We developed a framework to assess and compare dengue forecasts produced from different types of models and evaluated the performance of seasonal autoregressive models with and without climate variables for forecasting dengue incidence in Mexico. Climate data did not significantly improve the predictive power of seasonal autoregressive models. Short-term and seasonal autocorrelation were key to improving short-term and long-term forecasts, respectively. Seasonal autoregressive models captured a substantial amount of dengue variability, but better models are needed to improve dengue forecasting. This framework contributes to the sparse literature of infectious disease prediction model evaluation, using state-of-the-art validation techniques such as out-of-sample testing and comparison to an appropriate reference model.
Similar content being viewed by others
Introduction
Dengue is a substantial public health problem in most of the tropical and subtropical regions of the world1. In most of these areas, dengue is endemic with cases occurring year-round, yet there is marked variation in incidence of dengue both within and between years. In Mexico, for example, yearly reported incidence over the last few decades has varied from several thousand cases to over 100,000 cases in 20092. Even understanding the current burden of dengue can be challenging. There is often an extended delay between symptom onset and official reports reflecting care-seeking behavior or confirmed clinical reports of illness. In some settings, complex, multi-tiered reporting systems may contribute to delays. Because of the vastly greater burden of disease in larger epidemic years and difficulty in understanding current and future needs, much effort has been placed on developing early warning systems to predict or detect large epidemics as early as possible with the hope of being able to control epidemics in their early stages3,4.
Numerous mechanistic models have been developed to use detailed knowledge of dengue virus transmission biology to predict the evolution of dengue epidemics5,6. However difficulties emerge when attempting to use mechanistic models for forecasting, often the key mechanistic assumptions are unclear and the data needed to parameterize and feed the model are often difficult or impossible to obtain.
Models for large-scale dengue early warning systems have therefore mostly focused on two components, temporal autocorrelation and an association with weather or climate. Temporal autocorrelation results from the infectious nature of dengue viruses; cases are more likely in the near future when the current prevalence of infection is high. The influence of weather is due to the mosquito vectors of dengue viruses, Aedes aegypti and Ae. albopictus. Temperature, humidity and precipitation are important determinants of mosquito reproduction and longevity7,8,9 and temperature has a strong influence on the ability of the mosquitoes to transmit dengue viruses10.
These two components, autocorrelation and weather or climate, form the basis for a wide variety of efforts to predict dengue incidence in countries such as Australia11, Bangladesh12, Barbados13, Brazil14,15,16,17, Colombia18,19,20, Costa Rica21, China22, Ecuador23, Guadeloupe24, India25, Indonesia26,27, Mexico28, New Caledonia29, Peru30, Philippines31,32, Puerto Rico33, Singapore34,35,36,37,38, Sri Lanka39, Taiwan40,41, Thailand42,43,44,45,46 and Vietnam47.
In this manuscript, we focus on developing prediction models for dengue incidence in Mexico based on observed dengue incidence and weather. We focus explicitly on building models that directly predict dengue incidence rather than those designed to classify future transmission, for example as low or high29,30,34,42. Although classification may be more useful for public health decision-making, the classification process is subjective48, making estimation of uncertainty a less straightforward process compared to direct prediction of incidence.
Autoregressive integrated moving average (ARIMA) models49 have been used extensively in dengue prediction efforts14,18,19,35,37,40,45, often incorporating a seasonal component (SARIMA)11,14,15,24,25,27,43,46,47. We used the SARIMA framework to define a dynamic suite of prediction models for dengue in Mexico that is at once flexible and wide-ranging, while remaining manageable in size for the purposes of careful evaluation and comparison. While the fundamental biology leading to autocorrelation and associations with weather and dengue incidence is clear, the specific contributions of these two components to dengue prediction remains less so. In other words, we wanted to answer the question, to what extent does incorporating climate data into models improve dengue forecasts at different spatial scales? Therefore, we assessed three specific features of these dengue prediction models: (i) the most important autoregressive and climatological components for predicting dengue incidence; (ii) the variability in importance of these components across different geographical areas; and (iii) the limits of prediction accuracy across models at different time horizons. Another important motivation of this study was to establish a forecast assessment framework that can serve as a reference for any infectious disease forecasting problem, including comparison to a non-naïve baseline model and validation on completely out-of-sample data.
Materials and Methods
Data
The number of dengue and dengue hemorrhagic fever cases reported for each month from January 1985 to December 2012 was obtained from the Mexican Health Secretariat2. To model these counts as a linear process, we log-transformed the highly skewed monthly dengue cases after adding one to the observed count. This eliminates computational problems associated with taking the log of zero and can be thought of as accounting for the potential entrance of new cases50. Weather data from January 1985 to December 2012 were obtained from the National Oceanic and Atmospheric Administration North American Regional Reanalysis dataset (www.esrl.noaa.gov/psd/ accessed on May 1st, 2013). For each month and state, we extracted the average temperature (°C), daily precipitation (mm) and relative humidity (%).
Models
We analyzed three different types of temporal models: linear models, autoregressive (AR) models and seasonal autoregressive models (SAR). We label these models as (p,d,q)(P,D,Q)s + covarL. For the ARIMA component, (p,d,q), p indicates the autoregressive order, d indicates differencing and q is the order of the moving average49. For the seasonal component, (P,D,Q)s, s indicates the season length (s = 12 months for the monthly data presented here), P indicates the autoregressive order, D indicates differencing and Q is the order of the moving average. The final component, + covarL, indicates a particular covariate at a lag of L months included as a linear regression term.
We used a systematic procedure to select SARIMA models to fit to the data and evaluate for predictive performance. Each time series was assessed for stationarity using the Augmented Dickey-Fuller test51. We used domain-specific knowledge about infectious disease models to create a limited model space that we could explore fully and justify scientifically. Defining the model space in this way mitigated the risk of overfitting the model in the training period. Specifically, we chose to focus on models that (a) included lagged observations of up to three months (p = 1, 2, or 3) and three years (P = 0, 1, 2, or 3), (b) included differencing terms of up to order 1 (i.e. d or D = 0 or 1) and (c) excluded all consideration of moving averages (i.e. q and Q both fixed at 0).
Prediction models that include a differencing term (i.e. d = 1 or D = 1) have a term added to the model formula that captures the difference between the lag-1 and lag-2 case counts. These models therefore incorporate information about the most recently observed slope of dengue incidence: e.g. are reported cases increasing or decreasing? In some formulations, this can be considered a crude approximation to the reproductive rate of the disease, an important parameter for judging the trajectory of the outbreak52. As an example of a formula for a model including differencing, a (1,0,0)(2,1,0)12 multiplicative SARIMA model can be expressed as:

where  are the observed numbers of cases of dengue at time
are the observed numbers of cases of dengue at time  ;
;  are the residual error terms, assumed to be normally distributed; and the coefficients
are the residual error terms, assumed to be normally distributed; and the coefficients  ,
,  and
and  are determined to minimize the residual squared error.
are determined to minimize the residual squared error.
To evaluate the added predictive value of weather variables, we examined the best SARIMA models from the model space defined above by adding individual weather variables as covariates, with lags of 1, 2 and 3 months and the month with the maximum Pearson correlation with dengue incidence (labeled with the sub-script MX in the figures) and assessing the change in predictive performance. Our aim was to single out the effect of each variable (precipitation, relative humidity and temperature). Additional models including multiple weather variables at once were considered. Ultimately, the models presented represent a given SARIMA model plus the most highly correlated lagged weather covariate. All models were fitted in R53, using the arima function from the stats package.
Model evaluation
The data was separated into three subsets. The first five years of data (1985-1989) was reserved for model training. Models trained on that data were used to dynamically predict dengue incidence over an 18-year model evaluation period (1990–2007). The final five-year dataset (2008–2012) was reserved for a complete out-of-sample validation after model selection.
At the end of the training period, predictions were made for the next 1–6 months (e.g., predictions are made for January–June based on data through December of the preceding year). Then the model was refitted with data from the next month (i.e., January) and predictions were made for the following 1–6 months (February–July). This process was repeated over all months of the evaluation period. Predictions were evaluated by comparing observed incidence with model-predicted incidence using two metrics: mean absolute error (MAE) and the coefficient of determination (R2). For comparisons of predictions across different locations and predictions horizons, we calculated the change in MAE relative to the best prediction among all models for a given location and horizon:

where mi is a single model in the set of models M for a given time and location. Thus the model with the best point prediction has relMAE = 1 and predictions further from the observations will have increasing relMAE values.
To compare two specific models (m1 and m2), we calculated the relMAE:

State-level models
We systematically assessed the predictive performance of a wide range of models at different spatial scales, using data aggregated at the national level and at the level of states. The primary interest of this manuscript is to assess models for forecasting dengue incidence in endemic locations, so we restricted the analysis to the 17 states reporting cases in at least half of the months in the training and development time period (1985–2007). Some of the other states, such as Sonora, Coahuila and San Luis Potosi, had high median annual incidence over this period due to sporadic outbreaks but reported cases in less than 50% of the months.
Using the selection algorithm described briefly above in the “Models” subsection and in more detail below in the “National dengue forecasts” subsection, we fitted and evaluated 39 models at each spatial scale. The same selection process was repeated for each location separately. We assessed the predictions of all models across each location using the average relative MAE and R2 for each prediction horizon. For each state we selected an optimal model for short-term forecasts by identifying the model with minimum average relative MAE across the 1–3 month prediction horizons, for each state we refer to this model as the “local” model. Assessing model performance across all spatial scales in the training period, we identified a single “common” model that performed well across all spatial scales. During the prospective out-of-sample forecast phase, after model selection, we compared the performance between the common and local models.
Results
National dengue forecasts
During the 5-year training period (1985–1989) and 18-year evaluation period (1990–2007) the monthly dengue incidence in Mexico showed strong seasonality (Fig. 1A). Incidence also varied substantially between years, with less than 2,000 cases reported in 2000 and more than 50,000 reported in 1997.
National-level forecast metrics.
National-level incidence is shown during the training period (1985–1989) and evaluation period (1990–2007). (A) For each of 39 models considered, the MAE (B) and R2 (C) values for prospective forecasts over the entire evaluation period are shown for each prediction horizon (dark red to yellow, corresponds to 1–6 months). For models including lagged weather covariates, forecasts were not possible at prediction horizons beyond the lag and are not shown. An equivalent plot for each state is shown in Figure S1.
We first compared two naïve models for predicting national dengue incidence several months into the future, one estimating that future incidence follows the historical average incidence and another assuming that future incidence for a specific month will be the historical average for that particular month of the calendar year (Fig. 1B). These models were implemented at the beginning of the evaluation period, with predictions made for months 1 through 6 of that period. An additional month of data was then acquired (month 1), the model was refitted and predictions for the next 6 months (i.e., months 2–7) were made, ensuring that all forecasts were made on out-of-sample data. As predictions were made at each month throughout the 18-year evaluation period, a total of 216 predictions were analyzed for each prediction horizon and each model. For all models, we used the same dynamically increasing training set strategy to calculate the respective out-of-sample predictions, strictly avoiding the use of forward-looking information. This allowed the use of predictive metrics to compare models directly.
Across all of these out-of-sample predictions, the model using the month of the year outperforms the long-term mean model by both MAE (lower error) and R2 (higher correlation). Despite being relatively naïve, predictions from the seasonal model have an R2 of approximately 0.24.
We then assessed twelve linear models including data on average temperature, daily precipitation and relative humidity in previous months. The maximum cross-correlation between each of these weather variables and dengue incidence was 1 month for relative humidity, 3 months for precipitation and 4 months for temperature. We assessed lags of 1–3 months for each variable and also a 4-month lag for temperature. The 4-month lag temperature model performed best, but did not outperform the simple monthly model by either metric.
Next we assessed sixteen models with only autocorrelation and differencing terms: eight models including only short-term autocorrelation and eight models including both short-term and seasonal autocorrelation. The first-order AR model (1,0,0)(0,0,0)12, substantially improved the 1-month predictions compared to all previous models. At 2-months, the predictions were less accurate than those from the monthly model and some of the covariate models. Increasing the order of the AR model slightly improved the predictions, while differencing decreased their accuracy. Adding a seasonal component markedly improved the predictions; the (1,0,0)(1,0,0)12 SAR model outperformed all of the previous models with lower MAE and higher R2 at all prediction times. Increasing the short-term AR component slightly decreased accuracy and 1-month differencing decreased accuracy substantially. Adding a seasonal differencing term however, improved accuracy by both metrics for longer prediction horizons (e.g. (1,0,0)(1,1,0)12). Increasing the order of the seasonal AR term to (1,0,0)(3,1,0)12 further improved predictions.
Finally, we assessed nine AR and SAR models with weather covariates. At all prediction horizons, models containing first order autoregressive terms and covariates consistently outperformed models containing only the covariate information (e.g. (1,0,0)(0,0,0)12+tempMX versus tempMX) and simple AR models (e.g. (1,0,0)(0,0,0)12+tempMX versus (1,0,0)(0,0,0)12). The SAR models with covariates have very similar accuracy to the SAR models without covariates at 1–4 month prediction horizons. For 5- and 6-month horizons, the covariate models could not make predictions as they extended beyond the 4-month lag for temperature. Additional analyses showed that once about 12 years of training data were used, the predictive performance of the models reached a stable average value (between 0.85 and 0.9 correlation), although year-specific values showed some variation around the average (data not shown). Finally, in a non-exhaustive search, we noticed that using all weather variables at once as input in a given model did not yield noticeable improvements.
Overall, the best performing models were (1,0,0)(3,1,0)12 for horizons of 1–2 months, (1,0,0)(3,1,0)12+tempMX for the 3-month horizon, (1,0,0)(1,1,0)12 for the 4-month horizon and (2,0,0)(1,1,0)12 for 5- and 6-month horizons (Fig. 1C). The best model across all horizons was (1,0,0)(3,1,0)12, followed by (1,0,0)(1,1,0)12 and (1,0,0)(2,1,0)12.
State-level dengue forecasts
Dengue incidence varies substantially between states within Mexico (Fig. 2). Similar to the national-level results, the first-order AR model (1,0,0)(0,0,0)12 outperformed the monthly model at shorter prediction horizons of 1–3 months (Fig. 3, Supplementary Figure 1). However across all horizons and states, the most accurate model was the (1,0,0)(2,1,0)12 model, which we now refer to as the “common” model. The coefficients for the (1,0,0)(2,1,0)12 model in each state varied, but the pattern was consistent across all states: the monthly autoregressive component was positive in each state and the seasonal autoregressive components were negative, with decreasing magnitude at longer lags (Supplementary Table). The next best model was (1,0,0)(3,1,0)12. Adding meteorological covariates to either of these generally resulted in increased error.
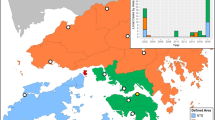
Map of included states.
States with median monthly incidence greater than zero during the training and development periods (1985–2007) were selected for forecasting model development (labeled). This figure was produced using the statistical computing environment R, version 3.2.3 (http://www.R-project.org).
Forecasting metrics for all models in Mexico and 17 Mexican states.
MAE (A) and R2 (B) values are shown for each of 39 models at every prediction horizon (grey lines). The optimum local (red, dashed) and common (blue, solid) models are superimposed. Full detail for all models is shown in Fig. 1 for all of Mexico and Figure S1 for each state.
Nine of the seventeen local models, i.e. the models with minimum average relative MAE across the 1–3 month prediction horizons, included meteorological variables (Fig. 3). Post-evaluation period coefficients for the local and common models are shown in the Supplementary Table.
Prospective forecasts
At the national and state level we used the analysis described above to implement prospective forecasts for the validation period, 2008–2012, using the local and common models. Both models tended to capture seasonality and some of the inter-annual variability (Fig. 4A). However, they underestimated the magnitude on numerous occasions in different locations, particularly during the epidemic of 2010. This was most pronounced in Jalisco and Nayarit. Of the 18 time-series analyzed (17 state-level, 1 national-level), stationarity varied, with 7 potentially non-stationary states.
Prospective prediction evaluation over the 5-year validation period (2008–2012).
The local (red) and common (blue) 3-month ahead forecasts are compared to reported dengue incidence (black, dashed lines) (A). The relative MAE compares the local model (red) to the common model (blue) over the entire 5-year validation period for individual locations (B). Values less than one indicate decreased error, i.e. improved performance, of the local model relative to the common model. Across all locations the number of locations in which the local model is more accurate than the common model declines at increasing prediction horizons (C) (red = local, blue = common, grey = the local and common models are the same). The relative MAE over all locations for the local model increases at longer prediction horizons.
The relative performance of the two models varied by location and prediction horizon (Fig. 4B). In most locations, the local models were more accurate than the common model for predictions at 1–2 months (Fig. 4C). At 3–4 months, the accuracy was similar and at 5–6 months the common model was more accurate. Generally, the difference between the two models was small. The local model was at least 10% more accurate than the common model at a total of 6 horizons in three states – Colima (1-month horizon), Jalisco (1–2 month horizons) and Morelos (3–5 month horizons). The common model was 10% better than the local model in seven states for a total of 17 prediction horizons. Taking the average of the differences across all locations (national and states), the common model was approximately 0.1% more accurate than the local model at 1- and 2-month horizons, with this difference increasing at longer horizons (Fig. 4D). Averaged across all locations, the common model was more than 4% more accurate at horizons of 3–6 months.
Finally, we assessed the uncertainties in predictions (Fig. 5 - national, Supplementary Figure 2 – national and states). Forecasts for 1-month horizons had some ability to confidently distinguish a low season from a high season and to a lesser extent at a 2-month horizon. However at 3-months and beyond, the expected number of cases in the peak transmission season generally ranged from zero or a very low number of cases to more cases than have ever been reported for both the local and common models.
Prospective predictions with uncertainty.
Forecasts from the national (1,0,0)(3,1,0)12 model with 95% Confidence Intervals are compared to reported dengue incidence (black, dashed lines). The (1,0,0)(2,1,0)12 model and models for each state are shown in Figure S2.
Discussion
Increasing data availability and novel analytical tools have led to a growth in research on infectious disease forecasting. As these efforts move towards real-time implementation for use by public health decision makers, it is vital that we move towards a common understanding of how forecasts and the accompanying uncertainty should be reported, how models should be evaluated and what methodologies work well in which situations. Prediction efforts should start with a key public health objective. For dengue, a global public health problem that can affect millions of people per year, prediction of epidemics is a valuable objective because local incidence varies substantially from year to year. If dengue epidemics could be predicted, interventions such as vector control and preparing healthcare systems for a surge of patients, could reduce the impact. The accuracy and uncertainty of those predictions would have a direct effect on the cost-effectiveness of those measures.
Here we evaluated the forecasting capability of SARIMA models for predicting dengue incidence in Mexico and 17 Mexican states up to 6 months into the future. Importantly, this is a mature statistical framework used by many other dengue forecasters11,14,15,18,19,24,25,27,35,37,40,43,45,46,47. We compared 39 different models from the most simplistic, expecting future incidence to be the average of past incidence, to relatively complex seasonal autoregressive models incorporating weather covariates.
For each state and all prediction horizons, models including seasonality via a naïve monthly term or weather variables were more accurate than the constant model (Fig. 6). For some states, weather data slightly improved prediction at short time scales compared to the naïve seasonal model. These differences may result from ecological heterogeneities that lead to different transmission dynamics in different places54. Alternatively, they may represent slightly better correlated covariates from a selection of highly correlated lagged variables that capture seasonality or confound seasonality with autocorrelation. This potentially leads to overfitting. In Michoacán for example, the local model including temperature performed poorly in the out-of-sample validation period. Regardless of their cause, the improvements resulting from inclusion of weather variables were generally very slight and only Jalisco had a clear improvement in relative accuracy in both the evaluation and validation datasets.
Prediction horizons.
The relative MAEs compared to the constant model (grey line) are shown in transparent lines for all locations at all prediction horizons. Models including only weather covariates are shown in orange, models containing only short-term autocorrelation are shown in red and models containing both short-term autocorrelation and seasonality (using weather variables or seasonal autocorrelation) are shown in blue. The average relative MAE across all locations is shown in solid lines for four key representative models.
Models including short-term autocorrelation meanwhile had improved accuracy for short-term prediction compared to seasonal models (Fig. 6). However, the strongest performance was attained by combining short-term autocorrelation and seasonality. The strong performance of the (1,0,0)(2,1,0)12 and (1,0,0)(3,1,0)12 models across states indicates that this type of model is a good reference model for dengue prediction. These models captured the short-term autocorrelation, but also a long-term negative autocorrelation of seasonal differences with coefficients of declining strength at increasing lags. In more general terms, this means that following a season with a substantial increase in cases, there will likely be fewer cases in subsequent seasons with that dampening decreasing over time. This makes sense for dengue as heterologous and homologous immunity can transiently limit transmissibility following large outbreaks55 and endemic dengue exhibits clear multiyear periodicity56.
While we have used a set of common climate variables in our analysis, considering additional climate covariates could provide additional information or benefits in predictive accuracy. Numerous studies have shown correlations between dengue cases and temperature, relative humidity and precipitation as indicated in the introduction as well as absolute humidity, more recently57,58. Since temperature, relative humidity and precipitation are closely related to absolute humidity, we do not expect that absolute humidity or other highly correlated climate variables will yield significant improvements to the model performance presented here. The framework nonetheless provides a straightforward and comprehensive procedure for assessing the predictive value of these variables or any others.
While this investigation revealed clear differences between models, it also revealed clear limitations to all the assessed models. At the 1 month horizon, R2 for the optimal models rarely exceeded 0.8 and accuracy rapidly declined for longer horizons. Furthermore, although R2 and mean absolute error can be used to assess and compare model fit, they are not sufficient for determining public health utility. As shown in Fig. 4A, in many cases both the local and common models failed to predict major epidemics at a 3-month horizon. The uncertainty in the predictions shown in Fig. 5 and Figure S2 reflects this and is large enough that there can be little expected public health utility at prediction horizons beyond a month with these models alone.
These findings capture broader challenges in the field of infectious disease forecasting. Published models vary in both approach and results. As shown here, numerous approaches can yield similar results, yet there is still variability in results. That variability may capture true heterogeneity or it may represent practically insignificant differences between essentially very similar models. For dengue model development, models incorporating both autocorrelation and seasonality, such as the (1,0,0)(2,1,0)12 model, should always be used as a baseline for comparison. Despite not including any data other than historical dengue data, this model captured a substantial amount of variation in dengue incidence. It therefore provides an easy benchmark for identifying substantive advances in dengue prediction.
We did not explore an exhaustively large space of possible prediction models, choosing instead to focus on the SARIMA framework. These models are widely used and accepted as robust tools for time-series prediction, but their limitations for dengue are clear. Other types of model frameworks and data could and should be explored for use instead of or in combination with these types of models. Other approaches used for forecasting dengue incidence include a variety of generalized linear models, machine learning techniques and incorporation of novel data sources12,13,16,19,20,21,22,23,26,27,28,31,33,34,36,37,38,39,41,43,44,47. Mechanistic approaches may also be required specifically to capture changes in human immunity in response to past infection5,6,55. Other types of data such as vector surveillance data and DENV serotype- and genotype-specific data may also be critical. Furthermore, the inclusion of information from disparate (and complementary) disease-related data sources, such as cloud-based electronic health records, Twitter micro-blogs and Google searches has been shown to improve short-term influenza forecasts substantially59.
With new approaches, robust benchmarking, testing and validation will be critical to advancing the dengue forecasting. Here, we used 28 years of historical data to establish three datasets: training, evaluation and validation. For every model considered, forecasts were made stepwise for every month of the evaluation period. Performance over this period was used to select two models, the common, baseline model and a local short-term model. The relative performance of these two models was then evaluated on the independent validation dataset. This framework follows the standard for evaluating prediction models as developed for machine learning60. Modeling efforts that leave out or combine the testing and validation components can lead to over-fitted models that perform poorly when used for prospective prediction, the ultimate goal. For example, if the original Google Flu Trends (GFT) work on influenza prediction61 used a similar framework, the benefits and limitations of the approach could have been better understood. Several years later, it became clear that at key times the GFT-based predictions were substantially off and that a simple autoregressive model had comparable performance62,63.
This study, like most, was restricted to archived historical data. While we took care to limit every forecast to data from before that time point and separate the evaluation and validation datasets, this is not the same as making truly prospective forecasts. Real-time forecasting is the objective and requires an extensive operational pipeline that can take raw real-time surveillance data (usually only partially observed) and produce accurate, calibrated forecasts with appropriately stated uncertainty. The work presented here does not meet these criteria. Rather, it helps to build the foundation for those systems, as a robust assessment of forecast performance on historical data is the best indicator of prospective performance.
We anticipate that the next decade will bear witness to a rapid maturation of techniques, methods and frameworks that will increase our capacity to generate accurate, timely and appropriately calibrated disease forecasts. With the growth of this field it is essential to establish robust methods for forecast development and evaluation. The first step in this process is to work with public health decision makers to identify appropriate targets and data. Next, as shown here, the data need to be clearly defined and separated into development and validation datasets comparing predictions to at least one baseline model that is not completely naïve. Model development coupled with systematic evaluation is critical for the future implementation of infectious disease forecasting to address real-time public health needs.
Additional Information
How to cite this article: Johansson, M. A. et al. Evaluating the performance of infectious disease forecasts: A comparison of climate-driven and seasonal dengue forecasts for Mexico. Sci. Rep. 6, 33707; doi: 10.1038/srep33707 (2016).
References
Brady, O. J. et al. Refining the global spatial limits of dengue virus transmission by evidence-based consensus. PLoS Negl Trop Dis 6, e1760, 10.1371/journal.pntd.0001760 (2012).
Mexico Secretariat of Health. Anuarios de Morbilidad, http://www.epidemiologia.salud.gob.mx/anuario/html/anuarios.html (accessed on May 1st, 2013).
Beatty, M. E. et al. Best practices in dengue surveillance: a report from the Asia-Pacific and Americas Dengue Prevention Boards. PLoS Negl Trop Dis 4, e890, 10.1371/journal.pntd.0000890 (2010).
Racloz, V., Ramsey, R., Tong, S. & Hu, W. Surveillance of dengue fever virus: a review of epidemiological models and early warning systems. PLoS Negl Trop Dis 6, e1648, 10.1371/journal.pntd.0001648 (2012).
Johansson, M. A., Hombach, J. & Cummings, D. A. Models of the impact of dengue vaccines: a review of current research and potential approaches. Vaccine 29, 5860–5868, S0264-410X(11)00906-6 [pii]. 10.1016/j.vaccine.2011.06.042 (2011).
Reiner, R. C. et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. Journal of The Royal Society Interface 10, 20120921 (2013).
Christophers, S. R. Aedes aegypti (L.): The Yellow Fever Mosquito . (The University Press, 1960).
Focks, D. A., Haile, D. G., Daniels, E. & Mount, G. A. Dynamic life table model for Aedes aegypti (Diptera: Culicidae): analysis of the literature and model development. J. Med. Entomol. 30, 1003–1017 (1993).
Brady, O. J. et al. Modelling adult Aedes aegypti and Aedes albopictus survival at different temperatures in laboratory and field settings. Parasites & vectors 6, 351, 10.1186/1756-3305-6-351 (2013).
Chan, M. & Johansson, M. A. The incubation periods of dengue viruses. PLoS One 7, e50972, 10.1371/journal.pone.0050972 (2012).
Hu, W., Clements, A., Williams, G. & Tong, S. Dengue fever and El Nino/Southern Oscillation in Queensland, Australia: a time series predictive model. Occup. Environ. Med. 67, 307–311, 10.1136/oem.2008.044966 (2010).
Karim, M. N., Munshi, S. U., Anwar, N. & Alam, M. S. Climatic factors influencing dengue cases in Dhaka city: a model for dengue prediction. Indian J. Med. Res. 136, 32–39 (2012).
Depradine, C. & Lovell, E. Climatological variables and the incidence of Dengue fever in Barbados. Int. J. Environ. Health Res. 14, 429–441 (2004).
Luz, P. M., Mendes, B. V., Codeco, C. T., Struchiner, C. J. & Galvani, A. P. Time series analysis of dengue incidence in Rio de Janeiro, Brazil. Am. J. Trop. Med. Hyg. 79, 933–939 (2008).
Martinez, E. Z., Silva, E. A. & Fabbro, A. L. A SARIMA forecasting model to predict the number of cases of dengue in Campinas, State of Sao Paulo, Brazil. Rev. Soc. Bras. Med. Trop. 44, 436–440 (2011).
Lowe, R. et al. The development of an early warning system for climate-sensitive disease risk with a focus on dengue epidemics in Southeast Brazil. Stat. Med. 32, 864–883, 10.1002/sim.5549 (2013).
Gomes, A. F., Nobre, A. A. & Cruz, O. G. Temporal analysis of the relationship between dengue and meteorological variables in the city of Rio de Janeiro, Brazil, 2001-2009. Cad. Saude Publica 28, 2189–2197 (2012).
Rua-Uribe, G. L., Suarez-Acosta, C., Chauca, J., Ventosilla, P. & Almanza, R. Modelling the effect of local climatic variability on dengue transmission in Medellin (Colombia) by means of time series analysis. Biomedica: revista del Instituto Nacional de Salud 33 Suppl 1, 142–152 (2013).
Eastin, M. D., Delmelle, E., Casas, I., Wexler, J. & Self, C. Intra-and interseasonal autoregressive prediction of dengue outbreaks using local weather and regional climate for a tropical environment in Colombia. The American journal of tropical medicine and hygiene 91, 598–610 (2014).
Torres, C., Barguil, S., Melgarejo, M. & Olarte, A. Fuzzy model identification of dengue epidemic in Colombia based on multiresolution analysis. Artif. Intell. Med. 60, 41–51 (2014).
Fuller, D. O., Troyo, A. & Beier, J. C. El Nino Southern Oscillation and vegetation dynamics as predictors of dengue fever cases in Costa Rica. Environmental research letters: ERL [Web site] 4, 140111–140118, 10.1088/1748-9326/4/1/014011 (2009).
Wang, C., Jiang, B., Fan, J., Wang, F. & Liu, Q. A Study of the Dengue Epidemic and Meteorological Factors in Guangzhou, China, by Using a Zero-Inflated Poisson Regression Model. Asia. Pac. J. Public Health, 10.1177/1010539513490195 (2013).
Stewart-Ibarra, A. M. & Lowe, R. Climate and non-climate drivers of dengue epidemics in southern coastal Ecuador. The American journal of tropical medicine and hygiene 88, 971–981 (2013).
Gharbi, M. et al. Time series analysis of dengue incidence in Guadeloupe, French West Indies: forecasting models using climate variables as predictors. BMC Infect Dis 11, 166, 10.1186/1471-2334-11-166 (2011).
Bhatnagar, S., Lal, V., Gupta, S. D. & Gupta, O. P. Forecasting incidence of dengue in Rajasthan, using time series analyses. Indian J. Public Health 56, 281–285, 10.4103/0019-557X.106415 (2012).
Halide, H. & Ridd, P. A predictive model for Dengue Hemorrhagic Fever epidemics. Int. J. Environ. Health Res. 18, 253–265, 10.1080/09603120801966043 (2008).
Sitepu, M. S. et al. Temporal Patterns and a Disease Forecasting Model of Dengue Hemorrhagic Fever in Jakarta Based on 10 Years of Surveillance Data. The Southeast Asian journal of tropical medicine and public health 44, 206–217 (2013).
Hurtado-Díaz, M., Riojas-Rodríguez, H., Rothenberg, S. J., Gomez-Dantés, H. & Cifuentes, E. Short communication: impact of climate variability on the incidence of dengue in Mexico. Trop. Med. Int. Health 12, 1327–1337 (2007).
Descloux, E. et al. Climate-based models for understanding and forecasting dengue epidemics. PLoS Negl Trop Dis 6, e1470, 10.1371/journal.pntd.0001470 (2012).
Buczak, A. L., Koshute, P. T., Babin, S. M., Feighner, B. H. & Lewis, S. H. A data-driven epidemiological prediction method for dengue outbreaks using local and remote sensing data. BMC medical informatics and decision making 12, 124, 10.1186/1472-6947-12-124 (2012).
Su, G. L. Correlation of climatic factors and dengue incidence in Metro Manila, Philippines. Ambio 37, 292–294 (2008).
Buczak, A. L. et al. Prediction of high incidence of dengue in the Philippines. PLoS Negl Trop Dis 8, e2771, 10.1371/journal.pntd.0002771 (2014).
Schreiber, K. V. An investigation of relationships between climate and dengue using a water budgeting technique. Int. J. Biometeorol. 45, 81–89 (2001).
Wu, Y., Lee, G., Fu, X. & Hung, T. Detect climatic factors contributing to dengue outbreak based on wavelet, support vector machines and genetic algorithm. Institute of High Performance Computing. URL http://oar.a-star.edu.sg:80/jspui/handle/123456789/700 (2008).
Wilder-Smith, A., Earnest, A., Tan, S., Ooi, E. & Gubler, D. Lack of association of dengue activity with haze. Epidemiol. Infect. 138, 962–967 (2010).
Earnest, A., Tan, S. & Wilder-Smith, A. Meteorological factors and El Nino Southern Oscillation are independently associated with dengue infections. Epidemiol. Infect. 140, 1244–1251 (2012).
Earnest, A., Tan, S. B., Wilder-Smith, A. & Machin, D. Comparing statistical models to predict dengue fever notifications. Computational and mathematical methods in medicine 2012 (2012).
Hii, Y. L., Zhu, H., Ng, N., Ng, L. C. & Rocklöv, J. Forecast of dengue incidence using temperature and rainfall. PLoS Negl Trop Dis 6.11, e1908 (2012).
Goto, K. et al. Analysis of effects of meteorological factors on dengue incidence in Sri Lanka using time series data. PLoS One 8, e63717, 10.1371/journal.pone.0063717 (2013).
Wu, P. C., Guo, H. R., Lung, S. C., Lin, C. Y. & Su, H. J. Weather as an effective predictor for occurrence of dengue fever in Taiwan. Acta Trop . 103, 50–57 (2007).
Yu, H.-L., Yang, S.-J., Yen, H.-J. & Christakos, G. A spatio-temporal climate-based model of early dengue fever warning in southern Taiwan. Stochastic Environmental Research and Risk Assessment 25, 485–494 (2011).
Barbazan, P., Yoksan, S. & Gonzalez, J. P. Dengue hemorrhagic fever epidemiology in Thailand: description and forecasting of epidemics. Microbes Infect 4, 699–705 (2002).
Silawan, T., Singhasivanon, P., Kaewkungwal, J., Nimmanitya, S. & Suwonkerd, W. Temporal patterns and forecast of dengue infection in Northeastern Thailand. Southeast Asian J. Trop. Med. Public Health 39, 90–98 (2008).
Tipayamongkholgul, M., Fang, C.-T., Klinchan, S., Liu, C.-M. & King, C.-C. Effects of the El Niño-Southern Oscillation on dengue epidemics in Thailand, 1996-2005. BMC public health 9, 422 (2009).
Wongkoon, S., Jaroensutasinee, M. & Jaroensutasinee, K. Development of temporal modeling for prediction of dengue infection in Northeastern Thailand. Asian Pacific journal of tropical medicine 5, 249–252 (2012).
Wongkoon, S., Jaroensutasinee, M. & Jaroensutasinee, K. Assessing the temporal modelling for prediction of dengue infection in northern and northeastern, Thailand. Tropical biomedicine 29, 339–348 (2012).
Phung, D. et al. Identification of the prediction model for dengue incidence in Can Tho city, a Mekong Delta area in Vietnam. Acta Trop . 141, 88–96, 10.1016/j.actatropica.2014.10.005 (2015).
Brady, O. J., Smith, D. L., Scott, T. W. & Hay, S. I. Dengue disease outbreak definitions are implicitly variable. Epidemics 11, 92–102, 10.1016/j.epidem.2015.03.002 (2015).
Box, G. E., Jenkins, G. M. & Reinsel, G. C. Time series analysis: forecasting and control . Vol. 734 (John Wiley & Sons, 2011).
Zeger, S. L. & Qaqish, B. Markov regression models for time series: a quasi-likelihood approach. Biometrics 44, 1019–1031 (1988).
Said, S. E. & Dickey, D. A. Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 71, 599–607 (1984).
Nishiura, H., Chowell, G., Heesterbeek, H. & Wallinga, J. The ideal reporting interval for an epidemic to objectively interpret the epidemiological time course. Journal of The Royal Society Interface, rsif20090153 (2009).
R Core Team. R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria. URL http://www.R-project.org (2013).
Johansson, M. A., Dominici, F. & Glass, G. E. Local and Global Effects of Climate on Dengue Transmission in Puerto Rico. PLoS Negl Trop Dis 3, e382 (2009).
Reich, N. G. et al. Interactions between serotypes of dengue highlight epidemiological impact of cross-immunity. J R Soc Interface 10, 20130414, 10.1098/rsif.2013.0414 (2013).
Johansson, M. A., Cummings, D. A. & Glass, G. E. Multiyear climate variability and dengue–El Nino southern oscillation, weather and dengue incidence in Puerto Rico, Mexico and Thailand: a longitudinal data analysis. PLoS Med . 6, e1000168, 10.1371/journal.pmed.1000168 (2009).
Xu, H.-Y. et al. Statistical modeling reveals the effect of absolute humidity on dengue in Singapore. PLoS Negl Trop Dis 8, e2805 (2014).
Campbell, K. M., Lin, C., Iamsirithaworn, S. & Scott, T. W. The complex relationship between weather and dengue virus transmission in Thailand. The American journal of tropical medicine and hygiene 89, 1066–1080 (2013).
Santillana, M., Nguyen, A. T., Dredze, M., Paul, M. J. & Brownstein, J. S. Combining Search, Social Media and Traditional Data Sources to Improve Influenza Surveillance. arXiv preprint arXiv. 1508, 06941 (2015).
Murphy, K. P. Machine learning: a probabilistic perspective . (MIT press, 2012).
Ginsberg, J. et al. Detecting influenza epidemics using search engine query data. Nature 457, 1012–1014 (2009).
Lazer, D., Kennedy, R., King, G. & Vespignani, A. The parable of Google Flu: traps in big data analysis. Science 343 (2014).
Yang, S., Santillana, M. & Kou, S. Accurate estimation of influenza epidemics using Google search data via ARGO. Proceedings of the National Academy of Sciences 112, 14473–14478 (2015).
Acknowledgements
This work was supported by the National Institute of General Medical Sciences at the National Institutes of Health (Grant 1U54GM088558), the National Institute of Allergy and Infectious Diseases at the National Institutes of Health (Grants R21 AI115173-01 and R01 AI102939-01) and the National Library of Medicine at the National Institutes of Health (Grant R01 LM010812-04).
Author information
Authors and Affiliations
Contributions
M.A.J., J.S.B. and M.S. planned research; M.A.J., A.H. and M.S. collected data; M.A.J., N.G.R., A.H. and M.S. conducted analyses; all authors wrote and approved of manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Johansson, M., Reich, N., Hota, A. et al. Evaluating the performance of infectious disease forecasts: A comparison of climate-driven and seasonal dengue forecasts for Mexico. Sci Rep 6, 33707 (2016). https://doi.org/10.1038/srep33707
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33707
This article is cited by
-
An interpretable hybrid predictive model of COVID-19 cases using autoregressive model and LSTM
Scientific Reports (2023)
-
Weather integrated multiple machine learning models for prediction of dengue prevalence in India
International Journal of Biometeorology (2023)
-
Comparing Short-Term Univariate and Multivariate Time-Series Forecasting Models in Infectious Disease Outbreak
Bulletin of Mathematical Biology (2023)
-
Impact of environmental factors on the spread of dengue fever in Sri Lanka
International Journal of Environmental Science and Technology (2022)
-
Incorporating human mobility data improves forecasts of Dengue fever in Thailand
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.