Abstract
The one-parameter scaling theory of localization predicts that all states in a disordered two-dimensional system with broken time reversal symmetry are localized even in the presence of strong spin-orbit coupling. While at constant strong magnetic fields this paradigm fails (recall the quantum Hall effect), it is believed to hold at weak magnetic fields. Here we explore the nature of quantum states at weak magnetic field and strongly fluctuating spin-orbit coupling, employing highly accurate numerical procedure based on level spacing distribution and transfer matrix technique combined with one parameter finite-size scaling hypothesis. Remarkably, the metallic phase, (known to exist at zero magnetic field), persists also at finite (albeit weak) magnetic fields, and eventually crosses over into a critical phase, which has already been confirmed at high magnetic fields. A schematic phase diagram drawn in the energy-magnetic field plane elucidates the occurrence of localized, metallic and critical phases. In addition, it is shown that nearest-level statistics is determined solely by the symmetry parameter β and follows the Wigner surmise irrespective of whether states are metallic or critical.
Similar content being viewed by others
Introduction
The one-parameter scaling theory (1PST) of localization1,2,3,4 has been instrumental in our current understanding of the metal-insulator transition (MIT) in disordered non-interacting systems. This theory assumes that the scaling function β(g), determining how the dimensionless conductance g changes with system size, depends only on g itself, and predicts that the occurrence of a MIT depends on the system dimensionality and its symmetry under time reversal (TR) and spin rotation (SR)5,6,7,8,9. In two dimensions (2D), for both the Gaussian orthogonal ensemble (GOE), where TR and SR symmetries are preserved, and the Gaussian unitary ensemble (GUE), where TR symmetry is violated, the 1PST asserts that all states are localized. On the other hand, for the Gaussian symplectic ensemble (GSE), where TR symmetry is preserved while SR symmetry is violated, there is a MIT. Thus, according to 1PST, despite the presence of spin-orbit scattering (SOS), even an infinitesimal magnetic field that breaks TR causes all states to be localized. At high magnetic fields, the occurrence of the quantum Hall effect indicates that extended states do exist, since in this regime, 1PST should be modified to incorporate two scaling parameters (e.g. the longitudinal conductance and the Hall conductance)10,11,12,13. The question addressed in this work is whether 1PST is still valid (as is widely believed) at weak magnetic fields and spatially fluctuating SOS. Our answer is negative. We show that under these conditions, the band of extended states that exists at zero magnetic field persists at weak magnetic fields, and eventually, with increasing magnetic field, crosses over at some critical field Bc into a band of critical states that has been shown to exist at strong magnetic fields14. For 0 ≤ B < Bc the bandwidth [−Ec(B), Ec(B)] between the two mobility edges is a slowly decreasing function of B.
To substantiate our claim, we study the nature of non-interacting electronic states in 2D under the influence of weak magnetic field, disorder potential and strongly fluctuating SOS, and carry out two kinds of numerical calculations: The first one studies the nearest level spacing distribution in various energy regimes, in order to identify the localized phase and the appropriate universality classes5,6,7,8,9. The second one consists of highly accurate procedure for identifying MIT, based on the transfer matrix technique and finite-size scaling arguments.
Results
Model
In weak magnetic fields, the Landau levels mix and projection on the lowest Landau level is meaningless. An appropriate and convenient procedure is then to consider a tight-binding model for 2D electrons hopping on a square lattice of unit lattice constant. The lattice sites are labeled as i = (ni, mi), with 1 ≤ ni ≤ L and 1 ≤ mi ≤ M integers. The Hamiltonian reads,

Here  (ci,σ) is the electron creation (annihilation) operator at site i with spin projection σ = ±, and 〈ij〉 denotes nearest-neighbor lattice sites. The on-site energies εi are randomly distributed in [−W/2, W/2], (hereafter we take W = 1 and as long as
(ci,σ) is the electron creation (annihilation) operator at site i with spin projection σ = ±, and 〈ij〉 denotes nearest-neighbor lattice sites. The on-site energies εi are randomly distributed in [−W/2, W/2], (hereafter we take W = 1 and as long as  , the results are similar. The model does not support any extended states for W > Wc.), and the magnetic field is introduced by the Peierls substitution in which phase factors
, the results are similar. The model does not support any extended states for W > Wc.), and the magnetic field is introduced by the Peierls substitution in which phase factors  multiply the hopping amplitudes, where
multiply the hopping amplitudes, where  is the vector potential15,16. The dimensionless parameter B is defined such that magnetic flux through a unit cell is Bϕ0 where ϕ0 ≡ hc/e is the quantum flux unit. Accordingly, B is a measure of the magnetic field strength in this lattice model. The SOS is encoded by random SU(2) matrices Vij acting on the electron spin that hops between sites i and j, defined as,
is the vector potential15,16. The dimensionless parameter B is defined such that magnetic flux through a unit cell is Bϕ0 where ϕ0 ≡ hc/e is the quantum flux unit. Accordingly, B is a measure of the magnetic field strength in this lattice model. The SOS is encoded by random SU(2) matrices Vij acting on the electron spin that hops between sites i and j, defined as,

where αij and γij are uniformly and independently distributed in a range [0, 2π], while cosβij is uniformly distributed in [−1, 1]. This model is hereafter referred to as the 2DSU model. For B = 0 it displays the (so called) symplectic MIT, pertaining to systems with conserved TR and broken SR symmetries, as also predicted within 1PST17. For strong magnetic field (e.g. B ≥ 1/5) the 2DSU model exhibits a Berezinskii-Kosterlitz-Thouless transition (BKTT) between a band of localized states and a band of critical states14. In the following we concentrate on the physics at weak magnetic fields, (explicitly, we even consider B < 10−4).
Level statistics
Consider first the distribution P(s) of nearest level spacings s (in units of the mean level spacing). This analysis enables the distinction between localized and extended states, and in the latter case, identification of the relevant universality class: More concretely, for localized states, it is expected to follow the Poisson distribution PLoc(s) = exp[−s], while for extended states, Pβ(s) is specified by the symmetry parameter β = 1, 2, 4 (corresponding respectively to GOE, GUE and GSE). These three distributions are excellently approximated by the Wigner surmise expressions Pβ(s) = C1(β)sβexp[−C2(β)s2]. (The constants C1 and C2 are determined by normalization conditions for probability and unit mean level-spacing 〈1〉 = 〈s〉 = 1).
For the actual computation, a finite lattice of size M × (M + 1) is considered and periodic boundary conditions are imposed on both directions using the almost antisymmetric gauge (see methods). That makes it possible to treat a weak field  . The Hamiltonian (1) is diagonalized, yielding all eigenvalues {E} and normalized wave functions {ψE(ni, mi)} for each value of B and M. As shown in Fig. 1, P(s) for B = 0 and strong SOS displays, for a wide energy range −2.5 ≤ E ≤ −0.5, GSE statistics (data in black squares, theory in black curve). It suggests the existence of a band of extended states within the symplectic ensemble, commensurate with the prediction of 1PST17. Remarkably, adding a single flux through the entire area, corresponding to B = 1/10100 for M = 100 (red circles) is already sufficient to modify Pβ=4(s) into Pβ=2(s), where the level statistics follows the GUE Wigner surmise (red line in Fig. 1). In any case, the fact that in both cases P(s) follows the Wigner surmise and not Poisson distribution indicates that these are metallic-like states, where level repulsion occurs at small s. This behavior persists for different system sizes and for all B > 0. On the other hand, for energies below the mobility edge (blue shapes and curve in Fig. 1), P(s) obeys Poisson statistics, as expected for localized states. Thus, our analysis of nearest level spacing distribution suggests that states in the same energy range (as for B = 0) are still extended at finite magnetic field even though this 2D system now belongs to the unitary class. The wide range of parameters and energies where the GUE statistics has been observed, substantiates that this result is robust, namely, it is not due to finite size effects.
. The Hamiltonian (1) is diagonalized, yielding all eigenvalues {E} and normalized wave functions {ψE(ni, mi)} for each value of B and M. As shown in Fig. 1, P(s) for B = 0 and strong SOS displays, for a wide energy range −2.5 ≤ E ≤ −0.5, GSE statistics (data in black squares, theory in black curve). It suggests the existence of a band of extended states within the symplectic ensemble, commensurate with the prediction of 1PST17. Remarkably, adding a single flux through the entire area, corresponding to B = 1/10100 for M = 100 (red circles) is already sufficient to modify Pβ=4(s) into Pβ=2(s), where the level statistics follows the GUE Wigner surmise (red line in Fig. 1). In any case, the fact that in both cases P(s) follows the Wigner surmise and not Poisson distribution indicates that these are metallic-like states, where level repulsion occurs at small s. This behavior persists for different system sizes and for all B > 0. On the other hand, for energies below the mobility edge (blue shapes and curve in Fig. 1), P(s) obeys Poisson statistics, as expected for localized states. Thus, our analysis of nearest level spacing distribution suggests that states in the same energy range (as for B = 0) are still extended at finite magnetic field even though this 2D system now belongs to the unitary class. The wide range of parameters and energies where the GUE statistics has been observed, substantiates that this result is robust, namely, it is not due to finite size effects.
P(s) for W = 1, various magnetic field strengths B = 0, 1/10100, 1/5, various system sizes M = 50, 100, and in various energy ranges.
Data are averaged over 1500 ensembles. It is evident that for B > 0 (no matter how small), P(s) corresponding to both critical and extended states fits well into the Wigner surmise for GUE (red solid line), whereas P(s) corresponding to extended states at B = 0 agree with the Wigner surmise for GSE (black solid line). The dashed line corresponds to the distribution suggested in refs 27, 28, 29 assuming ν = ∞ ⇒ γ = 1 since the localization length at a BKTT diverges faster than a power-law. For localized states with energies −3.55 ≤ E ≤ −3.50 far from BKTT mobility edge ( for B = 1/5), whose localization length is much smaller than the sample size (M = 100), P(s) agrees with the Poisson distribution (blue solid line).
for B = 1/5), whose localization length is much smaller than the sample size (M = 100), P(s) agrees with the Poisson distribution (blue solid line).
Localization length
In order to corroborate our finding on the existence of extended states at weak magnetic field (that is so far based on level spacing analysis of finite size systems), we directly evaluate the localization length ξ(E, B) of the 2D system (up to a multiplicative constant) employing the transfer matrix technique18,19. Within this procedure, one evaluates the localization length λM of a stripe of width M and (virtually infinite) length L > 106. According to the scaling analysis, the renormalized localization length of the strip,  , increases (decreases) with M for extended (localized) states and is independent of M for critical states. For the 2DSU model, Fig. 2(a,c,e) display
, increases (decreases) with M for extended (localized) states and is independent of M for critical states. For the 2DSU model, Fig. 2(a,c,e) display  vs E for B = 0, B = 1/1000, and B = 1/500. It is clear from these figures that the system undergoes an Anderson MIT, since all curves for different M cross at two mobility edges at which
vs E for B = 0, B = 1/1000, and B = 1/500. It is clear from these figures that the system undergoes an Anderson MIT, since all curves for different M cross at two mobility edges at which  changes sign. The results of Fig. 2(a) just reconfirm the familiar symplectic MIT, but the MIT displayed in Fig. 2(c,e) occurring at mobility edges Ec = ±3.245 and ±3.242 is novel, and agrees with the conclusion based on level-spacing analysis: In the presence of strong SOS fluctuations, a band of extended states occurs in 2D systems even when its Hamiltonian breaks TR symmetry.
changes sign. The results of Fig. 2(a) just reconfirm the familiar symplectic MIT, but the MIT displayed in Fig. 2(c,e) occurring at mobility edges Ec = ±3.245 and ±3.242 is novel, and agrees with the conclusion based on level-spacing analysis: In the presence of strong SOS fluctuations, a band of extended states occurs in 2D systems even when its Hamiltonian breaks TR symmetry.
The left panel displays  vs E calculated for disorder strength W = 1 and for three values of the magnetic field (a) B = 0, (c) B = 1/1000, and (e) B = 1/500 for M = 32 (squares), 48 (circles), 64 (up-triangles), 80 (down-triangles), and 96 (left-triangles). The scaling function obtained from (a,c,e) by collapsing data of
vs E calculated for disorder strength W = 1 and for three values of the magnetic field (a) B = 0, (c) B = 1/1000, and (e) B = 1/500 for M = 32 (squares), 48 (circles), 64 (up-triangles), 80 (down-triangles), and 96 (left-triangles). The scaling function obtained from (a,c,e) by collapsing data of  near the transition points into a single curve ξ ~ (E − Ec)−ν are shown in (b) for B = 0, (d) for B = 1/1000, and (f) for B = 1/500.
near the transition points into a single curve ξ ~ (E − Ec)−ν are shown in (b) for B = 0, (d) for B = 1/1000, and (f) for B = 1/500.
One parameter finite-size scaling
To substantiate that these results are not merely due to finite size effects, we employ the one parameter finite-size scaling formalism, which is based on the hypothesis  , where x = M/ξ = CM/(E − Ec)−ν. Here C is a constant and ν is the localization-length critical exponent. For optimal values of Ec and ν, the scaling function f(x) should be smooth (actually there are two functions, one for the insulator and one for the metallic side). The numerical values of ν characterize the universality class of the MIT20. In Fig. 2(b) the different curves of Fig. 2(a), when plotted as function of x, indeed collapse on a smooth curve that represents the scaling function f(x). Here, for B = 0, this result reconfirms the criticality of the symplectic MIT. The value of ν (see first row of the Table 1) agrees with previous ones20,21,22. Remarkably, inspection of Fig. 2(d,f) shows that the collapse scenario occurs also at finite magnetic field, namely the different curves in Fig. 2(c,e) fall on a single smooth curve. Moreover, for these novel MIT at B > 0, the dependence of ν(B) on B is dramatic and even puzzling (see Table 1). This gradual increase of ν is most likely due to the transition from Anderson MIT to BKKT (where, by definition, ν → ∞, that occurs whenever B > Bc).
, where x = M/ξ = CM/(E − Ec)−ν. Here C is a constant and ν is the localization-length critical exponent. For optimal values of Ec and ν, the scaling function f(x) should be smooth (actually there are two functions, one for the insulator and one for the metallic side). The numerical values of ν characterize the universality class of the MIT20. In Fig. 2(b) the different curves of Fig. 2(a), when plotted as function of x, indeed collapse on a smooth curve that represents the scaling function f(x). Here, for B = 0, this result reconfirms the criticality of the symplectic MIT. The value of ν (see first row of the Table 1) agrees with previous ones20,21,22. Remarkably, inspection of Fig. 2(d,f) shows that the collapse scenario occurs also at finite magnetic field, namely the different curves in Fig. 2(c,e) fall on a single smooth curve. Moreover, for these novel MIT at B > 0, the dependence of ν(B) on B is dramatic and even puzzling (see Table 1). This gradual increase of ν is most likely due to the transition from Anderson MIT to BKKT (where, by definition, ν → ∞, that occurs whenever B > Bc).
 for different values of magnetic field.
for different values of magnetic field.It is known that at strong magnetic fields the Pruisken-Khmelnitzkii renormalization-group (RG) formalism is based on the two parameters σxx and σxy. Inclusion of SOS probably requires an additional parameter in the RG scheme, making it necessary to study the RG flow in three-dimensional space. Such an advanced calculation is beyond the scope of this work. However, we would like to analyze the results based on the general and standard RG approach23. Generically one has several fixed points, each with its own basin of attraction, separated by separatrices, such that crossing a separatrix corresponds to a phase transition. In this case, all the physical points within the same basin of attraction flow to the same fixed point, and are described by the same critical exponent. This is the case, for example, for the Anderson transition for finite SOS at zero magnetic field. In accordance with these lines that a RG flow persists for finite small magnetic fields until the separatrix to the BKT fixed points at Bc, we want to have a single power-law divergence for B < Bc and a BKTT above. So we expect the following behavior,

such that F(E, B) will be some number in the limit E → Ec(B) for B < Bc, and  for B ≥ Bc. A possible choice is
for B ≥ Bc. A possible choice is

where G and μ are arbitrary constants. The effective crossover exponent ν(B) is defined by

where we eliminate the step function since we are looking at B < Bc. If we were to estimate Ec(B) perfectly, then, as mentioned above, the critical exponent will remain ν0 all the way to Bc. However, if we have an error because of the presence of the critical point at Bc, then our estimation  of Ec(B) will be somewhere between the true Ec(B) and Ec(Bc), say
of Ec(B) will be somewhere between the true Ec(B) and Ec(Bc), say  . Such that we substitute
. Such that we substitute  in the above expression:
in the above expression:

Fitting the numerical data with the expression above (see Fig. 3), we get  , α = 1/4, and Bc = 1/50 (G = 0.02 but is immaterial). The effective crossover exponent ν(B) demonstrates a good agreement with the numerical data. It is also shown there that the critical magnetic field is
, α = 1/4, and Bc = 1/50 (G = 0.02 but is immaterial). The effective crossover exponent ν(B) demonstrates a good agreement with the numerical data. It is also shown there that the critical magnetic field is  . The two analyses confirm the existence of extended states for
. The two analyses confirm the existence of extended states for  . Thus, our results indicate that in the presence of both magnetic field and strongly fluctuating spin-orbit interaction, the one-parameter scaling theory of localization fails and one needs more than one length scale to characterize the system.
. Thus, our results indicate that in the presence of both magnetic field and strongly fluctuating spin-orbit interaction, the one-parameter scaling theory of localization fails and one needs more than one length scale to characterize the system.
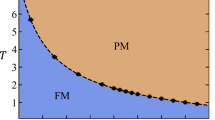
Phase diagram
A broader picture of the nature of states in the 2DSU model is obtained by combining the results of the present study with those of ref. 14, where the existence of a band of critical states at strong magnetic fields (B ≥ 1/5) has been demonstrated. It is found that Ec(B) is a slowly increasing function, and that somewhere around  the Anderson MIT (discussed here) crosses over into a BKTT discussed previously14. Elucidating the nature of this crossover is beyond our scope. It requires the calculations of
the Anderson MIT (discussed here) crosses over into a BKTT discussed previously14. Elucidating the nature of this crossover is beyond our scope. It requires the calculations of  for many points in the E-B plane, with the hope to establish a critical curve separating the two bands of metallic and critical states. The resulting phase diagram in the E-B plane is depicted in Fig. 4. The emerging picture is that the band of extended states known to exist at B = 0, persists for finite B, until strong enough magnetic field
for many points in the E-B plane, with the hope to establish a critical curve separating the two bands of metallic and critical states. The resulting phase diagram in the E-B plane is depicted in Fig. 4. The emerging picture is that the band of extended states known to exist at B = 0, persists for finite B, until strong enough magnetic field  it crosses over (either sharply or smoothly) into a band of critical states as discussed in ref. 14.
it crosses over (either sharply or smoothly) into a band of critical states as discussed in ref. 14.
Schematic phase diagram in the E-B plane displaying the occurrence of three phases of localized states (pink), metallic states (blue), and critical states (green).
Here the metallic states spread over the whole space (e.g. plane waves and Bloch states) which are distinct from the critical states who possess non-trivial multi-fractal structure. The black curve is Ec(B). See text for further details.
Discussion
Starting from the 2DSU model Hamiltonian (1), we focus on the localization issue at the weak field regime, starting at B = 0 where it is known to display MIT for system with the symplectic symmetry. Based on analyses of level statistics (Fig. 1) and localization length (Fig. 2), it has been demonstrated that a band of metallic states persists also for finite magnetic field  . Combined with our previous results14, we can suggest a schematic phase diagram in Fig. 4, that elucidates the nature of localization in the E-B plane under the influence of spatially random spin-orbit potential. Thus, the paradigm that all states in 2D disordered systems with unitary symmetry are localized should be reviewed when strong spin-orbit fluctuations are present. In other words, in contrast to the prediction of the one-parameter scaling theory of localization3, localization in 2D disordered systems is not unambiguously determined by its symmetry. This suggests that, similar to what happens in the quantum Hall regime (occurring at strong magnetic field, without SOS), a second parameter is required to describe the scaling of the dimensionless conductance. Obvious questions are how to introduce such a parameter, and how the RG flow will look like in the presence of this additional parameter. Presently, the answers remain a theoretical challenge. To experimentally detect our results, we predict that in thin layers of Mott insulators with spin-orbit coupling (like 5d transition metal oxides SrIrO3 and Sr2IrO424,25,26), the novel MIT occurs in the presence of small magnetic field.
. Combined with our previous results14, we can suggest a schematic phase diagram in Fig. 4, that elucidates the nature of localization in the E-B plane under the influence of spatially random spin-orbit potential. Thus, the paradigm that all states in 2D disordered systems with unitary symmetry are localized should be reviewed when strong spin-orbit fluctuations are present. In other words, in contrast to the prediction of the one-parameter scaling theory of localization3, localization in 2D disordered systems is not unambiguously determined by its symmetry. This suggests that, similar to what happens in the quantum Hall regime (occurring at strong magnetic field, without SOS), a second parameter is required to describe the scaling of the dimensionless conductance. Obvious questions are how to introduce such a parameter, and how the RG flow will look like in the presence of this additional parameter. Presently, the answers remain a theoretical challenge. To experimentally detect our results, we predict that in thin layers of Mott insulators with spin-orbit coupling (like 5d transition metal oxides SrIrO3 and Sr2IrO424,25,26), the novel MIT occurs in the presence of small magnetic field.
Remarkably, (and unlike the localization issue), level statistics is found to be determined solely by symmetry, whether states are metallic or critical. As shown in Fig. 1, for B = 0, P(s) follows the Wigner surmise for the GSE, while for B = 1/10100, P(s) follows the Wigner surmise for the GUE. Moreover, P(s) obeys the GUE statistics also for the band of critical states discussed in ref. 14. This latter band is obtained following BKTT at strong magnetic field. In contrast, for critical states around a mobility edge in a standard Anderson MIT, a novel P(s) statistics is suggested27,28,29. What we conclude here is that P(s) is the same for metallic and critical states and depends solely on symmetry.
Methods
In this section we show how to realize weak magnetic fields in a finite lattice model with periodic boundary conditions. Within the standard procedure of the Azbel-Hofstadter butterfly problem, one considers a square lattice of constant a and size q × q (where q is an integer) with site coordinates (na, ma) ≡ (n, m), and imposes the Landau gauge Ax = By. This means putting a vector potential equals ϕ0mp/(qa) on the link joining sites (n, m) and (n + 1, m), where ϕ0 = hc/e is the flux quantum and p = 1, 2, …, q represents the strength of the magnetic field. All site coordinates are considered modulo q to assure periodic boundary conditions. The magnetic flux per square is then equal to ϕ0p/q and the magnetic flux through the entire system is ϕ0pq.
In many cases, however, we need to tune the variation of flux through the entire system by a much smaller amount. As in the main text, we would like to study the system at very low magnetic fields, such that the total flux through the entire system is just ϕ0 and not qϕ0. Beside the important physical aspect, there is also a natural curiosity to expose how the energy curves behave “in between” the grid points p/q and (p + 1)/q. Here we suggest a very simple construction that requires a slight deviation of the geometry from a perfect square system, but this should not affect the physics in any way.
Consider a square lattice of size (q + 1) × q and vector potentials

the +sign before Ay is in contrast with the symmetric gauge, namely (Ax, Ay) = →↑. Since |Ay| is just slightly greater than |Ax| and they are counter-oriented, we call this construction an almost antisymmetric gauge. The total flux per square is then

and the flux through the entire system is pϕ0 with p = 1, 2, …, q(q + 1). Thus, the minimum flux through the entire system is just by ϕ0.
The above construction can easily be checked for consistency when p divides q(q + 1). For example, when p = (q + 1) the flux per square is ϕ0/q and the spectrum can be obtained by solving the problem either with the gauge (7) with p = (q + 1) or with the Landau gauge Ay = ϕ0 × 1/q, following the substitution ψnm =  , and solving the set of Harper equations with k = 1, 2, …q + 1, m = 1, 2, …q applied to the original rectangle of size (q + 1)qa2 (in this case the argument of the cosine function is 2π[k/(q + 1) + mp/q]) and p = 1, 2, …q. The corresponding spectra should then be identical. We have checked that this is indeed the case.
, and solving the set of Harper equations with k = 1, 2, …q + 1, m = 1, 2, …q applied to the original rectangle of size (q + 1)qa2 (in this case the argument of the cosine function is 2π[k/(q + 1) + mp/q]) and p = 1, 2, …q. The corresponding spectra should then be identical. We have checked that this is indeed the case.
Additional Information
How to cite this article: Su, Y. et al. Absence of localization in disordered two-dimensional electron gas at weak magnetic field and strong spin-orbit coupling. Sci. Rep. 6, 33304; doi: 10.1038/srep33304 (2016).
References
Edwards, J. T. & Thouless, D. J. Numerical studies of localization in disordered systems. J. Phys. C: Solid State Phys. 5, 807 (1972).
Licciardello, D. C. & Thouless, D. J. Conductivity and mobility edges for two-dimensional disordered systems. J. Phys. C: Solid State Phys. 8, 4157 (1975).
Abrahams, E., Anderson, P. W., Licciardello, D. C. & Ramakrishnan, T. V. Scaling theory of localization: absence of quantum diffusion in two dimensions. Phys. Rev. Lett. 42, 673 (1979).
Lee, P. A. & Ramakrishnan, T. V. Disordered electronic systems. Rev. Mod. Phys. 57, 287 (1985).
Wigner, E. P. Group theory and its application to the quantum mechanics of atomic spectra (Academic Press, New York, 1959).
Dyson, F. J. Statistical theory of the energy levels of complex systems. I. J. Math. Phys. 3, 140 (1962).
Dyson, F. J. Statistical theory of the energy levels of complex systems. II. J. Math. Phys. 3, 157 (1962).
Dyson, F. J. Statistical theory of the energy levels of complex systems. III. J. Math. Phys. 3, 166 (1962).
Mehta, M. L. Theory of random matrices (Academic Press, New York, 1991).
Levine, H., Libby, S. B. & Pruisken, A. M. M. Theory of the quantized Hall effect (I). Nucl. Phys. B 240, 30 (1984).
Levine, H., Libby, S. B. & Pruisken, A. M. M. Theory of the quantized Hall effect (II). Nucl. Phys. B 240, 49 (1984).
Levine, H., Libby, S. B. & Pruisken, A. M. M. Theory of the quantized Hall effect (III). Nucl. Phys. B 240, 71 (1984).
Khmelnitskii, D. E. Quantum Hall effect and additional oscillations of conductivity in weak magnetic fields. Phys. Lett. A 106, 182 (1984).
Wang, C., Su, Y., Avishai, Y., Meir, Y. & Wang, X. R. Band of critical states in Anderson localization in a strong magnetic field with random spin-orbit scattering. Phys. Rev. Lett. 114, 096803 (2015).
Wang, X. R. Localization in fractal spaces: exact results on the Sierpinski gasket. Phys. Rev. B 51, 9310 (1995).
Wang, X. R. Magnetic-field effects on localization in a fractal lattice. Phys. Rev. B 53, 12035 (1996).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707 (1980).
Kramer, B. & Mackinnon, A. Localization: theory and experiment. Rep. Prog. Phys. 56, 1469 (1993).
Xie, X. C., Wang, X. R. & Liu, D. Z. Kosterlitz-Thouless-type metal-insulator transition of a 2D electron gas in a random magnetic field. Phys. Rev. Lett. 80, 3563 (1998).
Obuse, H., Furusaki, A., Ryu, S. & Mudry, C. Boundary criticality at the Anderson transition between a metal and a quantum spin Hall insulator in two dimensions. Phys. Rev. B 78, 115301 (2008).
Asada, Y., Slevin, K. & Ohtsuki, T. Anderson transition in two-dimensional systems with spin-orbit coupling. Phys. Rev. Lett. 89, 256601 (2002).
Janssen, M. Statistics and scaling in disordered mesoscopic electron systems. Phys. Rep. 295, 1 (1998).
Riedel, E. K. & Wegner, F. J. Effective critical and tricritical exponents. Phys. Rev. B 9, 294 (1974).
Kim, B. J. et al. Novel Jeff = 1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402 (2008).
Moon, S. J. et al. Dimensionality-controlled insulator-metal transition and correlated metallic state in 5d transition metal oxides Srn+1IrnO3n+1 (n = 1, 2, and ∞). Phys. Rev. Lett. 101, 226402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital Mott state in Sr2IrO4 . Science 323, 1329 (2009).
Shklovskii, B. I., Shapiro, B., Sears, B. R., Lambrianides, P. & Shore, H. B. Statistics of spectra of disordered systems near the metal-insulator transition. Phys. Rev. B 47, 11487 (1993).
Kravtsov, V. E., Lerner, I. V., Altshuler, B. L. & Aronov, A. G. Universal spectral correlations at the mobility edge. Phys. Rev. Lett. 72, 888 (1994).
Aronov, A. G., Kravtsov, V. E. & Lerner, I. V. Spectral correlations in disordered electronic systems: crossover from metal to insulator regime. Phys. Rev. Lett. 74, 1174 (1995).
Acknowledgements
This work is supported by NSF of China Grant No. 11374249 and Hong Kong RGC Grants No. 163011151 and No. 605413. The research of Y.A. is partially supported by Israel Science Foundation Grant No. 400/12. Y.A. acknowledges fruitful discussions with T. Ohtsuki. Y.M. acknowledges ISF Grant No. 292/15.
Author information
Authors and Affiliations
Contributions
Y.S. and C.W. performed the numerical simulations. Y.A., Y.M. and X.R.W. designed the project. X.R.W. supervised the research. All the authors contributed to data analysis and manuscript preparation.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Su, Y., Wang, C., Avishai, Y. et al. Absence of localization in disordered two-dimensional electron gas at weak magnetic field and strong spin-orbit coupling. Sci Rep 6, 33304 (2016). https://doi.org/10.1038/srep33304
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33304
This article is cited by
-
Structural-disorder-driven critical quantum fluctuation and localization in two-dimensional semiconductors
Nature Communications (2023)
-
Two-Dimensional Time-Reversal-Invariant Topological Insulators via Fredholm Theory
Mathematical Physics, Analysis and Geometry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.