Abstract
The superconductor-to-insulator transition (SIT) induced by means such as external magnetic fields, disorder or spatial confinement is a vivid illustration of a quantum phase transition dramatically affecting the superconducting order parameter. In pursuit of a new realization of the SIT by interfacial charge transfer, we developed extremely thin superlattices composed of high Tc superconductor YBa2Cu3O7 (YBCO) and colossal magnetoresistance ferromagnet La0.67Ca0.33MnO3 (LCMO). By using linearly polarized resonant X-ray absorption spectroscopy and magnetic circular dichroism, combined with hard X-ray photoelectron spectroscopy, we derived a complete picture of the interfacial carrier doping in cuprate and manganite atomic layers, leading to the transition from superconducting to an unusual Mott insulating state emerging with the increase of LCMO layer thickness. In addition, contrary to the common perception that only transition metal ions may respond to the charge transfer process, we found that charge is also actively compensated by rare-earth and alkaline-earth metal ions of the interface. Such deterministic control of Tc by pure electronic doping without any hindering effects of chemical substitution is another promising route to disentangle the role of disorder on the pseudo-gap and charge density wave phases of underdoped cuprates.
Similar content being viewed by others
Introduction
Heterointerfaces between dissimilar layers of semiconductors have long been at the forefront of condensed matter physics in topics ranging from charge transfer in a p−n junction to quantum Hall effects arising in two-dimensional electron gases. For the case of complex oxide interfaces, the past decade has witnessed a rapid growth in science and ability to synthesize interfaces between a wide variety of oxides with atomic layer precision1,2,3,4. Despite the marked progress, many fundamental questions still remain not well understood, particularly in regards to how charge carriers redistribute across interfaces in strongly correlated electron systems and how this process affects spin, charge and orbital degrees of freedom. Macroscopically, two factors seem to be of key importance: charge transfer localization at the interface and the presence of a longer scale charge transfer related to the balancing of the mismatch in chemical potential. The former has been observed at many perovskite interfaces where the local interactions drive a charge transfer. For example, in cases like LaB3+O3/LaNi3+O3, the B site ion and Ni form a redox couple resulting in B4+ and Ni2+ charges localized within a very short range of 1–2 unit cells (u.c.) of the interface5,6,7,8. As for the balancing of the chemical potential via charge transfer, which is well understood and successfully utilized for semiconductor junctions, it is still an open research area with many experimental and theoretical challenges due to the strongly correlated nature of the carriers9,10,11,12,13.
The case of YBa2Cu3O7−x/La0.67Ca0.33MnO3 (YBCO/LCMO) interface provides a ideal system where antagonistic combination of unconventional magnetism and high Tc superconductivity defines a number of intriguing phenomena governed by the charge redistribution between magnetic electrons of manganite and Cooper pairs of the cuprate to equalize chemical potential across the boundary (see ref. 4 and references therein). From the perspective of interfacial charge transfer and its impact on the overall materials properties of the YBCO/LCMO heterojunction, there has been a significant number of results including charge, spin and orbital reconstruction as revealed by electron microscopy14,15,16,17,18, neutron reflectometry19,20,21, resonant X-rays17,22,23,24,25,26,27, and cross-sectional STM15,28, where the reported length scales of charge transfer effects range from few Å to several nanometers. The variability in scale of these charge transfer effects stems from the exploration of thick YBCO7 and LCMO constituent layers of multiple unit cells (u.c.) for which the bulk physics of the inner layers can obscure the interface induced many-body behaviour. Based on this observation, we can then ask what happens when the LCMO and YBCO layers approach 1–2 u.c. limit and the entire structure becomes purely interfacial in nature.
To address this question, we explored a set of interface-controlled layered heterostructures composed of YBa2Cu3O7 (2 u.c.) and La0.67Ca0.33MnO3 (N = 1, 2 and 3 u.c.) to investigate the emergent behaviors due to the reconstructed charge and magnetic moments at the complex oxide interface. By utilizing the combined power of resonant X-ray absorption (XAS) and hard X-ray photoelectron spectroscopy (HXPS), we are able to elucidate how the large transfer of electrons from LCMO effectively tunes the YBCO layer across the doping phase space from being a superconductor (SC) into the antiferromagnetic (AFM) phase. Additionally, the electronic responses of Ba and La atoms demonstrate their important roles as electron acceptor and electron donor, respectively, sharing the doped charges with the CuO2 plane, thus revealing a strong similarity to doping by oxygen content, x in the bulk YBa2Cu3O7−x.
Results
The structure was determined by X-ray diffraction. The superlattice (SL) period of ∼22 Å from the spacing of the diffraction peaks (Fig. 1(a)) for N = 1 SL is consistent with the structure shown in Fig. 1(b). This particular superlattice structure was based upon the detailed electron microscopy studies from several groups, which found that the interfaces predominantly involved an MnO2-BaO-CuO2 sequence15,24,29,30. The superlattice spacing was consistent with extracting the value from the total thickness measured by the fringes. As shown in Fig. 1(c), electrical transport measurements demonstrate a clear superconductor-insulator (S-I) transition with increasing N, where the superconducting transition, as determined by the midpoint, is reduced from 50 K to zero and the N = 3 data is consistent with the anti-ferromagnetic insulating phase in the lightly hole doped region of the phase diagram. While the dependence of the Tc seems consistent with a decrease in hole doping with increasing LCMO layer thickness, it turns out that the data has a different evolution than is observed for the case of bulk YBa2Cu3O7−δ 31,32,33. The most notable is a linear T-dependence that disappears quickly in the bulk as a function of δ, while the resistivity in the normal state of the N = 1, 2 superlattices remains linear with temperature down to ∼100 K.
Crystal structure and electrical transport.
(a) XRD scan for Y2/L1 sample showing clear thickness fringes and superlattice (SL) peaks. (b) The lattice structure consistent with the diffraction data of panel (a). (c) Electrical transport measurements showing a clear superconductor to insulator transition as a function of LCMO layer thickness. Inset shows growth sequence for Y2/L1 sample.
To understand the transition from superconductor to insulating state, we made use of polarized soft-XAS and hard-XPS to extract an element-resolved picture of the electronic and magnetic states. Beginning with the Mn L-edge X-ray absorption spectroscopy (XAS), we find that, rather than the expected 3.33+ valence34,35, all the films demonstrate a Mn valence state of 4+ (see Fig. 2(a)). In the bulk phase diagram of manganites34, this doping level corresponds to an insulator and the magnetism is either paramagnetic (PM) or antiferromagnetic (AFM) as noted by the small X-ray magnetic circular dichroism at 5T, which vanishes as the field tends to zero. In addition, Fig. 2(b) shows HXPS spectra of Mn 2p3/2 of the Y2/L1, Y9/L25, and LCMO bulk samples. With comparison to the prior HXPS studies of LCMO and LSMO36,37, we note the effects of final-state core-hole screening in such spectra. For bulk LCMO, one can observe two shoulders in addition to the unscreened peak of Mn 2p3/2 at a binding energy (BE) of 641.1 eV. The shoulder at BE = 642.2 eV is attributed to the Mn 4+ states, whereas the unscreened peak is attributed to 3.33+ states. The other shoulder in the low BE region at 639.5 eV is assigned to well-screened states, which are associated with delocalized screening and metallic character in the 3d-based transition metal oxides36. In the Y2/L1 sample, we found that the component of Mn 4+ states is enhanced and the well-screened feature is suppressed, suggesting a charge transfer from LCMO to YBCO with the LCMO layer displaying an insulating behavior, consistent with the XAS results in Fig. 2(a). The Y9/L25 show features similar to both the LCMO bulk and to the Y2/L1 SL, so we can infer that the bulk-like part contributes to the 3.33+ valence state, and the YBCO/LCMO interface contributes to the 4+ valence state. We measured also the Mn 3s HXPS spectrum (not shown here) of the bulk LCMO sample. It has a multiplet splitting of ΔE3s = 5.2 eV that is directly related to the Mn spin moment and charge state. A prior study of Mn 3s exchange splittings in mixed-valence manganites permits concluding that the ΔE3s = 5.2 eV is consistent with the Mn nominal valence of 3.33+ 38, again qualitatively consistent with the XAS results for Y9/L25 with the thickest LCMO layer. Spectral interference of Mn 3s and Ba 4d in the SLs unfortunately prevented measuring Mn 3s for the superlattice samples. From these Mn XAS and HXPS results it is clear that the LCMO layer has lost 0.67 electrons per layer (Mn3.33+ → Mn4+) in these ultra-thin superlattices. If the electrons have been transferred from the LCMO into the YBCO layer, then we can search for signs of the altered YBCO charge state in the Cu XAS.
Heterostructuring effect on manganite layers.
(a) Mn L3-edge x-ray absorption spectroscopy demonstrating that for up to 3 unit cells of LCMO, the Mn valence is fixed close to 4+ rather than the expected 3.33+. For comparison, we show data from a thicker LCMO/YBCO superlattice (Y9/L25) with a nominal Mn valence of 3.33+. (b) HXPS spectra of Mn 2p3/2, demonstrating that in Y9/L25 and bulk LCMO, Mn has nominal valence of 3.33+, whereas Mn in the Y2/L1 SL has nominal valence of 4+.
To track the doping level of the CuO2 plane, we rely on a base knowledge built upon studies of bulk YBCO39,40,41. While the valence of Cu remains 2+ (3d9) with hole doping, there is a clear emergence of a ligand hole state (3d9L) on the oxygen site, which is important for Cooper pairing42,43. Detailed examination of the bulk cuprates have shown that this peak on both the Cu L-edge and O K-edge track directly with doping of the CuO2 plane44,45, which can be altered in the bulk by changing oxygen stoichiometry31, replacing Y with Ca46,47, or doping at Cu sites48. Figure 3(a) shows the evolution of the polarization dependent Cu L-edge with increasing N together with a comparison to a thicker YBCO superlattice with bulk like absorption. On this figure we note the location of the 3d9L feature associated with hole doping in the CuO2 plane. Note also the absence of the feature near 932.5 eV related with the partial oxidation of the chains associated with underdoped samples39,40,41, implying the presence of fully oxygenated chain layer in these superlattices.
Heterostructuring effect on cuprate layers.
(a) Cu L-edge XAS showing the trend in the electronic structure and orbital differences with LCMO layer thickness. While all show the strong polarization dependence expected for a pure  state, there is a clear drop in the
state, there is a clear drop in the  state. (b) HXPS spectra of Cu 2p3/2 of the Y2/L1, Y9/L25 and YBCO bulk samples, where the well screened peak of Cu 2p3/2 is observed at binding energy 932 eV and corresponds to the final state
state. (b) HXPS spectra of Cu 2p3/2 of the Y2/L1, Y9/L25 and YBCO bulk samples, where the well screened peak of Cu 2p3/2 is observed at binding energy 932 eV and corresponds to the final state  . The satellite peaks at binding energy 940–944 eV correspond to the 3d9 poorly screened final states.
. The satellite peaks at binding energy 940–944 eV correspond to the 3d9 poorly screened final states.
From Fig. 3(a) we see that the XAS of the N = 1 SL is very close to that of the thicker Y9/L25 superlattice, which has Tc of 75 K. With increasing N there is a drastic reduction in the 3d9L state and corresponding increase in the 3d9 feature. This evolution is directly associated with a decreasing doping level of the CuO2 plane due to the charge transfer from the LCMO layer into the YBCO layer. In order to analyze this on a more quantitative level, we have integrated the background subtracted Cu L3 spectra and done a direct comparison as a function of spectral weight ratio, 3d9L/3d9 (see inset of Fig. 3(a)). This ratio shows a clear drop with increasing N, consistent with a reduction of hole doping of the CuO2 plane with increasing N. In comparison we also include the ratio for optimal doping as determined by an identical analysis of optimally doped YBCO from ref. 41.
Figure 3(b) shows the HXPS spectra of Cu 2p3/2 of the Y2/L1, Y9/L25 and YBCO bulk samples, where the well screened peak of Cu 2p3/2 is observed at BE = 932 eV and corresponds to the final state 3d9L, implying charge transfer from oxygen due the positive core-hole potential. The satellite peaks at BE = 945–940 eV correspond to the Cu 2p3d9, poorly screened final state. Previous studies indicate that the monovalent Cu2O compounds show only the well screened peak and no satellites since the 3d shell is already filled in the initial state. Thus, the presence of the satellite peaks for Y2/L1 and Y9/L25 SLs implies Cu in the 2+ state49. The Cu 2p satellite peaks of the Y2/L1 are slightly more intense compared to those of bulk YBCO, although some of this could be due to a small difference in the inelastic background subtraction. However, the satellite intensity of Y9/L25 is dramatically different compared to that of bulk YBCO and Y2/L1 SLs. This result indicates that the Cu valence state at the YBCO/LCMO interface is much different from the YBCO bulk-like environment.
From the behavior of the XAS data, it is evident that the amount of electrons doped to Cu sites is much smaller than the 0.67 x N electrons donated by the LCMO block. In order to find out how the charge transfer influences energy levels, we consider HXPS results from other atoms in the SLs in Fig. 4, beginning with the YBCO side of the interface. Fig. 4(a) indicates that not only the Cu 2p features are different in the spectrum of Y9/L25 compared to that of Y2/L1, but also the Ba 3d core level. In addition to the main peak of Ba 3d5/2 at BE = 778 eV, there is a strong peak at BE = 780 eV which appears only as a shoulder in the spectrum of the Y2/L1 SL, and is essentially absent in bulk YBCO. We assign this two-peaked structure of Y9/L25 SL to the existence of two kinds of Ba in the superlattice structure, at the interface and away from it, consistent with the structure shown in the schematic of Fig. 1(b). In the case of the thick LCMO overlayer for the Y9/L25 sample, the interface sensitivity is enhanced due to the short inelastic mean free path (IMFP)50 giving rise to a large interface peak. This feature at BE = 780 eV, due to the interfacial sites, has a non-bulk-like electronic configuration. The Ba 3d5/2 core level of Y2/L1 SL has also been shifted towards higher binding energy by ∼0.4 eV as compared to the bulk YBCO film. The response of this core level to the depression of Tc, is similar to the chemical doping effect observed in bulk YBCO7−x and emphasizes that the Ba-O plane also acts as an electron reservoir51. The Y atoms, which are farther away from the interface, displayed in Fig. 4(b), only a small shift of ∼0.2 eV to higher binding energy and no significant change in spectral shape, which is consistent with the bulk doping behavior as well51,52, and the fact that Y maintains a bulk-like coordination in the superlattice geometry.
On the other side of interface, the La 3d5/2 BE of Y2/L1 moves to lower binding energy by about 0.5 eV compared to Y9/25 and bulk LCMO. A BE shift to lower energy of ∼0.5 eV is also observed for the case of the Ca 2p3/2 XPS data as shown in Fig. 4(d), with an additional broadening towards the low-BE side, that might indicate a greater degree of interdiffusion by Ca at the interface. A self-consistent picture of the BE shifts in Fig. 4 is also possible through a measurement of the valence-band offset (VBO) at the Y2/L1 interface using HXPS core-level and valence-band maximum (VBM) energies for Y2/L1 and the bulk reference samples of YBCO and LCMO, and a method introduced into oxide studies by Chambers et al.53,54. The VBO obtained in this way is 0.67 eV, with sign such that BEs in YBCO should increase and those in LCMO should decrease, just as seen in Fig. 4. The sign of the VBO is also consistent with the effective n doping of YBCO and p doping of LCMO. The fact that the magnitude of this VBO is of the same general magnitude as the shifts in Fig. 4 nicely supports this interpretation. From the behavior of the Mn and Cu XAS and HXPS data of the Y2/LN SLs, it is thus evident that there is charge transfer from the LCMO layer into the YBCO layer, with binding energy shifts in opposite directions on the two sides.
From a chemical structure standpoint, one can consider how balancing charge in a larger unit cell helps to understand the charge transfer. The key is the missing chains at the interface that lead to a partial and charge imbalanced YBCO unit cell that needs to be compensated by the LCMO layers15, which leads to the structure shown in Fig. 1(b). By constructing a larger unit cell composed of LCMO and YBCO unit cells together and counting the charges using the ionic values explains the direction of charge motion, but the change of the charge in the CuO2 layers comes out much larger than experimentally seen. This is because we are assuming that the other elements are passive, but as shown above the other ions in the lattice are participating in the charge compensation. The shift to higher energy on the YBCO side is consistent with the electron doping while the opposite shift on the La and Ca is due to electron depletion of the LCMO layer. The fact that Y reacts less than Ba, is potentially related to the distance from the interface and suggests that within 1–2 CuO2 layers, the YBCO electronic structure is returning to bulk-like properties, which is consistent with a recent study of the electronic interface with cross-sectional STM15. This length scale is also consistent with theoretical calculations that explore how the electronic structure evolves across the LCMO/YBCO interface11,14,16,55,56,57. Based upon simple arguments in the level of the chemical potential11, one can determine the expected trends that are consistent with that seen here in the experimental data.
Taking all the experimental results together, we can confirm that the suppression of the SC state is due to doping of electrons into YBCO from the LCMO layer. To quantify this, using the Tc data from the films together with data from the bulk58, we can estimate that each LCMO layer is doping 0.67 electrons to the whole of the YBCO layer, but only ∼0.05 electrons into the CuO2 planes as shown in Fig. 5. This discrepancy is perhaps not surprising though since in the bulk changing from YBa2Cu3O7 to YBa2Cu3O6, which is a total charge change of 2-, only leads to a small doping change in the CuO2 plane58. A similar effect was seen with electrostatic doping experiments, which explained why so little variation of Tc was found in ferroelectric/cuprate heterostructures59. This also highlights that it is important to track all of the potential charge reservoirs in order to create a physical picture of the process in a multicomponent system.
Phase diagram.
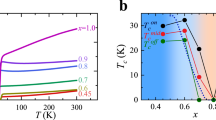
(a) XMCD of Cu L3,2 edges for Y2/LN SLs. (b) Doping level inferred from both Tc and the XAS analysis of Y2/LN SLs are overlayed with the bulk phase diagram for YBCO, adapted by permission from Macmillan Publishers Ltd: [Nature Communications] (63), copyright (2014). PG = pseudogap, FL = Fermi liquid. Superconducting Tc is defined as the midpoint of the transition and the width of transition has been marked as the corresponding error bar.
Together with this reduction in Tc, we also observed a significant increase in the Cu XMCD at high-fields (5 T) connected with increase in magnetic order associated with the onset of the AFM phase. The same trend using XMCD to probe Cu magnetism was recently seen for bulk YBCO as a function of doping60, which serves to support the idea that while we are doping via an interface into an ultra YBCO layer, much of the expected bulk physics remains intact. This results from the highly two-dimensional character of the cuprate high temperature superconductors, as was seen by the presence of superconductivity even in isolated CuO2 layers61,62.
Given the striking similarity between the effect of chemical doping and the interfacial “doping” by electron/hole transfer, there are a number of interesting questions which arise in the view of the recent discovery of a charge density wave (CDW) phase competing with SC pairing. Specifically, recent extensive works on underdoped YBCO revealed the presence of long-range charge fluctuations in CuO2 in a wide range of hole doping63,64,65,66,67,68,69, which act to suppress the SC order. As demonstrated above and summarized in Fig. 5(b), the charge transfer between manganite and cuprate layers in these superlattices brings the cuprate component to the under doped region of bulk YBCO phase diagram, where CDW phase would also appear. Based on this observation, it can be anticipated that similar charge fluctuations in CuO2 planes are also present in the case of heterojunctions. However, the situation is not that straightforward considering the fact that the CuO chains remain fully oxygenated in these SLs contrary to the chains with ordered oxygen vacancy of underdoped bulk YBCO. Moreover, the incipient CDW fluctuations may be strongly altered or even entirely suppressed because of the charge mismatch across the YBCO/LCMO interface4,27,70 leading to a possible new phase state without CDW (e.g. charge glass) for the underdoped part of cuprate phase diagram71. On the manganite side of the junction the charge transfer causes massive hole doping into the CMR layers. This in turn raises an interesting question if the hallmark CMR phenomena (e.g. electronic phase separation and Jahn-Teller like distortions from strong electron-lattice coupling) persist after pure hole doping into intact lattice by random chemical doping72.
In conclusion, by variable-polarization XAS, XMCD, and HXPS, we have shown a clear superconductor to insulator transition driven by interfacial doping in an ultra-thin cuprate-maganite superlattice. Without changing the concentration of vacancies in the chains, we can utilize the chemical potential imbalance at the LCMO/YBCO interface to dope electrons into YBCO over a wide range of the phase diagram. This offers an interesting route to examine the link between dopant disorder and phenomena in underdoped superconductors. As noted in recent work, there is a clear correlation between the spatial dopant arrangements and charge order observed in the cuprates73,74. Given the dramatic differences associated with how the ordering of dopants can affect the corresponding phase diagrams both in bulk75 and heterostructures76,77, this might suggest a modified phase diagram for the YBCO doped in this manner. As noted above, the deviation from linear T, which is associated with the onset of the pseudogap and associated q = 0 magnetic order in the bulk63,78, occurs at a much lower temperature and perhaps suggests a suppression of the onset of the pseudogap phase. Future work, will explore further how this type of doping into ultrathin YBCO affects the phase diagram.
Methods
The high-quality epitaxial superlattices (SL) consisting of 2 unit cell (uc) of YBa2Cu3O7 (YBCO) and N uc of La0.67Ca0.33MnO3 (LCMO) (N = 1, 2, 3) were grown by pulsed laser interval deposition on 5 × 5 mm2 SrTiO3 (001) substrate. The layer-by-layer growth of these 20 repeat superlattices (labelled as Y2/LN with N = 1,2,3) were monitored by in-situ reflection high energy electron diffraction (RHEED). In addition to these superlattices, thick bulk-like LCMO, YBCO, and (Y9/L25)3 were also grown as references. Samples were capped with a protective coating of 4 u.c. of SrTiO3, which is very stable in air.
The SL structures were studied by X-ray diffraction (XRD) in air at room temperature using a standard four-circle diffractometer, operating at Beamline 33-BM-C of the Advanced Photon Source (APS). The dc transport properties were measured from 300 to 2 K in a Physical Property Measurement System (PPMS, Quantum Design) using the van der Pauw geometry. The XAS measurements, X-ray Linear Dichroism measurements (XLD) and X-ray Magnetic Circular Dichroism (XMCD)) were performed at the Cu L3 edge and Mn L3 edge respectively at the 4-ID-C beam line of the APS. The XLD spectra were measured in bulk sensitive total-fluorescence-yield mode, and energy calibrations were carried out by measuring a CuO (Cu2+) standard simultaneously in the diagnostic section of the beamline. Each spectrum was normalized to the beam intensity monitored by a gold mesh set in front of the samples. In order to avoid spurious XMCD signals, XMCD spectra were recorded with both ±5 Tesla magnetic fields.
(HXPS) data were obtained at beamline 15XU of the SPring-8 Synchrotron. (Y2/L1) SL and the bulk YBCO and LCMO samples were measured at a photon energy of 3.238 keV and an overall energy resolution of 0.25 eV. A Y9/L25 SL, with the structure from top to bottom of 4 u.c. STO/[25 u.c. LCMO/9 u.c. YBCO]x3/STO substrate, was measured at a photon energy of 2.2 keV and a resolution of 0.1 eV. Using these multi-keV photon energies yields more buried interface sensitivity than normal soft x-ray photoemission, through increased mean depths of emission, as controlled by the photoelectron inelastic mean free path (IMFP): as estimated from the TPP-2M formula50, the IMFP at 3.238 keV will be ∼46 Å, and at 2.2 keV ∼33 Å. Thus, our HXPS measurements are sensitive to approximately the first two bilayers in the Y2/LN SL, and to the bulk behavior in the thicker reference samples. The binding energies of the HXPS spectra were calibrated using Au 4f and Au EF before and after each data acquisition. The experiment was performed at room temperature and at T = 20 K, below the normal superconducting TC for YBCO; however, it is noteworthy that cooling to the superconducting state did not induce any significant changes in any of the SL spectra, and the data reported here are thus only those collected at room temperature.
Additional Information
How to cite this article: Gray, B. A. et al. Superconductor to Mott insulator transition in YBa2Cu3O7/LaCaMnO3 heterostructures. Sci. Rep. 6, 33184; doi: 10.1038/srep33184 (2016).
References
Zubko, P., Gariglio, S., Gabay, M., Ghosez, P. & Triscone, J.-M. Interface Physics in Complex Oxide Heterostructures. Annual Review Of Condensed Matter Physics 2, 141 (2011).
Bibes, M., Villegas, J. E. & Barthelemy, A. Ultrathin oxide films and interfaces for electronics and spintronics. Advances in Physics 60, 5–84 (2011).
Bhattacharya, A. & May, S. J. Magnetic Oxide Heterostructures. Annual Review Of Materials Research 44, 65–90 (2014).
Chakhalian, J., Freeland, J. W., Millis, A. J., Panagopoulos, C. & Rondinelli, J. M. Colloquium: Emergent properties in plane view: Strong correlations at oxide interfaces. Rev. Mod. Phys. 86, 1189–1202 (2014).
Hoffman, J. et al. Charge transfer and interfacial magnetism in (LaNiO3)n/(LaMnO3)2 superlattices. Phys. Rev. B 88, 144411 (2013).
Disa, A. S. et al. Orbital Engineering in Symmetry-Breaking Polar Heterostructures. Phys. Rev. Lett. 114, 026801 (2015).
Cao, Y. et al. Engineered Mott ground state in a LaTiO3+δ/LaNiO3 heterostructure. Nature Communications 7, 10418 (2016).
Grisolia, M. N. et al. Hybridization-controlled charge transfer and induced magnetism at correlated oxide interfaces. Nature Physics 12, 484–492 (2016).
Okamoto, S. & Millis, A. J. Electronic reconstruction at an interface between a Mott insulator and a band insulator. Nature 428, 630 (2004).
Oka, T. & Nagaosa, N. Interfaces of Correlated Electron Systems: Proposed Mechanism for Colossal Electroresistance. Phys. Rev. Lett. 95, 266403 (2005).
Yunoki, S. et al. Electron doping of cuprates via interfaces with manganites. Phys. Rev. B 76, 064532 (2007).
Lee, W.-C. & Macdonald, A. Electronic interface reconstruction at polar-nonpolar Mott-insulator heterojunctions. Phys. Rev. B 76, 075339 (2007).
Charlebois, M., Hassan, S. R., Karan, R., Sénéchal, D. & Tremblay, A.-M. S. Mott p-n junctions in layered materials. Phys. Rev. B 87, 035137 (2013).
Salafranca, J. & Okamoto, S. Unconventional Proximity Effect and Inverse Spin-Switch Behavior in a Model Manganite-Cuprate-Manganite Trilayer System. Phys. Rev. Lett. 105, 256804 (2010).
Chien, T. Y. et al. Visualizing short-range charge transfer at the interfaces between ferromagnetic and superconducting oxides. Nature Communications 4, 2336 (2013).
Salafranca, J. et al. Competition between Covalent Bonding and Charge Transfer at Complex-Oxide Interfaces. Phys. Rev. Lett. 112, 196802 (2014).
Cuellar, F. A. et al. Reversible electric-field control of magnetization at oxide interfaces. Nature Communications 5, 4215 (2014).
Biškup, N., Das, S., Gonzalez-Calbet, J. M., Bernhard, C. & Varela, M. Atomic-resolution studies of epitaxial strain release mechanisms in La1.85Sr0.15CuO4/La0.67Ca0.33MnO3superlattices. Phys. Rev. B 91, 205132 (2015).
Stahn, J. et al. Magnetic proximity effect in perovskite superconductor/ferromagnet multilayers. Phys. Rev. B 71, 140509 (2005).
Hoffmann, A. et al. Suppressed magnetization in La0.7Ca0.3MnO3YBa2Cu3O7−δ superlattices. Phys. Rev. B 72, 140407 (2005).
Hoppler, J. et al. Giant superconductivity-induced modulation of the ferromagnetic magnetization in a cuprate-manganite superlattice. Nature Materials 8, 315–319 (2009).
Chakhalian, J. et al. Orbital reconstruction and covalent bonding at an oxide interface. Science 318, 1114–1117 (2007).
Werner, R. et al. YBa2Cu3O7/La0.7Ca0.3MnO3 bilayers: Interface coupling and electric transport properties. Phys. Rev. B 82, 224509 (2010).
Visani, C. et al. Symmetrical interfacial reconstruction and magnetism in La0.7Ca0.3MnO3/YBa2Cu3O7/La0.7Ca0.3MnO3 heterostructures. Phys. Rev. B 84, 060405 (2011).
Satapathy, D. et al. Magnetic Proximity Effect in YBa2Cu3O7/La2/3Ca1/3MnO3 and YBa2Cu3O7/LaMnO3+δ Superlattices. Phys. Rev. Lett. 108, 197201 (2012).
Liu, Y. et al. Effect of Interface-Induced Exchange Fields on Cuprate-Manganite Spin Switches. Phys. Rev. Lett. 108, 207205 (2012).
Frano, A. et al. Long-range charge-density-wave proximity effect at cuprate/manganate interfaces. Nature Materials 15, 831–834 (2016).
Fridman, I., Gunawan, L., Botton, G. A. & Wei, J. Y. T. Scanning tunneling spectroscopy study of c-axis proximity effect in epitaxial bilayer manganite/cuprate thin films. Phy. Rev. B 84, 104522 (2011).
Zhang, Z. L., Kaiser, U., Soltan, S., Habermeier, H.-U. & Keimer, B. Magnetic properties and atomic structure of La2/3Ca1/3MnO3/YBa2Cu3O7 heterointerfaces. Appl. Phys. Lett. 95, 242505 (2009).
Zhang, H., Gauquelin, N., Botton, G. A. & Wei, J. Y. T. Attenuation of superconductivity in manganite/cuprate heterostructures by epitaxially-induced CuO intergrowths. Appl. Phys. Lett. 103, 052606 (2013).
Ito, T., Takenaka, K. & Uchida, S. Systematic deviation from T-linear behavior in the in-plane resistivity of YBa2Cu3O7−y: Evidence for dominant spin scattering. Phys. Rev. Lett. 70, 3995–3998 (1993).
Ando, Y., Komiya, S., Segawa, K., Ono, S. & Kurita, Y. Electronic Phase Diagram of High-Tc Cuprate Superconductors from a Mapping of the In-Plane Resistivity Curvature. Phys. Rev. Lett. 93, 267001 (2004).
Barišić, N. et al. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors. Proceedings of the National Academy of Sciences 110, 12235–12240 (2013).
Schiffer, P., Ramirez, A. P., Bao, W. & Cheong, S.-W. Low Temperature Magnetoresistance and the Magnetic Phase Diagram of La1−xCaxMnO3 . Phys. Rev. Lett. 75, 3336–3339 (1995).
Chmaissem, O. et al. Structural and magnetic phase diagrams of La1−xSrxMnO3 and Pr1−ySryMnO3 . Phys. Rev. B 67, 094431 (2003).
Horiba, K. et al. In vacuo photoemission study of atomically controlled La1−xSrxMnO3 thin films: Composition dependence of the electronic structure. Phys. Rev. B 71, 155420 (2005).
Mannella, N. et al. Temperature-dependent evolution of the electronic and local atomic structure in the cubic colossal magnetoresistive manganite La1−xSrxMnO3 . Phys. Rev. B 77, 125134 (2008).
Galakhov, V. R. et al. Mn 3s exchange splitting in mixed-valence manganites. Phys. Rev. B 65, 113102 (2002).
Nücker, N. et al. Site-specific and doping-dependent electronic structure of YBa2Cu3Ox probed by O 1s and Cu 2p x-ray-absorption spectroscopy. Phys. Rev. B 51, 8529–8542 (1995).
Merz, M. et al. Site-Specific X-Ray Absorption Spectroscopy of Y1−xCaxBa2Cu3O7−y: Overdoping and Role of Apical Oxygen for High Temperature Superconductivity. Phys. Rev. Lett. 80, 5192–5195 (1998).
Hawthorn, D. G. et al. Resonant elastic soft x-ray scattering in oxygen-ordered YBa2Cu3O6+δ . Phys. Rev. B 84, 075125 (2011).
Zhang, F. & Rice, T. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759–3761 (1988).
Meyers, D. et al. Zhang-Rice physics and anomalous copper states in A-site ordered perovskites. Scientific Reports 3, 1834 (2013).
Peets, D. C. et al. X-Ray Absorption Spectra Reveal the Inapplicability of the Single-Band Hubbard Model to Overdoped Cuprate Superconductors. Phys. Rev. Lett. 103, 075105 (2009).
Chen, Y.-J. et al. Doping evolution of Zhang-Rice singlet spectral weight: A comprehensive examination by x-ray absorption spectroscopy. Phys. Rev. B 88, 134525 (2013).
Neumeier, J. J., Bjørnholm, T., Maple, M. B. & Schuller, I. K. Hole filling and pair breaking by Pr ions in YBa2Cu3O6.95±0.02 . Phys. Rev. Lett. 63, 2516–2519 (1989).
Niedermayer, C. et al. Common Phase Diagram for Antiferromagnetism in La2−xSrxCuO4 and Y1−xCaxBa2Cu3O6 as Seen by Muon Spin Rotation. Phys. Rev. Lett. 80, 3843–3846 (1998).
Tallon, J., Bernhard, C., Williams, G. & Loram, J. Zn-induced Tc Reduction in High- Tc Superconductors: Scattering in the Presence of a Pseudogap. Phys. Rev. Lett. 79, 5294–5297 (1997).
Maiti, K. et al. Doping dependence of the chemical potential and surface electronic structure in YBa2Cu3O6+x and La2−xSrxCuO4 using hard x-ray photoemission spectroscopy. Phys. Rev. B 80, 165132 (2009).
Tanuma, S., Powell, C. J. & Penn, D. R. Calculations of electron inelastic mean free paths. IX. Data for 41 elemental solids over the 50 eV to 30 keV range. Surface And Interface Analysis 43, 689–713 (2011).
Yang, I.-S., Schrott, A. & Tsuei, C. Ba core-level shift in x-ray photoemission spectroscopy on single-phase Y1−xPrxBa2Cu3O7 and YBa2Cu3O7−y compounds. Phys. Rev. B 41, 8921–8926 (1990).
Yang, I.-S., Schrott, A., Tsuei, C., Burns, G. & Dacol, F. Electronic states in rare-earth 1:2:3 oxides: Photoemission and Raman studies. Phys. Rev. B 43, 10544–10547 (1991).
Chambers, S. A. et al. Band discontinuities at epitaxial SrTiO3/Si(001) heterojunctions. Appl. Phys. Lett. 77, 1662 (2000).
Chambers, S. A., Droubay, T., Kaspar, T. C. & Gutowski, M. Experimental determination of valence band maxima for SrTiO3, TiO2, and SrO and the associated valence band offsets with Si(001). Journal Of Vacuum Science & Technology B 22, 2205 (2004).
Pavlenko, N., Elfimov, I., Kopp, T. & Sawatzky, G. A. Interface hole doping in cuprate-titanate superlattices. Phys. Rev. B 75, 140512 (2007).
Pavlenko, N. Mechanism of orbital reconstruction at the interfaces of transition metal oxides. Phys. Rev. B 80, 075105 (2009).
Yang, X., Yaresko, A. N. Antonov, V. N. & Andersen, O. K. Electronic structure and x-ray magnetic circular dichroism of YBa2Cu3O7/LaMnO3 superlattices from first-principles calculations. arXiv:0911.4349 (2010).
Liang, R., Bonn, D. A. & Hardy, W. N. Evaluation of CuO2 plane hole doping in YBa2Cu3O6+x single crystals. Physical Review B 73, 180505 (2006).
Salluzzo, M. et al. Indirect electric field doping of the CuO2 planes of the cuprate NdBa2Cu3O7 superconductor. Phys. Rev. Lett. 100, 056810 (2008).
De Luca, G. M. et al. Weak magnetism in insulating and superconducting cuprates. Phys. Rev. B 82, 214504 (2010).
Logvenov, G., Gozar, A. & Bozovic, I. High-Temperature Superconductivity in a Single Copper-Oxygen Plane. Science 326, 699 (2009).
Di Castro, D. et al. High- T, cSuperconductivity at the Interface between the CaCuO2 and SrTiO3 Insulating Oxides. Phys.Rev. Lett. 115, 147001 (2015).
Tabis, W. et al. Charge order and its connection with Fermi-liquid charge transport in a pristine high-Tc cuprate. Nature Communications 5, 5875 (2014).
Wu, T. et al. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy . Nature 477, 191–194 (2011).
Chang, J. et al. Direct observation of competition between superconductivity and charge density wave order in YBa2Cu3O6.67 . Nature Physics 8, 871 (2012).
Ghiringhelli, G. et al. Long-Range Incommensurate Charge Fluctuations in (Y,Nd)Ba2Cu3O6+x . Science 337, 821–825 (2012).
Le Tacon, M. et al. Inelastic X-ray scattering in YBa2Cu3O6.6 reveals giant phonon anomalies and elastic central peak due to charge-density-wave formation. Nature Physics 10, 52–58 (2013).
Comin, R. et al. Symmetry of charge order in cuprates. Nature Materials 14, 796–800 (2015).
Comin, R. & Damascelli, A. Resonant X-Ray Scattering Studies of Charge Order in Cuprates. Annu. Rev. Condens. Matter Phys. 7, 369–405 (2016).
He, J. et al. Observation of a three-dimensional quasi-long-range electronic supermodulation in YBa2Cu3O7/LaCaMnO3 heterostructures. Nature Communications 7, 10852 (2016).
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Tokura, Y. Critical features of colossal magnetoresistive manganites. Reports On Progress In Physics 69, 797 (2006).
Ricci, A. et al. Multiscale distribution of oxygen puddles in 1/8 doped YBa2Cu3O6.67 . Scientific Reports 3, 2383 (2013).
Campi, G. et al. Inhomogeneity of charge-density-wave order and quenched disorder in a high-Tc superconductor. Nature 525, 359–362 (2015).
Akahoshi, D. et al. Random potential effect near the bicritical region in perovskite manganites as revealed by comparison with the ordered perovskite analogs. Phys. Rev. Lett. 90, 177203 (2003).
Santos, T. S. et al. Delta Doping of Ferromagnetism in Antiferromagnetic Manganite Superlattices. Phys. Rev. Lett. 107, 167202 (2011).
Nelson-Cheeseman, B. B. et al. Polar Cation Ordering: A Route to Introducing >10% Bond Strain Into Layered Oxide Films. Advanced Functional Materials 24, 6884 (2014).
Li, Y. et al. Unusual magnetic order in the pseudogap region of the superconductor HgBa2CuO4+δ . Nature 455, 372–375 (2008).
Acknowledgements
We thank Eun Ju Moon for discussions and help with transport measurements. J.W.F. would like to thank David Hawthorne for sharing the bulk YBCO XAS data. S.M. was supported by DOD-ARO under Grant No. 0402-17291. J.C. was supported by Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant No. GBMF4534. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DEAC02-06CH11357. This work was supported by the US Department of Energy under Contract No. DE-AC02-05CH11231, and through the Laboratory Directed Research Development program, of the Lawrence Berkeley National Laboratory; and under Contract No. DE-SC0014697 through the University of California Davis. C.S.F. also acknowledges support from the APTCOM Project of the Labex Program (France) during the writing of this paper. A.X.G. acknowledges support from the US Army Research Office, under Grant No. W911NF-15-1-0181 during the writing of this paper.
Author information
Authors and Affiliations
Contributions
B.A.G. and M.K. prepared the sample. B.A.G., S.M., D.M., I.C.T., J. L., J.C. and J.W.F. acquired and analyzed the XAS data at Argonne National Laboratory. G.C., A.X.G., C.-T.K., A.M.K., S.U., K.K. and C.S.F. carried out HXPS experiments and analysis. All authors contributed to the interpretation of the data. B.A.G., S.M., C.S.F., J.C. and J.W.F. wrote the manuscript with input from all the authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gray, B., Middey, S., Conti, G. et al. Superconductor to Mott insulator transition in YBa2Cu3O7/LaCaMnO3 heterostructures. Sci Rep 6, 33184 (2016). https://doi.org/10.1038/srep33184
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33184
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





 (b) Y 3d (c) Ca 2p3/2 and (d) La 3d5/2. All of these data were recorded at T = 300 K and the energy was calibrated using Au.
(b) Y 3d (c) Ca 2p3/2 and (d) La 3d5/2. All of these data were recorded at T = 300 K and the energy was calibrated using Au.