Abstract
We propose a simple two-dimensional acoustic crystal to realize topologically protected edge states for acoustic waves. The acoustic crystal is composed of a triangular array of core-shell cylinders embedded in a water host. By utilizing the point group symmetry of two doubly degenerate eigenstates at the Γ point, we can construct pseudo-time-reversal symmetry as well as pseudo-spin states in this classical system. We develop an effective Hamiltonian for the associated dispersion bands around the Brillouin zone center, and find the inherent link between the band inversion and the topological phase transition. With numerical simulations, we unambiguously demonstrate the unidirectional propagation of acoustic edge states along the interface between a topologically nontrivial acoustic crystal and a trivial one, and the robustness of the edge states against defects with sharp bends. Our work provides a new design paradigm for manipulating and transporting acoustic waves in a topologically protected manner. Technological applications and devices based on our design are expected in various frequency ranges of interest, spanning from infrasound to ultrasound.
Similar content being viewed by others
Introduction
Topological insulators have witnessed a lot of success in the last decade. In various electronic systems, from the artificially designed Haldane lattice1, to graphene2,3 and HgTe/CdTe quantum well structures4,5, the topology – a mathematical property describing the quantized behavior of the wavefunctions over the associated dispersion bands – has been found to have a profound influence on the transportation properties of electronic wave functions6,7. The concept of topology was thereafter borrowed from quantum systems and transplanted into classical systems, offering researchers a new degree of freedom in controlling and manipulating electromagnetic8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27, acoustic28,29,30,31,32,33 and elastic waves34,35,36,37,38,39,40,41,42 in their corresponding artificial structures.
Both electromagnetic and elastic waves satisfy vector wave equations. Electromagnetic wave has two transverse polarizations/modes that are perpendicular to the propagation direction. Elastic wave contains not only two transverse polarizations/modes but also one longitudinal polarization/mode. The polarization degree of freedom is naturally exploited to emulate spins in quantum systems in the realization of unidirectional propagation of classical waves. In contrast, acoustic wave satisfies scalar wave equation and has only one longitudinal polarization, making the realization of unidirectional propagation in acoustics nontrivial. Thus, the reported topological nontrivial phases in acoustic systems were enabled either by rotating fluids to break the time-reversal symmetry29,30,31, or by utilizing chiral interlayer coupling to break the inversion symmetry32. Although topologically protected edge states were numerically demonstrated in these works, the need of integrating rotational fluids into resonators or the fabrication of complex inversion-breaking chiral structures remains technically challenging. Very recently, another artificial structure was designed to realize the unidirectional propagation of acoustic waves33. The graphite-like structure is a bit complex, which involves two scatterers in each primitive unit cell, and its lattice constant has to be on the wavelength scale to support the associated unidirectional propagation. Here, we propose a different and simple way to realize topologically protected edge states for acoustic waves in the subwavelength region without introducing rotational fluids or complex unit cells.
The system is a two-dimensional acoustic crystal (AC) composed of a triangular array of core-shell cylinders embedded in a water host. We show that by utilizing the rotational symmetry of the unit cell, pseudo-time-reversal symmetry23 can be constructed and, as a result, the acoustic analogue of the quantum spin Hall effect can be emulated. We develop an effective Hamiltonian for the associated system, and unveil the inherent link between the band inversion and the topological phase transition. We unambiguously demonstrate topologically protected acoustic one-way edge states with robust propagation against scattering from defects.
Results
Design and characteristics
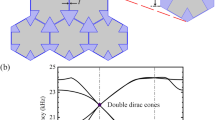
A schematic of the two-dimensional (2D) AC is shown in Fig. 1(a). Each core-shell cylinder has a steel rod with radius r as its core, which is coated by a layer of silicone rubber. The outer radius of the cylinder is R, and a is the lattice constant. The acoustic wave equation is
Band structures for the 2D acoustic crystals (ACs).
(a) Each 2D AC consists of a triangular array of core-shell cylinders embedded in a water host. (b) The band structure for r = 0.2822a and R = 0.3497a; a double Dirac cone is seen at the Γ point. (c) The band structure for r = 0.265a and R = 0.322a; a trivial gap is formed between the third and fourth bands. (d) The band structure for r = 0.295a and R = 0.35a; a nontrivial gap is formed. The frequency range of the gap is almost the same as that in (c).

where p is the pressure, with ρr = ρ/ρ0 and Br = B/B0 being the relative mass density and bulk modulus, respectively.  is the speed of sound in water. The mass densities for water, rubber and steel are ρ0 = 1000 kg/m3, ρ1 = 1300 kg/m3, and ρ2 = 7670 kg/m3, respectively. The longitudinal wave velocities in water, rubber and steel are c0 = 1490 m/s, c1 = 489.9 m/s, and c2 = 6010 m/s, respectively. Due to the strong mismatch between the longitudinal velocities in these media, the shear wave modes in the solid components are ignored here, and this simplification does not alter the essential physics of the system43,44.
is the speed of sound in water. The mass densities for water, rubber and steel are ρ0 = 1000 kg/m3, ρ1 = 1300 kg/m3, and ρ2 = 7670 kg/m3, respectively. The longitudinal wave velocities in water, rubber and steel are c0 = 1490 m/s, c1 = 489.9 m/s, and c2 = 6010 m/s, respectively. Due to the strong mismatch between the longitudinal velocities in these media, the shear wave modes in the solid components are ignored here, and this simplification does not alter the essential physics of the system43,44.
It was shown in ref. 44 that a four-fold degeneracy is achieved at the Г point at frequency ωD = 0.6092(2πc0/a) when r = 0.2822a and R = 0.3497a, and, as a result, a double Dirac cone was formed at the center of the Brillouin zone as shown in Fig. 1(b). Here, we use COMSOL Multiphysics, a commercial package based on the finite-element method, to calculate the band structures.
The four-fold degeneracy is realized when the doubly degenerate dipolar states coincide with the doubly degenerate quadrupolar states at ωD. The degeneracy is thus accidental. That is to say, if we alter the geometric parameters, e.g., the inner and/or outer radii of the core-shell cylinders, the four-fold degeneracy will be lifted, and the dipolar states will be separated from the quadrupolar states. In Fig. 1(c,d), we plot the band structures for r = 0.265a and R = 0.322a, and for r = 0.295a and R = 0.35a, respectively, where the four-fold degeneracy is lifted and the dipolar states are separated from the quadrupolar states.
For the AC we mentioned above, the point group at the center of the Brillouin zone (BZ) is C6v, which has two 2D irreducible representations45: E1 with basis functions (x,y) and E2 with basis functions (2xy, x2 − y2). E1 modes have odd spatial parity, while E2 modes have even spatial parity. From the distribution of the eigenfields shown in Fig. 2, it is easy to recognize that the E1 [Fig. 2(a,b)] and E2 [Fig. 2(c,d)] representations have, respectively, the same symmetry as the (px,py) and  orbitals of electrons in quantum systems. We note that relative eigenfrequencies corresponding to different irreducible representations change as the geometry of the core-shell cylinder changes. To be more specific, the eigenfrequency associated with the E1 representation is lower than that of E2 as shown in Fig. 1(c), but it is higher in Fig. 1(d), indicating that a band inversion process occurs as the geometry changes. Later, we will show that this band inversion is inherently associated with a topological phase transition.
orbitals of electrons in quantum systems. We note that relative eigenfrequencies corresponding to different irreducible representations change as the geometry of the core-shell cylinder changes. To be more specific, the eigenfrequency associated with the E1 representation is lower than that of E2 as shown in Fig. 1(c), but it is higher in Fig. 1(d), indicating that a band inversion process occurs as the geometry changes. Later, we will show that this band inversion is inherently associated with a topological phase transition.
Pressure field distributions of the E1 and E2 representations for the topologically nontrivial AC shown in Fig. 1(d).
In (a,b), px – and py –like pressure fields are seen, while in (c,d) d2xy – and  –like patterns are recognized. Red and blue denote the positive and negative maxima, respectively.
–like patterns are recognized. Red and blue denote the positive and negative maxima, respectively.
In the Method section, we demonstrate that the spatial symmetry of the E1 and E2 representations can be utilized to construct pseudo-time-reversal symmetry. Here we refer only to the main results. From the E1 basis functions (px,py), we can construct the pseudo-spin states as  , with p+ (p−) being the pseudo spin-up (spin-down) state. The same conclusion can be made on
, with p+ (p−) being the pseudo spin-up (spin-down) state. The same conclusion can be made on  , which is another pair of pseudo spin-up/spin-down states associated with the E2 representation.
, which is another pair of pseudo spin-up/spin-down states associated with the E2 representation.
Effective Hamiltonian
To understand the topological property of the band gaps shown in Fig. 1(b,c), we construct an effective Hamiltonian for the current system around the Γ point from a  perturbation method44,45,46. We assume Γα (α = 1, 2, 3, 4) are the four eigenstates at the Γ point: Γ1 = px, Γ2 = py,
perturbation method44,45,46. We assume Γα (α = 1, 2, 3, 4) are the four eigenstates at the Γ point: Γ1 = px, Γ2 = py,  , and Γ4 = d2xy, with the px(y) and
, and Γ4 = d2xy, with the px(y) and  states corresponding to the E1 and E2 representations, respectively. The effective Hamiltonian around the Γ point then is given by
states corresponding to the E1 and E2 representations, respectively. The effective Hamiltonian around the Γ point then is given by  , where
, where 
 is the eigenfrequency of Γ1,2 (Γ3,4), and
is the eigenfrequency of Γ1,2 (Γ3,4), and  is the
is the  perturbation term for the acoustic wave equation (1), obtained by expanding the Bloch eigenstates at point
perturbation term for the acoustic wave equation (1), obtained by expanding the Bloch eigenstates at point  as the linear combinations of the Bloch eigenstates at point Γ. Rewriting the above Hamiltonian on the basis [p+, d+, p−, d−], we arrive at the following effective Hamiltonian in the vicinity of the Γ point,
as the linear combinations of the Bloch eigenstates at point Γ. Rewriting the above Hamiltonian on the basis [p+, d+, p−, d−], we arrive at the following effective Hamiltonian in the vicinity of the Γ point,

wherek± = kx ± iky and  is the frequency difference between E2 and E1 representations at the Γ point, which is positive (negative) before (after) the band inversion. A comes from off-diagonal elements of the first-order perturbation term
is the frequency difference between E2 and E1 representations at the Γ point, which is positive (negative) before (after) the band inversion. A comes from off-diagonal elements of the first-order perturbation term  with m = 1, 2 and n = 3, 4. B is determined by the diagonal elements of the second-order perturbation term
with m = 1, 2 and n = 3, 4. B is determined by the diagonal elements of the second-order perturbation term  , and is typically negative. We note that to derive the above Hamiltonian, the spatial symmetries of the eigenstates, Γα, are utilized. The effective Hamiltonian,
, and is typically negative. We note that to derive the above Hamiltonian, the spatial symmetries of the eigenstates, Γα, are utilized. The effective Hamiltonian,  , shown in Eq. (2) takes a similar form as that proposed in the Bernevig-Hughes-Zhang (BHZ) model for the CdTe/HgTe/CdTe quantum well system4.
, shown in Eq. (2) takes a similar form as that proposed in the Bernevig-Hughes-Zhang (BHZ) model for the CdTe/HgTe/CdTe quantum well system4.
We note that, in Fig. 1(c), the bands above (below) the gap belong to the E2 (E1) representation, which means that  . For the Hamiltonian expressed in Eq. (2), the spin Chern numbers can be evaluated as4,47
. For the Hamiltonian expressed in Eq. (2), the spin Chern numbers can be evaluated as4,47

Since C± = 0, we conclude that the band gap shown in Fig. 1(c) is trivial. However the situation is different in Fig. 1(d), where the bands above (below) the gap exhibit E1 (E2) characteristics around the Γ point, meaning that M < 0. Applying Eq. (3), we immediately know that C± = ±1 and the gap in Fig. 1(d) is nontrivial. It is evident that the topological property of the effective Hamiltonian is determined by the signs of M and B rather than their absolute values. It is also interesting to find the topological phase transition from a trivial one [Fig. 1(c)] to a nontrivial one [Fig. 1(d)] that is associated with the band inversion between the E1 and E2 representations around the Γ point. Our finding shares a similar physical mechanism with that in the BHZ model developed for the CdTe/HgTe/CdTe quantum well system4. Therefore, we expect that our AC system can support an acoustic ‘spin Hall effect’, although our system is quite different from the BHZ quantum system: we are dealing with a system governed by the classical acoustic wave equation rather than the Schrödinger equation.
Topological edge states
We consider a ribbon of topologically nontrivial crystal (i.e., the AC that produces the band structure shown in Fig. 1(d)) with its two edges cladded by two topologically trivial crystals (the AC that produces the band structure shown in Fig. 1(c)). The frequency regime, [955.18 Hz, 990.43 Hz], is common for the trivial and nontrivial gaps to create true edge states that are spatially confined around the interface between two crystals. In Fig. 3(a), we plot the projected band structures along the ΓK direction for such a ribbon. We find that in addition to the bulk states represented by black dots, there are doubly degenerate states, represented by red dots within the bulk gap region. After examining the eigenfield distributions at the red dots (e.g., points A and B), we find that the pressure field decays exponentially into bulk crystals on both sides, which means that the red curves represent the dispersion relations of edge states that are tightly confined around the interface between the nontrivial and trivial phases. In Fig. 3(b), we plot the pressure field distribution on one interface for the eigenstates at points A and B, respectively, and a magnified view is plotted in Fig. 3(c), where black arrows indicate the time-averaged Poynting vectors. The clockwise and anticlockwise distributions of the Poynting vector at the interface unveil the characteristics of the pseudo spin-up and spin-down states, respectively. The locking of the (pseudo) spin-up and spin-down states with counter-propagations of edge states is reminiscent of the quantum spin Hall effect in electronic systems. We want to note that the working frequency of points A and B is in the subwavelength region, where the lattice constant is only 0.64λ0.
Projected band structure and topological edge states.
(a) The projected band structure along the ΓK direction for a ribbon of topologically nontrivial crystal with its two edges cladded by topologically trivial crystals. The ribbon has 1 unit cell in one direction and 86 unit cells along the other direction (46 nontrivial unit cells cladded by 20 trivial unit cells on both sides). The red and black dots represent edge and bulk states, respectively. (b,c) Pressure field distributions around the interface between the trivial and nontrivial phases at points A and B, i.e., at kx = −0.05π/a and 0.05π/a, respectively. Red and blue denote positive and negative maxima, respectively. Black arrows indicate the time-averaged Poynting vector.
Because the pseudo-time-reversal symmetry and the pseudo-spin states are constructed on the basis of the C6ν point group symmetry, any deviation from the crystal symmetry would mix the two pseudo-spin channels as in other topological systems11,15,23. Actually, there is a tiny gap (not evident in Fig. 3(a)) at the Γ point, arising from the reduction of the C6ν symmetry at the interface between the trivial and nontrivial phases. However, the topological properties of the corresponding structures remain valid even with a moderate deformation in the lattice symmetry, as will be explicitly shown below.
Discussion
As a first example, we consider a flat edge between a topologically nontrivial phase (upper part) and a trivial phase (lower part), as shown in Fig. 4, where the whole structure is surrounded by perfectly matched layers (PMLs) to absorb outgoing waves. When an acoustic wave carrying a leftward (rightward) wave vector is excited in the middle part of the edge, unidirectional propagation of the acoustic wave towards the left (right) direction can be observed in Fig. 4(a,b). When these edge waves arrive at the left (right) boundary of the simulation domain, they are guided without reflections along the interface of the nontrivial crystal to continue propagating upwards. At the same time, they gradually decay into the PMLs. Negligible reflection occurs at the left (right) boundary of the edge, which is expected from the topological properties of the edge states.
Unidirectional propagation of edge states.
Realization of unidirectional acoustic wave propagation towards the (a) left and (b) right directions along the interface between a nontrivial phase (upper part) and a trivial phase (lower part), with the whole structure surrounded by perfectly matched layers. The acoustic waves that carry the leftward (rightward) wave vector is excited by using a couple of point sources located in the middle part of the interface at a distance of λ0/4, and the two sources have a phase difference of π/2(−π/2).
One of the most important features of topological edge states is that they are immune to defects/imperfections. In the following, we demonstrate edge wave propagation around a specific type of imperfection: four sharp bends of the edge shown in Fig. 5(b), which is constructed from the structure in Fig. 4 by further replacing a region of the nontrivial topological phase  with that of the trivial one. When a left-heading wave is excited, it propagates along the edge and can go around the rhombic defect without reflections at the four sharp corners. It also maintains its unidirectional propagation as shown in Fig. 5(a). This result confirms the topological robustness of the edge states against a sharply curved interface.
with that of the trivial one. When a left-heading wave is excited, it propagates along the edge and can go around the rhombic defect without reflections at the four sharp corners. It also maintains its unidirectional propagation as shown in Fig. 5(a). This result confirms the topological robustness of the edge states against a sharply curved interface.
To conclude, we have designed a 2D acoustic crystal consisting of a triangular array of core-shell cylinders embedded in a water host. We have shown that a topological phase transition can be obtained by using the band inversion mechanism in such a simple system. A pseudo-time-reversal symmetry can be constructed by utilizing the C6ν point group symmetry of the p and d eigenstates at the Γ point, and it follows that pseudo spin-up and spin-down states can be realized in this classical wave system in the same spirit as the quantum spin Hall effect in electronic systems. An effective Hamiltonian is developed for the current acoustic system around the Γ point, and the Hamiltonian unveils the underlying mechanism that links the band inversion to a topological phase transition. Numerical simulations unambiguously demonstrate the unidirectional propagation of the pseudo-spin edge states and the robustness of these edge states against sharp bends. The simple design of our proposed structure suggests that experimental realization is feasible. Since the underlying principle is valid for different scales, we expect that it will have potential applications in manipulating and controlling acoustic waves over a very large frequency range, spanning from infrasound to ultrasound.
Methods
Derivation of pseudo-time-reversal symmetry
In the following, we demonstrate that the spatial symmetry of the E1 and E2 representations can be utilized to construct pseudo-time-reversal symmetry23. Let DE1(C6) and  denote the E1 irreducible representations of the π/3 and 2π/3 rotations, respectively. Their matrix representations on basis (x, y)T are therefore
denote the E1 irreducible representations of the π/3 and 2π/3 rotations, respectively. Their matrix representations on basis (x, y)T are therefore


It turns out that they can be combined together in a unitary operator, U, as

where σy is the Pauli matrix. Obviously, U2 = −I. Thus, we can construct an anti-unitary operator, T, as T = UK = −iσyK, where K is the complex conjugate operator. It follows that

which yields T2 = −I. Similarly, the E2 matrix representations of rotational operators C6 and  on basis (x2 − y2, 2xy)T are
on basis (x2 − y2, 2xy)T are


And the unitary operator, U, can be constructed as  . It is easy to check that we also have T2 = −I, the same as in the E1 irreducible representation. Therefore, for both E1 and E2 modes, the pseudo-time-reversal symmetry, T = UK, in the current acoustic system indeed satisfies T2 = −I, which is similar to the real time-reversal symmetry in electronic systems and which also guarantees the appearance of a Kramers doublet at the Γ point. From the derivations shown above, it is clear that the role played by the crystal symmetry of the unit cell in constructing the pseudo-time-reversal symmetry is crucial.
. It is easy to check that we also have T2 = −I, the same as in the E1 irreducible representation. Therefore, for both E1 and E2 modes, the pseudo-time-reversal symmetry, T = UK, in the current acoustic system indeed satisfies T2 = −I, which is similar to the real time-reversal symmetry in electronic systems and which also guarantees the appearance of a Kramers doublet at the Γ point. From the derivations shown above, it is clear that the role played by the crystal symmetry of the unit cell in constructing the pseudo-time-reversal symmetry is crucial.
Following this analysis, we can construct the pseudo-spin states as  , with p+ (p−) being the pseudo spin-up (spin-down) state. On the (p+, p−)T basis, the pseudo-time-reversal operator, T′ = U′K, [U′ and T′ are defined on the (p+, p−)T basis, while U and T are defined on the (px, py)T basis] exhibits the following desired properties:
, with p+ (p−) being the pseudo spin-up (spin-down) state. On the (p+, p−)T basis, the pseudo-time-reversal operator, T′ = U′K, [U′ and T′ are defined on the (p+, p−)T basis, while U and T are defined on the (px, py)T basis] exhibits the following desired properties:

From Eq. (10), it is clear that the wave functions (p+, p−) are the two pseudo-spin states in the E1 representation of our acoustic system because the pseudo-time-reversal operator, T′, transforms the pseudo spin-up state into a spin-down state, and vice versa. The same conclusion can be made on  , which is another pair of pseudo spin-up/spin-down states associated with the E2 representation.
, which is another pair of pseudo spin-up/spin-down states associated with the E2 representation.
Numerical simulations
All the numerical simulations presented in this article are performed using COMSOL Multiphysics, a commercial package based on the finite-element method. Figures 1, 2 and 3 are computed using the eigenfrequency study in the pressure acoustics module. The Bloch boundary conditions are imposed on the boundaries of the unit cells. Figures 4 and 5 are calculated using the frequency domain study in the pressure acoustics module, where the acoustic crystal structures are surrounded by perfectly matched layers so that there is no reflected wave from the boundaries of the simulation domains.
Additional Information
How to cite this article: Mei, J. et al. Pseudo-time-reversal symmetry and topological edge states in two-dimensional acoustic crystals. Sci. Rep. 6, 32752; doi: 10.1038/srep32752 (2016).
References
Haldane, F. D. M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).
Kane, C. L. & Mele, E. J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 95, 226801 (2005).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 314, 1757–1761 (2006).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Klitzing, K. v., Dorda, G. & Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 49, 405–408 (1982).
Haldane, F. D. M. & Raghu, S. Possible Realization of Directional Optical Waveguides in Photonic Crystals with Broken Time-Reversal Symmetry. Phys. Rev. Lett. 100, 013904 (2008).
Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljăcić, M. Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys. Rev. Lett. 100, 013905 (2008).
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljăcić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).
Poo, Y., Wu, R.-X., Lin, Z., Yang, Y. & Chan, C. T. Experimental Realization of Self-Guiding Unidirectional Electromagnetic Edge States. Phys. Rev. Lett. 106, 093903 (2011).
Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photonics 6, 782–787 (2012).
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).
Khanikaev, A. B. et al. Photonic topological insulators. Nat. Mater. 12, 233–239 (2013).
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photonics 7, 1001–1005 (2013).
Liang, G. Q. & Chong, Y. D. Optical Resonator Analog of a Two-Dimensional Topological Insulator. Phys. Rev. Lett. 110, 203904 (2013).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photonics 8, 821–829 (2014).
Chen, W. J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 5782 (2014).
Xiao, M., Zhang, Z. Q. & Chan, C. T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys. Rev. X 4, 021017 (2014).
Ochiai, T. Photonic realization of the (2 + 1)-dimensional parity anomaly. Phys. Rev. B 86, 075152 (2012).
Ma, T., Khanikaev, A. B., Mousavi, S. H. & Shvets, G. Guiding Electromagnetic Waves around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides. Phys. Rev. Lett. 114, 127401 (2015).
Wu, L.-H. & Hu, X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys. Rev. Lett. 114, 223901 (2015).
Estep, N. A., Sounas, D. L., Soric, J. & Alù, A. Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nat. Phys. 10, 923–927 (2014).
Wang, Y.-P., Yang, W.-L., Hu, Y., Xue, Z.-Y. & Wu, Y. Detecting topological phases of microwave photons in a circuit quantum electrodynamics lattice. npj Quantum Information 2, 16015 (2016).
Wang, Y.-P. et al. Realizing and characterizing chiral photon flow in a circuit quantum electrodynamics necklace. Sci. Rep. 5, 8352 (2015).
He, C. et al. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl. Acad. Sci. USA 113, 4924–4928 (2016).
Xiao, M. et al. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 11, 240–244 (2015).
Yang, Z. et al. Topological Acoustics. Phys. Rev. Lett. 114, 114301 (2015).
Ni, X. et al. Topologically protected one-way edge mode in networks of acoustic resonators with circulating air flow. New J. Phys. 17, 053016 (2015).
Chen, Z. G. & Wu, Y. Tunable Topological Phononic Crystals. Phys. Rev. Applied 5, 054021 (2016).
Xiao, M., Chen, W. J., He, W.-Y. & Chan, C. T. Synthetic gauge flux and Weyl points in acoustic systems. Nat. Phys. 11, 920–924 (2015).
He, C. et al. Acoustic topological insulator and robust one-way sound transport. arXiv:1512.03273 (unpublished).
Prodan, E. & Prodan, C. Topological Phonon Modes and Their Role in Dynamic Instability of Microtubules. Phys. Rev. Lett. 103, 248101 (2009).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45 (2014).
Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).
Paulose, J., Chen, B. G. & Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 11, 153–156 (2015).
Khanikaev, A. B., Fleury, R., Mousavi, S. H. & Alù, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260 (2015).
Mousavi, S. H., Khanikaev, A. B. & Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 6, 8682 (2015).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological Phases of Sound and Light. Phys. Rev. X 5, 031011 (2015).
Wang, P., Lu, L. & Bertoldi, K. Topological Phononic Crystals with One-Way Elastic Edge Waves. Phys. Rev. Lett. 115, 104302 (2015).
Swinteck, N. et al. Bulk elastic waves with unidirectional backscattering-immune topological states in a time-dependent superlattice. J. Appl. Phys. 118, 063103 (2015).
Kafesaki, M. & Economou, E. N. Multiple-scattering theory for three-dimensional periodic acoustic composites. Phys. Rev. B 60, 11993–12001 (1999).
Li, Y., Wu, Y. & Mei, J. Double Dirac cones in phononic crystals. Appl. Phys. Lett. 105, 014107 (2014).
Dresselhaus, M. S., Dresselhaus, G. & Jorio, A. Group Theory: Application to the Physics of Condensed Matter (Springer-Verlag, Heidelberg, Germany, 2008).
Mei, J., Wu, Y., Chan, C. T. & Zhang, Z.-Q. First-principles study of Dirac and Dirac-like cones in phononic and photonic crystals. Phys. Rev. B 86, 035141 (2012).
Shen, S.-Q., Shan, W.-Y. & Lu, H.-Z. Topological insulator and the Dirac equation. Spin 1, 33–44 (2011).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos 11274120 and 11574087) and King Abdullah University of Science and Technology (KAUST).
Author information
Authors and Affiliations
Contributions
J.M. proposed the research direction, derived the analytic formulae, conducted numerical simulations and wrote the initial manuscript. Z.C. drew the figures, calculated the coefficients and revised the manuscript. Y.W. supervised the work and revised the manuscript. All authors participated in the discussion.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mei, J., Chen, Z. & Wu, Y. Pseudo-time-reversal symmetry and topological edge states in two-dimensional acoustic crystals. Sci Rep 6, 32752 (2016). https://doi.org/10.1038/srep32752
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep32752
This article is cited by
-
Spin-dependent properties of optical modes guided by adiabatic trapping potentials in photonic Dirac metasurfaces
Nature Nanotechnology (2023)
-
Topological acoustics
Nature Reviews Materials (2022)
-
Phononic topological insulators based on six-petal holey silicon structures
Scientific Reports (2019)
-
Experimental characterisation of the bound acoustic surface modes supported by honeycomb and hexagonal hole arrays
Scientific Reports (2019)
-
Reflected wave manipulation via acoustic metamaterials with decoupled amplitude and phase
Applied Physics A (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.