Abstract
In the interfacial superconductor Bi2Te3/Fe1+yTe, two dimensional superconductivity occurs in direct vicinity to the surface state of a topological insulator. If this state were to become involved in superconductivity, under certain conditions a topological superconducting state could be formed, which is of high interest due to the possibility of creating Majorana fermionic states. We report directional point-contact spectroscopy data on the novel Bi2Te3/Fe1+yTe interfacial superconductor for a Bi2Te3 thickness of 9 quintuple layers, bonded by van der Waals epitaxy to a Fe1+yTe film at an atomically sharp interface. Our data show highly unconventional superconductivity, which appears as complex as in the cuprate high temperature superconductors. A very large superconducting twin-gap structure is replaced by a pseudogap above ~12 K which persists up to 40 K. While the larger gap shows unconventional order parameter symmetry and is attributed to a thin FeTe layer in proximity to the interface, the smaller gap is associated with superconductivity induced via the proximity effect in the topological insulator Bi2Te3.
Similar content being viewed by others
Introduction
Tailoring a topological superconductor by combining the topologically protected surface states of a TI with a superconductor via the proximity effect is of enormous theoretical and technological interest, principally due to the possibility of finding the Majorana fermionic states which are predicted to exist in the vortex cores of topological superconductors1,2. A novel Bi2Te3/Fe1+yTe heterostructure3 may represent a promising material. Although both parent materials are non-superconducting, the interface becomes a 2D superconductor which undergoes a characteristic 2D Berezinski-Kosterlitz-Thouless (BKT) superconducting transition4,5,6. Bi2Te3 is a 3D topological insulator (TI) whose surface states consist of a single Dirac cone at the Γ point7, while Fe1+yTe is the parent compound of the ‘11’ family of Fe-based superconductors. Despite the exact mechanism for superconductivity in Bi2Te3/Fe1+yTe remaining unknown, it has been shown previously that any doping effect by O, Bi or Te impurities can be excluded3. Evidence that TI surface states play a role in the emergence of superconductivity is found in the fact that a critical thickness of the Bi2Te3 layer is required3. As the number of Bi2Te3 quintuple layers (QL) increases, Tc rises from ~1.2 K (1 QL) to 12 K (5 QL) and then saturates. This correlates with the 5 QL critical thickness required to form a fully-developed surface state in Bi2Te38,9. The heterostructure may thus represent a model system to study proximity-induced topological superconductivity in the Bi2Te3 layer and a highly complex superconducting mechanism is likely involved in the interfacial superconductivity.
In this article, we report directional point-contact data measured for current injection (a) parallel to the interface into the edge of the heterostructure, simultaneously probing both layers and (b) perpendicular to the interface into the top Bi2Te3 layer. We observe a pronounced twin gap structure with a large gap of unconventional pairing symmetry, corresponding to the interfacial superconductivity and a smaller gap which opens below the characteristic BKT temperature and is associated with proximity-induced superconductivity in the topologically insulating Bi2Te3 layer. In addition, a pseudogap is observed which extends up to 40 K.
Point-contact spectroscopy is an energy-resolved technique directly probing the amplitude, symmetry and temperature-dependence of the superconducting gap10. Our data were acquired using bilayers of Bi2Te3(9QLs)/Fe1+yTe, chosen for their high Tc = 12 K. The Van-der-Waals bonding between the materials results in extremely high quality atomically-sharp interfaces.
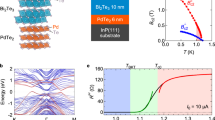
Figure 1 displays the temperature-dependent resistance of the heterostructure, as measured with 4 contacts established by silver-loaded paint on top of the Bi2Te3 surface. An insulator-to-metal transition is visible in the form of a broad maximum at 76 K, which we associate with the antiferromagnetic transition of the bulk Fe1+yTe layer. At lower temperatures, the resistance passes through a minimum at 24 K before increasing steeply. The overall resistive behavior (including this increase) is typical for FeTe with a high content of interstitial excess Fe11 and can therefore be attributed to the bulk FeTe layer of our heterostructure. Indeed, high-resolution energy-dispersive X-ray spectroscopy in a scanning transmission electron microscope indicates that y = 0.15 ± 0.02 in our Fe1+yTe bulk layer. It should be noted that FeTe does not exist in stoichiometric form and always has some excess Fe in the form of individual interstitial ions12. Superconductivity in the vicinity of the Bi2Te3/Fe1+yTe interface reveals itself by a rapid resistance decrease below Tc = 12 K until zero resistance is reached at T0 = 8 K. From Fig. 1, the overall behavior of our heterostructure is in good agreement with our previous work3, in which we have shown that the broadness of the resistance drop associated with the superconducting transition between 12 K and 8 K is intrinsic and the transition falls into the 2D-XY universality class of a BKT transition. It is important to note that the resistance is composed of 3 parallel components: the Bi2Te3 layer, the bulk Fe1+yTe layer and the intermediate thin interfacial layer. The resistance drop below 12 K is associated with the diverging superconducting correlation length in the interfacial layer upon approaching the BKT transition. However, 12 K is not necessarily the onset of the superconducting transition: the rapidly increasing resistance of the interface will cause the current to gradually move away from the interfacial region into the 140 nm thick bulk Fe1+yTe layer, which then begins to shunt the interface resistance. Therefore, the normal state resistance of the interface will be largely hidden due to the large Fe1+yTe thickness (140 nm) relative to that of the thin superconducting interfacial layer.
Temperature dependence of the electrical resistance of the device.
The drop below 12 K is associated with the superconducting BKT transition of the interface region3, while the resistance above ~12 K is dominated by the bulk Fe1+yTe layer. TSDW is the antiferromagnetic spin density wave ordering temperature of the bulk FeTe layer12.
Figure 2a shows the temperature dependent point-contact spectra for the nano-contact on the heterostructure edge. At the highest temperatures a smooth parabolic background is seen, with little difference in data acquired at 70, 50 and 40 K. Below 40 K a pseudogap develops symmetrically around Vb = 0, gradually deepening as the temperature falls. Until 15 K, the gap is rounded at low energy, but at 12 K the conductance flattens around Vb = 0 prior to the emergence of a zero bias conductance peak (ZBCP) below ~10 K. Concurrently, shoulder-like structures develop at ~10 mV and ~5 mV, which as we will now demonstrate correspond to a phase-coherent superconducting twin-gap structure13.
(a) Temperature-dependent differential conductance spectroscopy. The data was taken on a point-contact on the edge of the Bi2Te3(9QLs)/Fe1+yTe heterostructure. Offsets have been added for clarity. The dotted lines illustrate the normal-state background. (b) Data from 2(a) normalized to a polynomial background from the 70 K spectrum, together with fits using superconducting 2-gap BTK and Dynes models. Offsets have been added for clarity. The low voltage range containing the ZBCP (±3.5 mV) was excluded from the fit. (c,d) Temperature dependence of the two superconducting gaps Δ1,2 determined from BTK and Dynes models. (e) The energy dependent Dynes parameter Γ2 describing the quasiparticle lifetime in Δ2 obtained from the fits to the 2-gap Dynes and BTK models.
To fit the temperature dependence of our data, we primarily employ a modified Blonder-Tinkham-Klapwijk (BTK) model for finite-transparency tunnel junctions14, excluding the energy range of the ZBCP. Our fits are based on a 1D BTK model for simplicity, since higher-dimensional models are equivalent to the 1D case except for small shifts in the barrier heights Z. In such a highly two-dimensional superconductor, fluctuations are expected to significantly reduce the quasiparticle lifetime; we account for this in our model with an energy-dependent Dynes parameter15 of the form Γexp[(│Vb│−Δ)/W] where Γ and W are free parameters. The shoulders at ~5 and ~10 mV are modeled by an anisotropic two-band s-wave order parameter Δ(α+(1 − α) cos θ)16, in which we determine the gap anisotropies α1,2 from a fit at our lowest achievable temperature 0.27 K, then fix α1,2 at these values for all other temperatures.
The fitting results are shown in Fig. 2b: we are able to accurately reproduce our experimental data – including the double-gap structure – across the entire energy range. Since our BTK fits indicate large barrier heights (Z1 ≥ 0.35 for Δ1 and Z2 ~ 1000 for Δ2), we also attempt to model our data using a two-band Dynes model (with a metallic conduction component to compensate for the lower barrier Z1). Both models yield similar results: at 0.27 K, Δ1 = 6 meV and Δ2 = 12 meV from the BTK model, while Δ1 = 4 meV and Δ2 = 13 meV from the Dynes fit. Δ1 exhibits a pronounced anisotropy α ~ 0.7, whereas Δ2 is approximately isotropic (α = 1). In each case, Δ2 provides the dominant contribution to the spectral weight: 60 ± 5% versus 40 ± 5% for Δ1 in the BTK model, compared with a Δ1:Δ2:metallic ratio of 8 ± 0.5%: 46 ± 4% : 46 ± 4% in the Dynes model. The smaller values for Δ1 and its spectral weight from the Dynes fit are due to non-negligible Andreev reflections, which cannot be perfectly simulated by the metallic component within this model. To account for the presence of the ZBCP, we also attempted to reproduce this data using a two-gap d-wave model, but no improvement of the fit or significant variation of the gap values were observed compared to the anisotropic s-wave case. Δ1 closes at 8 K while Δ2 appears to close at 40 K. The magnitude of Δ2 abruptly increases above 8 K. As we will demonstrate later, Δ2 actually consists of a large superconducting gap which transforms continuously into a pseudogap in the temperature range between 8 and 12 K. The pseudogap then closes at 40 K.
In Fig. 3 we present the differential conductance upon injecting the current through a scanning probe tip on the Bi2Te3 surface. The current was injected perpendicular to the film and hence only probes the Bi2Te3 layer. A small 5.4 meV gap dominates the conductance at low temperature, in excellent agreement with the small gap Δ1 observed upon injecting the current into the edge of the interface. The conductance saturates for Vb > 6 mV and no signature of the larger gap Δ2 is observed. This suggests that the Bi2Te3 layer becomes superconducting and is responsible for Δ1, similar to what has been observed in Bi2Sr2CaCu2O8+δ/Bi2Se317,18, Bi2Sr2CaCu2O8+δ/Bi2Te318 or Bi2Sr2CaCu2O8+δ/Bi2Te2Se19 junctions grown on a cuprate high-temperature superconductor, or in proximity contact with classical superconductors20. Here it should be noted that certain other groups have reported the absence of a proximity effect in Bi2Sr2CaCu2O8+δ/Bi2Se3 junctions21,22. Additional point contact data can be found in the supplementary information.
Zero-field conductance of a point contact on the Bi2Te3 surface.
The same Bi2Te3(9QLs)/Fe1+yTe heterostructure was used as in Fig. 2. Data were acquired by injecting the current perpendicular to the film plane through a tungsten scanning probe tip in contact with the surface. A fit using an anisotropic s-wave single-gap BTK model is also shown: α = 0.7 and Δ = 5.4 meV, thus corroborating our results for Δ1 from our edge-contacted heterostructures.
In Fig. 4 we plot the point-contact spectra in 0 and 15 T applied (a) perpendicular and (b) parallel (field perpendicular to the current injection direction) to the film plane. Note that for technical reasons, different edge contacts on the same sample have been used and the spectra in Fig. 4b are somewhat broader but show qualitatively the same features. The gap structure and ZBCP are quite robust with respect to magnetic fields, irrespective of their orientation. The spectra hardly change in 15 T: the gap becomes marginally shallower, but the gap energies Δ1,2 do not shrink significantly. This resilience of the overall gap structure demonstrates that the Cooper pairing strength is almost impervious to strong fields, in direct contrast with the critical field Hc2 = 17 T which has been estimated from resistance data3. We deduce that Hc2 merely corresponds to a field-induced loss of phase coherence. We observe reductions in the ZBCP height of 20% and 30% in 15 T applied in-plane and perpendicular to the interface, respectively, measured with respect to the minimum in the dI/dV curve. The ZBCP does not experience any splitting, regardless of the magnetic field orientation. In Fig. 4c we show the effect of a 9T magnetic field on the pseudogap: a magnetic field has a weak suppressing effect at temperatures up to 40 K.
Differential conductance of the edge contact in magnetic fields.
(a,b) Differential conductance of the edge contact in 0 T and 15 T at 0.27 K applied perpendicular (a) and parallel (b) to the interface. The spectra in (b) have been obtained on a different edge contact on the same sample, which show slightly broader spectra than at the contact in (a). (c) Pseudogap in the normalized spectra in 0 T and 9 T, illustrating a partial suppression of the pseudogap by the applied field at temperatures below 40 K.
The large size of Δ2 ≥ 12 meV is a striking feature of our Bi2Te3/Fe1+yTe heterostructure. It exceeds the superconducting gap in bulk FeSe23 or FeSe1−xTex24 by at least a factor of 4, despite the Tc of our heterostructures being comparable to Tc in these bulk materials. Our data constitute a demonstration of the potential for strong-coupling superconductivity which could persist up to far higher temperatures than the critical temperatures observed in the bulk iron-chalcogenides. The origin of this gap enhancement is unclear, but since the presence of the Bi2Te3 layer is essential for the appearance of superconductivity3, it is possible that the topological surface states of Bi2Te3 play a certain role.
Multiband superconductivity with various gaps has been reported in various Fe-based superconductors10,25,26 and is usually attributed to multiple electronic bands crossing the Fermi level in the same material. However, as we are probing the properties of the FeTe and Bi2Te3 layers in parallel, the twin-gap feature could also originate from two spatially separated regions each with its corresponding electronic bands involved. Superconductivity induced by the proximity effect in the Bi2Te3 layer could therefore play a role in the opening of the second gap. A proximity-induced small gap has previously been observed in devices of Bi2Se3 and Bi2Te3 which were mechanically bonded to the cuprate high-Tc Bi2Sr2CaCu2O8+δ: these showed a similar reduction of the gap in the cuprate when the TI became superconducting18.
The temperature dependence of the gaps extracted from the BTK and Dynes fits is shown in Fig. 2c,d: it is clear that both models yield qualitatively identical results. Below 2 K the smaller gap Δ1 is approximately constant; upon increasing the temperature its magnitude decreases rapidly, reaching zero at ~8 K. In contrast, the larger gap Δ2 is almost temperature-independent between 10 K and 25 K, gradually decreasing towards zero when the temperature is increased further up to 40 K. Between 10 K and 8 K, Δ2 is slightly reduced, which clearly correlates with the opening of Δ1. Below 8 K, the sample exhibits zero resistance3 and is hence globally phase-coherent. Although the pronounced coherence peaks, which are characteristic of superconducting tunneling spectra, are absent from our data due to the short quasiparticle lifetimes imposed by low-dimensional fluctuations, we may nevertheless infer the presence of coherence by the sharp falls in dI/dV close to Δ1,2. Above 8 K, global phase coherence is lost, the resistance gradually increases until the normal state is reached at 12 K and Δ1 vanishes, while Δ2 becomes a pseudogap which persists up to 40 K. The Dynes parameter Γ2 describing the quasiparticle lifetime in Δ2 also rises steeply above 8 K (Fig. 2e), supporting our observed loss of phase coherence above this temperature.
The edge contact data does not allow us to judge whether Δ2 closes at 8 K and is replaced by a pseudogap due to a competing order, or if it transforms continuously into the high-temperature pseudogap, thus suggesting a phase-incoherent superconducting (i.e. pairing) origin. A pronounced pseudogap state above the superconducting critical temperature is most famous in the cuprate high temperature superconductors27 and its origin is still widely debated. In addition, various Fe-based superconductors display signatures of a pseudogap well above Tc10,24,28,29,30,31 and its origin has been suggested to be due to fluctuations of a nematic electronic order31,32,33.
The pseudogap opens well below the antiferromagnetic transition at ~80 K of the bulk Fe1+yTe layer as seen in the resistivity (Fig. 1)34 and thus does not appear to be related to its magnetic ordering. Similar to Se-doped FeTe, it is likely that the magnetic order in the interface region is weakened by charge transfer across the interface from the n-doped Bi2Te3 layer. In addition, the topological surface state may contribute electrons with a strong spin-orbit coupling, thus further suppressing the interfacial magnetic order and paving the way for the emergence of superconductivity. In Ba0.85K0.15Fe2As2 it has been shown by angle resolved photoemission spectroscopy that the SDW order is associated with a ~20 meV gap which forms below the SDW ordering temperature35. At low temperature the SDW gap is reduced concurrently with the onset of superconducting order, in a very similar manner to what we observe for the larger gap Δ2 above 8 K in Fig. 2c,d. A normal state origin is thus compatible with the increase of Δ2 above 8 K, which is suggestive of a replacement of the superconducting gap by a normal state pseudogap. This suggests that the pseudogap which we observe has a competitive relationship with superconductivity and is presumably related to SDW and/or nematic order, which are therefore likely to develop below ~40 K in the interface region.
On the other hand, we have previously shown that the interfacial superconductivity in our heterostructures lies in the extreme 2D limit and the resistance drop and IV characteristics can be perfectly modelled by a BKT transition3. This represents a pure 2D phase-ordering transition of Cooper pairs which are already formed at higher temperature, where the phase of the superconducting order parameter is stabilized below a characteristic temperature TBKT (lying just above T0), at which thermally-induced vortices and anti-vortices are bound into pairs4,5,6. This naturally implies the existence of phase-incoherent Cooper pairs within a certain temperature range above TBKT, creating a pseudogap in the density of states. The 10 meV magnitude of this superconducting gap indicates a potential for strong coupling superconductivity with stable Cooper pairing at temperatures well above 12 K. Superconducting fluctuations have been observed at temperatures many times higher than Tc in strongly-underdoped layered cuprate HTSCs36,37, where they contribute in part to the pseudogap formation. Furthermore, scanning tunneling spectroscopy on ultrathin titanium nitride films has shown that the strong phase fluctuations associated with two-dimensionality can induce a pseudogap in conventional superconducting films at temperatures up to 14 times Tc38. A superconducting origin for the pseudogap in the interfacial superconductor Bi2Te3(9QLs)/Fe1+yTe is supported by the fact that the pseudogap is partially suppressed by a magnetic field of 9 T in temperatures up to 40 K (Fig. 4c), which could be a consequence of pair-breaking effects and is not expected for the SDW gap in an Fe based superconductor. If the pseudogap had an entirely phase-incoherent superconducting origin, then the reduction of the gap upon transformation into a real superconducting gap Δ2below ~8 K could be caused by the opening of the proximity-induced gap Δ1 in the Bi2Te3 layer, similar to the reduction of the superconducting gap observed in Bi2Sr2CaCu2O8+δ in proximity contact to a TI18.
However, in a pseudogap which is caused entirely by fluctuations of the superconducting order parameter, it is expected that the zero-bias conductance GN should vary linearly with ln(ln(T/T0))38,39, where T0 is the phase coherence temperature, represented by the establishment of zero resistivity at 8 K. From Fig. 5 this trend is not observed in our data, thus suggesting that a competing normal-state pseudogap at least partially contributes to the spectra. The most likely explanation of the pseudogap is thus a mixture of a normal state pseudogap (e.g. caused by interfacial SDW or nematic order) and a phase incoherent superconducting pseudogap caused by the strong phase fluctuations of a 2D superconductor.
Temperature dependence of the zero-bias conductance.
The graph shows temperature dependence of the normalized zero-bias conductance GN above the phase-coherence temperature T0 as a function of the reduced temperature ε = ln(T/T0) for various choices of T0 surrounding our experimentally-determined T0 = 8 K (the dotted line is a guide to the eye). The absence of linear behavior over a sufficiently large range of ε suggests a competitive normal state contribution to the pseudogap, which likely competes with phase-incoherent pairing38,39.
As demonstrated by our point contact data on the top of the Bi2Te3 layer, interfacial contact with the Fe1+yTe induces superconductivity in Bi2Te3, which is therefore a potential candidate to host a topological superconducting state40. The combination of superconductivity with the non-trivial topological symmetry of the surface states in a TI naturally evokes the question whether the ZBCP could be caused by Majorana bound states41,42,43. Care has been taken to eliminate any spurious origin for the ZBCP, e.g. heating or proximity effects44: (1) our high-resistance point-contact lies comfortably within the ballistic spectroscopic tunneling regime, (2) the spectra were verified to be identical upon increasing and decreasing the tunnel current and (3) the ZBCP width remains roughly constant at all temperatures below 8 K (Fig. 2a), despite the gap energy Δ1 increasing from zero to 5 meV within this temperature range. The ZBCP is therefore of intrinsic origin. The proximity effect of an s-wave superconductor on a TI1 creates a fully gapped energy spectrum without any in-gap states; in this case, Majorana modes would only be created in the vortex cores in an applied magnetic field. Since the pairing symmetry in Bi2Te3(9QLs)/Fe1+yTe remains unclear, two possible mechanisms exist for the formation of Majorana edge states. One possibility is that the contact with FeTe drives the Bi2Te3 layer to become an intrinsic topological superconductor with Majorana surface states40,41,45,46, e.g. by a charge transfer effect, instead of a proximity-induced superconductor. This would explain the ZBCP observed in the point contact spectra of both the edge (Fig. 2) and the top contacts (Fig. 3). In a magnetic field the ZBCP should be suppressed due to broken time-reversal symmetry: a reduction in the ZBCP height is indeed observed in high magnetic fields, but the effect is only ~20% in 14T. This could be a consequence of a particularly strong Rashba spin-orbit coupling at the interface as well as the extremely high critical field for pairing. A detailed theoretical study of the possible pairing symmetries in Bi2Te3 would be required to confirm this possibility. The alternative mechanism requires nodal dx2−y2 superconductivity (associated with the Fe1+yTe) combined with Rashba spin-orbit coupling (enhanced by the topological surface states of Bi2Te3)47. Although a d-wave order parameter alone could create a fermionic ZBCP at the sample edge, a ZBCP composed of the fermionic edge states and Majorana fermions should form in the presence of strong spin-orbit coupling at zero field. It has been predicted that an in-plane applied field will split and shift the fermionic states to finite energy via the Zeeman effect, while the Majorana state remains at zero energy47. However, no splitting of the ZBCP is observed up to 15 T for applied fields parallel or perpendicular to the interface (Fig. 4a,b) and its height is rather small, thus rendering such a d-wave scenario unlikely. Furthermore, the ZBCP visible in our top contact (Fig. 3) is at odds with a d-wave scenario.
A more conventional explanation for the ZBCP is related to the large Fe excess in the Fe1+yTe layer: scanning probe measurements have recently shown that excess iron in Fe(Te,Se) superconductors causes pronounced local in-gap states, which do not split, shift or vanish in applied magnetic fields48. However, the presence of a ZBCP when tunneling directly into the Bi2Te3 layer (in which Fe impurities are absent) discourages this interpretation and rather points to an unconventional pairing mechanism as its origin.
A similar ZBCP was observed in Bi2212/Bi2Te2Se junctions with a very similar temperature and magnetic field dependence as in our heterostructure19. This suggests that such a ZBCP could be an universal feature of interfaces between unconventional superconductors and topological insulators. Its origin remains a mystery and requires further experiments such as angle resolved photoemission to clarify the exact electronic density of states in Bi2Te3/Fe1+yTe heterostructures.
Our Bi2Te3(9QLs)/Fe1+yTe heterostructures reveal a highly unusual superconducting state with an extraordinarily large superconducting gap, a pronounced pseudogap and compelling evidence for proximity-induced superconductivity in the topological insulating Bi2Te3 top layer. Our experiments alone are not able to prove the topological nature of this superconductivity, nor provide an indisputable explanation of the origin of the interfacial superconductivity. Nevertheless, it is clear that Bi2Te3(9QLs)/Fe1+yTe interfaces display a similarly rich behavior to the cuprate superconductors, which remain one of the major unsolved mysteries in physics.
Methods
Film growth
The heterostructure studied in this work was synthesized by a VG-V80H MBE system. A 50 nm ZnSe buffer was first grown on a GaAs(100) semi-insulating substrate. A 140 nm thick FeTe layer is then deposited on the buffer layer, followed by a 9QL thick Bi2Te3 film. Detailed information about the quality and characterization of this interface, including scanning transmission microscope micrographs and resistivity data may be found in Ref. 3. Our data were acquired using bilayers of Bi2Te3(9QLs)/Fe1+yTe, chosen for their high Tc = 12 K.
Device fabrication and point contact spectroscopy
To fabricate a point-contact device on the edge of the bilayer, a thin slab was attached to a silicon substrate with one edge facing upwards. Ordinary low-Ohmic contacts were prepared by RS 186–3593 silver conductive paint on the Bi2Te3 surface. The edge of the sample was finely polished, instantly covered by a thin layer of Au and an isolated 100 nm wide Au strip was separated using a focused-ion-beam. The maximum contact area is ~100 × 149 nm2 (from the width of the Au strip and the total thickness of the FeTe/Bi2Te3 bilayer, respectively). A schematic drawing of the contact configuration is shown in Fig. 6. In order to reduce the effect of Ag pollution at the interface through our surface electrical contacts, we prepared all surface electrical contacts at a distance of at least 1 mm from the point contact junctions.
Schematic model of the point contact devices.
(a) For the fabrication of a point contact at the edge of the Bi2Te3(9QLs)/Fe1+yTe heterostructure, a thin polished slab was glued onto a substrate with its edge facing upwards. A point contact was fabricated in form of a narrow 100 nm wide gold strip over the edge. An AC current (IAC) superimposed on a DC current (IDC) was injected from the strip to an ordinary highly conducting contact on the Bi2Te3 surface, while the resulting AC and DC voltages were measured between the strip and a second low-Ohmic contact by a lock-in amplifier and a DC voltmeter, respectively. (b) The point contact on the top Bi2Te3 surface was established by gently pressing a W tip against the surface. The measurements were then conducted in the same manner as described above for the edge contact.
The edge contacts typically had resistances in the kΩ range and the data reproducibility was verified on 4 different devices. The point-contact spectral shape is strongly dependent on the tunnel barrier height parameter Z10, which is linked to the contact resistance. Z = 0 corresponds to pure Andreev reflection, while larger values represent the spectroscopic tunneling regime. In our contacts we consistently achieve Z ≥ 0.35 and our nanoscale contact area ensures that our experimental tunneling regime is ballistic and not thermal or diffusive, i.e. the applied bias voltage Vb corresponds to the electron injection energy. This is confirmed by the temperature-independent value of the normal-state contact resistance. A point contact with similar properties was established on the Bi2Te3 surface for perpendicular current injection with the help of a scanning probe device, by gently approaching a tungsten tip to the Bi2Te3 surface. The differential conductance dI/dV vs Vb was measured at temperatures from 0.27 K to 70 K in magnetic fields up to 15 T with a quasi-four-probe method, using a Keithley 6221 AC/DC current source to generate a small, constant-amplitude (10 nA) AC current IAC with frequency 5 Hz, superposed on a ramped DC bias current. A standard lock-in technique in combination with a DC multimeter was used to measure dI/dV and Vb = VDC across the junction.
Additional Information
How to cite this article: He, M. Q. et al. Pseudogap and proximity effect in the Bi2Te3/Fe1+yTe interfacial superconductor. Sci. Rep. 6, 32508; doi: 10.1038/srep32508 (2016).
References
Fu, L. & Kane, C. L. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Xu, J.-P. et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure, Phys. Rev. Lett. 114, 017001 (2015).
He, Q. L. et al. Two-dimensional superconductivity at the interface of a Bi2Te3/FeTe heterostructure. Nat. Commun. 5 4247 (2014).
Kosterlitz, J. M. & Thouless, D. M. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys.C 6, 1181–1203 (1973).
Kosterlitz, J. M. The critical properties of the two-dimensional XY model. J. Phys. C 7, 1046–1060 (1974).
Berezinskii, V. L. Destruction of long-range order in one-dimensional and two-dimensional systems having a continuous symmetry group I. classical systems. Sov. Phys. JETP 32, 493–500 (1971).
Chen,Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Li, Y.-Y. et al. Intrinsic topological insulator Bi2Te3 thin films on Si and their thickness limit. Adv. Mater. 22, 4002–4007 (2010).
Taskin, A. A., Sasaki, S., Segawa, K. & Ando, Y. Manifestation of topological protection in transport properties of epitaxial Bi2Se3 thin films. Phys. Rev. Lett. 109, 066803 (2012).
Daghero, D., Tortello, M., Ummarino, G. A. & Gonnelli, R. S. Directional point-contact Andreev-reflection spectroscopy of Fe-based superconductors: Fermi surface topology, gap symmetry and electron–boson interaction. Rep. Prog. Phys. 74, 124509 (2011).
Koz, C., Rößler, S., Tsirlin, A. A., Wirth, S. & Schwarz, U. Low-temperature phase diagram of Fe1+yTe studied using x-ray diffraction. Phys. Rev. B 88, 094509 (2013).
Bao, W. et al. Tunable (δπ, δπ)-Type Antiferromagnetic Order in α-Fe(Te,Se) Superconductors. Phys. Rev. Lett. 102, 247001 (2009).
Eskildsen, M. R. et al.Vortex imaging in magnesium diboride with H⊥c. Phys. Rev. B 68, 100508 (2003).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting microconstrictions: excess current, charge imbalance and supercurrent conversion. Phys. Rev. B 25, 4515 (1982).
Dynes, C., Naraynamurti, V. & Garno, J. P. Direct measurement of quasiparticle-lifetime broadening in a strong-coupled superconductor. Phys. Rev. Lett. 41, 1509 (1978).
Petrović, A. P. et al. Multiband superconductivity in the Chevrel phases SnMo6S8 and PbMo6S8 . Phys. Rev. Lett. 106, 017003 (2011).
Wang, E. et al. Fully gapped topological surface states in Bi2Se3 films induced by a d-wave high-temperature superconductor. Nat. Phys. 9, 621–625 (2013).
Zareapour, P. et al. Proximity-induced high-temperature superconductivity in the topological insulators Bi2Se3 and Bi2Te3 . Nat. Commun. 3, 1056 (2012).
Zareapour, P. et al. Evidence for a new excitation at the interface between a high-Tc superconductor, and a topological insulator, Rev. B 90, 241106 (R) (2014).
Zhang, D. et al. Superconducting proximity effect and possible evidence for Pearl vortices in a candidate topological insulator. Phys. Rev. B 84, 165120 (2011).
Yilmaz, T. et al. Absence of a proximity effect for a thin-films of a Bi2Se3 topological insulator grown on top of a Bi2Sr2CaCu2O8+δ cuprate superconductor. Phys. Rev. Lett. 113, 067003 (2014).
Xu, S.-Y. et al. Fermi-level electronic structure of a topological-insulator/cuprate-superconductor based heterostructure in the superconducting proximity effect regime. Phys. Rev. B 90, 085128 (2014).
Song, C.-L. et al. Suppression of superconductivity by twin boundaries in FeSe. Phys. Rev. Lett. 109, 137004 (2012).
Kato, T. et al. Local density of states and superconducting gap in the iron chalcogenide superconductor Fe1+δSe1−xTex observed by scanning tunneling spectroscopy. Phys. Rev. B 80, 180507 (2009).
Hardy, F. et al. Calorimetric evidence of multiband superconductivity in Ba(Fe0.925Co0.075)2As2 single crystals. Phys. Rev. B 81, 060501 (R) (2010).
Tortello, M. et al. Multigap superconductivity and strong electron-boson coupling in Fe-based superconductors: a point-contact Andreev-reflection study of Ba(Fe1−xCox)2As2 single crystals. Phys. Rev. Lett. 105, 237002 (2010).
Timusk, T. & Statt, B. The pseudogap in high-temperature superconductors: an experimental survey. Rep. Prog. Phys. 62, 61–122 (1999).
Xu, Y.-M. et al. Fermi surface dichotomy of the superconducting gap and pseudogap in underdoped pnictides. Nat. Commun. 2, 392 (2011).
Shimojima, T. et al. Pseudogap formation above the superconducting dome in iron pnictides. Phys. Rev. B 89, 045101 (2014).
Kwon, Y. S. et al. Evidence of a pseudogap for superconducting iron-pnictide Ba0.6K0.4Fe2As2 single crystals from optical conductivity measurements. New J. Phys. 14, 063009 (2012).
Arham, H. Z. et al. Detection of orbital fluctuations above the structural transition temperature in the iron pnictides and chalcogenides. Phys. Rev. B 85, 214515 (2012).
Chu, J.-H. et al. In-plane resistivity anisotropy in an underdoped iron arsenide superconductor. Science 329, 824–826 (2010).
Harriger, L. W. et al. Nematic spin fluid in the tetragonal phase of BaFe2As2 . Phys. Rev. B 84, 054544 (2011).
Karki, A. B. et al. Interplay between superconductivity and magnetism in Fe1−xPdxTe. PNAS 110, 9283–9288 (2013).
Yi, M. et al. Dynamic competition between spin-density wave order and superconductivity in underdoped Ba1−xKxFe2As2 . Nat. Commun. 5, 3711 (2012).
Meingast, C. et al. Phase fluctuations and the pseudogap in YBa2Cu3Ox . Phys. Rev. Lett. 86, 1606 (2001).
Wang, Y. et al. The onset of the vortex-like Nernst signal above Tc in La2−xSrxCuO4 and Bi2Sr2−yLayCuO6 . Phys. Rev. B 64, 224519 (2001).
Sacépé, B. et al. Pseudogap in a thin film of a conventional superconductor. Nat. Commun. 1, 140 (2010).
Varlamov, A. A. & Dorin, V. V. Fluctuation resistance of Josephson junction, Soviet Phys. JETP 57, 1089–1096 (1983).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Sasaki, S. et al. Topological Superconductivity in CuxBi2Se3 . Phys. Rev. Lett. 107, 217001 (2011).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Con. Mat. Phys. 4, 113–136 (2013).
Sheet, G., Mukhopadhyay, S. & Raychaudhuri, P. Role of critical current on the point-contact Andreev reflection spectra between a normal metal and a superconductor. Phys. Rev. B 69, 134507 (2004).
Fu, L. & Berg, E. Odd-parity topological superconductors: theory and application to CuxBi2Se3 . Phys. Rev. Lett. 105, 097001 (2010).
Hsieh, T. H. & Fu, L. Majorana fermions and exotic surface Andreev bound states in topological superconductors: application to CuxBi2Se3 . Phys. Rev. Lett. 108, 107005 (2012).
Yuan, N. F. Q., Wong, C. L. M. & Law, K. T. Probing Majorana flat bands in nodal dx2−y2-wave superconductors with Rashba spin–orbit coupling. Physica E 55, 30–36 (2014).
Yin, J.-X. et al. Observation of a robust zero-energy bound state in iron based superconductor Fe(Te,Se). Nat. Phys. 11, 543–546 (2015).
Acknowledgements
We thank M. L. Cohen, Y.-R. Shen and S. G. Louie for stimulating discussions and U. Lampe for technical support. This work was supported by grants from the Research Grants Council of the Hong Kong Special Administrative Region, China (603010, 16304515, 604910, 602813, SEG_HKUST03, CRF3/HKUST/13G, FSGRF13SC23, FSGRF14SC25, SRFI11SC02).
Author information
Authors and Affiliations
Contributions
R.L. initiated this study; M.Q.H., R.L. and J.Y.S. designed the experiments; M.Q.H. and J.Y.S. conducted the experiment with contributions from Y.Z., C.H.W. and Q.H.C; Q.L.H. carried out the sample growth and structural characterization with contributions from H.C.L. and J.N.W.; A.P.P. performed the fitting analysis of the data with contributions from M.Q.H. and J.Y.S.; I.K.S. designed the material and initiated the sample growth; K.T.L. contributed the theoretical interpretation of the data and all authors contributed to the scientific planning and discussions. R.L. and M.Q.H. and A.P.P. wrote the manuscript with contributions from the other authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
He, M., Shen, J., Petrović, A. et al. Pseudogap and proximity effect in the Bi2Te3/Fe1+yTe interfacial superconductor. Sci Rep 6, 32508 (2016). https://doi.org/10.1038/srep32508
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep32508
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.