Abstract
Observations of robust superconductivity in some of the iron based superconductors in the vicinity of a Lifshitz point where a spin density wave instability is suppressed as the hole band drops below the Fermi energy raise questions for spin-fluctuation theories. Here we discuss spin-fluctuation pairing for a bilayer Hubbard model, which goes through such a Lifshitz transition. We find s± pairing with a transition temperature that peaks beyond the Lifshitz point and a gap function that has essentially the same magnitude but opposite sign on the incipient hole band as it does on the electron band that has a Fermi surface.
Similar content being viewed by others
Introduction
The microscopic mechanism of pairing that gives rise to superconductivity in the iron based superconductors remains an unsettled issue1. Spin-fluctuation mediated pairing2,3,4, in which electrons form pairs by exchanging virtual S = 1 particle hole excitations, is a leading candidate mechanism, since superconductivity appears near the onset of a magnetic phase. However, this picture relies on the nesting properties of the electronic band structure with both hole and electron Fermi surface pockets present and the absence of hole pockets in some of the iron based superconductors5,6,7,8,9,10,11 has challenged these theories. In these systems, the hole like band drops below the Fermi energy after a Lifshitz transition12,13. Nevertheless, pairing remains strong, as evidenced e.g. by the high Tc superconductivity reported in mono-layer FeSe films grown on SrTiO39,10,11,14. Scanning tunneling microscopy experiments12 as well as ARPES measurements11,13 on these FeSe mono-layers find that there are no hole pockets. Furthermore, the ARPES measurements of the variation of the gap magnitude around the electron pockets13 makes the possibility of d-wave pairing, arising from pair scattering between the electron pockets, unlikely. However, these experiments also report the existence of an incipient hole band laying 50 to 100 meV below the Fermi energy, implying that the system is just beyond a Lifshitz transition15 where the hole Fermi surface has disappeared. In addition, photoemission measurements find evidence that superconductivity occurs in the monolayer FeSe film, when SDW order is suppressed by electron doping11 and density functional theory calculations16 predict that in the absence of electron doping, the ground state of the mono-layer FeSe film would have SDW order. Thus, it appears that superconductivity is induced in the FeSe mono-layer when the SDW order is suppressed by a Lifshitz transition arising from electron doping or strain11. Motivated by these results, we have investigated the suppression of SDW order and the onset of superconductivity near a Lifshitz transition in a two-layer Hubbard model. This model was previously shown to have both s± and d-wave pairing depending upon the strength of the interlayer hopping17. Here using this model, we show that spin-fluctuation scattering of pairs between an electron and an incipient hole band can lead to s± pairing for a system that has undergone a Lifshitz transition.
Results
The Hamiltonian for the two layer Hubbard model that we study is

Here  creates/annihilates a fermion with spin σ on the nth layer (n = 1 or 2). The intralayer hoping is t, the interlayer hoping is t⊥ and μ is the chemical potential. The band structure for this model is,
creates/annihilates a fermion with spin σ on the nth layer (n = 1 or 2). The intralayer hoping is t, the interlayer hoping is t⊥ and μ is the chemical potential. The band structure for this model is,

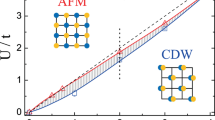
with t⊥/t = 3.5 and μ set so that the site filling 〈n〉 = 1.05 is shown in Fig. 1(a). If the filling is kept constant as t⊥/t is increased, the system has a Lifshitz transition such that for t⊥ > 3.67 the hole Fermi surface at the Γ point disappears as illustrated in Fig. 1(b). We are interested in studying the pairing for parameters such that the spin density wave (SDW) instability is suppressed by this Lifshitz transition.
In a random phase approximation (RPA) the spin susceptibility is given by

with

Here T is the temperature, G0(k, ωn) = (iωn − ξk)−1 and ωn = (2n + 1)πT and Ωm = 2mπT are the usual fermionic and bosonic Matsubara frequencies. For a fixed filling, as t⊥/t is increased and the Lifshitz transition is approached, χ0 which peaks near wavevector (π, π, π), decreases. For 〈n〉 = 1.05, we take U = 2.4t so that the SDW instability determined from Eq. (3) is suppressed by the Lifshitz transition as shown in Fig. 2. With this suppression of the SDW order, one can imagine that superconductivity may appear following the usual paradigm. However, the Lifshitz transition that has suppressed the SDW instability can also lead to a suppression of the s± pairing associated with the scattering of pairs between the electron Fermi surface and the incipient hole band. For a fixed pairing strength, Tc decreases as the hole band moves below the Fermi energy18.
To explore this, we solve the Bethe-Salpeter equation

and determine Tc from the temperature at which the leading eigenvalue of Eq. (5) goes to 1. Here we use a spin-fluctuation mediated interaction19,

Here the first term in the effective interaction is the bare interaction U which is momentum independent. The effect of this term is small due to the sign change of the gap between the two bands. In Eq. (5) we set G(k, ωn) = [iωn − ξk − Σ(k, ωn)]−1 with

Note that we keep the Fermi surface unchanged in the dressed Green’s function. For 〈n〉 = 1.05 and U = 2.4t, the resulting value of Tc, interpolated from the temperature at which λ crosses 1, is plotted in Fig. 2 as a function of t⊥/t. As shown in this figure, after the SDW instability is suppressed by the Lifshitz transition, a pairing transition occurs at a Tc which peaks as t⊥/t increases and then falls off as the hole band is pushed further below the Fermi energy.
The momentum dependence of the superconducting gap function Δ(k, ω = πT) ≡ Φ(k, πT)/Z(k, πT) is shown in Fig. 3. This is an A1g (s±) state in which the sign of Δ changes between kz = 0 (bonding) and kz = π (antibonding) bands. One can see that the magnitudes of the two gaps Δ(kx, ky, kz = 0) and Δ(kx, ky, kz = π) are comparable even though the hole band is below the Fermi energy.
The momentum dependence of eigenvectors at the lowest Matsubara frequency (πT) for 〈n〉 = 1.05 and U = 2.4t at t⊥ = 3.8t.
The eigenvector is normalized to its maximum value. The momentum dependence for the incipient hole band is shown in panel (a) and for the electron band is shown in panel (b) with the electronlike Fermi surface.
In order to understand the peak in Tc that occurs as the hole band drops below the Fermi energy, it is useful to separately examine the dependence of Tc on the changes in  and
and  that occur as the Tc at which the eigenvalue of Eq. (5) goes to 1 as a functional of χ and the pair propagator GG. We can calculate the variation in Tc due to the change in χ with GG unchanged when t⊥ increases by Δt⊥,
that occur as the Tc at which the eigenvalue of Eq. (5) goes to 1 as a functional of χ and the pair propagator GG. We can calculate the variation in Tc due to the change in χ with GG unchanged when t⊥ increases by Δt⊥,

and the variation due to the change in pair propagator GG when χ is unchanged and t⊥ increases by Δt⊥,

We set Δt⊥ = 0.01t. The results of the calculation are shown in Fig. 4. Here one sees that the initial increase in Tc arises from both the changes in χ and GG. The latter effect is associated with an increase in the quasi-particle spectral weight Z−1(k, ω) on the electron Fermi surface that occurs as the hole band drops below the Fermi energy. This increase in the quasi-particle spectral weight initially ameliorates the decrease in Tc resulting from the submergence of the hole band. The initial positive contribution associated with the variation in χ reflects the change in the frequency structure of the spin-fluctuations. As the hole band drops below the Fermi energy, a gap opens in the low energy qz = π spin fluctuation spectrum and spectral weight is transfered to higher energies as shown in Fig. 5, which leads to stronger pairing20. The ultimate decrease in Tc is due to the decrease of the pair propagator  as t⊥ increases and the hole band drops further below the Fermi energy, as well as the decreasing strength of the spin-fluctuations.
as t⊥ increases and the hole band drops further below the Fermi energy, as well as the decreasing strength of the spin-fluctuations.
The variation of Tc with changes in χ (solid blue curve) and the pairfield propagators GG (dashed red curve) versus t⊥/t.
Here one sees that initially as t⊥/t increases beyond 3.7 and the SDW order is suppressed, both the change in χ and the change in GG lead to an increase in Tc. Then, as t⊥/t increases further and the hole band drops deeper below the Fermi energy, the changes in both χ and GG lead to a reduction in Tc.
The imaginary part of RPA χ(π, π, π, Ω) at T = 0.1t versus Ω for U = 2.4t for different values of t⊥, which continuously increases in units of 0.01t from t⊥ = 3.7t (red curve)to t⊥ = 4t (blue curve).
The thick line represents the value of t⊥ = 3.77t corresponding to the maximum value of Tc. As t⊥ increases and the hole band drops below the Fermi energy, the spin fluctuation spectral weight is shifted to higher frequencies, of order 5 to 10Tc, where it is more effective for pairing. However, as t⊥ increases further and the spectral weight moves to still higher frequencies, the strength of the pairing decreases and this combined with the suppression of the pair propagator GG leads to a rapid decrease of Tc.
Discussion
To conclude, we have studied a two-layer Hubbard model with parameters chosen so that a SDW instability is suppressed by a Lifshitz transition in which the hole band at the Γ point drops below the Fermi energy. Here, we have kept the site filling fixed and varied the interlayer hopping to tune the system through the Lifshitz point. For a physical system this might by obtained via strain11. Following the suppression of the SDW order, we find the onset of an s± superconducting state whose transition temperature Tc initially increases as the system is pushed beyond the Lifshitz point by further increasing t⊥/t. We find that this increase in Tc is associated with both an increase in the quasi-particle spectral weight and an increase in the strength of the pairing interaction, which are related to the incipient hole band and the resulting change in the spectral distribution of the spin-fluctuations. We find that the gap function on the incipient hole band is similar in magnitude but of the opposite sign to that on the electron band which crosses the Fermi surface.
Additional Information
How to cite this article: Mishra, V. et al. s± pairing near a Lifshitz transition. Sci. Rep. 6, 32078; doi: 10.1038/srep32078 (2016).
References
Norman, M. R. The Challenge of Unconventional Superconductivity. Science 332, 196–200 (2011).
Mazin, I. I., Singh, D. J., Johannes, M. D. & Du, M. H. Unconventional Superconductivity with a Sign Reversal in the Order Parameter of LaFeAsO1−xFx . Phys. Rev. Lett. 101, 057003 (2008).
Kuroki, K. et al. Unconventional Pairing Originating from the Disconnected Fermi Surfaces of Superconducting LaFeAsO1−xFx . Phys. Rev. Lett. 101, 087004 (2008).
Hirschfeld, P. J., Korshunov, M. M. & Mazin, I. I. Gap symmetry and structure of Fe-based superconductors. Rep. Prog. Phys. 74, 124508 (2011).
Guo, J. G. et al. Superconductivity in the iron selenide KxFe2Se2 (0 ≤ x ≤ 1.0). Phys. Rev. B 82, 180520 (2010).
Mou, D. X., Zhao, L. & Zhou, X. Structural, Magnetic and Electronic Properties of the Iron-Chalcogenide AxFe2−ySe2 (A = K, Cs, Rb, Tl and etc.) Superconductors. Front. Phys. 6, 410–428 (2011).
Zhang, Y. et al. Nodeless superconducting gap in AxFe2Se2 (A = K, Cs) revealed by angle-resolved photoemission spectroscopy. Nat. Mater. 10, 273–277 (2011).
Liu, X. et al. Electronic structure and superconductivity of FeSe-related superconductors. Journal of Physics: Condensed Matter 27, 183201 (2015).
Wang, Q.-Y. Interface-Induced High-Temperature Superconductivity in Single Unit-Cell FeSe Films on SrTiO3 Chin. Phys. Lett. 29, 037402 (2012).
He, S. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605–610 (2013).
Tan, S. Interface-induced superconductivity and strain-dependent spin density waves in FeSe/SrTiO3 thin films. Nat. Mater. 12, 634–640 (2013).
Huang, D. Bounds on nanoscale nematicity in single-layer FeSe/SrTiO 3. Phys. Rev. B 93, 125129 (2016).
Zhang, Y. Superconducting gap anisotropy in monolayer FeSe thin film. arxiv:1512.06322.
Ge, J.-F. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3 . Nat. Mater. 14, 285 (2015).
Lifshitz, I. M. Anomalies of Electron Characteristics of a Metal in the High Pressure Region. Zh. Eksp. Teor. Fiz. 38, 1569 (1960) [Soy. Phys. JETP 11, 1130–1135 (1960)].
Liu, K., Gao, M., Lu, Z.-Y. & Xiang, T. First-principles study of FeSe epitaxial films on SrTiO3 . Chin. Phys. B 24, 117402 (2015).
Bulut, N., Scalapino, D. J. & Scalettar, R. T. Nodeless d-wave pairing in a two-layer Hubbard model. Phys. Rev. B 45, 5577 (1992).
Chen, X., Maiti, S., Linscheid, A. & Hirschfeld, P. J. Electron pairing in the presence of incipient bands in iron-based superconductors. Phys. Rev. B 92, 224514 (2015).
Maier, T. A. & Scalapino, D. J. Pair structure and the pairing interaction in a bilayer Hubbard model for unconventional superconductivity. Phys. Rev. B 84, 180513(R) (2011).
Monthoux, P. & Scalapino, D. J. Variations of Tc for changes in the spin-fluctuation spectral weight. Phys. Rev. B 50, 10339 (1994).
Acknowledgements
Research sponsored by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the U. S. Department of Energy. DJS and TAM acknowledge the support of the Center for Nanophase Materials Sciences, a US DOE Office of Science User Facility. We acknowledge the Valinor cluster for computational resources. We thank A. Linscheid, S. Maiti, P. Hirschfeld for useful discussion.
Author information
Authors and Affiliations
Contributions
V.M., D.J.S. and T.A.M. contributed equally.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Mishra, V., Scalapino, D. & Maier, T. s± pairing near a Lifshitz transition. Sci Rep 6, 32078 (2016). https://doi.org/10.1038/srep32078
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep32078
This article is cited by
-
Evolution of spin excitations from bulk to monolayer FeSe
Nature Communications (2021)
-
Anisotropic resonance modes emerging in an antiferromagnetic superconducting state
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.