Abstract
We demonstrate the use of a compound optical cavity as linear displacement detector, by measuring the thermal motion of a silicon nitride suspended membrane acting as the external mirror of a near-infrared Littrow laser diode. Fluctuations in the laser optical power induced by the membrane vibrations are collected by a photodiode integrated within the laser, and then measured with a spectrum analyzer. The dynamics of the membrane driven by a piezoelectric actuator is investigated as a function of air pressure and actuator displacement in a homodyne configuration. The high Q-factor (~3.4 · 104 at 8.3 · 10−3 mbar) of the fundamental mechanical mode at ~73 kHz guarantees a detection sensitivity high enough for direct measurement of thermal motion at room temperature (~87 pm RMS). The compound cavity system here introduced can be employed as a table-top, cost-effective linear displacement detector for cavity optomechanics. Furthermore, thanks to the strong optical nonlinearities of the laser compound cavity, these systems open new perspectives in the study of non-Markovian quantum properties at the mesoscale.
Similar content being viewed by others
Introduction
The fast progress of cavity optomechanics has produced extraordinary advances in fabrication and characterization of nanomechanical objects1, with impressive results towards the achievement of quantum effects in mesoscopic systems2,3,4,5,6. Routinely dealing with sub-picometer displacements, the measure of an optomechanical system often requires complicated and expensive setups composed by optical interferometers and local oscillators to perform homodyne or heterodyne experiments. In this paper we show how a table-top, well known vibrometric technique such as the laser self-mixing7,8,9 can be pushed to measure the thermal motion of a typical optomechanical device, that is a metallic mirror mounted on a trampoline membrane10,11,12. By shining a laser beam back into its resonant cavity after interacting with the external environment, an interferometric system is created which does not require any complicated arrangement or frequency demodulation. Showing the capability of detecting tens of pm displacements in its linear, stable regime, this technique would allow for detection of thermal noise up to cryogenic temperatures, making it an easy to implement, fast characterization benchmark for optomechanical resonators. At odds with standard optomechanical devices, such as whispering gallery mode resonators and optomechanical crystals, in which the displacement sensitivity is pushed towards the standard quantum limit, our technique offers a different advantage, integrating the high optical nonlinearities of the laser diode directly within the system. Moreover, by reaching the unstable dynamical regime, a rich and interesting physics can be accessed, which falls in the almost unexplored topic of active cavity optomechanics13,14. Using the chaotic dynamics readily attainable in self-mixed lasers15,16 scenarios in which chaotic mechanical objects are created through radiation pressure effects can be easily imagined17.
Experimental setup
Optical bench and signal analysis
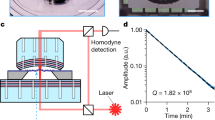
The optomechanical laser setup is sketched in Fig. 1(a). The optical bench is a compound cavity working as a displacement sensor7,8,9,15. The source includes a Littrow external cavity diode laser (ECDL), with lasing wavelength  . The light-emitting, active medium is coupled to a Littrow angle reflection grating, placed at a distance L = 1 cm from the left facet of the diode. The zeroth diffraction order is reflected outside the ECDL and focused by an achromatic doublet (focal length 75 mm) onto a gold mirror placed on top of a silicon nitride trampoline membrane10,11,12. The membrane is mounted on a piezo ceramic actuator and placed inside a vacuum chamber, in order to drive its motion and control the environment pressure when needed. The piezo actuator is a polymer covered multilayer, capable of elongating in one direction when biased, at a maximum frequency of some hundreds of kHz. The chip frame with the membrane is directly glued on its top surface and therefore is moving integrally with it. The membrane is then aligned to the optical path in such way that light is reflected back into the ECDL to form a compound cavity. As the membrane moves, it changes the oscillation condition of the cavity. Normally this would simply cause a frequency shift in the lasing modes of the cavity: in our case, thanks to the feedback interferometric effect this translates into a modulation of the field amplitude in the laser cavity7,8,9,18. The resulting laser radiation emitted from the right active region (AR) facet (labeled as 1 in Fig. 1(a)) is collected by an integrated photodiode (labeled as PD in Fig. 1(a)), which returns an electric potential proportional to the emitted power. For a fixed current bias, this potential, called readout voltage in the following, is composed by a static part V0, and a dynamic term ΔV(t). V0 is measured with an oscilloscope, while ΔV(t) is acquired by a spectrum analyzer and read out in the frequency domain. This is the essential quantity to be measured in order to demonstrate the working principle of the setup: by recording the modulation in the laser emitted power, informations about the motion of the membrane are recorded. A micrograph of the silicon nitride trampoline membrane employed in this work is shown in Fig. 1(b). A square-shaped, 5/45 nm Ti/Au layer is deposited on top of the 200 nm nitride, in order to improve its reflectivity. The first resonant mechanical mode oscillates orthogonally to the mirror surface, bending the tethers while keeping the central square parallel to the substrate. The mode frequency is f0 = 73279.0 ± 0.3 Hz with a quality factor Q = 34000 ± 3000 (at 0.0083 mbar), limited by both squeeze film effect19,20, and thermoelastic damping of the four tethers21. When the motion of the membrane is driven by a phase-coherent external displacement source, such as a piezo-ceramic actuator, the two quadratures of motion can be measured through the readout voltage. A typical measurement of amplitude and phase spectrum is shown in Fig. 1(c).
. The light-emitting, active medium is coupled to a Littrow angle reflection grating, placed at a distance L = 1 cm from the left facet of the diode. The zeroth diffraction order is reflected outside the ECDL and focused by an achromatic doublet (focal length 75 mm) onto a gold mirror placed on top of a silicon nitride trampoline membrane10,11,12. The membrane is mounted on a piezo ceramic actuator and placed inside a vacuum chamber, in order to drive its motion and control the environment pressure when needed. The piezo actuator is a polymer covered multilayer, capable of elongating in one direction when biased, at a maximum frequency of some hundreds of kHz. The chip frame with the membrane is directly glued on its top surface and therefore is moving integrally with it. The membrane is then aligned to the optical path in such way that light is reflected back into the ECDL to form a compound cavity. As the membrane moves, it changes the oscillation condition of the cavity. Normally this would simply cause a frequency shift in the lasing modes of the cavity: in our case, thanks to the feedback interferometric effect this translates into a modulation of the field amplitude in the laser cavity7,8,9,18. The resulting laser radiation emitted from the right active region (AR) facet (labeled as 1 in Fig. 1(a)) is collected by an integrated photodiode (labeled as PD in Fig. 1(a)), which returns an electric potential proportional to the emitted power. For a fixed current bias, this potential, called readout voltage in the following, is composed by a static part V0, and a dynamic term ΔV(t). V0 is measured with an oscilloscope, while ΔV(t) is acquired by a spectrum analyzer and read out in the frequency domain. This is the essential quantity to be measured in order to demonstrate the working principle of the setup: by recording the modulation in the laser emitted power, informations about the motion of the membrane are recorded. A micrograph of the silicon nitride trampoline membrane employed in this work is shown in Fig. 1(b). A square-shaped, 5/45 nm Ti/Au layer is deposited on top of the 200 nm nitride, in order to improve its reflectivity. The first resonant mechanical mode oscillates orthogonally to the mirror surface, bending the tethers while keeping the central square parallel to the substrate. The mode frequency is f0 = 73279.0 ± 0.3 Hz with a quality factor Q = 34000 ± 3000 (at 0.0083 mbar), limited by both squeeze film effect19,20, and thermoelastic damping of the four tethers21. When the motion of the membrane is driven by a phase-coherent external displacement source, such as a piezo-ceramic actuator, the two quadratures of motion can be measured through the readout voltage. A typical measurement of amplitude and phase spectrum is shown in Fig. 1(c).
(a) Sketch of the setup. The laser block is composed by: an active region (light orange bar in the picture), with an anti-reflection coated facet (labeled as 2); an external Littrow grating (multi-colored milled bar) placed at distance L from the facet 2; a coupling mirror (grayscale bar near the Littrow grating); an integrated photodiode (labeled as PD). The emitted radiation is focused by a lens (sky blue curved bar) onto an external mirror (yellow bar) placed at distance Lext from the facet 2, and then reflected back into the laser in order to form a compound cavity. Within a traveling wave approximation, the lasing conditions can be found as function of the effective right and left reflectivities calculated at the facet 2 interface. The radiation emitted by the facet labeled as 1 is collected by the integrated photodiode, and the resulting voltage V0 + ΔV(t) is recorded by an oscilloscope and a spectrum analyzer. In the main experiment the external mirror is a gold layer deposited onto a silicon nitride membrane, which is mounted on a piezo actuator in order to drive its displacement by a voltage VD. The resulted device is placed inside a vacuum chamber in order to control the environment pressure. When the membrane is displaced along the optical axis, the output signal is modulated according to equation (1). (b) SEM image of the Si3N4 membrane. The yellow-colored square at the center of the membrane is the deposited gold layer. The white bar is 200 μm. (c) The spectrum analyzer reports the power spectral density, and the total amount of displacement can be obtained through proper calibration. An example of measurement is reported for the membrane moved by the piezo actuator. The homodyne approach enables to collect the two motion quadratures of the membrane.
Connection between readout voltage and displacement: theoretical prediction
In this paragraph the relation between the readout voltage and the external mirror displacement is calculated within the semiclassical framework, in order to predict the sensitivity of the apparatus. The full derivation of the calculations is reported in section 1 of the Supplementary Information (SI). We consider a model system like the one sketched in Fig. 1(a). The Littrow ECDL is characterized essentially by the optical and electronic properties of the AR and the optical properties of the blazed angle grating22. In the traveling wave approximation the laser oscillation condition can be expressed with the following set of coupled equations23,24:


The coefficients rR and rL are related to the amplitude of the right and left traveling wave at the AR facet interface, labeled as 2 in Fig. 1(a). The effective index n and the modal gain g are in principle spectral functions of the laser carrier density N and the photon number P; the other parameters employed are defined in Table 1. More details on the reflectivities, effective index and modal gain are reported in the SI. Equations (1) can be solved numerically to find N, P and the lasing frequency fL of the cavity modes, while the stability analysis for small signals24 will determine which modes are currently lasing. The ECDL is coupled to an external mirror (i.e. the Si3N4 membrane) with reflectivity rext, which directly affects the rR coefficient: this becomes a function of the delay time τext = 2Lext/c0:

When the external mirror is moving, rR is modified, changing the solution of equations (1) as well. The cavity mode radiation envelope evolves with two different timescales: TL, defined by the laser relaxation damping, and TM, defined by the oscillation frequency of the membrane as  . We numerically solved equations (1) with the parameters relative to our ECDL and found TL ∼ 10 ns for the lasing modes, roughly three orders of magnitude smaller than TM. In this case the e.m. radiation envelope can be assumed to evolve through states which verify equations (1) instantaneously25. This allows us to solve equations (1) for different static displacements of the membrane around its equilibrium position. For each position we can define the variation of intracavity photon number ΔP with respect to the photon number at the equilibrium position P0. Within the linear regime26 these two quantities are related to the readout voltage by ΔP/P0 = ΔV/V0. To estimate the sensitivity of our setup we roughly evaluated the numerical solution of equations (1) for displacements from 0 to 1 μm around the initial position. Given a readout voltage V0 + ΔV(t), the predicted linear displacement is
. We numerically solved equations (1) with the parameters relative to our ECDL and found TL ∼ 10 ns for the lasing modes, roughly three orders of magnitude smaller than TM. In this case the e.m. radiation envelope can be assumed to evolve through states which verify equations (1) instantaneously25. This allows us to solve equations (1) for different static displacements of the membrane around its equilibrium position. For each position we can define the variation of intracavity photon number ΔP with respect to the photon number at the equilibrium position P0. Within the linear regime26 these two quantities are related to the readout voltage by ΔP/P0 = ΔV/V0. To estimate the sensitivity of our setup we roughly evaluated the numerical solution of equations (1) for displacements from 0 to 1 μm around the initial position. Given a readout voltage V0 + ΔV(t), the predicted linear displacement is

It is important to stress that the linear operation regime we found is valid only if there is no mode competition inside the cavity. If that is not the case, TL is not well defined anymore, and the Relative Intensity Noise (RIN) rises sensibly23,24.
Connection between readout voltage and displacement: experimental calibration
Using equation (3) we can link the measured voltage to the membrane displacement. To verify that our model well reproduces the experimental conditions, we carried out a calibration of the system by employing a commercial atomic force microscope (AFM). As the cantilever of the AFM has a mass comparable to the Si3N4 membrane and a resonance frequency of ~80 kHz, it is not possible to follow the motion of the membrane without strongly perturbing it. Therefore we chose to calibrate the motion using a mirror with the same reflectivity of the membrane, but deposited directly on the chip nitride film. The piezoelectric actuator was driven with a sinusoidal tone at frequency f0 and amplitude ranging from 10 mVrms to 2 Vrms. The bulk displacement was then recorded with the AFM probe. We then measured the voltage readout obtained including the same mirror in the optomechanical setup, with the same driving conditions. The two sets of data are linearly proportional to the piezo drive, therefore we correlated the measured displacements with the voltage readout to get a calibrated setup sensitivity:

Given the experimental ΔV(t), it is now possible to define the experimental RMS displacement Δx ± δx, where δx includes different contributions coming from the laser RIN, detector noise, calibration-induced error and the error on the theoretical linear fit. A detailed explanation of the different terms is reported in section 1.3 of SI.
Results and Discussion
Air pressure effect on the mechanical spectrum
We first characterized the effect of the air pressure on the motion of the suspended mirror. The membrane was placed inside a vacuum chamber, where the internal pressure was changed from 1bar to 8.3 · 10−3 mbar. The motion of the mirror was forced by a piezoelectric ceramic actuator, driven by a flat spectrum voltage defined as:

At different pressures, we measured the spectrum of ΔV(t) in a homodyne scheme, by employing the piezo driving source as the local oscillator. The measurement resolution bandwidth (RBW) was 1.56 Hz, spanning over a 5 kHz spectral range centered on f0. For the point at lowest pressure the RBW was 250 mHz and the frequency span was 200 Hz.
Using equation (4) the power spectral density is translated into the calibrated displacement spectral density (DSD), which measurements are reported in Fig. 2(a). The amplitude spectrum at 1 bar is clearly asymmetric, denoting a nonlinear dynamics of the oscillator; symmetry is gradually recovered as the pressure decreases. This behaviour is confirmed if we compare the total RMS displacements Δx extracted from the spectra with the solutions of a classic forced linear harmonic oscillator (labeled ΔxHO), as shown in Fig. 2(b). The driving source has a fixed displacement spectrum, in order to resemble the effect of the piezo actuator, while f0 and the damping rate are taken from the experimental data. More details on the model are reported in section 2 of the SI. As can be seen our experiment and theory show a fair agreement at high pressures; on the other hand, a wide discrepancy is found at low pressure. We attribute this effect to nonlinear effects induced by large deformations of the membrane, due to the reduced thin film damping and increased Q factor of the resonator. While this is enough to get an amplitude saturation, the linewidth γtot, which is a parameter of the model, is basically unaffected and is still monotonically decreasing, as can be seen from the inset of Fig. 2(b). This fact produces the discrepancy, because  . At the lowest pressure point, Q factor assumes a value of Q = 3.4 ± 0.3 · 104, which we believe is still partially limited by thermoelastic damping12.
. At the lowest pressure point, Q factor assumes a value of Q = 3.4 ± 0.3 · 104, which we believe is still partially limited by thermoelastic damping12.
(a) Displacement spectral density as a function of the air pressure. Note that the lineshape gets slightly distorted close to atmospheric pressure due to mechanical nonlinearities. (b) RMS displacement extracted from measurements (blue squares) compared to the prediction made from a simple harmonic oscillator forced with a constant displacement (orange squares); the experimental linewidths are also reported in the upper inset. Note that the disagreement at the lowest pressures is likely due to anharmonic effects due to the large deformations suffered by the tethers.
Thermal and piezo-driven spectra
At the lowest achievable pressure (8.3 · 10−3 mbar), we focused on the displacement sensitivity of the apparatus, measuring the displacement spectra at different driving voltages of the piezo actuator. To increase the spectral resolution, the signals were acquired with a 250 mHz RBW, spanning over a 200 Hz spectral window centered on f0. The piezo driving voltage had the same functional shape described in equation (5), but its amplitude was varied in a range between 1 μVrms and 100 mVrms. Figure 3(a) shows the measured DSD for different driving voltages down to VD = 0. The Δx has been reported in panel (b). For large values of VD it does not vary linearly with the piezo voltage; this can be due to a nonlinearity in the emitted power arising from mode competition inside the cavity, or to the breakdown of the linear elastic regime caused by the strong bending of the tethers which reduces the oscillation amplitude. As VD is decreased, the linear behavior is recovered, and Δxrms converges to the displacement induced by Langevin thermal fluctuations. By switching off VD and directly acquiring the voltage signal, the thermal peak from the membrane is clearly visible, as reported in Fig. 3(c). Using again the results of our calibration (equation (4)), we estimate a thermal displacement of  . The experimentally found displacement has to be compared with the theoretical feedback evaluation, which gives a displacement of
. The experimentally found displacement has to be compared with the theoretical feedback evaluation, which gives a displacement of  , where equation (3) has been used on the integrated voltage spectrum (ΔV = 33.6 nV, V0 = 5.5 mV). Both experimental and theoretical results are in good agreement. By simply considering the phonon population at such temperature, we can have another rough theoretical estimate of the expected RMS thermal fluctuations by considering the equipartition theorem. The numerical simulations performed with a thermal transport finite-element-method solver (COMSOL Multiphysics) predict that the laser beam heats up the mirror to an average temperature of T = 354 K. The resulting thermal fluctuation is
, where equation (3) has been used on the integrated voltage spectrum (ΔV = 33.6 nV, V0 = 5.5 mV). Both experimental and theoretical results are in good agreement. By simply considering the phonon population at such temperature, we can have another rough theoretical estimate of the expected RMS thermal fluctuations by considering the equipartition theorem. The numerical simulations performed with a thermal transport finite-element-method solver (COMSOL Multiphysics) predict that the laser beam heats up the mirror to an average temperature of T = 354 K. The resulting thermal fluctuation is
(a) Displacement spectral density as a function of the piezo driving voltage VD. Each curve lies on the plane identified by the gray line on the base floor, starting from its relative VD. The sidepeaks ~45 Hz aside of the main peak in the blue curve come from environmental noise which couples to the vacuum system. (b) Extracted total rms displacement of the membrane Δx as function of the piezo driving voltage VD. (c) Displacement spectral density resulting from the thermal fluctuations of the membrane.

where kB is the Boltzmann’s constant and meff = 3.141 · 10−11 Kg the mechanical mode effective mass. Even in this case we have a reasonable agreement with the experimentally obtained displacement.
In conclusion, we employed a compound cavity laser diode for measuring small displacements of a silicon nitride trampoline membrane down to the thermal noise in the linear regime. The membrane movement directly shows in the laser emission thanks to the effect of optical feedback. By measuring average displacements as low as tens of picometers, our system can represent a fast, compact and cost effective optomechanical platform. Further upgrades of the setup, such as an improved environmental filtering and thermal and mechanical stabilization of the optical components, would push the resolution down to few pms, allowing for measurement of thermal motion at few K temperatures ( at 30 K). Moreover, the added functionality of getting a feedback directly on the laser source will enable the use of strong optical nonlinearities which can interact with mechanical elements through radiation pressure. In this active cavity optomechanical systems, schemes in which optical chaos is ingrained in a mechanical state can be readily imagined, opening the route to the investigation of a new class of mesoscale non-Markovian phenomena.
at 30 K). Moreover, the added functionality of getting a feedback directly on the laser source will enable the use of strong optical nonlinearities which can interact with mechanical elements through radiation pressure. In this active cavity optomechanical systems, schemes in which optical chaos is ingrained in a mechanical state can be readily imagined, opening the route to the investigation of a new class of mesoscale non-Markovian phenomena.
Methods
Sample fabrication and experimental setup
The trampoline membranes have been fabricated starting with a 300 nm LPCVD stoichiometric silicon nitride film grown on a 250 μm thick silicon FZ 2″ wafer. The high temperature at growth (~800 °C) and the different thermal expansion between Si and Si3N4 gives the thin film a considerable tensile stress at room temperature (~900 MPa). At first the metallic mirrors were defined through e-beam lithography followed by a 5/50 nm Ti/Au thermal deposition and lift-off. A second aligned beam-write defined the membrane pattern which was transferred on the sample with plasma etching (CF4/H2). Finally the full membrane was released in a hot KOH solution. The membrane was mounted on a flat piezoceramic actuator from PI with a fundamental resonant frequency of 300 kHz. The full block was then placed in a vacuum chamber with optical access and carefully aligned with the laser optical path. Sample alignment was performed by using not-suspended mirrors placed on the same chip which were shaken by the piezo actuator. The drive voltage was a flat band voltage coming from the source port of a Hewlett Packard 89441A vector signal analyzer, which collected the drive voltage at port 1 and the readout voltage by the laser integrated photodiode at port 2. The scattering coefficient S21 was then maximized to obtain a good optical alignment of the system. In order to exploit the linear operation regime for displacement detection, the laser was biased following the procedure described in section 1.3 of SI.
Theoretical modeling, simulations and calibration
Equation system (1) in the main text was numerically solved by using the commercial software Mathematica, with semi-empirical initial conditions and parameters independently extracted from the experiment. The membrane motion was simulated using a commercial FEM solver (Comsol Multiphysics) in order to predict the membrane frequency and motional mass. The simulation prediction was then independently confirmed by using a Polytech UHF-120 laser vibrometer. The calibration of the setup was performed with a Bruker Dimension Icon AFM. The deflection signal coming from the cantilever, in contact with the sample surface, was recorded in time using a high-speed detector (50 MHz bandwidth) following the Thermal Tune calibration protocol.
Additional Information
How to cite this article: Baldacci, L. et al. Thermal noise and optomechanical features in the emission of a membrane-coupled compound cavity laser diode. Sci. Rep. 6, 31489; doi: 10.1038/srep31489 (2016).
References
Aspelmeyer, M., Kippenberg, T. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391 (2014).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Teufel, J. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Brooks, D. W. et al. Non-classical light generated by quantum-noise-driven cavity optomechanics. Nature 488, 476–480 (2012).
Wollman, E. et al. Quantum squeezing of motion in a mechanical resonator. Science 349, 952–955 (2015).
Riedinger, R. et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 530, 313–316 (2016).
Giuliani, G., Norgia, M., Donati, S. & Bosch, T. Laser diode self-mixing technique for sensing applications. J. Opt. A-Pure Appl. Op. 4, S283–S294 (2002).
Giuliani, G., Bozzi-Pietra, S. & Donati, S. Self-mixing laser diode vibrometer. Measurement Science and Technology 14, 24 (2002).
Otsuka, K., Abe, K., Ko, J.-Y. & Lim, T.-S. Real-time nanometer-vibration measurement with a self-mixing microchip solid-state laser. Optics letters 27, 1339–1341 (2002).
Kleckner, D. et al. Optomechanical trampoline resonators. Opt. Expr. 19, 19708 (2011).
Norte, R. A., Moura, J. P. & Gröblacher, S. Mechanical resonators for quantum optomechanics experiments at room temperature. Physical review letters 116, 147202 (2016).
Reinhardt, C., Müller, T., Bourassa, A. & Sankey, J. Ultralow-noise sin trampoline mems for sensing and optomechanics. arXiv preprint arXiv 1511.01769 (2015).
Yang, W. et al. Laser optomechanics. Sci. Rep. 5 (2015).
Czerniuk, T. et al. Lasing from active optomechanical resonators. Nat. Comm. 5, 4038 (2014).
Kane, D. M. & Shore, K. A. Unlocking Dynamical Diversity: Optical Feedback Effects on Semiconductor Lasers vol. 1 (2005). URL https://books.google.com/books?id=DnSiDZ3UfLgC&pgis=1.
Uchida, A. Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization. Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization (Wiley, 2012). URL https://books.google.it/books?id=5eFVoxbcvWYC.
Monifi, F. et al. Optomechanically induced stochastic resonance and chaos transfer between optical fields. Nature Photonics 10, 399–405 (2016).
Lang, R. & Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Elect. 16, 347–355 (1980).
Blech, J. On isothermal squeeze films. J. Tribol-T. ASME 105, 615–620 (1983).
Bao, M. & Yang, H. Squeeze film air damping in mems. Sensor Actuat. A-Phys. 136, 3–27 (2007).
Schmid, S., Jensen, K., Nielsen, K. & Boisen, A. Damping mechanisms in high-q micro and nanomechanical string resonators. Phys. Rev. B 84, 165307 (2011).
Ye, C. Tunable External Cavity Diode Lasers (World Scientific, 2004). URL https://books.google.it/books?id=zVkYnwEACAAJ.
Tromborg, B., Mørk, J. & Velichansky, V. On mode coupling and low-frequency fluctuations in external-cavity laser diodes. Quantum Semicl. Opt. 9, 831 (1997).
Detoma, E., Tromborg, B. & Montrosset, I. The complex way to laser diode spectra: example of an external cavity laser strong optical feedback. IEEE J . Quantum Elect. 41, 171–182 (2005).
Mezzapesa, F. P. et al. Nanoscale displacement sensing based on nonlinear frequency mixing in quantum cascade lasers. IEEE Journal of Selected Topics in Quantum Electronics 21, 107–114 (2015).
Yariv, A. & Yeh, P. Photonics: optical electronics in modern communications (the oxford series in electrical and computer engineering) (Oxford University Press, Inc., 2006).
Acknowledgements
The authors wish to acknowledge fundings from the ERC Advanced Grant SOULMAN (ERC-FP7-321122) and QUANTOM project of the italian MIUR. D.N.U. acknowledges Ramon y Cajal Contract from spanish MINECO.
Author information
Authors and Affiliations
Contributions
A.T. conceived and supervised the whole work. L.B. and A.P. conducted the main experiment and analysed the results, L.B. performed the theoretical calculations, A.P. fabricated the sample. L.B., A.P., L.M. and D.N.-U. devised the setup, L.B., A.A. and F.C. performed the calibration. L.B. and A.P. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Baldacci, L., Pitanti, A., Masini, L. et al. Thermal noise and optomechanical features in the emission of a membrane-coupled compound cavity laser diode. Sci Rep 6, 31489 (2016). https://doi.org/10.1038/srep31489
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep31489
This article is cited by
-
Impact of the central frequency of environment on non-Markovian dynamics in piezoelectric optomechanical devices
Scientific Reports (2021)
-
Continuous-wave laser operation of a dipole antenna terahertz microresonator
Light: Science & Applications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.