Abstract
We study heterogeneous condensation growth of water droplets on micron-sized particles resting on a level substrate. Through numerical simulations on equilibrium droplet profiles, we find multiple wetting states towards complete wetting of the particle. Specifically, a partially wetting droplet could undergo a spontaneous transition to complete wetting during condensation growth, for contact angles above a threshold minimum. In addition, we find a competitive wetting behavior between the particle and the substrate and interestingly, a reversal of the wetting dependence on contact angles during late stages of droplet growth. Using quasi-steady assumption, we simulate a growing droplet under a constant condensation flux and the results are in good agreement with our experimental observations. As a geometric approximation for particle clusters, we propose and validate a pancake model and with it, show that a particle cluster has greater wetting tendency compared to a single particle. Together, our results indicate a strong interplay between contact angle, capillarity and geometry during condensation growth.
Similar content being viewed by others
Introduction
Condensation often occurs when water vapor undergoes physical change in state on a solid surface1. This subject has many applications in many fields such as thin film growth2, heat transfer3, recovery of atmospheric water4,5 and polymer templating6. Relevant experimental and theoretical works can be found in the review paper of Ucar et al.7.
Of particular importance and interest is the growth rate of water droplets on a flat substrate7. Beysen and co-workers8,9,10,11 observed a power-law growth rate of one-third and explained it using a diffusive growth mechanism, where adsorbed water monomers diffuse laterally towards the droplet perimeter. The one-third power law exponent is corroborated by other studies, including those of Briscoe and Galvin12, Ucar and Erbil13,14 and Ichikawa et al.15. In contrast, direct condensation of saturated water vapor onto the droplet surface leads to a power law growth exponent of one-half16,17,18,19,20. The same one-half power law is experimentally observed for the droplet growth on hydrophobic substrate21,22. Still others found a linear relationship between droplet radius and time during condensation growth, due to an assumed constant water flux23,24,25. Together, this suggests that typical droplet growth exponent could range from one-third to unity.
A closely related phenomenon, capillary condensation, could occur at under-saturated pressures26 and find particular importance in porous media condensation26 and atomic force microscopy (AFM) measurement27,28,29. On a concave curvature meniscus, the saturation pressure on the meniscus reduces follows the Kelvin equation30. For capillary condensation on AFM tip, a thin layer of liquid atom is first absorbed on the flat substrate and particle surfaces, before coalescence occurs forming a liquid neck.
Generally, droplet growth is governed by transport mechanisms, namely, molecular diffusion, Knudsen diffusion, surface diffusion and thin film dynamics27,28,29. For molecular diffusion, the rate of growth of capillary condensates follows a limited diffusion model based on Langmuir theory of growth31. For Knudsen diffusion, the mean free path is much larger than the geometric gap size between the particle and flat substrate, so condensation rates are controlled by collisions between water vapor molecules and solid surfaces27,29. For surface diffusion, the accumulation of drop mass depends on the diffusivity of water monomers on the substrate11. Lastly, for thin film dynamics, thin adsorbed water film on the flat substrate flows towards the liquid neck, so condensation rates depends on the viscosity of the water liquid layer.
Here, we investigate the condensation growth of a water droplet on spherical solid particles on a flat substrate. To that, we develop and present a numerical model based on capillary pressure, contact angle and droplet morphology and compare results against our experimental observations. In particular, we distinguish the behavior of droplet on a single spherical particle with that of a monolayer cluster on a flat substrate.
Methods
Theory
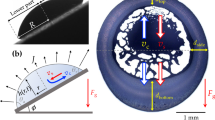
Consider a liquid meniscus adhering to a spherical particle on a flat surface as shown in Fig. 1a. Using polar coordinates (r, ϕ, z), we define r0 as the radius of the particle, ϕ ∈ {0, 180°} as the polar angle taken from the negative direction (−z) on the vertical axis, Φ0 as the polar angle of the locus where the meniscus contacts the particle (wetting edge), θ as the in-plane tangential meniscus contact angle, h(ϕ) as the meniscus depth taken from the particle surface and rd is the droplet-substrate contact radius taken from the axis of symmetry.
The droplet shape profile is governed by the Young-Laplace equation32,

where PC = r0pc/σ is the normalized capillary pressure, σ is the surface tension, pc is the capillary pressure, η(ϕ) = h(ϕ)/r0 is the normalized meniscus thickness and  denotes the spatial derivative in polar coordinates. In Eq. (1), the terms on the left-hand side represent the in-plane and out-plane curvatures of the meniscus respectively and the right-hand side the capillary pressure effect.
denotes the spatial derivative in polar coordinates. In Eq. (1), the terms on the left-hand side represent the in-plane and out-plane curvatures of the meniscus respectively and the right-hand side the capillary pressure effect.
Based on our experimental study (detailed later), the droplet radius grows almost proportionally in time. The observed linear growth rate suggests a mechanism whereby water vapor condenses directly on the liquid meniscus during droplet growth23,24,25.
Following mass conservation, the droplet volume evolves as

where Γ is the direct condensation mass flux, s is the meniscus surface area, v is the droplet volume, ρ is liquid density and t is time. For convenience, we can also express Eq. (2) in dimensionless form as  , where V = v/r03 is the normalized droplet volume, S = s/r02 is the normalized meniscus surface and
, where V = v/r03 is the normalized droplet volume, S = s/r02 is the normalized meniscus surface and  is the normalized condensation time.
is the normalized condensation time.
The equilibrium meniscus droplet shape is obtained by solving Eq. (1) using an iterative shooting procedure implemented by a fourth order Runge-Kutta method. For a given meniscus contact point Φ0 (where η(Φ0) = 0) and surface contact angle θ (where  ), we vary the capillary pressure pc until the resultant droplet profile intersects the flat substrate at the imposed contact angle of θ. At a given time, the resultant droplet profile is compared against the desired droplet volume obtained by Eq. (2) and the process is repeated iteratively until volume convergence is achieved.
), we vary the capillary pressure pc until the resultant droplet profile intersects the flat substrate at the imposed contact angle of θ. At a given time, the resultant droplet profile is compared against the desired droplet volume obtained by Eq. (2) and the process is repeated iteratively until volume convergence is achieved.
The above numerical procedure assumes that thermodynamic equilibrium time-scale is fast compared to droplet growth time-scale, so that droplet growth is quasi-steady. Furthermore, we assume that both droplet-particle and droplet-substrate contact angles are of the same constant value, since both particle and substrate used in our experiments are made of silica.
Experiment
We directly visualize water droplet growing on spherical particles via condensation, using an experimental setup shown in Fig. 1(b). To prepare the substrate, glass cover-slips (Menzel Glaser, Germany) were sonicated for 20 minutes each in acetone, isopropyl alcohol and ethanol and dried in a fast stream of nitrogen air. Separately, we determined the contact angle of a water droplet on the prepared glass slides to be approximately 22°. The particles were introduced via a stock solution of 1 μm silicon dioxide particles (1%, Thermo Scientific, United States), which was diluted by a factor of 10 in water before it was dispensed on the coverslip. The experiment was performed within a fluid cell (Bruker Corporation, United States) sealed by a silicone O-ring. Apart from inlet and outlet ports (closed during the experiment), the fluid cell is fully sealed at all times.
As a source of water vapor, liquid water was piped via silicone tubing up to the point just outside the inlet of the cell. We point out that no liquid water was delivered directly into the cell. The evaporating water creates a humid environment within the cell, which in turn promotes the condensation of water on the particles. We imaged the condensation and droplet growth from below the cover-slip via a 60x microscope objective (Olympus, Japan). The recording was performed with a CCD camera (Pixelfly QE, PCO AG, Germany) at a temporal resolution of 10 frames per second and a spatial resolution of 100 nm per pixel.
Results
Wetting transition
First we consider the wetting of the particle and how it relates to the droplet volume and contact angle. For contact angle θ = 45°, we vary the wetting edge at the polar angle Φ0 from 30° to 180° (complete wetting) and numerically solve for droplet profiles against associated droplet volumes. Figure 2a shows that the drop volume increases monotonically with increasing wetting Φ0, until the turning point P3 is reached. Thereafter, the droplet volume at equilibrium apparently decrease with further wetting until complete wetting is reached at point P1′. This apparent reversal in wetting and volume trends can be attributed to a dramatic increase in out-plane curvature term in the Young-Laplace equation, which tends towards singularity as 1/r. This we corroborated using a separate analysis on droplet growth on an infinite 2D cylinder and accordingly did not observe any wetting-volume reversal.
(a) Plot of wetting edge Φ0 on spherical particle against normalized droplet volume V, for a droplet contact angle of θ = 45°. Different wetting states are possible for a given droplet volume due to out-of-plane curvature effects. P1 indicates the onset of multiple wetting states, P2 the spontaneous transition from partial to complete wetting based on Gibbs free energy consideration and P3 the partial wetting limit. Here, with increasing droplet volume, continuous partial wetting occurs, until P2 where it jumps discontinuously to a complete wetting state at P2′ (b) Phase diagram of Gibbs energy difference ΔG between complete (upper right) and partial (lower left) wetting states and the dependence on contact angles θ and droplet volumes V. The red contour depicts the transition curve ΔG = 0. The inset is a close-up on the dashed box region with the same parameter space used in (a).
The dash section of the curve (Fig. 2a) from P1 to P3 represents multiple wetting states for the same droplet volume. Here the intermediate point P2 indicates spontaneous transition from partial wetting to complete wetting based on free energy considerations. The apparent wetting-volume reversal reflects a duality in wetting states, for instance the loci pair P1-P1′ and P2-P2′ represent partial and complete wetting states at the same droplet volume V (Fig. 2a). The thermodynamic consideration is that the droplet tends to adopt the wetting state which corresponds to a lower Gibbs free energy. Here, the Gibbs free energy G is expressed in dimensionless form as33,34,35

where G is scaled by σr02, θ is the contact angle between droplet and flat surface and between droplet and spherical particle, ASL is the scaled solid-liquid surface, S is the scaled water-air interface area and Ω0 is an constant.
Here we define ΔG as the difference in Gibbs energies between complete wetting (e.g. P1′ and P3′) and partial wetting (e.g. P1 and P3) states. Figure 2b shows a phase diagram of energy difference ΔG and its dependence on contact angle θ and droplet volume V. Here, we sketch the red contour curve for ΔG = 0, which separates distinct regions of positive (lower left) and negative (upper right) energy differences and thus represents the threshold for complete wetting transition. Specifically, the inset shows a close-up of the dashed box region and covers the parameter space used in Fig. 2a. The inset clearly shows that ΔG is positive between the loci range P1-P1′ to P2-P2′, but is negative between P2-P2′ to P3-P3′. This means that in the absence of wetting energy barriers, an initial partial wetting state could transit spontaneously to a complete wetting state with increasing droplet volume between P1 and P3.
Capillary pressure and droplet shape
Next we turn to the droplet profile and its surface curvature at equilibrium. Figure 3a shows the phase diagram of the capillary pressure Pc as a function of the wetting edge Φ0 and contact angle θ. As indicated by the Young Laplace equation, the capillary pressure represents the sum of in-plane and out-of-plane surface curvature components. Due to the inherent centerline axisymmetry, the out-of-plane component is always negative, so the capillary pressure sums to zero if a positive in-plane curvature exactly cancels the out-of-plane component. The null capillary isobar Pc = 0 is sketched on Fig. 3a as red dotted curve, separating regions of surface concavity (lower left) and convexity (upper right). Here we define a minimum capillary isobar Pc,min, which also represents the minimum in surface concavity, sketched as dashed curve. For comparison, we plot the null capillary isobar for the case of a 2D cylinder solved analytically as θ = (π−Φ0)/2, sketched here as red line.
(a) The non-dimensional capillary pressure Pc of the droplet growth on the particle for various contact angles from 10° to 60°. (b) Droplet shape on the particle for contact angle θ = 45° and wetting edge Φ0 = 80° at zero capillary pressure Pc = 0 and at minimum non-dimensional capillary pressure Pc = Pc min. The menisci are concave and convex for Pc = 0 and Pc = Pc min cases, respectively.
Figure 3b shows in-plane droplet profiles held at either Pc = 0 or Pc,min for contact angle θ of 45° and wetting edge Φ0 of 80°. The corresponding parameter loci are indicated in Fig. 3a as red and black dot markers for reference. It is clear that the in-plane curvatures are consistently concave for null capillary pressure Pc = 0 and more linear for minimum capillary pressure Pc,min.
Of further interest are the in-plane droplet growth profiles and its dependence on contact angles. Figure 4a shows the growth of in-plane droplet profiles on a single particle simulated using a condensation rate constant  s−1 obtained from experiments (detailed later), in dimensionless time increments of 0.42 τ and we compare the effects of contact angles θ of 60° (left) and 22° (right). Initially concave, the in-plane curvatures become increasingly convex with time, due to the effects of decreasing capillary pressure (Fig. 3). This evolution of in-plane curvatures is particularly evident at higher contact angles.
s−1 obtained from experiments (detailed later), in dimensionless time increments of 0.42 τ and we compare the effects of contact angles θ of 60° (left) and 22° (right). Initially concave, the in-plane curvatures become increasingly convex with time, due to the effects of decreasing capillary pressure (Fig. 3). This evolution of in-plane curvatures is particularly evident at higher contact angles.
(a) Snapshots of droplet meniscus profiles taken in time increments of 0.42 τ, for contact angles of 22° on the right and 60° on the left side of the vertical aSxis. The initial volume of the droplet is V = 0.05 and the condensation rate is  s−1. (b) The substrate wetting rate dR/dτ increases with droplet radius R at early times but tapers off later. (c) The particle wetting rate dΦ0/dτ decreases with wetting edge Φ0 at early times, but increases significantly as it approaches complete particle wetting. Both (b) and (c) are shown for contact angles θ = 22°, 45°, 60°.
s−1. (b) The substrate wetting rate dR/dτ increases with droplet radius R at early times but tapers off later. (c) The particle wetting rate dΦ0/dτ decreases with wetting edge Φ0 at early times, but increases significantly as it approaches complete particle wetting. Both (b) and (c) are shown for contact angles θ = 22°, 45°, 60°.
Figure 4b shows the droplet growth rate as a function of its instantaneous dimensionless radius R scaled by particle radius r0. Smaller droplets tend to spread laterally on the substrate slower compared to larger droplets, due to the competitive wetting of the particle at smaller droplet volumes. In addition, smaller contact angles correspond to faster spreading rates compared to larger contact angles, across all droplet sizes investigated. This is expected because a small contact angle is indicative of a hydrophilic surface, which tends to wet more easily compared to a hydrophobic one.
Figure 4c shows the rate of wetting as a function of its wetting edge Φ0. For a small wetting edge, the wetting rate decreases with wetting edge Φ0, as liquid accumulates preferentially in the bulk of the droplet due to curvature changes; the trend is however reversed towards complete wetting. As before, smaller contact angles θ (hydrophilic surface) lead to faster initial wetting rates, but this trend is reversed within a wetting interval of 120° and 150°, such that larger contact angles (hydrophobic surface) correspond to faster wetting rates.
The latter observation is, in particular, of interest, for it suggests an interaction between the contact angle, capillarity and the geometric constraint imposed by the spherical particle. Although the substrate and the particle are made of a common material with the same contact angle, the competition for surface wetting is unbalanced and preferential wetting occurs depending on the specific drop volume, geometry and thermodynamics.
Condensation growth rates
In our experiment, water vapor nucleates as a liquid meniscus preferentially in the cavity between the particle and the substrate; no unattached droplet is found on the substrate over a region of about 100 μm × 100 μm. Initially, the nucleated droplet is not well resolved, since the contact line is obscured by the particle itself. Later, the growing droplet radius exceeds the particle radius and could be resolved.
Figure 5 shows images of droplet growth on a single particle, three-particle and six-particle clusters in ten-second increments from initial time t = 0 s, when the first flicker of droplet contact line is observed at the edge of the particles. During early times, the nascent droplet perimeter follows the peripheral outline of the cluster; the droplet outline becomes circular by t = 30 s onwards. The apparent radius is determined by close-fitting the droplet outline to a circle, an example illustrated in the image for t = 40 s. Based on the even illumination and lack of optical distortion throughout the experiment, it appears likely that the droplet has not completely wetted the particle up to t = 50 s.
For a tightly grouped particle cluster, we approximate the collective geometry as a single pancake model structure as shown in Fig. 6a (for a three particle cluster). The pancake model consists of a cylindrical core, conjoined and wrapped around the sides by a revolved semi-circle of radius r0, which is equivalent to the radius of a single particle. The apparent centerline radius of the pancake r1 is set by equating the centerline pancake area πr12 and the sum of all actual particle areas nπr02, where n is the number of particles in a cluster (Fig. 6b). This geometric reshape, while simplistic, retains features of dimensional scaling and morphological consistency at the edges.
For the pancake model, we express the Young-Laplace equation in Eq. (1) as

where ε scales the interior cylindrical core as (r1/r0) − 1. The numerical solution follows the same scheme as indicated earlier for the case of a single particle.
The droplet is simulated using a contact angle of 22° (experimentally determined) and an initial wetting edge Φ0 of 30°. The resulting droplet wets the substrate to a radius of approximately R so the contact line is at the threshold of experimental visibility. The droplet grows at rate determined by the condensation mass flux Γ. As shown in Fig. 7a, we fit the simulated droplet growth rate to experimental data (obtained from Fig. 5), using a condensation rate constant  s−1. For a water droplet of density ρ = 1000 kg/m3 and particle radius r0 = 1 μm, the dimensional mass flux Γ = 21 mg/m2s.
s−1. For a water droplet of density ρ = 1000 kg/m3 and particle radius r0 = 1 μm, the dimensional mass flux Γ = 21 mg/m2s.
(a) Logarithmic time-plot of non-dimensional droplet radius for the cases of single particle, 3-particle and 6-particle clusters for both experimental (markers) and simulated (lines) data. Condensation rate is  s−1 and the contact angle is 22°. Eye-guide of slope 1 refers to an idealized growth rate of a particle-free droplet. (b) Plot of droplet aspect ratio represented by wetting edge Φ0 and the non-dimensional radius R.
s−1 and the contact angle is 22°. Eye-guide of slope 1 refers to an idealized growth rate of a particle-free droplet. (b) Plot of droplet aspect ratio represented by wetting edge Φ0 and the non-dimensional radius R.
Here, we make the case that a good trend fit is not assured simply by tuning a single free parameter. In particular, we find that the direct condensation mechanism, which predicts a linear growth rate23,24,25, caters sufficiently to the fit on a constant flux. Other condensation models, for example substrate monomer diffusion and limited directed condensation, predict a growth power law between one-third8,9,10,11 to one-half20, but they do not fit the experimental data trend reasonably. In addition, we found that the apparent initial deviation from linear growth of slope one occurs due to the geometric and wetting effects of the particle. This observed deviation diminishes as the droplet size becomes large compared to the particle, such that the growth behavior approaches that of homogeneous condensation.
As further validation, we simulate the cases for three and six particle clusters using the pancake model as described earlier. Using the same condensation rate constant  s−1 as for the single particle case, the simulated growth curves are found to be in good agreement with the actual experimental data, without any fitting (Fig. 7a). This result indicates that both the pancake geometric approximation and the assumed condensation flux are reasonable assumptions for our simulations.
s−1 as for the single particle case, the simulated growth curves are found to be in good agreement with the actual experimental data, without any fitting (Fig. 7a). This result indicates that both the pancake geometric approximation and the assumed condensation flux are reasonable assumptions for our simulations.
Further, we compare the respective late time growth rates against the theoretical linear growth rate of a particle-free droplet due to a constant condensation flux (see eye-guide of slope 1). Interestingly, we note that the growth curve for the particle clusters (pancake model) finds better agreement with the indicated slope than for the single particle. To clarify this, we plot the aspect ratio based on the wetting edge Φ0 and non-dimensional droplet radius R, as shown in Fig. 7b. This plot essentially describes the ratio of wetting on the particle against the substrate and indeed, the droplet wets the particle clusters faster than the single particle case, so that further droplet growth tends to wet the substrate instead of the particle. This results in a growth rate similar to that of a homogeneous droplet (slope 1).
For the case of a single particle, we note that the out-of-plane curvature term rapidly becomes singular as the droplet approach complete wetting, leading to a wetting-volume transition as previously discussed (Fig. 2). Conversely, for the case of particle cluster (pancake model), this problem is alleviated, for even as wetting edge Φ0 approaches 180°, the out-of-plane radius of curvature tends to  and not zero. Therefore, the wetting-volume transition is not significant for the particle clusters. This is particularly evident for the 6-particle case as depicted in Fig. 7b for larger values of Φ0.
and not zero. Therefore, the wetting-volume transition is not significant for the particle clusters. This is particularly evident for the 6-particle case as depicted in Fig. 7b for larger values of Φ0.
Discussion
We had presented herein an analysis on the condensation of water on micron-sized particle or cluster of particles on a substrate, specifically on drop growth and wetting behavior. Notably, alternative thermodynamic wetting states are accessible as the growing droplet approach complete wetting of the particle. Partially wetting droplet profiles become less favorable as the out-of-plane curvatures approach singularity. This, we supported with calculations of Gibbs energy subjected to contact angle and wetting edge and obtained a transition curve where a jump from partial to complete wetting may occur.
In addition, we simulated droplet growth under experimental conditions and found a good agreement with experimental results using a single fitting condensation mass flux constant. The analysis was extended to particle clusters using a simple geometric approximation in the form of a pancake and our results are also consistent with experimental observations.
With that, we ask the question of how droplet profiles evolve during condensation growth, but constrained by geometric and wetting considerations. Here, we present a case where the wetting behavior of either the particle or the substrates is competitive and unbalanced, even with the same contact angles. This result highlights a gap in our understanding of condensation and surface wettability at small scales. The present work could be extended to problems involving capillary adhesion between wetted particles and substrates, or wetted fine particulates and granules commonly used in chemical industries.
Additional Information
How to cite this article: Quang, T. S. B. et al. Growth and wetting of water droplet condensed between micron-sized particles and substrate. Sci. Rep. 6, 30989; doi: 10.1038/srep30989 (2016).
References
Khandekar, S. & Muralidhar, K. Dropwise condensation on inclined textured surfaces (Springer, 2014).
Lewis, V. B. & Anderson, J. C. Nucleation and growth of thin films (Academic Press, 1978).
Ma, X., Rose, J. W., Xu, D., Lin, J. & Wang, B. Advances in dropwise condensation heat transfer: chinese research. Chemical Engineering Journal 78, 87–93 (2000).
Clus, O., Ortega, P., Muselli, M., Milimouk, I. & Beysens, D. Study of dew water collection in humid tropical islands. J. Hydrol. 361, 159–171 (2008).
Sharan, G., Clus, O., Singh, S., Muselli, M. & Beysens, D. A very large dew and rain ridge collector in the Kutch area (Gujarat, India). J. Hydrol. 405, 171–181 (2011).
Widawski, G., Rawiso, M. & Francois, B. Self-organized honeycomb morphology of star-polymer polystyrene films. Nature 369, 387–389 (1994).
Ucar, I. O. & Erbil, H. Y. Droplet condensation on a polymer surfaces: a review. Turk. J. Chem. 37, 643–674 (2013).
Viovy, J. L., Beysens, D. & Knobler, C. M. Scaling description for the growth of condensation patterns on surfaces. Phys. Rev. A 37, 4965–4970 (1988).
Beysens, D., Knobler, C. M. & Schaffar, H. Scaling in the growth of aggregates on a surface. Phys. Rev. B 41, 9814–9818 (1990).
Steyer, A., Guenoun, P., Beysens, D. & Knobler, C. M. Growth of droplets on a substrate by diffusion and coalescence. Phys. Rev. A 44, 8271–8277 (1991).
Beysens, D. Dew nucleation and growth. C. R. Phys. 7, 1082–1100 (2006).
Briscoe, B. J. & Galvin, K. P. An experimental study of the growth of breath figures. Colloids Surf. 56, 263–278 (1991).
Ucar, I. O. & Erbil, H. Y. Dropwise condensation rate of water breath figures on polymer surfaces having similar surface free energies. Appl. Surf. Sci. 259, 515–523 (2012).
Ucar, I. O. & Erbil, H. Y. Use of diffusion controlled drop evaporation equations for dropwise condensation during dew formation and effect of neighboring droplets. Colloids Surf. A 411, 60–68 (2012).
Ichikawa, M., Magome, N. & Yoshikawa, K. Rhythmic growth and collapse of a micro water droplet. Europhys. Lett. 66, 545–551 (2004).
Kulmala, M. & Vesala, T. Condensation in the continuum regime. J. Aerosol Sci. 22, 337–346 (1991).
Heidenreich, S. Condensational droplet growth in the continuum regime - a critical review for the system air-water. J. Aerosol Sci. 25, 49–59 (1994).
Vesala, T., Kulmala, M., Rudolf, R., Vrtala, A. & Wagner, P. E. Models for condensational growth and evaporation of binary aerosol particles. J. Aerosol Sci. 28, 565–598 (1997).
Lauri, A., Riipinen, I., Ketoja, J. A., Vehkamaki, H. & Kulmala, M. Theoretical and experimental study on phase transitions and mass fluxes of supersaturated water vapor onto different insoluble flat surfaces. Langmuir 22, 10061–10065 (2006).
Sokuler, M., Auernhammer, G. K., Liu, C. J., Bonaccurso, E. & Butt, H. J. Dynamics of condensation and evaporation: effect of inter-drop spacing. Europhys. Lett. 89, 36004 (2010).
Miljkovic, N., Enright, R. & Wang, E. N. Effect of droplet morphology on growth dynamics and heat transfer during condensation on superhydrophobic nanostructured surfaces. ACS Nano 6, 1776–1785 (2012).
Rykaczewski, K. Microdroplet growth mechanism during water condensation on superhydrophobic surfaces. Langmuir 28, 7720–7729 (2012).
Zheng, L., Wang, Y.-X., Plawsky, J. L. & Wayner, P. C. Effect of curvature, contact angle and interfacial subcooling on contact line spreading in a microdrop in dropwise condensation. Langmuir 18, 5170–5177 (2002).
Gokhale, S. J., Plawsky, J. L. & Wayner, P. C. Jr.. Experimental investigation of contact angle, curvature and contact line motion in dropwise condensation and evaporation. J. Colloid Interface Sci. 259, 354–366 (2003).
Leach, R. N., Stevens, F., Langford, S. C. & Dickinson, J. T. Dropwise condensation: experiments and simulations of nucleation and growth of water drops in a cooling system. Langmuir 22, 8864–8872 (2006).
Gregg, S. J. & Sing, K. S. W. Adsorption, surface area and porosity (Academic Press, 1982).
Wei, Z. & Zhao, Y. Growth of liquid bridge in AFM. J. Phys. D 40, 4368–4375 (2007).
Rabinovich, Y. I., Singh, A., Hahn, M., Brown, S. & Moudgil, B. Kinetics of liquid annulus formation and capillary forces. Langmuir 27, 13514–13523 (2011).
Sirghi, L. Transport mechanisms in capillary condensation of water at a single-asperity nanoscopic contact. Langmuir 28, 2558–2566 (2012).
Israelachivili, J. N. Intermolecular and surface forces (Academic Press, 1992).
Kohonen, M. M., Maeda, N. & Christenson, H. K. Kinetics of capillary condensation in a nanoscale pore. Phys. Rev. Lett. 82, 4667–4670 (1999).
Silin, D. & Virnovsky, G. A variational model of disjoining pressure: liquid film on a nonplanar surface. Transport Porous Med. 82, 485–505 (2010).
Michielsen, S., Zhang, J., Du, J. & Lee, H. J. Gibbs free energy of liquid drops on conical fibers. Langmuir 27, 11867–11872 (2011).
Liang, Y. E., Tsao, H. K. & Sheng, Y. J. Drops on hydrophilic conical fibers: gravity effect and coexistent states. Langmuir 31, 1704–1710 (2015).
Liang, Y. E., Wu, C. J., Tsao, H. K. & Sheng, Y. J. Equilibrium morphological phase diagram of drops in hydrophilic cylindrical channels. J. Phys. Chem. C 119, 25880–25886 (2015).
Acknowledgements
This work is supported in part by the Singapore National Research Foundation under CRP Award No. NRF-CRP9-S2011-04.
Author information
Authors and Affiliations
Contributions
T.S.B.Q. and F.Y.L. conducted the numerical study and wrote the manuscript; F.Y.L. designed study; H.A., B.H.T. and C.-D.O. conducted the experiments and analyzed the results. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Quang, T., Leong, F., An, H. et al. Growth and wetting of water droplet condensed between micron-sized particles and substrate. Sci Rep 6, 30989 (2016). https://doi.org/10.1038/srep30989
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30989
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.