Abstract
When lightning strikes soil, it may generate a cylindrical tube of glass known as a fulgurite. The morphology of a fulgurite is ultimately a consequence of the energy of the lightning strike that formed it and hence fulgurites may be useful in elucidating the energy distribution frequency of cloud-to-ground lightning. Fulgurites from sand mines in Polk County, Florida, USA were collected and analyzed to determine morphologic properties. Here we show that the energy per unit length of lightning strikes within quartz sand has a geometric mean of ~1.0 MJ/m and that the distribution is lognormal with respect to energy per length and frequency. Energy per length is determined from fulgurites as a function of diameter and frequency is determined both by cumulative number and by cumulative length. This distribution parallels those determined for a number of lightning parameters measured in actual atmospheric discharge events, such as charge transferred, voltage and action integral. This methodology suggests a potential useful pathway for elucidating lightning energy and damage potential of strikes.
Similar content being viewed by others
Introduction
Cloud-to-ground lightning is a high-energy phenomenon that transfers electric charge, either positive or negative, between the atmosphere and the surface. Voltages associated with lightning strikes may exceed 108 V and the total energy of a strike may reach 109J, heating the air to temperatures exceeding 30,000 K1. This phenomenon is associated with several detrimental effects including human fatalities, forest fires and property damage and a few positive effects such as natural nitrogen fixation2 and production of reduced oxidation state phosphorus compounds that may improve the solubility of phosphorus in soil3.
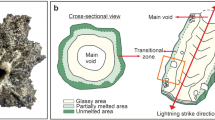
When cloud-to-ground lightning strikes an appropriate target material such as sand, soil, rock, or clay, the current flows through the target, heating the material to temperatures that exceed its vaporization point, followed by rapid cooling that results in quenching to form a hollow cylinder of glass known as a fulgurite (Fig. 1). The morphology of fulgurites is strongly dependent on material composition4,5,6 and for natural fulgurites, the thickness of the glass is inversely related to fraction of material composed of SiO2. Lightning is a ubiquitous phenomenon on Earth, with a global flash rate of about 45 times per second7, a majority (75–90%) of which occur over continental landmass8. About a quarter of these strikes occur from a cloud to the ground9 and hence the number of potential fulgurite-forming events is significant, with up to 10 fulgurites formed globally per second. This estimate depends on the efficiency of fulgurite formation by lightning, which is highest when striking barren sand, soil, or rock10. Lightning striking forested areas may not necessarily form a fulgurite, though fulgurites are known to form when lightning strikes trees11. Fulgurites have also been known to form associated with human-made objects such as steel pylons, where the metallic structure may actually induce lightning to travel along its length12.
(A) Exemplary fulgurites collected from the field area. Surficial differences likely result from different initial physical conditions (e.g., percent water in sand). Color differences are apparently due difference between the thicknesses of the glass wall, which are 1.1 ± 0.1, 0.9 ± 0.3 and 1.6 ± 0.3 mm from top to bottom (taken from 10 measurements, with 1 standard deviation given as the error). (B) Fulgurite found in situ. Diameter is about 1.2 cm.
Fulgurites that are formed in a homogenous target may preserve the probability distribution of a key lightning parameter—the energy of a strike—in their morphology. To this end, we determined the relationship between numerical frequency and energy of cloud-to-ground lightning strikes by studying a set of 266 fulgurites from two quartz sand mines in Polk County, Florida, USA (Fig. 2). We then compared these results to predicted distributions calculated using simulated energy and length parameters, coupled to a simple fracture model. Our motivating hypothesis within this work is that fulgurites might also follow a lognormal distribution with respect to energy, as many other lightning parameters follow lognormal distributions.
Polk County, Florida, USA digital elevation map showing sample localities for fulgurites.
This map was prepared with QGIS software (QGIS Development team, 2016, http://osgeo.org). Base map was modified from USGS National Elevation Dataset 1/3 arc-second, (www.nationalmap.gov). County boundaries were modified from the Florida Geographic Data Library (www.fgdl.org) after the United State Census Bureau, 1999, Florida County Boundaries – Statewide (www.census.gov). City information was modified from the Florida Geographic Data Library (www.fgdl.org) after the National Atlas of the United States, 2004, Cities and Towns of Florida (www.nationalatlas.gov).
Results
The fulgurites were arranged according to decreasing diameter. Each fulgurite was given a number corresponding to the number of fulgurites equal to or larger than its diameter. Correspondingly, the frequency distribution of the fulgurites may be calculated by ordering the fulgurites in terms of energy per length (MJ/m) and then from 1) the length of each fragment with cumulative length becoming the dependent variable, or 2) by using total number as the dependent variable. Alternatively, the distribution of total energy (MJ/m × length) to total number can also be used to provide a distribution. These frequency diagrams are given as Fig. 3. All three methods generate linear relationships between the log of energy (MJ/m or total MJ) vs. frequency (number of occurrences, or cumulative length).
Lognormal frequency distributions.
(A) Distribution of energy per length (MJ/m) vs. number. Each fulgurite, is assigned a number corresponding to the number of fulgurites equal to or larger than it with respect to energy per unit length. These numbers are then divided by the total number of fulgurites collected (266). (B) Distribution of energy per length (MJ/m) vs. cumulative length. As above, each fulgurite is arranged in descending energy per unit length. The energy is then graphed against the cumulative length of each fulgurite bearing that energy or more. This length is then divided by the total length (14.659 m). (C) Distribution of total energy (MJ) vs. number. The total energy is obtained by multiplying the energy per unit length determined from the diameter of the fulgurite by its length. Fulgurites are then arranged in order of decreasing total energy and each fulgurite is given a number based on the number of fulgurites equal to or greater than the calculated total energy. These numbers are then divided by 266, the total number of fulgurites collected.
We also prepared simulations of fulgurite distributions that might arise from specific energy distributions. We find that lognormal distributions of energy per length with a normal distribution or constant length of each fulgurite are most consistent with the natural fulgurite distributions (see supporting information). These simulations help to provide some confidence in the approaches taken below.
Three approaches (energy per meter vs. cumulative length, energy per meter vs. cumulative number, total energy vs. cumulative number) were chosen to allow for multiple approaches to the estimating lightning energy distributions. Cumulative length is used as it allows for a direct comparison to frequency of events for a fractured material in which all parts may not be recovered. There is little change in fulgurite diameter across the length of a fulgurite1, even if the fulgurite has a total length greater than one meter. Hence, two fragments of the same fulgurite should have the same diameter. To this end, comparing energy to cumulative length helps eliminate the possibility of double-counting two fragments of a single strike. For comparison, the longest documented fulgurite yet discovered has a length of 5 meters1 and hence this single individual is about a third of the total length of all of the fulgurites recovered in the present study. The median length of the fulgurites from these sand mines in the present collection is about 5 cm, with no significant variations in diameter across these lengths. As a result, the systematic collection of fulgurites might yield distributions where length is proportional to the abundance of each fulgurite of a specific width.
Alternatively, if we treat each fulgurite as a separate event, then there exists the possibility that a single event may be counted multiple times if the fulgurite fragmented before collection. However, if multiple events have the same energy, then counting by numerical frequency considers this multiplicity. Regardless, both approaches give very similar slopes between log E (MJ/m) and frequency/cumulative length (Table 1) and the median (50%) energy associated with fulgurite formation in both cases is about 1.4 MJ/m and the standard deviation is ×/÷ 3.
The total energy recorded within the fulgurite tube can also be approximated by multiplying the energy per unit length by the length of a given fulgurite. Such a calculation assumes that breakage of the glass was minimal since formation. This scenario is presented for the sake of completeness, but given the fragile nature of fulgurites, is likely inaccurate. However, since most of the fulgurite fragments have similar lengths, the energy distribution is also lognormal, like the energy per unit length distributions. The regression line fit to the lognormal total energy vs. frequency distribution is the strongest of these calculations (R2 = 0.9852), though the slope differs from the prior two approaches.
Comparison between the fulgurite distributions and between the simulations (SI) suggests that, as long as the fulgurite fragments are collected without bias and as long as the fulgurites have experienced roughly the same fracturing history, then the fulgurite distributions are most consistent with being lognormal with respect to energy per length. Consequently, the resulting distribution of total energy should also be lognormal even when fractured, as is borne out by the above data.
The density of a subset of the fulgurites subset is found to be 1.8 ± 0.1 g/cm3 (1σ). The density of the accompanying sand is 1.7 g/cm3 and of the individual quartz grains that make up the sand 2.6 g/cm3.
Discussion
The relationship between the energy E per unit length of a given lightning strike and frequency of that given strike having energy E or more follows a lognormal distribution. Many lightning parameters follow a log-normal distribution with respect to the frequency of that parameter occurring, including flash duration, voltage, charge transferred, stroke interval, current duration and action integral13,14,15. The slopes of the log E (MJ/m) plots vs. frequency or cumulative length (normalized to probability 1) are both close to −0.6. Intriguingly, the slope of frequency vs. charge or impulse peak current measured by Pichler et al.14 also bear slopes of −0.6, nearly identical to these fulgurite morphology slopes14.
For a poorly conductive target material that does not vary significantly in composition in aerial extent, the electric field must exceed the breakdown field strength of the material to propagate a spark. For sand, this strength is less than 8 MV/m, the breakdown strength of quartz. Air has a lower breakdown strength (~1 MV/m at 1 sea level)16, hence the breakdown strength of sand should be less than quartz alone. Thus the energy per unit length deposited by lightning into the sand should be a function of the number of electrons that propagate through the sand as the insulating capability of the sand fails, in addition to the amount of thermal energy transferred by the column of heated plasma adjacent to the fulgurite. The amount of charge transferred by lightning is known to follow a lognormal distribution function14 and hence the energy deposited by lightning might be expected to follow the same. The lognormal nature of charge transferred may hence be the source of lognormal distribution of fulgurite energy per unit length, though other parameters may also play a role.
Accuracy of “fossilization” of energy per unit length in fulgurites
The density of the fulgurites appears to have not changed substantially from the quartz sand during heating. This implies that there was little movement of the molten silica during the lightning strike. If the column of heated air had pushed the molten glass radially outward by the expansion of gas, the glass would have increased in density to arrive at a value closer to the density of silica glass (~2.6 g/cm3) as air was displaced from pore spaces. Instead, the similarity in density between sand and glass suggests the glass is as porous as the sand. The increase of about 0.1 g/cm3 may be attributed to the presence of unmelted grains of quartz captured on the exterior of the fulgurite. These grains, when frozen onto the surface of the fulgurite, will increase the density of the fulgurite, especially if the size of the sand grains is not significantly smaller than the size of the fulgurite wall. Given the sand grains range from 0.1 to 0.5 mm and the fulgurite glass walls are commonly about 1 mm thick, the embedding of quartz grains alone would give an increase in density from sand. Thus, we conclude that the fulgurites capture the original energy of the lightning without significant modification or post-lightning fluid movement.
Distribution residuals
We postulate that the energy vs. frequency reported in Fig. 3 may record up to four separate phenomena. The data residuals with respect to the calculated regression line demonstrate three points where discontinuities occur (Fig. 4). These deviations occur for all three lognormal plots. One of these occurs at the high-energy regime (6 MJ/m and larger, or 0.2 MJ total energy). This group constitutes about 3–4% of all fulgurites and we speculate that this discontinuity occurs when the lightning that forms the fulgurites becomes positive. Positive lightning strikes have a higher mean energy than negative lightning strikes and are known to comprise about 4% of all strikes annually17,18. The lower energy per unit length (<6 MJ/m) likely represents fulgurites formed by negative lightning strikes, by far the most common type of cloud-to-ground lightning event. The discontinuity in frequency that occurs from 1 to 6 MJ/m (0.08 to 0.2 MJ) may hence be due to a mixing of two different lightning types with differing distributions in lognormal space: a high energy variety that is tapering off as the energy decreases and a low energy variety that becomes more important at lower energies. Alternatively, these deviations are also demonstrated in the fulgurite distribution simulations and result from the stronger nature of thicker fulgurite fragments. If bigger fulgurites don’t fragment as easily as smaller fulgurites, then these changes to slope are expected. From 1 MJ/m to below 0.3 MJ/m (or 0.005 to 0.08 MJ total energy), the residuals are roughly constant, implying a match to the calculated regression slope in lognormal space. Finally, below 0.3 MJ/m (0.005 MJ total energy) are the lowest energy fulgurites. These probably deviate from the trend as fulgurites that are very thin are also more fragile, are smaller and are more difficult to recover, hence the accurate collection of fulgurites within this size range is difficult. Proof of any of these points would require characterization of specific lightning strikes followed by observation of the morphology of fulgurites formed.
Energy dissipated to form fulgurites
The average energy required to form these fulgurites in quartz sand is about 1.4 MJ/m, with a standard deviation of ×/ ÷ 3. In contrast, the energy per unit length of lightning traveling through air is between 103 and 104 J/m19. If the total energies along these lengths are considered, a 5 km lightning strike through air dissipates about 5 MJ and a corresponding 10 cm fulgurite dissipates only about 0.1 MJ. The energy estimates20 of Maggio et al. also suggest lightning strike energies of 108–109 J, implying 1% or less of the energy of lightning is captured in fulgurite formation. However, within the ground material in which a fulgurite forms, the energy per unit length is much higher than the energy per unit length in the atmosphere by about a factor of 100–1000. This is likely a result of the higher density of the target material (1700 kg/m3) compared to the atmosphere (~1 kg/m3), which also vary by a factor of 1000. Thus the energy dissipation by lightning is a function of the density of the material through which it travels.
Conclusions
We have reported here the first attempt to determine the lightning energy distribution from fulgurites and one of the first datasets of cloud-to-ground lightning energy delivery measured as a function of damage to the solid earth surface. The frequency distribution of the energy required to form a fulgurite follows a lognormal relationship, consistent with many lightning phenomena. Lognormal relationships are a natural consequence of the multiplication of normal probabilistic distributions and imply the energy transferred to the ground, like other lightning phenomena, is skewed towards high energy events with higher frequency than a typical normal distribution.
The current work presents a new approach to determining lightning parameters. Measurements of these lightning parameters are typically done either by analyzing lightning initiated by launching rockets21 or by analysis of strikes to towers and tall buildings22. These methods have provided most of the parameters of lightning as it relates to these discharges striking a conductive target. The work here provides a means of directly determining energy as a lightning parameter in cloud-to-ground strikes on an insulating material (fine quartz sand). With an average energy of 1.4 MJ/m in conductive materials and a peak of >20 MJ/m, this data may be of use in anticipating lightning damage from cloud-to-ground strikes. If fulgurites occurring in other materials, such as clays or rock, could be investigated in a fashion similar to the present study, better resolution on the energy of lightning may be possible as clay and rock fulgurites are usually better at preserving the thermal effects resulting from lightning6.
Methods
Locality
Fulgurites from two sand mines, Pit #1 and Pit #4 operated by C. C. Calhoun, Inc., in central peninsular Polk County, Florida (USA) were chosen for this analysis (Fig. 2). These mines are located along and near, the crest of the Lake Wales Ridge, in Polk County, Florida. Up to 20 meters of siliciclastic sediments, mapped by Campbell as the Cypresshead Formation23,24,25, are exposed in the pits. These sands consist of at least 98% SiO2 with the remainder clay and oxide minerals and have similar grain size distributions. Materials from the Cypresshead Formation were transported from Georgia into Florida by longshore currents26 and deposited in the Late Pliocene to Early Pleistocene27. Depositional environments have been interpreted as nearshore marine to brackish26,28,29.
Fulgurites found at these mines and others in the region are most abundant in clean, white, fine-to-medium-grained quartz sand (~30–35% porosity). We suspect the white sand unit to be aeolian (wind-deposited) in origin: at Pit #1 the unit consists of a single set of large-scale, high-angle, cross-beds measuring about 10 meters thick. The unit is somewhat thinner (about 7 m) at Pit #4; and bedding is massive, exhibiting little sedimentary depositional features. These characteristics suggest that sand was deposited as a dune and has been above sea level for a long time. A total of 266 fulgurites were collected from these mines, for a cumulative length of over 14 meters (Fig. 1). Note that fulgurites with incomplete cylinders are not considered in this study, as it is difficult to estimate the diameter and correct length of broken fulgurites. No branching fulgurites—fulgurites with bifurcations—were collected amongst these fulgurites; fulgurites forming in sand usually are unbranched6. Fulgurites, when found in situ, were oriented vertically and had no indication of radial outward development. Every fulgurite we observed within the field area (~0.02 km2) was collected and the internal void diameters (measured four times, twice at the top of each fulgurite and again at the bottom) and total fulgurite lengths were measured and recorded in centimeters. Since complete fulgurites are difficult to collect as these objects are prone to fracturing, for most of these fulgurites we do not have the full length. Additionally, the sand mines are still actively producing sand as a construction material hence heavy equipment crushes and distributes fulgurite fragments across the surface of the mine.
The process of mining inhibits the collection of complete fulgurites as the glasses are frequently cleaved during excavation. Fulgurites that are excavated during mining are separated from the sand and usually end up in waste spoil piles; fulgurites from these locations were not collected. The remainder of the fulgurites exposed to the surface erode out, frequently fracturing and becoming further distributed to the surface. Although it would be ideal to collect and excavate all of the complete fulgurites within a sand mine, this is not feasible financially. However, mining typically cuts through sand in ~1 m high layers (the height of the excavator). To this end, fulgurites that are cleaved and erode out represent a cross-section of the lightning that has struck over about a 1 m region in height within these dunes as the mining proceeds through the sand.
Sand and Fulgurite Composition
The sand mines here are characterized by being composed of almost exclusively quartz sand and similar mines in the region are over 99.2% SiO230. Quartz is the only mineral identified in X-ray diffractograms of powdered samples of the sand and Raman analysis of the sand also only shows quartz (see SI). Raman data from a subset of five of these fulgurites only detected SiO2 phases, principally quartz and lechatelierite glass (SI)4. Additionally, a single ICP-MS analysis of a fulgurite had ~99% SiO2 (SI). Consequently, the calculations done here assume the mineralogy of the sand consists exclusively of quartz.
These findings are consistent with prior work done on sand fulgurites. The fulgurites found here would be considered to be type I fulgurites according to the scheme of Pasek et al. (2012)6. Other studies of type I fulgurites have shown that these objects are typically composed of >98% SiO26,31,32.
Calculations
The energy required to vaporize quartz as SiO2 from room temperature is calculated using HSC Chemistry, a thermodynamic equilibrium modeling code that has been previously used to determine the Solar system chemistry of sulfur33, the composition of Europa’s subsurface ocean34 and fulgurite formation processes6. This model determines the energy at one bar of pressure required to promote the reactions:


where the vaporization of SiO2 is accompanied by the decomposition of this material to SiO2, SiO and O2 gases. The code determined the vaporization of SiO2 approximately 0.94 MJ per mole (~15.7 MJ/kg,). Correspondingly, the relationship between fulgurite internal diameter and energy per unit length (E) required to vaporize the material to make a fulgurite is equal to:

where ρS is the density of sand (here at ~1.65 g/cm3), ΔHvap is the energy required to vaporize SiO2 from room temperature (the above 0.94 MJ/mole), MW is the molecular weight of SiO2 (60.08 g/mole) and d is the internal diameter of the fulgurite in centimeters. We do not consider further energy transfer in the formation of the glass wall (e.g., the melting of the sand to form the fulgurite and heating of adjacent sand) that may store up to 20% of the energy of a lightning strike and the heating and ionization of the gas column within the fulgurite is not considered. These data cannot be readily determined from the fulgurites collected. These energy estimates are necessarily minima and the actual energy transfer may be more than 25% of our calculated values.
We also omit the enthalpy of vaporization of water from these calculations (40 kJ/mol). This omission is based on two factors: 1) given that the geologic setting of these sand dunes is consistent with being above sea level since their deposition35, it is reasonable to assume that the conducting subsurface aquifer is suitably distant from the surface of the sand dunes such that the fulgurites occurring within the sand were not saturated with water. Water saturation requires about 2.5 cm of rainfall to saturate 5 cm of sand and 5 cm being the median fulgurite fragment length found here. While a rainfall of 2.5 cm in a single storm event is not uncommon in Florida, most lightning precedes the heaviest rainfall36. 2) The sand has a porosity that allows about one mole of water per mole of sand and the exclusion of 40 kJ/mol (vs. 940 kJ/mol) from these calculations should not introduce significant error (about 0.02 log units in MJ/m). However, the surfaces of individual fulgurites range from smooth to wrinkled to covered in fractal-like branching patterns (Fig. 1). These differences are likely attributable to differences in the physical conditions at the time of formation, including water content. Additionally, differences in fulgurite glass thickness may be partially attributed to sand water content, as wetter sand should transfer heat more readily than dry sand. Thus, thicker-walled fulgurites may be more common in wet sand.
In addition to measuring the shape of fulgurite cylinders, we also determined the density of a subset (n = 12) of the glasses in fulgurites using Archimedes’ displacement of water technique to determine volume. The fulgurites chosen were completely open tubes, so that a measurement of the density of the glass could be performed without also measuring gas that might have been pinched in by the collapse of the tube. The density of the accompanying sand was also measured by both a mass per unit volume technique and by the Archimedes displacement principle. The latter was used specifically to estimate the bulk density of the quartz grains.
Model Distributions
Since we do not presume to have the complete length of most of the fulgurites within our collection as nearly all were discovered exposed on the sand surface, we performed a set of calculations to determine how the measured collection compares to a simulated distribution.
We modeled the distribution of fulgurite fragments as a function of energy per meter vs. cumulative length and vs. cumulative number and total energy vs. cumulative number to determine the resulting distributions (see SI). These models tested six scenarios: energy per length distributions that were normal or lognormal and length distributions that were constant across all energy per length distributions (in other words, one meter fulgurites were formed at the lowest energy per unit length and at the highest energy), or length distributions that were normal or lognormal. Each fulgurite was assigned a specific energy and a specific length.
To these distributions we applied a “fracture event” that broke each simulated fulgurite into smaller, equal parts. This fracture event assumed the following: since the weakest point of a fulgurite will be at the midpoint of its length, each fulgurite was assumed to fracture in half and the fragments may then fracture subsequently in half. A fulgurite will fracture as many times as possible until it reaches a specific length, which we establish empirically (SI). The diameter of the fulgurites is weakly correlated with length (R = 0.38), which establishes the maximum length allowed in the simulation. Thicker fulgurites should be expected to be somewhat stronger and hence produce longer lengths. From these fragments and energy per unit length distributions, we compare our simulated distributions with those from the actual suite of fulgurites.
Additional Information
How to cite this article: Pasek, M. A. and Hurst, M. A Fossilized Energy Distribution of Lightning. Sci. Rep. 6, 30586; doi: 10.1038/srep30586 (2016).
References
Uman, M. A. The art and science of lightning protection (Cambridge University Press, 2008).
Borucki, W. J. & Chameides, W. L. Lightning - Estimates of the rates of energy dissipation and nitrogen fixation. Rev. Geophys. Space Phys. 22, 363–372 (1984).
Pasek, M. A. & Block, K. Lightning-induced reduction of phosphorus oxidation state. Nature Geosci. 2, 553–556 (2009).
Carter, E. A., Hargreaves, M. D., Kee, T. P., Pasek, M. A. & Edwards, H. G. M. A Raman spectroscopic study of a fulgurite. Phil. Trans. Royal Soc. A 368, 3087–3097 (2010).
Carter, E. A. et al. Rapid Raman mapping of a fulgurite. Analyt. Bioanalyt. Chem. 397, 2647–2658 (2010).
Pasek, M. A., Block, K. & Pasek, V. D. Fulgurite morphology: a classification scheme and clues to formation. Contrib. Min. Pet. 164, 477–492 (2012).
Christian, H. J. et al. Global frequency and distribution of lightning as observed from space by the Optical Transient Detector. J. Geophys. Res. 108, 4005 (2003).
Lay, E. H., Jacobson, A. R., Holzworth, R. H., Rodger, C. J. & Dowden, R. L. Local time variation in land/ocean lightning flash density as measured by the World Wide Lightning Location Network. Journal of Geophysical Research, 112, D13111 (2007).
Boccippio, D. J., Cummins, K. L., Christian, H. J. & Goodman, S. J. Combined satellite- and surface-based estimation of the intracloud–cloud-to-ground lightning ratio over the continental United States. Month. Weath. Rev. 129, 108–122 (2001).
Jones, B. E. et al. Oxide reduction during triggered-lightning fulgurite formation. J. Atmo. Solar-Terrestr. Phys. 67, 423–428 (2005).
Essene, E. J. & Fisher, D. C. Lightning strike fusion: extreme reduction and metal-silicate liquid immiscibility. Science 234, 189–193 (1986).
Martin-Crespo, T., Fernandez, R. P. L. & Laguna, R. G. The fulgurite of Torre de Moncorvo (Portugal): description and analysis of the glass. Eur. J. Miner. 21, 783–794 (2009).
Berger, K., Anderson, R. B. & Kroninger, H. Parameters of lightning flashes. Electra 41, 23–37 (1975).
Pichler, H. & Diendorfer, G. Statistics of lightning current parameters measured at the Gaisberg tower. Int. Light. Detec. Conf. 18, 64 (2004).
Ballarotti, M. G., Medeiros, C., Saba, M. M. F., Schulz, W. & Pinto, O. Frequency distributions of some parameters of negative downward lightning flashes based on accurate-stroke-count studies. J. Geophys. Res. 117, D06112 (2012).
O’Dwyer, J. J. The theory of electrical conduction and breakdown in solid dielectrics (Claredon Press, 1973).
Reap, R. M. & MacGorman, D. R. Cloud-to-ground lightning: Climatological characteristics and relationships to model fields, radar observations and severe local storms. Month. Weath. Rev. 117, 518–535 (1989).
Rutledge, S. A., Lu, C. & MacGorman, D. R. Positive cloud-to-ground lightning in mesoscale convective systems. J. Atmos. Sci. 47, 2085–2100 (1990).
Borovsky, J. E. Lightning energetics: Estimates of energy dissipation in channels, channel radii and channel‐heating risetimes. J. Geophys. Res. Atmos. 103, 11537–11553 (1998).
Maggio, C. R., Marshall, T. C. & Stolzenburg, M. Estimations of charge transferred and energy released by lightning flashes. J. Geophys. Res. Atmos. 114, D14203 (2009).
Fieux, R., Gary, C. & Hubert, P. Artificially triggered lightning above land. Nature 257, 212–214 (1975).
Hussein, A. M. et al. Simultaneous measurement of lightning parameters for strokes to the Toronto Canadian National Tower. J. Geophys. Res. 100, 8853–8861 (1995).
Campbell, K. Geologic map of Polk County Florida. Florida Geological Survey, Open File Map Series No. 46 (1992).
Huddlestun, P. F. A revision of the lithostratigraphic units of the coastal plain of Georgia: The Miocene through Holocene. Georgia Geological Survey Bulletin 104 (1988).
Scott, T. M. The Cypresshead Formation in northern peninsular Florida in Southeastern Geological Society, Field Trip Guidebook No. 29 (ed. Pirkle, F. L. & Reynolds, J. G. ) (1988).
Kane, K. B. Origin of the Grandin (Plio-Pleistocene) sands, western Putnam County, Florida. M.S. Thesis. University of Florida, Gainesville, Florida (1984).
Scott, T. M. A geological overview of Florida. Florida Geological Survey, Open File Report No. 50 (1992).
Fountain, K. B. Origin and stratigraphic significance of kaolinitic sediments from the Cypresshead Formation: a sedimentological, mineralogical and geochemical investigation. Ph.D. dissertation. University of Florida, Gainesville, Florida (2009).
Fountain, K. B. Depositional and facies characteristics of the Cypresshead Formation in North-Central Florida In Southeastern Geological Society, Field Trip Guidebook No. 50 (ed. Hurst, M. V. ) (2010).
Anonymous. Retrieved from https://www.jahna.com/pdf_main/Haines_City_Concrete_Petro.pdf, June 2016.
Navarro-González, R. et al. Paleoecology reconstruction from trapped gases in a fulgurite from the late Pleistocene of the Libyan Desert. Geology 35, 171–174 (2007).
Sheffer, A. A. Chemical reduction of silicates by meteorite impacts and lightning strikes. Ph.D. Dissertation. University of Arizona, Tucson, Arizona (2007).
Pasek, M. A. et al. Sulfur chemistry with time-varying oxygen abundances during Solar System formation. Icarus 175, 1–14 (2005).
Pasek, M. A. & Greenberg, R. Acidification of Europa’s subsurface ocean as a consequence of oxidant delivery. Astrobiology 12, 151–159 (2012).
Adams, P. N., Opdyke, N. D. & Jaeger, J. M. Isostatic uplift driven by karstification and sea-level oscillation: Modeling landscape evolution in north Florida. Geology 38, 531–534 (2010).
Gungle, B. & Krider, E. P. Cloud-to-ground lightning and surface rainfall in warm-season Florida thunderstorms. J. Geophys. Res. 11, D19203 (2006).
Acknowledgements
This work was funded by a grant from NASA Exobiology and Evolutionary Biology (NNX14AN96G). The authors thank C.C. Calhoun, Inc. for allowing access to the two sand mines, Martin Uman and Brian Jackson for assistance with understanding lightning energy deposition and Virginia Pasek, Danny Lindsay and Jakob Centlivre for assistance in working with the fulgurites.
Author information
Authors and Affiliations
Contributions
M.A.P. and M.H. jointly collected fulgurites. M.A.P. performed the research and M.A.P. and M.H. wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Pasek, M., Hurst, M. A Fossilized Energy Distribution of Lightning. Sci Rep 6, 30586 (2016). https://doi.org/10.1038/srep30586
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30586
This article is cited by
-
Lightning-induced features on granitic gneiss and its implication for rare lightning scars from the geological record
Contributions to Mineralogy and Petrology (2022)
-
Finite Element Analysis of Electro-Thermal Coupling of Sandstone Under Lightning Currents
Geotechnical and Geological Engineering (2022)
-
The response of zircon to the extreme pressures and temperatures of a lightning strike
Scientific Reports (2021)
-
Lightning-induced high temperature and pressure microstructures in surface and subsurface fulgurites
Scientific Reports (2021)
-
Lightning-fast chemistry
Nature Chemistry (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.