Abstract
Layered compounds AMnBi2 (A = Ca, Sr, Ba, or rare earth element) have been established as Dirac materials. Dirac electrons generated by the two-dimensional (2D) Bi square net in these materials are normally massive due to the presence of a spin-orbital coupling (SOC) induced gap at Dirac nodes. Here we report that the Sb square net in an isostructural compound BaMnSb2 can host nearly massless Dirac fermions. We observed strong Shubnikov-de Haas (SdH) oscillations in this material. From the analyses of the SdH oscillations, we find key signatures of Dirac fermions, including light effective mass (~0.052m0; m0, mass of free electron), high quantum mobility (1280 cm2V−1S−1) and a π Berry phase accumulated along cyclotron orbit. Compared with AMnBi2, BaMnSb2 also exhibits much more significant quasi two-dimensional (2D) electronic structure, with the out-of-plane transport showing nonmetallic conduction below 120 K and the ratio of the out-of-plane and in-plane resistivity reaching ~670. Additionally, BaMnSb2 also exhibits a G-type antiferromagnetic order below 283 K. The combination of nearly massless Dirac fermions on quasi-2D planes with a magnetic order makes BaMnSb2 an intriguing platform for seeking novel exotic phenomena of massless Dirac electrons.
Similar content being viewed by others
Introduction
Three-dimensional topological semimetals, including Dirac semimetals (DSMs)1,2,3,4,5,6, Weyl semimetals (WSMs)7,8,9,10,11,12,13,14,15 and Dirac nodal-line semimetals16,17,18,19,20,21 represent new quantum states of matter and have stimulated intensive studies. These materials possess bulk relativistic quasiparticles with linear energy-momentum dispersion. DSMs feature linear band crossings at discrete Dirac nodes. In WSMs, the Weyl nodes with opposite chirality appear in pairs and each pair of Weyl nodes can be viewed as evolving from the splitting of Dirac node due to the lifted spin degeneracy arising from either broken spatial inversion symmetry or broken time reversal symmetry (TRS). The linear band dispersions in these materials are topologically protected by crystal symmetry and lead to many distinct physical properties such as large linear magnetoresistance and high bulk carrier mobility22. WSMs also show exotic surface “Fermi arc” connecting a pair of Weyl nodes of the opposite chirality7,8. These exotic properties of topological semimetals have potential applications in technology.
AMnBi2 (A = alkali earth/rare earth metal) is one of the established Dirac semimetals23,24,25,26,27,28,29,30,31,32,33. These materials share common structure characteristics, consisting of alternately stacked MnBi4 tetrahedral layers and A-Bi-A sandwich layers23,26,27,29,31,33. In an A-Bi-A sandwich layer, Bi atoms form a square net and harbor Dirac fermions, with coincident (e.g. SrMnBi234) or staggered (e.g. CaMnBi235) stacking of A atoms above and below the Bi plane. In the Mn centered edge sharing MnBi4 tetrahedral layers, antiferromagnetic (AFM) order usually develops near room temperature36,37 and such layers are expected to be less conducting23,27. Dirac fermions in AMnBi2 have been found to interplay with magnetism, leading to novel exotic properties. This has been demonstrated in YbMnBi215 and EuMnBi231. Evidence for Weyl state has been observed in YbMnBi2, which has been proposed to be caused by the TRS breaking due to the ferromagnetic (FM) component of a canted AFM state15. In EuMnBi2, half-integer bulk quantum Hall Effect (QHE) occurs due to the magnetic order induced two-dimensional (2D) confinement of Dirac fermions31.
One disadvantage of AMnBi2 as Dirac semimetals is that the strong spin orbit coupling (SOC) due to heavy Bi atoms opens gap at Dirac nodes23,38, leading to massive Dirac electrons. For instance, in SrMnBi2, the SOC-induced gap at the Dirac node is about 40 meV23 and the effective mass of Dirac fermions estimated from the analyses of Shubnikov-de Haas (SdH) oscillations is ~0.29m0 (m0, the mass of free electron)23, much heavier than the Dirac fermions in the 3D gapless DSM Cd3As2 where m* ~0.02–0.05m039,40,41,42. Therefore, one possible route to realize massless Dirac fermions in AMnBi2-type material is to replace Bi with other lighter main group elements such as Sb and Sn, whose SOC effect is much weaker. Under this motivation, we previously studied SrMnSb243 and found the 2D Sb layer can indeed harbor much lighter relativistic fermions with m* ~0.14m0. Moreover, this material shows FM properties: the Mn sublattice develops a FM order for 304 K < T < 565 K, but a canted AFM state with a FM component for T < 304 K. Coupling between ferromagnetism and quantum transport properties of relativistic fermions has also been observed43. These interesting results further motivated us to investigate the isostructural compound BaMnSb2, the material studied in this work.
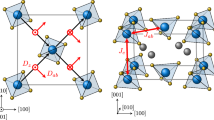
BaMnSb2 crystalizes in a tetragonal structure with the space group of I4/mmm34, similar to the structure of SrMnBi2 but different from the orthorhombic structure of SrMnSb243. The orthorhombic distortion in SrMnSb2 leads Sb atoms in the Sr-Sb-Sr sandwich layer to form zig-zag chains. However, in BaMnSb2, as Ba has larger ionic radius than Sr, the stronger interaction between Ba atoms and Sb atoms suppresses orthorhombic distortion38 and lead to a Sb square net lattice (Fig. 1a), which is an analogue of the Bi square net in SrMnBi2. In addition, the Ba layers are coincidently stacked along the Sb layer in BaMnSb2, which is also distinct from the staggeredly arranged Sr atoms in SrMnSb238. First principle calculations have predicted that BaMnSb2 exhibits Dirac fermion behavior and its SOC induced gap near the Dirac node is as small as ~20 meV, about half of the gap in SrMnBi238.
Crystal strucutre, magnetic and transport properties of BaMnSb2.
(a) Crystal and magnetic structure of BaMnSb2. (b) Susceptibility as a function of temperature measured with a 2T magnetic field applied along the c axis (χc) and along the ab plane (χab) under zero field cooling (ZFC) and field cooling (FC) histories. Red: χc of FC; dark red: χc of ZFC; purple: χab of FC; blue: χab of ZFC. Inset in (b), an optical image of a typical BaMnSb2 single crystal. (c) Isothermal magnetization along the c axis (red) and along the ab plane (blue). (d) Temperature dependence of the Bragg peak intensity at (101) indicates the magnetic order below 283 K. Inset in (d), the Bragg peak (101) scanned at the selected temperatures. (e) In-plane resistivity (ρin) and out-of-plane resistivity (ρout) as a function of temperature under zero magnetic field. (f) ρin and ρout plotted on logarithmic scale.
In this paper, we will show BaMnSb2 indeed is a Dirac material with the Dirac node being very close to the Fermi level. Through the analyses of SdH oscillations, we find this material hosts nearly massless Dirac fermions (m* ~0.052m0). As compared with AMnBi2 and SrMnSb2, BaMnSb2 possesses the smallest Fermi surface (FS) with the most significant 2D character. Additionally, BaMnSb2 also exhibits a G-type AFM order below 283 K. These findings suggest that BaMnSb2 is a promising candidate for seeking novel exotic phenomena of massless Dirac fermions.
Results and Discussions
The BaMnSb2 single crystals used in this study were synthesized using self-flux method (see Method). The composition measured by an energy dispersive X-ray spectrometer (EDS) can be expressed as Ba1-yMn1-zSb2, with y < 0.05 and 0.05 < z < 0.12. The nonstoichiometry of Sr and Mn was also found in SrMnSb2 where the actual composition measured by EDS can be described by Sr1-yMn1-zSb2 (y, z < 0.1)43. The neutron diffraction experiment on a piece of single crystal with the measured composition of Ba0.96Mn0.94Sb2 confirms the tetragonal structure with the space group I4/mmm reported by Cordier & Schafer34. The lattice parameters and atomic positions extracted from the structural confinement are summarized in Table 1. We note that the lattice constant c = 23.85 Å obtained from our structural refinement is smaller than the previously-reported value of 24.34 Å34, which may be attributed to the deficiencies of Ba and Mn in our sample.
From magnetic susceptibility measurements on BaMnSb2 single crystals, we have observed signatures of antiferromagnetism. As shown in Fig. 1b, at temperatures below 285 K, the susceptibility χ exhibits a striking decrease for the magnetic field applied along the c-axis (B//c), but a clear upturn for in-plane field (B//ab). As the temperature is lowered below 50 K, χ displays sharp upturns for both field orientations. Similar features have been observed in AMnBi2 (A = Ca, Sr and Ba)23,25,26,32,33,36. Neutron scattering studies on CaMnBi2 and SrMnBi2 have demonstrated that those magnetic anomalies probed in susceptibility originate from an AFM order formed on the Mn-sublattice36. Given the similar behavior in susceptibility between BaMnSb2 and AMnBi2, we can reasonably attribute the magnetic transition at 285 K seen in BaMnSb2 to an AFM transition. We note BaMnSb2 exhibits distinct magnetic anisotropy from AMnBi2. As seen in Fig. 1b, χ of B//c (χc) is much larger than χ of B//ab (χab) at temperatures both above and below TN. However, in AMnBi2, χab is almost equal to χc for T ≥ TN, but > χc for T < TN23,26,32. Additionally, the isothermal magnetization M(H) of BaMnSb2 (Fig. 1c) also looks different from that of AMnBi2. We have observed weak FM polarization behavior (Fig. 1c), in contrast with the nearly linear field dependence of M for BaMnBi232. These discrepancies imply that BaMnSb2 and AMnBi2 may not share an identical magnetic structure.
Magnetic structures of CaMnBi2, SrMnBi2 and YbMnBi2 have been determined from neutron scattering experiment36,37. Although these materials show similar Néel-type AFM coupling within the plane and the moments are oriented along the c-axis, their interlayer coupling is different. CaMnBi2 (space group P4/nmm) and YbMnBi2 (P4/nmm) features FM interlayer coupling, whereas SrMnBi2 (I4/mmm) is characterized by interlayer AFM coupling36,37. The magnetic structure of BaMnSb2 determined from our neutron scattering experiments is similar to that of SrMnBi2, i.e. both the interlayer and intralayer couplings between two nearest moments are AFM, which is also called the nearest neighbor G-type AFM order. The Néel temperature probed in the neutron scattering experiment is ~283 K, as shown in Fig. 1d which shows the Bragg peak at (101) (dominated by the magnetic scattering, see the inset) as well as the temperature dependence of the (101) Bragg peak intensity. The ordered moment of Mn at 4 K estimated from the magnetic structure refinement at 4 K is 3.950(85) μB/Mn, comparable to the ordered moments probed in CaMnBi2, SrMnBi2, YbMnBi2 and Sr1-yMn1-zSb236,37,43. As indicated above, the isothermal magnetization of BaMnSb2 exhibits weak FM polarization (Fig. 1c). This feature, together with the upturn of χab below TN, sharp upturns of χab and χc below 50 K and the small irreversibility of χab between field cooling (FC) and zero-field-cooling (ZFC) measurements, is reminiscent of a canted AFM state with a FM component. However, moment canting is generally not expected for a tetragonal structure for symmetry considerations. If the weak ferromagnetism turns out to be intrinsic for BaMnSb2, the possible origin may be associated with its actual nonstoichiometric composition Ba1-yMn1-zSb2 as mentioned above. In our previous studies on orthorhombic SrMnSb243, we have demonstrated a FM component arising from a canted AFM state; the saturated FM moment sensitively depends on Sr and Mn deficiencies, ranging from 0.6 μB/Mn to 0.005μB/Mn. With this in mind, we can speculate that Ba and Mn deficiencies possibly lead to local orthorhombic distortion, thus resulting in local canted AFM states. However, we have to point out that small FM components cannot be resolved in neutron scattering experiments. Hence it is not surprising to see the absence of FM response in our neutron scattering experiment.
We have also characterized the electronic transport properties of BaMnSb2 single crystals. In Fig. 1e we present both in-plane (ρin) and out-of-plane (ρout) resistivity as a function of temperature, from which we found several signatures distinct from that of (Ca/Sr/Ba)MnBi226,30,32,33. First, BaMnSb2 shows much stronger electronic anisotropy than (Ca/Sr/Ba)MnBi2, which is manifested in its larger ρout/ρin ratio. The ρout/ρin ratio at 2 K ranges from 15 to 100 for (Ca/Sr/Ba)MnBi226,30,32,33, but rises to 670 for BaMnSb2, which is comparable to the value of ρout/ρin (~609) seen in SrMnSb243. Such a large electronic anisotropy of BaMnSb2 suggests its electronic structure is quasi-2D like, which is further confirmed in our measurements of angular dependence of SdH oscillation frequency as shown below. Second, unlike (Ca/Sr/Ba)MnBi2 whose ρout(T) always exhibits a hump due to a crossover from high-temperature incoherent to low-temperature coherent conduction26,30,32,33, BaMnSb2 displays an opposite behavior in ρout(T) (Fig. 1e); a crossover from high-temperature metallic conduction to low-temperature localization is observed, which leads to a broad minimum in ρout(T) around 120 K. The temperature dependence of in-plane resistivity ρin(T) of BaMnSb2 also differs from that of (Ca/Sr/Ba)MnBi2. (Ca/Sr/Ba)MnBi2 features a quadratic temperature dependence for ρin in low temperature range23,26,32,33, while ρin of BaMnSb2 exhibits localization behavior below 80 K but crossovers to metallic behavior below 11 K. These differences imply the transport mechanism in BaMnSb2 is somewhat different from that in (Ca/Sr/Ba)MnBi2. We note that in the temperature region where the localization behavior occurs, both ρout(T) and ρin(T) follow a logarithmic temperature dependence, as denoted by the dashed lines in Fig. 1f which presents ρout(T) and ρin(T) on the logT scale. This observation is reminiscent of Kondo effect. Given that we have an AFM lattice formed from local moments of Mn ions, the presence of Kondo effect is possible in principle. But, this naturally leads to a question why such an effect occurs only to BaMnSb2, but not to (Ca/Sr/Ba)MnBi2 and SrMnSb2 with similar AFM lattices. Clear understanding of this issue requires further studies, but one possible interpretation is that the Kondo effect depends on the dimensionality of electronic structure and may be enhanced in BaMnSb2 due to its highly 2D electronic structure. Moreover, we would like to point out the localization behavior seen in BaMnSb2 cannot be attributed to disorder induced localization since in Sr1-yMn1-zSb2 with the level of disorders being comparable or higher than that of BaMnSb2, no localization behavior is observed43.
Like (Ca/Sr/Ba)MnBi2 and SrMnSb2, BaMnSb2 also exhibits quantum transport properties as revealed by our magnetotransport measurements, In Fig. 2a,d, we present the field dependences of in-plane (ρin) and out-of-plane (ρout) resistivity measured at various temperatures for BaMnSb2, respectively. Strong SdH oscillations, which sustain up to above 40 K, are observed in both ρin(B) and ρout(B). In Fig. 2b,e we present the oscillatory components of ρin and ρout, respectively. From Fast Fourier Transformation (FFT) analyses of Δρin and Δρout (see the insets to Fig. 2c,f), we find that the SdH oscillations of ρin consists of a single frequency (~22T), whereas the oscillations of ρout include two frequencies (i.e. Fα~25T and Fβ ~35T). Such a difference is likely caused by the non-stoichiometric composition. As mentioned above, the actual composition of our BaMnSb2 crystals involves Ba and Mn non-stoichiometry, which could lead to slight modification for electronic structure in different samples. To verify this speculation, we have measured many samples and find that their oscillation frequencies indeed show variation, ranging from 20T to 35T. Given that the quantum oscillation frequency is directly linked to the extremal Fermi surface cross-section area AF by the Onsager relation F = (Φ0/2π2)AF, a small oscillation frequency is generally expected for topological semimetals with the Dirac node being near the Fermi level. We note that the quantum oscillation frequency of 22T probed in our BaMnSb2 crystals is the smallest as compared with AMnBi2 and SrMnSb2, implying that if BaMnSb2 turns out to be a Dirac material, its Dirac band crossing points must be very close to the Fermi level.
Quantum transport properties of BaMnSb2.
(a) The in-plane resistivity, ρin, as a function of field up to 31T at different temperatures. (b) The oscillatory component of ρinvs. 1/B at different temperatures. (c) The temperature dependence of the normalized FFT amplitude. The dashed line curve is the fit to the Lifshitz-Kosevich (LK) formula from 2 to 40 K. Inset: FFT spectra of Δρin(B) at different temperatures (the FFT was done in the field range of 3T–31T). (d) The out-of-plane resistivity, ρout. as a function of field at different temperatures. (e) The oscillatory component of ρout vs. 1/B. (f) The temperature dependence of the normalized FFT amplitude. The dashed line is the fit to the LK formula. Inset: FFT spectra of Δρout(B) at different temperatures (the FFT was done in the field range of 5T–31T).
Evidence for Dirac fermions in BaMnSb2 has been obtained from the further analyses of the SdH oscillations. As shown in Fig. 2c,f, the effective cyclotron mass m* can be extracted from the fit of the temperature dependence of the normalized FFT peak amplitude to the thermal damping factor of Lifshitz-Kosevich (LK) equation44, i.e.  , where ρ0 is the zero field resistivity and α = (2π2kBm0)/(ħe). μ is the ratio of effective mass of cyclotron motion to the free electron mass.
, where ρ0 is the zero field resistivity and α = (2π2kBm0)/(ħe). μ is the ratio of effective mass of cyclotron motion to the free electron mass.  is the average inverse field for FFT analysis. We did the FFT within the field 3T–31T range for ρin and the 5T–31T range for ρout, with
is the average inverse field for FFT analysis. We did the FFT within the field 3T–31T range for ρin and the 5T–31T range for ρout, with  being 5.47T and 8.61T respectively. As seen in Fig. 2c,f, the best fits yield m* = 0.052m0 and 0.058m0, respectively, for the SdH oscillations of ρin and ρout. For ρout, the fit was performed for the component with the oscillation frequency of 35T, whose FFT peak can be clearly resolved. The effective mass of m* = 0.052m0 and 0.058m0 seen in BaMnSb2 is much smaller than that of other known AMnBi223,26,32,37 and SrMnSb243, but comparable to that of gapless Dirac semimetal Cd3As239,40,41,42. Detailed comparisons of m* as well as other parameters derived from SdH oscillations are shown in Table 2.
being 5.47T and 8.61T respectively. As seen in Fig. 2c,f, the best fits yield m* = 0.052m0 and 0.058m0, respectively, for the SdH oscillations of ρin and ρout. For ρout, the fit was performed for the component with the oscillation frequency of 35T, whose FFT peak can be clearly resolved. The effective mass of m* = 0.052m0 and 0.058m0 seen in BaMnSb2 is much smaller than that of other known AMnBi223,26,32,37 and SrMnSb243, but comparable to that of gapless Dirac semimetal Cd3As239,40,41,42. Detailed comparisons of m* as well as other parameters derived from SdH oscillations are shown in Table 2.
To further verify if the nearly massless electrons in BaMnSb2 is of topological nature of Dirac fermions, we extracted the Berry phase accumulated along cyclotron orbit from the analyses of SdH oscillations. Berry phase should be zero for a non-relativistic system with parabolic band dispersion, while a finite value up to π is expected for Dirac fermions45,46. We present the Landau level (LL) fan diagram constructed from the SdH oscillations of ρin for BaMnSb2 in Fig. 3a,b, where integer LL indices are assigned to the maxima of ρin. Our definition of LL index is based on the customary practice that integer LL indices are assigned to the minima of conductivity46,47. In-plane conductivity σxx can be converted from the longitudinal resistivity ρxx and the transverse (Hall) resistivity ρxy using σxx = ρxx/(ρxx2 + ρxy2). Since our measured ρxy (Fig. 3d) is about 1/3–1/4 of ρxx (Fig. 2a) for B < 9 T, σxx ≈1/ρxx, which justifies our definition of LL index. As seen in Fig. 3b, the intercept on the LL index axis obtained from the extrapolation of the linear fit in the fan diagram is 0.53, very close to the expected value of 0.5 for a 2D Dirac system with a π Berry phase. The oscillation frequency derived from the fit is 21.8T, nearly the same as the frequency obtained from the FFT analyses of the SdH oscillations of ρin (see the inset to Fig. 2c), suggesting that our linear fit in the fan diagram is reliable46. The Berry phase derived from the above fan diagram analyses clearly indicates that the nearly massless electrons probed in the SdH oscillations are Dirac fermions.
Berry phase, quantum mobility and Hall resistivity of BaMnSb2.
(a) The oscillatory component of in-plane resistivity, ρin, vs. 1/B at 2 K. As the longitudinal resistivity (ρin = ρxx) is much larger than transverse resistivity (ρxy), integer Landau level (LL) indices are assigned to the maximum of resistivity (see text). (b) LL fan diagram. The blue dashed line represents the linear fit. c, Dingle plot for the in-plane quantum oscillations Δρin at 2 K. (d) Hall resistivitivity as a function of field at various temperatures (T = 2, 5, 10, 20, 50, 100, 150, 200, 250 and 300 K).
Dirac Fermions are usually characterized by high quantum mobility, as seen in Cd3As222. This is also seen in BaMnSb2. The quantum mobility is directly related with the quantum relaxation time τq by μq = eτq/m*. τq characterizes quantum life time, the time scale over which a quasiparticle stays in a certain eigenstate. τq can be found from the field damping of quantum oscillation amplitude, i.e.,  . TD is the Dingle temperature and is linked with τq by TD = ħ/(2πkBτq). With m* being the known parameter, τq at T = 2 K can be extracted through the linear fit of ln ([B* sinh (αTμ/B)/αTμ]*Δρ/ρ0) against 1/B. As shown in Fig. 3c, we have obtained τq = 3.8 × 10−14 s, from which the quantum mobility μq(=eτq/m*) is estimated to be 1280 cm2V−1s−1, much higher than that of SrMnBi2 (250 cm2V−1s−1 23) or SrMnSb2 (~570 cm2V−1s−1 43) (see Table 2). In general, the transport mobility is one or two orders of magnitude higher than quantum mobility, since the transport mobility is sensitive only to large angle scattering of carriers, while the quantum mobility is sensitive to both small and large angle scatterings. However, this was not observed in BaMnSb2. Using the Hall coefficient RH data extracted from Hall resistivity data shown in Fig. 3d, the transport mobility μtr(=RH/ρxx) at 1.8 K is estimated to be ~1300 cm2V−1S−1 for BaMnSb2, much less than that of SrMnSb2 (μtr ~12500 cm2V−1S−1) at low temperature43. The low μtr in BaMnSb2 may be associated with the transport localization behavior seen in ρout and ρin.
. TD is the Dingle temperature and is linked with τq by TD = ħ/(2πkBτq). With m* being the known parameter, τq at T = 2 K can be extracted through the linear fit of ln ([B* sinh (αTμ/B)/αTμ]*Δρ/ρ0) against 1/B. As shown in Fig. 3c, we have obtained τq = 3.8 × 10−14 s, from which the quantum mobility μq(=eτq/m*) is estimated to be 1280 cm2V−1s−1, much higher than that of SrMnBi2 (250 cm2V−1s−1 23) or SrMnSb2 (~570 cm2V−1s−1 43) (see Table 2). In general, the transport mobility is one or two orders of magnitude higher than quantum mobility, since the transport mobility is sensitive only to large angle scattering of carriers, while the quantum mobility is sensitive to both small and large angle scatterings. However, this was not observed in BaMnSb2. Using the Hall coefficient RH data extracted from Hall resistivity data shown in Fig. 3d, the transport mobility μtr(=RH/ρxx) at 1.8 K is estimated to be ~1300 cm2V−1S−1 for BaMnSb2, much less than that of SrMnSb2 (μtr ~12500 cm2V−1S−1) at low temperature43. The low μtr in BaMnSb2 may be associated with the transport localization behavior seen in ρout and ρin.
The Dirac fermion behavior probed in our experiments for BaMnSb2 is in good agreement with the prediction by first principle calculations that BaMnSb2 is a Dirac material at ambient pressure38. Next, we will make more detailed comparisons between the predicted electronic band structure and our experimental observations. First, the Dirac bands are predicted to be generated by the Sb square net plane; thus the Fermi surface formed by Dirac bands is expected to be highly 2D, which is supported by our observations. As shown in Fig. 4a,d, systematic evolutions of SdH oscillation patterns for ρin and ρout are clearly observed as the magnetic field is rotated from the out-of-plane to the in-plane direction (see the insets to Fig. 4b,e for the experiment set-up). The oscillation frequency F(θ) extracted from the FFT for ρin measurements can be fitted to F(θ) = F(θ = 0°)/cosθ (Fig. 4c), suggesting that the Fermi surface responsible for SdH oscillations in BaMnSb2 is indeed 2D. However, in ρout(B,θ) measurements, we observed two frequency branches. As shown in Fig. 4f, the higher frequency branch also follows F(θ) = F(0°)/cosθ, while the lower frequency branch shows a weak angular dependence, suggesting the sample used for ρin measurements has slightly different morphology in its Fermi surface from the sample used for ρout measurements, which presumably originates from slightly different non-stoichiometric compositions. The 2D Fermi surface also explains the aforementioned large electronic anisotropy manifested in the large ρout/ρin ratio (~670). Second, the first principle calculations also predicted that the linear Dirac bands crossing occurs near the middle of ΓM, with the crossing point (i.e. the Dirac node) being right above the Fermi level, which implies the Fermi pocket hosting Dirac Fermions should be a hole pocket and small. In addition to the hole pocket enclosing the Dirac nodes, small electron pockets with quasi-linear band dispersion are also predicted to exist at X and Y points. The quantum transport properties of Dirac fermion revealed in our experiments provide strong support to these predictions. As shown in Fig. 3d, our measured Hall resistivity exhibits linear field dependence with positive slopes at all temperatures as well as remarkable SdH oscillations below 50 K. These features prove that holes are dominant carriers and responsible for the SdH oscillations. From the SdH oscillation frequency of 22T of ρin, the extremal cross-section area of the Fermi surface is estimated to be ~0.2 nm−2, about 0.1% of the total area of the first Brillouin zone, indicating an extremely small Fermi surface, the smallest as compared with AMnBi2 and SrMnSb2 (see Table 2). Third, the SOC-induced gap at the Dirac node in BaMnSb2 was predicted to be half of that in SrMnBi2 due to the weaker SOC of the Sb square net as mentioned above, which should result in lighter Dirac Fermions in BaMnSb2. Our observations of small cyclotron Frequency and effective mass of the Dirac fermions in BaMnSb2 are in line with these predicted results. Furthermore, the Dirac cone in BaMnSb2 was predicted to be anisotropic38, similar to that of SrMnBi2 and CaMnBi223,27,28. ARPES experiments are called in to verify it.
Angular dependences of SdH oscillations and the oscillation frequencies for BaMnSb2.
(a) The oscillatory component of in-plane resistivity, Δρin, vs. 1/B measured under different field orientations. The data has been shifted for clarity. (b) The FFT spectra of Δρin(B) at different field orientations. Inset: the diagram of the measurement setup; θ is defined as the angle between the magnetic field and the out-of-plane direction. (c) The angle dependence of SdH oscillation frequency determined from the FFT of Δρin(B). The dashed curve is the fit to F(θ) = F(0)/cosθ. (d) The oscillatory component of out-of-plane resistivity, Δρout. vs. 1/B measured under different field orientations. The data has been shifted for clarity. (e) The FFT spectra of Δρout(B) at different field orientations. Inset: the diagram of the measurement setup. (f) The angular dependence of SdH oscillation frequency determined from the FFT of Δρout(B). The dashed curves are the fits to F(θ) = F(0)/cosθ.
The signatures of Dirac fermions in BaMnSb2 imply that materials including 2D Sb square net planes can harbor Dirac electrons. We note many such candidate materials indeed exist, e.g. ReAgSb2 (Re = rare earth), for which small mass quasi-particles have been found48,49,50. Recent studies on LaAgSb2 have shown its small mass quasi-particles indeed originate from the Dirac-cone like band structure formed by Sb 5 Px,y orbitals51. Band structure calculations52 predicted that the Dirac cone in LaAgSb2 can host nearly massless Dirac fermions with m* ~0.06m0 and has a very small Fermi surface with a quantum oscillation frequency of ~20T. However, these predictions were not seen in experiments48,52; the smallest m* measured in experiments is 0.16m0 and the least quantum oscillation frequency is 72T48. Surprisingly, the Dirac electron behavior observed in BaMnSb2 is very close to that predicted for LaAgSb2. Note that the electronic structure of BaMnSb2 is much simpler than that of ReAgSb2. BaMnSb2 exhibits only a single frequency quantum oscillations (~22T) and its transport properties can almost be described by a single-band model, whereas LaAgSb2 possesses a much complicated band structure, showing four frequencies in quantum oscillations48,49.
Given that BaMnSb2 exhibits a G-type AFM order with possible FM components due to Ba and Mn non-stoichiometry as discussed above, a natural question is whether its FM component can be tuned by changing Ba and Mn non-stoichiometry and coupled to quantum transport properties. In our previous studies on Sr1-yMn1-zSb2, we have shown that its saturated FM moment Ms can be tuned from 0.6μB/Mn to 0.005μB/Mn by changing y and z43. The samples with heavier Sr deficiencies have larger Ms than the samples with heavier Mn deficiencies. The Ms (~0.04 μB/Mn at 7T, see Fig. 1c) probed in BaMnSb2 seems comparable to that of type B samples of our previously reported Sr1-yMn1-zSb2 where Ms ~0.04–0.06 μB/Mn. Although we have examined many samples, all measured samples show comparable Ms. Therefore, it is difficult to find samples with a wide range of Ms, which would allow us to examine the coupling between Dirac electron behavior and ferromagnetism as we did for Sr1-yMn1-zSb243.
Conclusion
In summary, we have demonstrated that in BaMnSb2 the Sb square net layers with coincident stacking of Ba atoms can host nearly massless Dirac fermions due to the weaker SOC effect of Sb, in contrast with massive Dirac fermions hosted by the Bi square net planes in AMnBi2. Compared with AMnBi2, BaMnSb2 displays much more significant 2D-like electronic band structure, with the out-of-plane transport showing non-coherent conduction below 120 K and the ρout/ρin ratio reaching ~670. Its quantum transport properties can be almost described by a single band model, consistent with its simple electronic band structure predicted by first principle calculations. In addition, BaMnSb2 also exhibits a G-type AFM order below 283 K and the Ba and Mn non-stoichiometries might cause a weak FM component. These findings establish BaMnSb2 as a promising platform for seeking novel exotic properties of massless Dirac fermions in low dimensions.
Methods
Single crystal growth and characterization
Single crystals of BaMnSb2 were synthesized using self-flux method with a stoichiometric ratio of Ba pieces, Mn and Sb powder. The starting materials were mixed in a small crucible, sealed into a quartz tube under Argon atmosphere and heated up to 1050 °C in one day. The temperature was maintained at 1050 °C for two days. After that, it was first cooled down to 1000 °C at a fast rate, 50 °C/h and then followed by a slowly cooling down to 450 °C at a rate 3 °C/h. Subsequently the furnace was turned off for fast cooling. Plate-like crystals with lateral dimensions of several millimeters (see the inset to Fig. 1b) can easily be obtained from the final product. The compositions of the crystals were measured using an energy dispersive X-ray spectrometer (EDS). The measured composition can be expressed as Ba1-yMn1-zSb2, with y < 0.05 and 0.05 < z < 0.12. The structure of the single crystals was characterized by an X-ray diffractometer.
Magnetization and magnetotransport measurements
The magnetization data were taken by a 7T SQUID magnetometer (Quantum Design). The magnetotransport properties were measured using standard four and five- probe method for longitudinal and Hall resistivity, respectively, in a Physics Property Measurement System (PPMS, Quantum Design) and the 31T resistive magnet at National High Magnetic Field Laboratory (NHMFL) in Tallahassee.
Neutron Scattering
Single-crystal neutron diffraction was performed at the HB-3A Four-circle Diffractometer equipped with a 2D detector at the High Flux Isotope Reactor(HFIR) at ORNL. Neutron wavelength of 1.546 Å was used from a bent perfect Si-220 monochromator53. The Rietveld refinement was performed using FullProf54.
Additional Information
How to cite this article: Liu, J. et al. Nearly massless Dirac fermions hosted by Sb square net in BaMnSb2. Sci. Rep. 6, 30525; doi: 10.1038/srep30525 (2016).
References
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A=Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Wang, Z., Weng, H., Wu, Q., Dai, X. & Fang, Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2 . Phys. Rev. B 88, 125427 (2013).
Liu, Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2 . Nat. Mater. 13, 677–681 (2014).
Liu, Z. K. et al. Discovery of a Three-Dimensional Topological Dirac Semimetal, Na3Bi. Science 343, 864–867 (2014).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nat. Commun. 5, 4786 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 5, 011029 (2015).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Xu, S. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613 (2015).
Lv, B. Q. et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 3426 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Xu, S. et al. Discovery of a sWeyl fermion state with Fermi arcs in niobium arsenide. Nat. Phys. 11, 748 (2015).
Xu, N. et al. Observation of Weyl nodes and Fermi arcs in TaP. Nat. Commun. 7, 11006 (2016).
Borisenko, S. et al. Time-reversal symmetry breaking Weyl state in YbMnBi2. arXiv:1507.04847v2 (2015).
Xu, Q. et al. Two-dimensional oxide topological insulator with iron-pnictide superconductor LiFeAs structure. Phys. Rev. B 92, 205310 (2015).
Schoop, L. M. et al. Dirac Cone Protected by Non-Symmorphic Symmetry and 3D Dirac Line Node in ZrSiS. Nat. Commun. 7, 11696, doi: 10.1038/ncomms11696 (2016).
Neupane, M. et al. Observation of Topological Nodal Fermion Semimetal Phase in ZrSiS. Phys. Rev. B 93, 201104(R) (2016).
Wu, Y. et al. Dirac Node Arcs in PtSn4 . Nat Phys, doi: 10.1038/nphys3712 (2016).
Bian, G. et al. Topological nodal-line fermions in spin-orbit metal PbTaSe2 . Nat. Commun. 7, 10556 (2016).
Hu, J. et al. Evidence of Topological Nodal-Line Fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 117, 016602 (2016).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in Cd3As2: protection from backscattering in a Dirac semimetal. Nat. Mater. 14, 280–284 (2015).
Park, J. et al. Anisotropic dirac fermions in a Bi square net of SrMnBi2 . Phys. Rev. Lett. 107, 126402 (2011).
Wang, K., Graf, D., Lei, H., Tozer, S. W. & Petrovic, C. Quantum transport of two-dimensional Dirac fermions in SrMnBi2 . Phys. Rev. B 84, 220401(R) (2011).
He, J. B., Wang, D. M. & Chen, G. F. Giant magnetoresistance in layered manganese pnictide CaMnBi2 . Appl. Phys. Lett. 100, 112405 (2012).
Wang, K., Graf, D. & Petrovic, C. Two-dimensional Dirac fermions and quantum magnetoresistance in CaMnBi2 . Phys. Rev. B 85, 041101(R) (2012).
Lee, G., Farhan, M. A., Kim, J. S. & Shim, J. H. Anisotropic Dirac electronic structures of AMnBi2 (A=Sr, Ca). Phys. Rev. B 87, 245104 (2013).
Feng, Y. et al. Strong anisotropy of Dirac cones in SrMnBi2 and CaMnBi2 revealed by angle-resolved photoemission spectroscopy. Sci. Rep. 4, 5385 (2014).
May, A. F., Mcguire, M. A. & Sales, B. C. Effect of Eu magnetism on the electronic properties of the candidate Dirac material EuMnBi2 . Phys. Rev. B 90, 075109 (2014).
Jo, Y. J. et al. Valley-Polarized Interlayer Conduction of Anisotropic Dirac Fermions in SrMnBi2 . Phys. Rev. Lett. 113, 156602 (2014).
Masuda, H. et al. Quantum Hall effect in a bulk antiferromagnet EuMnBi2 with magnetically confined two-dimensional Dirac fermions. Sci. Adv. 2(1), e1501117 (2016).
Li, L. et al. Electron-hole asymmetry, Dirac fermions and quantum magnetoresistance in BaMnBi2 . Phys. Rev. B 93, 115141 (2016).
Wang, Y.-Y., Yu, Q.-H. & Xia, T.-L. Large linear magnetoresistance in a new Dirac material BaMnBi2. arXiv:1603.09117 (2016).
Cordier, G. & Schafer, H. Preparation and crystal structure of BaMnSb2, SrMnBi2 and BaMnBi2 . Z. Naturforsch. 32b, 383–386 (1977).
Brechtel, E., Cordier, G. & Schäfer, H. Zur Darstellung und Struktur von CaMnBi2 . Z. Naturforsch. 35b, 1–3 (1980).
Guo, Y. F. et al. Coupling of magnetic order to planar Bi electrons in the anisotropic Dirac metals AMnBi2 (A=Sr, Ca). Phys. Rev. B 90, 075120 (2014).
Wang, A. et al. Two-dimensional Dirac fermions in YbMnBi2 antiferromagnet. arXiv:1604.01009 (2016).
Farhan, M. A., Lee, G. & Shim, J. H. AEMnSb2 (AE=Sr, Ba): a new class of Dirac materials. J. Phys. Condens. Matter 26, 042201 (2014).
He, L. P. et al. Quantum Transport Evidence for the Three-Dimensional Dirac Semimetal. Phys. Rev. Lett. 113, 246402 (2014).
Cao, J. et al. Landau level splitting in Cd3As2 under high magnetic fields. Nat. Commun. 6, 7779 (2015).
Narayanan, A. et al. Linear Magnetoresistance Caused by Mobility Fluctuations in n -Doped Cd3As2 . Phys. Rev. Lett. 114, 117201 (2015).
Xiang, Z. J. et al. Angular-Dependent Phase Factor of Shubnikov-de Haas Oscillations in the Dirac Semimetal Cd3As2 . Phys. Rev. Lett. 115, 226401 (2015).
Liu, J. Y. et al. Discovery of a magnetic topological semimetal Sr1-yMn1-zSb2 (y, z < 0.10). arXiv:1507.07978v2 (2015).
Lifshits, E. M. & Kosevich, A. M. Theory of the Shubnikov—de Haas effect. J. Phys. Chem. Solids 4, 1–10 (1958).
Mikitik, G. P. & Sharlai, Y. V. Manifestation of Berry’s Phase in Metal Physics. Phys. Rev. Lett. 82, 2147–2150 (1999).
Taskin, A. A. & Ando, Y. Berry phase of nonideal Dirac fermions in topological insulators. Phys. Rev. B 84, 035301 (2011).
Xiong, J. et al. High-field Shubnikov-de Haas oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 86, 045314 (2012).
Myers, K. et al. de Haas–van Alphen and Shubnikov–de Haas oscillations in RAgSb2 (R=Y, La-Nd, Sm). Phys. Rev. B 60, 13371 (1999).
Bud’ko, S. L. et al. Thermal expansion and magnetostriction of pure and doped RAgSb2 (R=Y, Sm, La) single crystals. J. Phys. Condens. Matter 20, 115210 (2008).
Arakane, T. et al. Electronic structure of LaAgSb2 and CeAgSb2 studied by high-resolution angle-resolved photoemission spectroscopy. J. Magn. Magn. Mater. 310, 396–398 (2007).
Shi, X. et al. Observation of Dirac-like band dispersion in LaAgSb2 . Phys. Rev. B 93, 081105 (2016).
Wang, K. & Petrovic, C. Multiband effects and possible Dirac states in LaAgSb2 . Phys. Rev. B 86, 155213 (2012).
Chakoumakos, B. C. et al. Four-circle single-crystal neutron diffractometer at the High Flux Isotope Reactor. Journal of Applied Crystallography, 44, 655–658 (2011).
Rodríguez-Carvajal, Juan Recent advances in magnetic structure determination by neutron powder diffraction. Physica B 192, 55–69 (1993).
Acknowledgements
The work at Tulane is supported by the U.S. Department of Energy under EPSCoR Grant No. DE-SC0012432 with additional support from the Louisiana Board of Regents (support for a graduate student, materials, travel to NHMFL). The work at NHMFL is supported by National Science Foundation Cooperative Agreement No. DMR-1157490 and the State of Florida (high field measurements). The work at ORNL HFIR was sponsored by the Scientific User Facilities Division, Office of Science, Basic Energy Sciences, U.S. Department of Energy.
Author information
Authors and Affiliations
Contributions
The single crystals used in this study were synthesized and characterized by J.L., Y.Z. and A.C. The magnetotransport measurements in PPMS were carried out by J.L., D.J.A., S.M.A.R., L.S. and Z.M. The high field measurements at NHMFL were conducted by J.L., D.G., J.H., S.M.A.R., I.C. and Z.M. J.L. and Z.M. analyzed the data and wrote the manuscript. H.C. performed neutron scattering experiments and data analyses. All authors read and commented on the manuscript. The project was supervised by Z.M.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Liu, J., Hu, J., Cao, H. et al. Nearly massless Dirac fermions hosted by Sb square net in BaMnSb2. Sci Rep 6, 30525 (2016). https://doi.org/10.1038/srep30525
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep30525
This article is cited by
-
High-entropy engineering of the crystal and electronic structures in a Dirac material
Nature Communications (2024)
-
Magnetic Properties of Topological Material Candidate EuZnBi2
Journal of Superconductivity and Novel Magnetism (2024)
-
Strong room-temperature bulk nonlinear Hall effect in a spin-valley locked Dirac material
Nature Communications (2023)
-
Exploration of two surfaces observed in Weyl semimetal BaMnSb2
npj Quantum Materials (2022)
-
Physical Properties of Antiferromagnetic Dirac Semimetal SrMnSb\(_{2}\)
Journal of Superconductivity and Novel Magnetism (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.