Abstract
There has been a puzzle between experiments and theoretical predictions on the charge ordering of layered titanium-oxypnictides superconductors. Unconventional mechanisms to explain this discrepancy have been argued so far, even affecting the understanding of superconductivity on the compound. We provide a new theoretical prediction, by which the discrepancy itself is resolved without any complicated unconventional explanation. Phonon dispersions and changes of nesting vectors in Fermi surfaces are clarified to lead to the variety of superlattice structures even for the common crystal structures when without CDW, including orthorhombic 2 × 2 × 1 one for BaTi2As2O, which has not yet been explained successfully so far, being different from tetragonal  for BaTi2Sb2O and BaTi2Bi2O. The electronic structure analysis can naturally explain experimental observations about CDW including most latest ones without any cramped unconventional mechanisms.
for BaTi2Sb2O and BaTi2Bi2O. The electronic structure analysis can naturally explain experimental observations about CDW including most latest ones without any cramped unconventional mechanisms.
Similar content being viewed by others
Introduction
Layered titanium oxypnictides, ATi2Pn2O [A = Na2, Ba, (SrF)2, (SmO)2; Pn = As, Sb, Bi]1,2,3,4,5,6,7, have the common undistorted structure, as shown in Fig. 1, including Ti2O-plane that leads to quasi two-dimensional (2D) electronic structures. Yajima et al.5 synthesized BaTi2Sb2O and reported its superconductivity with the transition temperature, Tc = 1.2 K. Doan et al.6 also synthesized Ba(1−x)NaxTi2Sb2O individually and reported its superconductivity with Tc = 5.5 K. Followed by their pioneering works, similar kinds of compounds, BaTi2Bi2O, BaTi2(Sb1−xBix)2O, BaTi2(Sb1−xSnx)2O, Ba1−xKxTi2Sb2O and Ba1−xRbxTi2Sb2O, have been synthesized to get superconductivities, achieving the current highest Tc around 6.1 K7,8,9,10,11,12. Based on Allen-Dynes formalism13,14 within DFT, Subedi suggested a conventional BCS-type superconductivity mechanism holds in BaTi2Sb2O15. This theoretical finding was supported afterward by experiments of specific heats, NMR and μSR16,17,18, confirming full-gap BCS mechanism with s-wave paring for this compound. Although their Tc values themselves are relatively low compared with possibly conventional BCS-type mechanism, the superconductivity of BaTi2Sb2O and its relatives attracts special interests in the sense that their nominal electronic configurations, Ti3 + (d1), are conjugate with those for cuprates superconductors19 with respect to the electron-hole symmetry. Quasi 2-dimensional (2D) transports in these systems also attract the common interest among those for cuprates19 as well as for iron arsenides superconductors20, leading to the arguments on the similarity of superconducting mechanisms5,6.
The possibilities of the density waves (DW) in these systems are one of the key concepts, which is common to low-dimensional transports possible for cuprates and iron arsenides. Anomalies in the temperature dependence of resistivity ρ(T) and magnetic susceptibility χ(T) at low temperature are sometimes observed in these systems, getting into an argument over if the anomalies can be attributed to the emergence of charge density waves (CDW) or spin density waves (SDW)1,2,4,5,6. Several DFT studies applied to BaTi2As2O and BaTi2Sb2O21,22,23 have reported the possibility of SDW, while it has not yet been observed experimentally, such as by NMR/NQR for Sb121/123 and μSR for BaTi2As2O and BaTi2Sb2O16,17,18. Focusing on CDW, the nesting of Fermi surface matters, which is enhanced by 2D nature of Ti2O planes. While conventional models take a simple picture of 2D transport with Ti-3dxy orbital only5, Singh21 clarified a more complicated 3D shape of Fermi surface in BaTi2Sb2O by taking into account several Ti-3d orbitals contributions. A similar shape was also predicted in BaTi2Bi2O, theoretically24. Indeed, such shapes have been recently observed by state-of-the-art Angle-Resolved Photo Emission Spectroscopy (ARPES) applied to BaTi2As2O and BaTi2Sb2O single crystals25,26. Subedi15 worked on BaTi2Sb2O using DFT and reported the possible lattice instability toward CDW with  superstructure at low temperature. Experimentally, however, no such superlattice peaks were found by neutron and electron diffractions for this compound17,27, reviving the argument over if the anomalies in ρ(T) and χ(T) can be really attributed to the phonon-driven CDW or not. Though Frandsen et al.27 observed tiny lattice displacements from tetragonal to orthorhombic in both BaTi2As2O and BaTi2Sb2O, theoretically predicted
superstructure at low temperature. Experimentally, however, no such superlattice peaks were found by neutron and electron diffractions for this compound17,27, reviving the argument over if the anomalies in ρ(T) and χ(T) can be really attributed to the phonon-driven CDW or not. Though Frandsen et al.27 observed tiny lattice displacements from tetragonal to orthorhombic in both BaTi2As2O and BaTi2Sb2O, theoretically predicted  superlattice peaks15 could not be found experimentally. To account for this, they proposed a bit complicated picture that the intra-unit-cell nematic charge order, such as that observed in cuprates28,29, might be the origin of the anomalies in ρ(T) and χ(T).
superlattice peaks15 could not be found experimentally. To account for this, they proposed a bit complicated picture that the intra-unit-cell nematic charge order, such as that observed in cuprates28,29, might be the origin of the anomalies in ρ(T) and χ(T).
Another important topic on this system is the ‘two-dome’ structure in the dependence of Tc(x) on the concentration of ionic substitutions, Pn = SbxBi(1−x) in BaTi2Pn2O8. Similar ‘two-dome’ structures are known also for cuprates30,31,32,33,34 and iron arsenides35,36 superconductors. The ‘two-dome’ structure can be regarded as a modification with a singularity put on the original single peak dependence. The singularity might be attributed to electron or spin orderings such as DW transition. Actually, a series of NMR experiments on LaFeAsO1−xHx37 identified the peak as being corresponding to the emergence of the new SDW phase related to the second Tc dome. This suggests that another origin of the second dome be different from that of the first dome. The ‘two-dome’ for BaTi2Pn2O, on the other hand, has not well been investigated so far.
As mentioned above, the layered titanium oxypnictides superconductors show a lot of similar phenomena to cuprates and iron-asenides superconductors. The investigation of DW transition in these oxypnictides could then be one of the most important clues to understanding of the physics of high-Tc superconducting mechanism. In the present study, we investigated the possibility of DW transition in BaTi2Pn2O (Pn = As, Sb, Bi) using DFT-based phonon analysis. Because of the common lattice structure when without DW, we could perform systematic and careful comparisons among the three compounds, putting the same computational conditions to suppress artifacts as less as possible. As a result, we found a new possibility of orthorhombic 2 × 2 × 1 superlattice structure for BaTi2As2O, which is different from the previous prediction by Subedi15 for BaTi2Sb2O, tetragonal  . Our theoretical finding can provide a more natural explanation for the structural transition and the weak superlattice peaks observed by Frandsen et al.27 in terms of the conventional phonon-driven CDW, not by such a complicated mechanism as intra-unit-cell nematic charge ordering, as given in their papers28,29. The finding might also account for the anomalies of ρ(T) and χ(T) being attributed to the lattice instability. While BaTi2Bi2O does not show anomalies in ρ(T) and χ(T), we found lattice instability possibly inducing a tetragonal
. Our theoretical finding can provide a more natural explanation for the structural transition and the weak superlattice peaks observed by Frandsen et al.27 in terms of the conventional phonon-driven CDW, not by such a complicated mechanism as intra-unit-cell nematic charge ordering, as given in their papers28,29. The finding might also account for the anomalies of ρ(T) and χ(T) being attributed to the lattice instability. While BaTi2Bi2O does not show anomalies in ρ(T) and χ(T), we found lattice instability possibly inducing a tetragonal  superlattice structure. Such a discrepancy is observed in a LaO0.5F0.5BiS2 superconductor as well38. To account for this, Yildirim39 argued the possibility of an unconventional superconducting mechanism in which the inherent lattice instability plays an important role in the Cooper paring. The similarity of the discrepancy for the present case might imply the similar unconventional mechanism for BaTi2Bi2O.
superlattice structure. Such a discrepancy is observed in a LaO0.5F0.5BiS2 superconductor as well38. To account for this, Yildirim39 argued the possibility of an unconventional superconducting mechanism in which the inherent lattice instability plays an important role in the Cooper paring. The similarity of the discrepancy for the present case might imply the similar unconventional mechanism for BaTi2Bi2O.
Results
Lattice instabilities from undistorted structures
Electronic band structures and densities of states (DOS) for undistorted structures are shown in Fig. 2. Figure 3 highlights the corresponding Fermi surfaces with possible nesting vectors. Overall features agree well with previous DFT results by Yu et al.23, Singh21 and Suetin et al.24 for each compound, justifying no specific artifacts due to any choices of computational conditions. Note that our optimized geometry parameters are also in good agreements with the previous calculations (See Supplementary Note 1).
Phonon dispersions for undistorted structures are shown in Fig. 4. Despite the common crystal structure, we see that the phonon instabilities appear around different points, M and A for Pn = Sb, Bi, while X and R for Pn = As [hereafter, all the  and
and  points are labeled according to Brillouin-zone database on the Bilbao Crystallographic Server40]. The former instabilities (for Pn = Sb, Bi) are consistent with the previous calculations by Subedi15 on Pn = Sb. The latter instability (for Pn = As), on the other hand, has been never reported before, so we carefully examined to confirm that the result does not depend on the choice of pseudo potentials. For Pn = Sb and Bi, the instability occurs around M and A, corresponding to (qx, qy) = (1/2, 1/2) [hereafter a unit of
points are labeled according to Brillouin-zone database on the Bilbao Crystallographic Server40]. The former instabilities (for Pn = Sb, Bi) are consistent with the previous calculations by Subedi15 on Pn = Sb. The latter instability (for Pn = As), on the other hand, has been never reported before, so we carefully examined to confirm that the result does not depend on the choice of pseudo potentials. For Pn = Sb and Bi, the instability occurs around M and A, corresponding to (qx, qy) = (1/2, 1/2) [hereafter a unit of  is 2π/a.]. For qz direction, there is no specific dependence, as shown in the dispersion along M to A in the right panel of Fig. 4(b,c). From phonon pDOS (partical DOS), we can identify which vibration modes lead to the instability toward the superlattice. It is found from phonon pDOS that the negative (imaginary) frequencies mainly come from Ti ‘in-plane’ (within xy plane) vibrations (See Supplementary Note 2). We therefore concentrate on the representative case with M, (qx, qy, qz) = (1/2, 1/2, 0), corresponding to
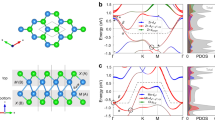
is 2π/a.]. For qz direction, there is no specific dependence, as shown in the dispersion along M to A in the right panel of Fig. 4(b,c). From phonon pDOS (partical DOS), we can identify which vibration modes lead to the instability toward the superlattice. It is found from phonon pDOS that the negative (imaginary) frequencies mainly come from Ti ‘in-plane’ (within xy plane) vibrations (See Supplementary Note 2). We therefore concentrate on the representative case with M, (qx, qy, qz) = (1/2, 1/2, 0), corresponding to  superlattice structure. By analyzing the dynamical matrices, we can further identify the superlattice structure shown in Fig. 5. Note that this is the same structure as that predicted previously by Subedi15 for Pn = Sb.
superlattice structure. By analyzing the dynamical matrices, we can further identify the superlattice structure shown in Fig. 5. Note that this is the same structure as that predicted previously by Subedi15 for Pn = Sb.
Atomic displacements corresponding to the negative (imaginary) phonon mode at M (1/2, 1/2, 0) point, leading to  superlattice for BaTi2Pn2O (Pn = Sb and Bi).
superlattice for BaTi2Pn2O (Pn = Sb and Bi).
Dashed lines in the left panel stand for the unit cell of the superlattice, drawn in the right panel again with displaced atomic positions after the rotation by 45 degree. The symmetry of the superlattice is P4/mbm (No. 127).
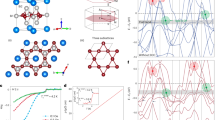
The same scheme is applied to Pn = As with the instability around X and R, corresponding to (qx, qy) = (0, 1/2): For qz direction, there is no specific dependence, as shown in the dispersion along X to R in the right panel of Fig. 4(a). From phonon pDOS, we can identify that the vibrations for the instability come from Ti and As ‘in-plane’ vibrations (See Supplementary Note 2). We therefore take a representative mode at X, (qx, qy, qz) = (0, 1/2, 0). By analyzing the dynamical matrices, we get the superlattice structure shown in Fig. 6, 1 × 2 × 1 superlattice.
Atomic displacements corresponding to the negative (imaginary) phonon mode at X (0, 1/2, 0) point, leading to 1 × 2 × 1 superlattice for BaTi2As2O.
Dashed lines in the left panel stand for the unit cell of the superlattice, drawn in the right panel again with displaced atomic positions. The symmetry of the superlattice is Pbmm (No. 51).
Superlattice structures and Tc
The negative modes appearing in Fig. 4 are expected to disappear when we further relax the lattices along the negative modes to get superlattices. Resultant phonon dispersions are shown in Fig. 7. For  superlattices of Sb and Bi, the negative modes have disappeared assuring the superlattice as the final stable structures [the negative mode seen around Γ for Bi is due to the well-known artifact coming from the discreteness of Fast Fourier Transform (FFT) grid]. For As, on the other hand, the negative modes at X and U point still remain. Taking the representative X point, this implies the further superlattice transition toward 2 × 2 × 1. The phonon pDOS analysis shows that the superlattice deformation still comes from ‘in-plane’ vibrations of Ti and As, actually leading to the superlattice structure as shown in Fig. 8. The geometry optimization along this deformation gives lattice parameters, a = 8.122 Å, b = 8.108 Å and c = 7.401 Å (See Supplementary Note 4). The orthorhombicity parameter is η = 2 × (a − b)/(a + b) = 0.171%. To finalize the verification, we ought to examine if the negative modes surely disappear in the 2 × 2 × 1 superlattice. It was, however, intractable because four times enlarged unit cell requires 43 times more computational cost and lower symmetry makes more demands for k- and q-mesh samplings over larger reciprocal space.
superlattices of Sb and Bi, the negative modes have disappeared assuring the superlattice as the final stable structures [the negative mode seen around Γ for Bi is due to the well-known artifact coming from the discreteness of Fast Fourier Transform (FFT) grid]. For As, on the other hand, the negative modes at X and U point still remain. Taking the representative X point, this implies the further superlattice transition toward 2 × 2 × 1. The phonon pDOS analysis shows that the superlattice deformation still comes from ‘in-plane’ vibrations of Ti and As, actually leading to the superlattice structure as shown in Fig. 8. The geometry optimization along this deformation gives lattice parameters, a = 8.122 Å, b = 8.108 Å and c = 7.401 Å (See Supplementary Note 4). The orthorhombicity parameter is η = 2 × (a − b)/(a + b) = 0.171%. To finalize the verification, we ought to examine if the negative modes surely disappear in the 2 × 2 × 1 superlattice. It was, however, intractable because four times enlarged unit cell requires 43 times more computational cost and lower symmetry makes more demands for k- and q-mesh samplings over larger reciprocal space.
Atomic displacements for 1 × 2 × 1 BaTi2As2O corresponding to the negative (imaginary) phonon mode at X (1/2, 0, 0) point, leading to orthorhombic 2 × 2 × 1 superlattice.
Dashed lines in the left panel stand for the unit cell of the superlattice, drawn in the right panel again with displaced atomic positions. The symmetry of the 2 × 2 × 1 superlattice is Pbam (No. 55).
Superconducting transition temperatures, Tc, are estimated using Allen-Dynes formula14, as shown in Table VI in Supplementary Information. The parameters used in the formula are also tabulated. Even with imaginary frequencies, Tc can be estimated just by ignoring the contributions15, being the case for 1 × 1 × 1. For  where all the negative modes disappear, the estimation gets to be more plausible. There seems, however, little change in the estimation from that in 1 × 1 × 1. The present estimations, Tc = 2.30 (2.45) K for Pn = Sb (Bi), are consistent with experiments reporting Tc = 1.2 (4.6) K for Pn = Sb (Bi)5,7, as well as that by previous DFT study, Tc = 2.7 K for Pn = Sb15. For 1 × 2 × 1 (Pn = As), the estimation was made still under the existence of negative modes and the more plausible estimation for 2 × 2 × 1 was intractable as mentioned above. The estimations, Tc = 6.93 K (1 × 1 × 1) and 8.31 K (1 × 2 × 1) seem incompatible with experiments of BaTi2As2O exhibiting no superconductivity so far4,8. We might expect much lower Tc obtained for the 2 × 2 × 1 superlattice structure.
where all the negative modes disappear, the estimation gets to be more plausible. There seems, however, little change in the estimation from that in 1 × 1 × 1. The present estimations, Tc = 2.30 (2.45) K for Pn = Sb (Bi), are consistent with experiments reporting Tc = 1.2 (4.6) K for Pn = Sb (Bi)5,7, as well as that by previous DFT study, Tc = 2.7 K for Pn = Sb15. For 1 × 2 × 1 (Pn = As), the estimation was made still under the existence of negative modes and the more plausible estimation for 2 × 2 × 1 was intractable as mentioned above. The estimations, Tc = 6.93 K (1 × 1 × 1) and 8.31 K (1 × 2 × 1) seem incompatible with experiments of BaTi2As2O exhibiting no superconductivity so far4,8. We might expect much lower Tc obtained for the 2 × 2 × 1 superlattice structure.
Discussions
Comparison with experiments
The orthorhombic 2 × 2 × 1 superlattice structure, obtained here for BaTi2As2O, would attract interests in connection with experimental observations. Frandsen et al. actually observed a lattice structural transition from tetragonal P4/mmm to orthorhombic Pmmm by neutron diffractions. They also reported very weak superlattice peaks corresponding to qHx = (1/2, 0, 0) or qHy = (0, 1/2, 0), which disappears at higher temperatures, by electron diffractions27. Since BaTi2As2O has the same P4/mmm parent structure as BaTi2Sb2O, they might expect a tetragonal  superlattice according to the previous DFT prediction by Subedi15 for Pn = Sb. The lack of the expected
superlattice according to the previous DFT prediction by Subedi15 for Pn = Sb. The lack of the expected  superlattice and the observation of the structural transition were explained by rather complicated mechanism such as intra-unit-cell nematic charge ordering, as an analogue of that in cupurates28,29. The observed weak peaks of qHx or qHy was then regarded as being non-intrinsic, attributed to poly-crystalline grain boundary effects. Our finding of orthorhombic 2 × 2 × 1 superlattice here can instead account for the observations, as intrinsic, more naturally in terms of the lattice instability due to conventional phonon-driven CDW. Note that our optimized geometry gives the orthorhombicity parameter, η = 2 × (a − b)/(a + b) = 0.171%, which is comparable with the experimental value η = 0.22%27. Though qHx or qHy is naturally explained, the present result also leads to the emergence of qHxy = (1/2, 1/2, 0), which is not explicitly reported in the work by Frandsen et al.27 Looking at their TEM photo in the paper27, it is actually quite difficult to distinguish the qHxy peak from much brighter spots in the immediate vicinity. Polycrystalline sample qualities and weak intensities of the peak might also matter. We expect that further careful investigation would find qHxy peak corresponding to the present 2 × 2 × 1 superlattice structure.
superlattice and the observation of the structural transition were explained by rather complicated mechanism such as intra-unit-cell nematic charge ordering, as an analogue of that in cupurates28,29. The observed weak peaks of qHx or qHy was then regarded as being non-intrinsic, attributed to poly-crystalline grain boundary effects. Our finding of orthorhombic 2 × 2 × 1 superlattice here can instead account for the observations, as intrinsic, more naturally in terms of the lattice instability due to conventional phonon-driven CDW. Note that our optimized geometry gives the orthorhombicity parameter, η = 2 × (a − b)/(a + b) = 0.171%, which is comparable with the experimental value η = 0.22%27. Though qHx or qHy is naturally explained, the present result also leads to the emergence of qHxy = (1/2, 1/2, 0), which is not explicitly reported in the work by Frandsen et al.27 Looking at their TEM photo in the paper27, it is actually quite difficult to distinguish the qHxy peak from much brighter spots in the immediate vicinity. Polycrystalline sample qualities and weak intensities of the peak might also matter. We expect that further careful investigation would find qHxy peak corresponding to the present 2 × 2 × 1 superlattice structure.
Unlike Pn = As, the other two compounds are predicted to have  superlattices in our calculations, which is consistent with the preceding work by Subedi15 for Pn = Sb. Then a question arises asking why only Pn = As takes the different superlattice structure. This can be explained by the nesting of Fermi surfaces, shown in Fig. 3. Because of the cylinderical shape, every compound has a nesting vector
superlattices in our calculations, which is consistent with the preceding work by Subedi15 for Pn = Sb. Then a question arises asking why only Pn = As takes the different superlattice structure. This can be explained by the nesting of Fermi surfaces, shown in Fig. 3. Because of the cylinderical shape, every compound has a nesting vector  [hereafter a unit of
[hereafter a unit of  is 2π/a]. around M and A points, as previously pointed out by Yu et al.23 for Pn = As . Another possible nesting around X and R is described by the vector
is 2π/a]. around M and A points, as previously pointed out by Yu et al.23 for Pn = As . Another possible nesting around X and R is described by the vector  , corresponding to the negative phonons we get around M and A in phonon Brillouin zones for Pn = Sb, Bi. This nesting has already been pointed out by Singh21 and Subedi15 for Pn = Sb. Looking carefully at the Fermi surface of Pn = As, we see the flattening of the cusp around X and R points (as shown by a dashed oval in Fig. 3(a)), leading to new nesting vectors,
, corresponding to the negative phonons we get around M and A in phonon Brillouin zones for Pn = Sb, Bi. This nesting has already been pointed out by Singh21 and Subedi15 for Pn = Sb. Looking carefully at the Fermi surface of Pn = As, we see the flattening of the cusp around X and R points (as shown by a dashed oval in Fig. 3(a)), leading to new nesting vectors,  and (1/2, 0). They correspond to the negative phonons around X and R appearing only for Pn = As. We note that
and (1/2, 0). They correspond to the negative phonons around X and R appearing only for Pn = As. We note that  have already been mentioned by Yu et al.23 for Pn = As, but its relation to the phonon instability has not been discussed so far. Possible reasons why the flattening occurs only for As are discussed in the next section. Since all the above stories can be made only within the electronic Fermi surfaces, one might consider the phonon evaluations not necessarily required. We note, however, that there are several 2D chalcogenide systems where CDW cannot be explained only by the electronic Fermi surfaces, but accounted for when the phonon dispersions are evaluated41,42,43,44,45. We discuss this in the later section. It is further interesting if CDW superlattice transitions predicted here could be related to the anomalies of ρ(T) and χ(T) at low temperature.
have already been mentioned by Yu et al.23 for Pn = As, but its relation to the phonon instability has not been discussed so far. Possible reasons why the flattening occurs only for As are discussed in the next section. Since all the above stories can be made only within the electronic Fermi surfaces, one might consider the phonon evaluations not necessarily required. We note, however, that there are several 2D chalcogenide systems where CDW cannot be explained only by the electronic Fermi surfaces, but accounted for when the phonon dispersions are evaluated41,42,43,44,45. We discuss this in the later section. It is further interesting if CDW superlattice transitions predicted here could be related to the anomalies of ρ(T) and χ(T) at low temperature.
The  superlattice structure for BaTi2Sb2O is predicted not only by the present work but also by Subedi15. However, such a superlattice has not yet been observed experimentally so far by any diffraction experiments such as neutron and electron diffractions17,27. Frandsen et al. observed a subtle structural distortion from P4/mmm to Pmmm by neutron diffraction measurement at low temperature27, which is not consistent with the prediction. Note that all the above diffraction experiments are applied to polycrystalline samples. Interestingly, Song et al. has very recently reported the existence of (1/2, 1/2) nesting vector by ARPES and STM measurements applied to high-quality single crystals, being consistent with the theoretical predictions26. The superlattice structure is hence expected to be detected by further diffraction measurements. The theoretically estimated distortion here is quite small, 0.14 Å (See Supplementary Note 4), being in agreement with the previous calculation by Subedi15, so careful detections would be required for experiments. As described in the previous section, the estimated Tc is almost consistent with experiments, supporting that the compound is a conventional BCS-type superconductor, being consistent with the previous conclusion by Subedi15.
superlattice structure for BaTi2Sb2O is predicted not only by the present work but also by Subedi15. However, such a superlattice has not yet been observed experimentally so far by any diffraction experiments such as neutron and electron diffractions17,27. Frandsen et al. observed a subtle structural distortion from P4/mmm to Pmmm by neutron diffraction measurement at low temperature27, which is not consistent with the prediction. Note that all the above diffraction experiments are applied to polycrystalline samples. Interestingly, Song et al. has very recently reported the existence of (1/2, 1/2) nesting vector by ARPES and STM measurements applied to high-quality single crystals, being consistent with the theoretical predictions26. The superlattice structure is hence expected to be detected by further diffraction measurements. The theoretically estimated distortion here is quite small, 0.14 Å (See Supplementary Note 4), being in agreement with the previous calculation by Subedi15, so careful detections would be required for experiments. As described in the previous section, the estimated Tc is almost consistent with experiments, supporting that the compound is a conventional BCS-type superconductor, being consistent with the previous conclusion by Subedi15.
In contrast to the other two compounds, there are little experiments on BaTi2Bi2O because of the difficulty of sample preparation mainly due to the significant instability under the air and moisture7. As far as we have known, there is no previous research on phonon dispersions on this system. The anomalies of ρ(T) and χ(T) disappear with increasing Tc when Sb is gradually substituted by Bi, as reported experimentally7. Though there is no direct evidence by diffraction experiments, it seems, then, the present consensus on this compound that there is no instability toward CDW, which would be contradicting to our result here. The spin polarization, not taken into account here, may be one of the possibilities to modify the nesting, for instance via the spin-orbit coupling, accounting for this discrepancy, but it is reported, at least for DOS, the effect matters little21. A similar discrepancy between negative phonon predictions39,46 and unobserved structural instability is known for a superconductor, LaO0.5F0.5BiS238. A large phonon instability toward a static CDW was estimated theoretically39, while no anomaly in ρ(T) and χ(T) has been observed experimentally38,47. Yildirim39 then argued the possibility of an unconventional superconducting mechanism in which inherent lattice instabilities have an important role on the Cooper paring in this compound. A more recent neutron diffraction experiment48 reported that the local distortion of the atomic position of S around Bi is detected under Tc, attracting an attention in connection with the unconventional mechanism. In our case of BaTi2Bi2O, the stabilization energy is evaluated around 23.3 meV/UnitCell, being much larger than that of LaO0.5F0.5BiS2 (~10 meV/UnitCell)39. In terms of the magnitude of the displacement, it is 0.16 Å for BaTi2Bi2O (See Supplementary Note 4), which is the same as 0.16 Å for LaO0.5F0.5BiS239. In addition, the  superlattice structure obtained by analyzing dynamical matrices for BaTi2Bi2O does not show any negative phonon frequency (Fig. 7(c)). Therefore, the lattice instability is also expected to be static. The similarity might imply the similar unconventional mechanism also for BaTi2Bi2O. If it were so, the substitution of Sb by Bi would introduce the unconventionality to the conventional BCS of BaTi2Sb2O16,17,18. The introduction might account for the two-dome structure appeared by the substitution8.
superlattice structure obtained by analyzing dynamical matrices for BaTi2Bi2O does not show any negative phonon frequency (Fig. 7(c)). Therefore, the lattice instability is also expected to be static. The similarity might imply the similar unconventional mechanism also for BaTi2Bi2O. If it were so, the substitution of Sb by Bi would introduce the unconventionality to the conventional BCS of BaTi2Sb2O16,17,18. The introduction might account for the two-dome structure appeared by the substitution8.
Possible mechanism for variety of superlattices
A natural question consequently arising would be asking why the new nesting vectors  appear only for Pn = As. The vectors are caused by the flattening of the ‘nose’ of Fermi surfaces directing toward the central cylinder from four equivalent outsides. Interestingly, the similar flattened ‘nose’ was actually reported in the paper by Singh21 (in its Fig. 7), shown as the ‘Fermi surfaces’ below EF by 0.1 eV for Pn = Sb. Looking at our Fig. 2, we observe that the Fermi level seems to be approaching down toward the DOS peak as Pn changes from Bi and Sb to As. This can be regarded as if EF effectively behaves like the ‘sea-level down’ Pn = As with a fixed landscape of Pn = Sb. The Fermi surface of Pn = As would therefore correspond to that of Pn = Sb with negative energy shift, as shown in ‘Fig. 7 by Singh’21. The ‘fixed landscape’, namely the ‘rigid band picture’ near to Fermi level, can be justified to some extent because they are mainly composed of Ti-d orbital contributions as shown in Fig. 2. The reason why the ‘sea-level’ gets down when Pn is substituted into As can roughly be accounted as follows: As a rough estimation of how Pn affects to shift EF, we can start with its ‘HOMO’ level of the isolated atom [HOMO stands for ‘Highest Occupied Molecular Orbital’ though the orbital in the present context is not molecular but isolated atomic orbital. We use ‘HOMO’ rather than HOAO just because the latter is not so commonly spread abbreviation. We expect this doesn’t matter so much even it is used for isolated atom.]. Namely, a negatively deeper ‘HOMO’ would contribute to attract Ti-electrons more strongly and make EF lower. Noticing the deeper ‘HOMO’ corresponds to the larger ionic potential, we expect that the lighter element (As) has deeper ‘HOMO’ because the potential is enhanced by the less screening of the nucleus attractions by fewer inner electrons49. The deeper ‘HOMO’ also corresponds to the larger electronegativity, which is actually 2.18 for As while 2.05 (2.02) for Sb (Bi) by Pauling scale. Similar negativities for Sb and Bi can account for the common nesting vectors of these compounds, being different from that of As. Summarizing the above, the negatively deeper ‘HOMO’ level of As can attract Ti-electrons more strongly and effectively push EF down when it forms pnictides and then the Fermi surface changes to get flattened ‘nose’ as depicted in ‘Fig. 7 of Singh’21.
appear only for Pn = As. The vectors are caused by the flattening of the ‘nose’ of Fermi surfaces directing toward the central cylinder from four equivalent outsides. Interestingly, the similar flattened ‘nose’ was actually reported in the paper by Singh21 (in its Fig. 7), shown as the ‘Fermi surfaces’ below EF by 0.1 eV for Pn = Sb. Looking at our Fig. 2, we observe that the Fermi level seems to be approaching down toward the DOS peak as Pn changes from Bi and Sb to As. This can be regarded as if EF effectively behaves like the ‘sea-level down’ Pn = As with a fixed landscape of Pn = Sb. The Fermi surface of Pn = As would therefore correspond to that of Pn = Sb with negative energy shift, as shown in ‘Fig. 7 by Singh’21. The ‘fixed landscape’, namely the ‘rigid band picture’ near to Fermi level, can be justified to some extent because they are mainly composed of Ti-d orbital contributions as shown in Fig. 2. The reason why the ‘sea-level’ gets down when Pn is substituted into As can roughly be accounted as follows: As a rough estimation of how Pn affects to shift EF, we can start with its ‘HOMO’ level of the isolated atom [HOMO stands for ‘Highest Occupied Molecular Orbital’ though the orbital in the present context is not molecular but isolated atomic orbital. We use ‘HOMO’ rather than HOAO just because the latter is not so commonly spread abbreviation. We expect this doesn’t matter so much even it is used for isolated atom.]. Namely, a negatively deeper ‘HOMO’ would contribute to attract Ti-electrons more strongly and make EF lower. Noticing the deeper ‘HOMO’ corresponds to the larger ionic potential, we expect that the lighter element (As) has deeper ‘HOMO’ because the potential is enhanced by the less screening of the nucleus attractions by fewer inner electrons49. The deeper ‘HOMO’ also corresponds to the larger electronegativity, which is actually 2.18 for As while 2.05 (2.02) for Sb (Bi) by Pauling scale. Similar negativities for Sb and Bi can account for the common nesting vectors of these compounds, being different from that of As. Summarizing the above, the negatively deeper ‘HOMO’ level of As can attract Ti-electrons more strongly and effectively push EF down when it forms pnictides and then the Fermi surface changes to get flattened ‘nose’ as depicted in ‘Fig. 7 of Singh’21.
Though we could not make clear explanations here, we must note that the nesting vector cannot solely account for the superlattice instabilities even in the present case. In addition to  for Pn = As,
for Pn = As,  and
and  may be regarded as possible nesting vectors. The Kohn anomalies corresponding to
may be regarded as possible nesting vectors. The Kohn anomalies corresponding to  and
and  are, however, not present in the phonon dispersion. This fact might be related to recent intensive discussions about the Kohn anomaly50: Some studies41,42,43,44,45 insist that the imaginary phonons in quasi 2D systems are dominated not mainly by the nesting of electronic structures but rather primarily by the wave vector dependence of the electron-phonon coupling,
are, however, not present in the phonon dispersion. This fact might be related to recent intensive discussions about the Kohn anomaly50: Some studies41,42,43,44,45 insist that the imaginary phonons in quasi 2D systems are dominated not mainly by the nesting of electronic structures but rather primarily by the wave vector dependence of the electron-phonon coupling,  . There exists, however, such quasi 2D systems51 where their superlattice instabilities can clearly be explained by the nesting vectors. To investigate if our system corresponds to which case or that lying in between, it is quite intriguing to analyze
. There exists, however, such quasi 2D systems51 where their superlattice instabilities can clearly be explained by the nesting vectors. To investigate if our system corresponds to which case or that lying in between, it is quite intriguing to analyze  for Pn = As, but unfortunately we cannot perform any of such phonon calculations under the perfect disappearance of imaginary frequencies because of too costly calculations for the 2 × 2 × 1 superlattice.
for Pn = As, but unfortunately we cannot perform any of such phonon calculations under the perfect disappearance of imaginary frequencies because of too costly calculations for the 2 × 2 × 1 superlattice.
Methods
All the calculations were done within DFT using GGA-PBE exchange-correlation functionals52, implemented in Quantum Espresso package53. After carefully examining the artifacts due to the choice of pseudo potentials (PP), we provide here the final results mainly obtained by the PAW54 framework of the valence/core separation of electrons. The implementation of PAW adopted here takes into account the relativistic effects within the extent of the scalar-relativistic theory upon a careful comparison with all-electron calculations by Wien2k55. We restricted ourselves to spin unpolarized calculations, anticipating that the spin polarization affects little as supported by several experiments16,17,18. Lattice instabilities are detected by the negative (imaginary) phonon dispersions evaluated for undistorted lattice structures. Taking each of the negative phonon modes, the structural relaxations along the mode are evaluated by the BFGS optimization scheme with the structural symmetries fixed to Pbmm (1 × 2 × 1) and Pbam (2 × 2 × 1) for BaTi2As2O, P4/mbm ( ) for BaTi2Sb2O and BaTi2Bi2O. For phonon calculations, we used the linear response theory implemented in Quantum Espresso package56. Crystal structures and Fermi surfaces are depicted by using VESTA57 and XCrySDen58, respectively.
) for BaTi2Sb2O and BaTi2Bi2O. For phonon calculations, we used the linear response theory implemented in Quantum Espresso package56. Crystal structures and Fermi surfaces are depicted by using VESTA57 and XCrySDen58, respectively.
To deal with the three compounds systematically, we took the same conditions for plane-wave cutoff energies (Ecut), k-meshes and smearing parameters. The most strict condition among the compounds is taken to achieve the convergence within ±1.0 mRy in the ground state energies of undistorted (superlattice) systems, resulting in  Ry for wavefunction and
Ry for wavefunction and  Ry for charge densities. For Tc evaluation, we adopted unshifted k-meshes centered at Γ-point. Denser k-meshes should be taken for electron-phonon calculations because of the double-delta integrations59. For undistorted systems, (8 × 8 × 4) k-meshes were used for the Brillouin-zone integration. Phonon dispersions were calculated on (8 × 8 × 4) q-meshes. Denser k-meshes, (24 × 24 × 12), were used for the double-delta integrations in electron-phonon calculations. For distorted BaTi2As2O superlattices, (8 × 4 × 4) and (4 × 4 × 4) k-meshes were used for 1 × 2 × 1 and 2 × 2 × 1 superlattices, respectively. Phonon dispersions were calculated on (8 × 4 × 4) and (4 × 4 × 4) q-meshes. Denser k-meshes, (24 × 12 × 12), were used for the double-delta integrations in electron-phonon calculations of the 1 × 2 × 1 superlattice. For distorted BaTi2Sb2O and BaTi2Bi2O superlattices, (6 × 6 × 6) k-meshes are used. Phonon dispersions were calculated on (6 × 6 × 6) q-meshes. Denser k-meshes, (18 × 18 × 18), were used for the double-delta integrations in electron-phonon calculations. The Marzari-Vanderbilt cold smearing scheme60 with a broadening width of 0.01 Ry was applied to all the compounds. To estimate Tc, we used Allen-Dynes formula13,14 implemented in Quantum Espresso53, with the effective Coulomb interaction μ*, being chosen 0.1 empirically (See Supplementary Note 3).
Ry for charge densities. For Tc evaluation, we adopted unshifted k-meshes centered at Γ-point. Denser k-meshes should be taken for electron-phonon calculations because of the double-delta integrations59. For undistorted systems, (8 × 8 × 4) k-meshes were used for the Brillouin-zone integration. Phonon dispersions were calculated on (8 × 8 × 4) q-meshes. Denser k-meshes, (24 × 24 × 12), were used for the double-delta integrations in electron-phonon calculations. For distorted BaTi2As2O superlattices, (8 × 4 × 4) and (4 × 4 × 4) k-meshes were used for 1 × 2 × 1 and 2 × 2 × 1 superlattices, respectively. Phonon dispersions were calculated on (8 × 4 × 4) and (4 × 4 × 4) q-meshes. Denser k-meshes, (24 × 12 × 12), were used for the double-delta integrations in electron-phonon calculations of the 1 × 2 × 1 superlattice. For distorted BaTi2Sb2O and BaTi2Bi2O superlattices, (6 × 6 × 6) k-meshes are used. Phonon dispersions were calculated on (6 × 6 × 6) q-meshes. Denser k-meshes, (18 × 18 × 18), were used for the double-delta integrations in electron-phonon calculations. The Marzari-Vanderbilt cold smearing scheme60 with a broadening width of 0.01 Ry was applied to all the compounds. To estimate Tc, we used Allen-Dynes formula13,14 implemented in Quantum Espresso53, with the effective Coulomb interaction μ*, being chosen 0.1 empirically (See Supplementary Note 3).
Additional Information
How to cite this article: Nakano, K. et al. Phonon dispersions and Fermi surfaces nesting explaining the variety of charge ordering in titanium-oxypnictides superconductors. Sci. Rep. 6, 29661; doi: 10.1038/srep29661 (2016).
References
III, E. A., Ozawa, T., Kauzlarich, S. M. & Singh, R. R. Phase Transition and Spin-gap Behavior in a Layered Tetragonal Pnictide Oxide. Journal of Solid State Chemistry 134, 423–426 (1997).
Ozawa, T. C., Kauzlarich, S. M., Bieringer, M. & Greedan, J. E. Possible Charge-Density-Wave/Spin-Density-Wave in the Layered Pnictide-Oxides:Na2Ti2Pn2O (Pn = As, Sb). Chemistry of Materials 13, 1804–1810 (2001).
Liu, R. H. et al. Physical properties of the layered pnictide oxides Na2Ti2P2O (P = As, Sb). Phys. Rev. B 80, 144516 (2009).
Wang, X. F. et al. Structure and physical properties for a new layered pnictide-oxide: BaTi2As2O. Journal of Physics: Condensed Matter 22, 075702 (2010).
Yajima, T. et al. Superconductivity in BaTi2Sb2O with a d1 square lattice. Journal of the Physical Society of Japan 81, 103706 (2012).
Doan, P. et al. Ba1−xNaxTi2Sb2O (0.0 ≤ x ≤ 0.33) A Layered Titanium-Based Pnictide Oxide Superconductor. Journal of the American Chemical Society 134, 16520–16523 (2012).
Yajima, T. et al. Synthesis and Physical Properties of the New Oxybismuthides BaTi2Bi2O and (SrF)2Ti2Bi2O with a d1 Square Net. Journal of the Physical Society of Japan 82, 013703 (2013).
Yajima, T. et al. Two Superconducting Phases in the Isovalent Solid Solutions BaTi2Pn2O (Pn = As, Sb and Bi). Journal of the Physical Society of Japan 82, 033705 (2013).
Zhai, H.-F. et al. Superconductivity, charge- or spin-density wave and metal-nonmetal transition in BaTi2(Sb1−xBix)2O. Phys. Rev. B 87, 100502 (2013).
Nakano, K. et al. Tc Enhancement by Aliovalent Anionic Substitution in Superconducting BaTi2(Sb1−xSnx)2O. Journal of the Physical Society of Japan 82, 074707 (2013).
Pachmayr, U. & Johrendt, D. Superconductivity in Ba1−xKxTi2Sb2O (0 ≦ x ≦ 1) controlled by the layer charge. Solid State Sciences 28, 31–34 (2014).
von Rohr, F., Nesper, R. & Schilling, A. Superconductivity in rubidium-substituted Ba1−xRbxTi2Sb2O. Phys. Rev. B 89, 094505 (2014).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1957).
Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905–922 (1965).
Subedi, A. Electron-phonon superconductivity and charge density wave instability in the layered titanium-based pnictide BaTi2Sb2O. Phys. Rev. B 87, 054506 (2013).
Kitagawa, S., Ishida, K., Nakano, K., Yajima, T. & Kageyama, H. s-wave superconductivity in superconducting BaTi2Sb2O revealed by 121/123Sb-NMR/nuclear quadrupole resonance measurements. Phys. Rev. B 87, 060510 (2013).
Nozaki, Y. et al. Muon spin relaxation and electron/neutron diffraction studies of BaTi2(As1−xSbx)2O: Absence of static magnetism and superlattice reflections. Phys. Rev. B 88, 214506 (2013).
von Rohr, F., Schilling, A., Nesper, R., Baines, C. & Bendele, M. Conventional superconductivity and charge-density-wave ordering in Ba1−xNaxTi2Sb2O. Phys. Rev. B 88, 140501 (2013).
Bednorz, J. & Müller, K. Possible high-Tc superconductivity in the Ba-La-Cu-O system. Zeitschrift für Physik B Condensed Matter 64, 189–193 (1986).
Kamihara, Y., Watanabe, T., Hirano, M. & Hosono, H. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. Journal of the American Chemical Society 130, 3296–3297 (2008).
Singh, D. J. Electronic structure, disconnected Fermi surfaces and antiferromagnetism in the layered pnictide superconductor NaxBa1−xTi2Sb2O. New Journal of Physics 14, 123003 (2012).
Wang, G., Zhang, H., Zhang, L. & Liu, C. The electronic structure and magnetism of BaTi2Sb2O. Journal of Applied Physics 113 (2013).
Yu, X.-L. et al. A site-selective antiferromagnetic ground state in layered pnictide-oxide BaTi2As2O. Journal of Applied Physics 115, 17A924 (2014).
Suetin, D. & Ivanovskii, A. Electronic properties and fermi surface for new Fe-free layered pnictide-oxide superconductor BaTi2Bi2O from first principles. JETP Letters 97, 220–225 (2013).
Xu, H. C. et al. Electronic structure of the BaTi2As2O parent compound of the titanium-based oxypnictide superconductor. Phys. Rev. B 89, 155108 (2014).
Song, Q. et al. Electronic structure of the titanium-based oxypnictide superconductor Ba0.95Na0.05Ti2Sb2O and direct observation of its charge density wave order. Phys. Rev. B 93, 024508 (2016).
Frandsen, B. A. et al. Intra-unit-cell nematic charge order in the titanium-oxypnictide family of superconductors. Nat. Commun. 5, 5761 (2014).
Lawler, M. J. et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 466, 347–351 (2010).
Fujita, K. et al. Direct phase-sensitive identification of a d-form factor density wave in underdoped cuprates. Proceedings of the National Academy of Sciences 111, E3026 (2014).
Koike, Y., Watanabe, N., Noji, T. & Saito, Y. Effects of the Cu-site substitution on the anomalous x dependence of Tc in La2−xBaxCuO4 . Solid State Communications 78, 511–514 (1991).
Koike, Y., Kawaguchi, T., Watanabe, N., Noji, T. & Saito, Y. Superconductivity and low-temperature structural phase transition in La1.98−xCe0.02BaxCuO4 . Solid State Communications 79, 155–158 (1991).
Tamegai, T. & Iye, Y. Universal transport anomaly in YBa2Cu3O7-type systems with reduced carrier density. Phys. Rev. B 44, 10167 (1991).
Koike, Y. et al. Anomalous x dependence of Tc and possibility of low-temperature structural phase transition in La2−xSrxCu0.99M0.01O4 (M = Ni, Zn, Ga). Solid State Communications 82, 889–893 (1992).
Ando, Y., Komiya, S., Segawa, K., Ono, S. & Kurita, Y. Electronic Phase Diagram of High-Tc Cuprate Superconductors from a Mapping of the In-Plane Resistivity Curvature. Phys. Rev. Lett. 93, 267001 (2004).
Iimura, S. et al. Two-dome structure in electron-doped iron arsenide superconductors. Nat. Commun. 3, 943 (2012).
Matsuishi, S., Maruyama, T., Iimura, S. & Hosono, H. Controlling factors of Tc dome structure in 1111-type iron arsenide superconductors. Phys. Rev. B 89, 094510 (2014).
Fujiwara, N. et al. Detection of Antiferromagnetic Ordering in Heavily Doped LaFeAsO1−xHx Pnictide Superconductors Using Nuclear-Magnetic-Resonance Techniques. Phys. Rev. Lett. 111, 097002 (2013).
Mizuguchi, Y. et al. Superconductivity in novel BiS2-based layered superconductor LaO1−xFxBiS2 . Journal of the Physical Society of Japan 81, 114725 (2012).
Yildirim, T. Ferroelectric soft phonons, charge density wave instability and strong electron-phonon coupling in BiS2 layered superconductors: A first-principles study. Phys. Rev. B 87, 020506 (2013).
Aroyo, M. I. et al. Brillouin-zone databases on the Bilbao Crystallographic Server. Acta Cryst. A70, 126–137 (2014).
Johannes, M. D., Mazin, I. I. & Howells, C. A. Fermi-surface nesting and the origin of the charge-density wave in NbSe2 . Phys. Rev. B 73, 205102 (2006).
Johannes, M. D. & Mazin, I. I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 77, 165135 (2008).
Calandra, M., Mazin, I. I. & Mauri, F. Effect of dimensionality on the charge-density wave in few-layer 2H-NbSe2 . Phys. Rev. B 80, 241108 (2009).
Calandra, M. & Mauri, F. Charge-Density Wave and Superconducting Dome in TiSe2 from Electron-Phonon Interaction. Phys. Rev. Lett. 106, 196406 (2011).
Zhu, X., Cao, Y., Zhang, J., Plummer, E. W. & Guo, J. Classification of charge density waves based on their nature. Proc. Natl. Acad. Sci. USA 112, 2367–2371 (2015).
Wan, X., Ding, H.-C., Savrasov, S. Y. & Duan, C.-G. Electron-phonon superconductivity near charge-density-wave instability in LaO0.5F0.5BiS2: Density-functional calculations. Phys. Rev. B 87, 115124 (2013).
Lee, J. et al. Crystal structure, lattice vibrations and superconductivity of LaO1−xFxBiS2 . Phys. Rev. B 87, 205134 (2013).
Athauda, A. et al. In-plane charge fluctuations in bismuth-sulfide superconductors. Phys. Rev. B 91, 144112 (2015).
Hongo, K. Interpretation of Hund's multiplicity rule for the carbon atom. J. Chem. Phys. 121, 7144–7147 (2004).
Kohn, W. Image of the Fermi Surface in the Vibration Spectrum of a Metal. Phys. Rev. Lett. 2, 393–394 (1959).
Kim, H., Kang, C., Kim, K., Shim, J. H. & Min, B. I. Phonon softenings and the charge density wave instability in R2O2Sb (R = rare-earth element). Phys. Rev. B 91, 165130 (2015).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. Journal of Physics: Condensed Matter 21, 395502 (2009).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Jollet, F., Torrent, M. & Holzwarth, N. Generation of projector augmented-wave atomic data: A 71 element validated table in the XML format. Computer Physics Communications 185, 1246–1254 (2014).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515 (2001).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. Journal of Applied Crystallography 44, 1272–1276 (2011).
Kokalj, A. XCrySDen-a new program for displaying crystalline structures and electron densities. Journal of Molecular Graphics and Modelling 17, 176–179 (1999).
Wierzbowska, M., de Gironcoli, S. & Giannozzi, P. Origins of low- and high-pressure discontinuities of Tc in niobium. eprint arXiv:cond-mat/0504077 (2006).
Marzari, N., Vanderbilt, D., De Vita, A. & Payne, M. C. Thermal Contraction and Disordering of the Al(110) Surface. Phys. Rev. Lett. 82, 3296 (1999).
Acknowledgements
The authors are grateful to Tomohiro Ichibha for assistance in DFT calculation, Takeshi Yajima for useful discussion and Hiroshi Kageyama for his encouragement. The authors also acknowledge the support by the Computational Materials Science Initiative (CMSI/Japan) for the computational resources, Project Nos hp120086, hp140150, hp150014 at K-computer and SR16000 (Center for Computational Materials Science of the Institute for Materials Research, Tohoku University/Japan). R.M. is grateful for financial support from MEXT-KAKENHI grants 26287063, 25600156, 22104011 and that from the Asahi glass Foundation. K.H. is grateful for financial support from MEXT-KAKENHI grants 15K21023 and 15H02672. The computation in this work has been partially performed using the facilities of the Center for Information Science in JAIST.
Author information
Authors and Affiliations
Contributions
K.N. initiated and performed main calculations under the supervision by R.M. Data is analysed by K.N. and K.H. All the authors wrote the paper, section by section, finally organized to a manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Nakano, K., Hongo, K. & Maezono, R. Phonon dispersions and Fermi surfaces nesting explaining the variety of charge ordering in titanium-oxypnictides superconductors. Sci Rep 6, 29661 (2016). https://doi.org/10.1038/srep29661
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep29661
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

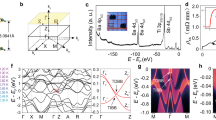







 and (c) Bi-
and (c) Bi- .
.