Abstract
Quantum metrology is the state-of-the-art measurement technology. It uses quantum resources to enhance the sensitivity of phase estimation over that achievable by classical physics. While single parameter estimation theory has been widely investigated, much less is known about the simultaneous estimation of multiple phases, which finds key applications in imaging and sensing. In this manuscript we provide conditions of useful particle (qudit) entanglement for multiphase estimation and adapt them to multiarm Mach-Zehnder interferometry. We theoretically discuss benchmark multimode Fock states containing useful qudit entanglement and overcoming the sensitivity of separable qudit states in three and four arm Mach-Zehnder-like interferometers - currently within the reach of integrated photonics technology.
Similar content being viewed by others
Introduction
Quantum metrology exploits particle entanglement in the probe state to enhance the precision of parameter estimation beyond what is reachable with classical resources (see refs 1,2 for reviews). The role of particle entanglement in the estimation of a single parameter has been clarified3,4,5,6 and investigated experimentally in Mach-Zehnder interferometers (MZIs)7. However, much less is known about the role of particle entanglement in the joint estimation of multiple parameters. Multiparameter estimation is relevant in many practical applications, including quantum imaging8, quantum process tomography9, as well as probing of biological samples10. Interestingly, the theory of multiphase estimation does not follow trivially from what is known about the single parameter case11,12. Indeed, ultimate multiphase estimation bounds are not saturable in general13, due to the non-commutativity of the operators generating the phase shift transformations14,15. First insights on this scenario have been recently reported16,17,18,19,20,21,22.
A natural platform for multiparameter quantum metrology is provided by multiport interferometry, generalizing conventional two-mode interferometry. Recent progresses in the realization of multiport devices have been achieved by exploiting integrated photonics23,24,25,26,27,28,29,30,31. Three- and four-port beam-splitters (tritters and quarters) have been produced with integrated optics31,32,33,34. This paves the way toward the realization of multiarm interferometers created by two tritters (quarters) in succession35. Quantum-enhanced single parameter estimation in integrated interferometers has been theoretically predicted17, while multiparameter estimation in multi-arm interferometers has been examined and compared with the sensitivity achievable by multiple single-parameter estimation18.
In this manuscript we provide conditions of useful particle entanglement for the simultaneous estimation of multiple phases. We study a general multimode scenario where each particle is treated as a qudit. Furthermore, we adapt the theory to the case of multiarm Mach Zehnder interferometers (MMZIs) considering an experimentally relevant framework, with multiphoton Fock states as probe and photon counting measurement. Our analysis generalizes the case of twin-Fock MZI which has attracted large experimental7,36,37,38 and theoretical39,40,41 interest for quantum-enhanced single phase estimation. From the analysis of the Fisher information and employing an adaptive multiphase estimation, we predict a multiparameter estimation sensitivity beyond the limit achievable with separable qudit probe states.
Results
Multiparameter estimation
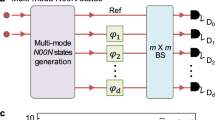
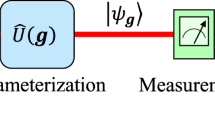
We consider here the estimation of a n-dimensional vector parameter λ = (λ1,  , λn)11,12. In our benchmark, every parameter corresponds to a phase to be estimated in a multiarm interferometer. A general approach (see Fig. 1a) consists in preparing a probe state
, λn)11,12. In our benchmark, every parameter corresponds to a phase to be estimated in a multiarm interferometer. A general approach (see Fig. 1a) consists in preparing a probe state  , applying a λ -dependent unitary transformation
, applying a λ -dependent unitary transformation  and performing independent measurements on ν identical copies of the output state
and performing independent measurements on ν identical copies of the output state  . The measurement is described by a positive-operator valued measure (POVM), i.e. a set
. The measurement is described by a positive-operator valued measure (POVM), i.e. a set  of positive operators satisfying
of positive operators satisfying  ,
,  being the probability of the detection event x. Finally, the sequence x ≡ (x1,
being the probability of the detection event x. Finally, the sequence x ≡ (x1,  , xν) of ν measurement results is mapped into a vector parameter Λ( x ) = (Λ1( x ),
, xν) of ν measurement results is mapped into a vector parameter Λ( x ) = (Λ1( x ),  , Λn( x )), representing our estimate of λ . A figure of merit of multiparameter estimation is the covariance matrix
, Λn( x )), representing our estimate of λ . A figure of merit of multiparameter estimation is the covariance matrix
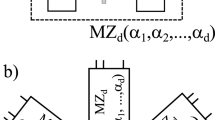
(a) General scheme of multiparameter estimation. (b) Three-mode MMZI for two-parameter phase estimation which can be obtained by two cascaded three-port beam-splitters. Phases (ϕ1, ϕ2) on modes (k1, k2) are the parameters to be estimated, while (ψ1, ψ2) are two additional controlled phase-shifts (c). Four-mode interferometer for two-parameter phase estimation which can be obtained by two cascaded four-port beam-splitters. Phases (ϕ1, ϕ2) on modes (k1, k2) are the parameters to be estimated, while (ϕ0, ψ1, ψ2) are assumed known and controlled. Controlled phases are introduced for adaptive estimation schemes.

where  and
and  is the mean value of the estimator vector. For locally unbiased estimators (i.e.
is the mean value of the estimator vector. For locally unbiased estimators (i.e.  ) the covariance matrix is bounded, via the Cramer-Rao theorem11, as
) the covariance matrix is bounded, via the Cramer-Rao theorem11, as

(in the sense of matrix inequality), where

is the Fisher information matrix (FIM). Notice that Eq. (2) can be derived only when the FIM is invertible. The equality sign in Eq. (2) is saturated asymptotically in ν by the maximum likelihood estimator11. Here we quantify the phase sensitivity by the variance of each estimator, (δλj)2 ≡ Cj,j. We have

where the first inequality is due to (2) and the second follows from a Cauchy-Schwarz inequality (see Supplementary Information). Since 1/(ν Fj,j) is the Cramer-Rao bound for single parameter estimation, inequality (4) tells us that sensitivity in the estimation of λj can be optimized when fixing all the other parameters to known values. We will also consider

The right-hand side inequality in Eqs (4) and (5) is saturated if and only if the FIM is diagonal. Furthermore, the FIM is bounded by the quantum Fisher information matrix (QFIM): F ≤ FQ (in the sense of matrix inequality), where

and  is the symmetric logarithmic derivative of ρλ with respect to parameter λj, defined by
is the symmetric logarithmic derivative of ρλ with respect to parameter λj, defined by 
 2 10. In the single parameter case, the QFIM reduces to a single scalar quantity and it is always possible to find a POVM for which F = FQ and δλ = 1/FQ holds42,43. In contrast, in the multiparameter case, it is generally not possible to achieve the Cramer-Rao bound13,14,15.
2 10. In the single parameter case, the QFIM reduces to a single scalar quantity and it is always possible to find a POVM for which F = FQ and δλ = 1/FQ holds42,43. In contrast, in the multiparameter case, it is generally not possible to achieve the Cramer-Rao bound13,14,15.
Sensitivity bounds for qudit-separable states
In the following we consider the estimation of n parameters in a system made of d = n + 1 modes (e.g. the number of arms in a MMZI, see below). A single particle occupying the n + 1 modes is generally indicated as a qudit. The notion of qudit generalizes the concept of qubit (a two-mode particle, n = 1) and is relevant in multimode interferometry2. Here we set sensitivity bounds for multiparameter estimation when the probe state is qudit-separable. A state  of N qudits is said to be qudit-separable if it can be written as
of N qudits is said to be qudit-separable if it can be written as  , where
, where  (l = 1,
(l = 1,  , N) is a single qudit state, pk > 0 and ∑k pk = 1. A state which is not qudit-separable is qudit-entangled. We take the generator of each phase shift,
, N) is a single qudit state, pk > 0 and ∑k pk = 1. A state which is not qudit-separable is qudit-entangled. We take the generator of each phase shift,  (j = 1, …, n labels the parameter), to be local in the qudit, i.e. it can be written as
(j = 1, …, n labels the parameter), to be local in the qudit, i.e. it can be written as  where
where  is an arbitrary operator acting on the lth qudit. In particular, the transformation
is an arbitrary operator acting on the lth qudit. In particular, the transformation  does not create entanglement among the N qudits. For simplicity, we will take the same operator
does not create entanglement among the N qudits. For simplicity, we will take the same operator  for each particle. For a generic separable probe state
for each particle. For a generic separable probe state  , the inequality
, the inequality

holds for all possible POVMs (see Supplementary Information), where gj,max and gj,min are the maximum and minimum eigenvalue of  , respectively. Inequality (7) gives a bound on the diagonal elements of the FIM. It corresponds, via the inequality (δλj)2 ≥ 1/ν Fj,j, to a bound on the sensitivity reachable with qudit-separable states for the estimation of the single parameter λj, when all other parameters are set to zero. Inequality (7) can be always saturated by optimal states and measurements (see Supplementary Information). For the estimation of a single parameter, the violation of Eq. (7) is a necessary and sufficient condition of useful qudit entanglement2,4: only those qudit-entangled states that violate Eq. (7) allow to estimate the parameter λj with a sensitivity overcoming the one reachable with any qudit-separable state. Regarding the simultaneous estimation of multiple parameters, we can use Eq. (7) and the chain of inequalities (4) to obtain
, respectively. Inequality (7) gives a bound on the diagonal elements of the FIM. It corresponds, via the inequality (δλj)2 ≥ 1/ν Fj,j, to a bound on the sensitivity reachable with qudit-separable states for the estimation of the single parameter λj, when all other parameters are set to zero. Inequality (7) can be always saturated by optimal states and measurements (see Supplementary Information). For the estimation of a single parameter, the violation of Eq. (7) is a necessary and sufficient condition of useful qudit entanglement2,4: only those qudit-entangled states that violate Eq. (7) allow to estimate the parameter λj with a sensitivity overcoming the one reachable with any qudit-separable state. Regarding the simultaneous estimation of multiple parameters, we can use Eq. (7) and the chain of inequalities (4) to obtain

Inequality (8) is a bound of sensitivity in the estimation of the single parameter λj with qudit-separable states, when all the parameters are unknown. Summing Eq. (8) over all parameters, we obtain

According to Eqs (8) and (9), for qudit-separable states such that the FIM is invertible, we recover – at best – the shot noise scaling of phase sensitivity, δλj ∝ N−1/2, which also characterizes single parameter estimation3,4. Notice that the quantity (gj,max − gj,min)2 is equal to one for any qubit transformation and might be larger than one for general qudit transformations. We finally recall that the phase estimation scenario we are considering – as well as the notion of useful qudit-entangement – refers to interferometric scheme involving liner qudit transformations and multiple independent measurements done with identical copies of the same probe. Inequalities (8) and (9) have no concern with the qudit-entanglement of the initial probe state for (nonlinear) parameter dependent processes that entangle/disentangle the probe or non-independent multiple measurements.
Multimode Mach-Zehnder interferometry
In the following we discuss the estimation of a phase vector ϕ = (ϕ1, …, ϕn) in a MMZI (see Fig. 1b,c). The MMZI can be obtained by cascading a d-mode balanced beam-splitter  , a phase shift transformation
, a phase shift transformation  , being
, being  the photon-number operator for the ith mode, and a second multiport beam-splitter
the photon-number operator for the ith mode, and a second multiport beam-splitter  . The d-mode beam-splitter
. The d-mode beam-splitter  is the natural extension of the standard 50-50 beam-splitter to more than two optical input-output modes41. Hence, the MMZI can be adopted as a benchmark to investigate simultaneous estimation of n = d − 1 optical phases. Indeed, it allows for a direct comparison between classical and quantum probe states and represents a flexible platform for the analysis of multiparameter scenario by changing the unitary transformation of the input and output multiport beam-splitters.
is the natural extension of the standard 50-50 beam-splitter to more than two optical input-output modes41. Hence, the MMZI can be adopted as a benchmark to investigate simultaneous estimation of n = d − 1 optical phases. Indeed, it allows for a direct comparison between classical and quantum probe states and represents a flexible platform for the analysis of multiparameter scenario by changing the unitary transformation of the input and output multiport beam-splitters.
In order to adapt the discussion of the previous section, we consider N particles as input of the MMZI and identify a single particle in the d arms of the interferometer as a qudit, whose Hilbert space has thus dimension d. The generator of phase shift in the jth mode is  . One can thus write
. One can thus write  where
where  as the operator projecting the lth qudit on the jth mode. Finally, gj,max − gj,min = 1 and the inequalities (8) and (9) read
as the operator projecting the lth qudit on the jth mode. Finally, gj,max − gj,min = 1 and the inequalities (8) and (9) read

respectively. The violation of one of these inequalities in the MMZI is a signature of useful qudit-entanglement in the probe state.
The recent experimental implementation of symmetric multiport beam-splitting31,32,33,34, by adopting integrated platforms, paves the way toward the future realization of optical MMZIs. For d = 3 modes, the tritter matrix  , corresponding to its unitary transformation
, corresponding to its unitary transformation  , has diagonal elements
, has diagonal elements  and off-diagonal elements
and off-diagonal elements  with i ≠ j. For d = 4 modes, the quarter matrix
with i ≠ j. For d = 4 modes, the quarter matrix  is
is  and
and  for i ≠ j. The overall matrix for the MMZI is then obtained as
for i ≠ j. The overall matrix for the MMZI is then obtained as  . The phase vector is estimated from the measurement of the number of particles in each mode. As probe, we focus on multimode Fock states with a single photon in each input mode of the interferometer18, |1, 1, 1〉 and |1, 1, 1, 1〉 for the three- and four-mode MZI, respectively. Here, |1, 1, 1〉 ≡ |1〉1 ⊗ |1〉2 ⊗ |1〉3 (and analogous definition for |1, 1, 1, 1〉), where |1〉j is a Fock state identifying a single particle in the jth mode.
. The phase vector is estimated from the measurement of the number of particles in each mode. As probe, we focus on multimode Fock states with a single photon in each input mode of the interferometer18, |1, 1, 1〉 and |1, 1, 1, 1〉 for the three- and four-mode MZI, respectively. Here, |1, 1, 1〉 ≡ |1〉1 ⊗ |1〉2 ⊗ |1〉3 (and analogous definition for |1, 1, 1, 1〉), where |1〉j is a Fock state identifying a single particle in the jth mode.
For the three-mode MZI, the results of the calculation for F−1 are shown in Fig. 2a–c. Analytic expression of the FIM is reported in the Supplementary Information. We observe that Tr[F−1] and the diagonal elements [F−1]1,1 and [F−1]2,2 depend on the phases ϕ1 and ϕ2. Notably, the inequalities (10) are violated at certain optimal values of the parameters, signaling that the Fock state |1, 1, 1〉 contains useful qudit entanglement: we find  (see Fig. 2a) and
(see Fig. 2a) and  (see Fig. 2b,c), which are smaller than the bound for qudit-separable states Tr[F−1] = 0.667 and [F−1]j,j = 0.33 (here N = 3 and n = 2), respectively. Additionally, we observe characteristic features. (i) F ≠ FQ, in particular, the minimum value of Tr[F−1] is greater than the corresponding minimum value of the QFIM:
(see Fig. 2b,c), which are smaller than the bound for qudit-separable states Tr[F−1] = 0.667 and [F−1]j,j = 0.33 (here N = 3 and n = 2), respectively. Additionally, we observe characteristic features. (i) F ≠ FQ, in particular, the minimum value of Tr[F−1] is greater than the corresponding minimum value of the QFIM:  (see Fig. 2a). (ii) The FIM is not always invertible: at the phase values for which det F = 0 the bound (2) is not defined. Around these points (white regions in Fig. 2a–c) [F−1]1,1 and/or [F−1]2,2 diverge. (iii) The working points to obtain the minimum of the multiparameter bound do not lead to symmetric errors on the single parameters ϕ1 and ϕ2. More specifically, when Tr[F−1] = 0.59, the bounds for the error on the single parameters are different:
(see Fig. 2a). (ii) The FIM is not always invertible: at the phase values for which det F = 0 the bound (2) is not defined. Around these points (white regions in Fig. 2a–c) [F−1]1,1 and/or [F−1]2,2 diverge. (iii) The working points to obtain the minimum of the multiparameter bound do not lead to symmetric errors on the single parameters ϕ1 and ϕ2. More specifically, when Tr[F−1] = 0.59, the bounds for the error on the single parameters are different:  . This is obtained for instance for working point Q1 = (ϕ1,ϕ2) = (0.892, 2.190), leading to
. This is obtained for instance for working point Q1 = (ϕ1,ϕ2) = (0.892, 2.190), leading to  and for working point Q2 = (ϕ1,ϕ2) = (2.190, 0.892), leading to
and for working point Q2 = (ϕ1,ϕ2) = (2.190, 0.892), leading to  , see Fig. 2a. In summary, with this choice of probe state and measurement it is not possible to saturate the quantum Cramer-Rao inequality simultaneously for the two parameters. Furthermore, according to point (iii) an adaptive estimation strategy (which we discuss below) is necessary to obtain the minimum sensitivity on both parameters with symmetric errors, and thus saturate the multiparameter Cramer-Rao bound.
, see Fig. 2a. In summary, with this choice of probe state and measurement it is not possible to saturate the quantum Cramer-Rao inequality simultaneously for the two parameters. Furthermore, according to point (iii) an adaptive estimation strategy (which we discuss below) is necessary to obtain the minimum sensitivity on both parameters with symmetric errors, and thus saturate the multiparameter Cramer-Rao bound.
(a–c) Optimal phase sensitivity of the three-mode balanced MZI with |1, 1, 1〉 probe state and photon-number measurement. Contour plots of (a) Tr[F−1], (b) (F−1)1,1, (c) (F−1)2,2, as a function of ϕ1 and ϕ2. Tr[F−1] is minimized at the working points Q1 and Q2 (see main text). (d–f) Optimal phase sensitivity of the four-mode balanced MZI with |1, 1, 1, 1〉 probe state and photon-number measurement. Contour plots of (d) Tr[ F−1], (e) (F−1)1,1, (f) (F−1)2,2, as a function of ϕ1 and ϕ2. These are shown for ϕ0 = 0.01 to avoid undetermined points in the plot. The QCRB is achieved, for instance, at the point O1 = [π, π]. Red areas indicate the violation of the separable bound defined in Eq. (10). Tables A and B report  and
and  for different input states and their comparison with the separable bound (Sep).
for different input states and their comparison with the separable bound (Sep).
We have repeated the above analysis for the four-mode interferometer (d = 4) with two unknown phases, ϕ1 and ϕ2, and a known control phase ϕ0 (see Fig. 1c). This configuration allows a comparison between three- and four-arm interferometers for the two parameter estimation. In the latter case the control phase ϕ0 gives us an additional degree of freedom. We choose as input the Fock State |1, 1, 1, 1〉. In Fig. 2d–f the results of our calculations are reported for a fixed value of ϕ0, as well as the numerical analysis of det F. We observe that as in the previous cases the FIM depends on the value of the parameter to be estimated. Furthermore, also in the four-mode the achievable sensitivity falls below the bound (10) for separable states: we have  ,
,  and
and  which are below the bounds 0.5 and 0.25 given by Eq. (10) (N = 4 and n = 2, here), respectively. The most notable difference with respect to the previous case is that the QCRB is achieved, for instance in working point O1 = [π, π]. In addition, both diagonal terms are equivalent and only a two step adaptive protocol is needed to reach the QCRB for any arbitrary phase vector (see discussion below).
which are below the bounds 0.5 and 0.25 given by Eq. (10) (N = 4 and n = 2, here), respectively. The most notable difference with respect to the previous case is that the QCRB is achieved, for instance in working point O1 = [π, π]. In addition, both diagonal terms are equivalent and only a two step adaptive protocol is needed to reach the QCRB for any arbitrary phase vector (see discussion below).
We have also compared the obtained results with the one achievable with other probe states. For instance, we consider a set of distinguishable particles  (where |q〉 stands for a single photon on mode kq), or an input coherent state
(where |q〉 stands for a single photon on mode kq), or an input coherent state  on input mode k1 with
on input mode k1 with  for d = 3 (α = 2 for d = 4) and no phase reference. We obtain
for d = 3 (α = 2 for d = 4) and no phase reference. We obtain  for both
for both  and
and  , within the bound Tr[F−1] ≥ 0.667 given by Eq. (10) for separable inputs. Similarly,
, within the bound Tr[F−1] ≥ 0.667 given by Eq. (10) for separable inputs. Similarly,  for both
for both  and
and  , within the bound Tr[F−1] ≥ 0.5. Results are summarized in Tables A and B.
, within the bound Tr[F−1] ≥ 0.5. Results are summarized in Tables A and B.
Adaptive phase estimation
In this section we present the adaptive estimation protocols required to maximize the precision on the simultaneous estimation of two arbitrary phases in a three- and four- mode MZI. The resources (the number of independent measurements ν) are split between multiple steps. A first step is needed to obtain a rough estimate of the unknown phases and requires a small subset of the resources which becomes negligible when the number of repetitions ν of the experiment is large enough. The subsequent steps exploit the available information to optimize the estimation procedure.
Regarding the three-mode interferometer, the above analysis has identified working points (Q1 and Q2) where the minimum uncertainty for the estimation of the two phases ϕ1 and ϕ2 does not give the same error on the two individual parameters. To overcome this limitation – and obtain approximatively a symmetric error in the joint estimation of the two phases – we exploited a three-step adaptive algorithm. The protocol requires ν independent measurements and the adoption of controlled phase shifts ψi on modes ki, with i = 1, 2, which have to be tuned during the protocol to perform the estimation at different working points (see in Fig. 1b). In a first step, we set ψ1,2 = 0 and obtain a rough estimate of the phases ϕi after a number of measurements much smaller than ν. Then, in step 2 the tunable phases ψi are adjusted so that ϕi + ψi on arms 1 and 2 are set to be close to the working point Q1. In this step essentially half of the remaining resources are spent so as to obtain  and
and  with an adequate estimator. Here
with an adequate estimator. Here  ,
,  represent respectively the estimation and the uncertainty of ϕi around working point Q1. In step 3 the same procedure is repeated for working point Q2. Finally the tunable phases ψ1.2 are subtracted so to recover ϕ1,2 ± δϕ1,2. The results of the adaptive algorithm are shown in Fig. 3a–d. Half of the measurements (ν1 = ν/2) are performed at point Q1, where
represent respectively the estimation and the uncertainty of ϕi around working point Q1. In step 3 the same procedure is repeated for working point Q2. Finally the tunable phases ψ1.2 are subtracted so to recover ϕ1,2 ± δϕ1,2. The results of the adaptive algorithm are shown in Fig. 3a–d. Half of the measurements (ν1 = ν/2) are performed at point Q1, where  and
and  , while the other half (ν2 = ν/2) are performed at point Q2, where
, while the other half (ν2 = ν/2) are performed at point Q2, where  and
and  . The expected error on a single phase δϕi after the two steps is then obtained as an appropriate combination of the values on the points Qi. More specifically, as the Fisher information is additive, the overall FIM reads F = ν1F1 + ν2F2, where Fi is the FIM in working points Qi. We observe that the protocol permits to achieve the bound of the working point, which for ν1 = ν2 is
. The expected error on a single phase δϕi after the two steps is then obtained as an appropriate combination of the values on the points Qi. More specifically, as the Fisher information is additive, the overall FIM reads F = ν1F1 + ν2F2, where Fi is the FIM in working points Qi. We observe that the protocol permits to achieve the bound of the working point, which for ν1 = ν2 is  . Note that the bound is lower than the bound (10) for separable states
. Note that the bound is lower than the bound (10) for separable states  .
.
The adaptive protocol (see text) aims at reaching a phase uncertainty δϕ1 ≈ δϕ2 after ν = 10000 independent measurements. (a,b) Uncertainties δϕ1/δϕm and δϕ2/δϕm obtained for different values of ϕ1 and ϕ2 (points) and normalized with respect to the expected value δϕm = 0.543/ (see text). As an example, we report the results obtained for the specific cases ϕ1 = π (c) and ϕ2 = π (d). In these panels the blue line is the estimated value of ϕ1, the red line is the estimated ϕ2. The inset shows the difference between the estimated value and the actual value of the phases, error bars are obtained by repeating 1000 times the numerical simulation of the protocol.
(see text). As an example, we report the results obtained for the specific cases ϕ1 = π (c) and ϕ2 = π (d). In these panels the blue line is the estimated value of ϕ1, the red line is the estimated ϕ2. The inset shows the difference between the estimated value and the actual value of the phases, error bars are obtained by repeating 1000 times the numerical simulation of the protocol.
The adaptive scheme for the four-mode interferometer is slightly different: in this case there are optimal working points, as the point O1, see Fig. 2, where QCRB is achieved for both phases. To reach the QCRB for arbitrary phases, we thus apply a two-step adaptive protocol. In the first step, we obtain a rough estimate of the parameters with an initial error δ. Then, in the second step we apply two supplementary phases ψ1 and ψ2 to translate the working point of the protocol to the neighbourhood of O1. It should be noticed that a convergent estimation protocol in the second step requires to set ϕ0 such that the quantity Tr[F−1] has no singularities. Note that the more ϕ0 deviates from ϕ0 = 0, the larger is the regular region around O1 (see Supplementary Information). The price to pay is a slightly increasing the error in the estimation process. The value of ϕ0 has to be chosen in order to move the singularity away from a neighbourhood of O1 larger than the inital error δ of the first step. The results of the protocol for the four-mode case with ϕ0 = 0.01 are then shown in Fig. 4a,b. Similarly to the three-mode case, we observe that the protocol permits to achieve the bound of the working point, which is  for ϕ0 = 0.01 (plane in Fig. 4), while the quantum Cramer-Rao bound reads
for ϕ0 = 0.01 (plane in Fig. 4), while the quantum Cramer-Rao bound reads  . This shows that achieving a convergent numerical protocol leads to a slight decrease in phase sensitivity due to singular points in the neighborhood of the working regions. Also in this case, the adaptive protocol allows to reach a sensitivity overcoming the bound of separable state for any vector parameter.
. This shows that achieving a convergent numerical protocol leads to a slight decrease in phase sensitivity due to singular points in the neighborhood of the working regions. Also in this case, the adaptive protocol allows to reach a sensitivity overcoming the bound of separable state for any vector parameter.
Conclusions
In this manuscript we have developed the general theory of quantum-enhanced multiphase estimation. In particular, we provide conditions of useful qudit-entanglement for the simultaneous estimation of multiple phases below the ultimate sensitivity limit achievable with qudit-separable states. We have focused on interferometers involving linear qudit transformations and multiple independent measurements. In a realistic experimental scenario, using multi-mode Mach-Zehnder interferometers and photo-counting measurements, Fock state probes can be exploited for multiphase estimation with quantum-enhancement phase sensitivity. With respect to the estimation of a single phase, where Fock states are known to be a useful resource, our analysis evidences a rich scenario: most notably, the phase sensitivity strongly depends on the phase value (the Cramer-Rao bound being not always definite) and on the interferometer configurations such as the three- and four-mode interferometers. Finally, we discuss and numerically simulate an adaptive estimation protocol which permits to achieve the expected bounds for any vector parameter. The adaptive strategy becomes crucial in multiparameter estimation since the simultaneous saturation of the ultimate limits for all parameters is in general not guaranteed.
During the completion of this manuscript, a first implementation of a tritter-based interferometer for single-phase estimation has been reported45.
Additional Information
How to cite this article: Ciampini, M. A. et al. Quantum-enhanced multiparameter estimation in multiarm interferometers. Sci. Rep. 6, 28881; doi: 10.1038/srep28881 (2016).
References
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222–229 (2011).
Pezzè, L. & Smerzi, A. Quantum theory of phase estimation. In Tino, G. & Kasevich, M. (eds.) Proceedings of the International School of Physics “Enrico Fermi”, Course CLXXXVIII “Atom Interferometry”, pag. 691 (Società Italiana di Fisica and IOS Press, Bologna, 2014). arXiv preprint. arXiv:1411.5164.
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401, doi: 10.1103/PhysRevLett.96.010401 (2006).
Pezzè, L. & Smerzi, A. Entanglement, nonlinear dynamics and the heisenberg limit. Phys. Rev. Lett. 102, 100401, doi: 10.1103/PhysRevLett.102.100401 (2009).
Hyllus, P. et al. Fisher information and multiparticle entanglement. Phys. Rev. A 85, 022321, doi: 10.1103/PhysRevA.85.022321 (2012).
Tóth, G. Multipartite entanglement and high-precision metrology. Phys. Rev. A 85, 022322, doi: 10.1103/PhysRevA.85.022322 (2012).
Krischek, R. et al. Useful multiparticle entanglement and sub-shot-noise sensitivity in experimental phase estimation. Phys. Rev. Lett. 107, 080504, doi: 10.1103/PhysRevLett.107.080504 (2011).
Preza, C., Snyder, D. L. & Conchello, J. A. Theoretical development and experimental evaluation of imaging models for differential-interference-contrast microscopy. J. Opt. Soc. Am. A 16, 2185–2199 (1999).
Zhou, X.Q. et al. Quantum-enhanced tomography of unitary processes. Optica 2, 510–516 (2015).
Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nature Photonics 7, 229–233 (2013).
Helstrom, C. W. Quantum Detection and Estimation Theory (Academic Press, 1976).
Paris, M. G. A. Quantum Estimation for Quantum Technology. Int. J. Quant. Inf. 7, 125–137 (2009).
Matsumoto, K. A new approach to the cramèr-rao-type bound of the pure-state model. J. Phys. A 35, 3111–3123 (2002).
Helstrom, C. W. & Kennedy, R. S. Noncommuting observables in quantum detection and estimation theory. IEEE Trans. Inform. Theory 20, 16–24 (1974).
Yuen, H. P. & Lax, M. Multiple-parameter quantum estimation and measurement of nonselfadjoint observables. IEEE Trans. Inform. Theory 19, 740–745 (1973).
Monras, A. & Illuminati, F. Measurement of damping and temperature: Precision bounds in gaussian dissipative channels. Phys. Rev. A 83, 012315, doi: 10.1103/PhysRevA.83.012315 (2011).
Spagnolo, N. et al. Quantum interferometry with three-dimensional geometry. Sci. Rep. 2, 862, doi: 10.1038/srep00862 (2012).
Humphreys, P. C., Barbieri, M., Datta, A. & Walmsley, I. A. Quantum enhanced multiple phase estimation. Phys. Rev. Lett. 111, 070403, doi: 10.1103/PhysRevLett.111.070403 (2013).
Genoni, M. G. et al. Optimal estimation of joint parameters in phase space. Phys. Rev. A 87, 012107, doi: 10.1103/PhysRevA.87.012107 (2013).
Crowley, P. J. D., Datta, A., Barbieri, M. & Walmsley, I. A. Multiparameter quantum metrology. Phys. Rev. A 89, 023845, doi: 10.1103/PhysRevA.89.023845 (2014).
Vidrighin, M. D. et al. Joint estimation of phase and phase diffusion for quantum metrology. Nat. Commun. 5, 3532, doi: 10.1038/ncomms4532 (2014).
Baumgratz, T. & Datta, A., Quantum Enhanced Estimation of a Multidimensional Field. Phys. Rev. Lett. 116, 030801 (2016).
Reck, M., Zeillinger, A., Herbert J, B. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 59–61 (1994).
Nolte, S., Will, M., Burghoff, J. & Tuennermann, A. Femtosecond waveguide writing: a new avenue to three-dimensional integrated optics. Appl. Phys. A 77, 109–111 (2003).
Kowalevicz, A. M., Sharma, V., Ippen, E. P., Fujimoto, J. G. & Minoshima, K. Three-dimensional photonic devices fabricated in glass by use of a femtosecond laser oscillator. Optics Letters 30, 1060–1062 (2005).
Liu, B. & Ou, Z. Y. Engineering multiphoton entangled states by quantum interference. Phys. Rev. A 74, 035802, doi: 10.1103/PhysRevA.74.035802 (2006).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & O’Brien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Matthews, J. C. F., Politi, A., Stefanov, A. & O’Brien, J. L. Manipulating multi-photon entanglement in waveguide quantum circuits. Nat. Photon. 3, 346–350 (2009).
Crespi, A. et al. Three-dimensional mach-zehnder interferometer in a microfluidic chip for spatially-resolved label-free detection. Lab Chip 10, 1167–1173 (2010).
Metcalf, B. J. et al. Multi-photon quantum interference in a multi-port integrated photonic device. Nat. Commun. 4, 1356, doi: 10.1038/ncomms2349 (2013).
Meany, T. et al. Non-classical interference in integrated 3d multiports. Opt. Express 20, 26895–26905 (2012).
Suzuki, K., Sharma, V., Fujimoto, J. G., Ippen, E. P. & Nasu, Y. Characterization of symmetric [3 × 3] directional couplers fabricated by direct writing with a femtosecond laser oscillator. Opt. Express 14, 2335–2343 (2006).
Peruzzo, A., Laing, A., Politi, A., Rudolph, T. & O’Brien, J. L. Multimode quantum interference of photons in multiport integrated devices. Nat. Commun. 2, 224, doi: 10.1038/ncomms1228 (2011).
Spagnolo, N. et al. Three-photon bosonic coalescence in an integrated tritter. Nat. Commun. 4, 1606, doi: 10.1038/ncomms2616 (2013).
Weihs, G., Reck, M., Weinfurter, H. & Zeilinger, A. All-fiber three-path mach-zehnder interferometer. Optics Letters 21, 302–304 (1996).
Nagata, T., Okamoto, R., O’Brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007).
Xiang, G. Y., Higgins, B. L., Berry, D. W., Wiseman, H. M. & Pryde, G. J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photon. 5, 43–47 (2011).
Kacprowicz, M., Demkowicz-Dobrzanski, R., Wasilewski, W., Banaszek, K. & Walmsley, I. A. Experimental quantum-enhanced estimation of a lossy phase shift. Nat. Photon. 4, 357–360 (2010).
Holland, M. & Burnett, K. Interferometric detection of optical phase shifts at the heisenberg limit. Phys. Rev. Lett. 71, 1355–1358 (1993).
Kim, T., Pfister, O., Holland, M. J., Noh, J. & Hall, J. L. Influence of decorrelation on heisenberg-limited interferometry with quantum correlated photons. Phys. Rev. A 57, 4004–4013 (1998).
Pezzè, L. & Smerzi, A. Ultrasensitive two-mode interferometry with single-mode number squeezing. Phys. Rev. Lett. 110, 163604, doi: 10.1103/PhysRevLett.110.163604 (2013).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).
Wasak, T., Smerzi, A., Pezzè, L., & Chwedenczuk, J. Optimal measurements in phase estimation: simple examples. Quantum information processing 15, 2231–2252 (2016).
Zukowski, M., Horne, M. A., Bernstein, J. & Greenberger, D. M. Quantum Interferometry (World Scientificd Scientific, 1993).
Chaboyer, Z., Meany, T., Helt, L. G., Withford, M. J. & Steel, M. J. Tuneable quantum interference in a 3d integrated circuit. Sci. Rep. 5, 9601, doi: 10.1038/srep09601 (2015).
Acknowledgements
This work was supported by ERC-Starting Grant 3D-QUEST (3D-Quantum Integrated Optical Simulation; grant agreement no. 307783, http://www.3dquest.eu), EU-STREP Project QIBEC and PRIN project Advanced Quantum Simulation and Metrology (AQUASIM). LP acknowledges financial support by MIUR through FIRB Project No. RBFR08H058.
Author information
Authors and Affiliations
Contributions
M.A.C., N.S., C.V., L.P., A.S. and F.S. contributed to design the ideas, perform the calculations, analyse the results and write the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ciampini, M., Spagnolo, N., Vitelli, C. et al. Quantum-enhanced multiparameter estimation in multiarm interferometers. Sci Rep 6, 28881 (2016). https://doi.org/10.1038/srep28881
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28881
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.





 and
and  obtained for different values of ϕ1 and ϕ2 (points) and normalized with respect to the achievable bound
obtained for different values of ϕ1 and ϕ2 (points) and normalized with respect to the achievable bound  . The horizontal red line in the legend corresponds to the quantum Cramer-Rao bound for the single-parameter.
. The horizontal red line in the legend corresponds to the quantum Cramer-Rao bound for the single-parameter.