Abstract
In recent years, the analysis of genomes by means of strings of length k occurring in the genomes, called k-mers, has provided important insights into the basic mechanisms and design principles of genome structures. In the present study, we focus on the proper choice of the value of k for applying information theoretic concepts that express intrinsic aspects of genomes. The value k = lg2(n), where n is the genome length, is determined to be the best choice in the definition of some genomic informational indexes that are studied and computed for seventy genomes. These indexes, which are based on information entropies and on suitable comparisons with random genomes, suggest five informational laws, to which all of the considered genomes obey. Moreover, an informational genome complexity measure is proposed, which is a generalized logistic map that balances entropic and anti-entropic components of genomes and is related to their evolutionary dynamics. Finally, applications to computational synthetic biology are briefly outlined.
Similar content being viewed by others
Introduction
The study of complexity in Biology is an old topic that often reemerges in theoretical biological investigations1,2,3. The study of complexity has very important implications for any deep understanding of the informational organization that life chooses in the different species to realize their specific biological functionalities. Entropy is a fundamental scientific concept that is naturally related to complexity and was the basis of statistical physics founded by Ludwig Boltzmann and the essence of his famous H theorem, which related the arrow of time to Boltzmann’s equation, where entropy is expressed in terms of mechanical microstates4. Essentially, the same function was the basis of the information theory founded by Claude Shannon in 19485, where entropy is defined on information sources, that is, probability distributions over finite sets of elements (symbols, words or signals). A genome is essentially a text; if read at pieces of length k (called k-mers), a genome becomes an information source. Therefore genomic k-entropies can be easily defined and the concepts and results of information theory can be applied6,7,8,9,10.
In recent years, many studies have approached the investigation of DNA strings and genomes by means of algorithms, information theory and formal languages11,12,13,14,15,16,17,18,19,20,21,22 and methods were developed for investigating whole genome structures. In particular, dictionaries of words occurring in genomes, distributions defined over genomes and concepts related to word occurrences and frequencies have been very useful and seem to characterize important genomic features relevant in biological contexts23,24,25,26,27,28,29,30. Dictionaries are, in essence, finite formal languages. In genome analyses based on dictionaries, concepts from formal language theory, probability and information theory are naturally combined by providing new perspectives in the investigation of genomes, which may disclose the internal logics of their structures.
The set of all k-mers, occurring in a given genome is a particular dictionary. A point that is crucial in genome analyses based on k-mers is the value of k that is more adequate for specific investigations. This issue becomes extremely evident when computing the entropy of a genome. We prove that preferential lengths exist for computing entropies and in correspondence with these lengths, some informational indexes can be defined that exhibit “informational laws” and characterize an informational structure of genomes. As we have already noticed, there is a long tradition in investigating genomes by using k-mers. However, comparing genomes of different lengths, by using the same value of k (usually less than 12) may result in the loss, in some cases, of important regularities. In fact, the genomic laws that we discover emerge when the values of k are suitably defined from the logarithmic length of the genomes.
When genomic complexity is considered, it is very soon clear that it cannot be easily measured by parameters such as genome length, number of genes, CG-content, basic repeatability indexes, or their combinations. Therefore, we follow an information theoretic line of investigation based on k-mer dictionaries and entropies16,26,27,31,32,33, which is aimed at defining and computing informational indexes for a representative set of genomes. This task is not trivial when genome sizes increase, so a specific software package is used to this end31. Moreover, an aspect that is missing in classical Shannon’s conceptual apparatus is relevant in our approach: random strings and pseudo-random generation algorithms, which now can be easily produced and analyzed34. In fact, it is natural to assume that the complexity of a genome increases with its “distance” from randomness35,36, as identified by means of a suitable comparison between the genome under investigation and random genomes of the same length. This idea alone provides important clues about the correct k-mer length to consider in our genome analyses, because theoretical and experimental analyses show that random genomes reach their entropic maxima for k-mers of length lg2(n), where n is the genome length. No assumption on the distribution of probability of k-mers is assumed or inferred (as in Markov Models-based approaches); rather, data processing is developed on the basis of the empirical distributions of k-mers computed over the investigated genomes.
To this end, two basic indexes are introduced, which we call entropic and anti-entropic components. These indexes and other related indexes, are computed over the chosen seventy genomes, ranging from prokaryotes to primates. The obtained values suggest some laws of genome structure. These laws hold in all of the investigated genomes and motivate the definition of the genomic complexity measure BB proposed in the paper. This measure depends on the entire structure of a genome and considers, together, the components of genomes (e. g., repeats, CpG, long range correlations, surely affecting entropies) without considering them separately. Moreover, as demonstrated below, BB is related to phylogeny but does not coincide with phylogenetic ordering. Certainly, primate genomes are usually more complex than, say, bacterial or insect genomes, but the situation is surely more critical because evolution is always active and a bacterium that we sequence today is not a type of bacteria that firstly arose in the tree of life. For this reason, genomes that are phylogenetically older can cumulate, even along different paths, “distances” from their corresponding random genomes comparable with those gained by “more evolved” genomes.
Results
The results presented in this paper are based on comparing real genomes with random genomes of the same length. As we show, any genome  of length n defines a partition of lg4(n) in two addends
of length n defines a partition of lg4(n) in two addends  and
and  such that
such that  .
.
The fundamental informational components of genomes
We denote by  the value
the value  . Of course,
. Of course,  . We call
. We call  the logarithmic length of
the logarithmic length of  and
and  the double logarithmic length of
the double logarithmic length of  . When no possible confusion can arise, we avoid explicitly indicating
. When no possible confusion can arise, we avoid explicitly indicating  , so we write in short LG and consequently we denote the entropy
, so we write in short LG and consequently we denote the entropy  over the
over the  -mers of
-mers of  by
by  (analogous abbreviations are also adopted for other indexes). We also refer to the interval
(analogous abbreviations are also adopted for other indexes). We also refer to the interval  as the critical entropic interval. In the following, when 2LG is not integer,
as the critical entropic interval. In the following, when 2LG is not integer,  denotes the linear interpolation between
denotes the linear interpolation between  and
and  , where k1, k2 are the smallest integers such that k1 < 2LG < k2. In the case of the human genome, 2LG is between 31 and 32; in the genomes considered in this paper (from microbes to primates), it ranges between 16 and 36.
, where k1, k2 are the smallest integers such that k1 < 2LG < k2. In the case of the human genome, 2LG is between 31 and 32; in the genomes considered in this paper (from microbes to primates), it ranges between 16 and 36.
We prove, by using well-known results of information theory, that the values LG and 2LG have the following properties (see section Methods):
-
i
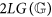 is an upper bound to the values that entropy can reach over the genomes with the same length of
is an upper bound to the values that entropy can reach over the genomes with the same length of  ;
; -
ii
if k belongs to the critical interval
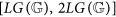 and
and 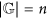 , then entropies Ek, for k ≤ n, reach, on suitable genomes, the best approximations to
, then entropies Ek, for k ≤ n, reach, on suitable genomes, the best approximations to  with an error close to zero, which is inferior to
with an error close to zero, which is inferior to  , being
, being  the closest integer greater than x.
the closest integer greater than x. -
iii
entropy
 reaches its maximum in random genomes of length
reaches its maximum in random genomes of length  . This result follows from the fact that in random genomes of length n all lg2(n)-mers are hapaxes, that is, they occur once in the whole genome37.
. This result follows from the fact that in random genomes of length n all lg2(n)-mers are hapaxes, that is, they occur once in the whole genome37.
In conclusion, the maximum of  is almost equal to
is almost equal to  and this maximum is reached by random genomes of length
and this maximum is reached by random genomes of length  . It was realized that for all of the investigated genomes the following inequality immediately holds:
. It was realized that for all of the investigated genomes the following inequality immediately holds:

Therefore, we know that  belongs to the (open) real interval of bounds
belongs to the (open) real interval of bounds  and
and  . Then, we can define the following values
. Then, we can define the following values  and
and  , which we call Entropic Component and anti-entropic Component of
, which we call Entropic Component and anti-entropic Component of  , respectively:
, respectively:


Summing Equations (2) and (3), we obtain  . The value
. The value  corresponds to the gap between the double logarithmic entropy
corresponds to the gap between the double logarithmic entropy  and the logarithmic length
and the logarithmic length  , which is always positive according to the equations above. Moreover,
, which is always positive according to the equations above. Moreover,  is the gap between the double logarithmic length
is the gap between the double logarithmic length  and the entropy
and the entropy  , which is positive because
, which is positive because  is an upper bound to the entropies in the critical entropic interval. The term “anti-entropic” stresses an important difference with the analogous concept of neghentropy, which is frequently used to denote the other side of the order/disorder dichotomy associated with entropy (and its time arrow)38,39,40,41. In fact, in anti-entropy, no change of sign is involved, but a difference from an upper bound of the entropy is instead considered.
is an upper bound to the entropies in the critical entropic interval. The term “anti-entropic” stresses an important difference with the analogous concept of neghentropy, which is frequently used to denote the other side of the order/disorder dichotomy associated with entropy (and its time arrow)38,39,40,41. In fact, in anti-entropy, no change of sign is involved, but a difference from an upper bound of the entropy is instead considered.
Informational genomic laws
Let us define  , called lexical index, as the ratio:
, called lexical index, as the ratio:

The numerator is essentially the number of words of length 2LG occurring in random genomes, which as we already noticed are all hapaxes and therefore, coincides with the number of possible occurrences of 2LG-mers in  . The denominator is the number of words of length 2LG occurring in
. The denominator is the number of words of length 2LG occurring in  . This ratio is related to the degree of order that
. This ratio is related to the degree of order that  gains with respect to random genomes. In fact, in a random genome R, we have LX(R) = 1; therefore, in a real genome
gains with respect to random genomes. In fact, in a random genome R, we have LX(R) = 1; therefore, in a real genome  ,
,  . The lexical index is smaller than the ratio
. The lexical index is smaller than the ratio  but is greater than
but is greater than  . Moreover, by dividing and multiplying LX by
. Moreover, by dividing and multiplying LX by  and
and  , it is possible to obtain lower and upper bounds to
, it is possible to obtain lower and upper bounds to  . The value
. The value  , given by
, given by  , corresponds to the eccentricity of an ellipse associated with
, corresponds to the eccentricity of an ellipse associated with  (see Supplementary Information, Sup. Fig. 3). The product of
(see Supplementary Information, Sup. Fig. 3). The product of  with
with  differs by 1 less than
differs by 1 less than  . In conclusion, the following laws hold for all seventy investigated genomes:
. In conclusion, the following laws hold for all seventy investigated genomes:





Biobit: a measure of genomic complexity
As we already noticed, AC is an index measuring the informational distance between genomes and random genomes with the same length. This means that the more biological functions a genome  has acquired, the further the genome is from randomness. However, if we directly identify the complexity of
has acquired, the further the genome is from randomness. However, if we directly identify the complexity of  with
with  , we obtain some biologically inconsistent results. For example, Zea mays has an LG value of 15.4701 but an AC value of 3.6678 (primates have AC less than 1). These types of anomalies suggested to us that AC is surely related to the biological complexity of a genome, but this complexity is not a linear function of AC because also the EC component also has to be considered in a more comprehensive definition of complexity. Our search focused on a function that combines AC with EH, which is strictly related to EC. If x briefly denotes the anti-entropic fraction AF = AC/LG, it is easy to verify that because EC = LG − AC, then EH = (EC − AC)/LG = (1 − 2x); therefore, the product AC * EH can be represented by:
, we obtain some biologically inconsistent results. For example, Zea mays has an LG value of 15.4701 but an AC value of 3.6678 (primates have AC less than 1). These types of anomalies suggested to us that AC is surely related to the biological complexity of a genome, but this complexity is not a linear function of AC because also the EC component also has to be considered in a more comprehensive definition of complexity. Our search focused on a function that combines AC with EH, which is strictly related to EC. If x briefly denotes the anti-entropic fraction AF = AC/LG, it is easy to verify that because EC = LG − AC, then EH = (EC − AC)/LG = (1 − 2x); therefore, the product AC * EH can be represented by:

This function (after a simple change of variables) is a type of logistic map ax(1 − x), with a constant and x variable ranging in [0, 1], which is very important in population dynamics.
If we generalize x(1 − 2x) in the class of functions xγ(1 − 2x)δ, with γ and δ positive rationals weighting the two factors, then we discover that these functions have maxima for values approaching to zero when γ ≤ 1 decreases and δ increases. Therefore, because AC is supposed to have a predominant role in the complexity measure, we define BBγ,δ as BBγ,δ = xγ(1 − 2x)δ by choosing the values of the exponents in such a way that maxima of BBγ,δ fall close to the values that the anti-entropic fraction AF assumes for the most part in genomes with high values of AC (almost all of them have medium horizontal eccentricity; see Supplementary Information, Sup. Table 2). No genome on our list reaches the maximum of the chosen function because their AF value is always smaller (suboptimal genomes) or greater (super-optimal genomes) than the value where the maximum is reached.
In conclusion, we conjecture that the genomic complexity is a non-linear function of AC having the form (apart from a multiplicative constant):

In particular, the following definition, which is an instance of (10), was supposed to be the most appropriate ( and
and  ):
):

In Fig. 1, the biobit values, together with the other described informational indexes, of the seventy genomes are visualized in a diagram. In Fig. 2 a flowchart is given that, in general terms, expresses the main stages for computing the BB measure of a given genome.
A flowchart of the computational steps involved in calculating  .
.
Given an input genome  , an upper bound of maximum entropy is calculated, its value equals
, an upper bound of maximum entropy is calculated, its value equals  and the value also defines the appropriate word length. Then the entropic and anti-entropic components are computed as, respectively,
and the value also defines the appropriate word length. Then the entropic and anti-entropic components are computed as, respectively,  and
and  and are successively normalized and combined by a weighted product into
and are successively normalized and combined by a weighted product into  .
.
A further law could be associated with the biobit index, according to which genomes evolve by increasing the value of the BB function. This means that an ordering, denoted by  (a reflexive, antisymmetric and transitive relation), can be defined such that:
(a reflexive, antisymmetric and transitive relation), can be defined such that:

Table 1 reports the main informational indexes based on the two entropic components of the logarithmic length of genomes. Figure 3 depicts graphically the values of these informational indexes for all of the investigated genomes (see Supplementary Information, Sup. Table 4, for the exact numerical values). The lengths of genomes are naturally linearly ordered, thus allowing us to arrange them along the x-axis. Apart from the EC curve, which is quite coincident with LG, the other indexes presents peaks that correspond to the genomes differing only slightly in lengths but differing greatly in other indexes.
It is interesting that, in essence, biological evolution is anti-entropic because the AC component, representing the tendency toward order, increases with the increase of biological functionalities, under the constraint of keeping the ratio AC/EC under a threshold, as expressed by the factor (1 − 2x)3 of BB.
A 3D-visualization of our seventy genomes, by means of the AC, LX, BB informational indexes (see Supplementary Information, Sup. Fig. 2), reveals that genomic complexity does not coincide with classical phylogenetic classifications, as argued in the next section.
Discussion
We think that our informational indexes and the laws relating them, confirm a very simple and general intuition. If life is information represented and elaborated by means of (organic) molecules, then the laws of information necessarily have to reveal the deep logic of genome structures.
The laws presented in the previous section represent universal aspects of genome structure and may rarely hold for strings of the same lengths that are not genomes. Therefore, the genomic complexity measure BB, obtained by means of informational indexes, is not a mathematical trick but must to be related to the way genomes are organized and to the way in which the genomes were generated. Figure 2 shows the values of BB along the 70 investigated genomes and it is clear that BB is related to the evolutionary positions of organisms. However, our approach has an important biological implication in clarifying the difference between phylogenesis and genomic complexity, which are related but different concepts. In fact, several cases have been found (see Fig. 2 and Sup. Fig. 2 in Supplementary Information) where organisms that are phylogenetically more primitive than others, for example bacteria, have biobit values greater than those of “more evolved” organisms. The reason could be the following. A bacterium that we sequence today is an evolutionary product of some primitive bacterium. Even if we do not know the path from the bacterium’s (possibly unknown) ancestor to the bacterium, its complexity along this path grew over time because its evolutionary age is the same as H. sapiens (even along different branches). The genomic complexity of  is, in a sense, a measure of the relevant steps from random genomes to
is, in a sense, a measure of the relevant steps from random genomes to  . Surely, these steps reflect the evolutionary pressure and the biological interactions and competitions among species. However, if we forget this perspective, we lose an important aspect of evolutionary dynamics. This is why complexity-driven classifications that completely agree with phylogenesis are almost impossible. For example, we found that bacteria associated with human diseases have BB values significantly higher than others phylogenetically comparable to them. The BB measure is a sort of absolute distance from random, whereas phylogenesis concerns similarity or dissimilarity between species. Therefore, a very natural question arises, which suggests the development of the presented theory. Can entropic divergences (Kullback-Leibler divergence or similar concepts) be applied to phylogenetic analysis of genomes by means of “common words” and their probability distributions in the compared genomes? Finally, what is the applicability of our indexes in the identification of informational features that are relevant in specific pathological genetic disorders? Of course, these questions deserve specific investigations; however, our informational indexes with the related laws and computational tools, provide a framework on which these informational analyses may be fruitfully set. We argue that it is almost impossible that functional changes do not correspond to precise informational alterations in the relationships expressed by the genomic laws. The challenge is in discovering the specific keys of these correspondences.
. Surely, these steps reflect the evolutionary pressure and the biological interactions and competitions among species. However, if we forget this perspective, we lose an important aspect of evolutionary dynamics. This is why complexity-driven classifications that completely agree with phylogenesis are almost impossible. For example, we found that bacteria associated with human diseases have BB values significantly higher than others phylogenetically comparable to them. The BB measure is a sort of absolute distance from random, whereas phylogenesis concerns similarity or dissimilarity between species. Therefore, a very natural question arises, which suggests the development of the presented theory. Can entropic divergences (Kullback-Leibler divergence or similar concepts) be applied to phylogenetic analysis of genomes by means of “common words” and their probability distributions in the compared genomes? Finally, what is the applicability of our indexes in the identification of informational features that are relevant in specific pathological genetic disorders? Of course, these questions deserve specific investigations; however, our informational indexes with the related laws and computational tools, provide a framework on which these informational analyses may be fruitfully set. We argue that it is almost impossible that functional changes do not correspond to precise informational alterations in the relationships expressed by the genomic laws. The challenge is in discovering the specific keys of these correspondences.
We developed some computational experiments showing a direct applicability of informational indexes and related genomic laws to the emergent field of synthetic biology. In fact, recent experiments on minimal bacteria42 are based on the search for genome sequences obtained by manipulating and reducing some real genomes. It has been proved that after removing some parts of the M. mycoides genome, the resulting organism, JCVI-syn3.0 (531 kilobase pairs, 473 genes), is able to survive and has a genome smaller than that of any autonomously replicating cell found in nature (very close to M. genitalium). Of course, in this manner a better understanding of biological basic functions is gained, which directly relates with the investigated genome (removing essential portions results in life disruption). On the basis of this principle, we considered M. genitalium and removed some portions of its genome through a greedy exploration of the huge space of possibilities. At every step of our genome modifications (of many different types), we checked the validity of our genomic laws. We found that, after removing portions of the genome, some of our laws do not hold in the resulting sequences (see Supplementary Information, Sup. Table 6). Of course, these methods need to be carefully analyzed and validated with other examples and comparisons. However, a clear indication seems to emerge about the applicability of informational indexes and laws, possibly after suitable improvements to support and complement the development of genome synthesis and analysis, in the spirit of new trends in synthetic biology.
The starting point of our investigation was the comparisons of real genomes with random genomes of the same length. To accomplish this purpose, the right length of k-mers equal to the double logarithmic length of genomes was identified as being more appropriate for this comparison because for this length random genomes reach their maximum entropy. The difference between entropies was considered a measure of the order acquired by real genomes and corresponded to their capability of realizing biological functions. This intuition was supported by the values of indexes that we computed for an initial list of genomes. In fact, Sup. Table 3 in Supplementary Information provides AC values that, apart from two evident exceptions, seem to confirm the increasing of the AC value in accordance with the macroscopic biological complexity of organisms (independently from length, number of genes, or other typical genomic parameters). However, when we extended our analysis by including other genomes43, we found AC values that were anomalous with respect to those already collected. In particular, plants provided extreme values, with no coherence with our interpretation of the AC index. To solve this puzzle, we considered a more comprehensive framework where AC and EC values interact in a trade-off between order and randomness. Genomes deviate from randomness, though to some extent, because genomes need a level of randomness that is sufficient to keep their evolutionary nature, based on a random exploration of new possibilities of life (filtered by natural selection).
In this picture, the two quantities  and
and  seem to correspond to the informational measure of two important aspects of genomes: evolvability and programmability (in the sense of2). Evolvability measures the random component of genomes, whereas programmability measures the order that genomes gain with respect to pure random genomes by acquiring biological functions. The non-random meaning of AC can be mathematically characterized in terms of Kullback-Leibler entropic divergence between the probability distribution of words of
seem to correspond to the informational measure of two important aspects of genomes: evolvability and programmability (in the sense of2). Evolvability measures the random component of genomes, whereas programmability measures the order that genomes gain with respect to pure random genomes by acquiring biological functions. The non-random meaning of AC can be mathematically characterized in terms of Kullback-Leibler entropic divergence between the probability distribution of words of  and the probability distribution of the same words in random genomes44.
and the probability distribution of the same words in random genomes44.
Genome evolution is realized through an interplay of programmability and evolvability. The anti-entropic component AC cannot increase beyond a percentage of the logarithmic length because LG = AC + EC and therefore increase of AC implies a decrease of EC by reducing the evolutionary ability. Therefore, the only way to increase AC, by keeping a good balance of the two components, is to increase the value of LG, i. e., the genome length, which explains why genomes increase their length during evolution. However, this increase is only indirectly correlated with biological complexity, as apparent in Fig. 1 (see also Supplementary Information, Sup. Table 3).
The definition of genomic complexity, in terms of a nonlinear function of AC, is related to the balance between AC and EC values. Some of the genome entropic laws continue to also hold for k-mers with  , but almost none of the laws continue to hold when
, but almost none of the laws continue to hold when  . For example, for k = 6 and
. For example, for k = 6 and  , the values of AC completely lose the logic that they have for
, the values of AC completely lose the logic that they have for  , by showing dramatic changes with respect to
, by showing dramatic changes with respect to  , on which our indexes are based (see Supplementary Information, Sup. Table 4). Of course, we could compare real and random genomes also for values shorter than
, on which our indexes are based (see Supplementary Information, Sup. Table 4). Of course, we could compare real and random genomes also for values shorter than  , but in this case, we need to generate random genomes and compute the corresponding entropies, whereas for
, but in this case, we need to generate random genomes and compute the corresponding entropies, whereas for  , we do not need such generations and computations, because we know, by theoretical arguments (see Proposition 3) that in random genomes, entropies at double logarithmic lengths can be assumed to be equal to
, we do not need such generations and computations, because we know, by theoretical arguments (see Proposition 3) that in random genomes, entropies at double logarithmic lengths can be assumed to be equal to  .
.
Our investigation can be compared to the astronomical observations measuring positions and times in the orbits of celestial objects. Kepler’s laws arose from the regularities found in planetary motions and from Kepler’s laws, the laws of mechanics emerged. This astronomical comparison, which was an inspiring analogy, revealed a surprising coincidence when ellipses were introduced in the representation of entropic and anti-entropic components. Kepler’s laws were explained by Newton’s dynamical and gravitational principles. Continuing our analogy, probably deeper informational principles are the ultimate reason for the laws that we found.
Methods
The seventy investigated genomes include prokaryotes, algae, amoebae, fungi, plants and animals of different types. In Sup. Table 5 of Supplementary Information, source data bases, assembly identifiers, genome lengths and percentages of unknown nucleotides are given. Basic concepts from information theory, probability theory and formal language theory can be found in classical texts in these fields5,45,46.
Basic definitions and notation
Strings are finite sequences of contiguous symbols. Mathematically, strings are functions from a set of positions, viewed as a subset of the set  of natural numbers,
of natural numbers,  to a set of symbols, called alphabet. The number n is called the length of the string. We denote generic strings with Greek letters (possibly with subscripts) and reserve λ for the empty string (useful for expressing mathematical properties of strings). The length of a string α is denoted by |α| and α[i] is the symbol occurring in α at position i, whereas α[i, j] is the string occurring in α between the positions i and j (both included).
to a set of symbols, called alphabet. The number n is called the length of the string. We denote generic strings with Greek letters (possibly with subscripts) and reserve λ for the empty string (useful for expressing mathematical properties of strings). The length of a string α is denoted by |α| and α[i] is the symbol occurring in α at position i, whereas α[i, j] is the string occurring in α between the positions i and j (both included).
Let us consider the genomic alphabet of four symbols (characters, or letters, associated with nucleotides) {a, c, g, t}. The set {a, c, g, t}*, as usual, denotes the set of all possible strings over {a, c, g, t}. A genome  is representable by a string of {a, c, g, t}*, where symbols that occur, from the first to the last position, are written in the order that they occur, from left to right, according to the standard writing system of Western languages and according to the chemical orientation 5′–3′ of DNA molecules.
is representable by a string of {a, c, g, t}*, where symbols that occur, from the first to the last position, are written in the order that they occur, from left to right, according to the standard writing system of Western languages and according to the chemical orientation 5′–3′ of DNA molecules.
Substrings  of length k, where
of length k, where  , are also called k-words, k-factors, k-mers of
, are also called k-words, k-factors, k-mers of  (k may be omitted, when it is not relevant). We remark that the absolute value notation |−| used for string length has different meaning when applied to sets or multisets. In fact, for a finite set A, then |A| denotes its cardinality, whereas for a finite multiset X (set of elements that possibly occur in many “identical” copies, with no relevance for occurrence order) |X| denotes its size (the sum of the elements of X each counted all the times that the element occurs).
(k may be omitted, when it is not relevant). We remark that the absolute value notation |−| used for string length has different meaning when applied to sets or multisets. In fact, for a finite set A, then |A| denotes its cardinality, whereas for a finite multiset X (set of elements that possibly occur in many “identical” copies, with no relevance for occurrence order) |X| denotes its size (the sum of the elements of X each counted all the times that the element occurs).
A dictionary of is a set of strings occurring in
is a set of strings occurring in  . We denote by
. We denote by  the dictionary of all k-mers occurring in G. It is easy to verify that the number of occurrences of k-mers in
the dictionary of all k-mers occurring in G. It is easy to verify that the number of occurrences of k-mers in  is
is  (
( is the length of
is the length of  ) and corresponds to the maximum cardinality
) and corresponds to the maximum cardinality  reachable by a dictionary of k-mers within genomes of the same length of
reachable by a dictionary of k-mers within genomes of the same length of  .
.
A word α of D can occur in  many times. We denote by
many times. We denote by  its multiplicity in
its multiplicity in  , that is, the number of times α occurs in
, that is, the number of times α occurs in  . A word of
. A word of  with multiplicity greater than 1 is called a repeat of
with multiplicity greater than 1 is called a repeat of  , whereas a word with multiplicity equal to 1 is called a hapax of
, whereas a word with multiplicity equal to 1 is called a hapax of  . This term is used in philological investigation of texts, but it is also adopted in document indexing and compression37. The values of word multiplicities can be normalized if we divide the word multiplicities by the sum of the multiplicities of all the words occurring in
. This term is used in philological investigation of texts, but it is also adopted in document indexing and compression37. The values of word multiplicities can be normalized if we divide the word multiplicities by the sum of the multiplicities of all the words occurring in  . This normalization corresponds to replacing multiplicities with frequencies, which can be seen as percentages of multiplicity.
. This normalization corresponds to replacing multiplicities with frequencies, which can be seen as percentages of multiplicity.
Many important indexes related to characteristics of genome dictionaries can be defined on genomes. For example,  is the length of the longest repeats of
is the length of the longest repeats of  . Of course,
. Of course,  is the minimum length, such that k-mers with k greater than
is the minimum length, such that k-mers with k greater than  are all hapaxes.
are all hapaxes.
Shannon used the term information source as synonymous with discrete probability distribution to introduce the notion of (information) entropy. Given a distribution of probability p, over a finite set A, its entropy is given by  . We remark that if −lg2(p(x)) is considered to be the information associated with the occurrence of x∈A (the more improbable x is, the more its occurrence is informative), then entropy is the mean (in a probabilistic sense) quantity of information emitted by the information source (A, p).
. We remark that if −lg2(p(x)) is considered to be the information associated with the occurrence of x∈A (the more improbable x is, the more its occurrence is informative), then entropy is the mean (in a probabilistic sense) quantity of information emitted by the information source (A, p).
An intrinsic property of entropy is its Equipartition Property, that is, in the finite case, the fact that entropy reaches its maximum value lg2(|A|), when p is equally distributed, that is, when p(x) = 1/|A|, for all x ∈ A (|A| is the number of elements of A).
A genome  is any sequence over the alphabet {a, c, g, t}. This definition includes real genomes and ideal genomes, with no biological meaning, which are important in the mathematical analysis of genomes, as “material points” are essential in physics for discovering motion laws. Any subsequence of contiguous symbols of
is any sequence over the alphabet {a, c, g, t}. This definition includes real genomes and ideal genomes, with no biological meaning, which are important in the mathematical analysis of genomes, as “material points” are essential in physics for discovering motion laws. Any subsequence of contiguous symbols of  is called a string, word, or k-mer of
is called a string, word, or k-mer of  (k explicitly expresses the length).
(k explicitly expresses the length).
The empirical k-entropy of
of  is given by (the adjective empirical refers to the use of frequencies):
is given by (the adjective empirical refers to the use of frequencies):

We remark that the entropy  is computed only with the k-mers occurring in
is computed only with the k-mers occurring in  (see definition of
(see definition of  ). The computation of
). The computation of  becomes prohibitive when
becomes prohibitive when  has length of order 109 and k > 20. Therefore, we used suffix arrays47 in the computation of genomic dictionaries.
has length of order 109 and k > 20. Therefore, we used suffix arrays47 in the computation of genomic dictionaries.
A Bernoullian, or random, genome is a synthetic genome generated by means of casual (blind) extractions (with insertion after extraction) from an urn containing four types of balls, in equal numbers of copies, completely identical apart from their colors, denoted by the genomic letters a, c, g, t. Pseudo-Bernoullian genomes can be generated by means of (pseudo) random generators available in programming languages (by suitable encoding of genomic symbols). We denote by RNDn the class of Bernoullian genomes of length n.
The computations of the main informational indexes, given in Table 1, extract the set of  -mers occurring in the considered genomes, where
-mers occurring in the considered genomes, where  varies from 16 to 36, by means of a dedicated software, based on suffix arrays, called InfoGenomics Tools (shortly IGTools)31, which is an efficient suite of interactive tools mainly designed for extracting k-dictionaries, computing on them distributions and set-theoretic operations and finally evaluating empirical entropies Ek and informational indexes, for different and even very large values of k.
varies from 16 to 36, by means of a dedicated software, based on suffix arrays, called InfoGenomics Tools (shortly IGTools)31, which is an efficient suite of interactive tools mainly designed for extracting k-dictionaries, computing on them distributions and set-theoretic operations and finally evaluating empirical entropies Ek and informational indexes, for different and even very large values of k.
In Supplementary Information, a 3D-visualization (Sup. Fig. 2) of 70 genomes is given with respect to BB, AC, LX axes, where Principal Component Analysis is applied for a better visualization. A taxonomy tree of the 70 genomes has been built via the NCBI taxonomy48 (see Supplementary Information, Sup. Fig. 1).
Mathematical Backgrounds
In the following, some propositions are given, which were essential to the identification of parameters on which information entropies are computed. Let us start with the following question. Given a genome length n and a value k ≤ n, which is the maximum value of  in the class of genomes of length n? We answer to the question above with Proposition 3, which is based on two Lemmas.
in the class of genomes of length n? We answer to the question above with Proposition 3, which is based on two Lemmas.
Lemma 1Given a genome of length n, if
of length n, if , then
, then is the maximum value that Ekcan reach in the class of all possible genomes of length n.
is the maximum value that Ekcan reach in the class of all possible genomes of length n.
Proof. The minimum value of k such that all k-mers are hapaxes of  is
is  . Therefore, if
. Therefore, if  , then
, then  is maximum, according to the entropy Equipartition Property, because we have the maximum number of words occurring once in
is maximum, according to the entropy Equipartition Property, because we have the maximum number of words occurring once in  and all these words have the same probability of occurring in
and all these words have the same probability of occurring in  . ☐
. ☐
Lemma 2If R is a random genome of length n, then

Proof. Let RNDn the class of random genomes of length n. If k = mrl(R) + 1, the probability that a k-mer occurs in R∈RNDn is (n − k + 1)/4k and the probability that it occurs exactly once in R (being all k-mer hapaxes) is 1/(n − k + 1). Therefore, by equating these two probabilities we get:

that is:

that implies (k has to be an integer) that the minimum length k for having all hapaxes in R is:

whence

that is

therefore

that implies the asserted inequality.☐
Table 2 shows an experimental validation of Lemma 2. It confirms that lg2(|R|) results to be a good estimation of the average of mrl(R) + 1 in  .
.
Proposition 3In the class of genomes of length n, for every k < n, the following relation holds

Moreover, random genomes of length n have entropies differing from the upper bound lg2(n) less than (close to zero).
(close to zero).
Proof. According to Lemma 1,  reaches its maximum, when
reaches its maximum, when  . In this case:
. In this case:

therefore, the difference  is given by:
is given by:

If  belongs to the class of random genomes of length n, according to Lemmas 1 and 2, the maximum entropy is given by
belongs to the class of random genomes of length n, according to Lemmas 1 and 2, the maximum entropy is given by  , for
, for  , with
, with  . Therefore, by substituting in equation (22) the upper bound of k, giving the upper bound of lg2(n/(n − k + 1)), we get:
. Therefore, by substituting in equation (22) the upper bound of k, giving the upper bound of lg2(n/(n − k + 1)), we get:  .☐
.☐
Additional Information
How to cite this article: Bonnici, V. and Manca, V. Informational laws of genome structures. Sci. Rep. 6, 28840; doi: 10.1038/srep28840 (2016).
Change history
28 February 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41598-023-30108-x
References
Conrad, M. Adaptability (PlenumPress, 2001).
Conrad, M. The price of programmability. In A half-century survey on The Universal Turing Machine, 285–307 (Oxford University Press, 1988).
Holland, J. & Mallot, H. Emergence: from chaos to order. Nature 395, 342–342 (1998).
Cercignani, C. The Boltzmann Equation and Its Application (Springer, 1988).
Shannon, C. E. A mathematical theory of communication. Bell Sys Tech J 27, 623–656 (1948).
Pincus, S. M. Approximate entropy as a measure of system complexity. P Nat Acad Sci 88, 2297–2301 (1991).
Crochemore, M. & Vérin, R. Zones of low entropy in genomic sequences. Computers & chemistry 23, 275–282 (1999).
Vinga, S. & Almeida, J. S. Local Renyi entropic profiles of DNA sequences. BMC bioinformatics 8, 393 (2007).
Koslicki, D. Topological entropy of dna sequences. Bioinformatics 27, 1061–1067 (2011).
Wang, D., Xu, J. & Yu, J. KGCAK: a K-mer based database for genome-wide phylogeny and complexity evaluation. Biol direct 10(1), 1–5 (2015).
Head, T. Formal language theory and DNA: an analysis of the generative capacity of specific recombinant behaviors. B Math Biol 49, 737–759 (1987).
Deonier, R. C., Tavaré, S. & Waterman, M. Computational genome analysis: an introduction (Springer, 2005).
Manca, V. & Franco, G. Computing by polymerase chain reaction. Math Biosci 211, 282–298 (2008).
Searls, D. B. Molecules, languages and automata. In Grammatical Inference: Theoretical Results and Applications, 5–10 (Springer, 2010).
Vinga, S. Information theory applications for biological sequence analysis. Brief Bioinform, doi: 10.1093/bib/bbt068 (2013).
Manca, V. Infobiotics: information in biotic systems (Springer, 2013).
Gatlin, L. L. The information content of DNA. J Theor Biol 10(2), 281–300 (1966).
Kraskov, A. & Grassberger, P. MIC: mutual information based hierarchical clustering. Info Theor Stat Learn, 101–123 (Springer, 2009).
Campbell, A., Mrázek, J. & Karlin, S. Genome signature comparisons among prokaryote, plasmid and mitochondrial DNA. P Nat Acad Sci 96(16), 9184–9189 (1999).
Ebeling, W. & Jiménez-Montaño, M. A. On grammars, complexity and information measures of biological macromolecules. Math Biosci 52(1), 53–71 (1980).
Weiss, O., Jiménez-Montaño, M. A. & Herzel, H. Information content of protein sequences. J Theor Biol 206(3), 379–386 (2000).
Holste, D., Grosse, I. & Herzel, H. Statistical analysis of the DNA sequence of human chromosome 22. Phys Rev E 64(4), 041917 (2001).
Fofanov, Y. et al. How independent are the appearances of n-mers in different genomes? Bioinformatics 20, 2421–2428 (2004).
Kurtz, S., Narechania, A., Stein, J. C. & Ware, D. A new method to compute K-mer frequencies and its application to annotate large repetitive plant genomes. BMC genomics 9(1), 517 (2008).
Chor, B. et al. Genomic dna k-mer spectra: models and modalities. Genome Biol 10, R108 (2009).
Castellini, A., Franco, G. & Manca, V. A dictionary based informational genome analysis. BMC genomics 13, 485 (2012).
Bonnici, V. & Manca, V. Recurrence distance distributions in computational genomics. Am J Bioinformat Comput Biol 3, 5–23 (2015).
Wen, J., Chan, R. H., Yau, S.-C., He, R. L. & Yau, S. S. k-mer natural vector and its application to the phylogenetic analysis of genetic sequences. Gene 546, 25–34 (2014).
Almirantis, Y., Arndt, P., Li, W. & Provata, A. Editorial: Complexity in genomes. Comp Biol Chem 53, 1–4 (2014).
Hashim, E. K. M. & Abdullah, R. Rare k-mer DNA: Identification of sequence motifs and prediction of CpG island and promoter. J Theor Biol 387, 88–100 (2015).
Bonnici, V. & Manca, V. Infogenomics tools: A computational suite for informational analysis of genomes. J Bioinfo Proteomics Rev 1, 8–14 (2015).
Manca, V. Infogenomics: genomes as information sources. Chap. 21, 317–324 (Elsevier, Morgan Kauffman, 2016).
Manca, V. Information theory in genome analysis. In Membrane Computing, LNCS 9504, 3–18 (Springer, 2015).
Knuth, D. The art of computer programming, volume 2: Seminumerical algorithms (Addison-Wesley, 1998).
Kong, S. G. et al. Quantitative measure of randomness and order for complete genomes. Phys Rev E 79(6), 061911 (2009).
Jiang, Y. & Xu, C. The calculation of information and organismal complexity. Biol Direct 5(59), 565 (2010).
Witten, I. H., Moffat, A. & Bell, T. C. Managing gigabytes: compressing and indexingdocuments and images (Morgan Kaufmann, 1999).
Wiener, N. Cybernetics or control and communication in the animal and the machine (Hermann, Paris, 1948).
Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell and Mind (Cambridge University Press, 1944).
Brillouin, L. The negentropy principle of information. J Appl Phys 24, 1152–1163 (1953).
Volkenstein, M. V. Entropy and information (Springer, 2009).
Venter, J. C. et al. Design and synthesis of a minimal bacterial genome. Science 351, 6280 (2016).
Lynch, M. & Conery, J. S. The origins of genome complexity. Science 302, 1401–1404 (2003).
Kullback, S. & Leibler, R. A. On information and sufficiency. Ann Math Stat, 79–86 (1951).
Feller, W. An Introduction to Probability Theory and Its Applications (Wiley & sons, 1968).
Rozenberg, G. & Salomaa, A. Handbook of Formal Languages: Beyonds words vol. 3 (Springer, 1997).
Abouelhoda, M. I., Kurtz, S. & Ohlebusch, E. Replacing suffix trees with enhanced suffix arrays. J Discrete Algorithms 2, 53–86 (2004).
Federhen, S. The NCBI taxonomy database. Nucleic acids res 40, D136–D143 (2012).
Acknowledgements
The authors are grateful to Andres Moya for his support and help and to Rosalba Giugno for her important suggestions.
Author information
Authors and Affiliations
Contributions
V.M. conceived the theoretical and mathematical setting of the paper, V.B. developed the software and computations and V.M. and V.B. analyzed the results. V.M. wrote the paper and both authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Bonnici, V., Manca, V. Informational laws of genome structures. Sci Rep 6, 28840 (2016). https://doi.org/10.1038/srep28840
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28840
This article is cited by
-
Environment and taxonomy shape the genomic signature of prokaryotic extremophiles
Scientific Reports (2023)
-
Uncovering patterns of the evolution of genomic sequence entropy and complexity
Molecular Genetics and Genomics (2021)
-
Intrinsic laws of k-mer spectra of genome sequences and evolution mechanism of genomes
BMC Evolutionary Biology (2020)
-
Driven progressive evolution of genome sequence complexity in Cyanobacteria
Scientific Reports (2020)
-
On the length, weight and GC content of the human genome
BMC Research Notes (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


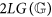 is an upper bound to the values that entropy can reach over the genomes with the same length of
is an upper bound to the values that entropy can reach over the genomes with the same length of  ;
;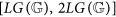 and
and 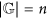 , then entropies Ek, for k ≤ n, reach, on suitable genomes, the best approximations to
, then entropies Ek, for k ≤ n, reach, on suitable genomes, the best approximations to  with an error close to zero, which is inferior to
with an error close to zero, which is inferior to  , being
, being  the closest integer greater than x.
the closest integer greater than x. reaches its maximum in random genomes of length
reaches its maximum in random genomes of length  . This result follows from the fact that in random genomes of length n all lg2(n)-mers are hapaxes, that is, they occur once in the whole genome
. This result follows from the fact that in random genomes of length n all lg2(n)-mers are hapaxes, that is, they occur once in the whole genome
 as the abscissa and their biobit value
as the abscissa and their biobit value  as the ordinate.
as the ordinate.
