Abstract
Ball lightning, a fireball sometimes observed during lightnings, has remained unexplained. Here we present a comprehensive theory for the phenomenon: At the tip of a lightning stroke reaching the ground, a relativistic electron bunch can be produced, which in turn excites intense microwave radiation. The latter ionizes the local air and the radiation pressure evacuates the resulting plasma, forming a spherical plasma bubble that stably traps the radiation. This mechanism is verified by particle simulations. The many known properties of ball lightning, such as the occurrence site, relation to the lightning channels, appearance in aircraft, its shape, size, sound, spark, spectrum, motion, as well as the resulting injuries and damages, are also explained. Our theory suggests that ball lighting can be created in the laboratory or triggered during thunderstorms. Our results should be useful for lightning protection and aviation safety, as well as stimulate research interest in the relativistic regime of microwave physics.
Similar content being viewed by others
Introduction
Since Arago1 first extensively discussed ball lightning in 1838, this rare natural phenomenon still remains a riddle. Ball lightning2,3,4,5 exhibits very diverse characteristics, such as close association with ordinary lightning, globate structure with steady glow for 1–5 seconds and mostly horizontal motion. Ball lightning can be formed even inside aircraft and closed rooms, permeate glass plates, decay explosively or silently and produce sound and acrid odours. Many models of ball lightning have been proposed, but none have been fully accepted6. In particular, these theories do not explain the inscrutable appearance of ball lightning inside fully-screened aircraft7. Here, we propose a theory for ball lightning formation, which can explain its appearing in aircraft and many other properties.
Lodge8 considered that ball lightning might be excited by a standing electrical wave from lightning. Kapitza9 argued that ball lightning could be formed through air ionization at antinodes of electromagnetic standing waves in the microwave regime. Dawson and Jones10 proposed that ball lightning could be a microwave bubble confined inside a globate plasma shell. Continuous air ionization by the trapped microwave maintains the plasma shell11. By dimensional analysis, we have pointed out12 that a microwave bubble can be formed similarly as light solitons observed in the laser-plasma interaction. Such a microwave bubble contains a half-cycle standing-wave mode and is sketched in Fig. 1a. The microwave-type model of ball lightning can explain its permeation through glass plates. However, the origin of microwave emission from lightning was never found.
Ball lightning model.
(a) Microwave bubble model. (b) Relativistic electron bunch generation. In the last leader step, a bunch of runaway electrons emerges from the leader tip, accelerates by electric fields between the leader and ground and undergoes an avalanche. (c) Coherent transition radiation (CTR) of the electron bunch striking the ground or passing through aircraft skins. γ is the relativistic factor of electrons.
In this article, we propose a mechanism for microwave generation from lightning. As shown in Fig. 1b, we assume that in a ball lightning event a relativistic electron bunch is generated by lightning. When this bunch strikes the ground or passes various media, powerful microwaves are emitted by coherent transition radiation (Fig. 1c). We further verify that this specific microwave in air plasmas naturally evolves into a microwave bubble. These results are demonstrated by particle-in-cell (PIC) simulation using the code JPIC12.
Results
Relativistic electron bunch
The assumption of isolated relativistic electron bunches in ball lightning events is based on high-energy phenomena13,14 discovered in cloud-to-ground lightning. A lightning flash5 starts with a negative leader propagating downward in a stepping process with each step tens of metres. This stepped leader has a corona 1–10 m in width. Moore et al.15 first detected >1 MeV radiation from a stepped leader. It was then observed that each step emits an x-ray burst16, which intensifies when the leader approaches the ground. Recent data17 shows that the last step or the so-called leader burst closest to the ground produces the strongest x-rays. Electrons accelerated by the stepped leader account for these detected x-rays, so that the electron acceleration is the most violent in the last step.
Friction force of electron motion in air is maximum at an energy of 100 eV, which defines a critical electric field Ec ≈ 30 MV/m14. Fields above Ec at the leader tip can accelerate thermal electrons to several keV18. This thermal runaway process19 can produce ~1011 electrons. The hot electrons can be further accelerated by the electric field between the leader tip and the ground and serve as seed electrons to undergo avalanche in air20. The electron flux quickly rises as exp(z/L), where L is the avalanche length. The electron energy follows a Boltzmann distribution exp(−ke/7.3 MeV), such that the average energy is 7.3 MeV. Latest data analysis21 shows that collimating relativistic electrons are required to explain observed x-rays from the stepped leader and should be either Boltzmann-distributed at 7 MeV or monoenergetic from 1 to 10 MeV.
The isolated x-ray bursts from the stepped leader are much shorter than 1 μs16. On the other hand, metre-scale laboratory sparks in air22 can emit very similar x-rays as in natural lightning. Duration of x-ray bursts from laboratory sparks is generally sub-10 ns23 and can be as short as 1 ns24. Accelerated electrons are expected to have the same temporal structure as the x-rays from lightning or sparks.
Accordingly, it can be expected that the last leader step generates a spatially well-defined relativistic electron bunch in a ball lightning event (see Fig. 1b). For simplicity, we assume that this bunch has a density profile nb = nb0 exp(−r2/2σ2), where nb0 is the peak density and σ is the characteristic radius. We take a bunch size (≃4σ) of tens of cm, i.e. ~1 ns in duration. As discussed later, a bunch with total electron number Nb = (2π)3/2nb0σ3 ≈ 1014 will lead to a microwave bubble. In the avalanche mechanism, this would need an avalanche path of 7L, corresponding to a multiplication rate of exp(7) ≈ 103. The avalanche length L is 7–30 cm near the ground14 and should support the rapid amplification of these nanosecond bunches. Another mechanism25 predicts that the leader can directly generate ~1016 energetic electrons on a timescale of 1 ns without avalanche.
Microwave generation
Transition radiation is generated from medium surfaces when an electron enters or emerges26 and can be coherent for an isolated electron bunch27. As the electron bunch reaches relativistic energies, its self-fields are predominantly transverse i.e. Eb ≃ cBb28, which is very close to an electromagnetic wave. In this case, coherent transition radiation can be considered as the reflected wave of the bunch field from the medium surface29. Therefore, we can write the radiation energy as

where  is the Fresnel reflection formula, Wb,f refers to the total bunch field energy and ε is the medium permittivity. The radiation is strongest for a metal or perfect conductor where ε → ∞ and ℛ ≈ 1 in microwave region. In addition, a Boltzmann-distributed electron bunch turns out to produce almost the same transition radiation pulse as a monoenergetic one30.
is the Fresnel reflection formula, Wb,f refers to the total bunch field energy and ε is the medium permittivity. The radiation is strongest for a metal or perfect conductor where ε → ∞ and ℛ ≈ 1 in microwave region. In addition, a Boltzmann-distributed electron bunch turns out to produce almost the same transition radiation pulse as a monoenergetic one30.
The leftmost panel of Fig. 2 shows the transverse field Eb,x of a monoenergetic 7 MeV electron bunch with σ = 4 cm, which is normalized to the peak field  . The bunch field is a unipolar wave with the same profile exp(−z2/2σ2) as the electron density along the direction of motion. Using JPIC12, we simulate the coherent transition radiation from a perfect conductor in Fig. 2. The radiation field Ex is initially opposite to Eb,x due to the conductor boundary, diffracts transversely and quickly evolves into a bipolar pulse. This radiation has a central wavelength λ ≈ 7.5σ = 30 cm (i.e. 1 GHz). The rapid field evolution into the bipolar shape is due to diffraction losses of longer wavelength components in an unipolar pulse31. At normal incidence in Fig. 2, the radiation field is radially polarised with a ring-like intensity distribution. Oblique incidence32 can enhance the radiation production and lead to an asymmetric intensity pattern. Considering surface fluctuations and non-axisymmetric bunches, the actual radiation could contain only one high-intensity emission spot, which is linearly-polarised and will make bubble formation more easily.
. The bunch field is a unipolar wave with the same profile exp(−z2/2σ2) as the electron density along the direction of motion. Using JPIC12, we simulate the coherent transition radiation from a perfect conductor in Fig. 2. The radiation field Ex is initially opposite to Eb,x due to the conductor boundary, diffracts transversely and quickly evolves into a bipolar pulse. This radiation has a central wavelength λ ≈ 7.5σ = 30 cm (i.e. 1 GHz). The rapid field evolution into the bipolar shape is due to diffraction losses of longer wavelength components in an unipolar pulse31. At normal incidence in Fig. 2, the radiation field is radially polarised with a ring-like intensity distribution. Oblique incidence32 can enhance the radiation production and lead to an asymmetric intensity pattern. Considering surface fluctuations and non-axisymmetric bunches, the actual radiation could contain only one high-intensity emission spot, which is linearly-polarised and will make bubble formation more easily.
PIC results of microwave generation.
Distribution of the initial bunch field and microwave fields at times 0.8 ns, 1.5 ns and 2 ns. The field is normalized to the bunch peak field Eb0. In the leftmost panel, the bunch is left-going to the plasma surface at z = 0. The white circle marks the bunch region with a density of 0.5nb0. The radiation is a reflection of the bunch field and propagates along z. Arrows point to the field propagation direction. Parameters are given in the text and Methods.
Microwave bubble formation
Laser solitons have been observed in both PIC simulations33,34 and experiments35,36,37 on relativistic laser-plasma interaction. The laser needs to exceed the relativistic field threshold Er = mcω/e38 and is typically multi-cycle. The plasma is underdense with an initial density n0 < nc, where nc = ε0mω2/e2 is the critical density39. During the laser propagation in the plasma, the self-phase modulation effect40 leads to a dramatic spectral broadening, which makes some part of laser energy to shift even below the background plasma frequency. Hence this part gets trapped in a plasma cavity with a half-cycle standing wave mode. The cavity is spherical and formed by evacuating electrons through the relativistic ponderomotive force41. The entire formation process takes tens of light cycles.
Here, we discuss the bubble formation for a mono-cycle microwave in Fig. 2. The microwave must get trapped within a few cycles before it is diffracted. In contrast to the mechanism discussed above, we find that the initial plasma must be overdense with n0 ≥ nc, where nc ≈ 1.2 × 1010cm−3 at ω/2π = 1 GHz. The existence of such a bubble-formation regime for single-cycle waves indicates self-consistency of our theory. The collisional effect is included by embedding air friction14,18 into JPIC. We launch microwave pulses with wavelength λ = 30 cm into a uniform plasma. The simulation shows that the threshold field required for bubble formation is

At 1 GHz, we have Er ≈ 10.7 MV/m and Ebl ≈ 11Er ≈ 120 MV/m, which is highly relativistic. Equation (2) clearly shows that the field needs to be greater than Ec to efficiently accelerate electrons and reach the relativistic regime to completely expel electrons by the relativistic pondermotive force. Surprisingly, Er matches with Ec to make the bubble formation possible. Here, we check the bunch parameters for giving the threshold field Ebl. For the case in Fig. 2, we get nb0 ≈ 3.7 × 1011cm−3 and Nb ≈ 3.7 × 1014.
In Fig. 3, we take n0 = 4nc and a microwave field of 310 MV/m and let t = 0 when the field touches the plasma. Snapshots of microwave field and plasma density from t = 1 ns to 11 ns illustrate the entire process of microwave self-trapping and bubble formation. The radiation pressure of microwave first pushes electrons to pile up into a semicircular shell at t = 1 ns and leaves a low-density region at the rear. As the field is reflected by the front shell, peripheric electrons return to the low-density region and close up the cavity at t ≈ 3 ns. The field gets trapped and then evolves into a standing-wave mode. At t = 11 ns, a motionless electron cavity forms about 45 cm deep into the plasma and then it becomes circular and keeps stable after t ≈ 15 ns. Meantime, heavy ions are slowly pulled out by the charge separation field.
In Fig. 4a,b, snapshots of the stable bubble at t = 19 ns show that the fields take on a half-cycle standing wave pattern, electrons have been almost emptied and ions are partially evacuated. The electrostatic force between electrons and ions is balanced by the radiation pressure ε0E2/4 ≈ 64 kPa, where E = 170 MV/m is the standing wave amplitude. The periodic conversion between electric and magnetic energies in Fig. 4c confirms the standing wave mode. The confined field oscillates at a longer period of 1.6 ns. This redshift is caused by the Doppler effect and self-phase modulation. The cavity diameter is about 24 cm, half of the wavelength of the trapped field. For a ball shape, the confined field energy in Fig. 4b is about 800J. Tuning the microwave field, the trapped field energy in the bubble ranges from 200J to 1500J.
PIC results of stable microwave bubble.
(a) Snapshots of the microwave electric field E, magnetic field B, electron density ne and ion density ni at t = 19 ns. White arrows mark the magnetic field direction. (b) Field energy density and plasma density ne,i verses y across the bubble centre. (c) Evolution of the electric field, electric field energy We and magnetic field energy Wm in the bubble. Parameters are the same as Fig. 3.
Three-dimensional field structure of microwave bubbles can be close to that of the light solitons observed in PIC simulation34. With energy loss of microwave by collisional absorption, the bubble is expected to convert into an electromagnetic cavity resonator. The fundamental mode at the lowest eigenfrequency in a spherical resonator26 is similar to that in a cylindrical cavity28, which resembles that shown in Fig. 4a.
Explanation of the diverse properties
The properties of ball lightning2,3,4,5 are summarized from about 5000 published sighting reports.
Site of occurrence
As shown in Fig. 2, a planar surface is necessary for microwave generation at least with a size of ball lightning, which can be easily fulfilled in reality. Microwave emission is also affected by the ground reflectivity  . The soil permittivity ε increases with its moisture ms42. At 1 GHz, we get
. The soil permittivity ε increases with its moisture ms42. At 1 GHz, we get  and
and  , which correspond to
, which correspond to  ≈ 25% and 56%, respectively. Rainfall can lead to ms > 60%43 and thus is favorable for the ball lightning formation. As stated by Stenhoff4, more than 50% of reports show that medium or heavy rainfall happens before the observation. Moreover, there is
≈ 25% and 56%, respectively. Rainfall can lead to ms > 60%43 and thus is favorable for the ball lightning formation. As stated by Stenhoff4, more than 50% of reports show that medium or heavy rainfall happens before the observation. Moreover, there is  ≈ 65% for either pure or sea water44. Indeed, there are 18 reports at sea2 and a few reports over rivers2,4. Certainly, metal holds the highest chance of ball formation due to
≈ 65% for either pure or sea water44. Indeed, there are 18 reports at sea2 and a few reports over rivers2,4. Certainly, metal holds the highest chance of ball formation due to  ≈ 1.
≈ 1.
Relation to lightning channels
The lightning channel refers to the bright return stroke occurring after the stepped leader attaches with a positive leader rising from the ground. The starting place of this positive leader would be the lightning strike point. We show that ball lightning is caused by the stepped leader, which is invisible with the naked eye. The stepped leader and its mirror charge underground establish a dark channel for electron acceleration and avalanche. Obviously, the ball formation site is unrelated to the lightning strike point. Their separation should be within one step length of tens of metres typically. This successfully explains the reports where ball lightning does not form near the lightning channel or strike point4.
Appearance in aircraft
First, the avalanche electron energy 7.3 MeV is independent of the air density13, i.e. altitude. When lightning strikes an aircraft, the same bunch is presumably produced and enters the aircraft with an energy loss of ~2 MeV due to the ~0.6 cm aluminium skin45. Second, transition radiation26 is not sensitive to the energy of the relativistic electrons and its efficiency from the electron emerging surface of the medium is almost the same as the reflection side discussed above. Therefore, the same intense microwave will arise inside the aircraft and form ball lightning there. In the same manner, ball lightning can appear in enclosed rooms.
Permeation through glass plates
Ball lightning is observed to enter rooms by passing through closed glass windows. In interference experiments of low-power microwave in metal cavity46, generated fireballs in air are observed to pass through a 3 mm ceramic plate intact. This is a direct result of the ability of microwave passage across dielectrics. The microwave bubble resembles a laser cavity. According to laser theory47, the internal standing wave will not be disturbed if a glass plate (~5 mm) is much thinner than the wavelength of microwave.
Shape
From dimensional analysis12, the microwave bubble of Fig. 4 in reality should be ball-shaped as its micrometre-scale counterpart in laser-plasma experiments35,36,37. The full trapping of the field in Fig. 2 can account for the 62 ring-shaped ball lightning reports2.
Size
Ball lightning has a common diameter of 20–50 cm4. Our theory shows that the diameter of microwave bubbles approximately equals the electron bunch length in the direction of motion. The bunch length of tens of cm is supported by x-ray duration measured from lightning and laboratory sparks, which can be as short as 1 ns.
Sound
Hissing, buzzing or fluttering sounds from ball lightning have been reported, which can be perfectly explained by the microwave hearing effect48,49. At 0.1 mJ/cm2, a microwave pulse (microsecond or shorter) at 0.2–3 GHz can induce an audible sound wave. The sound can only be heard by persons whose heads are irradiated by the microwave and has been described as a hiss, buzz or knocking. Therefore, ball lightning can be silent during its lifetime. In Jennison’s sighting50, he was only 0.5 m from a cruising ball and did not report any noise.
Spark
Ball lightning sometimes emits sparks, which can be caused by the ejection of charged particles along the electric field. Especially, the sparks are toward opposite directions in two reports2, which agrees with the linear polarisation of standing wave in the bubble.
Spectrum
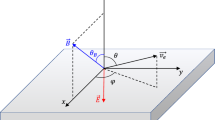
Recently, Cen et al.51 recorded an optical spectrum of ball lightning. The spectrum contains emission lines of atoms in air and soil. Interestingly, the spectral intensities of O and N atoms oscillate at 100 Hz, twice the frequency of the adjacent power lines (35 kV, 50 Hz). The latter is only 20 m from the ball and can produce a 50 Hz electric field of ~1 V/cm52 at the ball. This field can induce electron drift on the ball surface by tens cm (see Methods). This drift motion can perturb the spectral emission in the plasma shell. The spectral intensity should be independent of drift direction and varies at 100 Hz. The ball is attached to the soil on a hillside, where electrons cannot feel the oscillating field due to the screening effect. Thus, Si, Fe and Ca in soil glow steadily51.
Odour
Ionized air can produce O3 and NO25,53, both of which have an acrid smell.
Decay
The microwave bubble decays silently once the internal radiation is exhausted. When it is strongly disturbed or pierced by a conductor, the leaking radiation can launch a shock wave like an explosion.
Injury and damage
Most reported injuries and damages can readily be attributed to ordinary lightning2,4. However, Stenhoff4 noticed that some superficial burns are difficult to explain. In the Smethwick event4,54, the female witness did not get an electric shock but felt a burning heat all over. Wooding55 estimated that she received 250J whole-body ionizing radiation, which can be due to the electrons from the stepped leader and also be responsible for the redness on her hand and legs. She heard a knocking-like sound (rattle) from the microwave hearing effect. Her legs were numbed, which can be due to nerve damage by the microwave at 0.1J/cm2 56. When she brushed the ball away with her hand, the ring was burning into her finger. Wooding calculated that this rapid heating would need a resonant microwave at 1 GHz with an field of ~1 MV/m, which agrees well with our model. Others57 reported skin redness, vomiting and loss of hair, which are typical results of ionizing radiation58. As reported by X. Zhang and Q. Yan in Shanxi Daily (8 Aug. 2014), during a thunderstorm on 5 Aug. 2014, a red ball of fire 40 cm in diameter was witnessed entering an office through an open window at the local Water Conservancy Bureau in Xinjiang, Shanxi, China. The ball lasted for less than one second and then exploded loudly. Five computers in the room were damaged, which is a direct result of high-power microwaves56.
Motion
Near the ground, ball lightning moves mostly horizontally at about 2 m/s2 and usually travels with the wind3. A light breeze typically at 1.5–3 m/s59 can account for this motion speed. However, air convection will raise the ball if the background air is heated up by the ionized plasmas. Assuming a constant heat power of 100 W, we obtain a convection speed 23 cm/s for the ball of size 30 cm (see Methods). Thus, the upward motion is not notable compared with the horizontal motion. Several models2,4 speculate that the ball could take a positive charge due to the greater mobility of electrons compared with ions. The charged ball can further resist the buoyancy or air convection by an attractive force from its mirror charge underground. Moreover, like a charged particle self-accelerating into an open waveguide60, the ball can enter rooms through chimneys.
Lifetime
The typical lifetime of ball lightning is 1–5 seconds. Statistical analysis61 shows that increase in humidity decreases the lifetime of the ball, which can be due to microwave absorption by vapour. Experiments62 show that fireballs in air produced by a 5 kW, 2.45 GHz microwave can last for ~0.5 s after the source is turned off. Our self-organized microwave bubble can have the same potential to persist for a scale of seconds. Zheng11 calculated that hundreds of joule microwaves can maintain the plasma shell of the bubble for a few seconds. Air plasmas continuously depleted by recombination are refilled by microwave heating. Non-neutral plasmas shown in Fig. 4b can further resists the recombination loss.
Discussion
Experiments are required to verify our theory. First, forming a microwave bubble in laboratory will need hundreds of gigawatt microwave, which is one order of magnitude higher than the manmade sources. As stated in ref. 56, it is technically feasible to enhance current microwave devices to 100 GW. Alternatively, one can adopt a high-power electron beam63 to directly simulate the mechanism proposed in Fig. 1. Second, on the lightning research, we suggest to detect microwave radiation at GHz near a lightning strike point. We already show that trans-ionospheric pulse pairs from lightning are caused by the same radiation mechanism64, which supplies a physical evidence of our theory. On attempts to create ball lightning by rocket-triggered lightning65, we propose to use ungrounded wires5 rather than grounded ones because ball lightning is thought to be only related to the stepped leader. Perhaps intense lasers can trigger lightnings by producing an ungrounded plasma channel near thunderclouds66. For in situ investigation of ball lightning, we suggest to look for evidence of high-flux energetic electrons. Finally, we note that relativistic terahertz waves could be produced from laser-accelerated hot electrons emerging from solid foils by coherent transition radiation67 or laser-driven plasma waves in gas target68. In particular, the former scenario is very close to the scheme in Fig. 1 and may lead to a millimetre-scale terahertz radiation bubble.
Conclusion
In conclusion, based on a reasonable assumption on the electron bunch, we have constructed a self-consistent theory on the microwave generation and ball lightning formation. The theory successfully explains many properties of ball lightning. For the first time, we revel that ball lightning is an alarm signal of the existence of ultrastrong microwaves and abundantly hazardous electrons near the ground or aircraft. This result is of great significance for lightning protection and aviation safety. Moreover, it is hoped that our work will stimulate research activities in relativistic microwave physics and technology, an unexplored area before.
Methods
Dimensional analysis
The interaction of relativistic electromagnetic wave and collisionless plasmas is governed by the Maxwell’s equations and relativistic Lorentz equation of electrons and ions. When time and space are normalized to the cycle and wavelength of electromagnetic wave respectively, the whole system only depends on two dimensionless quantities  and
and  , where n0 is the initial plasma density, nc = ε0mω2/e2 is the critical density, E0 is the initial field amplitude, e is the fundamental charge, m is the electron mass, c is the light speed, ω is the angular frequency and ε0 is the vacuum permittivity. If
, where n0 is the initial plasma density, nc = ε0mω2/e2 is the critical density, E0 is the initial field amplitude, e is the fundamental charge, m is the electron mass, c is the light speed, ω is the angular frequency and ε0 is the vacuum permittivity. If  and
and  are same for any systems with different wavelengths λ = 2πc/ω, the physical process should be identical in these systems12. By the way,
are same for any systems with different wavelengths λ = 2πc/ω, the physical process should be identical in these systems12. By the way,  defines the relativistic field threshold Er = mcω/e. For a microwave at λ = 30 cm, we have Er = 10.7 MV/m (Ir = 1.5 × 107W/cm2) and nc = 1.2 × 1010cm−3.
defines the relativistic field threshold Er = mcω/e. For a microwave at λ = 30 cm, we have Er = 10.7 MV/m (Ir = 1.5 × 107W/cm2) and nc = 1.2 × 1010cm−3.
PIC simulation
All simulations are done with the JPIC code12, which self-consistently solves the Maxwell’s equations and relativistic Lorentz equations for electrons and ions in a two-dimensional space. JPIC applies a field solver free of numerical dispersion in the propagation axis and can accurately simulate the dynamics of half-cycle electromagnetic waves31. The simulation of transition radiation in Fig. 2 is performed in the xz plane. An overdense plasma is used to represent the conductor and its density has a negligible effect on the results. In Fig. 2, we take a density n0 = 50nc and resolution of 100 and 80 grids per wavelength (λ = 30 cm) along the z- and x-axes, respectively. The simulation of bubble formation in Figs 3 and 4 is done in the yz-plane. Since the collision frequency in air is ~1012Hz, i.e., thousands of collisions per cycle, which makes the resolution of individual collisions unrealistic in the present work. For the simulation, we embed the effective air friction force within an electron energy range [1 eV, 1 GeV]14,18 into the Lorentz equation of electrons. The microwave field Ex is perpendicular to the simulation plane and propagates from a vacuum to a uniform plasma along the z-axis. The microwave pulse has the form  , where E0 = 310 MV/m is the field amplitude, R = 9 cm is the spot size, τ = 2 ns is the duration and ω/2π = 1 GHz is the central frequency. The full width at half maximum of the field envelope is τ/2 = 1 ns. There are 80 and 64 grids per wavelength along the z and y axes respectively. Air molecules take an average molecular weight 28.97 and charge state Z = 1. In Fig. 3, to clearly recognize the bubble structure, color bars are based on specific values at each moment and therefore no quantitative relation exists among the different panels.
, where E0 = 310 MV/m is the field amplitude, R = 9 cm is the spot size, τ = 2 ns is the duration and ω/2π = 1 GHz is the central frequency. The full width at half maximum of the field envelope is τ/2 = 1 ns. There are 80 and 64 grids per wavelength along the z and y axes respectively. Air molecules take an average molecular weight 28.97 and charge state Z = 1. In Fig. 3, to clearly recognize the bubble structure, color bars are based on specific values at each moment and therefore no quantitative relation exists among the different panels.
Microwave effects on humans
Microwave can penetrate deeply into the tissue and cause an influence by thermal effects. Microwave hearing48,49,56 is the lowest power effect on humans and occurs when the absorbed energy in the brain tissue reaches 10 μJ/g for a 10 μs pulse. For a typical adult brain with 14 cm in diameter and 1.4 kg in weight, we get an energy flux threshold of 0.1 mJ/cm2. Experiments48,49 show this hearing effect induced by 0.2–3 GHz microwave pulses with 1−100 μs in duration. Theoretical analysis reveals that rapid (~μs) temperature rise (~10−6 degree) leads to a thermoelastic expansion of tissue, which launches an acoustic wave travelling by the skull to the inner ear. The audio frequency is located at an audible high-frequency band of 7–15 kHz, which is responsible for the sounds of hiss, buzz, knocking or clicking48. Although rather resistant to ionizing radiation69, sensory nerves in the peripheral nervous system are found to be particularly sensitive to the microwave70. Occurring at 0.1 J/cm2 56, nerve damage can lead to a numbness in the limbs71. In our theory, the microwave reaches ~1 J/cm2 for the ball formation, which is enough to induce both microwave hearing and nerve damage on witnesses.
Electron drift in air
In an electric field Ef sin(2πf t) with frequency f, electrons in air gain a drift velocity Ve = μeEf sin(2πft)13, where μe is the electron mobility. The amplitude of electron drift is then  . Taking Ef = 1 V/cm, f = 50 Hz and μe = 0.6 m2/V/s18, we have δ ≈ 38 cm. Ions have δ ≈ 0.1 mm due to its small mobility.
. Taking Ef = 1 V/cm, f = 50 Hz and μe = 0.6 m2/V/s18, we have δ ≈ 38 cm. Ions have δ ≈ 0.1 mm due to its small mobility.
Air convection
The microwave bubble will heat up the initially uniform air by electron-molecule collisions. When the temperature rises, air will expand and be lifted up by buoyancy, which leads to air convection. Assuming the temperature change ΔT is small, the convection speed is given by  72, where g = 9.8 m/s2 is the gravitational acceleration, D is the bubble size and T0 is the initial air temperature. If thermal energy is transferred primarily by the air convection, one has H = Cpρ0SuΔT, where H is the total heat power of bubble, Cp is the specific heat capacity of air, ρ0 is the air density and S = π(D/2)2 is the cross sectional area of bubble. From these relations, we obtain
72, where g = 9.8 m/s2 is the gravitational acceleration, D is the bubble size and T0 is the initial air temperature. If thermal energy is transferred primarily by the air convection, one has H = Cpρ0SuΔT, where H is the total heat power of bubble, Cp is the specific heat capacity of air, ρ0 is the air density and S = π(D/2)2 is the cross sectional area of bubble. From these relations, we obtain


At the room temperature T0 = 293 K, we have ρ0 = 1.2 kg/m3 and Cp = 1 × 103J/K/kg73. For a bubble with D = 30 cm and H = 100 W, the convection speed is u ≈ 23 cm/s and temperature increase is ΔT ≈ 5 K. We also get the Reynolds, Peclet and Rayleigh numbers of this system as 4.5 × 103, 3.2 × 103 and 1.4 × 107 respectively. These dimensionless numbers confirm that convection is the dominant mechanism of heat transport72.
Additional Information
How to cite this article: Wu, H.-C. Relativistic-microwave theory of ball lightning. Sci. Rep. 6, 28263; doi: 10.1038/srep28263 (2016).
References
Arago, F. Sur le tonnerre. Annuaire au Roi par le Bureau des Longitudes. Notices Scientifiques p. 221 (1838).
Singer, S. The nature of ball lightning (Plenum, New York, 1971).
Barry, J. D. Ball lightning and bead lightning: Extreme forms of atmospheric electricity (Plenum, New York, 1980).
Stenhoff, M. Ball lightning: An unsolved problem in atmospheric physics (Kluwer Academic and Plenum Publishers, New York, 1999).
Rakov, V. A. & Uman, M. A. Lightning: Physics and effects (Cambridge Univeristy Press, Cambridge, 2003).
Ball, P. First spectrum of ball lightning. Physics 7, 5 (2014).
Dijkhuis, G. C. A model of ball lightning. Nature 284, 150–151 (1980).
Lodge, O. J. Lightning conductors and lightning guards (Whittaker and Co. and Bell and Sons, London, 1892).
Kapitza, P. L. On the nature of ball lightning. Doklady Acad. 101, 245–248 (1955).
Dawson, G. A. & Jones, R. C. Ball lightning as a radiation bubble. Pure Appl. Geophys. 75, 247–262 (1969).
Zheng, X.-H. Quantitative analysis for ball lightning. Phys. Lett. A 148, 463–469 (1990).
Wu, H.-C. JPIC & How to make a PIC code. Preprint at http://arxiv.org/abs/1104.3163 (2011).
Dwyer, J. R. & Uman, M. A. The physics of lightning. Phys. Rep. 534, 147–241 (2014).
Dwyer, J. R., Smith, D. M. & Cummer, S. A. High-energy atmospheric physics: Terrestrial gamma-ray flashes and related phenomena. Space Sci. Rev. 173, 133–196 (2012).
Moore, C. B. et al. Energetic radiation associated with lightning stepped-leaders. Geophys. Res. Lett. 28, 2141–2144 (2001).
Dwyer, J. R. et al. X-ray bursts associated with leader steps in cloud-to-ground lightning. Geophys. Res. Lett. 32, L01803 (2005).
Howard, J. et al. RF and X-ray source locations during the lightning attachment process. J. Geophys. Res. 115, D06204 (2010).
Moss, G. D. et al. Monte Carlo model for analysis of thermal runaway electrons in streamer tips in transient luminous events and streamer zones of lightning leaders. J. Geophys. Res. 111, A02307 (2006).
Gurevich, A. V. On the theory of runaway electrons. Sov. Phys. JETP 12, 904–912 (1961).
Gurevich, A. V., Milikh, G. M. & Roussel-Dupre, R. A. Runaway electron mechanism of air breakdown and preconditioning during a thunderstorm. Phys. Lett. A 165, 463–468 (1992).
Babich, L. P. et al. Analysis of the experiment on registration of X-rays from the stepped leader of a cloud-to-ground lightning discharge. J. Geophys. Res. 118, 2573 (2013).
Dwyer, J. R. et al. X-ray bursts produced by laboratory sparks in air. Geophys. Res. Lett. 32, L20809 (2005).
Nguyen, C. V., J van Deursen, A. P. & Ebert, U. Multiple x-ray bursts from long discharges in air. J. Phys. D 41, 234012 (2008).
Kochkin, P. O., J van Deursen, A. P. & Ebert, U. Experimental study on hard x-rays emitted from metre-scale negative discharges in air. J. Phys. D 48, 025205 (2015).
Celestin, S. & Pasko, V. P. Energy and fluxes of thermal runaway electrons produced by exponential growth of streamers during the stepping of lightning leaders and in transient luminous events. J. Geophys. Res. 106, A03315 (2011).
Landau, L. D. & Lifshitz, E. M. Electrodynamics of continuous media (Pergamon, Oxford, 1984).
Happek, U., Sievers, A. J. & Blum, E. B. Observation of coherent transition radiation. Phys. Rev. Lett. 67, 2962–2965 (1991).
Jackson, J. D. Classical electrodynamics (Wiley, New York, 1975).
Casalbuoni, S. et al. Ultrabroadband terahertz source and beamline based on coherent transition radiation. Phys. Rev. ST Accel. Beams 12, 030705 (2009).
Tilborg, J. V. et al. Pulse shape and spectrum of coherent diffraction-limited transition radiation from electron beams. Laser Part. Beams 22, 415–422 (2004).
Wu, H.-C. & Meyer-ter-Vehn, J. Giant half-cycle attosecond pulses. Nature Photon. 6, 304–307 (2012).
Zheng, J. et al. Theoretical study of transition radiation from hot electrons generated in the laser-solid interaction. Phys. Plasmas 10, 2994–3003 (2003).
Naumova, N. M. et al. Formation of electromagnetic postsolitons in plasmas. Phys. Rev. Lett. 87, 185004 (2001).
Esirkepov, T. et al. Three-dimensional relativistic electromagnetic subcycle solitons. Phys. Rev. Lett. 89, 275002 (2002).
Sarri, G. et al. Observation of plasma density dependence of electromagnetic soliton excitation by an intense laser pulse. Phys. Plasmas 18, 080704 (2011).
Sylla, F. et al. Anticorrelation between ion acceleration and nonlinear coherent structures from laser-underdense plasma interaction. Phys. Rev. Lett. 108, 115003 (2012).
Zhu, B. et al. Observation of a strong correlation between electromagnetic soliton formation and relativistic self-focusing for ultra-short laser pulses propagating through an under-dense plasma. Phys. Plasmas 19, 102304 (2012).
Salamina, Y. I. et al. Relativistic high-power laser-matter interactions. Phys. Rep. 427, 41–155 (2006).
Kruer, W. L. The physics of laser plasma interactions (Addison-Wesley Publishing Company, California, 1988).
Watts, I. et al. Measurements of relativistic self-phase-modulation in plasma. Phys. Rev. E 66, 036409 (2002).
Sun, G.-Z. et al. Self-focusing of short intense pulses in plasmas. Phys. Fluids 30, 526–532 (1987).
Hallikainen, M. T. et al. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sensing GE-23, 25–34 (1985).
Xu, Q. et al. Effects of rainfall on soil moisture and water movement in a subalpine dark coniferous forest in southwestern China. Hydrol. Process. 26, 3800–3809 (2012).
Meissner, T. & Wentz, F. J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sensing 42, 1836–1849 (2004).
Dwyer, J. R. et al. Estimation of the fluence of high-energy electron bursts produced by thunderclouds and the resulting radiation doses received in aircraft. J. Geophys. Res. 115, D09206 (2010).
Ohtsuki, Y. H. & Ofuruton, H. Plasma fireballs formed by microwave interference in air. Nature 350, 139–141 (1991).
Siegman, A. E. Lasers (University Science Books, Mill Valley, CA, 1986).
Frey, A. H. Human auditory systems response to modulated electromagnetic energy. J. App. Physiol. 17, 689–692 (1962).
Lin, J. C. & Wang, Z. Hearing of microwave pulses by humans and animals: Effects, mechanism and thresholds. Health Phys. 92, 621–628 (2007).
Jennison, R. C. Ball lightning. Nature 224, 895 (1969).
Cen, J., Yuan, P. & Xue, S. Observation of the optical and spectral characteristics of ball lightning. Phys. Rev. Lett. 112, 035001 (2014).
Tzinevrakis, A., Tsanakas, D. & Mimos, E. Analytical calculation of the electric field produced by single circuit power lines with horizontal arrangement of the conductors. 51st Internationales Wissenschaftliches Kolloquium, Technische Universitaet Ilmenau. Sept. 11–15 (2006).
Petit, Y. et al. Production of ozone and nitrogen oxides by laser filamentation. Appl. Phys. Lett. 97, 021108 (2010).
Stenhoff, M. Ball lightning. Nature 260, 596–597 (1976).
Wooding, E. R. Ball lightning in Smethwick. Nature 262, 379–380 (1976).
Benford, J., Swegle, J. A. & Schamiloglu, E. High power microwaves (Taylor and Francis, New York, 2007).
Shmatov, M. L. Expected spectrum of high-energy photons from ball lightning. J. Plasma Phys. 72, 277–284 (2006).
Mettler, F. A. & Upton, A. C. Medical effects of ionizing radiation (Elsevier, USA, 2008).
Beaufort Scale. Royal Meteorological Society. http://www.rmets.org/weather-and-climate/observing/beaufort-scale.
Tyukhtin, A. V. Self-acceleration of a charge traveling into a waveguide. Phys. Rev. ST Accel. Beams 17, 021303 (2014).
Amirov, A. K. & Bychkov, V. L. Observational and computer assisted analysis of data from SKB data base. Proceedings: 5th International Symposium on Ball Lightning p. 42 (1997).
Ofuruton, H. et al. Experimental conditions for ball lightning creation by using air gap discharge embedded in a microwave field. J. Geophys. Res. 106, 12367–12369 (2001).
Humphries, S. Charged particle beams (Dover, USA, 2013).
Wu, H.-C. An explanation for trans-ionospheric and sub-ionospheric pulse pairs from lightning, The 1st International Symposium on Lightning and Storm Related Phenomena (Aurillac, France, July 2–3, 2015).
Hill, J. D. et al. Attempts to create ball lightning with triggered lightning. J. Atmos. Solar-Terr. Phys. 72, 913–925 (2010).
Graydon, O. & Kasparian, J. Lightning control by lasers. Nature Photon. 3, 120–121 (2009).
Ding, W. J., Sheng, Z. M. & Koh, W. S. High-field half-cycle terahertz radiation from relativistic laser interaction with thin solid targets. Appl. Phys. Lett. 103, 204107 (2013).
Wu, H.-C., Sheng, Z. M. & Zhang, J. Single-cycle powerful megawatt to gigawatt terahertz pulse radiated from a wavelength-scale plasma oscillator. Phys. Rev. E 77, 046405 (2008).
Gusev, I. A., Guskova, A. K. & Mettler, F. A. Medical management of radiation accidents. (CRC Press, Florida, 2000).
Sullivan, J. B. & Krieger, G. R. Clinical environmental health and toxic exposures. (Lippincott Williams & Wilkins, USA, 2001).
Latov, N. Peripheral neuropathy: When the numbness, weakness and pain won’t stop. (AAN Enterprises, USA, 2007).
Chenvidyakarn, T. Buoyancy effects on natural ventilation. (Cambridge University Press, Cambridge, 2013).
Bergman, T. L. et al. Fundamentals of heat and mass transfer. (John Wiley & Sons, USA, 2011).
Acknowledgements
This work was supported by the Thousand Youth Talents Plan, NSFC (No. 11374262) and Fundamental Research Funds for the Central Universities. We thank W. M. Wang and S. M. Weng for discussions on collisional PIC, Z. H. Wang for instruction in laser cavities and M. Y. Yu for helpful comments.
Author information
Authors and Affiliations
Ethics declarations
Competing interests
The author declares no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Wu, HC. Relativistic-microwave theory of ball lightning. Sci Rep 6, 28263 (2016). https://doi.org/10.1038/srep28263
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28263
This article is cited by
-
Changes in the Contents of Podophyllotoxin and other Phenolic Compounds in Acetone Extracts of Suspension Cell Cultures of Podophyllum peltatum L. at Different Stages of Cultivation
Pharmaceutical Chemistry Journal (2023)
-
Summary of basic plasma physics sessions at the first Asia Pacific Plasma Conference, 2017
Reviews of Modern Plasma Physics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


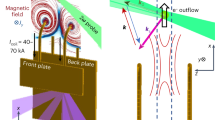



 , electron density ne and ion density ni from t = 1 ns to 11 ns. Vertical dashed line marks the plasma surface. Parameters are given in the text and Methods.
, electron density ne and ion density ni from t = 1 ns to 11 ns. Vertical dashed line marks the plasma surface. Parameters are given in the text and Methods.