Abstract
We report on a method of nanoSQUID modulation which uses kinetic inductance rather than magnetic inductance to manip-ulate the internal fluxoid state. We produced modulation using injected current rather than an applied magnetic field. Using this injected current, we were able to observe the triangle-wave shaped modulation of the device critical current which was periodic according to the London fluxoid quantization condition. The measurement results also confirmed that the fluxoid state inside a superconducting loop can be manipulated using primarily kinetic inductance. By using primarily kinetic inductance rather than magnetic inductance, the size of the coupling inductor was reduced by a factor of 10. As a result, this approach may provide a means to reduce the size of SQUID-based superconducting electronics. Additionally, this method provides a convenient way to perform kinetic inductance characterizations of superconducting thin films.
Similar content being viewed by others
Introduction
The nanoSQUID is a nanoscale superconducting quantum interference device (SQUID) in which the weak-link elements are often Dayem bridges1 instead of Josephson junctions (JJs)2,3. These devices have have been fabricated from a number of materials, including aluminum4, niobium5,6,7, and lead8, and have demonstrated flux sensitivities as low as  8, sufficient to resolve a single electron spin. The use of Dayem bridges instead of multilayer JJs allows the nanoSQUID to be patterned from a single-layer thin film, to reach diameters below 100 nm, and to be realized in high-Tc superconductors9,10. At these scales, the magnetic inductance of the nanoSQUID superconducting ring is small, on the order of 100 fH for a ring of size 100 nm. However, the kinetic inductance of the thin film can be significant even at these sizes, ranging from just comparable to the geometric inductance to several orders of magnitude larger.
8, sufficient to resolve a single electron spin. The use of Dayem bridges instead of multilayer JJs allows the nanoSQUID to be patterned from a single-layer thin film, to reach diameters below 100 nm, and to be realized in high-Tc superconductors9,10. At these scales, the magnetic inductance of the nanoSQUID superconducting ring is small, on the order of 100 fH for a ring of size 100 nm. However, the kinetic inductance of the thin film can be significant even at these sizes, ranging from just comparable to the geometric inductance to several orders of magnitude larger.
In general, SQUID and nanoSQUID device inductances need to be controlled to implement feedback and bias. To shrink device sizes as small as possible–for applications such as superconducting electronics–it becomes convenient to use kinetic rather than geometric inductors where possible. Since kinetic inductances do not couple to magnetic fields11, nanoscale devices which are dominated by kinetic inductance are best controlled by injected currents. Current injection has been demonstrated before as a viable means to control SQUIDs12,13,14 dominated by geometric inductance. These directly-coupled SQUIDs used a large pickup loop to convert an applied magnetic field into a current bias which was injected a smaller, more sensitive readout SQUID. Although the readout SQUIDs in these devices were smaller than the pickup loops, they still used large geometric inductors to route the injected current. This injection method was also used to build a SQUID-based logic family15 similar to RSFQ16,17 which also used geometric inductors. Here we report the results of modulating a nanoSQUID by coupling to the device kinetic inductance instead of its magnetic inductance. We have been able to demonstrate nanoSQUID modulation without the induction of any magnetic field, by using kinetic inductance to route currents injected asymmetrically into the nanoSQUID. This approach permits similar capabilities to a field-based approach, but with reduced dimensions.
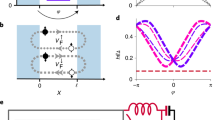
The kinetically-controlled nanoSQUID device geometry is shown in Fig. 1 and is composed of a superconducting ring, with four connecting terminals and two constrictions, all patterned on a 10-nm-thick niobium film. Terminals 1 and 4 were used to measure the switching current of the nanoSQUID, while terminals 2 and 3 were used to inject modulation current. The fabricated constrictions were 105 nm wide, ~3× larger than the coherence length of thin-film niobium, but significantly smaller than the thin-film penetration depth λthin = λ2/d where d is the thickness of the film and λ is the penetration depth18.
(a) Scanning-electron micrograph of a kinetically-controlled nanoSQUID device, fabricated from a thin niobium film. The inset shows a zoomed image one of the nanoSQUID constrictions. These constrictions were measured to be 105 nm wide at their narrowest point. (b) Equivalent circuit of the nanoSQUID device. Shown are the four terminals of the device and their inputs. Ibias, which was used to measure the switching current of the device, flowed in from terminal 1 at the top and was carried out through terminal 4 at the bottom. The modulation current Imod entered and left through the terminals 2 and 3 on the right. I+ and I− are the symmetric and circulating components of Imod, respectively.
Although the constriction shown in Fig. 1 are larger than the coherence length, they still form a type of superconducting weak link: the Dayem bridge1. Depending on its dimensions, a Dayem bridge may have a significantly different current-phase relationship (CPR) than the typical Josephson relation I = Ic sin(ϕ). Our constrictions are wider than the coherence length, and so likely have a different CPR19. However, as long as the bridge cross section is significantly smaller than the thin-film magnetic penetration depth (λthin is ~2 μm for our 10-nm-thick Nb), the CPR of the bridge is expected to be 2π-periodic and allow phase slippage20. The exact nature of the CPR determines the method of phase slippage. In wider bridges like the ones used here, phase slippage occurs by the passage of vortices across the wire. However, the modulation technique reported here is not dependent on the form of the bridge CPR, and so should extend to narrower, more Josephson-like bridges as well.
The device was fabricated from ~10 nm niobium deposited on sapphire by DC magnetron sputtering using the process described in ref. 21. The film had a Tc of 8.2 K, a room-temperature sheet resistance of 30.4 Ω/□, and a residual resistance ratio (RRR) of 3.3. Contact pads were created by evaporating titanium and gold onto the surface using a liftoff process. The nanoSQUID geometry was then patterned by electron-beam lithography, using ~50 nm HSQ as a resist. The pattern was transferred into the film by reactive-ion etching at 50 W (distributed across a 100 mm backing wafer) for 3 min in 1.3 Pa (10 m Torr) CF4. All tests were performed in liquid helium at 4.2 K.
To measure the nanoSQUID characteristics, we injected a fixed modulation current Imod into the device, as shown in the circuit schematic of Fig. 1. We then measured the switching current Isw of the device using current applied through the bias terminals. Specifically, the Isw discussed here represents the total amount of current passing through the constrictions just before the constrictions switched to the normal state.
The nanoSQUID Isw distribution measurements took place with the sample submerged in a bath of liquid helium. The sample was placed in a copper-shielded sample holder. The modulation current Imod was supplied using a variable battery source with two 20 kΩ resistors, one in series with each terminal of the battery source. With Imod fixed, the distribution of Isw was then measured by ramping Ibias until a nonzero voltage appeared at the Ibias terminal, indicating that the constrictions switched to the normal state. The current ramp for Ibias was provided by an arbitrary waveform generator (AWG) in series with a 10 kΩ resistor. The AWG output a 5 Vpp, 200 Hz triangle wave, corresponding to a current ramp rate of ~0.3 A/s.
As we varied the injected current Imod, we observed the modulation of the device Isw shown in Fig. 2. Since the nanoSQUID forms an unbroken superconducting loop, the shape of the Isw modulation can be understood as follows. To maintain phase single-valuedness, current injected by Imod splits between the two paths around the loop according to each path’s relative inductance. One of the paths has a smaller inductance, and so carries a larger fraction of Imod. The resulting imbalance of current flowing through the two constrictions reduces the total Isw of the device. To make this analysis clearer, we can break up the contributions of Imod into two constituent currents: I+, the portion of the modulation current which is divided equally between the two constrictions, and I−, a circulating current which has equal and opposite values through each constriction. These components are shown in Fig. 1. Since our measurement of interest, Isw, is defined as total amount of current passing through both constrictions when they switch, the measurement of I+ is automatically absorbed into Isw, leaving only I− to affect the value of Isw. Thus, we can view the effect of Imod as solely producing a loop current, similar to how a magnetic field would induce a loop current in a conventional SQUID. The triangle-wave pattern seen in Fig. 2 is similar to that seen in ref. 22, indicating a multi-valued, approximately-linear current-phase relationship–confirmation that the Dayem bridge constrictions are wider than the coherence length.
Shown is the the distribution of the nanoSQUID switching current (Isw) varying as a function of the injected modulation current (Imod). Each vertical slice of the graph corresponds to a a measurement of the Isw distribution for that value of Imod. (inset) Two slices showing the distribution of Isw when maximally and minimally modulated by Imod.
The periodicity of the Isw modulation arrives from the London quantization condition, which enforces an integer number of fluxoids in the loop. When Imod produces enough circulating current, the device can counteract the induced current by allowing a fluxoid in through one of the constrictions. Thus, the difference between adjacent maxima of the triangle wave shape correspond to Imod inducing a circulating current equivalent to one fluxoid. One feature of note is that the distribution is not at an extrema when Imod is zero. This distribution shift can be explained by a 4% variation in Ic between the two constrictions23. We additionally verified that the triangle-wave shape of the current modulation matched that of magnetic modulation by independently measuring the effect of applying a magnetic field to the device.
This device has proven to be a convenient metrological tool for extracting the kinetic inductance of superconducting thin films since it only requires low-frequency DC currents. The design of superconducting devices which have kinetic inductances often requires characterization of that inductance to achieve optimal device performance, for example tuning the L/R times of superconducting nanowire single photon detectors24 or nTrons25. Typically, these Lk values are measured by microwave reflection measurements using a network analyzer26, or by measuring the magnetic penetration of the film using two-coil mutual inductance measurements27. By patterning a kinetically-modulated nanoSQUID on the same film as these devices, it instead becomes possible to directly extract the thin-film inductance per square using only low-frequency current measurements–no microwave characterization or tunable magnetic fields are required.
Following the same principles of general SQUIDs28, we used the flux period to extract several parameters from the device including the total device inductance, the kinetic inductance per square, and the total inductance of each current path. To extract the material’s kinetic inductance, we assumed that the kinetic inductance per square was uniform over the entire patterned film. Kinetic inductance is expected to increase with current density29, but such increases are small except within a few percent of the critical current. It is likely this assumption was violated in the vicinity of the constrictions26, but the constrictions represent a small fraction of the total device inductance. From our numerical calculations, the inductances split Imod such that for every 1 μA of current that flowed into the left constriction, 7.2 μA of current flowed through the right constriction, resulting in the relation I− = 0.38 Imod. From the experimental results shown in Fig. 2 we found an  of 24.3 ± 0.1 μA, where
of 24.3 ± 0.1 μA, where  is the period of modulation of the device switching current. We then calculated the loop’s total inductance Ltot by comparing the loop current induced by
is the period of modulation of the device switching current. We then calculated the loop’s total inductance Ltot by comparing the loop current induced by  to the current that would be induced by one flux quantum, Ltot/Φ0, and found a total inductance of 225 pH.
to the current that would be induced by one flux quantum, Ltot/Φ0, and found a total inductance of 225 pH.
Since the total inductance is just the summation of the magnetic and kinetic contributions, the film’s kinetic inductance per square was then Lk = Ltot − Lg, where the magnetic inductance Lg was numerically calculated, giving a value of 16.7 pH. This value was less than 10% of the total inductance, meaning if we wanted to achieve a similar inductance value with purely geometric inductance, the device loop length would need to be at least ten times larger. We then numerically calculated that there were 60.1 squares in the loop, resulting in a kinetic inductance per square of 3.7 pH/□. This sheet inductance was larger than the value predicted26 by  = 1.8 pH/□, where Rs is the sheet resistance just above Tc and Δ is the superconducting gap energy at 4.2 K. This difference is likely due to degradation of the film during the fabrication process, increasing Rs or decreasing the RRR.
= 1.8 pH/□, where Rs is the sheet resistance just above Tc and Δ is the superconducting gap energy at 4.2 K. This difference is likely due to degradation of the film during the fabrication process, increasing Rs or decreasing the RRR.
In summary, we have demonstrated modulation of a nanoSQUID by using kinetic induction rather than magnetic induction to couple and route injected currents. By adding current asymmetrically to the two constrictions of the nanoSQUID, we were able to modulate the switching current of the device. Although the device described here has a large total inductance, and thus low sensitivity when operated as a magnetometer, this method of modulation should generalize to nanoSQUIDs of any design. This technique has applications as a means to reduce device sizes in SQUID-based supeconducting electronics.
Additional Information
How to cite this article: McCaughan, A. N. et al. nanoSQUID operation using kinetic rather than magnetic induction. Sci. Rep. 6, 28095; doi: 10.1038/srep28095 (2016).
Change history
12 January 2017
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Dayem, A. & Wiegand, J. Behavior of Thin-Film Superconducting Bridges in a Microwave Field. Phys. Rev. 155, 419–428 (1967).
Foley, C. P. & Hilgenkamp, H. Why NanoSQUIDs are important: an introduction to the focus issue. Supercond. Sci. Technol. 22, 064001 (2009).
Fink, H., Grünfeld, V. & López, A. Quantum-interference device without Josephson junctions. Phys. Rev. B 35, 35–37 (1987).
Finkler, A. et al. Self-aligned nanoscale SQUID on a tip. Nano Lett. 10, 1046–1049 (2010).
Troeman, A. G. P. et al. NanoSQUIDs Based on Niobium Constrictions. Nano Lett. 7, 2152–2156 (2007).
Hasselbach, K., Veauvy, C. & Mailly, D. MicroSQUID magnetometry and magnetic imaging. Phys. C Supercond. its Appl. 332, 140–147 (2000).
Lam, S. K. H., Clem, J. R. & Yang, W. A nanoscale SQUID operating at high magnetic fields. Nanotechnology 22, 455501 (2011).
Vasyukov, D. et al. A scanning superconducting quantum interference device with single electron spin sensitivity. Nat. Nanotechnol. 8, 639–44 (2013).
Wu, C. H. et al. Fabrication and characterization of high-T(c) YBa(2)Cu(3)O(7-x) nanoSQUIDs made by focused ion beam milling. Nanotechnology 19, 315304 (2008).
Arpaia, R. et al. Ultra low noise YBa2Cu3O7-δ nano superconducting quantum interference devices implementing nanowires. Appl. Phys. Lett. 104, 0–4 (2014).
Luomahaara, J., Vesterinen, V., Grönberg, L. & Hassel, J. Kinetic inductance magnetometer. Nat. Commun. 5, 4872 (2014).
Matsuda, M. et al. Directly-coupled DC-SQUID magnetometers made of Bi-Sr-Ca-Cu oxide films. IEEE Trans. Magn. 27, 3043–3046 (1991).
Ketchen, M. B., Goubau, W. M., Clarke, J. & Donaldson, G. B. Superconducting thin-film gradiometer. J. Appl. Phys. 49, 4111 (1978).
Koelle, D. et al. dc SQUID magnetometers from single layers of YBa2Cu3O7-x. Appl. Phys. Lett. 63, 2271 (1993).
Gheewala, T. A 30-ps Josephson current injection logic (CIL). IEEE J. Solid-State Circuits 14, 787–793 (1979).
Likharev, K. & Semenov, V. RSFQ logic/memory family: a new Josephson-junction technology for sub-terahertz-clock-frequency digital systems. IEEE Trans. Appiled Supercond. 1, 3–28 (1991).
Volkmann, M. H., Sahu, A., Fourie, C. J. & Mukhanov, O. a. Implementation of energy efficient single flux quantum digital circuits with sub-aJ/bit operation. Supercond. Sci. Technol. 26, 015002 (2013).
Gubin, A., Il’in, K., Vitusevich, S., Siegel, M. & Klein, N. Dependence of magnetic penetration depth on the thickness of superconducting Nb thin films. Phys. Rev. B 72, 1–8 (2005).
Troeman, A. et al. Temperature dependence measurements of the supercurrent-phase relationship in niobium nanobridges. Phys. Rev. B 77, 024509 (2008).
Likharev, K. Superconducting weak links. Rev. Mod. Phys. 51, 101–159 (1979).
Najafi, F. et al. Fabrication process yielding saturated nanowire single-photon detectors with 24-ps jitter. IEEE J. Sel. Top. Quantum Electron. 21, 1–7 (2015).
Michotte, S., Lucot, D. & Mailly, D. Fluxoid quantization in the critical current of a niobium superconducting loop far below the critical temperature. Phys. Rev. B 81, 100503 (2010).
Gurtovoi, V. L., Dubonos, S. V., Karpii, S. V., Nikulov, A. V. & Tulin, V. A. Contradiction between the results of observations of resistance and critical current quantum oscillations in asymmetric superconducting rings. J. Exp. Theor. Phys. 105, 262–267 (2007).
Kerman, A., Yang, J., Molnar, R., Dauler, E. & Berggren, K. Electrothermal feedback in superconducting nanowire single-photon detectors. Phys. Rev. B 79, 1–4 (2009).
McCaughan, A. N. & Berggren, K. K. A superconducting-nanowire three-terminal electrothermal device. Nano Lett. 14, 5748–53 (2014).
Annunziata, A. J. et al. Tunable superconducting nanoinductors. Nanotechnology 21, 445202 (2010).
Fiory, A. T., Hebard, A. F., Mankiewich, P. M. & Howard, R. E. Penetration depths of high Tc films measured by two-coil mutual inductances. Appl. Phys. Lett. 52, 2165–2167 (1988).
Clarke, J. & Braginski, A. I. (eds) The SQUID Handbook (Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, FRG, 2004).
Clem, J. & Kogan, V. Kinetic impedance and depairing in thin and narrow superconducting films. Phys. Rev. B 86, 174521 (2012).
Acknowledgements
The authors would like to thank James Daley and Mark Mondol of the MIT Nanostructures Laboratory for technical support. This work was supported by the Air Force Office of Scientific Research (AFOSR). Adam McCaughan was supported by a fellowship from the NSF iQuISE program, award number 0801525.
Author information
Authors and Affiliations
Contributions
A.N.M. conducted the experiments; A.N.M., Q.Z. and K.K.B analysed the results. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
McCaughan, A., Zhao, Q. & Berggren, K. nanoSQUID operation using kinetic rather than magnetic induction. Sci Rep 6, 28095 (2016). https://doi.org/10.1038/srep28095
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28095
This article is cited by
-
High operating temperature in V-based superconducting quantum interference proximity transistors
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.