Abstract
Deep connections are known to exist between scale-free networks and non-Gibbsian statistics. For example, typical degree distributions at the thermodynamical limit are of the form  , where the q-exponential form
, where the q-exponential form  optimizes the nonadditive entropy Sq (which, for q → 1, recovers the Boltzmann-Gibbs entropy). We introduce and study here d-dimensional geographically-located networks which grow with preferential attachment involving Euclidean distances through
optimizes the nonadditive entropy Sq (which, for q → 1, recovers the Boltzmann-Gibbs entropy). We introduce and study here d-dimensional geographically-located networks which grow with preferential attachment involving Euclidean distances through  . Revealing the connection with q-statistics, we numerically verify (for d = 1, 2, 3 and 4) that the q-exponential degree distributions exhibit, for both q and k, universal dependences on the ratio αA/d. Moreover, the q = 1 limit is rapidly achieved by increasing αA/d to infinity.
. Revealing the connection with q-statistics, we numerically verify (for d = 1, 2, 3 and 4) that the q-exponential degree distributions exhibit, for both q and k, universal dependences on the ratio αA/d. Moreover, the q = 1 limit is rapidly achieved by increasing αA/d to infinity.
Similar content being viewed by others
Introduction
Networks emerge spontaneously in many natural, artificial and social systems. Their study is potentially important for physics, biology, economics, social sciences, among other areas. For example, many empirical studies have identified peculiar properties in very different networks such as the Internet and online social networks (e.g., Facebook), citations networks, neurons networks1,2,3, to quote but a few. An ubiquitous class of such networks is constituted by the scale-free ones (more precisely, asymptotically scale-free). As we shall soon verify, these networks can be seen as a particular application of nonextensive statistical mechanics, based on the nonadditive entropy  , where BG stands for Boltzmann-Gibbs)4,5,6. This current generalization of the BG entropy and corresponding statistical mechanics has been widely successful in clarifying the foundations of thermal statistics as well as for applications in complex systems in high-energy collisions at LHC/CERN (CMS, ALICE, ATLAS and LHCb detectors) and at RHIC/Brookhaven (PHENIX detector)7,8,9,10,11,12,13,14,15,16, cold atoms17, dusty plasmas18, spin-glasses19, trapped ions20, astrophysical plasma21,22, biological systems23, type-II superconductors24, granular matter25, the Kuramoto model at the edge of chaos26, low-dimensional maps, for instance the (area-preserving) standard map27 (see Bibliography in http://tsallis.cat.cbpf.br/biblio.htm). Many other physical situations are described which are analogous, such as long-range-interacting Hamiltonians, for example, gravitational problems like globular clusters, spins systems, like the Ising, XY and Heisenberg long-range models. We may also point out random-walk anomalous diffusion where the jumps obey a power low probability distribution function. Some (naturally not all) of the properties of long-range-interacting systems may be described as forming complex network where the sites are linked according to power-law preferential attachment. In the present work we address a wide class of this kind of problems focusing on some basic universality relations.
, where BG stands for Boltzmann-Gibbs)4,5,6. This current generalization of the BG entropy and corresponding statistical mechanics has been widely successful in clarifying the foundations of thermal statistics as well as for applications in complex systems in high-energy collisions at LHC/CERN (CMS, ALICE, ATLAS and LHCb detectors) and at RHIC/Brookhaven (PHENIX detector)7,8,9,10,11,12,13,14,15,16, cold atoms17, dusty plasmas18, spin-glasses19, trapped ions20, astrophysical plasma21,22, biological systems23, type-II superconductors24, granular matter25, the Kuramoto model at the edge of chaos26, low-dimensional maps, for instance the (area-preserving) standard map27 (see Bibliography in http://tsallis.cat.cbpf.br/biblio.htm). Many other physical situations are described which are analogous, such as long-range-interacting Hamiltonians, for example, gravitational problems like globular clusters, spins systems, like the Ising, XY and Heisenberg long-range models. We may also point out random-walk anomalous diffusion where the jumps obey a power low probability distribution function. Some (naturally not all) of the properties of long-range-interacting systems may be described as forming complex network where the sites are linked according to power-law preferential attachment. In the present work we address a wide class of this kind of problems focusing on some basic universality relations.
The deep relationship between scale-free networks and q-statistics started being explored in 200528,29,30, and is presently very active31,32,33,34,35. The basic connection comes (along the lines of the BG canonical ensemble) from the fact that, if we optimize the functional  with the constraint
with the constraint  or analogous (k being the degree of a generic site, i.e., the number of links connected to a given site; P(k) denotes the degree or connectivity distribution), we straightforwardly obtain
or analogous (k being the degree of a generic site, i.e., the number of links connected to a given site; P(k) denotes the degree or connectivity distribution), we straightforwardly obtain  , which turns out to be the generic degree distribution for virtually all kinds of scale-free networks. The q-exponential function is defined as
, which turns out to be the generic degree distribution for virtually all kinds of scale-free networks. The q-exponential function is defined as  . We verify that, for q > 1 and k → ∞, P(k) ~ 1/kγ with γ ≡ 1/(q − 1). The classical result γ = 336 corresponds to q = 4/3.
. We verify that, for q > 1 and k → ∞, P(k) ~ 1/kγ with γ ≡ 1/(q − 1). The classical result γ = 336 corresponds to q = 4/3.
In the present work we address the question of how universal such results might be, and more specifically, how P(k) varies with the dimension d of the system?
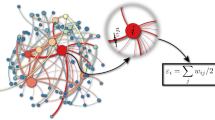
Our growing model starts with one site at the origin. We then stochastically locate a second site (and then a third, a fourth, and so on up to N) through the d-dimensional isotropic distribution

where r ≥ 1 is the Euclidean distance from the newly arrived site to the center of mass of the pre-existing system (in one dimension, r = |x|; in two dimensions,  ; in three dimensions
; in three dimensions  , and so on); we assume angular isotropy; p(r) is zero for 0 ≤ r < 1; the subindex G stands for growth. We consider αG > 0 so that the distribution P(r) is normalizable; indeed,
, and so on); we assume angular isotropy; p(r) is zero for 0 ≤ r < 1; the subindex G stands for growth. We consider αG > 0 so that the distribution P(r) is normalizable; indeed,  , which is finite for αG > 0, and diverges otherwise. See Fig. 1.
, which is finite for αG > 0, and diverges otherwise. See Fig. 1.
Every new site which arrives is then attached to one and only one site of the pre-existing cluster. The choice of the site to be linked with is done through the following preferential attachment probability:

where ki is the connectivity of the i-th pre-existing site (i.e., the number of sites that are already attached to site i), and rij is the Euclidean distance from site i to the newly arrived site j; subindex A stands for attachment.
For αA approaching zero and arbitrary d, the physical distances gradually loose relevance and, at the limit αA = 0, all distances becomes irrelevant in what concerns the connectivity distribution, and we therefore recover the Barabási-Albert (BA) model36, which has topology but no metrics. The BA model was extended37 in such a way that it would be able to yield an exponent γ such that 2 < γ < 3, thus making the model more realistic. In this work they showed a topological phase transition which range from scale-free networks to exponential networks through three control parameters (addition of links, redirection of edges, and addition of new sites). In the present paper we show that, for arbitrary dimensionality, γ can be controlled in a kind of simpler manner, namely by metric changes through only one control parameter (namely the ratio αA/d) in the structure of the network. Notice, however, that the BA generalized model is not a particular case of our model, and neither the other way around.
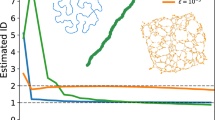
Large-scale simulations have been performed for the (d = 1, 2, 3, 4) models for fixed (αG, αA), and we have verified in all cases that the degree distribution P(k) is completely independent from αG: see Fig. 2. Using this fact, we have arbitrarily fixed αG = 2, and have numerically studied the influence of (d, αA) on P(k): see Figs 3 and 4. In all cases, the q-exponential fittings  with q > 1 and κ > 0 have been remarkably good. To test the goodness of fit, we performed Kolmogorov-Smirnov test38 (see Table 1). To deal with the problem that the data are very sparse in the tail, we excluded data points with sample probability less than 10−6. The best fitting values for (q, κ) are indicated in Fig. 5. From normalization of P(k), P(0) can be expressed as a straightforward function of (q, κ).
with q > 1 and κ > 0 have been remarkably good. To test the goodness of fit, we performed Kolmogorov-Smirnov test38 (see Table 1). To deal with the problem that the data are very sparse in the tail, we excluded data points with sample probability less than 10−6. The best fitting values for (q, κ) are indicated in Fig. 5. From normalization of P(k), P(0) can be expressed as a straightforward function of (q, κ).
 , where
, where .
.The data are those of Fig. 3. Top: log-log representation. Bottom: lnq[P(k)/P(0)] versus k representation. Notice that straight lines in a lnq–linear representation univocally determine the q-exponential function. The fitting parameters are exhibited in Fig. 5. The numerical failure, at large enough values of k, with regard to straight lines are finite-size effects that gradually disappear when we approach the thermodynamic limit N → ∞. Logarithmic binning was used whenever convenient.
For αA = 0 and ∀d, we recover the Barabási-Albert universality class q = 4/3 (hence γ = 3)36, which has no metrics.
Our most remarkable results are presented in Fig. 6, namely the fact that both the index q and the characteristic degree (or “effective temperature”) κ do not depend from (αA, d) in an independent manner but only from the ratio αA/d. This nontrivial fact puts the growing d-dimensional geographically located models that have been introduced here for scale-free networks, on similar footing as long-range-interacting many-body classical Hamiltonian systems such as the inertial XY planar rotators39,40,41,42 (possibly the generic inertial n-vector rotators as well43,44) and Fermi-Pasta-Ulam oscillators, assuming that the strength of the two-body interaction decreases with distance as 1/(distance)α. Moreover, as first pointed out generically by Gibbs himself45, we have the facts that the BG canonical partition function of these classical systems anomalously diverges with size for 0 ≤ α/d ≤ 1 (long-range interactions, e.g., gravitational and dipole-monopole interactions) and converges for α/d > 1 (short-range interactions, e.g., Lennard-Jones interaction), and the internal energy per particle is, in the thermodynamical limit, constant for short-range interactions whereas it diverges like N1−α/d for long-range interactions, N being the total number of particles.
We see that q = 4/3 for 0 ≤ αA/d ≤ 1, and a nearly exponential behavior emerges for αA/d > 1 (∀d); similarly for κ. These results exhibit the universality of both q and κ. The red dot indicates the Barabási-Albert (BA) universality class q = 4/336. In what concerns the universal q = 4/3 cut-off (i.e., the 1/(q − 1) = 3 cut-off), see50 and references therein.
If all these meaningful scalings are put together, we obtain a highly plausible scenario for the respective domains of validity of the Boltzmann-Gibbs (additive) entropy and associated statistical mechanics, and that of the nonadditive entropies Sq (with q ≠ 1) and associated statistical mechanics.
Finally, we notice in Fig. 6 that both q and κ approach quickly their BG limits (q = 1) for αA/d → ∞. Moreover, the same exponential e1−α/d appears in both heuristic expressions for q and κ. Consequently, the following linear relation can be straightforwardly established:

In fact, this simple relation is numerically quite well satisfied as can be seen in Fig. 7. Its existence reveals an interesting peculiarity of the nature of q-statistics. If in the celebrated BG factor e−energy/kT, corresponding to q = 1, we are free to consider an arbitrary value for T, how come in the present problem, κ is not a free parameter but has instead a fixed value for each specific model that we are focusing on? This is precisely what occurs in the high-energy applications of q-statistics, e.g., in quark-gluon soup46 where q = 1.114 and T = 135.2 Mev, as well as in all the LHC/CERN and RHIC/Brookhaven experiments7. Another example which is reminiscent of this type of behavior is the sensitivity to the initial conditions at the edge of chaos (Feigenbaum point) of the logistic map; indeed, the inverse q-generalized Lyapunov exponent satisfies the linear relation 1/λq = 1 − q47,48. The cause of this interesting and ubiquitous feature comes from the fact that q-statistics typically emerges at critical-like regimes and is deeply related to an hierarchical occupation of phase space (or Hilbert space or Fock space), which in turn points towards asymptotic power-laws (see also49). In other words, κ plays a role analogous to a critical temperature, which is of course not a free parameter but is instead fixed by the specific model.
Additional Information
How to cite this article: Brito, S. et al. Role of dimensionality in complex networks. Sci. Rep. 6, 27992; doi: 10.1038/srep27992 (2016).
References
Strogatz, S. H. Exploring complex networks. Nature 410(6825), 268 (2001).
Newman, M. E. J. The structure and function of complex networks. SIAM Review 45(2), 167 (2003).
Costa, L. D. F. et al. Analyzing and modeling real-world phenomena with complex networks: a survey of applications. Advances in Physics 60(3), 329–412 (2011).
Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 52, 479–487 (1988).
Gell-Mann, M. & Tsallis, C. Nonextensive entropy - Interdisciplinary applications (ed. Oxford University Press) (New York, 2004).
Tsallis, C. Introduction to nonextensive statistical mechanics - Approaching a complex world. (ed. Springer) (New York, 2009).
Khachatryan, V. et al. Transverse-Momentum and Pseudorapidity Distributions of Charged Hadrons in pp Collisions at . Phys. Rev. Lett. 105, 022002 (2010).
Chatrchyan, S. et al. Search for new physics with jets and missing transverse momentum in pp collisions at . J. High Energy Phys. 8, 1–46 (2011).
Aamodt, K. et al. Transverse momentum spectra of charged particles in proton-proton collisions at with ALICE at the LHC. Phys. Lett. B 693(2), 53–68 (2010).
Abelev, B. et al. Measurement of electrons from semileptonic heavy-flavor hadron decays in p p collisions at s = 7 TeV. Phys. Rev. D 86(11), 112007 (2012).
Aad, G. et al. Charged-particle multiplicities in pp interactions measured with the ATLAS detector at the LHC. New J. Phys. 13, 053033 (2011).
Adare, A. et al. Measurement of neutral mesons in p+ p collisions at s = 200 GeV and scaling properties of hadron production. Phys. Rev. D 83(5), 052004 (2011).
Adare, A. et al. Production of ω mesons in p+ p, d+ Au, Cu+ Cu, and Au+ Au collisions at s N N = 200 GeV. Phys. Rev. C 84(4), 044902 (2011).
Wong, C. Y. & Wilk, G. Tsallis fits to p T spectra and multiple hard scattering in p p collisions at the LHC. Phys. Rev. D 87(11), 114007 (2013).
Marques, L., Andrade-II, E. & Deppman, A. Nonextensivity of hadronic systems. Phys. Rev. D 87(11), 114022 (2013).
Aaij, R. et al. Study of the production of ∧ b 0 and B 0 hadrons in pp collisions and first measurement of the ∧ b 0 → J/ψpK-branching fraction. Chinese Physics C 40(1), 11001–011001 (2016).
Douglas, P., Bergamini, S. & Renzoni, F. Tunable Tsallis distributions in dissipative optical lattices. Phys. Rev. Lett. 96(11), 110601 (2006).
Liu, B. & Goree, J. Superdiffusion and non-Gaussian statistics in a driven-dissipative 2D dusty plasma. Phys. Rev. Lett. 100(5), 055003 (2008).
Pickup, R. M., Cywinski, R., Pappas, C., Farago, B. & Fouquet, P. Generalized spin-glass relaxation. Phys. Rev. Lett 102(9), 097202 (2009).
DeVoe, R. G. Power-law distributions for a trapped ion interacting with a classical buffer gas. Phys. Rev. Lett. 102(6), 063001 (2009).
Burlaga, L. F., Vinas, A. F., Ness, N. F. & Acuna, M. H. Tsallis statistics of the magnetic field in the heliosheath. Astrophys J. 644(1), L83 (2006).
Livadiotis, G. & McComas, D. J. Invariant kappa distribution in space plasmas out of equilibrium. Astrophys. J. 741(2), 88 (2011).
Upadhyaya, A., Rieu, J. -P., Glazier, J. A. & Sawada, Y. Anomalous diffusion and non-Gaussian velocity distribution of Hydra cells in cellular aggregates. Physica A 293(3), 549–558 (2001).
Andrade, J. S., da Silva, Jr. G. F. T., Moreira, A. A., Nobre, F. D. & Curado, E. M. F. Thermostatistics of overdamped motion of interacting particles. Phys. Rev. Lett 105(26), 260601 (2010).
Combe, G., Richefeu, V., Stasiak, M. & Atman, A. P. F. Experimental Validation of a Nonextensive Scaling Law in Confined Granular Media. Phys. Rev. Lett. 115(23), 238301 (2015).
Miritello, G., Pluchino, A. & Rapisarda, A. Central limit behavior in the Kuramoto model at the “edge of chao”. Physica A 388(23), 4818–4826 (2009).
Tirnakli, U. & Borges, E. P. The standard map: from Boltzmann-Gibbs statistics to Tsallis statistics. Nature/Scientific Reports 6, 23644 (2016).
Soares, D. J. B., Tsallis, C., Mariz, A. M. & da Silva, L. R. Preferential attachment growth model and nonextensive statistical mechanics. EPL 70(1), 70 (2005).
Thurner, S. & Tsallis, C. Nonextensive aspects of self-organized scale-free gas-like networks. EPL 72(2), 197 (2005).
Thurner, S. Nonextensive statistical mechanics and complex scale-free networks. Europhysics News 36(6), 218–220 (2005).
Andrade, J. S., Herrmann, Jr. H. J., Andrade, R. F. & da Silva, L. R. Apollonian networks: Simultaneously scale-free, small world, Euclidean, space filling, and with matching graphs. Phys. Rev. Lett. 94(1), 018702 (2005).
Lind, P. G., da Silva, L. R., Andrade, J. S. Jr. & Herrmann, H. J. Spreading gossip in social networks. Phys. Rev. E 76(3), 036117 (2007).
Mendes, G. A., da Silva, L. R. & Herrmann, H. J. Traffic gridlock on complex networks. Physica A 391(1), 362–370 (2012).
Almeida, M. L., Mendes, G. A., Viswanathan, G. M. & da Silva, L. R. Scale-free homophilic network. European Phys. J. B 86(2), 1–6 (2013).
Macedo-Filho, A., Moreira, D. A., Silva, R. & da Silva, L. R. Maximum entropy principle for Kaniadakis statistics and networks. Phys. Lett. A 377(12), 842–846 (2013).
Barabási, A. L. & Albert, R. Emergence of scaling in random networks. Science 286(5439), 509–512 (1999).
Barabási, A. L. & Albert, R. Topology of evolving networks: local events and universality. Phys. Rev. Lett. 85(24), 5234 (2000).
Bickel, P. J. & Doksum, K. A. Mathematical Statistics: Basic Ideas and Selected Topics, volume I (1977).
Antoni, C. M. & Ruffo, S. Clustering and relaxation in Hamiltonian long-range dynamics. Phys. Rev. E 52(3), 2361 (1995).
Anteneodo, C. & Tsallis, C. Breakdown of exponential sensitivity to initial conditions: Role of the range of interactions. Phys. Rev. Lett. 80(24), 5313 (1998).
Campa, A., Giansanti, A., Moroni, D. & Tsallis, C. Classical spin systems with long-range interactions: universal reduction of mixing. Phys. Lett. A 286(4), 251–256 (2001).
Cirto, L. J. L., Assis, V. R. V. & Tsallis, C. Influence of the interaction range on the thermostatistics of a classical many-body system. Physica A 393, 286–296 (2014).
Nobre, F. D. & Tsallis, C. Classical infinite-range-interaction Heisenberg ferromagnetic model: Metastability and sensitivity to initial conditions. Phys. Rev. E 68(3), 036115 (2003).
Cirto, L. J. L., Lima, L. S. & Nobre, F. D. Controlling the range of interactions in the classical inertial ferromagnetic Heisenberg model: analysis of metastable states. J. Stat. Mech. P04012 (2015).
Gibbs, J. W. Elementary Principles in Statistical Mechanics – Developed with Especial Reference to the Rational Foundation of Thermodynamics (C. Scribner’s Sons, New York, 1902; Yale University Press, New Haven, 1948); OX Bow Press, Woodbridge, Connecticut, 1981).
Walton, D. B. & Rafelski, J. Equilibrium distribution of heavy quarks in Fokker-Planck dynamics. Phys. Rev. Lett. 84(1), 31 (2000).
Lyra, M. L. & Tsallis, C. Nonextensivity and multifractality in low-dimensional dissipative systems. Phys. Rev. Lett. 80(1), 53 (1998).
Baldovin, F. & Robledo, A. Nonextensive Pesin identity: Exact renormalization group analytical results for the dynamics at the edge of chaos of the logistic map. Phys. Rev. E 69(4), 045202(R) (2004).
Plastino, A., Curado, E. M. F. & Nobre, F. D. Deriving partition functions and entropic functionals from thermodynamics. Physica A 403, 13–20 (2014).
Emmerich, T., Bunde, A. & Havlin, S. Structural and functional properties of spatially embedded scale-free networks. Phys. Rev. E 89(6), 062806 (2014).
Acknowledgements
We have benefitted from fruitful discussions with D. Bagchi, E.M.F. Curado, F.D. Nobre, P. Rapcan and G. Sicuro. We also appreciate the suggestions of an anonymous referee which helped us to improve this work. We gratefully acknowledge partial financial support from CNPq and Faperj (Brazilian agencies) and from the John Templeton Foundation-USA.
Author information
Authors and Affiliations
Contributions
C.T. conceived the research, analyzed the results, contributed to the manuscript text and revised it. S.B. developed and carried out the numerics, prepared figures, analyzed the results, contributed to the manuscript text and revised it. L.R.d.S. offered constructive suggestions, analyzed the results, contributed to the manuscript text and revised it.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Brito, S., da Silva, L. & Tsallis, C. Role of dimensionality in complex networks. Sci Rep 6, 27992 (2016). https://doi.org/10.1038/srep27992
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep27992
This article is cited by
-
Universality Classes and Information-Theoretic Measures of Complexity via Group Entropies
Scientific Reports (2020)
-
Thermoelectric properties of BiSbTe alloy nanofilms produced by DC sputtering: experiments and modeling
Journal of Materials Science (2020)
-
Null Model and Community Structure in Multiplex Networks
Scientific Reports (2018)
-
Coexisting crystal and liquid-like properties in a 2D long-range self-consistent model
Scientific Reports (2018)
-
Physical mechanism for biopolymers to aggregate and maintain in non-equilibrium states
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.









 (
(