Abstract
The structural human connectome (i.e. the network of fiber connections in the brain) can be analyzed at ever finer spatial resolution thanks to advances in neuroimaging. Here we analyze several large data sets for the human brain network made available by the Open Connectome Project. We apply statistical model selection to characterize the degree distributions of graphs containing up to  nodes and
nodes and  edges. A three-parameter generalized Weibull (also known as a stretched exponential) distribution is a good fit to most of the observed degree distributions. For almost all networks, simple power laws cannot fit the data, but in some cases there is statistical support for power laws with an exponential cutoff. We also calculate the topological (graph) dimension D and the small-world coefficient σ of these networks. While σ suggests a small-world topology, we found that D < 4 showing that long-distance connections provide only a small correction to the topology of the embedding three-dimensional space.
edges. A three-parameter generalized Weibull (also known as a stretched exponential) distribution is a good fit to most of the observed degree distributions. For almost all networks, simple power laws cannot fit the data, but in some cases there is statistical support for power laws with an exponential cutoff. We also calculate the topological (graph) dimension D and the small-world coefficient σ of these networks. While σ suggests a small-world topology, we found that D < 4 showing that long-distance connections provide only a small correction to the topology of the embedding three-dimensional space.
Similar content being viewed by others
Introduction
The neural network of the brain can be considered on structural (wired) as well as on functional connection levels. Precise structural maps exist only on very small scales. Functional networks, based on fMRI, are available on larger datasets. However a clear-cut relationship between them is largely unknown. Drawing parallels between neural and socio-technological networks, neuroscientists have hypothesized that in the brain we have small-world networks, both on a structural1 and functional level2. Small-world networks are at the same time highly clustered on a local scale, yet possess some long-distance connections that link different clusters of nodes together. This topology is efficient for signal processing3,4, but doubts have remained if the small-world assumption is generally true for the brain. Despite some evidence that functional networks obtained from spatially coarse-grained parcellations of the brain are small worlds5, at a structural cellular level the brain may be a large-world network after all4,6.
Like the small-world property, the hypothesis that functional brain networks have scale-free degree distributions became popular around the turn of the millennium7,8. The degree ki of node i is defined as the number of edges adjacent to i. Because the degree is a basic measure of a node’s centrality, the probability Pr(k) that a node has degree k has played a key role in network science for a long time9. Especially physicists have popularized power law fits to observed degree distributions10,11. When such a fit is statistically justified, the network is called formally “scale-free”. Power laws play a crucial role in statistical physics, where they arise at transitions between an ordered and unordered phase because of the absence of a characteristic length scale. There are theoretical and empirical arguments that the brain operates near such a critical point12,13,14,15. For this reason it is plausible to assume that, on a functional level, the connectome’s degree distribution is also scale-free. More sophisticated statistical analyses of the functional connectome justify skepticism about the scale-free hypothesis16,17,18. Until now there are only few results for degree distributions of structural brain networks and these do not show clear evidence for power laws19.
In this article we answer whether the structural connectome at an intermediate spatial resolution can be viewed as a scale-free, small-world network. We analyze large data sets collected by the Open Connectome project (OCP)20 that describe structural (rather than functional) brain connectivity. The particular data sets chosen by us were processed by members of the OCP from the raw diffusion tensor imaging data by Landman et al.21. Earlier studies of the structural network have analyzed much smaller data. For example the network obtained by Sporns et al., using diffusion imaging techniques22,23, consists of a highly coarse-grained mapping of anatomical connections in the human brain, comprising N = 998 brain areas and the fiber tract densities between them. The entire brain is made up of ~9 × 1010 neurons24, but current imaging techniques cannot resolve such microscopic detail. The networks investigated in this article have up to ~106 nodes, which puts them on a scale that is halfway between the earlier coarse-grained view and the complete neural network.
One important measure which could not have been estimated previously because of too coarse-grained data is the topological (graph) dimension D. It is defined by

where Nr is the number of node pairs that are at a topological (also called “chemical”) distance r from each other (i.e. a signal must traverse at least r edges to travel from one node to the other). The topological dimension characterizes how quickly the whole network can be accessed from any of its nodes: the larger D, the more rapidly the number of r-th nearest neighbors expands as r increases. Different small-world networks can possess different D, for example due to their distinct clustering behavior6. Therefore, the level of small-worldness (quantified for example by the coefficient defined by Humphries and Gurney25) and the topological dimension contain different information.
Distinguishing between a finite and infinite topological dimension is particularly important theoretically. It has been conjectured that heterogeneities can cause strong rare-region effects and generic, slow dynamics in a so-called Griffiths phase26, provided D is finite27. Criticality28 or even a discontinuous phase transition is smeared over an extended parameter space. As a consequence, a signalling network can exhibit behavior akin to criticality, although it does not operate precisely on a unique critical point that sharply divides an ordered from a disordered phase. This phenomenon is pronounced for the Contact Process29, a common model for the spread of activity in a network. Subsequent studies found numerical evidence for Griffiths effects in more general spreading models in complex networks, although the scaling region shrinks and disappears in the thermodynamic limit if D → ∞30,31,32,33. Recently Griffiths phases were also reported in synthetic brain networks34,35,36 with large-world topologies and with modular organization, which enhances the capability to form localized rare-regions. Real connectomes have finite size, so they must possess finite D. If in real connectomes D remains small, these models hint at an alternative explanation why the brain appears to be in a critical state: instead of the self-tuning mechanisms that have been frequently postulated37,38, the brain may be in a Griffiths phase, where criticality exists without fine-tuning. Models with self-tuning require two competing timescales: a slow “energy” accumulation on the nodes and a fast redistribution by avalanches when the energy reaches the firing threshold. It is unclear if such a separation of timescales is realistic. Even if the brain were in a self-organized critical state with clearly separated timescales, Griffiths effects can play an important role due to the heterogeneous behavior of the system, frequently overlooked when modelling the brain.
Open Connectome brain network data
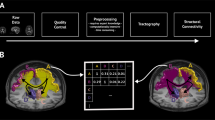
The data sets analyzed in this article were generated by members of the OCP with the MIGRAINE method described by Roncal et al.39. In this section we will briefly summarize their methods. Afterwards we will describe our analysis which was based on the graphs publicly available from the OCP web site20. The raw input data used by the OCP consist of both diffusion and structural magnetic resonance imaging scans with a resolution of  (i.e. the size of a single voxel). MIGRAINE combines various pieces of software into a “pipeline” to transform this input to a graph with 105–106 nodes.
(i.e. the size of a single voxel). MIGRAINE combines various pieces of software into a “pipeline” to transform this input to a graph with 105–106 nodes.
As an intermediate step, the processing software first generates a small graph of 70 nodes40. For this purpose the image is downsampled into 70 regions taken from the Desikan gyral label atlas41. During this step the software also identifies the fibers in the brain with deterministic tractography using the Fiber Assignment by Continuous Tracking (FACT) algorithm42. As stopping thresholds a gradient direction of 70 degrees and a stopping intensity of 0.2 were used.
These fibers are then reanalyzed in the next step of data processing. The Magnetic Resonance One-Click Pipeline outlined by Mhembere et al.43 generates a big graph where each voxel corresponds to one node. First a “mask” is defined, for example the 70 regions included in the small graph. Then all data outside the mask are discarded and an edge is assigned to each remaining voxel pair that is connected by at least one fiber staying within the boundaries of the mask. This procedure will naturally produce hierarchical modular graphs with (at least) two quite different scales.
At this point each scan has been turned into a network with  vertices and
vertices and  edges. However, due to the image processing algorithm (especially because the mask is chosen conservatively), many of these voxels will become disconnected and must be considered as noise. To clean up the data, all vertices outside the largest connected component are removed. According to Roncal et al.39 the remaining graph “keeps essentially all white matter voxels, consisting of ≈105 vertices and ≈108 edges”.
edges. However, due to the image processing algorithm (especially because the mask is chosen conservatively), many of these voxels will become disconnected and must be considered as noise. To clean up the data, all vertices outside the largest connected component are removed. According to Roncal et al.39 the remaining graph “keeps essentially all white matter voxels, consisting of ≈105 vertices and ≈108 edges”.
One important point to note is that two voxels A and C are linked by an edge even if there are other voxels B1, …, Bn between A and C on the same fiber. For example, if one traverses voxels A, B, C on a fiber, the edges (A, B), (A, C) and (B, C) are all part of the graph. Furthermore, the edges are undirected so that (B, A), (C, A) and (C, B) are also part of the graph because the FACT algorithm cannot provide information about the direction of an edge. Note that confounding factors such as the measurement technique, spatial sampling, measurement errors and the network-construction method can affect the graph data we downloaded44. We cannot control them, but tested the robustness of our conclusions by modifying one of the networks by neglecting a fraction of edges that might have arisen as a consequence of the transitivity rule. Additionally, we tested the effect of changing the reference null model from a nonspatial model (the ErdŐs-Rényi graph) to a spatial one (the random geometric graph, see section “Small-world coefficient” below).
To save space the OCP data files store only one of the directions (i.e. the upper triangle of the adjacency matrix) so that the opposite direction must be inferred from the data and inserted into the graph.
There were 3 different sets of big human brain graphs available from the OCP website20 with the abbreviations KKI (Kennedy Krieger Institute), MRN (Mind Research Network) and NKI (Nathan Kline Institute). The raw data are described by Landman et al.21, Jung et al.45 and Nooner et al.46, respectively. We analyzed the KKI graphs numbered 10 to 19 in more detail. Some graph invariants (e.g. degrees, clustering coefficients) were calculated and analyzed by Mhembere et al.43, but for the present study we have recalculated all invariants directly from the graph data available from the OCP website.
Degree distribution
Model selection
We want to assess how well different probability distributions fit the degrees of the OCP graphs. A first rough-and-ready visual attempt supports the hypothesis that the tails might be stretched exponentials, for example for the networks KKI-10 and KKI-18 in Fig. 1. However, such visual techniques have no inferential power. Even if the fitted parameters come from ordinary least-squares regression toolboxes, the fitted parameters in general do not converge to the true values even if the number of data points is large. Moreover, least-squares regression lacks a statistically principled criterion for comparing different models with each other.
Empirical degree distributions of the KKI-10 and KKI-18 graphs (solid lines).
Dashed lines show a rough-and-ready approach: ordinary least-squares fits for k > 1000 for the two graphs (short-dashed line for fit to KKI-18, long-dashed line for KKI-10) suggest stretched exponential tails. While ordinary least-squares fits are not a sound basis for model selection, we demonstrate in this article that there is indeed statistical evidence in favor of a generalized three-parameter Weibull distribution with a stretched exponential tail.
A statistically sound framework for model selection is information theory. Here we adopt the information-theoretic methodology proposed by Handcock and Jones47 who fitted different functions to degree distributions in sexual contact networks. The key idea is that a good model should perform well in terms of two opposing objectives. On one hand the model should have enough flexibility so that it is able to fit the observed distribution. On the other hand it should have only a minimal number of parameters. In general, the more parameters we have at our disposal, the better we can fit the observation.
The goodness of fit can be quantified by the likelihood function which, under the assumption of independent observations, has the form

Here v is the set of parameters in the model, N the number of observations and k1, …, kN are the observed degrees. Alternatively we can write the likelihood as

where kmin and kmax are the minimum and maximum observed degrees and ni is the number of times we observe the degree ki. In the graphs KKI-10 through KKI-19, kmin is always equal to 1; kmax ranges from 5154 to 11241. In the extreme case of allowing as many parameters as there are observed degrees we can achieve a maximal likelihood of e−NH, where  is the Shannon entropy of the data. However, such a highly parameterized model is no longer informative, because it fits only the particular connectome used as input and sheds little light on general features that different connectomes might have in common.
is the Shannon entropy of the data. However, such a highly parameterized model is no longer informative, because it fits only the particular connectome used as input and sheds little light on general features that different connectomes might have in common.
Statisticians have proposed several “information criteria” to address this problem of over-fitting (e.g. Bayesian, deviance or Hannan-Quinn information criteria). These are objective functions that rate the quality of a model based on a combination of the likelihood  and the number of parameters K. In this study we apply the Akaike information criterion with a correction term for finite sample size48,
and the number of parameters K. In this study we apply the Akaike information criterion with a correction term for finite sample size48,

where  is the set of parameters that maximizes
is the set of parameters that maximizes  ; as before, N is the number of observations. The last term in Eq. 4 is a second-order bias correction which, although not in Akaike’s original formula49, gives more accurate results if
; as before, N is the number of observations. The last term in Eq. 4 is a second-order bias correction which, although not in Akaike’s original formula49, gives more accurate results if  50.
50.
While the absolute size of AICc is not interpretable, differences in AICc are informative and allow us to quantitatively compare different models48. If we denote the AICc value of model j by  and the minimum over all models by
and the minimum over all models by  , then the difference
, then the difference

estimates the relative expected Kullback-Leibler distance between model j and the estimated best model51. As a rule of thumb, models with  have substantial empirical support; models with Δj > 10 on the other hand are unlikely candidates to explain the data48.
have substantial empirical support; models with Δj > 10 on the other hand are unlikely candidates to explain the data48.
Burnham and Anderson48 list many theoretical reasons in favor of model selection based on AICc. The Bayesian information criterion (BIC), although almost equally popular, has been reported to yield poor results when used to fit power-law tails in probability distributions52 because it tends to underestimate the number of parameters. The Akaike information criterion penalizes less severely for additional parameters: in the limit  the penalty is asymptotically equal to the term 2K in Eq. 4, whereas the equivalent term in the BIC grows as K In(N). We carried out Monte Carlo simulations on synthetically generated probability distributions of the type described in the next section (see supplementary material). We found that model selection by AICc came close to the true number of parameters. Although the BIC showed acceptable performance, we confirmed that it indeed favors a too small number of parameters. We therefore advocate the use of AICc rather than BIC for fitting degree distributions.
the penalty is asymptotically equal to the term 2K in Eq. 4, whereas the equivalent term in the BIC grows as K In(N). We carried out Monte Carlo simulations on synthetically generated probability distributions of the type described in the next section (see supplementary material). We found that model selection by AICc came close to the true number of parameters. Although the BIC showed acceptable performance, we confirmed that it indeed favors a too small number of parameters. We therefore advocate the use of AICc rather than BIC for fitting degree distributions.
Candidate models
The first step of AICc-based model selection is the definition of several candidate models that might generate the observed distribution. We denote as before by Pr(k) the probability that a node has degree k. The distinctive feature of different candidate models is the asymptotic decay of Pr(k) for  . Only in this limit we can hope to find scale-free behavior if it indeed exists. Of course, all real networks are finite so that, strictly speaking, we cannot take the limit k → ∞. If we restrict ourselves to only a few high-degree nodes, we have too few data points for a meaningful fit. On the other hand, if we include too many low-degree nodes, then we may misjudge the correct asymptotic behavior of Pr(k).
. Only in this limit we can hope to find scale-free behavior if it indeed exists. Of course, all real networks are finite so that, strictly speaking, we cannot take the limit k → ∞. If we restrict ourselves to only a few high-degree nodes, we have too few data points for a meaningful fit. On the other hand, if we include too many low-degree nodes, then we may misjudge the correct asymptotic behavior of Pr(k).
We therefore assume for all candidate models that there is an optimal cutoff point kc that separates nodes with degree ≤kc from the region where a hypothesized asymptotic function F (k) can fit the data47,

Each parameter Ak is chosen so that Pr (k) = Ak for k = 1, …, kc. Different families of candidate models can be defined by different functions F (k). We list all the functions F investigated in this study in Table 1. The exponential function (EXP) is the candidate that decays most rapidly in the right tail. The power law (POW) has two parameters: an exponent β > 0 and a constant α > 0 that shifts the function to the left or right. The tail  has the conventional power law form F (k) ∝ k−β. The discrete log-normal (LGN) and Weibull (WBL) distributions are represented by the usual distribution functions of their continuous namesakes. We also include two three-parameter models: a truncated power law (TPW) and the generalized Weibull distribution (GWB). In comparison to POW, TPW includes an additional exponential factor which is often used to mimic finite-size cutoffs in the right tail. GWB is a standard three-parameter generalization of WBL with an additional parameter γ, called location parameter, that shifts the distribution to the right or left53.
has the conventional power law form F (k) ∝ k−β. The discrete log-normal (LGN) and Weibull (WBL) distributions are represented by the usual distribution functions of their continuous namesakes. We also include two three-parameter models: a truncated power law (TPW) and the generalized Weibull distribution (GWB). In comparison to POW, TPW includes an additional exponential factor which is often used to mimic finite-size cutoffs in the right tail. GWB is a standard three-parameter generalization of WBL with an additional parameter γ, called location parameter, that shifts the distribution to the right or left53.
We can distinguish the members of each candidate model family by the choice of kc, the values of  and α, β, γ. Model selection by AICc gives a natural criterion for the optimal parameters matching an observed distribution. It is a simple exercise to prove that
and α, β, γ. Model selection by AICc gives a natural criterion for the optimal parameters matching an observed distribution. It is a simple exercise to prove that  is maximized if Ak equals the observed relative frequency of nodes with degree k,
is maximized if Ak equals the observed relative frequency of nodes with degree k,

For a fixed value of kc, standard numerical algorithms can optimize the remaining parameters α, β and γ in Table 1 to maximize  . After calculating these maximum-likelihood estimators for every kc between 0 and kmax, we search for the value of kc that minimizes AICc of Eq. 4. The number K of parameters that we have to insert into this equation is
. After calculating these maximum-likelihood estimators for every kc between 0 and kmax, we search for the value of kc that minimizes AICc of Eq. 4. The number K of parameters that we have to insert into this equation is
-
K = kc + 1 for EXP,
-
K = kc + 2 for POW, LGN and WBL,
-
K = kc + 3 for TPW and GWB.
Results of model selection
For each candidate model and each kc = 0, …, kmax we compute the AICc. We then determine the smallest  from the entire set and calculate for each model j the difference Δj defined in Eq. 5. In Fig. 2 we show for the example of the network KKI-18 the best-fitting distribution within each candidate model family. We have chosen a logarithmic scale for the ordinate to highlight the differences in the right tail. While the exponential and simple Weibull distributions decrease too rapidly, the power law and log-normal distributions decay too slowly. The truncated power law and generalized Weibull distributions are better in mimicking the overall shape of the distribution.
from the entire set and calculate for each model j the difference Δj defined in Eq. 5. In Fig. 2 we show for the example of the network KKI-18 the best-fitting distribution within each candidate model family. We have chosen a logarithmic scale for the ordinate to highlight the differences in the right tail. While the exponential and simple Weibull distributions decrease too rapidly, the power law and log-normal distributions decay too slowly. The truncated power law and generalized Weibull distributions are better in mimicking the overall shape of the distribution.
The maximum-likelihood distributions from each model family for matching the degree distribution of network KKI-18.
In this example the generalized Weibull distribution is the best compromise in the right tail (see Table 2).
We find that, broadly speaking, this observation is typical of the ten investigated connectomes. As we see from Table 2, in 9 out of the 10 investigated networks we can achieve Δj < 10 with the GWB distribution. In 6 out of 10 cases, there is a similar level of evidence for the TPW model which has been previously hypothesized for functional brain networks54,55,56. For all other candidate distributions there is either none or very sporadic statistical support. When interpreting Table 2, one should bear in mind that even the best-fitting model is only “best” compared with the other tested candidates. True brain networks are of course far more complicated than any of our candidate models. Even if there were a “true” model, searching for “the” degree distribution of the human connectome is not a sensible endeavor because it would certainly be a highly complex model that is unlikely ever to be discovered and included in the set of candidates. As we discuss in the supplementary information, we can nevertheless sensibly ask which candidate model comes closest to the truth in the sense that it minimizes the Kullback-Leibler divergence. With this interpretation, we conclude that GWB is generally the best of our candidates. The fact that not all of the ten data sets are best fitted by the same model does not call this conclusion into question. Just as in traditional p-value based hypothesis testing, we also expect in AICc-based model selection that the best general model is sometimes rejected by random chance for a concrete data sample.
 for each candidate degree distribution.
for each candidate degree distribution.A closer look at the fitted GWB values (Table 3) shows that, with the exception of KKI-16 where GWB is rejected by the AICc, the β exponents lie within one order of magnitude suggesting a common trend if not even universality. This order of magnitude also agrees with the least-squares fit in Fig. 1.
Dimension Measurements
To measure the dimension of the network57 we first computed the distances from a seed node to all other nodes by running the breadth-first search algorithm. Iterating over every possible seed, we counted the number of nodes Nr with graph distance r or less from the seeds and calculated the averages over the trials. As Fig. 3 shows, an initial power law crosses over to saturation due to the finite network sizes. We determined the dimension of the network, as defined by the scaling law (1), by attempting a power-law fit to the data N(r) for the initial ascent. This method resulted in dimensions between D = 3 and D = 4.
Number of nodes within graph distance r in the big KKI graphs.
Dashed lines show power-law fits. Inset: local slopes defined in Eq. 8. Crosses correspond to measurements on a regular 1003 lattice.
To see the corrections to scaling we determined the effective exponents of D as the discretized, logarithmic derivative of (1)

As the inset of Fig. 3 shows, Deff(r) tends to values below 4 even in the infinite size limit, but the narrow scaling region breaks down for r > 5. Furthermore, the extrapolated values for D of the connectomes exhibit an increasing tendency with N as we will now explain in detail.
For better understanding we have also performed the analysis for other graphs besides KKI, possessing graph sizes in different ranges of N. The finite size scaling results are summarized in Fig. 4, where we also extrapolate to N → ∞. As one can see, the dimension values follow the same trend for KKI-, MRN- and NKI-graphs without any clear sign of saturation. A power-law fit to the data with the form A + BNC is also shown, suggesting that D diverges for infinite N. It is tempting to extrapolate with this function to larger sizes or even to the infinite size limit. However, since we can rule out that the degree distributions are scale-free, we cannot assume that such extrapolated graphs faithfully represent connectomes of finer resolution. For example, using this power-law extrapolation we would overestimate their maximum degree kmax.
Thus the present data does not permit claiming any particular numeric value for the dimension D of the true (i.e. microscopically resolved) brain connectome.
We cannot modify the algorithms that generate the OCP graphs, but tested the robustness by randomly removing 20% of the directed graph connections in case of the KKI-18 network. This makes the network partially directed, more similar to a real connectome. As a result the graph dimension did not change much: D = 3.2(2) instead of 3.05(1). Since the majority of edges are short, a random removal results in a relative enhancement of long connections, but D increases only slightly.
Small-world coefficient
Small-worldness can be characterized by different definitions. One of them is the so-called small-world coefficient σ, which is defined as the normalized clustering coefficient (C/Cr) divided by the normalized average shortest path length (L/Lr),

where the normalization divides the observed quantity (C or L) by the expectation value (Cr or Lr) for an ErdŐs-Rényi (ER) random graph with the same number of nodes and edges25.
There are two different definitions of a clustering coefficient in the literature. The Watts-Strogatz clustering coefficient58 of a network of N nodes is

where ni denotes the number of direct edges interconnecting the ki nearest neighbors of node i. An alternative is the “global” clustering coefficient59, also called “fraction of transitive triplets” in the social networks literature60,

Both definitions are in common use, but values for CW and CΔ can differ substantially because Eq. 10 gives greater weight to low-degree nodes.
The average shortest path length is61

where d (i, j) is the graph distance between vertices i and j. L is only properly defined if the network is connected because otherwise the graph distance between some voxels is infinite.
We have calculated C and L for the largest connected components of several KKI networks directly from the edge lists on the OCP website20. The CΔ values are about half of those for CW (see Table 4). A finite size scaling analysis shows that the values of L, CΔ and CW decay by increasing the size N (see Fig. 5). For the average shortest path-length this decay is rather fast; a least-squares regression with the form a + b(1/N)c results in  and
and  . The constant is near zero within the precision of data, so in the infinite size limit we see small-world behavior. The clustering coefficients are almost constant; the power-law fit provides a very small slope:
. The constant is near zero within the precision of data, so in the infinite size limit we see small-world behavior. The clustering coefficients are almost constant; the power-law fit provides a very small slope:  in agreement with the behavior of modular graphs62. The decreasing trends for L, CW and CΔ as functions of N are statistically significant at the 5% significance level; the p-values for t-tests of zero slope for the log-transformed data are 0.03, 0.002 and 0.04 respectively. Again, finite size scaling has to be interpreted with caution given that the topology is not scale-free.
in agreement with the behavior of modular graphs62. The decreasing trends for L, CW and CΔ as functions of N are statistically significant at the 5% significance level; the p-values for t-tests of zero slope for the log-transformed data are 0.03, 0.002 and 0.04 respectively. Again, finite size scaling has to be interpreted with caution given that the topology is not scale-free.
Network invariants as a function of 1/N for the investigated KKI graphs from Table 4.
Lines show power-law fits.
As before, we tested the robustness, this time by deleting 10% randomly chosen undirected edges. We obtained very little changes: L = 11.37 (previously: 11.30), CW = 0.538 (previously: 0.598) CΔ = 0.322 (previously: 0.358).
Due to the transitivity of OCP graphs, one may question the validity of using ER graphs as a null model. Especially the high clustering can be at least partly attributed to the spatial embedding so that, for example, three-dimensional random geometric graphs63 are useful as comparison. Random geometric graphs have indeed a much higher clustering coefficient64, CW = 15/32, a similar value to CW in the OC graphs. To circumvent such problems Telesford et al.65 suggested another small-world criterion, using a “latticized” version of the graph for reference. However, as they pointed out, the latticization algorithm is computationally too demanding for large graphs. Their algorithm is in practice feasible only for up to  nodes, thus the necessary memory and run-times are prohibitive in our case.
nodes, thus the necessary memory and run-times are prohibitive in our case.
We therefore kept the ER graphs as our null model and calculated the corresponding small-world coefficient σ in Eq. 9. We determined the clustering coefficient of the corresponding random networks Cr = 〈k〉/N, where 〈k〉 is the mean degree. We have computed the average path length of the corresponding ErdŐs-Rényi networks with the formula66

where Nl is the size of the largest component.
Applying these formulas to the KKI graphs, the last two columns of Table 4 show that σW,  for all cases, suggesting small-world behavior according to this definition. These values do not show any tendency with respect to N: the t-tests for zero slope have p-values 0.45 and 0.72 for σW and σΔ, respectively.
for all cases, suggesting small-world behavior according to this definition. These values do not show any tendency with respect to N: the t-tests for zero slope have p-values 0.45 and 0.72 for σW and σΔ, respectively.
Conclusions
Let us return to our introductory question: are the structural connectome graphs from the OCP database scale-free, small-world networks? As far as the adjective “scale-free” is concerned, the answer is clearly no. We have applied model selection based on the Akaike information criterion to 10 graphs comparing 6 different degree distribution models. The observed distributions are best fitted by the generalized Weibull function with a stretched exponential tail ∝exp (−kβ). Most of the exponents β are between 0.2 and 0.5, which may hint at a universal trend. In some cases a truncated power law is a plausible alternative. However, the truncation occurs at a degree much smaller than the number of nodes in the network so that one cannot regard these distributions as scale-free.
Unlike the term “scale-free”, the adjective “small-world” does apply to the OCP connectomes in the sense that the small-world coefficients are much larger than 1. We have performed a finite size scaling analysis using several graphs and found no dependence between the number of nodes N and the small-world coefficients. The average path length, however, decreases as N increases. The resolution to this apparent paradox is that the average degree 〈k〉 increases with N so that there is an increasing number of shortcuts through the network. On the other hand, we obtained small topological dimensions characteristic of large-world networks. The dimensions show a tendency to grow as the sizes of the studied graphs increase. The limit N → ∞ here is taken by increasing N for a fixed voxel size. The absence of a scale-free degree distribution suggests that this limit may not be equivalent to fixing the brain volume and instead resolving the details of the connectome at an infinitely small scale. For this reason, it is difficult to judge whether Griffiths effects can be found in the brain, but the small topological dimensions that we have observed warrant further investigation.
Our analysis has been based on unweighted graphs. More realistically, however, the connectome is a weighted, modular network. Links between modules are known to be much weaker than the intra-module connections. Thus, future studies should take into account that signals in the brain propagate on a weighted, heterogeneous network, where generic slow dynamics is a distinct possibility67. The methods presented here to characterize degree distributions and topological dimensions can be generalized to the weighted case. We hope that, as more precise and finely resolved connectome data will become available, future research will be able to assess whether Griffiths phases can indeed occur in the brain.
Additional Information
How to cite this article: Gastner, M. T. and Ódor, G. The topology of large Open Connectome networks for the human brain. Sci. Rep. 6, 27249; doi: 10.1038/srep27249 (2016).
References
Hilgetag, C. C., Burns, G. A., O’Neill, M. A., Scannell, J. W. & Young, M. P. Anatomical connectivity defines the organization of clusters of cortical areas in the macaque monkey and the cat. Philos. Trans. R. Soc. B 355, 91–110 (2000).
Sporns, O. & Honey, C. J. Small worlds inside big brains. Proc. Natl. Acad. Sci. USA 103, 19219–19220 (2006).
Lago-Fernández, L. F., Huerta, R., Corbacho, F. & Sigüenza, J. A. Fast response and temporal coherent oscillations in small-world network. Phys. Rev. Lett. 84, 2758–2761 (2000).
Gallos, L. K., Makse, H. & Sigman, M. A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. Proc. Natl. Acad. Sci. USA 109, 2825–2830 (2012).
Salvador, R. et al. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 15, 1332–1342 (2005).
Hilgetag, C. C. & Goulas, A. Is the brain really a small-world network? Brain Struct. Func. 1–6, doi: 10.1007/s00429-015-1035-6 (2015).
Eguíluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M. & Apkarian, A. V. Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102 (2005).
van den Heuvel, M. P., Stam, C. J., Boersma, M. & Hulshoff Pol, H. E. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. NeuroImage 43, 528–539 (2008).
de Solla Price, D. A general theory of bibliometric and other cumulative advantage processes. J. Am. Soc. Inform. Sci. 27, 292–306 (1976).
Barabási, A.-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).
Caldarelli, G. Scale-free networks: complex webs in nature and technology, (Oxford University Press, Oxford, 2007).
Beggs, J. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003).
Expert, P. et al. Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J. R. Soc. Interface 8, 472–479 (2011).
Shew, W. L. & Plenz, D. The functional benefits of criticality in the cortex. Neuroscientist 19, 88–100 (2013).
Haimovici, A., Tagliazucchi, E., Balenzuela, P. & Chialvo, D. R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 110 178101 (2013).
Le, H. Complex network analysis: applications to human brain functional networks. Master’s thesis, Universitat Pompeu Fabra. Available at: http://www.upf.edu/csim/_pdf/_BestTheses/HoangLe_2012-13.pdf. Date of access: 22/03/2016 (2013).
Ferrarini, L. et al. Non-parametric model selection for subject-specific topological organization of resting-state functional connectivity. NeuroImage 56, 1453–1462 (2011).
Ruiz Vargas, E., Mitchell, D. G. V., Greening, S. G. & Wahl, L. M. Topology of whole-brain functional MRI networks: improving the truncated scale-free model. Physica A 405, 151–158 (2014).
Humphries, M. D., Gurney, K. & Prescott, T. J. The brainstem reticular formation is a small-world, not scale-free, network. Proc. R. Soc. B 273, 503–511 (2006).
Open Connectome Project, Available at: http://www.openconnectomeproject.org. Date of access: 25/05/2015.
Landman, B. A. et al. Multi-parametric neuroimaging reproducibility: a 3T resource study. NeuroImage 54, 2854–2866 (2011).
Hagmann, P. et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159 (2008).
Honey, C. J. et al. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. 106, 2035–2040 (2009).
Lent, R., Azevedo, F. A. C., Andrade-Moraes, C. H. & Pinto, A. V. O. How many neurons do you have? Some dogmas of quantitative neuroscience under revision. Eur. J. Neurosci. 35, 1–9 (2012).
Humphries, M. D. & Gurney, K. Network ‘small-world-ness’: a quantitative method for determining canonical network equivalence. PLoS One 3, e0002051 (2008).
Griffiths, R. B. Nonanalytic behavior above the critical point in a random Ising ferromagnet. Phys. Rev. Lett. 23, 17–19 (1969).
Muñoz, M. A., Juhász, R., Castellano, C. & Ódor, G. Griffiths phases on complex networks. Phys. Rev. Lett. 105, 128701 (2010).
Ódor, G. Universality in nonequilibrium lattice systems, (World Scientific, Singapore 2008).
Harris, T. E. Contact interactions on a lattice. Ann. Prob. 2, 969–988 (1974).
Ódor, G. & Pastor-Satorras, R. Slow dynamics and rare-region effects in the contact process on weighted tree networks. Phys. Rev. E 86, 026117 (2012).
Ódor, G. Rare regions of the susceptible-infected-susceptible model on Barabási-Albert networks. Phys. Rev. E 87, 042132 (2013).
Ódor, G. Spectral analysis and slow spreading dynamics on complex networks. Phys. Rev. E 88, 032109 (2013).
Cota, W., Ferreira, S. C. & Ódor, G. Griffiths effects of the susceptible-infected-susceptible epidemic model on random power-law networks. Phys. Rev. E 93, 032322 (2016).
Moretti, P. & Muñoz, M. A. Griffiths phases and the stretching of criticality in brain networks. Nat. Commun. 4, 2521 (2013).
Villegas, P., Moretti, P. & Muñoz, M. A. Frustrated hierarchical synchronization and emergent complexity in the human connectome network. Sci. Rep. 4, 5990 (2015).
Ódor, G., Dickman, R. & Ódor, G. Griffiths phases and localization in hierarchical modular networks. Sci. Rep. 5, 14451 (2015).
Bak, P., Tang, C. & Wiesenfeld, W. Self-organized criticality. Phys. Rev. A 38, 364–374 (1988).
Hesse, J. & Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 8, 166 (2014).
Roncal, W. G. et al., Technical report. Available at: http://arxiv.org/abs/1312.4875. Date of access: 22/03/2016 (2013).
Gray, W. R. et al. Magnetic resonance connectome automated pipeline: an overview. IEEE Pulse 3, 42–48 (2012).
Desikan, R. S. et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage 31, 968–980 (2006).
Mori, S., Crain, B. J., Chacko, V. P. & van Zijl, P. C. M. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 45, 265–269 (1999).
Mhembere, D. et al. Computing scalable multivariate glocal invariants of large (brain-) graphs. IEEE GlobalSIP 297–300 Available at: http://ieeexplore.ieee.org/xpl/abstractAuthors.jsp?reload=truearnumber=6736874. Date of access: 22/03/2016 (2013).
Bialonski, S., Horstmann, M. T. & Lehnertz, K. From brain to earth and climate systems: small-world interaction networks or not? Chaos. 20, 013134 (2010).
Jung, R. E. et al. Neuroanatomy of creativity. Hum. Brain. Mapp. 31, 398–409 (2010).
Nooner, K. B. et al. The NKI-Rockland sample: a model for accelerating the pace of discovery science in psychiatry. Front. Neurosci. 6, 152 (2012).
Handcock, M. S. & Jones, J. H. Likelihood-based inference for stochastic models of sexual network formation. Theor. Pop. Biol. 65, 413–422 (2004).
Burnham, K. P. & Anderson, D. R. Model selection and multimodel inference, (Springer, New York 1998).
Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).
Hurvich, C. M. & Tsai, C.-L. Regression and time series model selection in small samples. Biometrika 76, 297–307 (1989).
Burnham, K. P. & Anderson, D. R. Kullback-Leibler information as a basis for strong inference in ecological studies. Wildlife Res. 28, 111–119 (2001).
Clauset, A., Shalizi, C. R. & Newman, M. E. J. Power-law distributions in empirical data. SIAM Rev. 51, 661–703 (2009).
Teimouri, M. & Gupta, A. K. On the three-parameter Weibull distribution shape parameter estimation. J. Data Sci. 11, 403–414 (2013).
Achard, A., Salvador, R., Whitcher, B., Suckling, J. & Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 26, 63–72 (2006).
Hayasaka, S. & Laurienti, P. J. Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. NeuroImage 50, 499–508 (2010).
Joyce, K. E., Laurienti, P. J., Burdette, J. H. & Hayasaka, S. A new measure of centrality for brain networks. PLoS One 5, e12200 (2010).
Gastner, M. T. & Newman, M. E. J. The spatial structure of networks. Eur. Phys. J. B 49, 247–252 (2006).
Watts, D. J. & Strogatz, S. H. Collective dynamics of “small-world” networks. Nature 393, 440–442 (1998).
Newman, M. E. J., Moore, C. & Watts, D. J. Mean-field solution of the small-world network model. Phys. Rev. Lett. 84, 3201–3204 (2000).
Jackson, M. O. Social and economic networks, (Princeton University Press, Princeton 2008).
van den Heuvel, M. P., Stam, C. J., Kahn, R. S. & Hulshoff Pol, H. E. Efficiency of functional brain networks and intellectual performance. J. Neurosci. 29, 7619–7624 (2009).
Ravasz, E. & Barabási, A.-L. Hierarchical organization in complex networks. Phys. Rev. E 67, 026112 (2003).
Penrose, M. Random geometric graphs, (Oxford University Press, Oxford, 2003).
Dall, J. & Christensen, M. Random geometric graphs. Phys. Rev. E 66, 016121 (2002).
Telesford, Q. K., Joyce, K. E., Hayasaka, S., Burdette, J. H. & Laurienti, P. J. The ubiquity of small-world networks. Brain Connect. 1, 367–375 (2011).
Fronczak, A., Fronczak, P. & Hołyst, J. A. Average path length in random networks. Phys. Rev. E 70, 056110 (2004).
Ódor, G. Critical dynamics on a large human Open Connectome network. Preprint: arXiv:1604.02127.
Acknowledgements
We thank the staff of the Open Connectome project for help and discussions. Support from the Hungarian research fund OTKA (Grant No. K109577) and the European Commission (project number FP7-PEOPLE-2012-IEF 6-4564/2013) is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
Both authors designed the study and collected the data. M.T.G. performed the analysis of the degree distribution, prepared Figure 2, Tables 1–3 and wrote the supplementary information. G.Ó. conducted the dimension measurements and prepared Figures 1, 3–5 and Table 4. Both authors calculated the small-world coefficients and wrote and reviewed the main manuscript text.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gastner, M., Ódor, G. The topology of large Open Connectome networks for the human brain. Sci Rep 6, 27249 (2016). https://doi.org/10.1038/srep27249
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep27249
This article is cited by
-
Dependence of connectivity on geometric distance in brain networks
Scientific Reports (2019)
-
Critical synchronization dynamics of the Kuramoto model on connectome and small world graphs
Scientific Reports (2019)
-
Concurrence of form and function in developing networks and its role in synaptic pruning
Nature Communications (2018)
-
Griffiths phases in infinite-dimensional, non-hierarchical modular networks
Scientific Reports (2018)
-
Can local-community-paradigm and epitopological learning enhance our understanding of how local brain connectivity is able to process, learn and memorize chronic pain?
Applied Network Science (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.