Abstract
We have utilized ultrafast optical spectroscopy to study carrier dynamics in slightly underdoped (BaK)Fe2As2 crystals without magnetic transition. The photoelastic signals due to coherent acoustic phonons have been quantitatively investigated. According to our temperature-dependent results, we found that the relaxation component of superconducting quasiparticles persisted from the superconducting state up to at least 70 K in the normal state. Our findings suggest that the pseudogaplike feature in the normal state is possibly the precursor of superconductivity. We also highlight that the pseudogap feature of K-doped BaFe2As2 is different from that of other iron-based superconductors, including Co-doped or P-doped BaFe2As2.
Similar content being viewed by others
Introduction
Iron-based high-temperature superconductors have attracted great attention in recent years1. Among the more than six families based on their respective compositions of compounds, of which the 1111 (such as SmFeAsO), 122 (such as BaFe2As2), 111 (such as LiFeAs) and 11 (such as FeSe) systems have been widely studied. Compounds of the 122 system are the easiest among the iron-based superconductors to synthesize in the form of large single crystals and most publications have been devoted to 122 compounds2. Because superconductor-based devices require high quality crystals/films, the 122 system has also been employed most often among the iron-based compounds to demonstrate devices such as Josephson junctions3,4,5,6 and superconducting wires/tapes for high current applications7,8,9,10,11,12,13,14,15,16. Although the unconventional high-temperature superconductors (including copper-based and iron-based superconductors) have been applied for devices, the fundamental questions such as the forming mechanisms of Cooper pairs remain unclear17. K-doped BaFe2As2 was the first compound in the 122 system found to exhibit superconductivity18. It should be noted that its parent compound, BaFe2As2, has a structural and magnetic phase transition19, but Ba1−xKxFe2As2 is only superconducting (SC) for a range of x with maximum Tc at x = 0.420. Ba1−xKxFe2As2 does not have a structural and magnetic phase transition when x is close to the optimal value. The phase diagram and planar geometry of K-doped BaFe2As2 are similar to those of cuprate superconductors, leading to the intriguing question of whether K-doped BaFe2As2 and cuprate superconductors have the same mechanism of superconductivity.
One of the general features in cuprate superconductors is the presence of a pseudogap above Tc21. There are generally two energy scales for pseudogaps in cuprate superconductors and the low-energy pseudogap is believed to be the precursor of the SC gap21. However, there are contradictory results about the existence of pseudogap in optimally doped (BaK)Fe2As2 (BKFA) from angle-resolved photoemission spectroscopy (ARPES) measurements22,23. Although ARPES and scanning tunneling microscopy are capable of directly resolving band structures, they are surface-sensitive techniques. In contrast, ultrafast optical spectroscopy24,25,26,27,28,29,30 is not surface-sensitive and is a convenient tool to study the bulk property of materials. By observing the temperature-dependent quasiparticle-relaxation, a pseudogaplike feature has been observed in FeSe25, LiFeAs26, Ba(Fe,Co)2As2 27, Ca(Fe,Co)2As2 28, SmFeAsO0.8F0.2 29 and underdoped BKFA30.
In this article, we have utilized ultrafast optical spectroscopy to study carrier dynamics in slightly underdoped BKFA single crystals without magnetic transition. The signals of coherent acoustic phonons were quantitatively studied. We also found that the quasiparticle relaxation associated with the SC gap has temperature dependence that appears in the SC state and persists at least up to 70 K in the normal state. Our result supports the argument that the pseudogaplike feature in the normal state is possibly the precursor of superconductivity30,31. However, in most other iron-based superconductors26,28,32,33,34,35,36,37,38, the pseudogap is not associated with the SC gap and both of them coexist in the SC state. In addition, we suggest that the contradictory reports22,23 resulted from slightly different concentrations of K near optimally doped BKFA. The pseudogaplike feature could be found in slightly underdoped BKFA but was not found in optimally doped BKFA.
Results and Discussions
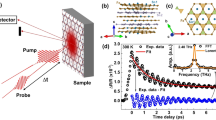
The magnetic susceptibilities of BKFA as a function of temperature were measured, as shown in Fig. 1. The SC temperature has been evaluated as 36 K. We conducted temperature-dependent transient optical reflectivity measurements of BKFA. Detailed experimental conditions can be found in the Methods section. Figure 2 shows the measurements for six representative temperatures. As shown in Fig. 2(f), the 110 K trace shows a fast exponential function with a time constant of < 1 ps, followed by a broad negative hump at ~12 ps. The ultrafast relaxation time within 1 ps should be attributed to thermalization of non-Fermi distribution of electrons39.
We ascribe the negative humps at ~12 ps to the effects of propagating coherent longitudinal acoustic phonons along the depth direction. In transparent or semi-transparent media, the propagation of coherent acoustic phonons induces temporal sinusoidal oscillation due to coherent Brillouin scattering40. The oscillation period of multiple cycles is experimentally resolvable and is determined by the refractive index, sound velocity, optical wavelength and incidence angle of the optical probe in the media40. However, the feature of transient reflectivity due to propagating phonons in highly absorptive materials, such as the BKFA we studied, is not trivial. In order to understand the acoustic signals, we have used the finite difference time domain method to simulate the temporal evolution of longitudinal strain distributions  (or longitudinal acoustic phonons) in BKFA41,42.
(or longitudinal acoustic phonons) in BKFA41,42.
The time-resolved optical reflectivity can be represented as43

where

n and  are respectively the real part and the imaginary part of the complex refractive index of the sample, z is the depth position from the surface, λ is the optical wavelength in vacuum and l is the optical absorption length. ϕ is a constant, which is related to n and
are respectively the real part and the imaginary part of the complex refractive index of the sample, z is the depth position from the surface, λ is the optical wavelength in vacuum and l is the optical absorption length. ϕ is a constant, which is related to n and  43.
43.  and
and  are the real part and the imaginary part of the photoelastic constant, respectively. The photoelastic constant can also be expressed as
are the real part and the imaginary part of the photoelastic constant, respectively. The photoelastic constant can also be expressed as  . For calculation, we assumed that the initial condition of
. For calculation, we assumed that the initial condition of  is proportional to exp(−z/l), where
is proportional to exp(−z/l), where  = 27.7 nm at 400 nm41. By using the indices of refraction
= 27.7 nm at 400 nm41. By using the indices of refraction  at 800 nm and
at 800 nm and  at 400 nm for BKFA41,
at 400 nm for BKFA41,  can be calculated following Eq. (1). Figure 3 shows the rescaled
can be calculated following Eq. (1). Figure 3 shows the rescaled  for a few representative phases of photoelastic constants (θ). Note that
for a few representative phases of photoelastic constants (θ). Note that  for different θ in Fig. 3 can be compared since all of the other parameters, including P, are kept the same. The centers of the negative hump vary for different values of θ. Therefore, one could not determine the phonon oscillation period simply from the first dip time. According to our fitting results in Fig. 3, the best fit of θ was 60° ± 5° for BKFA at 110 K. This is similar to the phase of the photoelastic constant of Cr metal thin film44. The amplitude of the photoelastic constant P could not be obtained in the present study because the strain under our experimental condition was unknown. Further information such as thermal expansion coefficients and heat capacities should be determined for P.
for different θ in Fig. 3 can be compared since all of the other parameters, including P, are kept the same. The centers of the negative hump vary for different values of θ. Therefore, one could not determine the phonon oscillation period simply from the first dip time. According to our fitting results in Fig. 3, the best fit of θ was 60° ± 5° for BKFA at 110 K. This is similar to the phase of the photoelastic constant of Cr metal thin film44. The amplitude of the photoelastic constant P could not be obtained in the present study because the strain under our experimental condition was unknown. Further information such as thermal expansion coefficients and heat capacities should be determined for P.
The calculated time-resolved optical reflectivity due to propagating acoustic phonons in BKFA.
The center of the negative hump, as shown by arrows, varies for different phases of the photoelastic constant. Note that the traces for some phases are scaled for easier comparison. The green line shows the rescaled trace at 110 K from Fig. 2(f).
Figure 4 shows the normalized traces from Fig. 2. Above Tc (36 K) in Fig. 4(a), the normalized traces are roughly the same after 10 ps. It should be noted that slower processes such as acoustic phonons, carrier diffusions and heat diffusions should not be sensitive to the temperature. However, we found additional relaxation components with time constants on the order of several tens of picoseconds in SC state such as at 14 K and 33 K, shown in Fig. 4(a). We attribute these temperature-dependent components to quasiparticle relaxation due to the SC gap45.
The normalized traces from Fig. 2.
(a) The traces below Tc (36 K), such as those at 14 K and 33 K, clearly show additional relaxation due to the SC gap. (b) The 49 K trace still has the SC-gap related relaxation component on the order of several tens of picoseconds.
In order to quantitatively study the temperature-dependence of the carrier dynamics, the transient reflectivity A(t) can be represented by

where  is the step function;
is the step function;  is used to account for the contribution from electron thermalization39;
is used to account for the contribution from electron thermalization39;  is used to represent the quasiparticle relaxation due to the SC gap;
is used to represent the quasiparticle relaxation due to the SC gap;  accounts for all of the slower processes such as acoustic phonons, carrier diffusions and heat diffusions. However, there is no simple analytical form for
accounts for all of the slower processes such as acoustic phonons, carrier diffusions and heat diffusions. However, there is no simple analytical form for  . Experimentally, we found the normalized traces above 110 K are almost the same. We assumed that
. Experimentally, we found the normalized traces above 110 K are almost the same. We assumed that  in Eq. (3) vanishes above 110 K. In order to experimentally obtain
in Eq. (3) vanishes above 110 K. In order to experimentally obtain  , we averaged 5 traces at 130 K, 135 K, 140 K, 145 K and 150 K.
, we averaged 5 traces at 130 K, 135 K, 140 K, 145 K and 150 K.  , primarily due to acoustic phonons, was thus obtained after further smoothing by adjacent averaging to eliminate the feature of
, primarily due to acoustic phonons, was thus obtained after further smoothing by adjacent averaging to eliminate the feature of  . In Eq. (3),
. In Eq. (3),  was used for fitting and
was used for fitting and  ,
,  ,
,  ,
,  , a and b are the fitting parameters. A(t) was convolved with the cross-correlation of pump and probe pulses to quantitatively fit the experimentally recorded
, a and b are the fitting parameters. A(t) was convolved with the cross-correlation of pump and probe pulses to quantitatively fit the experimentally recorded  traces below 110 K.
traces below 110 K.
According to our temperature-dependent analysis,  and
and  did not show any systematic trend and will not be discussed. Fig. 5(a,b) show the temperature-dependent
did not show any systematic trend and will not be discussed. Fig. 5(a,b) show the temperature-dependent  and
and  . From high temperature to low temperature,
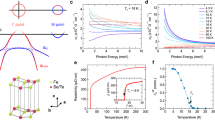
. From high temperature to low temperature,  dramatically increases beginning at Tc (36 K) and roughly saturates below 25 K.
dramatically increases beginning at Tc (36 K) and roughly saturates below 25 K.  also has a peak at Tc. These features were similar to those of quasiparticle relaxation due to the SC gap in other iron-based superconductors26,29,30,46. Although iron-based superconductors have multiple bands with different SC gaps, a temperature-dependent one-gap system based on the Rothwarf-Taylor (RT) model was still adequate to estimate the SC gap size for FeSe46, LiFeAs26, Ba0.6K0.4Fe2As2 30 and SmFeAsO0.8F0.2 29.
also has a peak at Tc. These features were similar to those of quasiparticle relaxation due to the SC gap in other iron-based superconductors26,29,30,46. Although iron-based superconductors have multiple bands with different SC gaps, a temperature-dependent one-gap system based on the Rothwarf-Taylor (RT) model was still adequate to estimate the SC gap size for FeSe46, LiFeAs26, Ba0.6K0.4Fe2As2 30 and SmFeAsO0.8F0.2 29.
(a) τS and (b)  of the SC quasiparticle relaxation term in slightly underdoped BKFA as a function of temperature. The black circles represent the experimental data and the solid red lines represent the fitting curve with Δ(0) = 12 meV. The dashed blue line in (b) represents the noise level. The error bars for τS are larger above Tc due to the relatively small amplitude
of the SC quasiparticle relaxation term in slightly underdoped BKFA as a function of temperature. The black circles represent the experimental data and the solid red lines represent the fitting curve with Δ(0) = 12 meV. The dashed blue line in (b) represents the noise level. The error bars for τS are larger above Tc due to the relatively small amplitude  .
.
We also used the RT model to interpret and fit our data45. The transient temperature near the surface of BKFA exceeds Tc after the optical pulses excite the quasiparticles. It thus creates high frequency bosons with energy  and breaks the Cooper pairs. The relaxation time reflects the population of high frequency bosons and the recovery time of the SC state when the heat escapes from the optically probed depth. In brief,
and breaks the Cooper pairs. The relaxation time reflects the population of high frequency bosons and the recovery time of the SC state when the heat escapes from the optically probed depth. In brief,  is the recovery time of superconductivity after suppression by photocarriers45,47.
is the recovery time of superconductivity after suppression by photocarriers45,47.
We assumed a temperature-dependent gap  , which is proportional to
, which is proportional to  following BCS temperature dependence.
following BCS temperature dependence.  , where P is the fitting parameter. The numerical solution
, where P is the fitting parameter. The numerical solution  without approximation was used for fitting.
without approximation was used for fitting.  , where
, where  is the Boltzmann constant and Tc = 36 K. According to the RT model, the excited population of quasiparticle
is the Boltzmann constant and Tc = 36 K. According to the RT model, the excited population of quasiparticle  . The relations between
. The relations between  ,
,  and
and  are
are

and

where δ and α are fitting parameters following the criteria described in ref. 30. The fitting curves were arbitrarily scaled due to the proportionality.
The gap size  was obtained from the fitting results based on the BCS temperature-dependent one-gap system. The red lines in Fig. 5(a,b) show the fitting curves with
was obtained from the fitting results based on the BCS temperature-dependent one-gap system. The red lines in Fig. 5(a,b) show the fitting curves with  . The temperature-dependent
. The temperature-dependent  below Tc shows good agreement with the RT model, while the temperature-dependent
below Tc shows good agreement with the RT model, while the temperature-dependent  does not agree well. However,
does not agree well. However,  still shows the characteristic trend of the RT model, the “U” shape below Tc. From low temperature to high temperature,
still shows the characteristic trend of the RT model, the “U” shape below Tc. From low temperature to high temperature,  first decreases and then dramatically increases when the temperature approaches Tc30. It should be noted that this is a simplified model. Actually, the transient optical reflectivity should be governed by the contribution of quasiparticle relaxation in all bands due to the multiband feature of iron-based superconductors. According to ARPES measurement results of optimally doped BKFA, Δ is ~12 meV at the inner/outer electron pockets (γ/δ bands) and the inner hole pocket (α band) while Δ is ~6 meV at the outer hole pocket (β band)22,23,48,49. Our obtained
first decreases and then dramatically increases when the temperature approaches Tc30. It should be noted that this is a simplified model. Actually, the transient optical reflectivity should be governed by the contribution of quasiparticle relaxation in all bands due to the multiband feature of iron-based superconductors. According to ARPES measurement results of optimally doped BKFA, Δ is ~12 meV at the inner/outer electron pockets (γ/δ bands) and the inner hole pocket (α band) while Δ is ~6 meV at the outer hole pocket (β band)22,23,48,49. Our obtained  agrees well with that of α, γ, δ bands in BKFA. The uncertainty of the fitting results with the simplified one-gap model might be attributed to different SC gaps of multi-bands in BKFA.
agrees well with that of α, γ, δ bands in BKFA. The uncertainty of the fitting results with the simplified one-gap model might be attributed to different SC gaps of multi-bands in BKFA.
From Fig. 5(b), we have noticed that  does not vanish above Tc, which is similar to the phenomenon observed in underdoped BKFA with magnetic transition30. The SC-related component of relaxation persists up to at least 70 K in our slightly underdoped BKFA without magnetic transition. Note that the noise level in Fig. 5(b) was obtained by a strict definition of peak-to-peak noise fluctuations in
does not vanish above Tc, which is similar to the phenomenon observed in underdoped BKFA with magnetic transition30. The SC-related component of relaxation persists up to at least 70 K in our slightly underdoped BKFA without magnetic transition. Note that the noise level in Fig. 5(b) was obtained by a strict definition of peak-to-peak noise fluctuations in  , which means the onset temperature could be even higher. It should be noted that the error bars for τS are larger above Tc due to the relatively small amplitude AS. However, the relaxation component AS (after consideration of the error bars and noise level) indeed persist from below Tc to above Tc. This phenomenon can also be clearly observed without quantitative analysis. The normalized traces in Fig. 4(b) reflect the percentage of different contributions from
, which means the onset temperature could be even higher. It should be noted that the error bars for τS are larger above Tc due to the relatively small amplitude AS. However, the relaxation component AS (after consideration of the error bars and noise level) indeed persist from below Tc to above Tc. This phenomenon can also be clearly observed without quantitative analysis. The normalized traces in Fig. 4(b) reflect the percentage of different contributions from  ,
,  and
and  in Eq. (3). For temperature above 110 K, the normalized traces are the same and are only composed of
in Eq. (3). For temperature above 110 K, the normalized traces are the same and are only composed of  (with
(with  ~1 ps) and
~1 ps) and  . However, for temperature below Tc such as 14 K and 33 K,
. However, for temperature below Tc such as 14 K and 33 K,  (with τS of several tens of ps) is relatively strong and overwhelms some features of
(with τS of several tens of ps) is relatively strong and overwhelms some features of  (as shown in Fig. 3 that the signal decreases prior to the minimum at ~12 ps). As shown in Fig. 4(b), these can be clearly observed in the normal state, 49 K trace, which still has the relaxation component
(as shown in Fig. 3 that the signal decreases prior to the minimum at ~12 ps). As shown in Fig. 4(b), these can be clearly observed in the normal state, 49 K trace, which still has the relaxation component  . According to our quantitative analysis in Fig. 5(b), the relaxation component due to the SC gap persists at least up to 70 K.
. According to our quantitative analysis in Fig. 5(b), the relaxation component due to the SC gap persists at least up to 70 K.
This phenomenon was similar to that found in underdoped BKFA with magnetic transition30 and was attributed to the pseudogap (or probably partial gaps) in the normal state. The main difference is that our slightly underdoped samples do not have magnetic transition. In addition, the pseudogap of slightly underdoped BKFA (without magnetic transition) was also found by optical conductivity measurement31. Kwon et al. found that the gap feature in the range between 50 cm−1 and 150 cm−1 (corresponding between 6 meV and 18 meV) continuously existed from the SC state to the normal state up to 100 K31. Our experimental results and previous reports30,31 support the proposition that the pseudogap in BKFA should be the precursor of the SC gap because the same SC-related relaxation component in the SC state persists up to the normal state.
It is worthy to note that Chia et al. also investigated the optimally doped BKFA and did not observe a significant pseudogap feature above Tc30. We argue that the BKFA sample of our present study should be slightly underdoped since its Tc = 36 K is slightly lower than the Tc = 37 K of BKFA reported in ref. 30. We also found a similar situation for ARPES measurements in that a pseudogap was found in BKFA with Tc = 35 K 22 but was not clearly found in BKFA with Tc = 37 K 23. A pseudogap was also clearly observed with optical conductivity measurement in slightly underdoped BKFA without magnetic transition31. We thus suggest that the contradictory reports22,23,30,31 actually resulted from the slightly different concentrations of K near optimally doped BKFA. Our results and previous reports22,31 indicate that a pseudogap still exists in slightly underdoped BKFA without magnetic transition. It is interesting that no strong evidence of a pseudogap has been found in optimally doped30 or overdoped BKFA, although a shadow gap was predicted recently50. Nevertheless, a pseudogap was found in the overdoped regime of other 122 system compounds28,32,33,34.
In the 111135,36, 11126,37,38 and cuprate51,52,53 systems, it was reported that a pseudogap can coexist with the SC gap. The infrared pseudogap in Co-doped and P-doped BaFe2As2 (122 systems) was also reported to be unrelated to superconductivity33. However, our findings and previous results30,31 lead us to suggest that the pseudogap in K-doped BaFe2As2 is the precursor of superconductivity. We suggest that partial gaps along certain momentum might be opened in the normal state and they evolve to complete SC gap below Tc. Note that the term “pseudogap” was widely used in the literature to specify a gap or a partial gap of which the physical origin is unknown. They may have different physical origins. Our experimental evidence indicates that the origin of the pseudogap in BKFA is different from that of other iron-based superconductors with coexisting pseudogap and SC gap in the SC state26,28,32,33,34,35,36,37,38. We would like to highlight that K atoms are doped out of the FeAs planes while Co and P are doped in the FeAs planes. It was suggested that in-plane doping or out-of plane doping would affect how SC gap forms54. A similar situation may occur in the formation of the pseudogap, leading to different features between (BaK)Fe2As2 (out-of-plane doping systems) and other in-plane systems such as BaFe2(CoAs)2 and BaFe2(AsP)2.
Conclusions
We have utilized ultrafast optical spectroscopy to investigate carrier dynamics in slightly underdoped BKFA without magnetic transition. The signals of acoustic phonons were quantitatively studied. We have also analyzed the quasiparticle relaxation due to the SC gap. Although the doping concentration of BKFA does not have a magnetic transition and is nearly optimally doped, we still found pseudogap feature at least up to 70 K in normal state. Our experimental results support the proposition that the pseudogap in BKFA should be the precursor of the SC gap. We have highlighted the unique pseudogap feature in K-doped BaFe2As2, which is different from that in other iron-based superconductors.
Methods
Experimental Setup
The sample was cleaved to reveal a shining surface and mounted on the holder of the cryostat in an Ar-filled glove box. After the cryostat was moved out from the glove box, the pressure of the chamber was immediately lowered to below 10−4 mtorr to avoid oxidation. Typical pump-probe (400 nm–800 nm) measurements were conducted. The polarization of the pump beam is orthogonal to that of the probe beam. But, the polarization was not intentionally aligned to the crystal axis of the sample. The repetition rate was 8 MHz and the optical pump fluence was 5~10 μJ/cm2. The pump was modulated at ~1 MHz with an acousto-optical modulator (AOM). The full width at half maximum (FWHM) of the temporal cross-correlation of the pump and probe pulse was ~400 fs, which determined the temporal resolution. Time constants close to the temporal resolution could still be accurately determined after the deconvolution process. A color filter was placed in front of the photodetector to eliminate pump light leakage. We recorded the reflectivity variation of the probe pulse as a function of time delay.
Under our experimental condition, the traces were in the linear region above 50 K. The normalized traces for optical pump fluence of both 5 μJ/cm2 and 10 μJ/cm2 did not show significant difference. At the lowest temperature cooled with liquid He, the normalized traces were different for optical pump fluence of 5 μJ/cm2 and 10 μJ/cm2. The steady-state laser heating still occurred under our experimental condition especially at low temperatures. The real temperature of the sample increased with increasing optical pump fluence. The temperature was calibrated as described in the next section. However, it should be noted that fluence-dependent measurements cannot be used to verify the linearity in the SC state of BKFA. It was reported that the decay rate of the quasiparticles due to the SC gap varies with optical pump fluence55. In our temperature-dependent measurements, the optical pump fluence was 5 μJ/cm2 below 50 K, which was reasonably low compared with previous experiments on iron-based superconductors25,26,29,30,46,55. For enhancement of the signal to noise ratio, the optical pump fluence was 10 μJ/cm2 for measurements above 50 K because they are in the linear region. The traces above 50 K were rescaled for comparison.
Temperature Calibration
The temperature of the sample was 10 K calibrated from the temperature measured by the thermometer. According to Fig. 2(b) in ref. 55, the features of normalized traces in SC and non-SC states under the same pumping fluence can be easily distinguished. We could thus obtain the temperature difference between the real temperature Tc of the sample and the temperature measured by the thermometer.
Additional Information
How to cite this article: Lin, K.-H. et al. Ultrafast dynamics of quasiparticles and coherent acoustic phonons in slightly underdoped (BaK)Fe2As2. Sci. Rep. 6, 25962; doi: 10.1038/srep25962 (2016).
References
Stewart, G. R. Superconductivity in iron compounds. Rev. Mod. Phys. 83, 1589–1652 (2011).
Haindl, S. et al. Thin film growth of Fe-based superconductors: from fundamental properties to functional devices. A comparative review. Rep. Prog. Phys. 77, 046502 (2014).
Zhang, X. et al. Observation of the Josephson Effect in Pb/Ba1−xKxFe2As2 Single Crystal Junctions. Phys. Rev. Lett. 102, 147002 (2009).
Reifert, D. et al. Preparation of hybrid Josephson junctions on Co-doped Ba-122 single crystals. Supercond. Sci. Tech. 27, 085003 (2014).
Katase, T. et al. Josephson junction in cobalt-doped BaFe2As2 epitaxial thin films on (La,Sr)(Al,Ta)O3 bicrystal substrates. Appl. Phys. Lett. 96, 142507 (2010).
Schmidt, S. et al. BaFe1.8Co0.2As2 thin film hybrid Josephson junctions. Appl. Phys. Lett. 97, 172504 (2010).
Choi, E.-M. et al. In situ fabrication of cobalt-doped SrFe2As2 thin films by using pulsed laser deposition with excimer laser. Appl. Phys. Lett. 95, 062507 (2009).
Katase, T. et al. Biaxially textured cobalt-doped BaFe2As2 films with high critical current density over 1 MA/cm2 on MgO-buffered metal-tape flexible substrates. Appl. Phys. Lett. 98, 242510 (2011).
Iida, K. et al. Scaling behavior of the critical current in clean epitaxial Ba(Fe1−xCox)2As2 thin films. Phys. Rev. B 81, 100507 (2010).
Maiorov, B. et al. Competition and cooperation of pinning by extrinsic point-like defects and intrinsic strong columnar defects in BaFe2As2 thin films. Phys. Rev. B 86, 094513 (2012).
Fang, L. et al. High, magnetic field independent critical currents in (Ba,K)Fe2As2 crystals. Appl. Phys. Lett. 101, 012601 (2012).
Kihlstrom, K. J. et al. High-field critical current enhancement by irradiation induced correlated and random defects in (Ba0.6K0.4)Fe2As2 . Appl. Phys. Lett. 103, 202601 (2013).
Yao, C. et al. Fabrication and transport properties of Sr0.6K0.4Fe2As2 multifilamentary superconducting wires. Appl. Phys. Lett. 102, 082602 (2013).
Zhang, X. et al. Realization of practical level current densities in Sr0.6K0.4Fe2As2 tape conductors for high-field applications. Appl. Phys. Lett. 104, 202601 (2014).
Tarantini, C. et al. Development of very high Jc in Ba(Fe1−xCox)2As2 thin films grown on CaF2 . Sci. Rep. 4, 7305 (2014).
Hanisch, J. et al. High field superconducting properties of Ba(Fe1−xCox)2As2 thin films. Sci. Rep. 5, 17363 (2015).
Pickett, W. E. Iron-based superconductors: Timing is crucial. Nat. Phys. 5, 87–88 (2009).
Rotter, M., Tegel, M. & Johrendt, D. Superconductivity at 38 K in the iron arsenide (Ba1−xKx)Fe2As2 . Phys. Rev. Lett. 101, 107006 (2008).
Dong, J. K. et al. Thermodynamic properties of Ba1−xKxFe2As2 and Ca1−xNaxFe2As2 . New J. Phys. 10, 123031 (2008).
Paglione, J. & Greene, R. L. High-temperature superconductivity in iron-based materials. Nat. Phys. 6, 645–658 (2010).
Damascelli, A., Hussain, Z. & Shen, Z. X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Zhao, L. et al. Multiple Nodeless Superconducting Gaps in (Ba0.6K0.4)Fe2As2 Superconductor from Angle-Resolved Photoemission Spectroscopy. Chin. Phys. Lett. 25, 4402–4405 (2008).
Nakayama, K. et al. Superconducting gap symmetry of Ba0.6K0.4Fe2As2 studied by angle-resolved photoemission spectroscopy. EPL 85, 67002 (2009).
Luo, C. W. et al. Ultrafast dynamics and phonon softening in Fe1+ySe1−xTex single crystals. New J. Phys. 14, 103053 (2012).
Wen, Y. C. et al. Gap Opening and Orbital Modification of Superconducting FeSe above the Structural Distortion. Phys. Rev. Lett. 108, 267002 (2012).
Lin, K.-H. et al. Observation of pseudogaplike feature above Tc in LiFeAs by ultrafast optical spectroscopy. Phys. Rev. B 90, 174502 (2014).
Stojchevska, L., Mertelj, T., Chu, J.-H., Fisher, I. R. & Mihailovic, D. Doping dependence of femtosecond quasiparticle relaxation dynamics in Ba(Fe,Co)2As2 single crystals: Evidence for normal-state nematic fluctuations. Phys. Rev. B 86, 024519 (2012).
Kumar, S., Harnagea, L., Wurmehl, S., Buechner, B. & Sood, A. K. “Signatures of superconducting and pseudogap phases in ultrafast transient reflectivity of Ca(Fe0.927Co0.073)2As2,” EPL 105, 47004 (2014).
Mertelj, T. et al. Distinct Pseudogap and Quasiparticle Relaxation Dynamics in the Superconducting State of Nearly Optimally Doped SmFeAsO0.8F0.2 Single Crystals. Phys. Rev. Lett. 102, 117002 (2009).
Chia, E. E. M. et al. Ultrafast Pump-Probe Study of Phase Separation and Competing Orders in the Underdoped (Ba, K)Fe2As2 Superconductor. Phys. Rev. Lett. 104, 027003 (2010).
Kwon, Y. S. et al. Evidence of a pseudogap for superconducting iron-pnictide Ba0.6+deltaK0.4-deltaFe2As2 single crystals from optical conductivity measurements. New J. Phys. 14, 063009 (2012).
Kasahara, S. et al. Electronic nematicity above the structural and superconducting transition in BaFe2(As1−xPx)2 . Nature 486, 382–385 (2012).
Moon, S. J. et al. Infrared Measurement of the Pseudogap of P-Doped and Co-Doped High-Temperature BaFe2As2 Superconductors. Phys. Rev. Lett. 109, 027006 (2012).
Shimojima, T. et al. Pseudogap formation above the superconducting dome in iron pnictides. Phys. Rev. B 89, 045101 (2014).
Ahilan, K. et al. 19F NMR investigation of the iron pnictide superconductor LaFeAsO(0.89)F(0.11) . Phys. Rev. B 78, 100501 (2008).
Mertelj, T. et al. Quasiparticle relaxation dynamics in spin-density-wave and superconducting SmFeAsO1−xFx single crystals. Phys. Rev. B 81, 224504 (2010).
Cai, P. et al. Visualizing the microscopic coexistence of spin density wave and superconductivity in underdoped NaFe1−xCoxAs. Nat. Commun. 4, 1596 (2013).
Ge, Q. Q. et al. Anisotropic but Nodeless Superconducting Gap in the Presence of Spin-Density Wave in Iron-Pnictide Superconductor NaFe1−xCoxAs. Phys. Rev. X 3, 011020 (2013).
Sun, C. K., Vallee, F., Acioli, L., Ippen, E. P. & Fujimoto, J. G. Femtosecond Investigation of electron thermalization in gold. Phys. Rev. B 48, 12365–12368 (1993).
Lin, K. H., Yu, C. T., Wen, Y. C. & Sun, C. K. Generation of picosecond acoustic pulses using a p-n junction with piezoelectric effects. Appl. Phys. Lett. 86, 093110 (2005).
Goto, T. et al. Quadrupole Effects of Layered Iron Pnictide Superconductor Ba(Fe0.9Co0.1)2As2 . J. Phys. Soc. Jpn. 80, 073702 (2011).
Wen, Y. C., Chern, G. W., Lin, K. H., Yeh J. J. & Sun, C. K. Femtosecond optical excitation of coherent acoustic phonons in a piezoelectric p-n junction. Phys. Rev. B 84, 205315 (2011).
Thomsen, C., Grahn, H. T., Maris, H. J. & Tauc, J. Surface Generation and Detection of phonons by picosecond light-pulses. Phys. Rev. B 34, 4129–4138 (1986).
Matsuda, O. & Wright, O. B. Reflection and transmission of light in multilayers perturbed by picosecond strain pulse propagation. J. Opt. Soc. Am. B 19, 3028–3041 (2002).
Kabanov, V. V., Demsar, J. & Mihailovic, D. Kinetics of a superconductor excited with a femtosecond optical pulse. Phys. Rev. Lett. 95, 147002 (2005).
Luo, C. W. et al. Quasiparticle Dynamics and Phonon Softening in FeSe Superconductors. Phys. Rev. Lett. 108, 257006 (2012).
Smallwood, C. L. et al. Time- and momentum-resolved gap dynamics in Bi2Sr2CaCu2O8+delta . Phys. Rev. B 89, 115126 (2014).
Ding, H. et al. Observation of Fermi-surface-dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2 . EPL 83, 47001 (2008).
Evtushinsky, D. V. et al. Momentum-resolved superconducting gap in the bulk of Ba1−xKxFe2As2 from combined ARPES and μSR measurements. New J. Phys. 11, 055069 (2009).
Bang, Y. A shadow gap in the over-doped (Ba1−xKx)Fe2As2 compound. New J. Phys. 16, 023029 (2014).
Cao, N. et al. Femtosecond optical detection of quasiparticle dynamics in single-crystal Bi2Sr2CaCu2O8+delta . Chin. Phys. Lett. 25, 2257–2260 (2008).
Liu, Y. H. et al. Direct observation of the coexistence of the pseudogap and superconducting quasiparticles in Bi2Sr2CaCu2O8+y by time-resolved optical spectroscopy. Phys. Rev. Lett. 101, 137003 (2008).
Nair, S. K. et al. Quasiparticle dynamics in overdoped Bi1.4Pb0.7Sr1.9CaCu2O8+delta: Coexistence of superconducting gap and pseudogap below Tc . Phys. Rev. B 82, 212503 (2010).
Dai, Y. M. et al. Optical conductivity of Ba0.6K0.4Fe2As2: The effect of in-plane and out-of-plane doping in the superconducting gap. EPL 104, 47006 (2013).
Torchinsky, D. H., Chen, G. F., Luo, J. L., Wang, N. L. & Gedik, N. Band-dependent Quasiparticle Dynamics in Single Crystals of the Ba0.6K0.4Fe2As2 Superconductor Revealed by Pump-Probe Spectroscopy. Phys. Rev. Lett. 105, 027005 (2010).
Acknowledgements
The authors would like to thank Yu-Da Chen and Prof. Yia-Chung Chang for ellipsometry measurement. This work is sponsored by Ministry of Science and Technology of Taiwan under Grant Nos: 104-2112-M-001-014-MY3. The work in Houston is supported in part by US Air Force Office of Scientific Research Grants No. FA9550-09-1-0656 and No. FA9550-15-1-0236, the T.L.L. Temple Foundation, the John J. and Rebecca Moores Endowment and the State of Texas through the Texas Center for Superconductivity at the University of Houston.
Author information
Authors and Affiliations
Contributions
K.-H.L. and M.-K.W. conducted the studies. K.-H.L. wrote the manuscript. K.-J.W. performed the pump-probe experiments. K.-H.L., K.-J.W. and Y.-C.W. analyzed the data. B.L. and C.-W.C. prepared the samples. B.L. and C.-C.C. characterized the sample with magnetic measurement.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lin, KH., Wang, KJ., Chang, CC. et al. Ultrafast dynamics of quasiparticles and coherent acoustic phonons in slightly underdoped (BaK)Fe2As2. Sci Rep 6, 25962 (2016). https://doi.org/10.1038/srep25962
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep25962
This article is cited by
-
Carrier dynamics of Mn-induced states in GaN thin films
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.