Abstract
Scaling up linear-optics quantum computing will require multi-photon gates which are compact, phase-stable, exhibit excellent quantum interference and have success heralded by the detection of ancillary photons. We investigate the design, fabrication and characterisation of the optimal known gate scheme which meets these requirements: the Knill controlled-Z gate, implemented in integrated laser-written waveguide arrays. We show device performance to be less sensitive to phase variations in the circuit than to small deviations in the coupler reflectivity, which are expected given the tolerance values of the fabrication method. The mode fidelity is also shown to be less sensitive to reflectivity and phase errors than the process fidelity. Our best device achieves a fidelity of 0.931 ± 0.001 with the ideal 4 × 4 unitary circuit and a process fidelity of 0.680 ± 0.005 with the ideal computational-basis process.
Similar content being viewed by others
Introduction
Recent advances in on-chip integration of efficient photon sources1,2,3,4 and detectors5,6,7 hold promise for significant progress in the linear optics architecture for quantum information processing and simulation. This architecture relies on the insight that entangling quantum gates can be realised probabilistically by interacting photonic qubits using effective optical nonlinearities induced by measurement8. However, efficient scaling in this architecture necessitates entangling gates which are both logically and physically scalable. Logical scalability requires successful operation to be heralded nondestructively, typically by the detection of additional ‘ancilla’ photons. Physical scalability, meanwhile, requires a compact and phase-stable architecture. Integrated, non-heralded entangling gates have been demonstrated9,10 as have heralded gates in bulk optics11,12. However, gates which are scalable in both the logical and physical senses have not been implemented to date due to their geometric complexity as well as the need for low circuit losses.
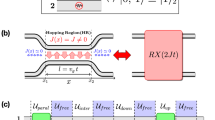
The simplest heralded entangling two-qubit photonic gate design, with the highest known success probability, was found by Knill13 and implements a controlled-Z operation with probability 2/27. This heralded cz design, henceforth called the hcz, relies on pairwise non-classical interference of four indistinguishable photons in a circuit with four particular beamsplitters (BSs), as shown in Fig. 1(a), as well as a stable phase shift of precisely π between the first and second BS pairs.
(a) The circuit for a hcz gate showing paths for ancillary photons A and B as well as the computational qubits; the control (target) photon is encoded across spatial paths C0 (T0) representing |0〉 and C (T) representing |1〉 . Modes are labeled C (Control), T (Target), A (Ancilla) and B (Ancilla). The |0〉 -modes do not interact in the gate; the four remaining modes undergo four beamsplitting operations with reflectivities R(θn) = cos2(θn) as described in Eq. (1). The light-coloured side indicates the surface yielding a relative π phase change upon reflection. (b) The four interacting circuit modes modelled as a waveguide array, showing the crossover and optimal reflectivities for the BSs implemented using evanescent coupling. The waveguides are separated by 127 μm at the device end facets; fan-in and fan-out regions are not shown. The input mode labeling is reversed compared to (a) due to the reflectance of the couplers being defined as the proportion of input light which couples from one waveguide to the other.
Integrated arrays of coupled waveguides could enable compact, phase-stable circuits with the requisite splittings and phase for Knill’s design. However, integrated hcz circuits require a physical swapping of neighboring modes; such crossovers are difficult to achieve lithographically. Laser-written waveguides have recently been used to demonstrate a wide variety of quantum photonics circuitry14,15. The femtosecond-laser direct-write (FLDW) technique in particular allows 3D waveguide arrays, simplifying waveguide crossovers, along with demonstrated high mode indistinguishability14 and has recently been employed for multiport and arbitrary-phase directional couplers16,17,18,19, all-optical routers20, circuits for small-scale quantum simulations21,22,23, quantum walks24 and non-heralded quantum gates10.
Here we investigate implementation of the hcz gate both theoretically and experimentally using the direct-write technique, with a particular focus on its action in the presence of deviations from optimal phase and reflectivity parameters. We derive the variation in gate performance as quantified by two metrics—the optical-circuit mode-fidelity and the computational-basis process-fidelity—with respect to such deviations. We further detail the fabrication of 12 prototype circuits including a novel and simple method for achieving the requisite internal phase and their full characterisation using coherent techniques as well as quantum interference, which confirms their excellent mode indistinguishability and suitability for the single-photon regime.
Materials and Methods
The optical circuit for the hcz gate is shown in Fig. 1(a). The control and target qubits are each encoded as single photons across a pair of modes, labelled C and C0 for the control and T and T0 for the target. C0 and T0, which encode |0〉 for their respective qubits, interact with neither the |1〉 -modes nor the ancillas; our fabricated circuits contain only the four interacting modes as shown in Fig. 1(b). Modulo local phases on the input and output modes, this circuit implements a heralded cz operation: conditioned on the detection of one photon in each ancilla mode it flips the sign of the |11〉 -term of an arbitrary two-qubit input state  .
.
Circuit Modelling and Design
Demonstrations of entangling linear optics quantum gates relying on post-selection of the computational photons go back more than a decade and include both free-space25,26 and integrated implementations9,10. In such gates, success relies on detecting the photonic qubits in particular output modes, precluding their use in subsequent multi-qubit operations8. In contrast heralded gates—where success is signalled by detection of ancillary photons without measuring the output qubits—can be incorporated as modules in complex quantum computations. The effects of fabrication imperfections on post-selected gates have been modelled27,28. However such gates can effectively be simplified to include only a single instance of two-photon interference at one beamsplitter26; by contrast the hcz, despite its simplicity relative to other heralded gates, requires four distinct two-photon interference events at four beamsplitters. Here we quantify the effects of device imperfections on such a heralded gate.
We first model imperfect hcz device operation as follows. We assume four single-mode waveguides coupled by BSs as in Fig. 1(b). The quantum state of the light is described by four bosonic creation operators  ,
,  ,
,  and
and  which create a photon in the control, target and two ancillary modes respectively. We employ the symmetric BS convention so that two modes a1 and a2 transform as
which create a photon in the control, target and two ancillary modes respectively. We employ the symmetric BS convention so that two modes a1 and a2 transform as

We first consider a photon or coherent state in a superposition of the input modes injected into a circuit of the form in Fig. 1(b). Our model neglects intrinsic loss, as in our fabricated circuits such loss is nearly constant across the waveguides and therefore results only in a reduction in the output state amplitude and, thus, the gate success probability. The circuit then maps the input creation operators a† to the outputs b† via the transformation  , where Ucirc is a unitary matrix and the mode indices k and j are ordered {C, T, A, B}. We allow for arbitrary splitting parameter angles θn,
, where Ucirc is a unitary matrix and the mode indices k and j are ordered {C, T, A, B}. We allow for arbitrary splitting parameter angles θn,  . The requisite internal phase shift is implemented by an additional phase of π on BS3, equivalent to
. The requisite internal phase shift is implemented by an additional phase of π on BS3, equivalent to  . Using Eq. (1) and allowing for additional undesired phase shifts (
. Using Eq. (1) and allowing for additional undesired phase shifts ( ) between the BS pairs, we find that all these unwanted internal phases can be collected into a single net phase shift ϕN = ϕc + ϕa − ϕb − ϕt. For the total circuit action, modulo external local phases, we thus find:
) between the BS pairs, we find that all these unwanted internal phases can be collected into a single net phase shift ϕN = ϕc + ϕa − ϕb − ϕt. For the total circuit action, modulo external local phases, we thus find:

Up to external phases and in the absence of net phase ϕN, the ideal matrix Uhcz given by Knill13 is achieved by the target angles of  and
and  .
.
We employ two metrics to assess the design accuracy of a physical circuit for a hcz gate. The mode fidelity Fm directly compares the 4 × 4 circuit mapping matrix Ucirc to the ideal unitary matrix Uhcz and is given by the normalized Hilbert-Schmidt inner product29: Fm = Tr{Uhcz†Ucirc}2/N2, where N = 4 is the number of modes. This metric most closely captures the differences between the manufactured integrated device and the ideal target device, but only partially captures how the device would function with qubits since it ignores the effect of measurement heralding. For instance if the ancilla modes were swapped prior to detection, Fm would decrease without any operational effect on the function of the heralded gate on the qubits, as it is irrelevant which detector detects which ancilla. The second metric directly assesses the effect of the measurement-induced optical nonlinearity in the space of the qubits and thus will be independent of such irrelevant changes. A quantum process  can be represented abstractly as a quantum state
can be represented abstractly as a quantum state  via the Jamiolkowski isomorphism30 and the natural figure of merit for gate quality is then the process fidelity:
via the Jamiolkowski isomorphism30 and the natural figure of merit for gate quality is then the process fidelity:  which simply compares the state representing the implemented process and the state ρcz representing the process for an ideal cz gate31,32. While we would expect the two measures to be roughly similar, particularly for small imperfections in e.g. splitting ratios, there is in general no simple relationship between them, as they are differently sensitive to imperfections.
which simply compares the state representing the implemented process and the state ρcz representing the process for an ideal cz gate31,32. While we would expect the two measures to be roughly similar, particularly for small imperfections in e.g. splitting ratios, there is in general no simple relationship between them, as they are differently sensitive to imperfections.
The most direct way to calculate  is to consider a maximally-entangled state |ϕmax〉 between the Hilbert space on which the process acts and another fictitious space of the same dimension. The process acts on one half of the entangled state and the resulting total state is exactly
is to consider a maximally-entangled state |ϕmax〉 between the Hilbert space on which the process acts and another fictitious space of the same dimension. The process acts on one half of the entangled state and the resulting total state is exactly  . As our computational input is two qubits, the entangled state is
. As our computational input is two qubits, the entangled state is

After a cz operation on the first two qubits the result is

and the corresponding final state representing the process is  .
.
Given that each qubit comprises a photon in two modes, |ϕmax〉 involves four photons encoded across eight modes, where the fictitious additional control (target) mode has creation operator 
 . With the addition of the two ancillary modes, the entangled input state is thus represented using boson creation operators as
. With the addition of the two ancillary modes, the entangled input state is thus represented using boson creation operators as  where |0〉 is a multimode bosonic vacuum and creation operators for the non-interacting logical |0〉 modes are again omitted. The circuit transforms
where |0〉 is a multimode bosonic vacuum and creation operators for the non-interacting logical |0〉 modes are again omitted. The circuit transforms  ,
,  ,
,  and
and  according to Ucirc and gate success is heralded by measuring exactly one photon in each ancillary mode. This measurement removes these modes and induces a cz on the remaining modes.
according to Ucirc and gate success is heralded by measuring exactly one photon in each ancillary mode. This measurement removes these modes and induces a cz on the remaining modes.
A subtle problem arises when the photonic gate is not perfectly balanced. There is then a non-zero amplitude for the states proportional to  and
and  , which lie outside the qubit space and represent errors. In characterising circuit performance, we account for these errors by calculating the process fidelity against a version of ρcz which is extended to include these two states but with zero support and thus any weight on these terms will always reduce Fp.
, which lie outside the qubit space and represent errors. In characterising circuit performance, we account for these errors by calculating the process fidelity against a version of ρcz which is extended to include these two states but with zero support and thus any weight on these terms will always reduce Fp.
Figure 2 shows the variation of the process and mode fidelity due to a deviation in a single BS reflectivity or the net internal phase. Both fidelity metrics are much less sensitive to small deviations in phase than in splitting ratios. Figure 2 also shows two fidelity distributions each resulting from 2000 randomly-chosen gate simulations with simultaneous deviations in all five reflectivity and phase parameters. Perhaps unsurprisingly the mode fidelity is far less sensitive to errors overall.
Variation of the model mode fidelity Fm and process fidelity Fp with deviations Δ from the ideal BS angles and internal phase shift.
The ideal phase is zero and Δ Φ N represents any net extra phase introduced between beamsplitters. For the BSs Δ is the variation from the ideal angle; the total reflectivity will be cos2(θideal + Δ θ). In both cases Δ is a length variation in the physical device. The top graphs show the fidelity when one Δ parameter is varied and the rest are held at zero. The points shown represent the deviations found in our best experimentally-characterised circuit; see Fig. 3 for further details. Note that on this scale both the curves and points for BS1 and BS2 are indistinguishable. The bottom graphs show the fidelities for 2000 simulated instances of hcz gates with all Δ parameters drawn randomly from Gaussian distributions with mean 0 and standard deviation σΔ. The purple distribution has σΔ = 0.1, which is similar in magnitude to most of the Δ parameters from our best measured circuit; the green distribution has σΔ = 0.05 in order to show the fidelities achievable with a modest improvement in fabrication accuracy. The resulting green (purple) distributions have means of 0.994 (0.980) for Fm and 0.962 (0.863) for Fp. Note the logarithmic scale on the horizontal axes.
Device Fabrication
The circuits were fabricated using the FLDW technique wherein a tightly focused femtosecond laser generates a localised refractive index contrast in a glass substrate. By translating the glass in (x, y, z) with respect to the incident laser, arbitrary 3D regions of net-positive refractive index change can be produced. Our fabrication employed a Ti:Sapphire oscillator (800 nm centre wavelength, < 50 fs pulse duration) with 5.1 MHz repetition rate33,34. A telescope was used to overfill the input pupil of a 100× oil immersion objective which focused the laser into the boro-aluminosilicate sample (Corning Eagle 2000) for writing with 66 nJ pulses at a translation speed of 1200 mm/min. The sample was subsequently annealed to obtain a more symmetric and Gaussian refractive index profile35. This significantly improves waveguide throughput efficiency, as shown in (ref. 36). This process yields a mode field diameter of 5 μm which has excellent overlap with an 800 nm single-mode optical fibre and gives rise to fibre-to-fibre coupling loss of only 1.8 dB for straight waveguides of length 40 mm. Input- and output-coupling accounts for the majority of this loss, while intrinsic propagation loss is below 0.2 dB/cm36 and importantly intrinsic losses were found to be constant across the four waveguides to within measurement error.
The splitting ratios of the waveguide BSs—or directional couplers—can be adjusted by changing their coupling lengths. Using a symmetric phase convention, the amplitudes in an ideal directional coupler of total length L with uniform coupling constant C vary sinusoidally with propagation length z as  , where
, where  and 0 ≤ z ≤ L. Since the waveguides have nominally identical profiles, the reflectivity takes the simple form R = cos2 γ, where
and 0 ≤ z ≤ L. Since the waveguides have nominally identical profiles, the reflectivity takes the simple form R = cos2 γ, where  and we allow for variation in the coupling strength C(z) along the waveguide37.
and we allow for variation in the coupling strength C(z) along the waveguide37.
While specific, arbitrary phase shifts are difficult to realise precisely without active elements using FLDW19,23, adjustments in coupler length also allowed us to achieve the requisite internal phase shift of π. Extending L such that γ goes from θ to (2π − θ) changes the action of the splitter to 
 . Exploiting this identity, we implemented the requisite phase shift by lengthening BS3 from
. Exploiting this identity, we implemented the requisite phase shift by lengthening BS3 from  to
to  . For ideal couplers the relative phase is limited to ± π/2 and the application of this technique on BS3 yields no undesired internal phase ϕN, even for slight errors in L. In practice ϕN ≠ 0 can occur due to slight variations in local waveguide profile resulting from laser power fluctuations in fabrication, as well as from small internal path length variations. All arms of the device are however designed to have the same path length.
. For ideal couplers the relative phase is limited to ± π/2 and the application of this technique on BS3 yields no undesired internal phase ϕN, even for slight errors in L. In practice ϕN ≠ 0 can occur due to slight variations in local waveguide profile resulting from laser power fluctuations in fabrication, as well as from small internal path length variations. All arms of the device are however designed to have the same path length.
An extensive parameter study of directional couplers was completed in order to determine the optimal laser characteristics, writing algorithm and coupling lengths for achieving the desired reflectivities and internal phase. However, the performance of couplers written according to a particular algorithm will nevertheless vary from sample to sample, depending on the precise substrate and laser characteristics at the time of fabrication. In particular, slight refractive index differences between the two waveguides constitute a significant source of deviations from intended reflectivities. Such differences yield phase mismatch which prevents full power transfer between the waveguides, an effect which becomes more pronounced as coupling length increases. Twelve separate candidate circuits were thus fabricated, both to increase the likelihood of achieving near-optimal phase and reflectivity parameters in one or more circuits and in order to experimentally investigate the sensitivity of device operation to parameter variations. In our directional coupler parameter scan the waveguide separation was maintained at 7 μm while we varied the coupling length. We fixed the length of BS4 (2.5 mm) and tested all combinations of three values for BS1 & BS2 (0.25, 0.50 and 0.75 mm) and four different values of BS3 (5.50, 5.75, 6.00 and 6.25 mm). The necessity for testing different parameter combinations results from variability of the writing laser, which in turn ultimately arises from its passive mode locking and the length of the cavity necessary to achieve a balance of sufficiently high pulse energy (> 100 nJ) and repetition rates (5 MHz). This cavity is 30 m long and any perturbation can have a substantial knock-on effect on the resultant pulse energy at short (sub second) time scales. Small fluctuations in the pulse energy result in fluctuations in the refractive index of the waveguides, to which the directional couplers are extremely sensitive (our laser fluctuates by up to 5% during processing). In principle these laser fluctuations could be improved by temperature stabilisation of the cavity, or potentially operation in vacuo.
Results and Discussion
Coherent Device Characterisation
We characterised the fabricated candidate circuits using a recently-demonstrated technique38,39 which yields  using only single- and two-mode bright coherent states and output intensity measurements. The moduli
using only single- and two-mode bright coherent states and output intensity measurements. The moduli  result from intensity measurement at each output k for an input at mode j. The phases
result from intensity measurement at each output k for an input at mode j. The phases  are obtained as follows: a two-mode coherent state is injected into two inputs and a relative phase between the modes is induced via continuous path-length variation in one mode using motorised translation. The output interference fringes are recorded with fast photodiodes and an oscilloscope and the phases
are obtained as follows: a two-mode coherent state is injected into two inputs and a relative phase between the modes is induced via continuous path-length variation in one mode using motorised translation. The output interference fringes are recorded with fast photodiodes and an oscilloscope and the phases  are simply the phase differences between the pairs of resulting periodic output intensity signals {Ij(t)}. However, due to experimental noise and slight variations in the phase-setting translation velocity, it was more accurate in practice to determine the unknown phases
are simply the phase differences between the pairs of resulting periodic output intensity signals {Ij(t)}. However, due to experimental noise and slight variations in the phase-setting translation velocity, it was more accurate in practice to determine the unknown phases  by subtracting the discrete Fourier transforms of the output signals. Gate inputs must be identically polarized for optimal interference; we tested the circuits with both horizontal- and vertical-polarized inputs and found the differences to be insignificant, indicating little birefringence in the waveguides. The data presented is for the horizontal polarization.
by subtracting the discrete Fourier transforms of the output signals. Gate inputs must be identically polarized for optimal interference; we tested the circuits with both horizontal- and vertical-polarized inputs and found the differences to be insignificant, indicating little birefringence in the waveguides. The data presented is for the horizontal polarization.
The resulting 12 measured maps Umeas are nearly unitary within error: over all 12 circuits the maximum value of  was 0.050, with a mean of 0.010 and on average Djk differed from zero by just 1.6 standard deviations, as determined through Monte Carlo analysis using our uncertainties in
was 0.050, with a mean of 0.010 and on average Djk differed from zero by just 1.6 standard deviations, as determined through Monte Carlo analysis using our uncertainties in  and
and  . Those uncertainties were derived directly from the measured variance in output power ratios and relative phase respectively, taken over multiple trials. Comparison of the measured matrices Umeas to Ucirc in Eq. 2 allows nearly direct determination of the net phase ϕN; notably the values of
. Those uncertainties were derived directly from the measured variance in output power ratios and relative phase respectively, taken over multiple trials. Comparison of the measured matrices Umeas to Ucirc in Eq. 2 allows nearly direct determination of the net phase ϕN; notably the values of  are consistent with Ucirc to within error. The splitting parameters θn,
are consistent with Ucirc to within error. The splitting parameters θn,  can be determined from rmeas using numerical optimisation. The results for Fp, Fm, ϕN and θn for all 12 measured candidate circuits are shown in Fig. 3. Notably the fidelity values shown were calculated directly from the measured matrices Umeas, but agree to within error with the values calculated from the measured phase and reflectivity deviations in the manner depicted in Fig. 2. The relatively higher variance in θ3 is due largely to the increased sensitivity of longer couplers to slight index mismatches, as explained in Device Fabrication; BS3 has a coupling region almost six times the length of BS1 and BS2 in order to achieve the required internal phase shift.
can be determined from rmeas using numerical optimisation. The results for Fp, Fm, ϕN and θn for all 12 measured candidate circuits are shown in Fig. 3. Notably the fidelity values shown were calculated directly from the measured matrices Umeas, but agree to within error with the values calculated from the measured phase and reflectivity deviations in the manner depicted in Fig. 2. The relatively higher variance in θ3 is due largely to the increased sensitivity of longer couplers to slight index mismatches, as explained in Device Fabrication; BS3 has a coupling region almost six times the length of BS1 and BS2 in order to achieve the required internal phase shift.
Results from coherent circuit characterisation.
Error bars are too small to see and are thus absent. Top: Mode and process fidelity of the measured circuit mappings with the ideal hcz circuit unitary, optimised over local external phases. The mean uncertainty in Fm and Fp are 0.002 and 0.006 respectively; these uncertainties were determined via Monte Carlo methods using the measured uncertainties in phases and moduli. Centre: Net undesired internal phase ϕN. The displayed value is the mean of the four values determined from the four occurrences of ϕN in comparing Umeas for each circuit to Eq. 2. For all 12 candidate circuits these differ by a maximum of 0.07. The variation between these four values dominated that between our many phase measurement trials for each circuit and their standard deviation is thus taken to be our uncertainty; the mean resulting value over all 12 circuits is 0.0015. Bottom: Deviations Δ θ from the ideal reflectivity parameters for the four BSs. For all values of Δ θ the mean uncertainty—determined from repeated measurement trials—is 0.0026. In all 3 panels, the measured circuits are ordered by decreasing process fidelity.
For the best measured device, the mode and process fidelities determined were Fm(Umeas, Uhcz) = 0.931 ± 0.001 and Fp = 0.680 ± 0.005 respectively; the net internal phase found was ϕN = − 0.346 ± 0.013 and the splitting parameter deviations determined were  ,
,  ,
,  and
and  . As an illustration these parameter deviations are also depicted in Fig. 2 along with their individual effects on the fidelities. For all 12 devices BS4 was erroneously fabricated with a reflectivity near 60% rather than the ideal value of 90.8%. However we note that if Δ θ4 had been approximately the mean of the other splitting deviations achieved, with a value of 0.08, the process fidelity calculated according to those parameter errors would have been Fp = 0.882 and the mode fidelity Fm = 0.984.
. As an illustration these parameter deviations are also depicted in Fig. 2 along with their individual effects on the fidelities. For all 12 devices BS4 was erroneously fabricated with a reflectivity near 60% rather than the ideal value of 90.8%. However we note that if Δ θ4 had been approximately the mean of the other splitting deviations achieved, with a value of 0.08, the process fidelity calculated according to those parameter errors would have been Fp = 0.882 and the mode fidelity Fm = 0.984.
Verification Using Two-Photon Interference
Full operation of these circuits as gates using spontaneous parametric down-conversion (SPDC)—the current state-of-the-art in generating multiple single photons—requires a six-photon output state where two serve as triggers. This is to avoid heralding false positives due to the probabilistic nature of SPDC. Given the 2/27 gate success probability and our loss of at least 1.8 dB per waveguide, this would result in a success probability of less than 0.015 per six-photon input. With current six-photon SPDC generation capabilities40 we would thus expect a success rate of less than 3 mHz, necessitating prohibitively long integration times and low signal-to-noise for e.g. quantum process tomography, thereby limiting conclusions regarding actual gate fidelity.
However, despite requiring four input photons for full operation, the hcz circuit relies only on fourth-order interference effects (in field), i.e. two-photon quantum interference; any higher-order interference effects between the four input photons can only result in error terms where the control and target qubits along with the two ancillary modes do not output exactly one photon each. In order both to confirm the ability of the circuits to support high-visibility quantum interference and to verify the results of their coherent characterisation, we therefore measured the visibility of two-photon quantum interference in the best-performing circuit for all possible input-output mode combinations. These measured visibilities are compared against both predictions from our classical characterisation and the ideal hcz circuit visibilities in Fig. 4.
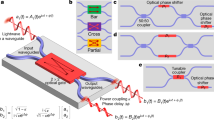
(a) Setup for measuring two-photon interference. Degenerate photon pairs at 820 nm are created via spontaneous parametric down-conversion (SPDC) in a nonlinear β-barium-borate (BBO) crystal pumped by a 410 nm frequency-doubled Ti:Sapphire laser. Manual polarisation controllers (POL) enable alignment of SPDC polarisation with the axes of polarisation-maintaining fibers coupled to the test device. We detect photons in coincidence using avalanche photo diodes (APDs). (b) Representative observed non-classical interference patterns, showing anti-coalescent and coalescent interference for two different output mode combinations as well as fits to the data with Gaussian and sinc components. The error bars shown are calculated from Poissonian counting statistics. (c) Two photon interference results for the best hcz circuit. We compare predictions (left) from the coherently-characterised circuit against measured two-photon interference visibilities (centre). The right panel shows visibilities for the ideal circuit Uhcz; most of the difference between this panel and the other two is due to the deviation in the best circuit from the ideal reflectivity for BS4 and unwanted net phase ϕN, as shown in Fig. 3. For the residuals after subtracting the measured visibilities from the predictions the mean and standard deviation are − 0.002 and 0.061, while after subtracting the measured values from the ideal values they are − 0.022 and 0.282 respectively.
The apparatus for measuring the quantum interference effects is depicted schematically in Fig. 4(a). The ratio of two-fold coincidences to those resulting from higher order terms may be calculated according to Broome et al.41. We estimate the percentage of 4-folds to 2-folds of 0.02% resulting in a maximum 95.6% two-photon interference visibility. We measured two-photon quantum interference visibility for all  combinations of two input and two output ports. The interference visibility V is calculated as V = (Cmax − Cmin)/Cmax, where C is the rate of coincident photon detection events as a function of the temporal delay between the input photons and Cmax and Cmin are calculated from a fit to the data as shown in Fig. 4(b).
combinations of two input and two output ports. The interference visibility V is calculated as V = (Cmax − Cmin)/Cmax, where C is the rate of coincident photon detection events as a function of the temporal delay between the input photons and Cmax and Cmin are calculated from a fit to the data as shown in Fig. 4(b).
The measured visibilities are shown in Fig. 4(c), along with those predicted from Umeas as determined via coherent characterisation and the visibilities for an ideal hcz circuit. The mean of the residuals after subtracting the measured visibilities from the predictions is only − 0.002 with a standard deviation of 0.061. Perhaps a better comparison is achieved by numerically calculating the unitary Uvis which would yield the minimum root-mean-square difference from the measured visibilities; this unitary has mode fidelities of Fm(Umeas, Uvis) = 0.983 and Fm(Uhcz, Uvis) = 0.931 with the measured circuit and the ideal hcz respectively. The small differences between predicted and measured visibilities can be attributed largely to three factors: polarisation non-degeneracy between the interfering photons in the FLDW circuit; the slightly differing spectra of the SPDC photons and the laser diode used for the coherent characterisation; and the effects of higher-order SPDC terms.
Conclusions
Along with further improvements in photon sources and detection, heralding will be required to concatenate multiple entangling linear optics quantum gates and thus enable more complex quantum computations and simulations. We have demonstrated that integrated waveguide arrays, particularly using femtosecond laser-writing, are capable of generating the required multimode interference circuits with both high fidelity and excellent quantum interference and allow simple implementation of mode crossover elements and π phase shifts. However further careful engineering will be required to precisely achieve the desired beamsplitter ratios and to avoid undesired phase accumulation. This study has outlined the challenges both experimentally and theoretically in achieving waveguide circuits with high operational fidelities.
The quantum process fidelity of candidate circuits can be calculated from known fabrication tolerances or classical characterisation results using the Jamiolkowski isomorphism and this metric has proven to be more sensitive and useful than mode fidelity for assessing such circuits. However any circuit imbalance will lead to error terms outside the computational subspace wherein two photons exit in either the control or target mode. The precise effects of such coherent error terms when multiple gates are concatenated, as well as possibilities for their correction or mitigation, could be a fruitful avenue for future investigation.
Additional Information
How to cite this article: Meany, T. et al. Engineering integrated photonics for heralded quantum gates. Sci. Rep. 6, 25126; doi: 10.1038/srep25126 (2016).
References
Schell, A. W. et al. Three-dimensional quantum photonic elements based on single nitrogen vacancy-centres in laser-written microstructures. Sci. Rep. 3, 1577 (2013).
Silverstone, J. W. et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photon. 8, 104–108 (2013).
Meany, T. et al. Hybrid photonic circuit for multiplexed heralded single photons. Laser Photon. Rev. 8, L42–L46 (2014).
Gazzano, O. et al. Entangling quantum-logic gate operated with an ultrabright semiconductor single-photon source. Phys. Rev. Lett. 110, 250501 (2013).
Calkins, B., Mennea, P. L. & Lita, A. E. High quantum-efficiency photon-number-resolving detector for photonic on-chip information processing. Opt. Express 21, 22657–22670 (2013).
Reithmaier, G. et al. On-chip time resolved detection of quantum dot emission using integrated superconducting single photon detectors. Sci. Rep. 3, 1901 (2013).
Sahin, D. et al. Waveguide photon-number-resolving detectors for quantum photonic integrated circuits. Appl. Phys. Lett. 103, 111116 (2013).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & O’Brien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Crespi, A. et al. Integrated photonic quantum gates for polarization qubits. Nat Commun 2, 566 (2011).
Pittman, T. B., Fitch, M. J., Jacobs, B. C. & Franson, J. D. Experimental controlled-NOT logic gate for single photons in the coincidence basis. Phys. Rev. A 68, 032316 (2003).
Okamoto, R., O’Brien, J. L., Hofmann, H. F. & Takeuchi, S. Realization of a Knill-Laflamme-Milburn controlled-NOT photonic quantum circuit combining effective optical nonlinearities. Proc. Natl. Acad. Sci. USA 108, 10067–10071 (2011).
Knill, E. Quantum gates using linear optics and postselection. Phys. Rev. A 66, 052306 (2012).
Marshall, G. D. et al. Laser written waveguide photonic quantum circuits. Opt. Express 17, 12546–12554 (2009).
Smith, B. J., Kundys, D., Thomas-Peter, N., Smith, P. G. R. & Walmsley, I. A. Phase-controlled integrated photonic quantum circuits. Opt. Express 17, 13516–13525 (2009).
Meany, T. et al. Non-classical interference in integrated 3D multiports. Opt. Express 20, 26895–26905 (2012).
Chaboyer, Z., Meany, T., Helt, L. G., Withford, M. J. & Steel, M. J. Tuneable quantum interference in a 3D integrated circuit. Sci. Rep. 5, 9601 (2014).
Spagnolo, N. et al. Three-photon bosonic coalescence in an integrated tritter. Nat. Commun. 4, 1606 (2013).
Heilmann, R., Keil, R., Gräfe, M., Nolte, S. & Szameit, A. Ultraprecise phase manipulation in integrated photonic quantum circuits with generalized directional couplers. Appl. Phys. Lett. 105, 061111 (2014).
Keil, R. et al. All-optical routing and switching for three-dimensional photonic circuitry. Scientific Reports 1, 94 (2011).
Di Giuseppe, G. et al. Einstein-Podolsky-Rosen spatial entanglement in ordered and Anderson photonic lattices. Phys. Rev. Lett. 110, 150503 (2013).
Tillmann, M. et al. Experimental boson sampling. Nat. Photon. 7, 540–544 (2013).
Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat Photon 7, 322–328 (2013).
Owens, J. O. et al. Two-photon quantum walks in an elliptical direct-write waveguide array. New J. Phys. 13, 75003 (2011).
O’Brien, J. L., Pryde, G. J., White, A. G., Ralph, T. C. & Branning, D. Demonstration of an all-optical quantum controlled-NOT gate. Nature 426, 264–267 (2003).
Langford, N. K. et al. Demonstration of a simple entangling optical gate and its use in Bell-state analysis. Phys. Rev. Lett. 95, 210504 (2005).
Ralph, T., Langford, N., Bell, T. & White, A. Linear optical controlled-NOT gate in the coincidence basis. Phys. Rev. A 65, 062324 (2002).
Mower, J., Harris, N. C., Steinbrecher, G. R., Lahini, Y. & Englund, D. High-fidelity quantum state evolution in imperfect photonic integrated circuits. Phys. Rev. A 92, 032322 (2015).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge U. P., Cambridge, 2010).
Jamiołkowski, A. Linear transformations which preserve trace and positive semidefiniteness of operators. Rep. Math. Phys. 3, 275–278 (1972).
Gilchrist, A., Langford, N. & Nielsen, M. Distance measures to compare real and ideal quantum processes. Phys. Rev. A 71, 062310 (2005).
White, A. G. et al. Measuring two-qubit gates. J. Opt. Soc. Am. B 24, 172 (2007).
Jovanovic, N. et al. Integrated photonic building blocks for next-generation astronomical instrumentation I: the multimode waveguide. Opt. Express 20, 17029–17043 (2012).
Gross, S. et al. Femtosecond direct-write Uberstructure waveguide Bragg gratings in ZBLAN. Opt. Lett. 37, 3999–4001 (2012).
Arriola, A. et al. Low bend loss waveguides enable compact, efficient 3D photonic chips. Opt. Express 21, 2978–2986 (2013).
Meany, T. et al. Towards low-loss lightwave circuits for non-classical optics at 800 and 1,550 nm. Appl. Phys. A 114, 113–118 (2013).
Okamoto, K. Fundamentals of optical waveguides (Academic Press, 2006).
Rahimi-Keshari, S. et al. Direct characterization of linear-optical networks. Opt. Express 21, 13450–13458 (2013).
Broome, M. A. et al. Photonic boson sampling in a tunable circuit. Science 339, 794–798 (2013).
Prevedel, R. et al. Experimental realization of Dicke states of up to six qubits for multiparty quantum networking. Phys. Rev. Lett. 103, 020503 (2009).
Broome, M. A., Almeida, M. P., Fedrizzi, A. & White, A. G. Reducing multi-photon rates in pulsed down-conversion by temporal multiplexing. Opt. Express 19, 22698–22708 (2011).
Acknowledgements
This research was supported in part by the Australian Research Council Centre of Excellence for Ultrahigh bandwidth Devices for Optical Systems (CE110001018), the Centre of Excellence for Quantum Computation and Communication Technology (CE110001027) and the Centre of Excellence for Engineered Quantum Systems (CE110001013). AF is supported by an Australian Research Council Discovery Early Career Research Award (DE130100240) and AGW by by a UQ Vice-Chancellor’s Research and Teaching Fellowship.
Author information
Authors and Affiliations
Contributions
T.M. fabricated device with guidance from M.J.W., M.J.S. and G.D.M. D.N.B. characterised devices with input from T.M., A.G.W., M.A.B. and A.F. M.D. and A.G. were responsible for theoretical performance calculations. All authors contributed to the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Meany, T., Biggerstaff, D., Broome, M. et al. Engineering integrated photonics for heralded quantum gates. Sci Rep 6, 25126 (2016). https://doi.org/10.1038/srep25126
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep25126
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.